Analisi di Regressione e Produttività

(1)

A

NALISI DI REGRESSIONE E PRODUTTIVITÁ

:

UN

’

INTRODUZIONE

In questo capitolo si vuole (a) offrire un’introduzione molto intuitiva alle principali procedure statistiche raccolte sotto il nome di analisi di regressione, (b) dedicare attenzione alla maniera in cui l’analisi di regressione permette di affrontare la stima di produttività ed efficienza tecnica delle unità produttive considerate, (c) dedicare attenzione alla maniera in cui l’analisi di regressione permette di affrontare la stima dello stato delle conoscenze tecniche delle unità produttive considerate, (d) esaminare il problema della distorsione ciclica di misure di produttività, accennando anche a possibili soluzioni del problema.

(2)

2.1) L’analisi di regressione lineare: un abbecedario.

Scopo del presente paragrafo è quello di fornire in modo conciso e intuitivo un richiamo alle nozioni fondamentali dell’analisi di regressione lineare. In particolare saranno illustrati il concetto stesso di regressione lineare, che cosa si intende per metodo dei minimi quadrati, per la relazione tra t-ratio e test di significatività, e per coefficiente di determinazione o R-quadro. In questa trattazione abbandoneremo per un attimo l’analisi della produzione (che sarà ripresa nel prossimo paragrafo), e ricorreremo come esempio alla stima (su dati fittizi) di una semplice funzione del consumo keynesiana e di una funzione lineare di domanda.

L’idea alla base della regressione lineare è che si possa stimare (vale a dire misurare) una relazione funzionale lineare tra una variabile dipendente e una o più variabili indipendenti. La stima di questa relazione è effettuata in maniera tale da tenere conto del fatto che la variabile dipendente è influenzata, oltre che dalle succitate variabili indipendenti, da un insieme di fattori aleatori (o stocastici), il cui ruolo può essere riassunto da un cosiddetto termine di errore (una variabile con media zero e varianza costante, perlomeno nel tipo di analisi più semplice e introduttivo). Partiamo proprio dalla funzione del consumo keynesiana, che individua una semplice relazione lineare tra una variabile dipendente (il consumo) e una variabile indipendente (il reddito).

Ammettiamo di essere nel paese di Agrolandia, un’isola in cui vi sono 33 regioni, in sostanza delle vallate separate da vallate assai scoscese. Dal 1970, anno in cui Agrolandia si è dotata di una contabilità nazionale, sino al 2000 il reddito e il consumo delle 33 regioni si è sempre mantenuto costante, ai livelli indicati nella Tab. 2.1. Gli economisti di Agrolandia hanno così potuto notare che tra consumo e reddito delle 33 regioni esisteva in quegli anni una relazione funzionale. Regioni a basso reddito avevano basso consumo, regioni ad alto reddito avevano alto consumo. In effetti, a partire dai dati della Tab. 2.1 essi hanno potuto notare che è esistita una perfetta relazione lineare tra consumo e reddito delle 33 regioni:

(3)

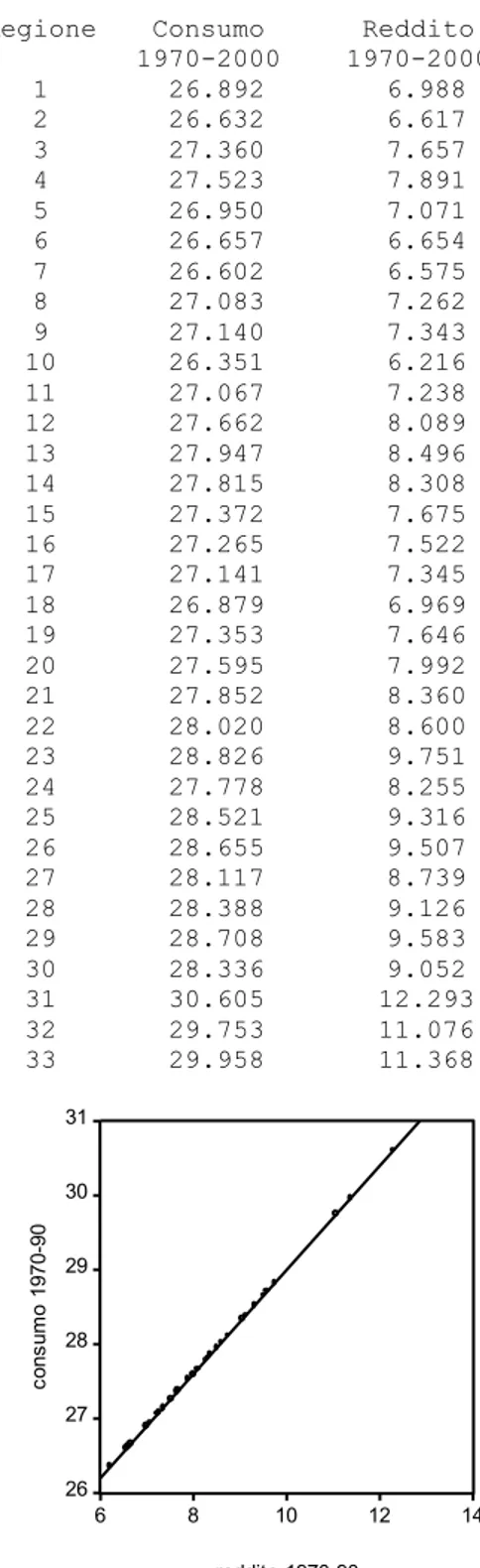
Dall’ubertosa natura del proprio paese, gli agrolandesi traggono la possibilità di consumare, indipendentemente dal reddito, beni (prevalentemente alimentari) per un valore annuale di 22 000 E. Ancora, per ogni E addizionale di reddito, essi consumano 0,7 E in più. Una relazione di questo tipo può essere adeguatamente descritta, nel diagramma a dispersione annesso alla Tab. 2.1, unendo tutti i punti consumo-reddito con una retta.

Tabella 2.1 Regione Consumo 1970-2000 1970-2000 Reddito 1 26.892 6.988 2 26.632 6.617 3 27.360 7.657 4 27.523 7.891 5 26.950 7.071 6 26.657 6.654 7 26.602 6.575 8 27.083 7.262 9 27.140 7.343 10 26.351 6.216 11 27.067 7.238 12 27.662 8.089 13 27.947 8.496 14 27.815 8.308 15 27.372 7.675 16 27.265 7.522 17 27.141 7.345 18 26.879 6.969 19 27.353 7.646 20 27.595 7.992 21 27.852 8.360 22 28.020 8.600 23 28.826 9.751 24 27.778 8.255 25 28.521 9.316 26 28.655 9.507 27 28.117 8.739 28 28.388 9.126 29 28.708 9.583 30 28.336 9.052 31 30.605 12.293 32 29.753 11.076 33 29.958 11.368 26 27 28 29 30 31 6 8 10 12 14 reddito 1970-90 co nsu m o 19 70 -9 0

(4)

Tuttavia, nel 2001, la (forse un po’ troppo) stabile economia di Agrolandia viene investita da un cambiamento epocale. I due miliardari più ricchi del paese (Topolino e Paperino) incominciano contemporaneamente due diversi tipi di campagna pubblicitaria. Topolino è diventato di colpo convinto delle qualità salutari dei prodotti alimentari naturali di Agrolandia, e vuole convincere i propri concittadini a coltivarne nei propri orti (nonché a consumarne) maggiori quantità (dunque, a spostare verso l’alto la propria funzione di consumo). Paperino si è invece accorto delle proprietà salutari della passeggiata in giardino, e vuole convincere i concittadini a trasformare gli orti in giardini, trascurando il consumo dei propri prodotti (e dunque, spostando verso il basso la propria funzione di consumo).

I due miliardari trasmettono campagne pubblicitarie a favore della propria idea dal monte più alto di Agrolandia, situato nel bel mezzo del paese, e hanno a disposizione lo stesso numero di ore di trasmissione. Poiché gli agenti pubblicitari dei due miliardari hanno la stessa abilità, se una regione è investita in uguale maniera dalle due campagne pubblicitarie, l’effetto sul consumo è nullo. Tuttavia, in ragione di fattori meteorologici casuali, occorrono interruzioni nelle trasmissioni dell’una e dell’altra campagna ricevute in ogni singola regione. Le regioni, in virtù di queste differenze, consumeranno di più o di meno rispetto a quanto facevano in precedenza (anche se il loro reddito non è cambiato), con i risultati rappresentati nella Tab. 2.2.

Come prima, regioni a basso reddito hanno basso consumo, e regioni ad alto reddito hanno alto consumo. Però, la presenza di un fattore stocastico (la differenza nelle ore di ricezione delle due campagne) fa sì che la relazione tra reddito e consumo non può più essere adeguatamente descritta unendo tutti i punti consumo-reddito con dei segmenti lineari (v. il diagramma a dispersione annesso alla Tab. 2.2). Come fare ora per descrivere questa relazione? Inoltre, a reddito immutato, le regioni in media consumeranno di più o di meno nel 2001 di quanto non avevano fatto negli anni precedenti? In altre parole la funzione di consumo si è spostata verso l’alto o verso il basso?

(5)

Tabella 2.2

Regione Consumo

Anno 2001 Anno 2001 Reddito

1 26.892 6.988 2 25.572 6.617 3 25.468 7.657 4 27.203 7.891 5 29.200 7.071 6 28.307 6.654 7 25.706 6.575 8 26.314 7.262 9 26.527 7.343 10 27.544 6.216 11 27.711 7.238 12 27.118 8.089 13 26.423 8.496 14 29.052 8.308 15 28.234 7.675 16 27.180 7.522 17 27.171 7.345 18 26.935 6.969 19 27.744 7.646 20 27.064 7.992 21 26.098 8.360 22 27.340 8.600 23 27.406 9.751 24 30.737 8.255 25 29.591 9.316 26 30.838 9.507 27 28.432 8.739 28 29.625 9.126 29 27.829 9.583 30 27.183 9.052 31 30.496 12.293 32 29.512 11.076 33 29.992 11.368 24 26 28 30 32 6 8 10 12 14 reddito 1991 co nsu m o 19 91

(6)

Per rispondere a queste domande, gli economisti di Agrolandia ricorrono al metodo dei minimi quadrati. Di che si tratta? Si considerino i grafici seguenti.

In questi grafici vengono rappresentate tre valori per la variabile x (1, 2 e 3) e y (2, 1,5 e 7). E’ possibile descrivere la relazione tra queste due variabili mediante i segmenti che uniscono le coppie di punti? Parrebbe proprio di no. A priori, non possiamo preferire un segmento all’altro, e a mano a mano che i punti sono più numerosi la relazione diventa sempre meno intelligibile.

Tuttavia, si potrebbe rappresentare in modo conciso la relazione tra le due variabili (vale a dire interpolare questa relazione) calcolando un qualche tipo di media della pendenza e intercetta dei tre segmenti. Per esempio, relativamente alla pendenza, possiamo prendere la media dei tre rapporti incrementali Δy/Δx ponderati per l’ampiezza delle variazioni nelle x:

(1,5 – 2)/(2 - 1) × (2 – 1)/[(2 – 1) + (3 – 2) + (3 – 1)] + + (7 - 1,5)/(3 - 2) × (3 – 2)/[(2 – 1) + (3 – 2) + (3 – 1)] +

+ (7 – 2)/(3 - 1) × (3 – 1)/[(2 – 1) + (3 – 2) + (3 – 1)] = -0,125 + 1,375 + 1,250 = = 2,500

Dunque, in questo caso la pendenza della relazione lineare tra y e x sarebbe uguale a 2,5. Quanto all’intercetta della funzione lineare, dato che dal suo valore dipendono i livelli delle due variabili, è ragionevole supporre che un’interpolazione soddisfacente della relazione tra le y e le x passi per il punto individuato dai valori

0 2 4 6 8 0.5 1.0 1.5 2.0 2.5 3.0 3.5 Y X

(7)

medi di y e x (3,5 e 2). Sotto questa ipotesi essa possiamo ottenere α, il termine di

intercetta, mediante l’uguaglianza:

(3,5 - α) = 2,5 × (2 – 0)

α = 3,5 - 5 = -1,5

La relazione lineare così calcolata, y = -1,5 + 2,5 x, è rappresentata nel grafico sottostante (assieme al punto medio (3,5 ; 2).

Si può dimostrare che la retta calcolata in questa maniera minimizza la somma dei quadrati degli scarti tra le coppie di punti (y, x) e la retta stessa. Cioè, per una data nuvola di punti, mediante questa procedura si è tracciata la retta che permette di minimizzare la somma dei quadrati degli scarti tra i punti e la retta stessa. Per questa ragione, il metodo di interpolazione lineare qui esposto viene definito dei minimi quadrati. Si noti che esso può venire impiegato, e mantiene la stessa giustificazione intuitiva, anche nel caso in cui vi è più di una variabile dipendente.

Applicando la procedura dei minimi quadrati alla relazione tra consumo e reddito delle 33 regioni agrolandesi nel 2001, si ottiene il seguente diagramma di dispersione:

0 2 4 6 8 0.5 1.0 1.5 2.0 2.5 3.0 3.5 Y X (3,5 ; 2)

(8)

Ci si può naturalmente chiedere quali sono intercetta e pendenza di questa retta interpolante. La risposta è:

consumo = 22 556 + 0,64 reddito VALORI PREVISTI !

A questo punto, parrebbe che i fattori meteorologici alla base delle interruzioni nelle trasmissioni dell’una e dell’altra campagna in regione non siano del tutto casuali, e che favoriscano le trasmissioni di Topolino. L’intercetta della funzione di consumo è infatti aumentata, e parrebbe pure che la pendenza della retta sia diminuita.

Per sapere se le cose stanno veramente così, bisogna formulare delle ipotesi sulla distribuzione statistica dei coefficienti della retta di regressione. In effetti, il metodo dei minimi quadrati permette pure di calcolare le deviazioni standard dei coefficienti di intercetta e pendenza, che nel presente caso sono rispettivamente uguali a 1,26 e 0,15. A partire da questi valori, e da un’ipotesi sulla distribuzione statistica dei coefficienti, è possibile fare inferenza statistica sui coefficienti e chiedersi se la differenza tra 22 556 e 22 000, 0,70 e 0,64 è statisticamente significativa o no.

Partiamo dall’assunto che la distribuzione statistica dei coefficienti rispecchia la distribuzione statistica dei fattori stocastici (in questo caso i fattori meteorologici). TORNA A PP. 6-7 ! FORMULA DELLA S.D. ! Cioè ipotizziamo che, se Paperino e Topolino ripetessero n volte le loro campagne pubblicitarie, otterremmo n coppie di coefficienti di pendenza e intercetta, e la distribuzione statistica di questi n valori rispecchierebbe la distribuzione statistica dei fattori meteorologici. Ma quest’ultima

24 26 28 30 32 6 8 10 12 14 reddito 1991 co nsu m o 19 91

(9)

distribuzione la possiamo desumere dai residui di una singola regressione, e cioè dagli scarti tra i consumi effettivi delle regioni agrolandesi e i valori previsti dalla retta di regressione (per il valore dato del reddito nelle varie regioni). Il grafico sottostante confronta un istogramma dei residui e la curva della distribuzione normale.

La distribuzione dei residui sembra sufficientemente vicina a quella della legge normale. Ciò autorizza a credere che pure i fattori meteorologici siano distribuiti secondo questa legge. Quindi, se Paperino e Topolino ripetessero n volte le loro campagne pubblicitarie, la distribuzione statistica delle n coppie di coefficienti di pendenza e intercetta così ottenute rispecchierebbe anch’essa la legge normale, e l’inferenza statistica sui coefficienti si può basare sull’ipotesi che essi siano distribuiti normalmente.

Come sapere quindi se 22 556 e 0,64 siano compatibili (non significativamente diversi) dai valori di 22 000 e 0,70 ricavati dagli anni passati? Non lo possiamo sapere con certezza, ma possiamo fare un’affermazione probabilistica. Definiamo con α il coefficiente di intercetta e con β il coefficiente di pendenza attesi a priori (cioè uguali ai ricavati dagli anni passati). Ancora, definiamo con α⌢ il coefficiente di intercetta e con β⌢ il coefficiente di pendenza stimati mediante il metodo dei minimi quadrati. Sotto l’ipotesi che α⌢ e β⌢ siano distribuiti normalmente, possiamo dire che, se:

3.00 2.50 2.00 1.50 1.00 .50 0.00 -.50 -1.00 -1.50 -2.00 Dev. Stad = 1.19 Medi a= - .0 N = 33 α

α

⌢ ⌢ s. d. α = z

(10)

dove d.s.α⌢ è la deviazione standard di α⌢, allora possiamo derivare dalle tavole

statistiche della legge normale la probabilità che z sia uguale a un dato valore, mettiamo 0,95:

P ( -1,96 ≤ z ≤ 1,96 ) = 0,95

La scelta di P ( . ) = 0,95 risponde al requisito di avere un livello di confidenza uguale al 95 %. Ciò vuol dire che se la nostra ipotesi è che α⌢ = α, sapremo che nel 95 % dei casi accettiamo (meglio sarebbe dire non rifiutiamo) correttamente questa ipotesi. Alternativamente, possiamo dire che solo nel 5 % dei casi rifiutiamo la nostra ipotesi anche essa corrisponde alla realtà (NB: 5% = 1 – livello di confidenza = livello di significatività. Gli statistici lo definiscono errore di tipo I, corrispondente alla condanna di un innocente).

Da P ( . ) = 0,95 deriviamo l’intervallo di confidenza per la nostra ipotesi:

P ( -1,96 × d.s.α⌢ ≤ α⌢ - α ≤ 1,96 × d.s.α⌢ ) = 0,95

P ( α - 1,96 × d.s.α⌢ ≤ α⌢ ≤ α + 1,96 × d.s.α⌢ ) = 0,95

P ( 22 000 - 1,96 × 1,26 ≤ α⌢ ≤ 22 000 + 1,96 × 1,26 ) = 0,95 P ( 19 530 ≤ α⌢ ≤ 24 470 ) = 0,95

Quindi, a un livello di confidenza uguale al 95 %, non rifiutiamo (accettiamo) l’ipotesi che α⌢ = α, poiché il nostro a (= 22 556) si trova ampiamente incluso nell’intervallo di confidenza. L’intercetta della funzione di consumo è compatibile col valore atteso, e in effetti potremmo dimostrare la stessa cosa per la pendenza della retta. Concludiamo che i fattori meteorologici alla base delle interruzioni nelle trasmissioni dell’una e dell’altra campagna in regione sono del tutto casuali, e che non vi è un fattore meteorologico strutturale che favorisca le trasmissioni di Topolino.

Le formule qui sopra esaminate servono pure a chiarire la natura della statistica detta t-ratio, che viene spesso affiancata ai valori stimati per i coefficienti di intercetta e di pendenza. Si supponga di voler sottoporre a verifica l’ipotesi che il reddito non abbia effetto sul consumo. In questo caso il valore ipotizzato a priori per β è 0, e z diventa:

(11)

Di conseguenza si avrà:

P ( -1,96 ≤ β⌢/d.s.β⌢ ≤ 1,96 ) = 0,95

Dunque, se il valore del coefficiente diviso per la sua deviazione standard è maggiore di 1,96 in valore assoluto il consumo sarà significativamente influenzato dal reddito. Il rapporto β⌢/d.s.β⌢ è per l'appunto ciò che viene solitamente definito t-ratio. Se esso

prende valori maggiore di 1,96 (o, come viene spesso approssimativamente indicato, di 2) in valore assoluto, l’ipotesi di non significatività della relativa variabile indipendente può essere rifiutata a un livello di confidenza del 95 %.

Come si sarà notato, non siamo entrati per nulla nei dettagli analitici e computazionali dei minimi quadrati. Esistono comunque molti programmi statistici che possono effettuare questi calcoli. Tipicamente, i loro risultati per il programma qui preso in considerazione avrebbero un aspetto simile a quello della seguente tabella.

N. osservazioni = 33 Variabile dipendente: Consumo

Variabile Coefficiente Dev. standard T-ratio

Costante 22 556 1,2565 17,9518

Reddito 0,6386 0,1500 4,2584

R-quadro 0,3691

R-quadro corretto 0,3487

P-VALUE !Il livello di probabilità associato alla statistica è la probabilità di ottenere, se l’ipotesi nulla è valida, un valore della statistica - p. es. il t-ratio - maggiore di quello osservato. Un p-value più basso del livello di significatività a cui effettuiamo il test implica il rifiuto dell’ipotesi nulla.

β β β

β

⌢ ⌢ ⌢ ⌢ ⌢ ⌢ s. d. s. d. 0 s. d. = = = β z

(12)

A parte le grandezze già prese in considerazione (valori dei coefficienti, deviazioni standard dei coefficienti, t-ratio) due elementi quasi sempre inclusi nei risultati delle stime sono l’R-quadro e l’R-quadro corretto. Si tratta di misure relative all’accostamento del modello ai dati, che hanno rispettivamente la formula seguente:

R-quadro =

∑

= = − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − n 1 i 2 y i n 1 i 2 i i 2 y i ) m (y ) y (y ) m (y ⌢ = 1

-

∑

= = − − n 1 i 2 y i n 1 i 2 i i ) m (y ) y (y ⌢ R-quadro corretto = 1

-

∑

= = − − − − n 1 i 2 y i n 1 i 2 i i 1) /(n ) m (y k) (n / ) y (y ⌢

dove n è il numero delle osservazioni e k è il numero delle variabili indipendenti (esclusa la costante). Con my definiamo la media delle yi, e con y⌢i i cosiddetti valori

previsti, ovverosia i valori che, per dati valori delle variabili indipendenti, si trovano sulla retta di regressione. Quindi, (yi - my) rappresenta la variabilità totale delle y,

mentre (yi - y⌢i) è la variabilità delle yi relativamente ai loro valori previsti dalla

regressione.

Il numeratore dell’R-quadro rappresenta la variabilità delle yi spiegata dalla regressione, e l’R-quadro stesso rappresenta la quota di variabilità delle yi spiegata dalla regressione. Questa quota varia tra zero e uno. Più essa si avvicina a uno, e migliore sarà l’accostamento della regressione (maggiore sarà il potere esplicativo delle variabili indipendenti).

La formula dell’R-quadro corretto penalizza l’inclusione di nuove variabili indipendenti nella regressione (a parità di altri fattori, diminuisce all’aumentare di k), ed è da preferire all’R-quadro “classico”, per il quale è possibile ottenere valori arbitrariamente vicini al 100 % semplicemente introducendo un numero di variabili indipendenti vicino a quello delle osservazioni.

(13)

Nel nostro caso, dei valori dell’R-quadro tra il 35 e il 37 % non sono molto alti. Per contro, rappresentiamo qui sotto la relazione tra retta di regressione e nuvola dei punti per una regressione il cui R-quadro sta attorno al 96 %.

Peraltro… potrebbe andare anche peggio di quanto capitato agli statistici agrolandesi! Nel caso in cui i valori di R-quadro fossero vicini a zero non vi sarebbe relazione lineare significativa tra la variabile dipendente e le variabili indipendenti e la pendenza della retta di regressione non sarebbe significativamente diversa da zero. Si veda per esempio che succede per valori dell’R-quadro attorno all’1 %.

Ribadiamo infine che si sono fatti esempi di regressione con una sola variabile indipendente unicamente per fini espositivi. Il metodo dei minimi quadrati mantiene la sua applicabilità (e la stessa giustificazione intuitiva) anche nel caso in cui vi sia più di una variabile dipendente. Ciò complica le cose dal solo punto di vista computazionale, che non è di nostro interesse in questa sede.

0 5 10 15 20 25 30 0 5 10 15 20 25 30

v alori prev isti di Q

v alo ri ef fe tt iv i d i Q 0 5 10 15 20 25 30 11.5 12.0 12.5 13.0 13.5 14.0 14.5 v alori prev isti di Q

v alo ri ef fe tt iv i d i Q

(14)