Verosimiglianza a coppie in modelli normali multivariati

U

NIVERSIT

A DEGLI

`

S

TUDI DI

P

ADOVA

F

`

S

S

C

L

IN

S

I

T E S I D I L A U R E A

VEROSIMIGLIANZA A COPPIE IN

MODELLI NORMALI MULTIVARIATI

R

: P

. ALESSANDRA SALVAN

C

: D

. NICOLA SARTORI

L

: EULOGE CLOVIS KENNE PAGUI

Indice

Introduzione III

1 Verosimiglianza composita 1

1.1 Introduzione . . . 1

1.2 Inferenza statistica . . . 2

1.3 Modelli statistici parametrici . . . 2

1.4 Funzione di verosimiglianza . . . 3 1.4.1 Informazione osservata . . . 4 1.4.2 Informazione attesa . . . 4 1.5 Verosimiglianza composita . . . 5 1.5.1 Introduzione . . . 5 1.5.2 Definizioni e propriet`a . . . 5

1.5.3 Quantit`a associate alla verosimiglianza composita . 8 1.5.4 Verifica delle ipotesi . . . 9

2 Verosimiglianza a coppie ed efficienza 11 2.1 Introduzione . . . 11

2.2 Un esempio con parametro scalare: normale simmetrica . . . 12

2.2.1 Verosimiglianza completa . . . 13

2.2.2 Verosimiglianza a coppie . . . 18

2.2.3 Efficienza asintotica . . . 20

2.3 Un esempio con parametro multidimensionale . . . 20

2.3.1 Verosimiglianza completa . . . 22

II INDICE

2.3.3 Efficienza . . . 36

3 Test basati sulla verosimiglianza a coppie 41 3.1 Introduzione . . . 41

3.2 Le statistiche test . . . 42

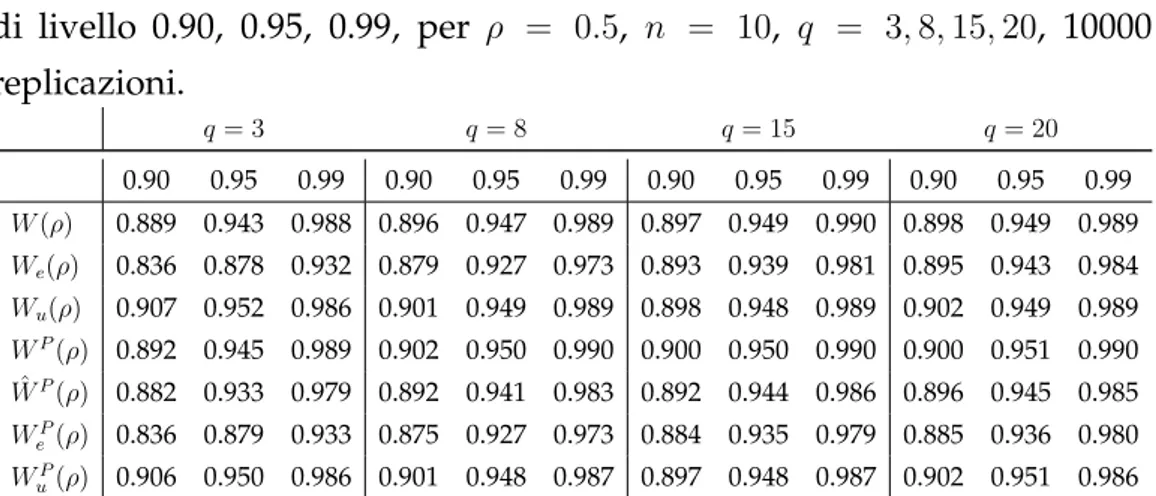
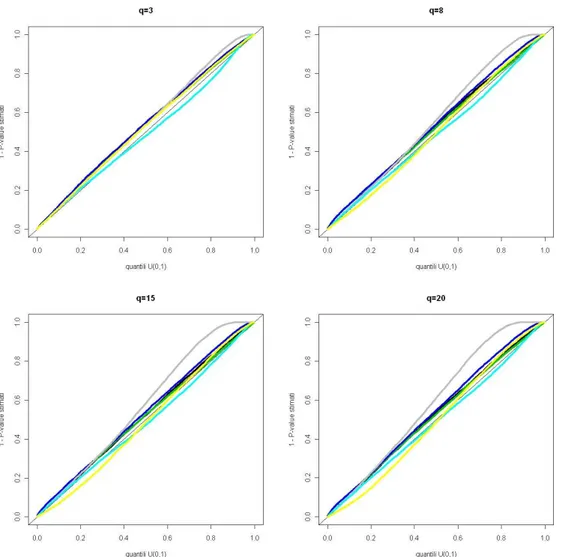
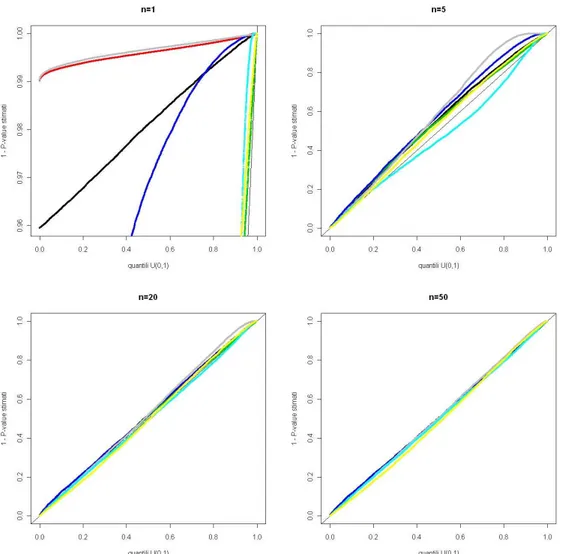
3.3 Distribuzione normale simmetrica: studio di simulazione . . 44

3.3.1 Distribuzioni nulle . . . 45

3.3.2 Potenza dei test . . . 49

3.4 Modello ad effetti casuali: studio di simulazione . . . 50

3.4.1 Risultati analitici . . . 51

3.4.2 Distribuzioni nulle . . . 51

Conclusioni 55

Appendice 57

Introduzione

Il ruolo della funzione di verosimiglianza `e centrale nell’inferenza sta-tistica. Tuttavia, per molti problemi riguardanti l’inferenza in modelli parametrici e semiparametrici, la funzione di verosimiglianza risulta dif-ficile da calcolare esplicitamente a causa di dipendenze complesse, di as-sunzioni fatte sul modello oppure nel caso di insiemi di dati di grandi dimensioni.

In queste situazioni, per risolvere il problema, vari autori hanno pro-posto diversi approcci basati su varianti della funzione di verosimiglian-za. Tra gli esempi pi `u conosciuti, si ricordano la pseudo-verosimiglianza di Besag (1974) per l’inferenza in modelli spaziali e la verosimiglianza parziale di Cox (1975), introdotta per l’inferenza in modelli con rischi pro-porzionali.

Un’idea alternativa alla verosimiglianza classica, `e quella di costruire pseudo-verosimiglianze semplici (Cox and Reid, 2004). In questa classe di pseudo-verosimiglianze, troviamo la verosimiglianza composita marginale che appartiene alla classe pi `u generale delle verosimiglianze composite (Lindsay, 1988). La verosimiglianza composita si ottiene combinando ade-guatamente validi oggetti di verosimiglianza relativi a piccoli sottoinsiemi di dati.

I vantaggi sono la riduzione della complessit`a computazionale rispetto alla verosimiglianza completa e la possibilit`a di non precisare la densit`a congiunta in assenza di una sufficiente conoscenza del meccanismo che ha generato i dati.

IV Introduzione L’impiego di questa metodologia `e presente in una variet`a di settori applicativi, per esempio nelle scienze ambientali, nel campo della geneti-ca, nell’analisi delle serie storiche e nell’analisi dei dati di sopravvivenza. Si veda Varin (2008) per una rassegna recente.

Sotto adeguate condizioni di regolarit`a, le varie procedure inferenziali basate sulla verosimiglianza composita, hanno propriet`a teoriche simili a quelle dei metodi basati sulla verosimiglianza completa, sebbene ci si aspetti una perdita di efficienza.

Questa tesi ha come obiettivo principale lo studio di un caso particolare di verosimiglianza composita marginale, detto verosimiglianza a coppie. Si focalizza l’attenzione sul comportamento della distribuzione dei test basati sulla verosimiglianza a coppie. In alcuni esempi in cui sia disponi-bile anche la verosimiglianza completa e sia possidisponi-bile svolgere analitica-mente gran parte dei calcoli necessari, si confrontano i risultati ottenuti utilizzando la verosimiglianza a coppie rispetto a quella completa e si va-luta la perdita di efficienza asintotica quando si utilizza la verosimiglianza a coppie.

Pi `u in dettaglio, si trattano due esempi di modelli normali multivariati con vincoli sulla matrice di covarianza. Alcuni aspetti del primo esem-pio, relativo ad un modello monoparametrico, sono gi`a trattati in lettera-tura, in particolare in Cox e Reid (2004). Qui si analizza in dettaglio un aspetto non ancora esplorato relativo alle statistiche test, e alla corrispon-dente costruzione degli intervalli di confidenza, basati sulla verosimiglian-za a coppie. Tramite un articolato studio di simulazione, si confrontano l’adeguatezza delle diverse approssimazioni delle distribuzioni. Il secon-do esempio, relativo a un caso multiparametrico, `e solo accennato in Cox e Reid (2004). Si mostra un risultato di efficienza della verosimiglianza a coppie e si analizza la struttura della verosimiglianza a coppie in relazione a quella completa. Come nell’esempio precedente, si valuta l’adeguatezza delle approssimazioni asintotiche disponibili per le statistiche di verosi-miglianza a coppie. Si studia inoltre una semplice approssimazione per la

Introduzione V distribuzione della statistica log-rapporto di verosimiglianza a coppie.

Nel Capitolo 1 vengono richiamati il concetto di modello statistico pa-rametrico e i principali risultati legati all’approccio di verosimiglianza. La teoria riassunta `e utile per l’introduzione del concetto di verosimiglian-za composita, che viene presentato assieme alle principali definizioni e propriet`a del metodo.

Il Capitolo 2 `e dedicato al caso particolare della verosimiglianza a cop-pie. Tramite due esempi viene studiata l’efficienza dello stimatore di mas-sima verosimiglianza a coppie rispetto all’analogo stimatore ottenuto dal-la verosimiglianza completa.

Nel Capitolo 3 si studia il comportamento delle statistiche test basate sulla verosimiglianza a coppie relativamente ai due esempi trattati nel Capitolo 2.

Capitolo 1

Verosimiglianza composita

1.1

Introduzione

In questo capitolo si concentra l’attenzione sul concetto e sulle propriet`a della verosimiglianza composita. Viene inoltre introdotto un caso partico-lare della verosimiglianza composita chiamato verosimiglianza

composi-ta marginale. La verosimiglianza composita `e una particolare pseudo-verosimiglianza (si veda ad esempio Pace e Salvan, 1997, capitolo 4; Molen-berghs e Verbeke, 2005, capitolo 9). Si richiamano preliminamente alcuni concetti fondamentali: inferenza statistica, modelli statistici parametrici, funzione di verosimiglianza, equazione di stima, informazione osservata e informazione di Fisher.

I primi quattro paragrafi richiamano alcuni risultati di base dell’in-ferenza basata sulla verosimiglianza, utili per comprendere meglio le pro-priet`a della verosimiglianza composita.

Il quinto paragrafo `e dedicato alla verosimiglianza composita ed alle sue propriet`a. In seguito,viene introdotto un caso particolare della verosi-miglianza composita, detta verosiverosi-miglianza composita marginale, perch´e costruita tramite adeguate densit`a marginali. Successivamente, vengono definite alcune quantit`a associate alla verosimiglianza composita come, ad esempio, l’equazione di stima, lo stimatore di massima verosimiglianza

2 Capitolo 1. Verosimiglianza composita composita. Infine vengono introdotti tre test basati sulla verosimiglianza composita.

1.2

Inferenza statistica

L’inferenza statistica `e il procedimento attraverso il quale si ottengono in-formazioni sulle caratteristiche di una popolazione dall’osservazione di un campione, cio`e un aggregato di unit`a selezionato solitamente medi-ante un esperimento casuale. L’obiettivo, `e quello di fornire strumenti e metodi per ricavare dai dati campionari informazioni sulla popolazione e per quantificare la fiducia da accordare a tali informazioni.

1.3

Modelli statistici parametrici

L’idea di base, su cui poggia l’inferenza statistica, `e che i dati osservati, 𝑦𝑜𝑠𝑠_{, costituiscono una realizzazione di un vettore casuale 𝑌 con legge di}

probabilit`a 𝑃0 <sub>e associata funzione di probabilit`a o di densit`a 𝑓</sub>0_{(𝑦). Si}

indica con 𝒴 lo spazio campionario di 𝑦𝑜𝑠𝑠_{. Ci `o si esprime concisamente}

con la scrittura 𝑦𝑜𝑠𝑠 _{realizzazione di 𝑌 ∼ 𝑃}0 _{con spazio campionario 𝒴.}

La legge di probabilit`a 𝑃0 <sub>`e almeno in parte ignota, e occore utilizzare</sub>

l’informazione portata dai dati stessi per ottenere una sua ricostruzione. La famiglia

ℱ = {𝑓 (𝑦; 𝜃) : 𝜃 ∈ Θ ⊆ ℝ𝑝_{, 𝑦 ∈ 𝒴}}

(1.1) di funzioni di densit`a (rispetto ad una fissata misura dominante) indi-cizzate dal vettore di parametri 𝜃 appartenente allo spazio parametrico Θ ⊆ ℝ𝑝 <sub>verr`a chiamata modello statistico parametrico.</sub>

Se 𝑓0 ∈ ℱ, si dice che il modello statistico `e correttamente specificato. Se il modello `e correttamente specificato, e se il parametro `e identificabile, ossia la corrispondenza fra Θ e ℱ `e biunivoca, si ha 𝑓0(𝑦) = 𝑓 (𝑦; 𝜃0_{) per}

uno e un solo valore 𝜃0 ∈ Θ, detto vero valore del parametro. Allora fare inferenza su 𝑃0, o su 𝑓0(⋅), `e equivalente a farla su 𝜃0.

1.4 Funzione di verosimiglianza 3

1.4

Funzione di verosimiglianza

I metodi di verosimiglianza sono molto importanti per l’inferenza in mo-delli statistici parametrici. Considerando un modello statistico parame-trico per i dati 𝑦 = (𝑦1, . . . , 𝑦𝑛) riferiti ad un campione casuale da 𝑌 =

(𝑌1, . . . , 𝑌𝑛), con funzione di densit`a congiunta 𝑓𝑌(𝑦; 𝜃) e 𝜃 ∈ Θ ⊆ ℝ𝑝

parametro non noto, la funzione 𝐿 : Θ −→ ℝ+, definita da 𝐿(𝜃) = 𝐿(𝜃; 𝑦) = 𝑓𝑌(𝑦; 𝜃),

`e detta funzione di verosimiglianza (likelihood) di 𝜃 basata sui dati 𝑦. Nel caso di osservazioni indipendenti, si ha

𝐿(𝜃; 𝑦) =

𝑛

∏

𝑖=1

𝑓𝑌𝑖(𝑦𝑖; 𝜃),

dove 𝑓𝑌𝑖(𝑦𝑖; 𝜃), 𝑖 = 1, . . . , 𝑛, rappresenta la densit`a marginale della

va-riabile casuale 𝑌𝑖. Spesso viene utilizzato la trasformata logaritmica di

𝐿(𝜃) 𝑙(𝜃) = log 𝐿(𝜃; 𝑦) = 𝑛 ∑ 𝑖=1 log 𝑓𝑌𝑖(𝑦𝑖; 𝜃),

chiamata funzione di log-verosimiglianza.

Frequentemente, nei modelli statistici considerati nelle applicazioni, Θ `e un sottoinsieme aperto di ℝ𝑝<sub>e 𝑙(𝜃) `e una funzione differenziabile almeno</sub>

tre volte, con derivate parziali continue in Θ. In tali casi si parla di modelli parametrici con verosimiglianza regolare.

Il metodo della massima verosimiglianza ricerca il valore pi `u verosi-mile di 𝜃, ossia ricerca, all’interno dello spazio Θ di tutti i possibili valori di 𝜃, il valore, o i valori, ˆ𝜃, del parametro che massimizzano la probabilit`a, o densit`a di probabilit`a di riottenere un campione uguale al campione da-to, in una ipotetica replicazione dell’esperimento. Questo valore, se unico, viene chiamato stima di massima verosimiglianza di 𝜃 e, formalmente,

ˆ

4 Capitolo 1. Verosimiglianza composita Non `e detto che tale massimo esista o che sia unico.

Il vettore di derivate parziali prime della funzione di log-verosimiglianza, 𝑙∗(𝜃) =

[ ∂𝑙(𝜃; 𝑦) ∂𝜃𝑟

]

= [𝑙𝑟(𝜃; 𝑦)] , 𝑟 = 1, . . . , 𝑝,

`e detto funzione punteggio o funzione score (score function).

Se il modello ha verosimiglianza regolare, spesso la stima di massi-ma verosimiglianza si individua come unica soluzione dell’equazione di

verosimiglianza

𝑙∗(𝜃) = 0,

dettata dalle condizioni del primo ordine per un massimo locale.

1.4.1

Informazione osservata

La matrice di dimensione 𝑝 × 𝑝 delle derivate parziali seconde di 𝑙(𝜃) cambiate di segno, 𝑗(𝜃) = −𝑙∗∗(𝜃) = [ −∂𝑙(𝜃; 𝑦) ∂𝜃𝑟∂𝜃𝑠 ] = [−𝑙𝑟𝑠(𝜃; 𝑦)] ,

`e detta matrice di informazione osservata, dove −∂𝑙(𝜃;𝑦)<sub>∂𝜃𝑟∂𝜃𝑠</sub> rappresenta l’ele-mento di posto (𝑟, 𝑠) della matrice 𝑗. A livello interpretativo si pu `o dire che l’informazione osservata calcolata nella stima di massima verosimiglian-za, 𝑗(ˆ𝜃), che non dipende dal parametro ma dal campione, `e una misura dell’informazione portata dal campione per il dato esperimento.

1.4.2

Informazione attesa

Si dice informazione attesa o informazione di Fisher la quantit`a 𝑖(𝜃) = 𝐸𝜃{𝑗(𝜃)} = [ −𝐸𝜃 ( ∂2_{𝑙(𝜃; 𝑌 )} ∂𝜃𝑟∂𝜃𝑠 )] ,

ossia il valore atteso dell’informazione osservata. `E una matrice di dimen-sione 𝑝 × 𝑝, dove −𝐸𝜃

(

∂2_{𝑙(𝜃;𝑌 )}

∂𝜃𝑟∂𝜃𝑠

)

1.5 Verosimiglianza composita 5 Sotto ulteriori condizioni di regolarit`a, l’informazione di Fisher pu `o essere calcolata tramite la funzione punteggio, ovvero

𝑖(𝜃) = Var𝜃{𝑙∗(𝜃)} = 𝐸𝜃{𝑙∗(𝜃; 𝑌 )𝑙∗(𝜃; 𝑌 )𝑇} . (1.2)

Sotto campionamento casuale semplice di numerosit`a 𝑛, l’informazione attesa `e proporzionale a 𝑛,

𝑖(𝜃) = 𝑛𝑖1(𝜃),

dove 𝑖1(𝜃) `e l’informazione attesa per una singola osservazione.

Sotto certe condizioni di regolarit`a, lo stimatore di massima verosimi-glianza `e consistente e ha distribuzione asintotica ˆ𝜃 ∼˙ 𝑁 (𝜃, 𝑖(𝜃)−1_).

1.5

Verosimiglianza composita

1.5.1

Introduzione

La verosimiglianza composita `e costruita da una combinazione di validi oggetti di verosimiglianza, di solito legati a piccoli sottoinsiemi di dati. Il vantaggio della verosimiglianza composita `e quello di ridurre la com-plessit`a computazionale in modo che sia possibile far fronte a grandi siemi di dati e modelli complessi che presentano difficolt`a a causa di in-terdipendenze di elevate dimensioni, che non rendono possibile l’utilizzo della verosimiglianza standard. Un altro aspetto vantaggioso della verosi-miglianza composita `e che si pu `o fare inferenza sui parametri di interesse senza fare assunzioni sulla distribuzione congiunta dei dati.

1.5.2

Definizioni e propriet`a

Sia 𝑌 = (𝑌1, . . . , 𝑌𝑛) un vettore di variabili casuali di dimensione 𝑛 con

densit`a congiunta 𝑓𝑌(𝑦; 𝜃) per un parametro incognito 𝜃 ∈ Θ ⊆ ℝ𝑝. Si

6 Capitolo 1. Verosimiglianza composita definizione della verosimigliamza per alcuni sottoinsiemi di dati sia pos-sibile. Pu `o quindi essere conveniente considerare pseudo-verosimiglianze ottenute combinando, in modo opportuno, tali oggetti di verosimiglianza. Quest’idea risale probabilmente a Besag (1974) ed `e stata definita

verosi-miglianza compositada Lindsay (1988).

Si considera un modello statistico parametrico (1.1). Date le osser-vazioni 𝑦 = (𝑦1, . . . , 𝑦𝑛), la verosimiglianza composita `e definita tramite

𝐾 eventi marginali o condizionati 𝐴𝑘(𝑦) su 𝒴, 𝑘 = 1, . . . , 𝐾, con

contribu-ti di verosimiglianza dacontribu-ti da 𝐿𝑘(𝜃; 𝑦) = 𝐿(𝜃; 𝐴𝑘(𝑦)). Allora, la

verosimi-glianza composita, ottenuta combinando queste singole verosimiglianze, `e definita come 𝐶𝐿(𝜃; 𝑦) = 𝐾 ∏ 𝑘=1 𝐿𝑘(𝜃; 𝑦)𝑤𝑘,

dove 𝑤𝑘, 𝑘 = 1, . . . , 𝐾, sono pesi positivi. Si indica con

𝐶𝑙(𝜃; 𝑦) = log 𝐶𝐿(𝜃; 𝑦), la funzione di log-verosimiglianza composita.

Questa classe contiene e quindi generalizza, l’usuale verosimiglianza ordinaria, insieme a tante altre interessanti alternative. Una possibile clas-sificazione delle verosimiglianze composite (Varin e Vidoni, 2005) prende in considerazione i seguenti due principali gruppi :

∙ Metodo di omissione

In questo gruppo, la pseudo-verosimiglianza si ottiene togliendo alcu-ni termialcu-ni che complicano la valutazione della verosimiglianza completa. L’auspicio `e che la parte omessa non sia molto informativa sul parametro di interesse e quindi la perdita di efficienza sia tollerabile. Alcuni esempi comprendono sia le pseudo-verosimiglianze di Besag (Besag, 1974, 1977) per dati spaziali, la verosimiglianza di ordine 𝑚 per processi stazionari (Azzalini, 1983) e la verosimiglianza di Stein (2004) per grandi insiemi di dati spaziali. Anche la famosa verosimiglianza parziale (Cox, 1975) pu `o essere inclusa in questa classe.

1.5 Verosimiglianza composita 7 ∙ Verosimiglianza composita marginale

In questo gruppo, la verosimiglianza composita viene costruita combi-nando verosimiglianze marginali (tramite distribuzioni congiunte di cop-pie, triplette,...). L’interesse `e focalizzato sulle composizioni di distribu-zioni marginali di piccole dimensioni, dato l’importante risparmio com-putazionale.

Un primo esempio riguarda le pseudo-verosimiglianze costruite utiliz-zando, le sole marginali univariate, come sotto l’ipotesi di indipendenza. Si ottiene quindi 𝐼𝐿(𝜃; 𝑦) = 𝑛 ∏ 𝑖=1 𝑓 (𝑦𝑖; 𝜃)𝑤𝑖,

che viene denominata verosimiglianza di indipendenza (independence like-lihood); si veda ad esempio, Chandler e Bate (2007).

Un secondo esempio `e quello in cui la verosimiglianza composita viene costruita utilizzando marginali bivariate. Si ottiene quindi

𝑃 𝐿(𝜃; 𝑦) = 𝑛−1 ∏ 𝑖=1 𝑛 ∏ 𝑗=𝑖+1 𝑓 (𝑦𝑖, 𝑦𝑗; 𝜃)𝑤𝑖𝑗,

che viene denominata verosimiglianza a coppie (pairwise likelihood). Si veda ad esempio Le Cessie e Van Houwelingen (1994). Si indica con

𝑃 𝑙(𝜃; 𝑦) = log 𝑃 𝐿(𝜃; 𝑦), la funzione di log-verosimiglianza a coppie.

In alcune circostanze sarebbe utile considerare dei sottogruppi pi `u gran-di come triplette d’osservazioni (Varin e Vidoni, 2005) o combinare vero-simiglianza di indipendenza e a coppie in un modo ottimale (Cox e Reid, 2004).

L’inferenza basata sulla verosimiglianza composita, pu `o essere guisti-ficata dal fatto che il valore atteso della log-verosimiglianza composita `e massimo in 𝜃0, ossia,

8 Capitolo 1. Verosimiglianza composita per ogni 𝜃 ∕= 𝜃0. Infatti

𝐸𝜃0[ 𝐾 ∑ 𝑘=1 𝑤𝑘log 𝐿𝑘(𝜃; 𝑌 )] = 𝐾 ∑ 𝑘=1 𝑤𝑘𝐸𝜃0[log 𝐿_𝑘(𝜃; 𝑌 )] = 𝐾 ∑ 𝑘=1 𝑤𝑘𝐸𝜃0[log 𝐿(𝜃; 𝐴_𝑘(𝑌 ))] < 𝐾 ∑ 𝑘=1 𝑤𝑘𝐸𝜃0[log 𝐿(𝜃0; 𝐴_𝑘(𝑌 ))],

per ogni 𝜃 ∕= 𝜃0 _{in base alla disuguaglianza di Wald che vale per ogni}

sin-golo addendo della sommatoria (si veda ad esempio Pace e Salvan, 2001, §5.4.1).

1.5.3

Quantit`a associate alla verosimiglianza composita

La funzione punteggio basata sulla verosimiglianza composita, si ottiene calcolando la derivata prima della log-verosimiglianza composita

𝐶𝑙∗(𝜃; 𝑦) = ∂𝐶𝑙(𝜃; 𝑦) ∂𝜃 = 𝐾 ∑ 𝑘=1 𝑤𝑘 ∂ log 𝐿𝑘(𝜃; 𝑦) ∂𝜃 .

L’equazione di stima basata sulla verosimiglianza composita, detta equa-zione di verosimiglianza composita `e data da,

𝐶𝑙∗(𝜃; 𝑦) = 0.

Lo stimatore di massima verosimiglianza composita `e la soluzione, se esiste ed `e unica, dell’equazione di verosimiglianza composita.

Essendo ogni singola componente della verosimiglianza composita una verosimiglianza propria, risulta che la funzione punteggio composita `e una combinazione lineare di funzioni di punteggio associate ad ogni sin-golo termine della verosimiglianza composita. Quindi l’equazione di sti-ma ad essa associata risulta non distorta e sotto le usuali condizioni di regolarit`a, lo stimatore ˆ𝜃𝐶 che massimizza 𝐶𝑙(𝜃; 𝑦) `e consistente e

asintoti-camente normale

ˆ

1.5 Verosimiglianza composita 9 dove 𝐺(𝜃) = 𝐻(𝜃)𝐽(𝜃)−1𝐻(𝜃), con 𝐻(𝜃) = 𝐸𝜃 { −∂𝐶𝑙∗(𝜃;𝑌 ) ∂𝜃 }

e 𝐽(𝜃) = Var𝜃{𝐶𝑙∗(𝜃; 𝑌 )} nota come

infor-mazione di Godambe(Godambe, 1960) o informazione sandwich.

La forma dell’informazione di Godambe `e dovuta al fatto che la verosi-miglianza composita non soddisfa un’identit`a analoga alla (1.2) valida per la verosimiglianza completa in modelli regolari. Il fatto che 𝐻(𝜃) non coin-cida con 𝐽(𝜃) pu `o comportare in genere una perdita di efficienza asintotica di ˆ𝜃𝐶 rispetto a ˆ𝜃 del modello completo.

1.5.4

Verifica delle ipotesi

Anche nel caso della verosimiglianza composita, per quanto riguarda la verifica delle ipotesi, esiste una opportuna procedura per verificare la con-formit`a dei dati a un sottomodello ℱ0 di ℱ, dove ℱ `e supposto

corretta-mente specificato.

Sebbene i test di Wald e score basati sulla verosimiglianza composi-ta siano semplici da ricavare, il loro uso pu `o tutcomposi-tavia essere discutibile a causa della ben nota mancanza di invarianza di riparametrizzazione (test di Wald) e possibile instabilit`a numerica (score test). Per queste ra-gioni, un analogo del test del rapporto di verosimiglianza basato sulla verosimiglianza composita pu `o essere pi `u interessante.

Si suppone di voler saggiare l’ipotesi nulla 𝐻0 : 𝜃 = 𝜃0,

dove 𝜃 `e un vettore 𝑝-dimensionale. Allora il test del rapporto di

verosi-miglianza compositarisulta 𝑊 (𝜃0) = 2

{

𝐶𝑙(ˆ𝜃𝐶; 𝑦) − 𝐶𝑙(𝜃0; 𝑦)

} ,

In questo caso la distribuzione asintotica di 𝑊 (𝜃0) non ha una forma

combi-10 Capitolo 1. Verosimiglianza composita nazione lineare di variabili casuali 𝜒21 indipendenti, ossia,

𝑊 (𝜃0) ˙∼ 𝑝 ∑ 𝑖=1 𝜆𝑖(𝜃0)𝑍𝑖2 dove 𝑍2

𝑖 sono variabili casuali 𝜒21 indipendenti e 𝜆𝑖(𝜃0), 𝑖 = 1, . . . , 𝑝, sono

gli autovalori della matrice 𝐽(𝜃0)−1𝐻(𝜃0); si veda Foutz e Srivastava (1997)

oppure Kent (1982).

Il test di Wald corrispondente `e dato da

𝑊𝑒(𝜃0) = (ˆ𝜃𝐶− 𝜃0)𝑇𝐺(𝜃0)(ˆ𝜃𝐶− 𝜃0),

mentre il test score `e

𝑊𝑢(𝜃0) = 𝐶𝑙∗(𝜃0; 𝑦)𝑇𝐽(𝜃0)𝐶𝑙∗(𝜃0; 𝑦).

Sia il test di Wald che il test score hanno l’usale distribuzione asintotica 𝜒2 𝑝.

Il risultato si generalizza al test del rapporto di verosimiglianza com-posita su un sottoinsieme di componenti di 𝜃 (si veda ad esempio, Varin, 2008, pagina 6).

Capitolo 2

Verosimiglianza a coppie ed

efficienza

2.1

Introduzione

Sono presenti in letteratura vari esempi di applicazione della verosimi-glianza a coppie, si veda ad esempio Lele and Taper (2002) o Varin (2008) per una rassegna recente.

In questo capitolo, saranno presentate due applicazioni della verosi-miglianza a coppie. Particolare attenzione sar`a posta sull’efficienza at-traverso il confronto tra i risultati ottenuti con la verosimiglianza a coppie e quelli ottenuti con il modello completo.

In particolare, nel secondo paragrafo tratteremo il primo esempio con-siderato da Cox e Reid (2004), ripercorrendone in dettaglio tutti i passaggi. Si tratta di un’applicazione della verosimiglianza a coppie per un modello normale multivariato monoparametrico. L’obiettivo `e valutare l’efficienza, confrontando i risultati con quelli ottenuti attraverso la verosimiglianza completa.

Nel terzo paragrafo viene trattato un esempio nuovo, in cui si applica la verosimiglianza a coppie ad un modello normale multivariato con tre parametri. Si sono ottenuti inoltre alcuni risultati analitici di rilevanza,

12 Capitolo 2. Verosimiglianza a coppie ed efficienza cos`ı sintetizzabili:

∙ l’informazione di Godambe e l’informazione di Fisher coincidono; ∙ vi `e una relazione lineare tra la funzione score basato sulla

verosimi-glianza a coppie e la funzione score basato su quella completa, con matrice della trasformazione dipendente da 𝜃, ma non da 𝑦.

Nel capitolo seguente verranno ripresi gli stessi esempi, considerando le distribuzioni di vari test basati sulla verosimiglianza a coppie.

2.2

Un esempio con parametro scalare: normale

simmetrica

Questo primo esempio `e stato gi`a trattato in Cox e Reid (2004). Vengono qui ricostruiti i vari passaggi, e aggiunte alcune spiegazioni. L’interesse `e focalizzato sulla perdita di efficienza dovuta all’impiego della verosi-miglianza a coppie per la stima di un parametro incognito rispetto alla verosimiglianza completa.

Sia 𝑦𝑖 = (𝑦𝑖1, . . . , 𝑦𝑖𝑞) realizzazione di una variabile casuale normale

𝑞-dimensionale 𝑌𝑖 = (𝑌𝑖1, . . . , 𝑌𝑖𝑞) con vettore delle medie nullo, varianze

unitarie e matrice di covarianza 𝑅, ovvero 𝑌𝑖 ∼ 𝑁𝑞(0, 𝑅), dove Cor𝜌(𝑌𝑖𝑟, 𝑌𝑖𝑠)

=𝜌 per 𝑟 ∕= 𝑠. Inoltre, si ha che ∣𝑅∣ > 0 per − 1

𝑞−1 < 𝜌 < 1, condizione

necessaria affinch´e 𝑅 sia una matrice di covarianza. Dunque

𝑅 = (1 − 𝜌) ( 𝐼𝑞+ 𝜌 1 − 𝜌1𝑞1 𝑇 𝑞 ) = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ 1 𝜌 ⋅ ⋅ ⋅ 𝜌 𝜌 1 ⋅ ⋅ ⋅ 𝜌 ... ... ... ... 𝜌 𝜌 ⋅ ⋅ ⋅ 1 ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ,

con 1𝑞 = (1, . . . , 1)𝑇, vettore 𝑞-dimensionale e 𝐼𝑞che rappresenta la matrice

identit`a di ordine 𝑞. Per facilitare il calcolo dell’inversa e del determinante della matrice 𝑅, si pu `o riscrivere l’elemento di posto (𝑟, 𝑠), 𝑟, 𝑠 = 1, . . . , 𝑞,

2.2 Un esempio con parametro scalare: normale simmetrica 13 nel seguente modo

𝑅𝑟,𝑠= (1 − 𝜌) ( 𝛿𝑟𝑠+ 𝜌 1 − 𝜌ℎ𝑟𝑠 ) , dove ℎ𝑟𝑠 = 1 per 𝑟, 𝑠 = 1, . . . , 𝑞 e 𝛿𝑟𝑠 = { 1 se 𝑟 = 𝑠 0 se 𝑟 ∕= 𝑠 . L’elemento (𝑟, 𝑠) di 𝑅−1risulta 𝑅𝑟𝑠₌ 1 1 − 𝜌 ( 𝛿𝑟𝑠− 𝜌 1−𝜌 1 + 𝑞_1−𝜌𝜌 ) = 1 1 − 𝜌 ( 𝛿𝑟𝑠− 𝜌 1 + 𝜌(𝑞 − 1) ) e quindi 𝑅−1 = 1 1 − 𝜌 ( 𝐼𝑞− 𝜌 1 + 𝜌(𝑞 − 1)1𝑞1 𝑇 𝑞 ) . Inoltre il determinante di 𝑅 si pu `o scrivere come

∣𝑅∣ = (1 − 𝜌)𝑞 ( 1 + 𝑞 𝜌 1 − 𝜌 ) = (1 − 𝜌)𝑞−1{1 + 𝜌(𝑞 − 1)} .

2.2.1

Verosimiglianza completa

Considerando una singola osservazione, la funzione di densit`a della dis-tribuzione normale 𝑞-dimensionale risulta

𝑓𝑌𝑖(𝑦𝑖; 𝜌) = 1 (2𝜋)𝑞2∣𝑅∣ 1 2 exp ( −1 2𝑦 𝑇 𝑖 𝑅−1𝑦𝑖 ) Sviluppando l’espressione 𝑦𝑇 𝑖 𝑅−1𝑦𝑖, si ottiente 𝑦𝑇 𝑖 𝑅 −1_𝑦 𝑖 = 1 1 − 𝜌 ( 𝑦𝑇 𝑖 𝑦𝑖− 𝜌 1 + 𝜌(𝑞 − 1)𝑦 𝑇 𝑖 1𝑞1𝑇𝑞𝑦𝑖 ) . Si nota che 𝑦𝑇 𝑖 𝑦𝑖 =∑𝑞_𝑟=1𝑦𝑖𝑟2 e 𝑦𝑇𝑖 1𝑞 = 1𝑇𝑞𝑦𝑖 = 𝑞𝑦𝑖 = ∑𝑞 𝑟=1𝑦𝑖𝑟. Di

conseguen-za, la funzione di densit`a diventa

𝑓𝑌𝑖(𝑦𝑖; 𝜌) = 1 (2𝜋)𝑞2(1 − 𝜌)𝑞−12 {1 + 𝜌(𝑞 − 1)} 1 2 exp { − 1 2(1 − 𝜌) ( _𝑞 ∑ 𝑟=1 𝑦𝑖𝑟2 − 𝜌𝑞2 1 + 𝜌(𝑞 − 1)𝑦 2 𝑖 )} .

14 Capitolo 2. Verosimiglianza a coppie ed efficienza La verosimiglianza completa calcolata per 𝑛 osservazioni indipendenti risulta 𝐿(𝜌) = 𝑛 ∏ 𝑖=1 𝑓𝑌𝑖(𝑦𝑖; 𝜌) = [ 1 (2𝜋)𝑞2(1 − 𝜌) 𝑞−1 2 {1 + 𝜌(𝑞 − 1)} 1 2 ]𝑛 exp { − 1 2(1 − 𝜌) 𝑛 ∑ 𝑖=1 ( _𝑞 ∑ 𝑟=1 𝑦2𝑖𝑟− 𝜌𝑞2 1 + 𝜌(𝑞 − 1)𝑦 2 𝑖 )} = (2𝜋)−𝑛𝑞2 (1 − 𝜌)− 𝑛(𝑞−1) 2 {1 + 𝜌(𝑞 − 1)}− 𝑛 2 exp { − 1 2(1 − 𝜌) 𝑛 ∑ 𝑖=1 ( _𝑞 ∑ 𝑟=1 𝑦2_𝑖𝑟− 𝜌𝑞 2 1 + 𝜌(𝑞 − 1)𝑦 2 𝑖 )} , e la log-verosimiglianza completa `e 𝑙(𝜌) = log 𝐿(𝜌) = −𝑛(𝑞 − 1) 2 log(1 − 𝜌) − 𝑛 2 log {1 + 𝜌(𝑞 − 1)} − 1 2(1 − 𝜌) 𝑛 ∑ 𝑖=1 [ _𝑞 ∑ 𝑟=1 𝑦_𝑖𝑟2 − 𝜌𝑞 2 1 + 𝜌(𝑞 − 1)𝑦 2 𝑖 ] = −𝑛(𝑞 − 1) 2 log(1 − 𝜌) − 𝑛 2 log {1 + 𝜌(𝑞 − 1)} − 1 2(1 − 𝜌) [ _𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 𝑦𝑖𝑟2 − 𝜌𝑞2 1 + 𝜌(𝑞 − 1) 𝑛 ∑ 𝑖=1 𝑦2𝑖 ] . L’espressione∑𝑛 𝑖=1 ∑𝑞

𝑟=1𝑦𝑖𝑟2 si pu `o riscrivere nel modo seguente 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 𝑦2𝑖𝑟 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟+ 𝑦𝑖− 𝑦𝑖)2 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖)2+ 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 𝑦2_𝑖 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖)2+ 𝑛 ∑ 𝑖=1 𝑞𝑦2𝑖 = 𝑆𝑆𝑊 +1 𝑞𝑆𝑆𝐵,

2.2 Un esempio con parametro scalare: normale simmetrica 15 dove 𝑆𝑆𝑊 = ∑𝑛 𝑖=1 ∑𝑞 𝑟=1(𝑦𝑖𝑟 − 𝑦𝑖)2 e 𝑆𝑆𝐵 = ∑𝑛 𝑖=1𝑦𝑖⋅2 con 𝑦𝑖⋅ = ∑𝑞_𝑟=1𝑦𝑖𝑟,

sono componenti della statistica sufficiente. Sostituendo le varie quantit`a ricavate, si ottiene infine

𝑙(𝜌) = −𝑛(𝑞 − 1) 2 log(1 − 𝜌) − 𝑛 2log {1 + 𝜌(𝑞 − 1)} − 1 2(1 − 𝜌)𝑆𝑆𝑊 − 1 2𝑞 {1 + 𝜌(𝑞 − 1)}𝑆𝑆𝐵. La funzione di punteggio risulta

𝑙∗(𝜌) = 𝑑𝑙(𝜌) 𝑑𝜌 = 𝑛(𝑞 − 1) 2 1 (1 − 𝜌) − 𝑛(𝑞 − 1) 2 1 {1 + 𝜌(𝑞 − 1)} − 1 2 1 (1 − 𝜌)2𝑆𝑆𝑊 + (𝑞 − 1) 2𝑞 1 {1 + 𝜌(𝑞 − 1)}2𝑆𝑆𝐵. e l’informazione osservata `e 𝑗(𝜌) = −𝑑 2_𝑙(𝜌) 𝑑𝜌2 = −𝑛(𝑞 − 1) 2 1 (1 − 𝜌)2 − 𝑛(𝑞 − 1)2 2 1 {1 + 𝜌(𝑞 − 1)}2 + 1 (1 − 𝜌)3𝑆𝑆𝑊 + (𝑞 − 1)2 𝑞 1 {1 + 𝜌(𝑞 − 1)}3𝑆𝑆𝐵.

Per calcolare l’informazione attesa 𝑖(𝜌) = 𝐸𝜌{𝑗(𝜌)}, `e necessario conoscere

i valori attesi di SSW e SSB. Si ha che, 𝑆𝑆𝑊 =∑𝑛 𝑖=1 ∑𝑞 𝑟=1(𝑌𝑖𝑟− 𝑌𝑖)2 =∑𝑛_𝑖=1𝑄𝑖, dove 𝑄𝑖 = 𝑞 ∑ 𝑟=1 (𝑌𝑖𝑟 − 𝑌𝑖)2 = 𝑞 ∑ 𝑟=1 𝑌𝑖𝑟2− 𝑞𝑌 2 𝑖 = 𝑞 ∑ 𝑟=1 𝑌_𝑖𝑟2−1 𝑞 𝑞 ∑ 𝑟=1 𝑌𝑖𝑟 𝑞 ∑ 𝑟=1 𝑌𝑖𝑟 = 𝑌𝑇 𝑖 ( 𝐼𝑞− 1 𝑞1𝑞1 𝑇 𝑞 ) 𝑌𝑖,

16 Capitolo 2. Verosimiglianza a coppie ed efficienza 𝑌𝑖 ∼ 𝑁𝑞(0, 𝑅). Poich`e la matrice 𝑅

(

𝐼𝑞− 1_𝑞1𝑞1𝑇𝑞

)

non risulta idempotente, si opera una trasformazione su 𝑌𝑖, ponendo 𝑍𝑖 = (1 − 𝜌)−

1 2𝑌_𝑖.

Allora 𝑍𝑖 ∼ 𝑁𝑞(0, Σ), con Σ = 𝐼𝑞+_1−𝜌𝜌 1𝑞1𝑇𝑞. Di conseguenza,

𝑌𝑇 𝑖 ( 𝐼𝑞−1_𝑞1𝑞1𝑇𝑞 ) 𝑌𝑖 = (1 − 𝜌)𝑍𝑖𝑇 ( 𝐼𝑞−1_𝑞1𝑞1𝑇𝑞 ) 𝑍𝑖.

Si nota ora che la matrice Σ(𝐼𝑞−1_𝑞1𝑞1𝑇𝑞

)

`e idempotente, quindi secondo il teorema 8.6 di Severini (2005), si ha 𝑍𝑇 𝑖 ( 𝐼𝑞− 1_𝑞1𝑞1𝑇𝑞 ) 𝑍𝑖 ∼ 𝜒2_𝑡𝑟 {Σ(𝐼𝑞−1_𝑞1𝑞1𝑇𝑞)}, con 𝑡𝑟 { Σ(𝐼𝑞− 1_𝑞1𝑞1𝑇𝑞 )} = 𝑞 − 1. Si deduce che 𝑄𝑖 1 − 𝜌 ∼ 𝜒 2 𝑞−1.

Quindi la distribuzione di SSW risulta 𝑆𝑆𝑊 =

𝑛

∑

𝑖=1

𝑄𝑖 ∼ (1 − 𝜌)𝜒2_{𝑛(𝑞−1)}.

Per quanto riguarda la distribuzione di 𝑆𝑆𝐵 =∑𝑛

𝑖=1𝑌𝑖⋅2, si ha che 𝑌𝑖⋅= 𝑞 ∑ 𝑟=1 𝑌𝑖𝑟 = 1𝑇𝑞𝑌𝑖 ∼ 𝑁 (0, 1𝑇𝑞𝑅1𝑞) ∼ 𝑁 (0, 𝑞 {1 + 𝜌(𝑞 − 1)}). Quindi 𝑆𝑆𝐵 pu `o essere riscritto in questo modo

𝑆𝑆𝐵 = 𝑞 {1 + 𝜌(𝑞 − 1)} 𝑛 ∑ 𝑖=1 [ [𝑞 {1 + 𝜌(𝑞 − 1)}]−12𝑌_𝑖⋅ ]2 = 𝑞 {1 + 𝜌(𝑞 − 1)} 𝑛 ∑ 𝑖=1 𝑍_𝑖2, dove 𝑍𝑖 ∼ 𝑁 (0, 1). Infine si ottiene che

𝑆𝑆𝐵 ∼ 𝑞 {1 + 𝜌(𝑞 − 1)} 𝜒2𝑛.

Si pu `o verificare che le variabili 𝑆𝑆𝑊 e 𝑆𝑆𝐵 sono indipendenti.

Infatti, visto che gli 𝑛 campioni sono indipendenti e 𝑆𝑆𝑊 `e funzione solo delle quantit`a ∑𝑞

𝑟=1(𝑌𝑖𝑟 − ¯𝑌𝑖)2 e 𝑆𝑆𝐵 solo delle 𝑌𝑖⋅, dimostrare che 𝑆𝑆𝑊

e 𝑆𝑆𝐵 sono indipendenti, corrisponde a dimostrare che∑𝑞

2.2 Un esempio con parametro scalare: normale simmetrica 17 e 𝑌𝑖⋅ sono indipendenti. Posto 𝐵 = 𝐼𝑞 − 1_𝑞1𝑞1𝑇𝑞, attraverso il risultato

(vi-ii) a pagina 188 di Rao (1973), la condizione necessaria e sufficiente per l’indipendenza `e che 𝑅𝐵𝑅1𝑞= 0. Ora 𝑅𝐵𝑅1𝑞 = (1 − 𝜌) ( 𝐼𝑞+ 𝜌 1 − 𝜌1𝑞1 𝑇 𝑞 ) ( 𝐼𝑞− 1 𝑞1𝑞1 𝑇 𝑞 ) (1 − 𝜌) ( 𝐼𝑞+ 𝜌 1 − 𝜌1𝑞1 𝑇 𝑞 ) 1𝑞 = (1 − 𝜌)2 { 𝐼𝑞− 1 𝑞1𝑞1 𝑇 𝑞 + 𝜌 1 − 𝜌 ( 1𝑞1𝑇𝑞 − 1 𝑞𝑞1𝑞1 𝑇 𝑞 )} ( 1𝑞+ 𝑞𝜌 1 − 𝜌1𝑞 ) = (1 − 𝜌)2 ( 𝐼𝑞− 1 𝑞1𝑞1 𝑇 𝑞 ) ( 1𝑞+ 𝑞𝜌 1 − 𝜌1𝑞 ) = (1 − 𝜌)2 { 1𝑞+ 𝑞𝜌 1 − 𝜌1𝑞− 1 𝑞 ( 𝑞1𝑞+ 𝑞2_𝜌 1 − 𝜌1𝑞 )} = (1 − 𝜌)2 ( 1𝑞+ 𝑞𝜌 1 − 𝜌1𝑞− 1𝑞− 𝑞𝜌 1 − 𝜌1𝑞 ) = 0.

Quindi, l’informazione di Fisher `e 𝑖(𝜌) = 𝐸𝜌{𝑗(𝜌)} = −𝑛(𝑞 − 1) 2 1 (1 − 𝜌)2 − 𝑛(𝑞 − 1)2 2 1 {1 + 𝜌(𝑞 − 1)}2 + 1 (1 − 𝜌)3𝐸𝜌(𝑆𝑆𝑊 ) + (𝑞 − 1)2 𝑞 1 {1 + 𝜌(𝑞 − 1)}3𝐸𝜌(𝑆𝑆𝐵), dato che 𝐸𝜌(𝑆𝑆𝑊 ) = 𝑛(1 − 𝜌)(𝑞 − 1) e 𝐸𝜌(𝑆𝑆𝐵) = 𝑛𝑞 {1 + 𝜌(𝑞 − 1)}, si ottiene che 𝑖(𝜌) = 𝑛𝑞(𝑞 − 1) 2 [ 1 + 𝜌2_{(𝑞 − 1)} (1 − 𝜌)2_{{1 + 𝜌(𝑞 − 1)}}2 ] .

18 Capitolo 2. Verosimiglianza a coppie ed efficienza

2.2.2

Verosimiglianza a coppie

Per quanto riguarda la verosimiglianza a coppie, questa si basa sulle dis-tribuzioni marginali bivariate, ovvero

( 𝑌𝑖𝑟 𝑌𝑖𝑠 ) ∼ 𝑁2 (( 0 0 ) , [ 1 𝜌 𝜌 1 ]) .

Per una sola osservazione la verosimiglianza a coppie combina le ( 𝑞 2 ) = 𝑞! 2!(𝑞 − 2)! = 𝑞(𝑞 − 1) 2 coppie possibili e risulta pari a

𝑃 𝐿(𝜌) = 𝑞−1 ∏ 𝑟=1 𝑞 ∏ 𝑠=𝑟+1 1 2𝜋√1 − 𝜌2 exp { − 1 2(1 − 𝜌2₎(𝑦 2 𝑖𝑟+ 𝑦𝑖𝑠2 − 2𝜌𝑦𝑖𝑟𝑦𝑖𝑠) } ,

quindi, date 𝑛 osservazioni, la log-verosimiglianza a coppie risulta 𝑃 𝑙(𝜌) = −𝑛𝑞(𝑞 − 1) 4 log(1 − 𝜌 2_{) −} 1 2(1 − 𝜌2₎ 𝑛 ∑ 𝑖=1 𝑞−1 ∑ 𝑟=1 𝑞 ∑ 𝑠=𝑟+1 (𝑦2𝑖𝑟+ 𝑦2𝑖𝑠− 2𝜌𝑦𝑖𝑟𝑦𝑖𝑠). Si nota che 𝑞−1 ∑ 𝑟=1 𝑞 ∑ 𝑠=𝑟+1 (𝑦𝑖𝑟2 + 𝑦𝑖𝑠2 − 2𝜌𝑦𝑖𝑟𝑦𝑖𝑠) = 𝑞 ∑ 𝑟=1 (𝑞 − 𝑟)𝑦2𝑖𝑟+ 𝑞 ∑ 𝑟=1 (𝑟 − 1)𝑦𝑖𝑟2 − 𝜌 ( _𝑞 ∑ 𝑟=1 𝑦𝑖𝑟 )2 + 𝜌 𝑞 ∑ 𝑟=1 𝑦_𝑖𝑟2.

Sostituendo quest’ultima forma nella verosimiglianza e semplificando, la log-verosimiglianza a coppie risulta pari a

𝑃 𝑙(𝜌) = −𝑛𝑞(𝑞 − 1) 4 log(1 − 𝜌 2_{) −}𝑞 − 1 + 𝜌 2(1 − 𝜌2₎𝑆𝑆𝑊 − (𝑞 − 1) 2𝑞(1 + 𝜌)𝑆𝑆𝐵,

2.2 Un esempio con parametro scalare: normale simmetrica 19 e la funzione punteggio risulta

𝑃 𝑙∗(𝜌) = 𝑑𝑃 𝑙(𝜌) 𝑑𝜌 = 𝑛𝑞(𝑞 − 1)𝜌 2(1 − 𝜌2₎ − 1 + 𝜌2_{+ 2(𝑞 − 1)𝜌} 2(1 − 𝜌2₎2 𝑆𝑆𝑊 + (𝑞 − 1) 2𝑞(1 + 𝜌)2𝑆𝑆𝐵.

Le quantit`a necessarie per il calcolo dell’informazione di Godambe sono: 𝑑2_{𝑃 𝑙(𝜌)} 𝑑𝜌2 = 1 (1 − 𝜌2₎3 { 𝑛𝑞(𝑞 − 1) 2 (1 − 𝜌 2_{)(1 + 𝜌}2_{) − [(𝑞 + 𝜌 − 1)(1 − 𝜌}2₎ +2𝜌(1 + 𝜌2+ 2(𝑞 − 1)𝜌)]𝑆𝑆𝑊 −(𝑞 − 1) 𝑞 (1 − 𝜌) 3_𝑆𝑆𝐵 } , 𝐻(𝜌) = 𝐸𝜌 { −𝑑 2_{𝑃 𝑙} (𝜌) 𝑑𝜌2 } = − 1 (1 − 𝜌2₎3 { 𝑛𝑞(𝑞 − 1) 2 (1 − 𝜌 4_{) − [(𝑞 + 𝜌 − 1)(1 − 𝜌}2₎ +2𝜌(1 + 𝜌2+ 2(𝑞 − 1)𝜌)]𝐸𝜌(𝑆𝑆𝑊 ) − (𝑞 − 1) 𝑞 (1 − 𝜌) 3_𝐸 𝜌(𝑆𝑆𝐵) } . Infine, dopo un po’ di algebra, si ottiene

𝐻(𝜌) = 𝑛𝑞(𝑞 − 1)(1 + 𝜌

2₎

2(1 − 𝜌2₎2 .

La quantit`a 𝐽(𝜌) invece risulta pari a 𝐽(𝜌) = Var𝜌{𝑃 𝑙∗(𝜌)} ={ (1 + 𝜌 2_{+ 2(𝑞 − 1)𝜌)} 2(1 − 𝜌2₎2 }2 Var𝜌(𝑆𝑆𝑊 ) + ( 𝑞 − 1 2𝑞(1 + 𝜌)2 )2 Var𝜌(𝑆𝑆𝐵).

Dato che Var𝜌(𝑆𝑆𝑊 ) = (1−𝜌)22𝑛(𝑞−1), Var𝜌(𝑆𝑆𝐵) = [𝑞 {1 + 𝜌(𝑞 − 1)}]22𝑛

e tenuto conto dell’indipendenza di 𝑆𝑆𝑊 e 𝑆𝑆𝐵. Dopo vari passaggi si ottiene

𝐽(𝜌) = 𝑛𝑞(𝑞 − 1)

20 Capitolo 2. Verosimiglianza a coppie ed efficienza dove 𝑐(𝑞, 𝜌) = (1 − 𝜌)2(3𝜌2_{+ 1) + 𝑞𝜌(−3𝜌}3_{+ 8𝜌}2 _{− 3𝜌 + 2) + 𝑞}2_𝜌2_{(1 − 𝜌)}2_.

L’informazione di Godambe risulta quindi pari a 𝐺(𝜌) = 𝐻(𝜌)𝐽(𝜌)−1𝐻(𝜌) = 𝐻(𝜌) 2 𝐽(𝜌) = 𝑛𝑞(𝑞 − 1)(1 + 𝜌 2₎2 2(1 − 𝜌)2_{𝑐(𝑞, 𝜌)} .

2.2.3

Efficienza asintotica

L’efficienza asintotica dello stimatore di massima verosimiglianza a cop-pie viene ottenuto dal rapporto tra le due varianze asintotiche basate, rispettivamente, sull’informazione di Fisher e Godambe,

𝐸 = 𝑖(𝜌)

−1

𝐺(𝜌)−1 =

(1 + 𝜌(𝑞 − 1))2(1 + 𝜌2₎2

(1 + 𝜌2_{(𝑞 − 1))𝑐(𝑞, 𝜌)} .

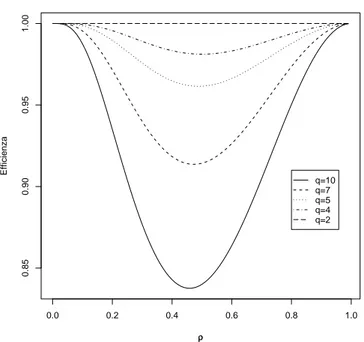
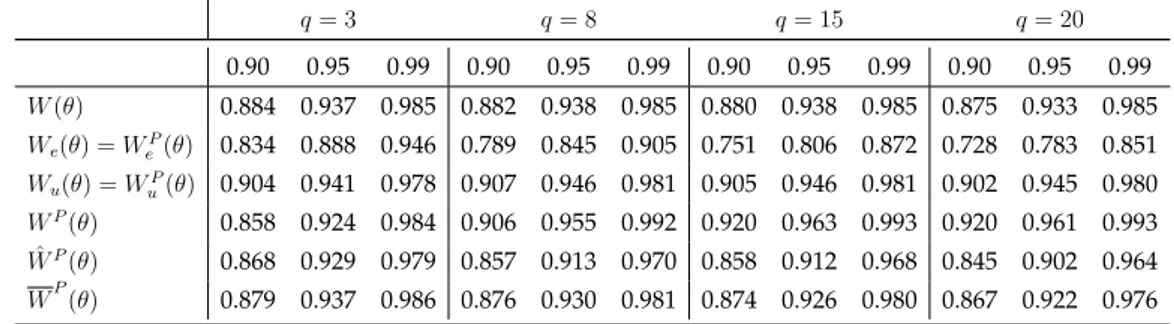
Questo rapporto vale 1 per 𝑞 = 2, in quanto la verosimiglianza a coppie coincide con quella standard. Risulta anche uguale a 1 anche se 𝜌 = 0 o 𝜌 = 1. Il grafico in Figura 2.1 illustra la perdita di informazione all’au-mentare di 𝑞. Gli stimarori ˆ𝜌 e ˆ𝜌𝑃 sono ottenuti rispettivamente con la

verosimiglianza completa e la verosimiglianza a coppie.

2.3

Un esempio con parametro

multidimensio-nale: modello ad effetti casuali

Il secondo esempio che si considera `e un’estensione del precedente (si ve-da ad esempio, Pace e Salvan, 1996, pagina 485) e riguarve-da sempre osser-vazioni normali multivariate equicorrelate. Ora, tuttavia, si considerano ignote e uguali tra di loro anche le medie e le varianze delle distribu-zioni marginali univariate. Il parametro `e dunque tridimensionale, con 𝜃 = (𝜇, 𝜎2, 𝜌).

2.3 Un esempio con parametro multidimensionale 21 0.0 0.2 0.4 0.6 0.8 1.0 0.85 0.90 0.95 1.00 ρρ Efficienza q=10 q=7 q=5 q=4 q=2

Figura 2.1: Rapporto asintotiche delle varianze di ˆ𝜌 e ˆ𝜌𝑃 in funzione di 𝜌

22 Capitolo 2. Verosimiglianza a coppie ed efficienza Considerando una singola osservazione, si assume che 𝑌𝑖 ∼ 𝑁𝑞(𝜇1𝑞, Σ),

dove 𝜇 ∈ ℝ. Indicando con Σ𝑟,𝑠l’elemento di posto (𝑟, 𝑠) della matrice Σ,

con Σ𝑟,𝑠= 𝜎2𝜌(1 − 𝜌) ( 𝛿𝑟𝑠+ 𝜌 1 − 𝜌ℎ𝑟𝑠 ) , dove 𝛿𝑟𝑠 = { 1 se 𝑟 = 𝑠 0 se 𝑟 ∕= 𝑠 e ℎ𝑟𝑠= 1. Allora si ha che Σ𝑟,𝑟 = 𝜎2(1 − 𝜌) ( 1 + 𝜌 1 − 𝜌 ) = 𝜎2(1 − 𝜌)1 − 𝜌 + 𝜌 (1 − 𝜌) = 𝜎2 Σ𝑟,𝑠 = 𝜎2(1 − 𝜌) 𝜌 (1 − 𝜌) = 𝜌𝜎2.

Quindi Cor𝜌(𝑌𝑖𝑟, 𝑌𝑖𝑠) = 𝜌, con −_𝑞−11 < 𝜌 < 1 in quanto questa `e condizione

necessaria affinch´e ∣Σ∣ > 0, ossia che Σ sia una matrice di covarianza. Un’applicazione importante si ha nell’ambito dell’analisi della vari-anza con effetti casuali, dove usualmente si assume 𝑌𝑖𝑟 = 𝜇 + 𝑎𝑖 + 𝑒𝑖𝑟

(𝑟 = 1, . . . , 𝑞, 𝑖 = 1, . . . , 𝑛), con l’effetto 𝑎𝑖 realizzazione di una normale

𝑁 (0, 𝜎2

𝑎), l’errore 𝑒𝑖𝑟 realizzazione di una normale 𝑁 (0, 𝜎𝑒2) e

indipenden-za fra tali realizindipenden-zazioni. Il modello statistico considerato `e del tipo sopra considerato con 𝜎2 = 𝜎2 𝑎+ 𝜎𝑒2e 𝜌 = 𝜎2𝑎 𝜎2 𝑎+𝜎2𝑒⋅

2.3.1

Verosimiglianza completa

Posto 𝑦𝑖 = (𝑦𝑖1, . . . , 𝑦𝑖𝑞), la funzione di verosimiglianza per 𝑛 osservazioni

risulta 𝐿(𝜇, 𝜎2, 𝜌) = 𝑛 ∏ 𝑖=1 1 (2𝜋𝜎2₎𝑞_{2(1 − 𝜌)}𝑞−1_{2 {1 + 𝜌(𝑞 − 1)}}12 exp ( − 1 2𝜎2_{(1 − 𝜌)} [ _𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝜇)2− 𝜌𝑞2 1 + 𝜌(𝑞 − 1)(𝑦𝑖− 𝜇) 2 ] )

2.3 Un esempio con parametro multidimensionale 23 = 1 (2𝜋𝜎2₎𝑛𝑞2 (1 − 𝜌) 𝑛(𝑞−1) 2 {1 + 𝜌(𝑞 − 1)} 𝑛 2 exp ( − 1 2𝜎2_{(1 − 𝜌)} 𝑛 ∑ 𝑖=1 [ _𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟 − 𝜇)2− 𝜌𝑞2 1 + 𝜌(𝑞 − 1)(𝑦𝑖− 𝜇) 2 ] ) ,

dove, analogamente al caso precedente, 𝑦𝑖 =

∑𝑞 𝑟=1𝑦𝑖𝑟/𝑞⋅ La log-verosimiglianza risulta 𝑙(𝜇, 𝜎2, 𝜌) = −𝑛𝑞 2 log 𝜎 2₋ 𝑛(𝑞 − 1) 2 log(1 − 𝜌) − 𝑛 2 log {1 + 𝜌(𝑞 − 1)} − 1 2𝜎2_{(1 − 𝜌)} [ _𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝜇)2− 𝜌𝑞2 1 + 𝜌(𝑞 − 1) 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝜇)2 ] = −𝑛𝑞 2 log 𝜎 2₋ 𝑛(𝑞 − 1) 2 log(1 − 𝜌) − 𝑛 2 log {1 + 𝜌(𝑞 − 1)} − 1 2𝜎2_{(1 − 𝜌)} [ 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖)2+ 𝑞 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝜇)2 − 𝜌𝑞 2 1 + 𝜌(𝑞 − 1) ( 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝑦)2+ 𝑛(𝑦 − 𝜇)2 )] = −𝑛𝑞 2 log 𝜎 2₋ 𝑛(𝑞 − 1) 2 log(1 − 𝜌) − 𝑛 2 log {1 + 𝜌(𝑞 − 1)} − 1 2𝜎2_{(1 − 𝜌)} [ 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖)2+ 𝑞(1 − 𝜌) 1 + 𝜌(𝑞 − 1) 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝑦)2 + 𝑛𝑞(1 − 𝜌) 1 + 𝜌(𝑞 − 1)(𝑦 − 𝜇) 2 ] = −𝑛𝑞 2 log 𝜎 2₋ 𝑛(𝑞 − 1) 2 log(1 − 𝜌) − 𝑛 2 log {1 + 𝜌(𝑞 − 1)} − 1 2𝜎2_{(1 − 𝜌)} 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖)2− 𝑞 2𝜎2_{{1 + 𝜌(𝑞 − 1)}} ( 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝑦)2 + 𝑛𝑦2 ) + 𝑛𝑞𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}𝑦 − 𝑛𝑞𝜇2 2𝜎2_{{1 + 𝜌(𝑞 − 1)}}⋅

24 Capitolo 2. Verosimiglianza a coppie ed efficienza Ponendo 𝑆𝑆𝑊 =∑𝑛 𝑖=1 ∑𝑞 𝑟=1(𝑦𝑖𝑟− 𝑦𝑖)2 e 𝑆𝑆𝐵 = ∑𝑛 𝑖=1(𝑦𝑖− 𝑦)2, si ottiene 𝑙(𝜇, 𝜎2, 𝜌) = − 1 2𝜎2_{(1 − 𝜌)}𝑆𝑆𝑊 − 𝑞 2𝜎2_{{1 + 𝜌(𝑞 − 1)}}(𝑆𝑆𝐵 + 𝑛𝑦 2₎ + 𝑛𝑞𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}𝑦 − 𝑛𝑞𝜇2 2𝜎2_{{1 + 𝜌(𝑞 − 1)}} − 𝑛𝑞 2 log 𝜎 2 − 𝑛(𝑞 − 1) 2 log(1 − 𝜌) − 𝑛 2log {1 + 𝜌(𝑞 − 1)} , dove 𝑦 = ∑𝑛𝑖=1 ∑𝑞 𝑟=1𝑦𝑖𝑟

𝑛𝑞 e avendo sfruttato le identit`a 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝜇)2 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖)2+ 𝑞 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝜇)2 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝜇)2 = 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝑦)2+ 𝑛(𝑦 − 𝜇)2.

La funzione punteggio ha componenti ∂𝑙(𝜃) ∂𝜇 = 𝑛𝑞 𝜎2_{{1 + 𝜌(𝑞 − 1)}}𝑦 − 𝑛𝑞𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}} ∂𝑙(𝜃) ∂𝜎2 = 1 2(𝜎2₎2_{(1 − 𝜌)}𝑆𝑆𝑊 + 𝑞 2(𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}(𝑆𝑆𝐵 + 𝑛𝑦 2₎ − 𝑛𝑞𝜇 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}𝑦 + 𝑛𝑞𝜇2 2(𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}− 𝑛𝑞 2𝜎2 ∂𝑙(𝜃) ∂𝜌 = − 1 2𝜎2_{(1 − 𝜌)}2𝑆𝑆𝑊 + 𝑞(𝑞 − 1) 2𝜎2_{{1 + 𝜌(𝑞 − 1)}}2(𝑆𝑆𝐵 + 𝑛𝑦 2₎ − 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}2𝑦 + 𝑛𝑞(𝑞 − 1)𝜇2 2𝜎2_{{1 + 𝜌(𝑞 − 1)}}2 + 𝑛(𝑞 − 1) 2(1 − 𝜌) − 𝑛(𝑞 − 1) 2 {1 + 𝜌(𝑞 − 1)}. La matrice d’informazione osservata

𝑗(𝜇, 𝜎2, 𝜌) = ⎛ ⎜ ⎜ ⎝ 𝑗𝜇𝜇 𝑗𝜇𝜎2 𝑗_𝜇𝜌 𝑗𝜇𝜎2 𝑗_𝜎2_𝜎2 𝑗_𝜎2_𝜌 𝑗𝜇𝜌 𝑗𝜎2_𝜌 𝑗_𝜌𝜌 ⎞ ⎟ ⎟ ⎠

2.3 Un esempio con parametro multidimensionale 25 `e formata dai seguenti elementi

𝑗𝜇𝜇 = − ∂2_𝑙(𝜃) ∂𝜇2 = 𝑛𝑞 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑗𝜇𝜎2 = −∂ 2_𝑙(𝜃) ∂𝜇∂𝜎2 = 𝑛𝑞 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}𝑦 − 𝑛𝑞𝜇 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}} 𝑗𝜇𝜌 = − ∂2_𝑙(𝜃) ∂𝜇∂𝜌 = 𝑛𝑞(𝑞 − 1) 𝜎2_{{1 + 𝜌(𝑞 − 1)}}2𝑦 − 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}2 𝑗𝜎2_𝜎2 = −∂ 2_𝑙(𝜃) ∂(𝜎2₎2 = 1 (𝜎2₎3_{(1 − 𝜌)}𝑆𝑆𝑊 + 𝑞 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}}(𝑆𝑆𝐵 + 𝑛𝑦 2₎ − 2𝑛𝑞𝜇 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}}𝑦 + 𝑛𝑞𝜇2 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}} − 𝑛𝑞 2(𝜎2₎2 𝑗𝜎2_𝜌 = −∂ 2_𝑙(𝜃) ∂𝜎2_∂𝜌 = − 1 2(𝜎2₎2_{(1 − 𝜌)}2𝑆𝑆𝑊 + 𝑞(𝑞 − 1) 2(𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2(𝑆𝑆𝐵 + 𝑛𝑦 2₎ − 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2𝑦 + 𝑛𝑞(𝑞 − 1)𝜇2 2(𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2 𝑗𝜌𝜌 = − ∂2_𝑙(𝜃) ∂𝜌2 = 1 𝜎2_{(1 − 𝜌)}3𝑆𝑆𝑊 + 𝑞(𝑞 − 1)2 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3(𝑆𝑆𝐵 + 𝑛𝑦 2₎ − 2𝑛𝑞(𝑞 − 1) 2_𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3𝑦 + 𝑛𝑞(𝑞 − 1)2_𝜇2 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3 − 𝑛(𝑞 − 1) 2(1 − 𝜌)2 − 𝑛(𝑞 − 1)2 2 {1 + 𝜌(𝑞 − 1)}2.

Prima di calcolare l’informazione attesa, `e opportuno ricavare la distri-buzione della statistica sufficiente (𝑌 , 𝑆𝑆𝑊, 𝑆𝑆𝐵)

∙ Distribuzione marginale di 𝑌 𝑌 = _𝑛𝑞1 ∑𝑛 𝑖=1 ∑𝑞 𝑟=1𝑌𝑖𝑟 ∼ 𝑁 ( 𝜇,𝜎2{1+𝜌(𝑞−1)}_𝑛𝑞 ), poich´e ∑𝑞 𝑟=1𝑌𝑖𝑟 = 1𝑇𝑞𝑌𝑖 ∼ 𝑁 (𝑞𝜇, 𝑞𝜎2_{[1 + 𝜌(𝑞 − 1)]).} ∙ Distribuzione marginale di 𝑆𝑆𝑊

Analogamente all’esempio precedente risulta che 𝑆𝑆𝑊 ∼ 𝜎2_{(1 − 𝜌)𝜒}2 𝑛(𝑞−1).

26 Capitolo 2. Verosimiglianza a coppie ed efficienza Si ha che 𝑌𝑖 = 𝑞−1 ∑𝑞 𝑟=1𝑌𝑖𝑟 = 𝑞−11𝑇𝑞𝑌𝑖 ∼ 𝑁 (𝜇, 𝑞−1𝜎2[1 + 𝜌(𝑞 − 1)]), pertan-to _𝑞−1𝜎2_{{1+𝜌(𝑞−1)}}𝑆𝑆𝐵 ∼ 𝜒2𝑛−1, e quindi 𝑆𝑆𝐵 ∼ 𝜎2{1+𝜌(𝑞−1)} 𝑞 𝜒 2 𝑛−1.

Tenendo conto che 𝐸𝜃(𝑌 ) = 𝜇, 𝐸𝜃(𝑆𝑆𝑊 ) = 𝜎2(1 − 𝜌)𝑛(𝑞 − 1) e 𝐸𝜃(𝑆𝑆𝐵 +

𝑛𝑌2) = 𝑛𝜎_𝑞2 {1 + 𝜌(𝑞 − 1)} + 𝑛𝜇2 _con 𝐸𝜃(𝑌 2 ) = Var𝜃(𝑌 ) + 𝜇2 = 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 + 𝜇 2_,

la matrice di informazione di Fisher

𝑖(𝜇, 𝜎2, 𝜌) = 𝐸𝜃{𝑗(𝜇, 𝜎2, 𝜌)} = ⎛ ⎜ ⎜ ⎝ 𝑖𝜇𝜇 𝑖𝜇𝜎2 𝑖_𝜇𝜌 𝑖𝜇𝜎2 𝑖_𝜎2_𝜎2 𝑖_𝜎2_𝜌 𝑖𝜇𝜌 𝑖𝜎2_𝜌 𝑖_𝜌𝜌 ⎞ ⎟ ⎟ ⎠ (2.1)

`e formata dai seguenti elementi 𝑖𝜇𝜇 = 𝑛𝑞 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑖𝜇𝜎2 = 𝑛𝑞 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}𝐸𝜃(𝑌 ) − 𝑛𝑞𝜇 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}} = 𝑛𝑞 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}𝜇 − 𝑛𝑞𝜇 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}} = 0 𝑖𝜇𝜌 = 𝑛𝑞(𝑞 − 1) 𝜎2_{{1 + 𝜌(𝑞 − 1)}}2𝐸𝜃(𝑌) − 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}2 = 𝑛𝑞(𝑞 − 1) 𝜎2_{{1 + 𝜌(𝑞 − 1)}}2𝜇 − 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}2 = 0 𝑖𝜎2_𝜎2 = 1 (𝜎2₎3_{(1 − 𝜌)}𝐸𝜃(𝑆𝑆𝑊 ) + 𝑞 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}}𝐸𝜃[(𝑆𝑆𝐵 + 𝑛𝑦 2_)] − 2𝑛𝑞𝜇 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}}𝐸𝜃(𝑌 ) + 𝑛𝑞𝜇2 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}} − 𝑛𝑞 2(𝜎2₎2 = 1 (𝜎2₎3_{(1 − 𝜌)}𝜎 2_{(1 − 𝜌)𝑛(𝑞 − 1) +} 𝑞 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}} ( 𝑛𝜎2 𝑞 {1 + 𝜌(𝑞 − 1)} + 𝑛𝜇 2 ) − 2𝑛𝑞𝜇 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}}𝜇 + 𝑛𝑞𝜇 2 (𝜎2₎3_{{1 + 𝜌(𝑞 − 1)}}− 𝑛𝑞 2(𝜎2₎2 = 𝑛𝑞 2(𝜎2₎2

2.3 Un esempio con parametro multidimensionale 27 𝑖𝜎2_𝜌 = − 1 2(𝜎2₎2_{(1 − 𝜌)}2𝐸𝜃(𝑆𝑆𝑊 ) + 𝑞(𝑞 − 1) 2(𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2𝐸𝜃[(𝑆𝑆𝐵 + 𝑛𝑦 2_)] − 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2𝐸𝜃(𝑌 ) + 𝑛𝑞(𝑞 − 1)𝜇2 2(𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2 = − 1 2(𝜎2₎2_{(1 − 𝜌)}2𝜎 2_{(1 − 𝜌)𝑛(𝑞 − 1) +} 𝑞(𝑞 − 1) 2(𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2 ( 𝑛𝜎2 𝑞 {1 + 𝜌(𝑞 − 1)} + 𝑛𝜇 2 ) − 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2𝜇 + 𝑛𝑞(𝑞 − 1)𝜇 2 2(𝜎2₎2_{{1 + 𝜌(𝑞 − 1)}}2 = − 𝑛𝑞(𝑞 − 1)𝜌 2𝜎2_{(1 − 𝜌) {1 + 𝜌(𝑞 − 1)}} 𝑖𝜌𝜌 = 1 𝜎2_{(1 − 𝜌)}3𝐸𝜃(𝑆𝑆𝑊 ) + 𝑞(𝑞 − 1)2 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3𝐸𝜃[(𝑆𝑆𝐵 + 𝑛𝑦 2_)] − 2𝑛𝑞(𝑞 − 1) 2_𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3𝐸𝜃(𝑌 ) + 𝑛𝑞(𝑞 − 1)2_𝜇2 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3 − 𝑛(𝑞 − 1) 2(1 − 𝜌)2 − 𝑛(𝑞 − 1)2 2 {1 + 𝜌(𝑞 − 1)}2 = 1 𝜎2_{(1 − 𝜌)}3𝜎 2_{(1 − 𝜌)𝑛(𝑞 − 1) +} 𝑞(𝑞 − 1)2 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3 ( 𝑛𝜎2 𝑞 {1 + 𝜌(𝑞 − 1)} + 𝑛𝜇 2 ) − 2𝑛𝑞(𝑞 − 1) 2_𝜇 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3𝜇 + 𝑛𝑞(𝑞 − 1) 2_𝜇2 𝜎2_{{1 + 𝜌(𝑞 − 1)}}3 − 𝑛(𝑞 − 1) 2(1 − 𝜌)2 − 𝑛(𝑞 − 1) 2 2 {1 + 𝜌(𝑞 − 1)}2 = 𝑛(𝑞 − 1) 2 [ 1 (1 − 𝜌)2 + 𝑞 − 1 {1 + 𝜌(𝑞 − 1)}2 ] .

2.3.2

Verosimiglianza a coppie

La verosimiglianza a coppie, si basa sulle distribuzioni marginali bivari-ate, ovvero ( 𝑌𝑖𝑟 𝑌𝑖𝑠 ) ∼ 𝑁2 (( 𝜇 𝜇 ) , 𝜎2 [ 1 𝜌 𝜌 1 ]) , 𝑟 ∕= 𝑠.

28 Capitolo 2. Verosimiglianza a coppie ed efficienza La densit`a bivariata `e 𝑝𝑌𝑖𝑟,𝑌𝑖𝑠(𝑦𝑖𝑟, 𝑦𝑖𝑠; 𝜃) = 1 2𝜋𝜎2_{√1 − 𝜌}2exp ( − 1 2𝜎2_{(1 − 𝜌}2₎ [ (𝑦𝑖𝑟− 𝜇)2 + (𝑦𝑖𝑠− 𝜇)2− 2𝜌(𝑦𝑖𝑟− 𝜇)(𝑦𝑖𝑠− 𝜇) ]) .

La log-verosimiglianza per una singola coppia di osservazioni risulta 𝑙(𝜃; 𝑦𝑖𝑟, 𝑦𝑖𝑠) = − log 𝜎2− 1 2log(1 − 𝜌 2_{) −} 1 2𝜎2_{(1 − 𝜌}2₎ [ (𝑦𝑖𝑟− 𝜇)2 + (𝑦𝑖𝑠− 𝜇)2− 2𝜌(𝑦𝑖𝑟 − 𝜇)(𝑦𝑖𝑠− 𝜇) ] , e il contributo di 𝑦𝑖alla log-verosimiglianza a coppie `e

𝑃 𝑙(𝜃; 𝑦𝑖𝑟, 𝑦𝑖𝑠) = 𝑞−1 ∑ 𝑟=1 𝑞 ∑ 𝑠=𝑟+1 𝑙(𝜃; 𝑦𝑖𝑟, 𝑦𝑖𝑠) = −𝑞(𝑞 − 1) 2 log 𝜎 2₋ 𝑞(𝑞 − 1) 4 log(1 − 𝜌 2_{) −} 1 2𝜎2_{(1 − 𝜌}2₎ 𝑞−1 ∑ 𝑟=1 𝑞 ∑ 𝑠=𝑟+1 [ (𝑦𝑖𝑟− 𝜇)2+ (𝑦𝑖𝑠− 𝜇)2− 2𝜌(𝑦𝑖𝑟− 𝜇)(𝑦𝑖𝑠− 𝜇) ] . Si nota che [ _𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟 − 𝜇) ]2 = 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝜇)2+ 2 𝑞 ∑ 𝑠>𝑟 (𝑦𝑖𝑟− 𝜇)(𝑦𝑖𝑟𝑠− 𝜇), 𝑞−1 ∑ 𝑟=1 𝑞 ∑ 𝑠=𝑟+1 (𝑦𝑖𝑟− 𝜇)2 = 𝑞−1 ∑ 𝑟=1 (𝑞 − 𝑟)(𝑦𝑖𝑟− 𝜇)2 = 𝑞 ∑ 𝑟=1 (𝑞 − 𝑟)(𝑦𝑖𝑟− 𝜇)2 e 𝑞−1 ∑ 𝑟=1 𝑞 ∑ 𝑠=𝑟+1 (𝑦𝑖𝑠− 𝜇)2 = 𝑞 ∑ 𝑟=1 (𝑟 − 1)(𝑦𝑖𝑟− 𝜇)2.

Dunque per 𝑛 osservazioni, la log-verosimiglianza a coppie risulta 𝑃 𝑙(𝜃; 𝑦) = −𝑛𝑞(𝑞 − 1) 2 log 𝜎 2₋ 𝑛𝑞(𝑞 − 1) 4 log(1 − 𝜌 2_{) −} 𝑞 − 1 + 𝜌 2𝜎2_{(1 − 𝜌}2₎ 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟 − 𝜇)2+ 𝜌 2𝜎2_{(1 − 𝜌}2₎ 𝑛 ∑ 𝑖=1 [ _𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝜇) ]2 .

2.3 Un esempio con parametro multidimensionale 29 Inoltre, considerando che

𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝜇) = 𝑞 ∑ 𝑟=1 𝑦𝑖𝑟− 𝑞𝜇 = 𝑞𝑦𝑖− 𝑞𝜇 = 𝑞(𝑦𝑖− 𝜇), 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝜇)2 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦+ 𝑦 − 𝜇)2 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦)2+ 𝑛𝑞(𝑦 − 𝜇)2 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖+ 𝑦𝑖− 𝑦)2 + 𝑛𝑞(𝑦 − 𝜇)2 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖)2+ 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖− 𝑦)2+ 𝑛𝑞(𝑦 − 𝜇)2 = 𝑛 ∑ 𝑖=1 𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝑦𝑖)2+ 𝑞 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝑦)2+ 𝑛𝑞(𝑦 − 𝜇)2 = 𝑆𝑆𝑊 + 𝑞𝑆𝑆𝐵 + 𝑛𝑞(𝑦 − 𝜇)2_, 𝑛 ∑ 𝑖=1 [ _𝑞 ∑ 𝑟=1 (𝑦𝑖𝑟− 𝜇) ]2 = 𝑛 ∑ 𝑖=1 𝑞2(𝑦𝑖− 𝜇)2 = 𝑞2 𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝜇)2 = 𝑞2 [ _𝑛 ∑ 𝑖=1 (𝑦𝑖− 𝑦)2+ 𝑛(𝑦 − 𝜇)2 ] = 𝑞2[𝑆𝑆𝐵 + 𝑛(𝑦 − 𝜇)2_{] ,} dove 𝑆𝑆𝑊 =∑𝑛 𝑖=1 ∑𝑞 𝑟=1(𝑦𝑖𝑟− 𝑦𝑖)2, e 𝑆𝑆𝐵 = ∑𝑛 𝑖=1(𝑦𝑖− 𝑦)2, alla fine si pu `o scrivere 𝑃 𝑙(𝜃; 𝑦) = − 𝑞 − 1 + 𝜌 2𝜎2_{(1 − 𝜌}2₎𝑆𝑆𝑊 − 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}(𝑆𝑆𝐵 + 𝑛𝑦 2_{) +} 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)} 𝑦 − 𝑛𝑞(𝑞 − 1)𝜇 2 2𝜎2_{(1 + 𝜌)} − 𝑛𝑞(𝑞 − 1) 2 log 𝜎 2₋ 𝑛𝑞(𝑞 − 1) 4 log(1 − 𝜌 2_).

30 Capitolo 2. Verosimiglianza a coppie ed efficienza Gli elementi della funzione di punteggio risultano

∂𝑃 𝑙(𝜃) ∂𝜇 = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 − 𝜌)}(𝑦 − 𝜇) ∂𝑃 𝑙(𝜃) ∂𝜎2 = 𝑞 − 1 + 𝜌 2(𝜎2₎2_{(1 − 𝜌}2₎𝑆𝑆𝑊 + 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)}(𝑆𝑆𝐵 + 𝑛𝑦 2_{) −} 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)}𝑦 + 𝑛𝑞(𝑞 − 1)𝜇 2 2(𝜎2₎2_{(1 + 𝜌)} − 𝑛𝑞(𝑞 − 1) 2𝜎2 ∂𝑃 𝑙(𝜃) ∂𝜌 = − 𝜌2_{+ 2𝜌(𝑞 − 1) + 1} 2𝜎2_{(1 − 𝜌}2₎2 𝑆𝑆𝑊 + 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}2(𝑆𝑆𝐵 + 𝑛𝑦 2_{) −}𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}2𝑦 +𝑛𝑞(𝑞 − 1)𝜇 2 2𝜎2_{(1 + 𝜌)}2 + 𝑛𝑞(𝑞 − 1)𝜌 2(1 − 𝜌2₎ ⋅ (2.2) La matrice 𝐻(𝜇, 𝜎2, 𝜌) = ⎛ ⎜ ⎜ ⎝ 𝐻𝜇𝜇 𝐻𝜇𝜎2 𝐻_𝜇𝜌 𝐻𝜇𝜎2 𝐻_𝜎2_𝜎2 𝐻_𝜎2_𝜌 𝐻𝜇𝜌 𝐻𝜎2_𝜌 𝐻_𝜌𝜌 ⎞ ⎟ ⎟ ⎠

`e formata dai seguenti elementi

𝐻𝜇𝜇 = 𝐸 ( −∂ 2_{𝑃 𝑙} ∂𝜇2 ) = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝐻𝜇𝜎2 = 𝐸 ( − ∂ 2_{𝑃 𝑙} ∂𝜇∂𝜎2 ) = 𝑛𝑞(𝑞 − 1) (𝜎2₎2_{(1 + 𝜌)}(𝐸(𝑦) − 𝜇) = 𝑛𝑞(𝑞 − 1) (𝜎2₎2_{(1 + 𝜌)}(𝜇 − 𝜇) = 0 𝐻𝜇𝜌= 𝐸 ( − ∂ 2_{𝑃 𝑙} ∂𝜇∂𝜎2 ) = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)}2(𝐸(𝑦) − 𝜇) = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)}2(𝜇 − 𝜇) = 0

2.3 Un esempio con parametro multidimensionale 31 𝐻𝜎2_𝜎2 = 𝐸 ( − ∂ 2_{𝑃 𝑙} ∂(𝜎2₎2 ) = 𝑞 − 1 + 𝜌 (𝜎2₎3_{(1 − 𝜌}2₎𝐸(𝑆𝑆𝑊 ) + 𝑞(𝑞 − 1) (𝜎2₎3_{(1 + 𝜌)}𝐸(𝑆𝑆𝐵 + 𝑛𝑦 2₎ − 2𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎3_{(1 + 𝜌)}𝐸(𝑦) + 𝑛𝑞(𝑞 − 1)𝜇2 (𝜎2₎3_{(1 + 𝜌)}− 𝑛𝑞(𝑞 − 1) 2(𝜎2₎2 = 𝑞 − 1 + 𝜌 (𝜎2₎3_{(1 − 𝜌}2₎𝜎 2_{(1 − 𝜌)𝑛(𝑞 − 1) +} 𝑞(𝑞 − 1) (𝜎2₎3_{(1 + 𝜌)} [ 𝑛𝜎2 𝑞 {1 + 𝜌(𝑞 − 1)} + 𝑛𝜇 2 ] − 2𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎3_{(1 + 𝜌)}𝜇 + 𝑛𝑞(𝑞 − 1)𝜇2 (𝜎2₎3_{(1 + 𝜌)} − 𝑛𝑞(𝑞 − 1) 2(𝜎2₎2 = 𝑛𝑞(𝑞 − 1) 2(𝜎2₎2 𝐻𝜎2_𝜌 = 𝐸 ( − ∂ 2_{𝑃 𝑙} ∂𝜎2_∂𝜌 ) = −𝜌 2_{+ 2𝜌(𝑞 − 1) + 1} 2(𝜎2₎2_{(1 − 𝜌}2₎2 𝐸(𝑆𝑆𝑊 ) + 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)}2𝐸(𝑆𝑆𝐵 + 𝑛𝑦 2₎ − 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)}2𝐸(𝑦) + 𝑛𝑞(𝑞 − 1)𝜇2 2(𝜎2₎2_{(1 + 𝜌)}2 = −𝜌 2_{+ 2𝜌(𝑞 − 1) + 1} 2(𝜎2₎2_{(1 − 𝜌}2₎2 𝜎 2_{(1 − 𝜌)𝑛(𝑞 − 1) +} 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)}2 [ 𝑛𝜎2 𝑞 {1 + 𝜌(𝑞 − 1)} + 𝑛𝜇 2 ] − 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)}2𝜇 + 𝑛𝑞(𝑞 − 1)𝜇 2 2(𝜎2₎2_{(1 + 𝜌)}2 = − 𝑛𝑞(𝑞 − 1)𝜌 2𝜎2_{(1 − 𝜌}2₎ 𝐻𝜌𝜌= 𝐸 ( −∂ 2_{𝑃 𝑙} ∂𝜌2 ) = 2𝜌 3_{− 6𝜌}2_{+ 6𝜌}2_{𝑞 + 6𝜌 + 2𝑞 − 2} 2𝜎2_{(1 − 𝜌}2₎3 𝐸(𝑆𝑆𝑊 ) + 𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)}3 𝐸(𝑆𝑆𝐵 + 𝑛𝑦2) − 2𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}3 𝐸(𝑦) + 𝑛𝑞(𝑞 − 1)𝜇2 𝜎2_{(1 + 𝜌)}3 − 𝑛𝑞(𝑞 − 1)(1 + 𝜌 2₎ 2(1 − 𝜌2₎2

32 Capitolo 2. Verosimiglianza a coppie ed efficienza = 2𝜌 3_{− 6𝜌}2_{+ 6𝜌}2_{𝑞 + 6𝜌 + 2𝑞 − 2} 2𝜎2_{(1 − 𝜌}2₎3 𝜎 2_{(1 − 𝜌)𝑛(𝑞 − 1) +} 𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)}3 [ 𝑛𝜎2 𝑞 {1 + 𝜌(𝑞 − 1)} + 𝑛𝜇 2 ] −2𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}3 𝜇 + 𝑛𝑞(𝑞 − 1)𝜇2 𝜎2_{(1 + 𝜌)}3 −𝑛𝑞(𝑞 − 1)(1 + 𝜌 2₎ 2(1 − 𝜌2₎2 = 𝑛𝑞(𝑞 − 1)(1 + 𝜌 2₎ 2(1 + 𝜌)2 ⋅

Per calcolare gli elementi della matrice 𝐽(𝜃), `e necessario calcolare i valori attesi e varianze di alcune variabili. Le variabili 𝑆𝑆𝑊, 𝑆𝑆𝐵 e 𝑌 sono indipendenti (si veda ad esempio, Davison, 2003, paragrafo 9.4).

∙ Valori attesi.

La variabile 𝑌 si distribuisce come una normale con media 𝜇 e varianza

𝜎2{1+𝜌(𝑞−1)}

𝑛𝑞 . Quindi la sua funzione generatrice dei momenti risulta

𝑀_𝑌(𝑡) = exp( 𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 2𝑛𝑞 𝑡 2_{+ 𝜇𝑡} ) . Dunque 𝐸𝜃[𝑌 2 ] = 𝑀_𝑌′′(0) = 𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 + 𝜇 𝐸𝜃[𝑌 3 ] = 𝑀_𝑌′′′(0) = 3𝜇𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 + 𝜇 3 𝐸𝜃[𝑌 4 ] = 𝑀_𝑌′′′′(0) = 𝜇4 +6𝜇 2_𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 + 3 [ 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 ]2 𝐸𝜃[𝑆𝑆𝑊2] = Var𝜃(𝑆𝑆𝑊 ) + [𝐸𝜃(𝑆𝑆𝑊 )]2 = 2𝑛(𝑞 − 1)[𝜎2_{(1 − 𝜌)]}2_{+ [𝑛𝜎}2_{(𝑞 − 1)(1 − 𝜌)]}2 = 2𝑛(𝑞 − 1)[𝜎2(1 − 𝜌)]2{2 + 𝑛(𝑞 − 1)}

2.3 Un esempio con parametro multidimensionale 33 𝐸𝜃[𝑆𝑆𝐵2] = Var𝜃(𝑆𝑆𝐵) + [𝐸𝜃(𝑆𝑆𝐵)]2 = 2(𝑛 − 1)[ 𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 ]2 +[ (𝑛 − 1)𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 ]2 = (𝑛2_{− 1)}[ 𝜎2{1 + 𝜌(𝑞 − 1)} 𝑞 ]2 𝐸𝜃[(𝑆𝑆𝐵 + 𝑛𝑌 2 )2] = 𝐸𝜃[(𝑆𝑆𝐵2]2+ 2𝑛𝐸𝜃[𝑆𝑆𝐵]𝐸𝜃[𝑌 2 ] + 𝑛2𝐸𝜃[𝑌 4 ] = (𝑛2+ 2𝑛)[ 𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 ]2 +2𝑛(𝑛 + 2)𝜇 2_𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 + 𝑛2𝜇4 𝐸𝜃[𝑛𝑌 2 (𝑦 − 𝜇)] = 2𝜇𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 𝐸𝜃[𝑌 (𝑌 − 𝜇)] = 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 𝐸𝜃[𝑌 (𝑆𝑆𝐵 + 𝑛𝑌 )] = (𝑛 − 1)𝜇𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 + 3𝜇𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 + 𝑛𝜇 3 ∙ Varianze. Var𝜃(𝑌 2 ) = 𝐸[𝑌4] − (𝐸[𝑌2])2 = 4𝜇 2_𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 + 2 [ 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 ]2 Var𝜃(𝑆𝑆𝐵 + 𝑛𝑌 2 ) = Var𝜃(𝑆𝑆𝐵) + 𝑛2Var𝜃(𝑌 2 ) = 2𝑛𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 [ 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 + 2𝜇 2 ] Cov𝜃((𝑆𝑆𝐵 + 𝑛𝑌 2 ), 𝑌 ) = 𝐸𝜃(𝑆𝑆𝐵𝑌 + 𝑛𝑌 3 ) − 𝐸𝜃(𝑆𝑆𝐵 + 𝑛𝑌 2 )𝐸𝜃(𝑌 ) = 2𝜇𝜎 2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 ⋅ La matrice 𝐽(𝜇, 𝜎2, 𝜌) = ⎛ ⎜ ⎜ ⎝ 𝐽𝜇𝜇 𝐽𝜇𝜎2 𝐽_𝜇𝜌 𝐽𝜇𝜎2 𝐽_𝜎2_𝜎2 𝐽_𝜎2_𝜌 𝐽𝜇𝜌 𝐽𝜎2_𝜌 𝐽_𝜌𝜌 ⎞ ⎟ ⎟ ⎠

34 Capitolo 2. Verosimiglianza a coppie ed efficienza `e formata dai seguenti elementi

𝐽𝜇𝜇 = Var𝜃 ( ∂𝑃 𝑙 ∂𝜇 ) =[ 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} ]2 Var𝜃(𝑌 ) = 𝑛𝑞(𝑞 − 1) 2_{{1 + 𝜌(𝑞 − 1)}} 𝜎2_{(1 + 𝜌)}2 𝐽𝜎2_𝜎2 = Var_𝜃 ( ∂𝑃 𝑙 ∂𝜎2 ) = [ 𝑞 − 1 + 𝜌 2(𝜎2₎2_{(1 − 𝜌}2₎ ]2 Var𝜃(𝑆𝑆𝑊 ) + [ 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)} ]2 Var𝜃(𝑆𝑆𝐵 + 𝑛𝑌 2 ) +[ 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)} ]2 Var𝜃(𝑌 ) − 2 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)} Cov𝜃((𝑆𝑆𝐵 + 𝑛𝑌 2 ), 𝑌 ) = [ 𝑞 − 1 + 𝜌 2(𝜎2₎2_{(1 − 𝜌}2₎ ]2 2𝑛(𝑞 − 1)[𝜎2(1 − 𝜌)]2+ [ 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)} ]2 2𝑛𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 [ 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 + 2𝜇 2 ] +[ 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)} ]2 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 − 2 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)} 2𝜇𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 = 𝑛(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)}2 {(𝑞 − 1 + 𝜌) 2_{+ (𝑞 − 1) {1 + 𝜌(𝑞 − 1)}}2} 𝐽𝜌𝜌 = Var𝜃 ( ∂𝑃 𝑙 ∂𝜌 ) =[ 𝜌 2_{+ 2𝜌(𝑞 − 1) + 1} 2𝜎2_{(1 − 𝜌}2₎2 ]2 Var𝜃(𝑆𝑆𝑊 ) + [ 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}2 ]2 Var𝜃(𝑆𝑆𝐵 + 𝑛𝑌 2 ) +[ 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}2 ]2 Var𝜃(𝑌 ) − 2 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}2 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}2 Cov𝜃((𝑆𝑆𝐵 + 𝑛𝑌 2 ), 𝑌 )

2.3 Un esempio con parametro multidimensionale 35 =[ 𝜌 2_{+ 2𝜌(𝑞 − 1) + 1} 2𝜎2_{(1 − 𝜌}2₎2 ]2 2𝑛(𝑞 − 1)[𝜎2(1 − 𝜌)]2+ [ 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}2 ]2 2𝑛𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 [ 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 + 2𝜇 2 ] +[ 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}2 ]2 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 − 2 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}2 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}2 2𝜇𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 = 𝑛(𝑞 − 1) 2(1 + 𝜌)4 { (𝜌2_{+ 2𝜌(𝑞 − 1) + 1)}2 (1 − 𝜌)2 + (𝑞 − 1) {1 + 𝜌(𝑞 − 1)} 2 } 𝐽𝜇𝜎2 = 𝐸_𝜃 ( ∂𝑃 𝑙 ∂𝜇 ∂𝑃 𝑙 ∂𝜎2 ) = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑞 − 1 + 𝜌 2(𝜎2₎2_{(1 − 𝜌}2₎𝐸𝜃(𝑌 − 𝜇)𝐸𝜃(𝑆𝑆𝑊 ) + 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)}𝐸𝜃[(𝑌 − 𝜇)(𝑆𝑆𝐵 + 𝑛𝑌 2 )] −𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)}𝐸𝜃[(𝑌 − 𝜇)𝑌 ] +𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇2 2(𝜎2₎2_{(1 + 𝜌)}𝐸𝜃(𝑌 − 𝜇) − 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1) 2𝜎2 𝐸𝜃(𝑌 − 𝜇) = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)}𝐸𝜃[(𝑌 − 𝜇)(𝑆𝑆𝐵 + 𝑛𝑌 2 )] −𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)}𝐸𝜃[(𝑌 − 𝜇)𝑌 ] = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)}𝐸𝜃[(𝑌 − 𝜇)𝑛𝑌 2 ] −𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)} 𝐸𝜃[(𝑌 − 𝜇)𝑌 ] = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑞(𝑞 − 1) 2(𝜎2₎2_{(1 + 𝜌)} 2𝜇𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 − 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 (𝜎2₎2_{(1 + 𝜌)} 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 = 0

36 Capitolo 2. Verosimiglianza a coppie ed efficienza 𝐽𝜇𝜌 = 𝐸𝜃 ( ∂𝑃 𝑙 ∂𝜇 ∂𝑃 𝑙 ∂𝜌 ) = −𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝜌2_{+ 2𝜌(𝑞 − 1) + 1} 2𝜎2_{(1 − 𝜌}2₎2 𝐸𝜃(𝑌 − 𝜇)𝐸𝜃(𝑆𝑆𝑊 ) + 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}2𝐸𝜃[(𝑌 − 𝜇)(𝑆𝑆𝐵 + 𝑛𝑌 2 )] −𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}2 𝐸𝜃[(𝑌 − 𝜇)𝑌 ] + 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇2 2𝜎2_{(1 + 𝜌)}2𝐸𝜃(𝑌 − 𝜇) +𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜌 2(1 − 𝜌2₎ 𝐸𝜃(𝑌 − 𝜇) = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}2𝐸𝜃[(𝑌 − 𝜇)(𝑆𝑆𝐵 + 𝑛𝑌 2 )] − 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}2𝐸𝜃[(𝑌 − 𝜇)𝑌 ] = 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑞(𝑞 − 1) 2𝜎2_{(1 + 𝜌)}2 2𝜇𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑞 − 𝑛𝑞(𝑞 − 1) 𝜎2_{(1 + 𝜌)} 𝑛𝑞(𝑞 − 1)𝜇 𝜎2_{(1 + 𝜌)}2 𝜎2_{{1 + 𝜌(𝑞 − 1)}} 𝑛𝑞 = 0 𝐽𝜎2_𝜌 = 𝐸_𝜃 ( ∂𝑃 𝑙 ∂𝜎2 ∂𝑃 𝑙 ∂𝜌 ) = 𝑛𝑞(𝑞 − 1)𝜌 2(𝜌 − 1)(𝜌 + 1)3_𝜎2 [𝑞 2_𝜌2_{− 3𝑞𝜌}2_{+ 3𝜌}2_{− 𝑞}2_{𝜌 + 5𝑞𝜌 − 4𝜌 + 1] .}

2.3.3

Efficienza

Mardia, Hughes e Charles (2007) mostrano che per questo esempio, le stime ottenute con la verosimiglianza a coppie sono uguali a quelle ot-tenute con la verosimiglianza completa, ossia, ˆ𝜃𝑃 = ˆ𝜃.

Quest’esempio, `e un caso particolare in cui non si ha perdita di efficien-za utilizefficien-zando la verosimiglianefficien-za a coppie. In aggiunta, si pu `o verificare analiticamente che l’informazione di Fisher e quella di Godambe coinci-dono, ossia, 𝑖(𝜃) = 𝐺(𝜃).