Capitolo 2 Metodi di ricostruzione

Capitolo 2

Metodi di ricostruzione

La luce nel vicino infrarosso viene sempre più applicata nella spettroscopia dei tessuti e nell’imaging ottico per la diagnostica. Il problema principale in queste tecniche è che la luce viaggia considerevolmente più lontano attraverso il tessuto biologico rispetto alla distanza fisica tra i suoi punti di input e di output a causa dello scattering multipli. Ciò crea difficoltà nel quantificare le misure tomografiche ottiche e fornisce una risoluzione ed un contrasto poveri delle immagini ricostruite.

Al fine di un’accurata quantificazione dei dati di tomografia ottica, è importante comprendere la natura del trasporto della luce attraverso un mezzo non omogeneo e conoscere la traiettoria effettiva all’interno delle varie parti che compongono un mezzo non omogeneo.

L’abilità di misurare direttamente la lunghezza ottica del percorso dal tempo di volo di brevi pulsazioni luminose attraverso il tessuto è stato un grande vantaggio ed ha aiutato a superare la gran parte dei problemi. Anche un’accurata modellizzazione per predire la propagazione della luce nel tessuto è importante sia per la quantificazione dei dati di tomografia ottica che per la ricostruzione delle distribuzioni delle proprietà ottiche perché i metodi inversi basati sulla descrizione deterministica della propagazione della luce sono essenziali per predire le proprietà ottiche del tessuto a partire dalle misure del tempo di volo.

Sono stati sviluppati diversi modelli per calcolare la propagazione della luce nei tessuti, e vengono classificati in metodi stocastici o deterministici. La modellizzazione Monte Carlo è un metodo stocastico che può essere applicato ad un mezzo non omogeneo che possegga una geometria complessa arbitraria ed ha il vantaggio di essere in grado di calcolare la lunghezza della traiettoria dei singoli fotoni in maniera diretta , ma richiede un

considerevole tempo di calcolo. Gli approcci basati sulle soluzioni dell’equazione di diffusione sono il metodo deterministico più popolare.

2.1 Modellizzazione del trasporto di fotoni nei tessuti

La propagazione della luce attraverso i tessuti è governata principalmente da interazioni di assorbimento e scattering, dove l’ultimo risulta essere il meccanismo dominante.

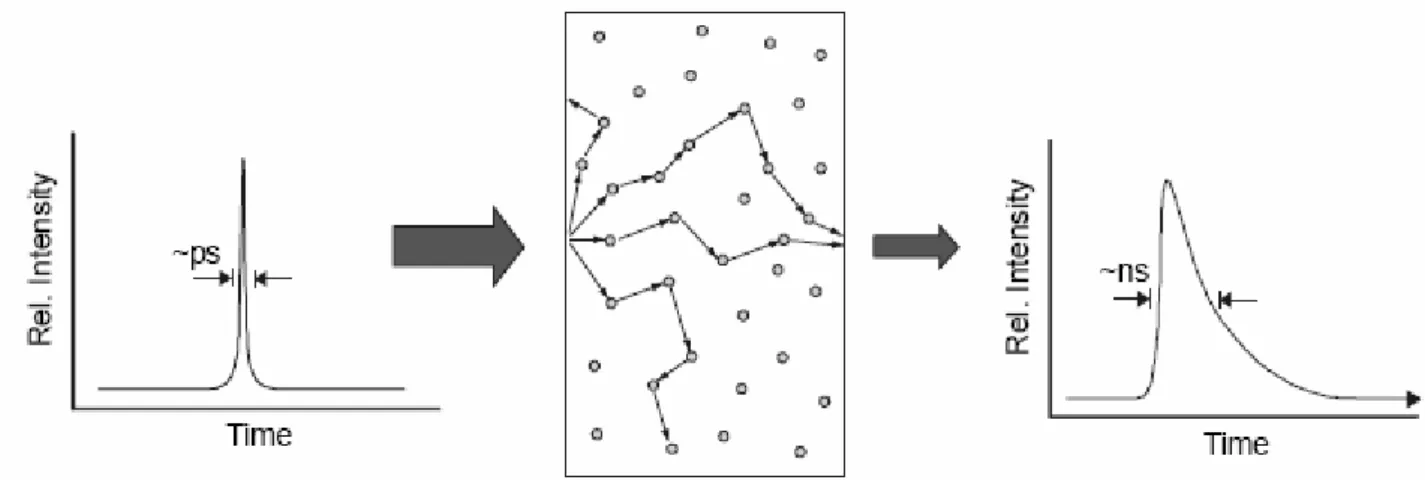
Fig. 2.1 Il diagramma illustra la propagazione diffusa della luce attraverso una sottile sezione di tessuto. Uno stretto

fascio di luce pulsata è iniettato e diventa dispersivo sia in termini temporali che spaziali attraverso eventi di scattering multiplo. Gli impulsi in uscita fortemente attenuati si allargono a causa della variazione nei tempi di volo del fotone.

Come conseguenza, un impulso molto breve di luce collimata in un mezzo altamente scatterante (come un tessuto) diventerà effettivamente diffuso e disperso nel tempo dopo pochi mm.

Questa sezione introduce i modelli matematici che sono stati usati per descrivere la propagazione della luce attraverso il tessuto. Questi modelli sono richiesti per risolvere il problema inverso nella tomografia ottica.

Il problema della ricostruzione dell’immagine in tomografia ottica è quello di stimare le proprietà ottiche all’interno dell’oggetto, una volta noti la quantità di luce fornita e i dati misurati sui bordi dell’oggetto in esame. Il problema della ricostruzione delle immagini in tomografia ottica è un problema inverso non lineare e mal posto. Non ci sono metodi diretti per la soluzione dei questo problema, e per questo motivo viene tipicamente formulato come un problema di minimizzazione. La soluzione

iterativa di questo problema richiede soluzioni ripetitive del problema diretto. Perciò, è essenziale avere un modello diretto di facile implementazione che descriva

la propagazione della luce nel mezzo in maniera accurata

2.1.1 Problema diretto

Il problema diretto in tomografia ottica è quello di risolvere i dati misurati allorché le proprietà ottiche del mezzo e le sorgenti di luce in ingresso siano noti. La propagazione della luce nei materiali biologici viene solitamente descritta attraverso la teoria del trasporto.

Nella teoria del trasporto, i modelli diretti che vengono più frequentemente applicati per descrivere la propagazione della luce nei tessuti sono l’equazione del trasporto radiativi e di diffusione.

L’equazione di trasferimento radiativo: la propagazione della luce nei tessuti può, per

principio, essere descritta usando la teoria elettromagnetica fondamentale. In questo caso il tessuto può essere considerato un mezzo casuale con una permeabilità spaziale variabile

( )r

ε , e le variazioni del campo elettrico saranno descritte usando le equazioni di Maxwell. Ma tale trattamento ad oggi non è possibile a causa della complessità del problema e di una non conoscenza precisa di ( )ε r . Il problema può essere semplificato ignorando i fenomeni ondulatori come la polarizzazione e l’interferenza, e le proprietà delle particelle come le collisioni anelastiche. Questa è un’ottima approssimazione per tessuti biologici di grande spessore (> alcuni mm).

L’assunzione di base nella teoria di trasferimento radioattivo è che viene considerato solo il flusso di energia attraverso il mezzo. L’equazione di Trasferimento Radiativo(RTE),

1

( , , )

s s

( , , ) (

s a s

) ( , ,

s

)

I r t e

e

I r t e

I r t e

c

t

µ µ

∂

_{+ ⋅∇}

₊

₊

∂

' ' 2 ' 4

( , ) ( , , )

( , , )

s

f e e I r t e d e

s s s s

q r t e

s π

µ

=

_∫

+

_(2.1)

è un’equazione integro-differenziale e descrive la variazione di energia radiante ( , ,I r t e _s)

alla posizione r nella direzione e . _s

Gli altri parametri sono:

c velocità della luce nel mezzo

s

µ

coefficiente di scattering '

( ,_{s s})

f e e funzione di fase di scattering

( , , )_s

q r t e sorgente radiante.

L’energia radiante ( , ,I r t e è l’energia trasferita per unità di tempo per unità di angolo s)

solido d e attraverso l’unità di area alla posizione r ed al tempo t. Integrando ( , ,2 s I r t e su s)

tutti gli angoli, si ottiene il flusso Γ attraverso un’unità di area data da e : _n

2 4

( , )

( , ,

)

n s s n s

r t

I r t e e e d e

π

Γ

=

_∫

⋅

_(2.2)

La RTE può essere derivata considerando il bilancio di energia radiante in un arbitrario volume elementare di tessuto. E’ un’equazione di bilancio che mette in relazione la variazione dell’energia radiante ( , ,I r t e nel tempo (primo termine) con la variazione del _s) flusso di energia (secondo termine), la perdita dovuta all’assorbimento e allo scattering (terzo termine), il guadagno dovuto alle sorgenti di scattering (quarto termine) e il guadagno dovuto alle sorgenti di radiazione (quinto termine). Benché la natura ondulatoria della luce venga ignorata nella sua derivazione, la polarizzazione può essere inclusa usando i parametri di Stokes, e derivando quattro invece che una sola equazione di trasferimento radioattivo. Mentre le soluzioni esatte per la RTE esistono per casi semplici come lo scattering isotropico in geometrie semplici [Patterson 1991], non c’è una soluzione generale. Perciò c’è bisogno di fare approssimazioni o calcolare soluzione numeriche. La maggior parte degli approcci correntemente utilizzati per la tomografia ottica usano l’approssimazione di diffusione (DA) alla RTE come modello diretto.

2.1.2 Approssimazione per la diffusione dell’Equazione di Trasporto

Radiativo

Espandendo la RTE in armoniche sferiche, si può derivare una gerarchia di equazioni [ Kaltenbach 1993], delle quali la più semplice, chiamata approssimazione P1 , è la

equazione di diffusione tempo-dipendente:

0

1

( , )

( )

( , )

_a

( ) ( , )

( , )

r t

D r

r t

r

r t

q r t

c

t

µ

∂Φ

_{− ∇ ⋅}

_∇Φ

₊

_Φ

₌

∂

(2.3)

dove Φè la densità fotonica 2

4

( , )r t I r t e d e( , , )_{s s} π

Φ =

_∫

(2.4)

e κè il coefficiente di diffusione definito come ' 1 ( ) 3 a( ) s( ) D r r r µ µ =  ₊    (2.5) 0

q rappresenta una sorgente isotropica.

Il flusso Γ lungo la normale e del confine nel punto ξ si dimostra essere _n

( , )

t

( )

( , )

t

n

ξ

κ ξ

∂

ξ

Γ

= −

Φ

∂

(2.6)

2.1.3 Condizioni al contorno

Le condizioni al contorno per la RTE specificano che nessun fotone si muove in una direzione all’interno del bordo ∂Ω (eccezion fatta per le posizioni della sorgente ε_k), come, per esempio,

φ

( , , )

r t s

ˆ

=

0,

r

∈ ∂Ω

,

s n

ˆ ˆ

⋅ <

0,

(2.7)

dove ˆn è l’unità diretta verso l’esterno normale a ∂Ω [Case 1967, Ishimaru 1978, Arridge 1999]. L’approssimazione di diffusione non riesce a soddisfare la condizione (2.7) esattamente [Arridge 1999]; per tale motivo, la condizione (2.7) è spesso sostituita da un’approssimazione per cui la corrente totale diretta verso l’interno risulta zero [Case 1967, Ishimaru 1978, Arridge 1999, Groenhuis 1983, Keijzer 1988] :

ˆ ˆ 0

ˆ

( , , )

ˆ

ˆ

0,

s n⋅ <

s r t s ds

φ

=

Se gli indici di rifrazione di Ω e del mezzo circostante sono diversi, una frazione dell’energia radiante incidente sul bordo ∂Ω dall’interno, Ω, verrà riflessa indietro in Ω [Groenhuis 1983, Keijzer 1988]. Per tenere di conto di questa disuguaglianza tra gli indici di rifrazione, la condizione al contorno (2.8) viene solitamente modificata nella forma

_{ˆ ˆ ˆ ˆ}

0

ˆ

( , , )

ˆ

ˆ

0

ˆ

( , , )

ˆ

ˆ

,

s n⋅ <

s r t s ds

φ

=

s n⋅ >

sR r t s ds

φ

∫

∫

r

∈ ∂Ω

,

(2.9)

dove R è un parametro che governa la rifrazione interna a ∂Ω [Groenhuis 1983, Keijzer 1988 , Arridge 1999]. All’interno della struttura dell’approssimazione di diffusione, l’equazione (2.9) può essere riscritta, dopo alcune manipolazioni algebriche, come:

( , )

( , ) 2

0,

ˆ

r t

r t

n

κϑ

∂Φ

Φ

+

=

∂

r

∈ ∂Ω

,

(2.10)

dove

ϑ

= +(1 R) (1−R) e il parametro R può essere approssimato dalla curva sperimentale [Groenhuis 1983, Keijzer 1988]

R

≈ −

1.4399

n

_in−2

+

0.7099

n

_in−1

+

0.6681 0.0636

+

n

_in.

In letteratura, la condizione (2.10) è conosciuta come condizione al contorno di tipo

Robyn. Si noti che esistono diverse espressioni per il coefficiente ϑ [Groenhuis 1983, Keijzer 1988, Contini 1997] ed il suo valore è stato il soggetto di accese discussioni.

2.1.4 Modelli di sorgente

La sorgente luminosa, negli esperimenti di tomografia ottica, è un fascio laser diretto verso l’interno che è perpendicolare a ∂Ω in ε_k ⊂ ∂Ω. Esistono due approssimazioni che vengono comunemente usate, il modello della sorgente collimata (CS) e il modello della sorgente diffusa sui contorni (DS); questi due modelli vengono usati frequentemente nell’approssimazione di diffusione per modellare i fasci laser anisotropici, vedi, ad esempio, [Schweiger 1995, Contini 1997, Hielscher 1995, Arridge 1999]. Nel modello CS la sorgente è modellata come una sorgente puntiforme isotropica

dove la posizione r è posizionata alla profondità di scattering _s 1 µ_s' sotto il sito della sorgente. Questa posizione risulta come la profondità media di sopravvivenza di una sorgente lineare che decade esponenzialmente, dove i fotoni che viaggiano nella direzione

ˆ

n

− percorrono una distanza x con una probabilità di sopravvivenza di

' exp(−µ_sx)

∼ [Haskell 1994, Hielscher 1995, Arridge 1999] . Nel modello DS, la sorgente

è modellata come una corrente Γs,diffusa ai bordi, diretta verso l’interno, che agisce sul

sito della sorgente ε_k ⊂ ∂Ω. In questo caso, la sorgente diventa parte della condizione al contorno (2.10). Come dato in [Schweiger 1995, Jenni Heino 1999] , la condizione al contorno di tipo Robin con il modello di sorgente diffusa può essere scritta come

,

4

( , )

( , )

2

ˆ

0,

\

s k k k k k

r

U

r t

r t

n

r

U

ω

ε

κϑ

ε

− Γ

∈



∂Φ

Φ

+

=



∂



∈ ∂Ω

(2.12)

dove il segno meno è dovuto al fatto che la corrente di sorgente è diretta verso l’interno e la funzione indicatrice ω_k per il sito della sorgente ε_k è o1 oppure 0 a seconda che la sorgente sia accesa o meno.

2.1.5 Validità dell’approssimazione di diffusione

La condizione di base per la validità della DA è che la distribuzione angolare della radianza sia circa uniforme. Al fine di ottenere ciò, nel mezzo lo scattering deve essere il fenomeno dominante, cioè deve valere µ_{a ≪}µ_s. La maggior parte dei tipi di tessuto sono altamente scatteranti e l’approssimazione di diffusione può essere considerata una buona approssimazione per la modellizzazione della propagazione della luce al loro interno. La DA è stata ricavata per descrivere la propagazione della luce con una buona accuratezza in situazioni nelle quali le sue assunzioni siano valide [Farrell 1992, Groenhuis 1983, Kim 1998, Okada 1996], ed è stata applicata con successo in molte applicazioni di tomografia ottica, come [Bluestone 2001, Boas 2004, Hebden 2003, Hillman 2001].

Comunque, la condizione per cui la distribuzione angolare della radianza debba essere circa uniforme viene violata nei pressi delle sorgenti altamente collimate che sono usate in tomografia ottica. In più, la condizione può non essere soddisfatta in tessuti fortemente

assorbenti o poco scatteranti come il fluido cerebrospinale che circonda il cervello e riempie i ventricoli cerebrali. In aggiunta alle condizioni riportate sopra, L’approssimazione di diffusione può non essere adattata alle condizioni al contorno realistiche o alle discontinuità presenti al livello delle interfacce. E’ stato provato che la teoria della diffusione fallisce in situazioni in cui le sue approssimazioni non sono valide, come vicino alle sorgenti [Alexandrakis 1998, Fantini 1997, Groenhuis 1983, Schweiger 1995] e all’interno di regioni poco scatteranti [Firbank 1996, Hielscher 1998, Okada 1997]. E’ stato inoltre dimostrato che queste limitazioni all’interno della teoria della diffusione possono portare a grandi errori nelle immagini ricostruite [Dehghani 2000]. Sono perciò stati studiati metodi per migliorare l’accuratezza della teoria della diffusione nei casi di regioni con basso scattering o in assenza di scattering [Bluestone 2004, Hayashi 2003, Okada 2003, Ripoll 2001] e per correggere la modellizzazione di contorni, interfacce e sorgenti [Alexandrakis 2000, Fantini 1997, Gaudette 2000, Spott 2000, Wang 1993].

Nella seguente sezione sono riassunti pochi approcci ibridi che sono stati sviluppati per superare le limitazioni della teoria della diffusione.

2.1.6 Modello radiativo ibrido di trasferimento-diffusione

Per superare le limitazioni della teoria della diffusione in corrispondenza delle sorgenti di luce, sono stati sviluppati alcuni metodi ibridi. Nel metodo ibrido Monte Carlo-diffusione, la simulazione Monte Carlo è combinata con la teoria della diffusione. Il metodo fu introdotto in [Wang 1993] per descrivere la riflettanza della luce in un mezzo torbido semi-infinito e, in seguito, venne esteso anche a sezioni torbide in [Wang 1998]. Dopodichè, il modello ibrido Monte Carlo-diffusione fu sviluppato per un mezzo torbido costituito da due strati nel dominio del tempo [Alexandrakis 2001, Alexandrakis 2000]. Nell’approccio ibrido Monte Carlo-diffusione, il metodo Monte Carlo è utilizzato per simulare la propagazione della luce in prossimità della sorgente luminosa e l’approssimazione di diffusione è risolta analiticamente altrove nel dominio. Il metodo Monte Carlo è noto per descrivere la propagazione della luce in maniera accurata. Nonostante ciò, ha lo svantaggio di richiedere un tempo di calcolo molto lungo. Questo aspetto ha effetti anche sui tempi di calcolo degli approcci ibridi Monte Carlo. Come ulteriore approccio, è stata usata l’equazione di Fokker-Planck per descrivere la

propagazione della luce in prossimità delle sorgenti luminose [Kim 2003]. L’equazione di Fokker-Planck è stata calcolata per descrivere la propagazione della luce in maniera accurata quando lo scattering raggiunge il suo massimo nella direzione diretta. Per tale motivo può essere utilizzata per piccole profondità al di sotto di sorgenti luminose fortemente collimate. Nonostante questa sua prerogativa, l’equazione di Fokker-Planck non descrive la propagazione della luce in maniera accurata a profondità maggiori nei tessuti biologici e nemmeno all’interno di mezzi non scatteranti o con basso scattering. [Tarvainen 2006] propone un modello ibrido radiativo di trasferimento-diffusione per descrivere la propagazione della luce in mezzi altamente scatteranti. Nel modello ibrido radiativo di trasferimento-diffusione, la propagazione della luce è modellata con la RTE in prossimità delle sorgenti luminose e la DA è utilizzata altrove nel dominio. La soluzione della RTE è usata per costruire una condizione al contorno di Dirichlet per la DA su un’interfaccia fittizia all’interno dell’oggetto. Questa condizione al contorno costituisce un modello di sorgente distribuita per la DA nella rimanente area.

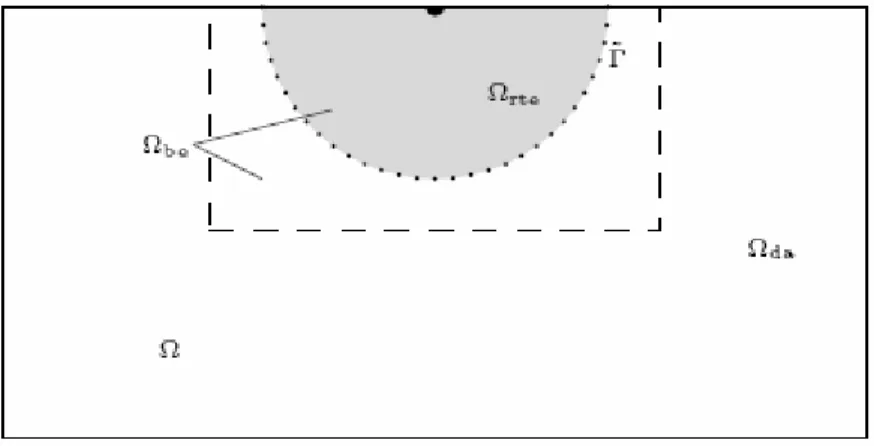
Fig. 2.2 Il dominioΩ con una sorgente al centro della parte superiore. La RTE è risolta nel sub-dominio Ω_be e la soluzione della RTE è usata per costruire una condizione al contorno di Dirichlet per la DA sull’interfaccia fittizia

Γɶ(linea punteggiata). La RTE è usata come modello diretto nel sub-dominio Ω_rte(in grigio) e la DA è usata come modello diretto nel sub-dominio Ω_da(in bianco)[tratta da Tarvenin 2006].

Sia Ω ⊂ n

ℝ , n=2o3 il dominio di calcolo, come mostrato in figura 2.2 per il caso n=2. La sorgente è posizionata al centro della parte superiore. Il modello ibrido proposto consiste di due parti: risolvere il modello di sorgente basato sulla RTE per la DA e risolvere la DA. La soluzione diretta si ottiene nel seguente modo: per prima cosa, la RTE

viene risolta nel sub-dominio Ω_be in prossimità della sorgente; dopodichè la soluzione della RTE è usata per costruire una condizione al contorno di Dirichlet per la DA sull’interfaccia fittizia Γɶ tra i sub-domini della RTE e della DA, Ω_rte e Ω_da. L’interfaccia Γɶ separa il dominio Ω in due sotto-gruppi Ω_rte, in cui la RTE è usata come modello diretto, e Ω_da, in cui la DA è usata come modello diretto. La posizione dell’interfaccia Γɶ dovrebbe essere scelta abbastanza distante dalla sorgente in modo che la distribuzione angolare della radianza φ( , )r sˆ sia ben approssimata con un’approssimazione del primo ordine.

Il modello ibrido utilizza la RTE in prossimità delle sorgenti, e perciò corregge l’inaccuratezza della teoria della diffusione vicino alle sorgenti. La DA è usata come modello diretto altrove nel dominio, dove le sue approssimazioni sono valide. In questo modo ci si aspetta che il modello ibrido descriva la propagazione della luce in maniera accurata nei mezzi altamente scatteranti sia vicino che lontano dalla sorgente. Un esempio di mezzo altamente scatterante è il tessuto cerebrale. Nonostante ciò, il modello ibrido non può essere utilizzato nelle situazioni in cui il mezzo altamente scatterante contiene regioni non scatteranti o con basso scattering.

2.1.7 Approssimazione di accoppiamento tra l’equazione del

trasferimento radiativi e la diffusione

Per superare le limitazioni della teoria della diffusione all’interno di regioni non scatteranti o con basso scattering, sono stati sviluppati diversi approcci ibridi e modelli approssimativi. Metodi che combinano la simulazione Monte Carlo con la teoria della diffusione sono stati applicati per mezzi torbidi con regioni a basso scattering. L’approssimazione agli elementi finiti della DA e la simulazione Monte Carlo sono stati combinati in [Hayashi 2003] per descrivere la propagazione della luce in un mezzo scatterante con uno strato a basso scattering. Anche in questo caso, l’approccio soffre a causa dell’alto costo computazionale in termini di tempo proprio dei metodi Monte Carlo. Per di più, i metodi ibridi Monte Carlo-diffusione spesso richiedono un mappaggio iterativo tra i modelli, passaggio che aumenta ulteriormente i tempi di calcoli. Il modello radiosità-diffusione [Arridge 2000, Firbank 1996, Ripoll 2000] può essere applicato per mezzi altamente scatteranti con regioni non scatteranti. Il metodo utilizza la DA per

modellare la propagazione della luce all’interno di regioni altamente scatteranti ed il modello di radiosità per modellare la propagazione della luce all’interno di regioni non scatteranti. L’analisi matematica del problema viene fornita in [Hyvönen 2002]. L’approccio radiosità-diffusione è stato testato con ricostruzioni ed è stato provato che migliora la qualità delle immagini ricostruite significativamente rispetto al modello tradizionale di diffusione [Dehghani 2000, Dehghani 2002, Riley 2000]. Un modello che propone l’accoppiamento di trasporto e diffusione è stato introdotto in [Bal 2002]. Nel modello, i modelli di trasporto e di diffusione sono accoppiati e viene applicato un mappaggio iterativo tra i modelli per ottenere la soluzione diretta. In più, è stato sviluppato un modello generalizzato di diffusione per la migrazione dei fotoni all’interno di mezzi altamente scatteranti con strati sottili non scatteranti e grandi inclusioni non diffusive [Bal 2002, Bal 2003]. E’ stato inoltre discusso l’accoppiamento tra le equazioni di trasporto e la teoria di diffusione in una sezione infinita [Tidriri 2001], e l’utilizzo dell’equazione di Fokker-Planck in una semplice geometria di un mezzo scatterante che contiene un piatto assorbente [Kim 2004]. Quest’ultimo metodo utilizza l’approssimazione di Kirchhoff per modellare il trasporto della luce in un piatto assorbente.

Come ultimo metodo, consideriamo quello proposto in [Tarvainen 2006] che accoppia l’equazione del trasferimento radiativi e l’approssimazione di diffusione per risolvere il problema diretto. In questo approccio, la RTE viene utilizzata come modello diretto nei sub-domini in cui le assunzioni della DA non risultano valide e la DA viene utilizzata altrove nel dominio. Nel modello, la RTE e la DA sono accoppiate per mezzo di condizioni al contorno tra i sub-domini della RTE e della DA. Messo a confronto con il precedente modello ibrido, il modello che accoppia RTE e DA non trascura il backscattering tra i sub-domini RTE e DA. In più, mentre il modello ibrido precedentemente proposto è stato sviluppato per eliminare l’inaccuratezza della teoria della diffusione in prossimità della sorgente, il modello di accoppiamento RTE-DA può essere utilizzato anche in altre situazioni in cui le assunzioni della DA non siano valide, per esempio vicino ai contorni del dominio e all’interno di regioni non scatteranti o con basso scattering.

Sia Ω ⊂_{ℝ ,} n n=2o3 il dominio di calcolo, come mostrato in figura 2.3 per il caso n=2. Nel modello di accoppiamento RTE-DA, il dominio Ω è separato in due sottosezioni disgiunte Ω_rtee Ω_da. La RTE è utilizzata come modello diretto nel sub-dominioΩ_rte, in

cui le assunzioni della DA non sono valide. La DA è utilizzata come modello diretto nel sub-dominio Ω_da, che include il restante dominio.

Fig. 2.3 Il dominio Ω ed il contorno∂Ω(linea solida). La RTE è usata come modello diretto nel sotto-dominioΩ_rte(in grigio) che ha il contorno ∂Ω_rte.La DA è usata come modello diretto nel sotto-dominio Ω_da(in bianco) che il contorno ∂Ω_da. I sotto-domini Ω_rtee Ω_dasono separati dall’interfacciaΓ ed hanno i contorni esterni

,

rte out

∂Ω e ∂Ω_{da out,} rispettivamente[ tratta da Tarvenin 2006 ].

Sia Ω_rte il confine del sub-dominio Ω_rte, e ∂Ω_da sia il confine del sub-dominio Ω_da; inoltre sia Γ l’interfaccia che separa i sub-domini Ω_rteeΩ_da. La RTE e la DA sono accoppiate attraverso condizioni al contorno sull’interfaccia Γ, che è indicata in figura 2.3 con la linea tratteggiata. Si noti che l’interfaccia Γ dovrebbe essere posizionata all’interno della regione in cui le assunzioni della DA sono valide.

Nel modello di accoppiamento RTE-DA, la RTE e la DA sono accoppiate per mezzo delle loro condizioni al contorno e le equazioni sono risolte simultaneamente. In questo modo, non è richiesto un mappaggio iterativo tra i due modelli. Il modello di accoppiamento RTE-DA è un approccio più generale per la propagazione della luce rispetto agli approcci ibridi che sono disegnati per superare le difficoltà della teoria della diffusione in prossimità della sorgente o per mezzi con regioni non scatteranti. Inoltre tale modello è in grado di descrivere il trasporto della luce accuratamente sia vicino che lontano dalla sorgente così come vicino al dominio del confine.

2.1.8 Problema inverso

Nel problema inverso della tomografia ottica, vengono ricostruite le funzioni di assorbimento e scattering, o in alcuni studi le funzioni di assorbimento e diffusione, all’interno dell’oggetto in esame. Se vengono utilizzate più di una lunghezza d’onda, la concentrazione di emoglobina, la saturazione di ossigeno, e le distribuzioni di acqua possono essere calcolate dallo spettro di assorbimento ed alcune caratteristiche di scattering dallo spettro di scattering [Durduran 2002, Srinivasan 2003]. Recentemente, ci sono stati studi in cui la ossi-emoglobina, la deossi-emoglobina, l’acqua, l’ampiezza di scattering e la potenza di scattering sono state stimate direttamente dalle misure effettuate a molte lunghezze d’onda [Corlu 2005, Li 2004, Srinivasan 2005 ]. In questo studio verrà discussa la ricostruzione dei coefficienti di scattering ridotto e di assorbimento (µ µ_a, _s').

I metodi di ricostruzione delle immagini in tomografia ottica possono essere divisi in due classi, che sono i metodi alle differenze ed i metodi basati sull’approccio non lineare regolarizzato ai minimi quadrati.

Metodi alle differenze

I metodi alle differenze sono basati sull’assunzione che i coefficienti di scattering e di assorbimento (µ µ_a, _s)non differiscono molto dai valori di riferimento (µ_{a ref,} ,µ_{s ref,} ). L’obiettivo è ricostruire una piccola perturbazione

, , a ref a a s s s ref

µ

δµ

µ

δµ

µ

µ







 



=

−







 

_{ }

_



 

 



Basata su un modello lineare

a s

δµ

δ

δµ





Ζ = Κ









(2.13)

dove δΖ = Ζ − Ζ_ref è la differenza tra i dati che vengono misurati con le proprietà ottiche (µ µ_a, _s), e con le proprietà ottiche di riferimento (µ_{a ref,} ,µ_{s ref,} ), rispettivamente. La matrice Κpuò essere ricostruita, per esempio, assumendo uno spazio infinito o una geometria infinita in cui può essere scritta un’espressione analitica [Gaudette 2000] o utilizzando una simulazione Monte Carlo [Chang 1996].

L’approccio più tipico per costruire la matrice K è attraverso metodi numerici in cui K è la matrice Jacobiana per il modello diretto [Arridge 1999].

In tomografia ottica, sono stati applicati metodi diversi negli studi funzionali sul cervello [Bluestone 2001, Culver 2003, Gibson 2006, Hebden 2004, Siegel 2003] dove viene monitorata la differenza prima e durante l’attivazione. E’ noto che l’imaging differenziale produce immagini con pochi artefatti; nonostante ciò, non può essere usata quando non è possibile acquisire una misura di riferimento.

Approccio non lineare ai minimi quadrati

La maggior parte degli approcci al problema inverso in tomografia ottica sono basati sul metodo ai minimi quadrati. In tale metodologia, viene utilizzata una singola acquisizione per stimare i valori assoluti per le proprietà ottiche del mezzo. Il problema regolarizzato non-lineare ai minimi quadrati è quello di stimare le distribuzioni di assorbimento e scattering (µ µ_a, _s)che minimizzano la funzione

Ψ =

L

(

Ζ −

F

(

µ µ

a

,

s

)

2₂

+

B

(

µ µ

a

,

s

)

(2.14)

quando sono forniti i dati misurati Z. Nell’equazione (2.14), F è il modello diretto per il trasporto della luce che mappa i parametri di assorbimento e scattering sui dati misurati. Per di più, il termine B(µ µ_a, _s)>0 è la funzione che rappresenta la penalità e la matrice L è la matrice dei pesi che corrisponde al fattore Cholesky dell’inverso della matrice di covarianza del rumore. La funzione che rappresenta la penalità è solitamente definita come

(

,

)

(

)

(

)

a s

a s a s

B

µ µ

=

α

_µ

Α

µ

+

α

_µ

Α

µ

(2.15) dove Α(µ_a) e Α(µ_s) sono le funzioni di penalità per il coefficiente di assorbimento e

per il coefficiente di scattering, rispettivamente, e

a µ

α e

s µ

α sono i parametri per

l’assorbimento e lo scattering. Benché sia possibile usare diverse funzioni di regolarizzazione della penalità per l’assorbimento e lo scattering, la scelta più usuale è l’uso della stessa funzione penalità per entrambi [Kolehmainen 2001]. Il problema della minimizzazione (2.14) viene di solito risolto utilizzando i metodi del

Nel metodo Gauss-Newton, il problema della minimizzazione può essere risolto iterativamente come

(

)

(

)

1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 1) ( )

1

1

,

2

2

a a T i T i i i i i i B i a s B s i s i

c

J WJ

H

J W Z

F

g

µ

µ

µ µ

µ

µ

− +











 



=

+

+

−

−











 





 











(2.16) dove i è l’indice di iterazione,

µ

_a =(

µ

_a,1,...,

µ

_{a M,} )T∈_ℝM e

,1 ,

( ,..., )T M

s s s M

µ

=

µ

µ

∈ℝ sono i vettori dei parametri discretizzati di

assorbimento e scattering, W =L LT , c è il parametro che indica la lunghezza del _{( )i}

passo, J è il Jacobiano per _{( )i} F

(

µ µ_a( )i , _s( )i

)

, e g e ( )_Bi H_B( )i sono il gradiente e l’Hessiano della funzione penalità (2. 15) [Kolehmainen 2001].

Al fine di garantire la veloce convergenza nella ricostruzione dell’immagine, i valori iniziali di assorbimento e scattering devono essere ragionevolmente vicini alle proprietà ottiche attuali. Le proprietà ottiche iniziali vengono solitamente scelte costanti se l’informazione a priori sulla struttura interna del dominio non è disponibile.

2.2 Metodi numerici per il trasporto della luce

Le soluzioni analitiche della RTE e della DA sono spesso limitate a determinate geometrie specifiche, e perciò la loro esportabilità in tomografia ottica è limitata. Perciò, in tomografia ottica, la RTE e la DA sono solitamente risolte con metodi numerici. I metodi numerici che più spesso vengono applicati sono il metodo alle differenze finite ed il metodo agli elementi finiti (FEM). Quest’ultimo è generalmente considerato il più flessibile quando vengono considerati i problemi dell’implementazione di diverse condizioni al contorno e del trattamento di geometrie complesse, e perciò viene scelto più spesso come metodo per risolvere le equazioni che governano il trasporto della luce nei tessuti. Il FEM è quindi usato per risolvere la RTE, la DA e anche gli approcci ibridi proposti.

2.2.1 Soluzioni analitiche

Le soluzioni analitiche dell’equazione di diffusione tempo-dipendente esistono per semplici geometrie [Patterson 1989, Arride 1992, Contini 1997]. Il caso più semplice è quello di una pulsazione infinitamente breve in un mezzo infinitamente omogeneo, così che la sorgente sia q r t( , )' ' =

δ

( , )r t' ' .

La soluzione per la densità fotonica Φ alla posizione r al tempo t, è la funzione di Green:

' 2 ') 3 ' ' ₂

1

(

)

( , )

exp

(

4

(

)

(4

(

))

a

r

r

r t

c t

t

c

t

t

c

t

t

µ

κ

π κ



₋



Φ

=



−

−

−



−





−

(2.17)

E’ inoltre possibile derivare una soluzione analitica per il caso di una fetta semi-infinita, che si estende oltre z≥0. Una sorgente puntiforme isotropica effettiva, che può essere pensata simulando un fascio laser strettamente collimato incidente a z₀ =0, è posizionata ad una profondità ₀ 1_'

s z

µ

Insieme con la condizione al contorno Φ =(z 0, )t , si dimostra che 2 ' 3 ' ' ₂

1

( , )

exp

(

)

4

(

)

(4

(

))

a

r t

c t

t

c

t

t

c

t

t

ρ

µ

κ

π κ





Φ

=



−

− −



⋅

−





−

2 2 0 0 ' '

(

)

(

)

exp

exp

4

(

)

4

(

)

z

z

z

z

c

κ

t

t

c

κ

t

t





_{− −}





_{− +}





−













−

−













(2.18) dove 1 ' 2 ' 2 2

(

x

x

)

(

y

y

)

ρ

₌



_

₋

_{+ −}



_

− _{è la distanza radiale dalla posizione di ingresso.}

La soluzione per una fetta infinita con confini a z=0 e z=d , e condizioni al contorno (z 0, )t (z d t, ) 0 Φ = = Φ = = , è 2 ' 3 ' ' ₂

1

( , )

exp

(

)

4

(

)

(4

(

))

a

r t

c t

t

c

t

t

c

t

t

ρ

µ

κ

π κ





Φ

=



−

− −



⋅

−





−

2 2 0 0 ' '

(

2

)

(

2

)

exp

exp

4

(

)

4

(

)

N N

z

Nd

z

z

Nd

z

c

κ

t

t

c

κ

t

t

=+∞ =−∞





_{− −}

₋





_{− −}

₊





−













−

−













∑

(2.19)

La derivazione di questa espressione coinvolge l’impiego del cosiddetto metodo delle immagini [Patterson 1989]. Per esempio, la TPSF calcolata per una fetta infinita di spessore d=50 mm, e proprietà ottiche µ_s' =1.0mm−1 e µ_a =0.01mm−1 è mostrata in figura 2.6.

2.2.2 Soluzioni numeriche

I metodi più comuni per risolvere numericamente l’equazione di diffusione tempo-dipendente per mezzi non omogenei di forma arbitraria sono i metodi alle differenze finite e agli elementi finiti. Mentre il primo è basato sulla discretizzazione dell’equazione di diffusione, il metodo agli elementi finiti (FEM) consiste nel dividere il mezzo in un gran numero di elementi di volume o di area, ognuno dei quali ha il suo set individuale di proprietà ottiche, µ_ae µ_s'.

Approssimazione agli elementi finiti della RTE

I metodi di soluzione numerica della RTE possono essere divisi in tecniche del primo ordine e del secondo ordine [Ackroyd 1997, Duderstadt 1979 ]. In tomografia ottica, i metodi del primo ordine sono stati usati, per esempio, in [Dorn 1998, Hielscher 1998, Klose 2002] e i metodi del secondo ordine sono stati usati, per esempio, in [Abdoulaev 2003, Aydin 2002, Wright 2005].

In tomografia ottica, un metodo per la risoluzione della RTE in stato stazionario, che usa il metodo alle differenze finite per la discretizzazione spaziale e coordinate discrete per la discretizzazione angolare, è stato proposto in [Klose 1999]. I problemi diretto ed inverso sono stati studiati ulteriormente in [Klose 2002 ] ed è stato sviluppato un algoritmo che usa gli elementi finiti ed i metodi ad ordinate discrete [Abdoulaev 2003].

Un approccio alla forma in stato stazionario della RTE, che usa il metodo ad elementi finiti per la discretizzazione spaziale e l’approssimazione ad armoniche sferiche per la discretizzazione angolare è stato introdotto in [Aydin 2002] e lo stesso approccio è stato studiato per mezzi con diverse proprietà ottiche [Aydin 2004]. Lo stesso metodo all’approssimazione P3 (approssimazione del terzo ordine) è stato studiato in [Jiang 2001]

e in [Wright 2005] è stato introdotto l’approccio adattativo PN (approssimazione all’ordine

n-esimo), in cui l’ordine della base angolare viene variato in accordo con le proprietà ottiche locali del dominio.

In [Iftimia 2000, Xu 2001] viene utilizzato un algoritmo basato sugli elementi finiti per la ricostruzione delle immagini che utilizza un metodo di Newton regolarizzato per inizializzare una distribuzione delle proprietà ottiche iterativamente al fine di minimizzare una funzione oggetto composta dalla somma pesata del quadrato della differenza tra i dati calcolati e quelli misurati.

L’algoritmo di ricostruzione per le immagini è basato sull’equazione di diffusione allo stato stazionario,che può essere scritta come

∇ ⋅

D r

( )

∇Φ

( )

r

−

µ

_a

( ) ( )

r

Φ

r

= −

S r

( )

, (2.20) dove S(r) è il termine di sorgente. Viene considerata una sorgente puntiforme,

0

(

0

)

S

=

S

δ

r

−

r

, nella quale S è la potenza della sorgente e ₀ δ(r−r₀) è la funzione delta di Dirac per una sorgente a r . ₀

Facendo uso di una discretizzazione ad elementi finiti, è possibile ottenere una matrice discreta e realizzare altre relazioni con matrici derivate grazie alla differenziazione, che porta ad un set di equazioni utile per la soluzione del problema inverso

[ ]

A

{ } { }

Φ =

b

, (2.21)

[ ]

{ }

b

A

A

χ

χ

χ



_∂Φ

 

_∂

 

_∂



=

−

Φ



 

_{ }

_

∂

∂

∂



 

 



, (2.22)

(

ℑ ℑ +

T

λ

I

)

∆ = ℑ Φ

χ

T





(m)

− Φ

( )c





(2.23) dove gli elementi della matrice

[ ]

A sono a_ij = − ∇ ⋅∇ −D φ_j φ µ φ φ_{j a j i} . indica l’integrazione sul dominio del problema; φie φj sono funzioni di Lagrange che variano

spazialmente ai nodi i e j, rispettivamente; χ esprime D o µ_a; ℑè la matrice Jacobiana

che dovrebbe essere formata da ∂Φ_∂

_χ

ai siti di misura dei bordi;

1 2 , ,1 ,2 ,

( D, D ,..., D_{N a} , _a ,...., _{a N})

χ µ µ µ

∆ = ∆ ∆ ∆ ∆ ∆ ∆ è il vettore di inizializzazione per i profili

delle proprietà ottiche, dove N è il numero totale dei nodi usati nel metodo ad elementi finiti; Φ = Φ( )m _{ 1}( )m ,Φ( )₂m,...,Φ( )_Mm _{ e} Φ = Φ Φ( )c _ ₁( )c , ( )₂c ,...,Φ( )_Mc _{ , dove} Φ_i( )m e Φ_i( )c , rispettivamente, sono dati calcolati e misurati per le posizioni dei bordi i=1,2,….,M. Nella ricostruzione di immagini ottiche, la finalità è inizializzare le distribuzioni di D e µ_a attraverso la soluzione del sistema di tre equazioni sopra, cosicché una somma pesata delle differenze al quadrato tra i dati calcolati e quelli misurati possa essere minimizzata.

Benché sia solitamente possibile fare una buona stima iniziale di D e µ_a per gli esperimenti di laboratorio, è difficile fare tali stime in situazioni cliniche. Allora si può dimostrare che è possibile usare un semplice schema di minimizzazione ai minimi quadrati per determinare questi parametri in maniera accurata.

Per illustrare questo schema, si dimostra come sia possibile determinare il coefficiente delle condizioni di bordo (BC)

α

; si calcola il valore diX come una funzione di 2

α

, 2 2 ( ) ( ) 1 M m c i i i

X

−





=

∑

_

Φ

− Φ

ɶ

_

_(2.24)

dove M è il numero delle misure di bordo, Φ( )_im è la densità fotonica misurata da un dato mezzo non omogeneo sperimentale, e Φɶ( )_ic è la densità fotonica calcolata da una simulazione numerica di un mezzo omogeneo con la stessa geometria del mezzo sperimentale.

Comunque, il metodo ad elementi finiti (FEM) è un metodo robusto ed efficiente per risolvere l’equazione di diffusione, e può essere applicato a geometrie complesse e mezzi non omogenei. In questo caso la soluzione dell’equazione di diffusione richiede la specificazione di appropriate condizioni di bordo, come la condizione di Dirichlet (DBC), per cui

Φ

( )

ξ

=

0

∀ ∈∂Ω

ξ

che è fisicamente equivalente ad un mezzo perfettamente assorbente che circonda il dominio Ω. Ogni fotone è assorbito immediatamente quando attraversa ∂Ω per cui la densità fotonica è uguale a zero fuori da Ω. Mentre questo approccio è comunemente usato in letteratura, un approccio più realistico porta alla condizione di bordo

Φ

( )

ξ

+

2

κ

n

ˆ

⋅∇Φ

( )

ξ

=

0

che è la condizione di bordo di Robin (RBC) e che rappresenta il modello fisico di un mezzo non scatterante che circonda Ω, assumendo che non avvenga alcuna riflessione superficiale a ∂Ω .

Un esempio dei risultati ottenuti con questo approccio è mostrato di seguito. In figura 2.4 è mostrata la geometria del fantoccio usato; i materiali utilizzati per il fantoccio consistono in intralipidi come scatteratore e inchiostro India come assorbitore. E’ stata usata polvere di agar (1-2 %) per solidificare le soluzioni intralipidiche e di inchiostro India [Cubeddu 1997]. Il fantoccio di base è un cilindro solido di 50 mm di diametro con µ_a =0.007mm−1

e µ_s' =1.0mm−1. Uno o due fori cilindrici del diametro di 14 mm sono stati ottenuti nel fantoccio di base in modo da poter inserire bersagli con diversi contrasti ottici.

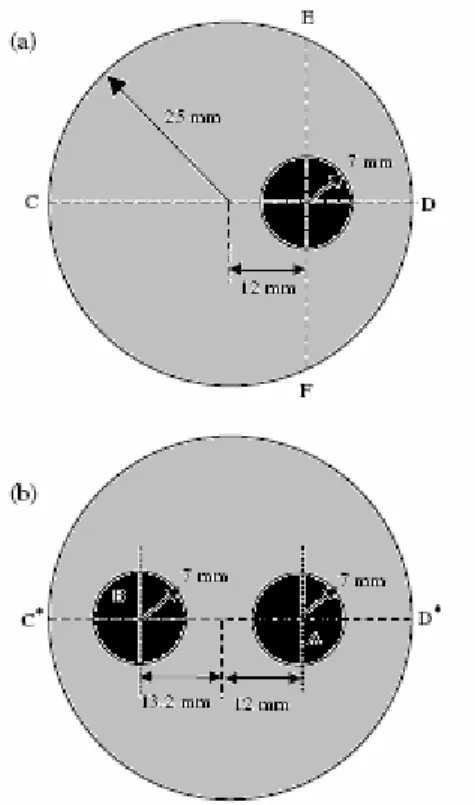
Fig. 2.4 Geometria del fantoccio nel caso di un bersaglio (a) e nel caso di due bersagli (b)

In questo esperimento sono stati usati cinque configurazioni del bersaglio: un bersaglio riempito con acqua pura allo 0.05% e 0.1% di soluzione intralipidica; due bersagli vuoti; e due bersagli con una regione vuota ed una regione altamente assorbente\scatterante.

Fig. 2.5 Immagini ricostruite di assorbimento e scattering

(a) immagine di assorbimento per un bersaglio di acqua pura e (b) immagine di scattering per un bersaglio di acqua pura

(c) immagine di assorbimento per un bersaglio di acqua più 0.05% di intralipidi e (d) immagine di scattering per un bersaglio di acqua più 0.05% di intralipidi;

(e) immagine di assorbimento per un bersaglio di acqua più 0.1% di intralipidi e (f) immagine di scattering per un bersaglio di acqua più 0.1% di intralipidi

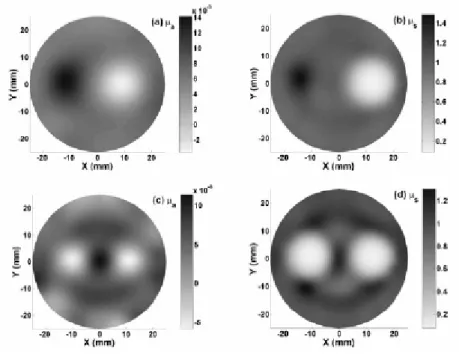
Fig. 2.5 Immagini ricostruite di assorbimento e scattering: (a) immagine di assorbimento per due bersagli (un bersaglio

vuoto sulla sinistra, un bersaglio altamente scatterante\assorbente sulla destra); (b) immagine di scattering per gli stessi due bersagli, come mostrato in (a); (c) immagine di assorbimento per due bersagli vuoti; (d) immagine di scattering per due bersagli vuoti [tratto da Xu , 2003]

2.3 Modelli stocastici per l’approssimazione dell’equazione di

trasferimento radiativo

Nei modelli stocastici di trasporto dei fotoni attraverso il tessuto (o qualsiasi altro mezzo altamente scatterante), i percorsi del singolo fotone sono simulati considerando la probabilità degli eventi di assorbimento e di scattering. I tree modelli stocastici più comunemente usati sono la teoria Random Walk, il metodo Markov Random Field ed il metodo Monte Carlo

2.3.1 Random Walk

Nella teoria del Random Walk (RWT), il comportamento statistico dei cammini random nello spazio è usato per risolvere alcune quantità, quali la dipendenza spaziale della riflettanza scatterata che si presenta da una sorgente puntiforme [Bonner 1987, Gandjbakhche 1995]. I cammini random del fotone avvengono in un reticolo cubico discreto, dove la spaziatura del reticolo è equivalente alla radice quadrata della distanza tra gli eventi di scattering, e l’assorbimento avviene nello spazio intermedio. Mentre ciò è equivalente allo scattering isotropico, il modello può essere esteso allo scattering anisotropico attraverso l’uso del cosiddetto “constrained walks”.

Nonostante il fatto che il numero di direzioni in cui il movimento è possibile è ristretto, RWT fornisce una valida descrizione della migrazione dei fotoni in mezzi random. Le previsioni ottenute da tali modelli sono state validate con simulazioni Monte Carlo, teoria della diffusione e misure sperimentali [Hebden 1995a]. Nel limite di un gran numero di passi nel cammino, si possono derivare le espressioni analitiche per quantità fisiche come la probabilità di trovare un fotone ad una certa distanza dalla sorgente puntiforme. Comunque, poiché un gran numero di passi corrisponde fisicamente ad una bassa probabilità di assorbimento, questo modello viene maggiormente usato nel regime dove anche la teoria della diffusione regge. [Chandrasekhar 1943] ha dimostrato l’equivalenza tra i due modelli di trasporto di fotoni attraverso mezzi altamente scatteranti.

2.3.2 Il metodo Markov Random Field

L’Università della California presso Berkeley ha sviluppato un modello stocastico molto diverso, completamente generale, basato sulle probabilità di transizione (Patch 1994, Grunbaum 1992, Grunbaum e Zubelli 1992). Il modello può recuperare le probabilità della transizione interna nel caso tempo-invariante, fornendo valori esatti delle probabilità sul confine di un dominio. Ciò che il modello si aspetta sono dati senza rumore. Nonostante tale modello porti ad una soluzione ottima del problema inverso non lineare, non è mai stato applicato a dati reali a causa della difficoltà nel mettere in relazione l’analisi invariante essenzialmente topologica alle condizioni reali.

2.3.3 Il metodo Monte Carlo

I problemi trattati con i metodi Monte Carlo sono di due tipi,detti probabilistici o deterministici a seconda che siano o meno direttamente connessi con il comportamento e il risultato di processi casuali. Nel caso di problemi probabilistici, l’approccio Monte Carlo più semplice è osservare i numeri casuali, scelti in modo che simulino direttamente i processi casuali fisici del problema originale, e desumere la soluzione desiderata a partire dal comportamento di questi numeri casuali.

L’idea che sta dietro all’approccio Monte Carlo ai problemi deterministici è quello di sfruttare la forza della matematica teorica evitando la sua debolezza nel rimpiazzare la teoria con gli esperimenti ogniqualvolta questa risulta incerta. Nello specifico, supponiamo di avere un problema deterministico che possiamo formulare in linguaggio teorico, ma che non siamo in grado di risolvere con gli strumenti teorici. Essendo deterministico, questo problema non è direttamente associabile con i processi casuali; ma, quando la teoria ha rivelato la sua struttura basilare, possiamo forse riconoscere che questa struttura o l’espressione formale descrivono anche alcuni processi casuali apparentemente non correlati, perciò possiamo risolvere il problema deterministico numericamente grazie ad una simulazione Monte Carlo del suo concomitante problema probabilistico.

Questa tecnica di risolvere un problema dato grazie ad una simulazione Monte Carlo di un problema diverso viene a volte chiamata “Monte Carlo sofisticato”, per distinguerlo dalla semplice simulazione del problema originale. Ci sono vari gradi di sofisticazione: per

discernere un secondo problema probabilistico descritto dalla teoria risultante, ed infine risolvere il primo problema probabilistico simulando il secondo. Il secondo problema può essere una maggiore o minore distorsione del primo, oppure può essere totalmente differente: la sola cosa che importa è che deve avere la stessa soluzione numerica del primo, o, più in generale, che le parti volute delle due soluzioni differiscano di una quantità trascurabile, non essendoci alcun bisogno di assicurare la concordanza tra le parti non volute delle due soluzioni.

Un modo per ridurre l’eventuale incertezza nella risposta è di basarla su un grande numero di osservazioni. C’è una relazione quadratica tra l’errore nella risposta ed il numero richiesto di osservazioni; per ridurre l’errore di un fattore dieci occorre aumentare di cento volte il numero delle osservazioni, e così via. Per eludere un’impraticabile ammontare di lavoro sperimentale, è vantaggioso modificare o almeno distorcere il problema originale in modo tale che l’incertezza nella risposta venga ridotta. Tale procedure sono conosciute come ‘tecniche di riduzione della varianza’, perché l’incertezza può essere misurata in termini di varianza.

Sebbene la procedura di base del metodo Monte Carlo sia la manipolazione di numeri casuali, essa non dovrebbe essere utilizzata generosamente. Ogni numero casuale è una potenziale fonte di incertezza nel risultato finale, e di solito si pagherà per esaminare ogni parte di un esperimento Monte Carlo e per vedere se quella parte non possa essere rimpiazzata dall’analisi teorica esatta che non introduce incertezza.

Il metodo Monte Carlo si riferisce a simulazioni numeriche basate sul campionamento random a partire da distribuzioni di probabilità appropriate. La luce viene considerata come un flusso di particelle (fotoni) che vengono iniettati nel mezzo, e che si muovono in linee rette all’interno del tessuto attraverso interazioni successive.I vantaggi del metodo Monte Carlo includono la semplice implementazione, l’abilità di trattare qualsiasi geometria complessa e disomogeneità, così come la possibilità di incorporare la dipendenza dal tempo. E’ anche possibile modellare i fenomeni ondulatori come la polarizzazione e l’interferenza. Il maggiore svantaggio è l’alto costo computazionale. Dato che i fotoni sono governati dalle statistiche di Poisson, il rapporto segnale rumore (SNR) della distribuzione campionata aumenta con la radice quadrata del numero di fotoni tracciati.

I parametri che sono richiesti per tracciare la traiettoria di un fotone attraverso un qualsiasi mezzo sono il coefficiente di assorbimento locale µ_a, il coefficiente di scattering µ_s, e la funzione di fase di scattering f e e . I fotoni sono emessi da una sorgente e viaggiano in ( ,_s '_s) linee rette finchè non vengono scatterati. La probabilità per un fotone di venire scatterato dopo una distanza dτ è definito da:

p

( )

τ τ

d

=

e

−µ τs

d

τ

(2.27) Perciò la probabilità totale di essere scatterato dopo aver viaggiato per una distanza

τ

è:

' 0

1

s s

e

e

r

τ µ τ µ τ −

_{= −}

−

_≡

∫

(2.28) dove r∈

[

0....1

]

è un numero a caso. La distanza tra gli eventi di scattering è data da

1

ln(1

)

s

r

τ

µ

= −

−

che è equivalente a

1

ln( )

s

r

τ

µ

= −

. (2.29) Gli angoli azimutale e polare, θ e φ, relativi alla precedente direzione del moto sono dati da

φ

=

2 r

π

1 e ' ' 2 0 ( ) f d r θ

θ θ

=

∫

dove r e ₁ r₂∈

[

0....1

]

sono numeri random uniformemente distribuiti.

L’assorbimento può essere tenuto in considerazione sia per terminare la traiettoria di un fotone assorbito o per introdurre uno schema pesato. Perciò il peso del fotone w∈

[ ]

0...1

viene ridotto attraverso successivi eventi di scattering in accordo con

w

=

w e

' −µ τa dove w è il peso prima dell’interazione, e '

τ

è la distanza percorsa dall’ultimo evento di scattering. Le traiettorie del fotone vengono terminate quando il peso diventa trascurabile, il fotone lascia la zona di confine o la regione di interesse, o colpisce il rivelatore. Nel caso in cui colpisca il rivelatore, la percentuale di rilevazione conteggiata viene aumentata del peso rimanentew del fotone. Questa tecnica, chiamata anche “survival weighting”, è una tra quelle denominate “tecniche di riduzione della varianza” che aiutano a rendere le

simulazioni Monte Carlo più accurate e allo stesso tempo efficienti dal punto di vista computazionale.