Capitolo 4 Approccio statistico bayesiano e test multipli in esperimenti di microarray

in esperimenti di microarray

I metodi empirici bayesiani si dimostrano particolarmente efficienti quando si vuole realizzare un test multiplo simultaneo di ipotesi su un insieme numeroso di soggetti, per ognuno dei quali sono disponibili poche osservazioni.

Questo è proprio il caso degli esperimenti di microarray, in cui il numero di osservazioni per lo stesso gene è generalmente molto basso rispetto al numero totale di geni analizzati.

In questo ambito, si possono ricordare gli studi di Efron et al. (2001), Lönnstedt et al. (2001), Efron (2003), Newton (2003) e Smyth (2004) che fanno uso di un approccio bayesiano al test delle ipotesi per la selezione dei geni differenzialmente espressi.

L’elemento in comune a questi lavori è lo sfruttamento della capacità insita in questi metodi di fare inferenza su ogni singolo gene, ossia di generare delle stime dei parametri statistici che lo possono descrivere, traendole da tutto l’insieme di dati: per questo motivo tali metodi vengono detti empirici.

Un contesto operativo o “framework” bayesiano genera queste stime avvalendosi del teorema di Bayes, di ipotesi sulle distribuzioni a priori dei parametri formulate dall’analista e dell’insieme dei dati: sono queste le componenti di un processo capace di produrre in maniera automatica un aggiornamento dei parametri delle distribuzioni coinvolte, al fine di generare gli elementi confrontati nella statistica caratteristica del “framework”.

4.1 Inferenza statistica classica e approccio bayesiano

empirico

Un processo di inferenza statistica su un insieme di dati ipotizza un modello delle osservazioni collezionate e lo verifica attraverso l’analisi dei dati stessi, producendo delle stime dei parametri descrittivi della distribuzione dei dati ipotizzata. Per fare inferenza statistica esistono due tipi di approcci:

ƒ Approccio frequentistico, detto anche analisi statistica classica; ƒ Approccio soggettivistico, detto anche analisi bayesiana.

4.1.1 Fondamenti del metodo classico: test delle ipotesi

Un’ipotesi statistica, come illustrato in Appendice A, è un’assunzione che viene fatta dal ricercatore sul problema di inferenza che sta affrontando.

Si supponga di ipotizzare un modello per un insieme di dati, cioè che essi si distribuiscano seguendo una determinata funzione di densità di probabilità. Per verificare la veridicità del modello occorre determinare l’incertezza sull’ipotesi formulata attraverso la probabilità condizionata che il modello ipotizzato sia vero sulla base dei dati osservati, ossia:

P ( Modello ipotizzato è vero | Dati osservati )

Purtroppo, una tale probabilità non è stimabile; è, invece, possibile esprimere la probabilità condizionata che si ottengano i dati osservati dato il modello ipotizzato:

P ( Dati osservati | Modello ipotizzato)

ossia è possibile ipotizzare il modello e verificare se i dati sono compatibili con esso. Questa verifica si può realizzare con un test delle ipotesi strutturato nel seguente modo:

Passo 1: Definire l’ipotesi di ricerca.

Un’ipotesi di ricerca o alternativa è un’assunzione derivata dalla teoria che il ricercatore intende verificare sui dati.

Passo 2: Definire l’ipotesi nulla.

L’ipotesi nulla è un’assunzione che non si deve mai verificare se l’ipotesi alternativa è consistente con la realtà.

Passo 3: Condurre un’analisi dei dati per determinare se l’ipotesi nulla è rigettabile con una determinata probabilità.

Attraverso questo procedimento è possibile rifiutare l’ipotesi nulla con un adeguato livello di confidenza nel risultato del test, affermando, così, che il modello ipotizzato per la distribuzione dei dati è effettivamente coerente con le osservazioni.

In un problema di inferenza statistica classica si suppone che i dati generati da un processo di misura possano essere considerati come un insieme di variabili aleatorie, cioè di osservazioni prodotte attraverso un processo statistico con distribuzione di probabilità sconosciuta sulla quale si vuole “riferire qualcosa”.

In un contesto del genere, la definizione di probabilità si basa sul concetto di realizzazioni del processo aleatorio, o uscite, ugualmente probabili: la probabilità, infatti, viene vista come la frequenza relativa con la quale una determinata uscita si realizza se si aumenta il numero di realizzazioni all’infinito.

Quando si fa inferenza statistica secondo una prospettiva frequentistica, si assume che i dati osservati siano un campione rappresentativo di un’intera popolazione molto più numerosa.

Tale popolazione può essere rappresentata attraverso la media e la varianza di popolazione, che sono parametri sconosciuti, mentre il campione può essere descritto grazie alla media e alla varianza campione, che possono, invece, essere calcolate e prendono il nome generico di statistiche.

Media e varianza campione procurano una stima della media e della varianza dell’intera popolazione; tuttavia, queste ultime non possono essere conosciute con precisione, ma sono affette da incertezza che viene riassunta con la distribuzione di campionamento o “sampling” del parametro che si sta considerando.

La distribuzione di “sampling” è un’ipotetica distribuzione di tutti i possibili valori della statistica di interesse per campioni di dimensione N, tratti da una data popolazione.Per fare un esempio di quanto detto, la media campione osservata non è altro che una realizzazione della sua distribuzione di “sampling”.

4.1.2 Approccio bayesiano e interpretazione soggettivistica della probabilità

Nell’approccio bayesiano, in contrasto con l’interpretazione frequentistica, la probabilità può essere interpretata come l’aspettativa che ciascuno esprime sulla possibilità che “verosimilmente” si possa ottenere una determinata uscita di un qualche processo. Ciò significa che individui differenti possono attribuire una diversa probabilità ad uno stesso evento. Il concetto di probabilità assume, dunque, il significato che gli viene attribuito nel linguaggio comune, ossia è una misura del “grado di fiducia” nel verificarsi dell’evento; conseguenza diretta di tale interpretazione è che si respinge il fondamento che vi sia un processo di generazione dei dati

verificabile attraverso un procedimento dicotomico quale il test delle ipotesi.

Il concetto intuitivo sfruttato nell’approccio bayesiano è che la probabilità dipende dallo stato di conoscenza (o di ignoranza) del fenomeno in esame; questa conoscenza è, in genere, differente da persona a persona.

Tali concetti sono in conflitto con l’impostazione classica della statistica, secondo cui le proprietà probabilistiche sono definite come proprietà asintotiche, ossia legate ad un numero infinito di dati ottenibili solo attraverso esperienze replicabili, e l’inferenza sui parametri è effettuata escludendo l’eventualità di utilizzare informazioni pregresse sul fenomeno che si sta analizzando.

Lo schema operativo dell’approccio Bayesiano alla modellazione dei dati ha la seguente struttura:

ƒ Passo 1: Fare inferenza basata su tutte le informazioni a disposizione e generare un’ipotesi di distribuzione a priori per il parametro che si sta considerando.

ƒ Passo 2: Aggiornare le stime avvalendosi del teorema di Bayes, illustrato nel paragrafo successivo, e delle distribuzioni a priori, al fine di generare una distribuzione a posteriori del parametro.

ƒ Passo 3: Verificare che i nuovi dati confermino le ipotesi a priori.

Il metodo bayesiano è iterativo, cioè le stime dei parametri generate al passo precedente sono gli ingressi del passo successivo e il processo si interrompe quando non si osservano apprezzabili variazioni sui parametri stimati.La differenza operativa più evidente fra l’approcco classico e quello bayesiano è che mentre la statistica classica considera i dati D come

realizzazioni di variabili aleatorie ed i parametri ignoti θ come deterministici, la statistica bayesiana considera i dati come costanti ed i parametri ignoti sono variabili aleatorie caratterizzate da una funzione densità di probabilità a priori P(θ).

4.1.3 Teorema di Bayes e inferenza sui parametri

L’approccio Bayesiano consente di aggiornare le informazioni a priori contenute nella funzione densità di probabilità P(θ) dei parametri, alla luce dei dati osservati. Tale aggiornamento si traduce, attraverso l’applicazione del teorema di Bayes, in una funzione densità di probabilità P(θ|D) a posteriori.

Il teorema di Bayes per eventi discreti può essere espresso nel modo seguente:

)

(B|A

)

(A

)

( B | A

)

( A

| B )

( A

k k k i i i

∑

=

Pr

Pr

Pr

Pr

Pr

dove:

ƒ Pr(Ai) = Probabilità a priori dell’evento Ai. Essa riassume le

convinzioni sulla probabilità dell’evento Ai prima che Ai o

l’evento B siano stati osservati

ƒ Pr( B | Ai ) = Probabilità condizionata di B dato Ai. Essa

riassume la probabilità che l’evento B si verifichi dopo che si è osservato Ai.

ƒ Σk Pr( Ak ) Pr( B | Ak ) = Costante di normalizzazione o

probabilità totale. Essa è uguale alla somma delle quantità al numeratore per tutti gli eventi Ak

ƒ Pr( Ai | B ) = Probabilità a posteriori di Ai dato B. Essa

rappresenta la probabilità dell’evento Ai dopo che l’evento B si

è verificato.

Dal punto di vista dell’approccio bayesiano alla stima dei parametri, ci sono quantità conosciute o osservabili, i dati D, e quantità sconosciute, i parametri θ.

Per fare inferenza sulle quantità sconosciute si stabilisce una probabilità congiunta p(θ,D) che descrive la personale “convinzione” dell’analista, fondata sul suo grado di conoscenza dei dati.

Questa probabilità congiunta può essere riscritta in modo da ottenere l’inferenza desiderata su θ:

( ) ( | )

( , )

( | )

( )

p

p D

p

D

p

D

p D

θ

θ

θ

=

θ

=

e utilizzando il teorema di Bayes diventa:

)

|

(

)

(

)

|

(

)

(

)

|

(

)

(

)

(

)

|

(

)

(

)

|

(

p

L

D

d

D

p

p

D

L

p

D

p

D

p

p

D

p

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

∝

=

=

∫

dove:

ƒ L( θ | D ) è la funzione di verosimiglianza o ”likelihood” per θ, ossia una misura della fiducia che si realizzi un determinato valore di θ quando i dati D sono stati osservati (Spiegel, 1979);

ƒ è la costante di normalizzazione, o distribuzione

predittiva a priori, che assicura che la probabilità a posteriori di θ integri a 1.

∫

θ θ θ θ)p(D | )d p(

4.1.4 Scelta della distribuzione a priori e stimatori della media e della varianza

La scelta della distribuzione a priori per i parametri che devono essere stimati può essere effettuata sulla base del significato che si vuole attribuire ad essa e delle diverse informazioni a disposizione dell’analista.

In generale esistono tre criteri per procedere a tale scelta e ognuno di essi esprime un differente modo di intendere questa distribuzione:

ƒ Metodo bayesiano classico: assume che la a priori non deve esprimere l’influenza del ricercatore, per cui si scelgono a priori che siano il meno informative possibile sull’insieme di dati.

ƒ Metodo bayesiano parametrico moderno: assume che la scelta della a priori deve essere funzionale ad avere un processo computazionale più snello, per cui si scelgono a priori con proprietà convenienti.

ƒ Metodo bayesiano soggettivo: assume che la a priori è un riassunto delle assunzioni del ricercatore, per cui si sceglie una a priori basata su conoscenze precedenti (risultati di precedenti studi, opinioni di altri gruppi di studio…).

4.1.5 Metodo bayesiano classico per la scelta delle distribuzioni a priori

Si supponga di avere un insieme di dati che si distribuisce come una variabile aleatoria normale

y ~ N( μ , σ2 ₎

dove μ e σ2 _{sono la media e la varianza della distribuzione e sono} entrambe variabili casuali sconosciute: per ottenere una stima dei due parametri della distribuzione è necessario generare un modello multi-parametro.

Il teorema di Bayes per due parametri si scrive:

p( μ , σ2 _{| y) ∝ p(μ , σ}2 _{) p(y | μ , σ}2₎

e, poichè si vogliono generare le distribuzioni di ogni singolo parametro condizionate all’insieme di dati osservati, cioè p(μ | y) e p(σ2_{|y), è conveniente studiare le distribuzioni marginali della} distribuzione condizionata p( μ , σ2 _{| y) nei due parametri, ossia :}

(

)

=

_∫

(

) (

)

2 2 2 2

_,

_|

|

|

σ

σ

σ

σ

μ

μ

y

p

y

p

y

d

p

(

)

=

_∫

(

)

(

)

μ

μ

μ

μ

σ

σ

y

p

y

p

y

d

p

2

|

2

|

,

|

Se l’intento dell’analista è optare per distribuzioni a priori che siano più generali possibile, senza sfruttare le informazioni disponibili

sull’insieme di dati, una buona scelta può essere una distribuzione a priori uniforme per entrambi i parametri, cioè:

p( μ ) ∝ c

-∞ < μ < +∞

p( σ

2

_{) ∝ 1/σ}

₀₂

_{0 < σ}

2

_{< +∞}

Nell’ipotesi che le distribuzioni dei due parametri siano indipendenti, ossia che valga p(μ , σ2 _{)= p( μ ) p( σ}2 _{), si ottiene per la} distribuzione congiunta:

p(μ , σ

2

_{) = c/σ}

₀₂

Si può dimostrare che (Spiegelhalter et al., 2004):

1

/

)

|

(

=

−

|y)~t

_n−

n

s

y

μ

p(

y

p

μ

p(σ

2

_{| y) ~ Inv-χ2 (n-1,s2) ≡ Inv-Γ( (n-1)/2), (n-1)s2/2 )}

dove:

ƒ y è la media di tutti i dati; ƒ n è il numero di osservazioni;

ƒ s è la devianza d’errore sul campione; ƒ s2 _{è la varianza campione;}

ƒ con tn-1 si indica una variabile aleatoria che segue una

ƒ con Inv-Γ( a,b ) si indica una variabile aleatoria che segue una distribuzione gamma inversa con parametri caratteristici a e b.

4.1.6 Metodo bayesiano parametrico moderno per la scelta delle distribuzioni a priori

L’ipotesi sui dati afferma che essi si distribuiscono seguendo una variabile aleatoria normale con media μ e varianza σ2_{, entrambe variabili} casuali sconosciute.

In questo approccio, la scelta delle distribuzioni a priori per i parametri viene effettuata in base a considerazioni di ordine pratico, ossia queste distribuzioni devono contribuire a semplificare il calcolo che conduce, attraverso l’applicazione del teorema di Bayes, all’aggiornamento del valore dei parametri considerati.

Si supponga di conoscere la varianza della popolazione σ2 _{= σ02 , che,} per esempio, in prima istanza può essere ritenuta uguale alla varianza campione. In quest’ottica una scelta conveniente per la distribuzione a priori della media è la distribuzione normale N( m, d2), dove m è la media campione e d2 è la varianza campione.

Questa scelta può essere operata sia in base alla congruenza con le ipotesi sulla media espresse dall’analista che, soprattutto, osservando che la distribuzione normale è una coniugata.

Una distribuzione a priori si definisce coniugata se, dopo aver applicato il teorema di Bayes ad essa, la distribuzione a posteriori risultante appartiene sempre alla stessa famiglia di distribuzioni, ad esempio se la a priori è una distribuzione normale anche la a posteriori sarà una distribuzione normale. Quello che cambia fra le due distribuzioni sono i parametri, che vengono modificati dall’applicazione del teorema di Bayes in virtù dei dati campionari disponibili.

)

2

ˆ

,

ˆ

(

μ

σ

_μ

N

p(μ)

~ N( m, d

2

)

p(

μ|y)

~ p(

μ)p(y| μ)

~

dove: 1 2 0 2 2 2 0 2 2 0 2

1

ˆ

1

1

ˆ

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

+

+

=

σ

σ

σ

σ

μ

_μ

n

d

d

y

d

m

e

sono i parametri della distribuzione a priori automaticamente aggiornati dal teorema.

Un discorso simile può essere fatto con la distribuzione a priori della varianza, per la quale una scelta opportuna è la distribuzione gamma inversa, che è anch’essa una coniugata.

Effettuando queste scelte la distribuzione congiunta a priori dei due parametri, nell’ipotesi che essi siano indipendenti, sarà una

Γ

normale-inversa:

p( μ, σ

2

_{) ~ N-Inv-Γ(μ}

₀

_{, σ}

₀₂

_/k

₀

_{; v}

₀

_{, σ}

₀₂

₎

dove

μ

₀

, σ

02

/k

0

, v

0

e σ

02 sono i parametri descrittivi della distribuzione.

Poiché il prodotto di due coniugate dà sempre una coniugata, la distribuzione a posteriori dei due parametri, condizionata all’insieme dei dati che si ottiene dall’applicazione del teorema di Bayes alla distribuzione

congiunta, appartiene alla stessa famiglia della distribuzione a priori, ma con i parametri aggiornati:

p(μ,σ

2

|y) ~ N-Inv-Γ(μ

_i

, σ

_i2

/k

_i

; ν

_i

, σ

_i2

)

dove: 2 0 0 0 2 2 0 0 2 0 0 0 0 0 0

)

(

)

1

(

μ

σ

σ

μ

μ

−

+

+

−

+

=

+

=

+

=

+

+

+

=

y

n

k

n

k

s

n

v

v

n

v

v

n

k

k

y

k

k

n

k

k

k

i i i i i n i

sono i parametri aggiornati ed i è il minimo indice di iterazione per il quale le stime non variano significativamente.

4.1.7 Metodo bayesiano soggettivo per la scelta delle distribuzioni a priori

In questo caso, la scelta delle distribuzioni a priori dei parametri che si stanno considerando viene operata in funzione dell’insieme delle informazioni a disposizione dell’analista, nonché degli accorgimenti utili a migliorare il carico computazionale del procedimento bayesiano di stima.

Le informazioni utilizzate non devono essere necessariamente relative all’insieme di dati osservato, ma possono anche provenire dalle considerazioni su esperimenti simili realizzati da altri gruppi. Inoltre, l’analista può modulare la scelta della distribuzione in base alla sua

conoscenza delle osservazioni o alla personale confidenza nel risultato che sta cercando di verificare.

Dall’analisi di questo e dei precedenti metodi, potrebbe sembrare che la scelta della distribuzione a priori non sia così vincolante.

In realtà non bisogna dimenticare che nel procedimento o “framework” bayesiano i risultati della stima al passo precedente vengono utilizzati come ingressi del passo successivo.

Essendo, inoltre, questo processo sempre convergente verso una stima corretta del parametro in esame, la scelta di un’opportuna distribuzione a priori comporta una riduzione del numero di iterazioni necessarie, ossia un aumento della velocità di convergenza.

4.2 Statistica “B” e modello gerarchico per i dati di

espressione genica

Sulla base degli argomenti appena trattati è ora possibile introdurre la statistica B, o fattore di Bayes, per la discriminazione dei geni differenzialmente espressi, inserendola in un “framework” bayesiano basato su di un modello gerarchico dei dati di espressione genica.

Si indichi con: ij ij ij

G

R

M

=

log

₂

il logaritmo del rapporto dei due canali per il gene i sull’array j, con i=1,…,N e j=1,…,n.

Sono stati già illustrati nel capitolo 3 i limiti dei metodi che stabiliscono una soglia su Mij per la selezione dei geni differenzialmente espressi.

Da un punto di vista più strettamente statistico, è necessario evidenziare alcuni problemi intrinseci alla struttura stessa dei dati; essi, infatti, sono generalmente costituiti da un insieme assai limitato di osservazioni per ogni singolo gene, rispetto al numero totale di geni presenti sul vetrino.

Questa caratteristica può invalidare l’uso di statistiche classiche, come la statistica t, per realizzare la selezione; ad esempio, un alto valore di t può essere determinato da un errore standard estremamente contenuto al suo denominatore e ciò può accadere anche quando la differenza fra le medie al numeratore sia molto piccola.

Un tipico esempio di soluzione a questo problema è stato illustrato con la statistica introdotta dal SAM, in cui la costante additiva al denominatore agisce proprio in funzione di una limitazione degli errori di primo tipo.

Un’alternativa ai metodi che fanno uso di statistiche t modificate può venire proprio da un approccio empirico bayesiano ai dati di espressione genica.

4.2.1 “Posterior odds” dell’espressione differenziale

Si supponga che i dati Mij, relativi ad ogni gene i, si distribuiscano seguendo una variabile aleatoria normale con media μi e varianza σi2:

Per indicare se un gene g è differenzialmente espresso oppure non ha mutato la sua espressione in seguito al trattamento effettuato, si può utilizzare un insieme di indicatori o indici definito nel modo seguente:

⎩

⎨

⎧

=

1

0

g

I

se il gene non è differenzialmente espresso

se il gene è differenzialmente espresso

Per ogni gene g, è possibile calcolare la probabilità a posteriori che esso sia differenzialmente espresso (Ig=1) dato l’insieme di osservazioni Mij e metterla in rapporto con la probabilità a posteriori che la sua espressione sia rimasta immutata (Ig=0) dato l’insieme di osservazioni Mij; ciò corrisponde a definire il rapporto degli “odds” a posteriori per il gene g.

La statistica B per ogni singolo gene viene definita come il logaritmo del rapporto dei suoi “odds” a posteriori:

)

|

0

Pr(

)

|

1

Pr(

log

ij g ij g g

M

I

M

I

B

=

=

=

per cui Pr(Ig=1|Mij) > Pr(Ig=0|Mij) se e solo se Bg > 0.

Applicando il teorema di Bayes all’espressione di Bg e nell’ipotesi che gli Mij siano indipendenti al variare di i, si può scrivere:

Pr(

|

1)

log

1

Pr(

|

0)

Pr(

|

1)

Pr(

|

1)

log

1

Pr(

|

0)

Pr(

|

0)

Pr(

|

1)

log

1

Pr(

|

0)

ij g g ij g i g i g g i g i g g _{i g} i g i g g i g g

M

I

p

B

p

M

I

M I

M

I

p

p

M

I

M I

M

I

p

p

M

I

= ≠ = _≠ = =

=

=

−

=

=

=

=

−

=

=

=

−

=

∏

∏

=

dove:

ƒ Mg è il vettore delle n osservazioni per il gene g;

ƒ p è la proporzione di geni differenzialmente espressi nell’esperimento, definita come p = Pr(Ii=1) per ogni i=1,…,N.

Per calcolare BBg è necessario quantificare l’espressione di Pr(Mg|Ig=1)

e Pr(Mg|Ig=0), che sono le distribuzioni marginali di Mg rispetto agli indici e

che possono essere indicate seguendo la notazione statistica con:

)

(

)

0

|

Pr(

)

(

)

1

|

Pr(

0 1 i I g i i I g i

M

f

I

M

M

f

I

M

i i = =

≡

=

≡

=

Ciò può essere realizzatto attraverso la definizione di un modello gerarchico dei dati, come si vedrà nel prossimo paragrafo.

4.2.2 Modello gerarchico e calcolo delle distribuzioni marginali

Si supponga di avere a disposizione le osservazioni relative ad una data variabile casuale Y e di averle collezionate da m popolazioni grazie ad n osservazioni per ogni popolazione.

Sia yij l’osservazione j della popolazione i e si supponga che ogni yij si distribuisca seguendo l’andamento di una variabile aleatoria caratterizzabile attraverso i suoi parametri descrittivi:

dove θi è il vettore dei parametri per la popolazione i.

Inoltre, per ogni θi sia possibile stabilire una distribuzione a priori anch’essa descrivibile attraverso i suoi parametri:

θ

i

~ f(Θ)

In questo modo sono stati realizzati i passi del procedimento bayesiano di stima dei parametri, come illustrato nei primi paragrafi di questo capitolo.

Si assuma, ora, che anche i parametri Θ siano delle variabili aleatorie casuali e che si debba specificare per esse una distribuzione f(a,b):

Θ ∼ f(a,b)

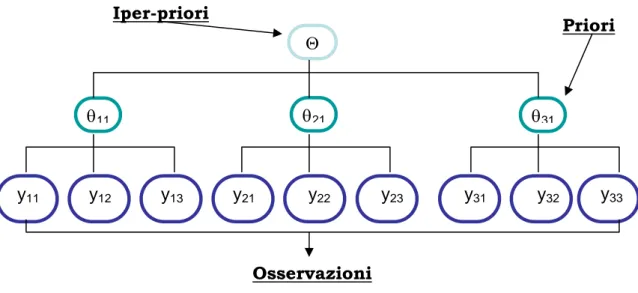
allora Θ viene chiamata iper-priori e il modello dei dati viene definito gerarchico, con ovvio riferimento ai diversi livelli di definizione delle distribuzioni, come si può osservare nella figura 4.1.

Θ

θ11 θ21 θ31

y11 y12 y13 y21 y22 y23 y31 y32 y33 Iper-priori

Priori

Osservazioni

Tipicamente le osservazioni relative ad ogni gene in un esperimento di microarray sono poche, mentre il numero di geni sul quale è necessario effettuare un test simultaneo delle ipotesi è molto grande.

Definendo un modello gerarchico per le osservazioni è possibile utilizzare le informazioni relative all’intero insieme di dati per descrivere le distribuzioni marginali della media μi e della varianza σi2, cioè dei parametri della distribuzione N(μi, σi2) relativa alle osservazioni del gene i-esimo.

Una possibile struttura gerarchica ipotizza che:

ƒ 1/σi2 si distribuisce seguendo una variabile aleatoria Γ ed essa è una iper-priori del modello;

ƒ la distribuzione di μi condizionata a 1/σi2 è normale ed essa è una priori del modello.

Seguendo questo modello gerarchico, se si definisce per la media μi una distribuzione tale che:

se Ii=0 se Ii=1

0

|

(0,

/ 2 )

i i

N

cna

μ τ

τ

⎧

⎨

⎩

i dove: ƒ τi = na/2σi2 ~ Γ(υ,1);

ƒ υ sono i gradi di libertà della distribuzione; ƒ a>0 e c>0 sono dei parametri di scala,

allora le distribuzioni marginali per ogni livello della gerarchia diventano:

( )

_{( )}

(

)

( )

( )

(

)

(

)

( )

(

)

(

)

(

)

( )

( )

2 2 1 2 1 1/ 2 1/ 2 1/ 2 ₂ 1 0 2 1 / 2 / 2 ₂ 1 1 1 0 1 (2 ) 2 0 , (2 ) 2 , , , i i i i i i ij i j i i i i i i cna I i i i I i n _M n _na i i i i I i I i i i i i i i i I i i i i i I i i i f e na f c e f na f M e e f M f M d d f M f f d d f M f M τ υ τ _μ τ _μ τ τ υ μ τ π τ μ δ μ τ π τ μ τ μ τ μ τ μ τ τ μ τ μ − − − ₋ − − = = − _{− −} − = = = = = Γ ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠ = ∑ ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠ = = = =

∫∫

∫∫

(

)

(

)

( )

(

)

( )

0 , 0, i i I i i i i i i i i i i f f d f M f d d τ μ τ τ μ τ μ τ τ τ = = = =

∫∫

∫

Dal risultato delle integrazioni si ottengono le espressioni delle due distribuzioni marginali che vengono messe a confronto per ogni gene nella statistica Bg:

( )

_{( ) ( )}

(

)

( )

_{( ) ( )}

(

)

⎟⎠ ⎞ ⎜ ⎝ ⎛ + − − − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − − − = ⎥⎦ ⎤ ⎢⎣ ⎡ _{+ +} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + Γ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + Γ = 2 2 . 2 2 / 2 / 0 2 2 . 2 2 / 1 2 / 2 / 1 1 1 2 2 2 1 1 1 1 2 2 2 n i i n n i I n i i n n i I M s a na n M f nc M s a nc na n M f i i υ υ π υ υ π υ υ

dove Mi. è la media delle osservazioni relative a tutti i geni. Quindi, per ogni gene g la statistica B assume la forma:

2 2 . 2 . 2

1

log

1

1

1

g g g g g

a s

M

p

B

M

p

nc

a s

nc

⎡

⎤

⎢

₊

₊

⎥

⎢

⎥

=

−

+

⎢

₊

₊

⎥

⎢

₊

⎥

⎣

⎦

La sola parte gene-specifica della statistica B è il rapporto fra parentesi quadre, che è sempre un numero ≥1 perché il denominatore è sempre minore o uguale al numeratore; ciò significa che un incremento nell’espressione differenziale, cioè un incremento della media Mg. fa

aumentare il valore della statistica anche quando la varianza è piccola e la presenza della costante di scala a garantisce che il rapporto non assuma valori troppo grandi a causa di medie Mg. troppo piccole.

E’ necessario, inoltre, porre l’attenzione sul fatto che, diversamente da altre statistiche, non esiste un valore di soglia di B rispetto al quale dichiarare che un gene è differenzialmente espresso. Al crescere del valore della statistica si incrementa la probabilità che il gene possa essere considerato a ragione differenzialmente espresso e, analogamente, per valori negativi di B è molto più verosimile supporre che l’espressione differenziale sia assente.