C
a
p
i
t
o
l
o
3
3
.
.
C
C
o
o
n
n
o
o
s
s
c
c
e
e
n
n
z
z
e
e
a
a
c
c
q
q
u
u
i
i
s
s
i
i
t
t
e
e
s
s
u
u
l
l
l
l
a
a
f
f
o
o
r
r
m
m
a
a
z
z
i
i
o
o
n
n
e
e
e
e
d
d
e
e
v
v
o
o
l
l
u
u
z
z
i
i
o
o
n
n
e
e
d
d
e
e
l
l
l
l
e
e
b
b
r
r
e
e
c
c
c
c
e
e
:
:
s
s
t
t
o
o
r
r
i
i
a
a
e
e
d
d
a
a
t
t
t
t
u
u
a
a
l
l
i
i
t
t
à
à
3.1. APPROCCI GENERALI ALLO STUDIO
La possibilità che si verifichi il crollo di un’opera di sbarramento e le relative conseguenze sono, come abbiamo più volte ricordato, alla base della comprensione e della valutazione del rischio che ciascuna struttura costituisce per l’ambiente dov’è costruita. Lo studio del fenomeno di rottura di una diga in materiale sciolto passa forzatamente attraverso la ricostruzione dell’idrogramma effluente dalla breccia. Solo successivamente si pone il problema di propagare l’idrogramma a valle, e quindi studiare gli effetti dell’inondazione. Concentrando l’attenzione sul primo punto, si può ulteriormente suddividere lo studio della stima dell’idrogramma di piena in due aspetti:
N per prima cosa si rende necessaria l’individuazione dei parametri di breccia;
N di seguito si può procedere con l’analisi del vuotamento del serbatoio attraverso tale breccia e quindi alla stima del picco di portata effluente.
Molto lavoro è già stato condotto da numerosi studiosi ed è possibile operare una semplice classificazione delle metodologie finora seguite. In generale, possiamo anticipare che molti metodi si sono basati su analisi di regressione statistica di una quantità di dati, più o meno vasta, ottenuti da storici collassi di dighe. Esse hanno dato origine a differenti espressioni empiriche che forniscono la stima dei parametri di breccia come anche del picco della portata. Nel tempo, si è arrivati alla messa a punto di metodi che si basano sulla comprensione dei reali fenomeni fisici causanti la rottura. Le grandi semplificazioni che sono contenute in questi modelli e, dalla parte opposta, la necessità di ottenere delle stime ad elevata precisione fanno sì che la ricerca in questo campo sia, ad oggi, di grande interesse ed attualità.
Possiamo riconoscere tre tipologie d’approccio all’analisi della formazione della breccia e della stima del picco di portata effluente:
A. Metodi empirici e statistici
Si individuano due differenti tecniche che possono essere considerate appartenenti a questo tipo di approccio. Le stime più semplici, ma che contengono le più grandi incertezze, possono essere fornite tramite “linee guida”. Significa che il valore del parametro che vogliamo stimare deve essere scelto all’interno di un intervallo stabilito tramite un’analisi di eventi già avvenuti in passato. Tale metodo può essere seguito nel caso in cui si riscontrino numerose analogie tra la diga in esame e le strutture che sono state alla base della determinazione dei valori guida. L’inconveniente è proprio quello che la grande variabilità di tecniche costruttive rende difficile qualsiasi ampia analogia.
La seconda tecnica è quella dell’analisi di regressione statistica su dati storici di collassi di sbarramenti in materiale sciolto. Uno studio di questo tipo porta all’individuazione di formule empiriche che legano i parametri di breccia, e quindi anche il picco di portata, alle caratteristiche geometriche e idrauliche della diga. Sebbene le formule di previsione sviluppate con questa tecnica siano un buon riferimento per la valutazione di larga massima dei parametri cercati, hanno anch’esse l’inconveniente di essere ricavate da dati disomogenei. Da informazioni scarse e non precise discendono dati dispersi e con un’incertezza tropo vasta.
B. Metodi matematici parametrici
Sono metodi che cominciano a mettere in conto i fenomeni fisici che determinano l’evoluzione del canale di breccia. A tale proposito, essi introducono delle relazioni parametriche per descrivere i principali meccanismi ai quali sarebbe complicato attribuire una soluzione analitica.
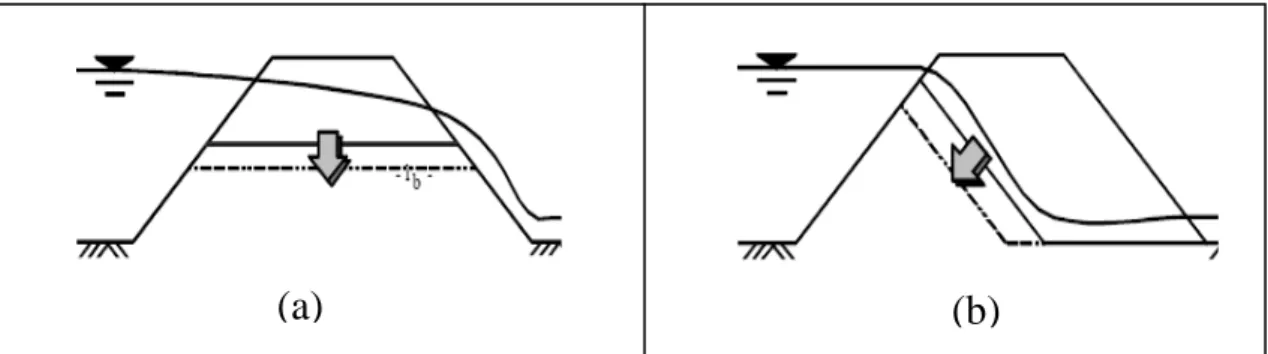
Figura 3. 1 – Evoluzione della breccia: a) cresta parallela al fondo; b) cresta parallela al paramento di valle
Per l’evoluzione della breccia fanno riferimento a schemi quali uno sviluppo parallelo alla cresta (figura 1a) o uno sviluppo parallelo al paramanto di valle (figura 1b). Il meccanismo d’allargamento del canale è scelto in accordo agli schema di figura 2.
Figura 3. 2 – Differenti meccanismi di allargamento del canale di breccia
La portata effluente dalla breccia è calcolata con le formule classiche dello stramazzo. La soglia di riferimento ha una preassegnata legge di evoluzione temporale. Il canale erodibile può avere geometria assegnata, l’assunzione più frequente è quella di figura 3.2b.
C. Metodi fisicamente basati
Si parla di metodi analitici quando, a differenza degli studi empirici, si ha la possibilità di ottenere delle previsioni su un certo evento, dati alcuni parametri idraulici, meccanici e topografici. Solo pochi metodi
analitici sono effettivamente derivati da principi fisici (ad esempio lo sono i modelli di Singh & Scarlatos, Singh & Quiroga e Waldeer & O’connor). Gli altri introducono varie leggi esponenziali che mettono in relazione l’efflusso con il carico solido (Cristofano, Kulisch). Il metodo utilizzato dai modelli analitici è semplice: in funzione della breccia viene calcolato l’efflusso attraverso una formula di stramazzo in parete
grossa; conoscendo la velocità e la profondità liquida si calcola la capacità di trasporto solido tramite una delle formule disponibili in letteratura; è inoltre necessario scegliere una tipologia di sviluppo della breccia (come in figura 3.1 e figura 3.3) e un tipo di allargamento del canale
di breccia (figura 3.2) per distribuire il materiale eroso che è stato precedentemente calcolato.
(a)
(b)
(c)
Figura 3. 3 – Evoluzione longitudinale della breccia con rotazione intorno al piede
La tipologia di modelli che più si adatta alla realtà fisica del fenomeno è costituita dai
modelli numerici. Per la simulazione dell’evoluzione arbitraria della breccia in una struttura
in materiale sciolto si sono inizialmente sviluppati modelli unidimensionali; in seguito si è cercato di estendere l’applicazione delle conoscenze raggiunte verso modelli bidimensionali. In questo ambito vengono usati differenti schemi numerici per la risoluzione delle equazioni in acque basse, l’equazione di Exners e equazioni del trasporto solido. L’osservazione importante da fare è che, con l’uso di modelli numerici, non deve essere fatta nessun’assunzione sullo sviluppo della breccia, proprio perché è la computazione numerica che lo genera automaticamente. E’ evidente che questi modelli sono i più completi all’interno di tutto il panorama di tecniche, per la stima delle conseguenze della formazione di una breccia, descritti nelle pagine precedenti.
3.2. REVISIONE CRONOLOGICA DELLA LETTERATURA TECNICA IN TEMA
Ritorniamo ora ai due aspetti, individuati a pag. 28, nei quali è stato suddiviso lo studio dell’idrogramma effluente da un potenziale crollo di diga. Analizziamo, dapprima, in modo più dettagliato l’approccio empirico che ha portato numerosi studiosi a generare semplici relazioni per l’identificazione dei principali parametri di breccia e per il picco di portata. Di seguito, sarà fatta una breve descrizione dei principali modelli fisicamente basati.
3.2.1. Metodi empirici: stima dei parametri di breccia
I parametri più rilevanti, che entrano in gioco nell’analisi dell’evoluzione della breccia, sono: la profondità e la larghezza della breccia stessa, la pendenza dei suoi fianchi, il tempo necessario affinché si cominci a generare e il tempo che impiega ad arrivare a completa rottura. Con riferimento alle metodologie sopra descritte, la stima dei parametri può essere condotta tramite approcci molto semplificati (analisi comparative o relazioni empiriche), attraverso più rigorosi metodi parametrici ed, infine, grazie alle più complesse, ma precise, modellazioni fisicamente basate. Nella tabella a pagina seguente sono riassunte tutte le relazioni empiriche che sono state elaborate, negli anni, utilizzando casi studio di dighe realmente crollate. Per ciascun autore si riporta anche il numero di casi cui ha fatto riferimento.
Singh e Snorrason (1982-1984) sono stati i primi a fornire una relazione tra la
MacDonald e Langridge-Monopolis (1984) hanno proposto il “fattore di breccia”
Vwhw dato dal prodotto tra il volume d’invaso al momento della rottura e l’altezza liquida in
corrispondenza dello sbarramento. Tale fattore è stato statisticamente correlato con la quantità di volume di materiale solido asportato dalla diga e con il picco della portata effluente. Vedremo, in dettaglio, i particolari del loro lavoro nel prossimo paragrafo.
Tabella 3. 1 – Raccolta delle relazioni empiriche dei parametri di breccia basate su analisi statistiche
Froehlich (1987) sviluppò un’analisi adimensionale per i principali parametri di
breccia. Successivamente egli ha aggiornato il suo lavoro nel 1995 basandosi su un numero molto maggiore di casi studio. La principale differenza con il primo lavoro è che le equazioni che sviluppa nel 1995 non sono più a carattere adimensionale. Il suo lavoro verrà presentato con maggiore attenzione nel prossimo paragrafo, qui ci limitiamo a sottolineare il fatto che le sue equazioni sono, ad oggi, considerate le più attendibili.
I valori guida che sono forniti dal Bureau of Reclamation (1988) servono soprattutto come limite superiore del “range” dei valori che possono essere assunti dalla larghezza di breccia e dal tempo di formazione della breccia; introducono cioè un fattore di sicurezza.
Singh e Scarlatos (1988), analizzando 52 collassi di dighe stabiliscono una relazione
tra la larghezza della breccia in sommità e al fondo. Inoltre valutano la pendenza dei fianchi del canale di breccia che va dai 10-15° fino all’essere verticale in molti casi.
Figura 3. 4 – Confronto di tre metodi empirici: larghezza del canale di breccia prevista e osservata rappresentata in scala aritmetica (sopra) e in scala logaritmica (sotto)
Von Thun e Gillette (1990) e Dewey e Gillette (1993) utilizzano i dati recuperati da
Froehlich (1987) e MacDonald and Langridge-Monopolis (1984) per determinare delle regole di stima dei più importanti parametri di breccia. Aggiungono, poi, particolari considerazioni sulla pendenza dei fianchi della breccia.
Von Thun and Gillette (1990) propongono la relazione : b w av
2
.
5
h
C
B
=
+
[m] (1) per la larghezza media della breccia, dove Cb è un coefficiente in funzione del volumed’invaso il cui valore si ricava dal riquadro a fianco. Nello stesso lavoro, questi autori rappresentano in un grafico il volume di materiale eroso in funzione del volume d’acqua effluente e in funzione della profondità liquida al di sopra del fondo del canale di breccia. Essi propongono anche due metodi per
stimare il tempo di formazione della breccia in base all’erodibilità del materiale.
(2)
(3) La quota dell’invaso, misurata sopra il fondo del canale di breccia, è in metri e si ottiene il tempo di formazione in ore. Se si fa riferimento alla velocità di erosione laterale della breccia, è possibile trovare altre due espressioni che si adattano meglio ai dati sperimentali:
(4)
(5)
In figura 3.4 a pagina precedente è riportato il confronto riguardo la capacità di previsione di tre differenti relazioni empiriche. La relazione di Von Thun and Gillette è applicata a 78 crolli contenuti nel database dei colassi storici (essa è stata statisticamente dedotta da 57 collassi contenuti proprio in questo database), la relazione di Froehlich è stata applicata a 77 casi studio (egli ha dedotto la sua equazione studiandoo 60 di questi casi), infine l’equazione prodotta dal Reclamation è calcolata per 80 casi studio. La relazione di froehlich risulta chiaramente quella che meglio riesce a prevedere la larghezza di breccia, soprattutto per valori inferiori ai 50m.
bassa erodibilità TF=0.20hw +0.25 Elevata erodibilità TF=0.015hw bassa erodibilità w av h 4 B TF= Elevata erodibilità 0 . 61 h 4 B TF w av + =
3.2.2. Metodi empirici: stima del picco di portata
In aggiunta ai parametri di breccia, molti ricercatori hanno proposto tecniche molto semplici e veloci per prevedere direttamente il picco d’efflusso. Nella tabella che segue troviamo una sintesi delle principali relazioni proposte, organizzate in ordine temporale:
Tabella 3. 2 - Raccolta delle espressioni di previsione del picco della portata effluente e del numero dei casi studio utilizzati.
La totalità delle equazioni sopra indicate è stata determinata grazie ad un’analisi di regressione statistica su dati d’incidenti passati. La sola eccezione è costituita dal lavoro di
Walder e O’Connor (1997), non riportato in tabella 3.2, che si basa sull’analisi di simulazioni
numeriche effettuate con dighe ipotetiche. Essi conducono le simulazioni su differenti dighe, diversi valori di volume d’invaso e studiano anche vari scenari d’erosione.
Propongono una distinzione tra grandi invasi (caratterizzati da erosione veloce) e piccoli invasi (con erosione lenta). Nel primo caso, il picco di portata occorre quando la breccia raggiunge la sua massima profondità ed è quindi indipendente dalla velocità d’erosione verticale. Per gli altri, invece, si ha un forte abbassamento di livello dell’invaso durante l’evoluzione della breccia ed il picco Qp dipende fortemente dalla velocità d’erosione
verticale.
Ripercorrendo quello che è mostrato in tabella, Kirkpatrick (1977) propone una relazione per l’interpolazione dei dati con la quale lega la portata d’efflusso al livello liquido d’invaso, subito a monte della diga, al momento del crollo. La relazione proposta è
5 . 2 w p
1
.
268
(
h
0
.
3
)
Q
=
+
[m3/s] (6) L’istituto del Soil Conservation Service (1981) utilizza gli stessi 13 casi studio del precedente autore. Si sviluppa una relazione esponenziale che lega la portata ancora al valore di hw, si tratta di una curva inviluppo. Successivamente, il SCS propone una metodologia per la previsione del picco Qp per le dighe in terra che prende il nome di “Earth” (1985):(7)
(8)
Dove Br è il fattore di breccia, definito alla pag 26 . Il volume d’invaso è in m3 mentre la sezione della struttura, in corrispondenza della breccia è in m2.
Anche il Bureau of Reclamation (1982) propone una curva di inviluppo, per 21 casi
studio, simile alla precedente:
85 . 1 w p
19
.
1
h
Q
=
⋅
[m3/s] (9) Negli anni 1982 – 1984, Singh e Snorrason analizzano le simulazioni di 8 crolli di dighe, condotte tramite i modelli DAMBRK e HEC-1. Alla fine del periodo di studio, essi mostrano che il picco della portata effluente può essere espresso sia come funzione dell’altezza della diga sia del volume d’invaso. Si ha:89 . 1 d p
13
.
4
H
Q
=
⋅
[m3/s] (10) 47 . 0 r p1
.
776
V
Q
=
⋅
[m3/s] (11) per hw ≥ 31.4 m 1.85 w p16
.
6
h
Q
=
⋅
[m3/s] per hw ≤ 31.4 mQ
p=
0
.
00042
⋅
B
1r..35[m3/s]MacDonald e Langridge-Monopolis (1984) oltre alla previsione dei parametri di
breccia propongono due curve, una interpolante (per le dighe non in terra) e una di inviluppo (per le dighe in terra), del picco d’efflusso in funzione del fattore di formazione della breccia. La relaziona individuata nell’ambito delle dighe in terra dà risultati ragionevoli e può essere ben approssimata dall’equazione:
41 . 0 r w p
3
.
85
(
h
V
)
Q
=
⋅
[m3/s] (12) Ciò non può essere fatto per le altre dighe in materiale sciolto (rocce sciolte, dighe con nucleo impermeabile, etc.) poiché i dati sono troppo dispersi.Costa (1985) si propone di studiare il comportamento di 31 crolli di dighe. Egli
presenta curve d’inviluppo ed equazioni derivate da analisi di regressione statistica. Egli individua tre relazioni: tra il picco di portata e l’altezza della diga; tra il medesimo picco e il volume d’invaso e, infine, l’equazione che lega la portata Qp al prodotto dei due parametri.
Ricordiamo: 42 . 0 r w p
0
.
981
(
h
V
)
Q
=
⋅
[m3/s] (13) 44 . 0 r w p2
.
634
(
h
V
)
Q
=
⋅
[m3/s] (14) Infine, poniamo l’accento sul lavoro di Froehlich (1995a). Egli utilizza 22 dighe per ottenere un’equazione d’interpolazione per la determinazione del picco Qp. Data l’importanzadel lavoro di Froehlich, se ne propone un’analisi più approfondita nel paragrafo seguente, insieme alla presentazione di altre ricerche più recenti e altrettanto interessanti.
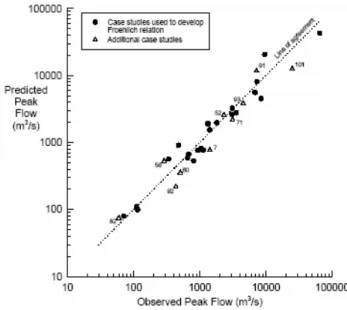
La figura a lato mostra l’applicazione della formula di Froehlich ai 22 casi studio più 10 dighe addizionali. Paragonata alle altre formule gli studiosi hanno dedotto che essa rappresenta il migliore strumento di stima per il picco di portata.
Figura 3. 5 – Picco di portata previsto ed osservato per 32 casi studio. Uso dell’equazione di Froehlich (1995a)
3.2.3. Metodi parametrici e metodi fisicamente basati
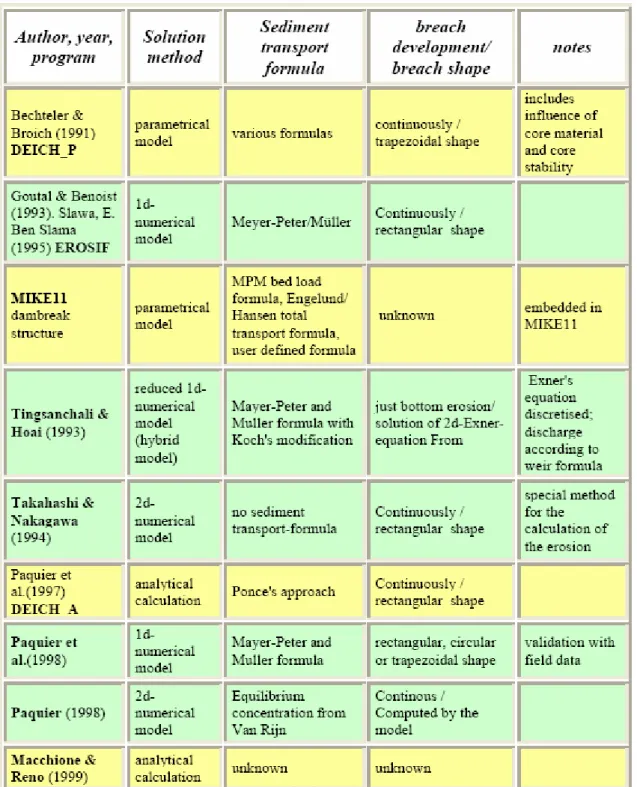
Una presentazione generale di queste due tipologie di approccio è già stata proposta alle pagine 29-31. Mentre i modelli parametrici continuano a fondarsi su varie ipotesi semplificative dedotte dall’esperienza, i modelli fisicamente basati si prefiggono di superare qualsiasi dipendenza da esse. Realizzare un modello di questo tipo significa affrontare non solo il problema delle corrette assunzioni per i principi idraulici, ma anche gestire con accuratezza la scelta di formule di trasporto solido. La quantità di materiale eroso e la distribuzione di questo sulla superficie del canale di breccia costituiscono gli aspetti chiave per gestire matematicamente o numericamente la forma della breccia. Nella tabella 3 si è cercato di raggruppare in modo dettagliato i modelli parametrici e fisicamente basati maggiormente citati nelle pubblicazioni. Segue una breve descrizione solo di alcuni di essi.
Cristofano (1967) rappresenta il primo tentativo do modello fisicamente basato. Il suo
lavoro lega la velocità di erosione del materiale solido lungo il canale di breccia con la velocità del deflusso all’interno del medesimo canale.
Harris e Wagner (1967) elaborano un modello nel quale assumono che la breccia inizi
contemporaneamente al sormonto e termini quando raggiunge la fondazione della struttura. Per il trasporto solido fanno uso della formula di Schoklitsch. Sulla base del loro lavoro, Brown & Rogers (1977 – 1981) presentano il modello “BRDAM” che può essere applicato sia al caso del sormonto sia alla rottura per sifonamento causata dell’erosione interna.
Lou (1981) e Ponce e Tsivoglou (1981) presentano un modello che mette in relazione
l’equazione di trasporto solido di Mayer-Peter e Müller all’equazione differenziale unidimensionale del flusso non stazionario e conservazione del materiale solido. La larghezza di breccia è legata empiricamente al deflusso attraverso il canale di breccia.
Un lavoro interessante è condotto da Fread (1984). Con il suo modello parametrico “DAMBRK” simula l’evoluzione continua di una breccia, la quale inizia in corrispondenza della cresta della diga e si sviluppa uniformemente. Le dimensioni finali sono raggiunte quando è trascorso un certo intervallo di tempo che è definito dall’utilizzatore del programma.
Gli altri parametri d’ingresso che devono essere formanti sono: la pendenza dei fianchi di breccia (Z), la larghezza finale del fondo della breccia (Bbr), la quota finale del fondo della breccia (Ybr) e l’altezza liquida sulla breccia Hf calcolata rispetto alla fondazione della struttura. Il modello è costruito sulla risoluzione delle equazioni di Saint Venant:
(15)
(16)
Dove A è la sezione trasversale soggetta a deflusso, A0 è la sezione inattiva di canale (emersa),
h è il livello liquido,
q è l’eventuale afflusso o efflusso laterale,
Sf è la pendenza della linea dell’energia valutata con la formula di Manning per il
moto stazionario uniforme,
Se è la pendenza di contrazione-dilatazione.
Le equazioni alle differenze parziali scritte sopra sono trasformate nelle corrispondenti equazioni alle differenze finite e risolte con il metodo Newton-Raphson. Il modello di Fread più utilizzato è, però, quello che sviluppa nel 1988: il noto “BREACH”. Per il trasporto solido si fa riferimento alla formula di Meyer-Peter e Müller modificata da Smart (1984) per i canali a forte pendenza. Il modello dà buoni risultati sia nel caso di rottura per sormonto sia nel caso di sifonamento. Si fa, infatti, riferimento ai meccanismi fisici che coinvolgono la resistenza e la stabilità delle porzioni di materiale soggette al deflusso nella breccia. Questo permette di elaborare una realistica evoluzione della forma della breccia.
Singh e Scarlatos (1985) sviluppano il modello BEED (Beach Erosion of
Embankments Dams) alla base del quale sta l’applicazione delle formule di Einstein-Brown e Bagnold per il calcolo dell’erosione. Nel 1998, Singh e Quiroga mettono a punto una formula particolare per il trasporto solido e conducono un’analisi del problema tramite espressioni adimensionalizzate.
Questi ed altri modelli più recenti sono riportati nel prospetto alle pagine seguenti.
equazione di continuità
(
)
q x Q t A A 0 = ∂ ∂ + ∂ + ∂ conservazione del momento(
)
0 S S x h A g x A Q t Q e f 2 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ∂ ∂ ⋅ + ∂ ∂ + ∂ ∂Tabella 3. 3 – Sequenza cronologica dei più importanti modelli: = Modelli Parametrici
Tabella 3. 4 – (Segue) Sequenza cronologica dei più importanti modelli: = Modelli Parametrici
3.3. DESCRIZIONE CRITICA DI ALCUNI METODI PIÙ SIGNIFICATIVI
Per entrare nello specifico di alcuni notevoli risultati, che costituiscono ancora oggi equazioni e modelli di riferimento, proponiamo una rivisitazione di 8 lavori svolti, singolarmente o in gruppo, da importanti ricercatori in questo campo. Sarà seguito l’ordine cronologico che ci porta dalle prime conoscenze fino agli strumenti disponibili attualmente.
3.3.1. Le formule empiriche di MacDonald e Langridge-Monopolis
Nel 1984, Thomas MacDonald e Jennifer Langridge-Monopolis pubblicano il loro studio condotto su ben 42 incidenti di dighe in materiale sciolto, avvenuti negli Stati Uniti. Il loro scopo è quello di dare una risposta alla necessità di stimare, con sempre maggiore precisione, la sicurezza di opere così imponenti. La necessità di sviluppare una buona metodologia per l’apprezzamento delle caratteristiche della breccia è ciò che sta alla base dell’impegno di questi autori.
I parametri sui quali è posta l’attenzione sono:
a
a)) Forma della breccia;
b
b)) La dimensione finale della breccia;
c
c)) Il tempo di formazione della breccia;
d
d)) Si sviluppa anche una relazione tra il picco Qp e il fattore di breccia BFF, introdotto
proprio in questo studio.
Molte altre variabili sono utilizzate per condurre questo studio, MacDonald e Langridge-Monopolis le raggruppano in tre categorie:
x Caratteristiche della struttura: la dimensione e la forma della diga, la dimensione e la coesione dei materiali, differenti zone di cui è composto lo sbarramento, metodologie costruttive;
x Caratteristiche del flusso idrico: volume d’invaso, la variabile hw che descrive la differenza di quota tra il livello d’invaso e il fondo della breccia, il picco di portata;
x Caratteristiche della breccia: abbiamo già fatto riferimento alla forma della breccia, larghezza finale e tempo di formazione, poi si ha la pendenza dei fianchi e il volume di materiale asportato.
Alcuni di questi dati sono stati direttamente disponibili, mentre quelli mancanti sono stati stimati dalle informazioni disponibili in letteratura. La scarsità e l’imprecisione di numerosi valori sono sicuramente causa di errori, d'altronde inevitabile, nelle analisi di regressione condotte dagli studiosi. Riassumiamo, quindi, i risultati ai quali sono arrivati gli autori:
a
a)) Forma della breccia: sia nel caso di dighe in terra che per tutte le altre, la forma della
breccia può essere assunta triangolare, se non si estende fino alla base della struttura, altrimenti si assume trapezoidale. Per entrambe le forme la pendenza dei fianchi 2V:1H. Nell’articolo che presenta il lavoro degli autori si descrive brevemente il progressivo sviluppo della breccia nel caso di sormonto e di sifonamento.
b
b)) Dimensioni finali della breccia: il limite fisico dell’allargamento della breccia è fornito
dagli argini della diga e dal terreno naturale, pertanto la metodologia proposta si applica solo alle dighe il cui materiale non viene completamente asportato. Adottando la forma della breccia descritta sopra, le dimensioni finali della breccia possono essere previste se si riesce a quantificare il volume di materiale del corpo diga che viene asportato. Combinando diversi parametri, si trova che un buon metodo per prevedere il volume solido asportato dalla struttura è il calcolo del fattore di formazione della breccia BFF:
Dighe in terra Ver =0.0261
(
Vw⋅hw)
0.769 [m3] (17) Altre dighe in materiale sciolto Ver =0.00348(
Vw⋅hw)
0.852 [m3] (18)Curva inviluppo per dighe in terra
Curva di migliore adattamento
Il grafico sottostante mostra che la relazione proposta dagli autori per la stima del volume di materiale eroso fornisce un risultato apprezzabile. I valori calcolati e misurati realmente si dispongono essenzialmente lungo la bisettrice. In generale, le dighe in terra mostrano un volume asportato più grande delle altre.
Figura 3. 7 – Volume di materiale eroso osservato e calcolato per 60 casi studio
c
c)) Tempo di formazione della breccia: si rappresenta in un grafico il tempo massimo di
sviluppo della breccia in funzione del volume di materiale rimosso. Per le dighe in terra è possibile tracciare la curva d’inviluppo che mantiene tutti i punti al di sopra. La stessa cosa non è fattibile per le altre tipologie di dighe:
( )
0.364 er f 0.0179 Vt = [sec] (19) E’ dunque possibile fare una stima dell’evoluzione delle caratteristiche geometriche e temporali di alcuni tipi di dighe, soprattutto per quelle in terra. Tali caratteristiche possono anche costituire il dato d’ingresso degli esistenti software che permettono di stimare il picco di efflusso di un ipotetico collasso di diga.
d
d)) Picco d’efflusso: avere una relazione che dà la possibilità di stimare direttamente il picco
della portata effluente è utile sia per una stima di massima che per un confronto con i risultati forniti dai modelli più avanzati. MacDonald e Langridge-Monopolis scoprono che c’è una relazione lineare tra il picco Qp e il fattore di formazione della breccia BFF se si dispongono i
valori in un grafico doppio logaritmico:
(
)
0.412 w w p 1.154 V h3.3.2. Le formule empiriche di Froehlich
Abbiamo già fatto cenno al lavoro elaborato da Froehlich nel 1995. Dagli anni ’70 in poi, molti studiosi hanno proposto formule empiriche per la stima dei parametri geometrici della breccia e del picco di portata. La scarsità d’informazioni precise sui numerosi incidenti passati, che sono alla base dell’individuazione di tali relazioni, hanno come conseguenza la notevole incertezza del risultato che le equazioni possono offrire.
Froehlich, già nel 1987, elabora delle relazioni adimensionali per stimare la larghezza media della breccia, un fattore di pendenza media dei fianchi e il tempo di formazione della breccia. Revisionando il suo lavoro, nel 1995 egli propone nuove equazioni dimensionali per la previsione della larghezza media della breccia e del tempo di formazione. Egli lavora usando 63 casi studio ed ottiene la seguente equazione
19 . 0 b 32 . 0 w 0 V h K 1803 . 0 B= ⋅ ⋅ ⋅ [m] (21) Si ricorda che:
Vw = volume d’invaso misurato rispetto al fondo della breccia
K0 = coefficiente sperimentale pari a 1.4 per sormonto e 1 negli altri casi
hb = altezza finale della breccia (spesso assunta quanto l’altezza della diga Hd)
Froehlich si interessa anche alla possibilità di ricavare un’equazione di previsione per il picco di portata effluente dalla breccia. Egli raccoglie, con accuratezza, i dati disponibili di 22 collassi di dighe in materiale sciolto. Per prima cosa, egli utilizza i dati disponibili sulle dighe per osservare il comportamento di alcune equazioni esistenti per il picco effluente. Sono alla sua attenzione le formule del SCS (“Earth, 1985), di Costa (1985) e McDonald e Langridge-Monopolis. Nella seconda parte del suo lavoro, Froehlich conduce una regressione multipla lineare grazie ai dati da lui raccolti. Passando attraverso il piano logaritmico egli calcola la retta interpolante dei dati ed ottiene, tramite l’operazione esponenziale, l’equazione:
24 . 1 w 295 . 0 w p
0
.
607
V
h
Q
=
⋅
⋅
[m3/s] (22) Con: Vw = volume d’invasohw = Altezza liquida nell’invaso al momento della rottura (spesso uguale a Hd)
3.3.3. Il modello parametrico elaborato da Macchione
Durante il meeting di CADAM nel 1999, è presentato un modello matematico semplificato di dam-breach elaborato da F. Macchione (1986-1989) presso l’Università della Calabria. Per permettere un’analisi computazionale della capacità erosiva del flusso liquido nei confronti della struttura di una diga in materiale sciolto occorre mettere in conto il principio fisico che spiega tale interazione tramite l’azione tangenziale. Vediamo quali sono i principi fondamentali:
x Il flusso sulla breccia è considerato critico
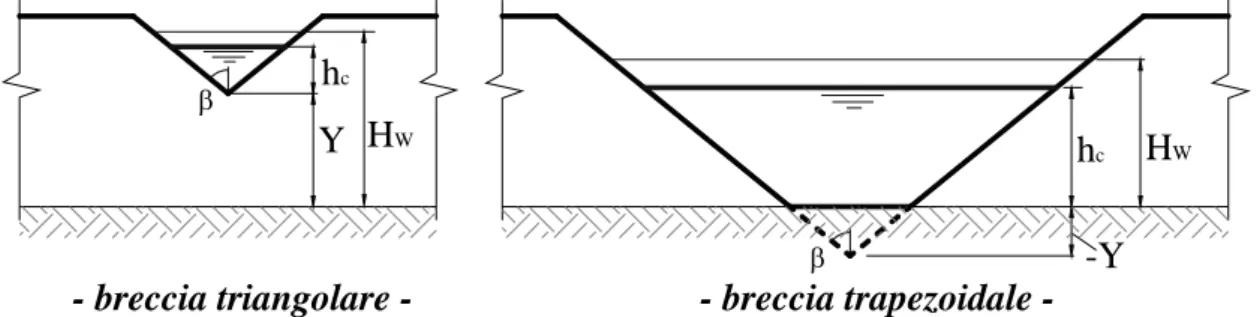
x La forma iniziale della breccia è assunta triangolare; quando, a seguito dell’ingrandimento, il vertice del triangolo raggiunge il fondo del canale la breccia diviene trapezoidale. Da questo momento si mette in conto solo l’erosione laterale.
Figura 3. 8 – Schematizzazioni delle assunzioni geometriche del modello L’efflusso nel caso di breccia triangolare è dato da:
(23)
mentre nel caso di breccia trapezoidale (Y < 0):
(24)
con l’altezza critica che si calcola come:
(25)
conoscendo la curva ipsografica (volume d’invaso – altezza d’invaso), espressa solitamente da: 0 w 0 r r W H W = α (26) HW hc Y hc HW -Y
- breccia triangolare - breccia trapezoidale -β β
(
)
β ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = H Y tg 5 4 g 2 1 Q 2 5 w 2 1(
)
[
−]
(
−)
β ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = h h 2Y h Y tg g 2 1 Q 12 c 2 3 c c 2 1(
)
[
12]
w 2 w 2 w c 2H 3Y 9Y 4H 8YH 5 1 h = + + + −e considerando l’equazione di continuità
(27) si ottiene la relazione
(28)
Inoltre, ricordando che A = sezione di breccia, PB = perimetro bagnato soggetto ad erosione e
RS
γ
=
τ
è l’azione tangenziale al fondo, si ottiene: con . . .( ) (
) (
(
)
)
(
)
⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ β − α ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = − − β γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = α − tg Y H W H 2 g 5 4 dt dH Y H Y H sin g k K 5 4 2 1 dt dY 2 5 w 0 r 0 1 w 2 1 2 5 w d 2 w 2 3 2 3 3 2 2 0( ) (
) (
)
(
)
(
)
(
)
⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ β ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − α − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − β − − β γ − = α − − tg h Y h Y 2 h 2 g h Y 2 h W H dt dH h Y sin h Y h H 2 Y 2 h sin g k K 2 1 dt dY 2 1 c c c c c 0 r 0 1 w w 2 c 2 1 c 2 3 c d 2 c 1 2 3 3 2 0Il rapporto K2n/K2=K3/K2 può essere considerato come un fattore di calibrazione del
modello e deve essere scelto in base alla similitudine del caso studio con un’altra situazione per cui tale valore è noto.
Un’ultima importante considerazione da fare è che, durante la presentazione di questo lavoro al convegno CADAM, è stata proposta un’analisi per verificare qualche valore dell’esponente n fornisse, effettivamente, le migliori capacità di previsione del modello. Usando i dati di alcune dighe, realmente crollate e ipotetiche, e facendo assumere ad n i valori di: 0.5, 1, 1.5, 2 e 2.5 si conclude che la scelta, operata originariamente dall’autore, di n=1.5 è la migliore. Breccia triangolare (29) Breccia trapezoidale (30) dt dW Q= r − 0 r 0 1 w W z Q dt dH 0 α − = −α n 2 BK P dt dA= τ ⎩ ⎨ ⎧ = = 2 3 2 n te tan cos K
3.3.4. Il modello numerico EDBREACH
Nel 1992 inizia una collaborazione scientifica-tecnologica tra la Cina e la Finlandia. Si giunge alla realizzazione di un modello che simula il processo erosivo durante il progressivo crollo di una diga in materiale sciolto. Il modello numerico prende il nome di “EDBREACH” ed portato a termine da E.Loukola e M.Houkuna nel 1998. Esso si indirizza soprattutto alla previsione del meccanismo di formazione della breccia nel caso di piccole dighe, o medio-alte, ma che garantiscono un grande volume d’invaso grazie alla loro estensione in lunghezza. Il modello può simulare sia il caso di sormonto che quello di sifonamento. Grazie a numerose osservazioni di test su campo condotti in Cina è stato sviluppato e calibrato il modello. Una validazione è stata poi fatta sulla base dei dati della rottura della diga di Teton.
Per utilizzare il modello bisogna essere in possesso delle seguenti informazioni:
Geometria della diga Materiale della diga e
del nucleo impermeabile Dati idrologici
-Quota della cresta della diga -Quota della cresta del nucleo impermeabile
-Larghezza della cresta della diga -Larghezza della cresta del nucleo impermeabile
-Quota del fondo non erodibile -Inclinazione dei paramenti del nucleo
impermeabile
-Inclinazione dei paramenti della diga
-Localizzazione del nucleo imp. all’interno della diga
-Peso specifico secco -Angolo d’attrito interno -Diametro d50 del materiale -Coesione
-Volume d’invaso (o sup. liquida) in funzione del livello d’invaso
-Condizione limite di valle: stima dell’efflusso o quota liquida in funzione del tempo
-Afflusso all’invaso o quota d’invaso in funzione del tempo
-Numero di sezioni usate nel modello
Vediamo la descrizione del modello EDBREACH. Il flusso che attraversa la breccia è simulato grazie all’uso di diverse sezioni trasversali della struttura che sono analizzate da monte verso valle. Per ogni sezione è valutato tale flusso e il relativo materiale eroso.
L’allargamento della breccia è calcolato in funzione della massima capacità di trasporto solido della corrente. Come mostrato in figura 8, si assume lo stato critico in corrispondenza della parte più a valle della cresta.
a
a)) Simulazione del flusso attraverso il corpo diga: il calcolo del flusso è diviso nelle tre
aree di: moto sub-critico a monte della sezione di controllo, moto super-critico a valle della sezione di controllo, area d’influenza della
corrente di valle (moto sub-critico). Durante ogni passo temporale si considera che il flusso sia stazionario. I calcoli si basano sulle seguenti formule (Chow, 1950):
(31)
dove Sf rappresenta la pendenza della linea
dell’energia data da: con
Per ogni sezione di controllo, le quantità con il pedice 1 rappresentano le quantità a monte mentre quelle con pedice 2 sono relative ai valori di valle; il pedice m ci indica che la quantità è calcolata come media aritmetica tra il valore di monte e quello di valle. Il coefficiente n di Manning è calcolato in funzione di quello di Chezy.
b
b)) Rottura per sormonto: la pendenza dei fianchi della breccia dipende dall’angolo d’attrito
β del materiale. La portata che attraversa la breccia è calcolata con la formula di Fread (1988b): 5 . 2 br w sub 5 . 1 br w sub br br 1.71B S (H Y ) 1.37ZS (H Y ) Q = − + − (32)
Figura 3. 9 – Sezione longitudinale della breccia L S g 2 V y g 2 V y f 2 2 2 2 1 1 + = + + ⋅ 3 4 m 2 2 m f R n V S = ⋅ 16 m R 1 n ⋅ χ =
Ssub è il fattore di correzione di portata ai piedi della diga (corrente di valle):
Hw2 rappresenta l’altezza liquida ai piedi della diga.
c
c)) Rottura per sifonamento: l’assunzione di partenza per il modello che analizza questo tipo
di crollo è il valore del diametro, solitamente molto piccolo, del canale circolare che si forma internamente al corpo diga, ad una certa quota dal fondo. La portata che attraversa il canale d’erosione è data dalla formula di Fread (1988a):
con (33)
Di queste formule ancora non sappiamo il significato di:
Hp = Quota, rispetto al fondo canale, del centro del canale d’erosione ∆Hp = Hw-Hp nel caso in cui Hp>Hw2
∆Hp = Hw-Hw2 nel caso in cui Hw2>Hp L = Lunghezza del canale interno
D = Diametro del canale interno
La dimensione del canale cresce in funzione della velocità del flusso idrico e delle proprietà del materiale. Gli autori di questo modello individuano un raggio critico, detto appunto Rcrit,
oltre il quale non può estendersi il canale interno giacché si verifica il crollo di tutto il materiale soprastante all’interno dalla breccia. Da questo momento in poi, la valutazione della portata effluente torna ad essere uguale al caso del sormonto.
(
) (
)
(
d p)
crit H H 2 tg tg 2 tg C 2 R − + ϕ ϕ + + ϕ ρ′ = (34) L’altezza della diga è espressa in metri, la coesione in kPa e la densità immersa del materiale in kg/m3 (densità del materiale – densità dell’acqua).) Y H ( 3 2 Y Hw2 − br≤ w − br
S
sub=
1
) Y H ( 3 2 Y Hw2 − br ≥ w − br ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − − = 0.67 Y H Y H 83 . 27 0 . 1 S br w br 2 w sub 6 1 50 D d 086137 . 0 f ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =( )
2 1 p br D fL 1 H g 2 A Q ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + ∆ =d
d)) Meccanismo d’allargamento della sezione a causa dell’erosione
Non è facile scegliere una formula di trasporto solido che ben si adatti a questo tipo di situazione, E.Loukola e M.Houkuna calcolano la quantità di materiale eroso tramite la formula di Mayer-Peter e Müller. Si considera che l’azione tangenziale causata dal flusso idrico è proprio l’azione critica per l’erosione. La portata volumetrica solida per unità di profondità è: (35) Con f wRS ρ = τ e 5 50 c
=
4
.
7
⋅
10
ρ′
d
τ
−Naturalmente ρw è la densità dell’acqua in kg/m3, R è il raggio idraulico e la pendenza della
linea dell’energia è valutata con la formula di Chezy:
con (36)
V è la velocità d’efflusso in m/s e Ks è la rugosità equivalente di Nikuradse, che nel presente
modello è fissata a
K
s=
d
50.Detto PB il perimetro della sezione bagnata, ma nel caso in cui la breccia raggiunga il fondo
non erodibile del canale o nel caso di Bbr > hbr assume il valore di
P
B=
2
P
1+
2
h
br, si hache la portata totale di sedimenti è data da:
s B
s
P
q
Q
=
⋅
[m/s] (37) Il modello che è stato presentato da questi autori può essere facilmente legato a modelli di propagazione della portata. Basandosi su semplici dati d’ingresso, i calcoli sono molto veloci e quindi è un ottimo strumento per ottenere una rapida stima dell’idrogramma d’efflusso.[m3/s/m]
(
)
32 c 2 1 w s 056 . 25 q τ−τ ρ′ ρ = R V S 2 2 f χ = 6 1 s K R 66 . 7 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = χ3.3.5. Le equazioni di Coleman, Andrews e Webby
Nella pubblicazione del Journal of Hydraulic Engineering, settembre 2002, è riportato l’articolo dei ricercatori S. E. Coleman, D. P. Andrews e M. G. Webby. Essi presentano delle equazioni adimensionali ricavate da un’accurata analisi dei dati di evoluzione della breccia, in dighe di materiale omogeneo non-coesivo, ottenuti da esperimenti di laboratorio a scala ridotta.
I dati sperimentali in esame derivano dal lavoro condotto da Jack (1996) e Andrews (1998) i quali realizzano piccole dighe, in canali sperimentali, con materiale avente differenti diametri. In particolare, Andrews utilizza un canale lungo 12 m e largo 2.4 m dotato di uno sfioratore laterale e di una vasca di raccolta, a valle, alimentata da uno stramazzo triangolare per il calcolo della portata.
Figura 3. 11 – Apparato sperimentale di Andrews
All’interno del canale sono posizionate anche due sonde per la rilevazione dei livelli liquidi e una particolare piastra ruotante a monte della diga, disposta inizialmente orizzontale sul fondo del canale, che blocca il flusso quando si vuole arrestare il processo erosivo. Quando la piastra si dispone verticalmente, e il flusso sulla diga si blocca, entra in funzione lo sfioratore laterale per lo smaltimento della portata in arrivo.
Le dighe sperimentali sono tutte alte 30 cm, la struttura di Andrews ha una larghezza in cresta di 6.5cm e una pendenza di fianchi di 2.7:1 (H:V), quella di Jack ha forma praticamente triangolare (larghezza di cresta nulla) e la pendenza dei fianchi è 2.5:1. Le caratteristiche dei materiali utilizzati per gli esperimenti si trovano nella tabella 5. Gli esperimenti sono condotti in modo tale che, raggiunto un grado d’erosione desiderato, si possa rilevare la superficie della struttura in modo molto accurato. Dopo che la portata liquida ha modificato la superficie della diga per un certo intervallo di tempo, si ruota la piastra metallica e si aspetta lo svuotamento del canale. A questo punto è possibile utilizzare un potenziometro digitale che registra la quota y e z dei punti desiderati. Sono così rilevate sezioni trasversali ogni 10 cm in direzione longitudinale. Per ogni sezione, analizzando i punti con coordinata massima ymax e zmax, si può
calcolare la lunghezza della linea che individua il fondo della breccia (Lb). Per questo ed altri
parametri geometrici utilizzati nelle relazioni adimensionali si rimanda il lettore alla figura 15.
Figura 3. 13 – Rappresentazione dei parametri di breccia di riferimento; metà-sezione del manufatto Figura 3. 12 – Proprietà dei materiali del corpo delle dighe
Analizziamo i punti essenziali in cui Coleman, Andrews e Webby dividono il loro studio:
a
a)) Processo d’erosione della breccia: Il deflusso, che riesce ad attraversare il canale pilota,
inizia l’erosione del paramento di valle fino al piede. La rottura evolve inizialmente con una predominanza d’erosione verticale e, dopo che il fondo della breccia ha raggiunto la fondazione, l’erosione dominante diviene quella alterale. La forza del flusso idrico causa l’instabilità del materiale collocato sui fianchi della breccia.
La conseguenza è che se verificano crolli improvvisi di blocchi di materiale all’interno del canale di breccia. Il fondo di tale canale, a seguito dell’erosione, si mantiene parallelo al paramento di valle, per un certo tempo. Dopo che il piede del canale è retrocesso fino al punto di rotazione (“pivot point”, figura 13b) la sua pendenza comincia a diminuire e l’appiattimento prosegue fino al raggiungimento di una pendenza limite Smin. E’ indicato che
tale valore è dell’ordine dell’1.5% per sbarramenti in materiale omogeneo e non coesivo.
b
b)) Geometria della breccia
La sezione di controllo per il deflusso uscente dalla breccia è collocata, in accordo con Coleman (1997), nella parte a monte della cresta.
Figura 3. 14 – (a) Sovrapposizione dei punti misurati e calcolati per la semi-sezione trasversale
(b) Profilo longitudinale del canale di breccia
Tipicamente, la forma della breccia è schematizzata come triangolare o trapezoidale ma, da queste esperienze, emerge chiaramente che la reale sezione trasversale della breccia è parabolica. Gli autori definiscono la seguente relazione adimensionale per la larghezza della breccia: 5 . 0 * * *
2
k
y
B
=
(38)con:
; ;
Il fattore k* rappresenta un coefficiente adimensionale per la forma parabolica e, in
corrispondenza della sezione B-B di figura 3.12, assume la forma di:
[
ln(
H
)
]
0
.
351
82
.
2
k
*=
−
b*+
(39) conE’ fornita anche una relazione per individuare la posizione del punto di rotazione alla base della diga, Xp dipende dal diametro d50 del materiale. Se tale materiale è relativamente grande
allora il punto di “pivot” è collocato proprio al piede della struttura.
c
c)) Velocità d’erosione: in base agli esperimenti considerati, la variazione della lunghezza
della linea che individua il fondo della breccia, in un piano verticale, è data da:
616 . 0 * 3 * e
1
.
29
10
(
t
)
L
=
⋅
− (40) con ePer la variazione della quota del fondo della breccia, in mezzeria, si propone:
1 * *
b
(
2
.
30
t
1
)
H
=
+
− (41) Le equazioni appena scritte sono valide per livello d’invaso costante e per geometrie delle strutture simili a quelle utilizzate da Andrews e Jack. La velocità d’erosione verticale si ottiene calcolando dHb*/dt*, mentre la velocità d’erosione laterale può essere calcolata comedLe*/dt*.
d
d)) Deflusso attraverso la breccia: gli autori confermano la scelta, adottata anche da molti
altri ricercatori, di valutare la portata effluente dalla breccia con la formula dello stramazzo in
parete grossa 5 . 0 d b
C
Ah
Q
=
. Con A si indica la sezione trasversale coinvolta nel deflusso e con h il carico idraulico sullo stramazzo, con precisione h è misurato sulla linea di mezzeria del canale di breccia. In questo modello, i parametri di breccia per la valutazione del coefficiente d’efflusso Cd sono calcolati in corrispondenza della cresta della breccia.s *
H
B
B
=
s *H
y
y
=
0.5 s *H
k
k
=
′
s b * bH
H
H
=
s e * eH
L
L
=
s 2 *H
gt
t
=
Con tale assunzione l’area A, adimensioanlizzata, prende il nome di Ab* e si valuta con:
)
h
L
(
672
.
0
A
b*=
b* b* (42) con ; ;La combinazione della (42) con la formula dello stramazzo fornisce l’equazione adimensionale per il picco di portata:
( )
1.5 * b * b * b0
.
242
L
h
Q
=
(43) (44)La relazione (43) indica che il coefficiente d’efflusso è stato considerato Cd = 0.758 m1/2/s. Grazie ai dati a disposizione, è stato possibile individuare un legame esponenziale tra la lunghezza del perimetro di breccia Lb e il carico liquido in corrispondenza della mezzeria
della breccia hb: 5 . 1 * b * b
16
(
h
)
L
=
(45) con 0 (livello d’invaso) ≤ hb≤ H (fondazione). Assumendo valida tale espressione la portata dipicco è, infine, valutata con:
( )
3 * b * b3
.
87
h
Q
=
(46) Per rendere applicabili le conoscenze sviluppate in questo lavoro alla valutazione della rottura di grandi dighe, le relazioni sopra descritte sono state usate per la creazione di un modello numerico. E’ stata naturalmente aggiunta anche un’equazione per il trasporto solido. Nonostante le numerose limitazioni, i risultati che si sono ottenuti applicando il modello al caso studio della diga di Teton indicano che il modello ha grandi potenzialità soprattutto nel fornire la descrizione della sezione di breccia.2 * b H A A = H L L b * b = H h h b * b = 5 . 2 5 . 0 b * b
H
g
Q
Q
=
3.4. Considerazioni sulle incertezze delle conoscenze attuali
Tutti i modelli che abbiamo presentato contengono inevitabilmente delle incertezze, esse sono evidenti nei metodi empirici ma possono essere riscontrate anche nel comportamento dei modelli fisicamente basati. I primi portano con sé la mancanza fondamentale che è quella di non avere nessun rapporto con i principi fisici che intervengono nella modellazione di un’opera in materiale sciolto. Questo implica che le relazioni derivanti da analisi statistiche di regressione, seppure il più accurate possibili, sono forzatamente legate alla natura dei casi studio sui quali si basano. I modelli fisici, sebbene si fondino sulla risoluzione di equazioni dell’idraulica e sull’analisi di principi strutturali e geotecnici, sono anch’essi caratterizzati da numerose assunzioni semplificative. Il risultato è che difficilmente c’è un alto grado d’affidabilità nell’applicazione delle metodologie esistenti ai più svariati casi di potenziale rottura di opere di sbarramento in materiale sciolto. La conseguenza peggiore si manifesta nell’incertezza della valutazione del rischio e quindi nell’incapacità di gestire situazioni di possibile emergenza.
Per comprendere quanto possano pesare, sulla potenzialità di previsione dei modelli, le incertezze delle assunzioni e la mancanza di dati misurati precisi è sufficiente mettere a confronto i loro risultati. Già nel 1984 Singh e Snorrason si sono accorti dell’importanza di confrontare i meriti teorici e pratici delle metodologie allora disponibili. Essi propongono di testare il modello HEC-1 e il modello DAMBRK, sui dati disponibili di 8 dighe dell’Illinois, facendo variare la portata di massima piena affluente e utilizzando diverse combinazioni dei parametri di breccia. Vedremo tra poco le conclusioni di questo studio che, oltre a fornire una relazione sperimentale per la stima di Qp, si presentano interessanti per dare una prima idea di
quanto possa incidere sul risultato la scelta di ogni singolo parametro.
Di seguito, si riporta una più accurata analisi d’incertezza condotta da Wahl nel 2001 sulle previsioni dei parametri di breccia, e picco d’efflusso, offerte da svariati metodi esistenti.
Ci chiediamo infine: disponiamo di tecniche veramente efficaci per affrontare con sicurezza la valutazione delle conseguenze della rottura di un’opera soggetta alla formazione
Cominciamo con ricordare le principali caratteristiche dei modelli HEC-1 e DAMBRK. Entrambi necessitano di un simile set di dati in ingresso ma gli algoritmi si basano su sistemi d’equazioni differenti. I parametri di breccia considerati sono: la pendenza dei fianchi di breccia (Z), la larghezza finale del fondo della breccia (Bbr), la quota finale del fondo della breccia (Ybr), il tempo di formazione della breccia (TF) e l’altezza liquida sulla breccia Hf calcolata rispetto alla fondazione della struttura.
- Il modello HEC usa il metodo di calcolo “modified Plus”, che trasforma l’equazione di continuità in un’equazione alle differenze finite (Chow, 1964):
- Il modello NWS DAMBRK si basa sulla risoluzione delle equazioni di Saint Venant, come già descritto al paragrafo 3.2.
Per effettuare il confronto tra i due modelli i ricercatori hanno scelto di attribuire i seguenti valori ai parametri di breccia sopra descritti:
Z: si assume 0.5 nel caso del sormonto e 0 nel caso di sifonamento Bbr: è sta posta uguale a 2Hd e 4Hd
hf: l’altezza di sormonto (Hf - Hd) è stata posta 0.15 o 0.61 TF: si sceglie il tempo di 0.25h, 0.5h e 1h
In generale, le portate di picco stimate dal modello del NWS sono maggiori del 10% rieptto a quelle prodotte da HEC. Analizzando, invece, la sensibilità del picco di portata in uscita dalla breccia nei confronti dei vari parametri si ha che: l’incremento della Qp dovuto ad un innalzamento della quota di rottura (Ybr) è relativamente basso, e si attesta tra il 2 e il 21% (molti casi rientrano nell’intervallo 14-21%); una riduzione del 50% del tempo di formazione della breccia provoca, invece, un incremento del picco di portata del 13-83% per dighe con piccoli invasi, e solo dell’1-5% per dighe con grandi invasi; l’allargamento del fondo della breccia (Bbr) nel caso di piccoli invasi ha generato un innalzamento del picco del 65-50% circa, per grandi invasi l’incremento è del 35-87% circa. L’aspetto più evidente è che il picco di portata risulta fortemente legato alla capacità d’invaso dello sbarramento.
E’ chiaro che tale sensibilità alle variazioni dei parametri di breccia implica la necessità di una loro stima molto accurata. Purtroppo Wahl, con la sua analisi d’incertezza condotta nel 2001, richiama l’attenzione sull’incapacità dei metodi esistenti di essere strumenti affidabili di previsione dei parametri chiave per l’evoluzione della rottura di una diga.
Se = deviazione standard (con ±2Se si rappresenta una fascia di confidenza del 95%
Tabella 3. 6 – Risultati dell’analisi d’incertezza proposta da Wahl per i parametri di breccia
Questo suggerisce che sarebbe utile considerare l’incertezza della previsione dei
parametri all’interno del processo di valutazione del rischio di un’opera in materiale sciolto. Significherebbe operare lo stesso procedimento, già seguito per le incertezze sulla natura dei materiali e sulle cause che possono portare al crollo, che si concretizza nella scelta di differenti condizioni di carico e scenari di rottura. Per sintetizzare il risultato della vasta analisi che Wahl conduce su 108 casi studio abbiamo riportato la tabella 3.4, ricavata dalla sua pubblicazione.
La previsione della larghezza della breccia ha evidenziato un’incertezza di circa ±1/3 dell’ordine di grandezza, per il tempo di formazione di breccia si arriva ad un’incertezza di ±1 ordine di grandezza mentre la stima diretta del picco di efflusso mostra l’incertezza da ±0.5 a ±1 ordine di grandezza, tranne per il risultato di Froehlich che è il più preciso con un’incertezza di solo ±1/3 dell’ordine di grandezza.
Per concludere, proviamo a dare una risposta all’ultimo quesito. Le tecniche a disposizione per operare delle supposizioni sulla formazione della breccia sono numerosissime. La continua ricerca è però sintomo d’inadeguatezza e, da questo, ecco la spiegazione del grande numero di risultati prodotti. Per una medesima diga in materiale sciolto analizzata, possiamo ricavare il valore del possibile picco Qp, effluente dalla breccia,
con una formula empirica (ad esempio quella di Froehlich (1995a) che è giudicata una delle migliori) ed ottenere il doppio di questo valore, cioè 2Qp, inserendo i parametri di breccia
stimati con formule empiriche (possiamo nuovamente usare i risultati di Froehlich (1995b)) in un modello parametrico tipo DAMBRK. Siamo costretti a concludere che i metodi per la previsione dei parametri di breccia sono lontani da offrire una loro stima realistica.
La strada da percorrere nel futuro è sicuramente quella della comprensione dei meccanismi fisici correlati allo sviluppo della breccia e, quindi, quella della realizzazione di modelli fisicamente basati per la determinazione dell’idrogramma effluente.