Capitolo 3 DESCRIZIONE DEL MODELLO MATEMATICO UTILIZZATO PER LO STUDIO DINAMICO

Capitolo 3

DESCRIZIONE DEL MODELLO MATEMATICO UTILIZZATO

PER LO STUDIO DINAMICO

3.1 Generalità

Sono molti i modelli matematici in grado di rappresentare, più o meno accuratamente, la dinamica di un sistema reale. In genere sono costituiti da un numero di parametri e di variabili gestibili con una certa semplicità, cercando di adempiere allo stesso tempo alle esigenze di un risultato preciso e di un sistema flessibile e facile da usare.

In commercio troviamo alcuni codici multi body, tra i quali MSC.ADAMS®, che grazie all’elevata potenza raggiunta dai moderni calcolatori consentono di simulare il comportamento dinamico di un sistema, fornendo una serie di dati con una precisione che fino a pochi anni fa era impensabile. Con tali software non è necessario scrivere le equazioni che governano l’evoluzione dinamica del sistema in studio, basta solamente realizzare un modello che possa essere considerato, dal punto di vista fisico, del tutto equivalente al sistema reale. Un lato negativo di questi software è che richiedono all’utente elevata preparazione e competenza specifiche nel loro utilizzo. Inoltre, è vero che forniscono dati molto precisi, ma ne pretendono molti di altrettanta precisione. Possono essere quindi difficili da gestire, ad esempio durante le fasi iniziali del progetto, dove certamente non sono ancora stati definiti completamente tutti i componenti. E’ comunque vero che un approccio troppo semplicistico si rileverebbe inefficace, ma uno troppo preciso potrebbe comportare un inutile spreco di risorse.

Una via alternativa è rappresentata dai cosiddetti modelli a parametri concentrati, nei quali un sistema meccanico viene semplificato operando una sua divisione in vari

componenti elementari, quali masse, molle, smorzatori, ecc., tramite i quali vengono poi impostate le equazioni che definiscono la dinamica del sistema. A questo punto è possibile simulare il comportamento del sistema, ad esempio in ambiente software Simulink®. Questo tipo di approccio offre una grande versatilità e permette di decidere molti fattori, tra cui il livello di precisione che si vuole raggiungere, quali fenomeni fisici considerare e quali trascurare, il numero di gradi di libertà.

Un ulteriore modo di procedere potrebbe essere l’utilizzo di modelli a parametri distribuiti, i quali pur semplificando la realtà, e quindi introducendo a loro volta delle approssimazioni, studiano il sistema come un insieme di elementi continui. Questa non discretizzazione del sistema consente di ottenere in genere una soluzione puntualmente più precisa. Lo svantaggio sta nella necessità di utilizzare pochi parametri, in modo da mantenere gestibile il calcolo.

E’ possibile tuttavia combinare i due metodi, in modo da sfruttare i vantaggi di entrambi.

3.2

Scelta del modello

La scelta del modello è stata effettuata in maniera tale da raggiungere due scopi principali. In primo luogo si è voluto realizzare un modello relativamente semplice, a tutto vantaggio della praticità e della velocità di utilizzo. Come seconda cosa si è cercato di ottenere un modello il più generale possibile, che consentisse cioè di essere adattato ad altre trasmissioni aventi disposizioni anche differenti da quella presa in esame.

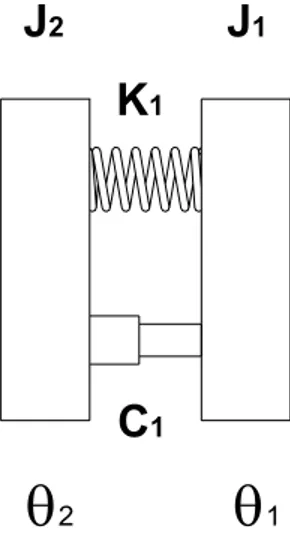
A seguito di queste prime valutazioni si è ritenuto più adatto il modello a parametri concentrati. Inizialmente ogni componente del drive train è stato sostituito con un volano avente un equivalente momento di inerzia polare. Come connessione tra questi è stata inserita una molla torsionale capace di ricreare l’azione del tratto di albero che collega i vari elementi della trasmissione. Oltre alla molla si è pensato che fosse importante introdurre anche un organo in grado di smorzare il moto, in modo da riprodurre l’effetto dello smorzamento interno che presentano i materiali. A tale scopo è stato inserito uno smorzatore viscoso. La Figura 3-1 mostra un esempio dove si sono collegati due volani di momento d’inerzia polare J1 e J2 con una molla

torsionale di costante elastica K1 e uno smorzatore viscoso C1. θ1 e θ2 sono gli angoli

J

J

K

θ

θ

C

Figura 3-1 – Schema a due volani con molla e smorzatore

3.3

Formulazione matriciale del problema

Una volta definito il sistema per prima cosa andremo a scrivere le equazioni del moto. Ci troveremo quindi di fronte ad un numero di equazioni differenziali del secondo ordine in θi con i=1÷n dove n è il numero di gradi di libertà del sistema,

ovvero il numero di volani. Vista la possibilità di lavorare anche con dieci gradi di libertà il problema può risultare difficile da gestire; è per questo che viene usata la notazione matriciale. Le equazioni scritte vengono raccolte in modo da ottenere il sistema

Jθ&&+Cθ& +Kθ =M (34)

Dove J è la matrice di massaa, C è la matrice di smorzamento, K è la matrice di rigidezza ed M il vettore dei momenti esterni applicati al sistema. θ invece è il vettore le cui componenti rappresentano gli spostamenti angolari dei vari gradi di libertà. Viste le caratteristiche del sistema analizzato C e K sono simmetriche e J è diagonale.

3.4

Analisi modale

Un importante aspetto da considerare nello studio del comportamento dinamico del sistema riguarda la ricerca dei suoi modi propri. Può infatti capitare che ad un preciso valore del numero di giri dell’albero motore il sistema venga forzato proprio in corrispondenza di una delle sue frequenze di risonanza. Ciò provocherebbe un aumento indesiderato dell’ampiezza delle vibrazioni, perturbando di conseguenza il moto di tutto il sistema ed amplificando gli effetti dei fenomeni dinamici.

Impostare il problema degli autovalori ci consente di calcolare le frequenze proprie del sistema [6].

Al fine di individuare le armoniche che rischiano di alimentare deleteri fenomeni di risonanza è necessario scomporre la forzante in serie di Fourier [7].

3.4.1 Calcolo delle frequenze di risonanza

E’ importante sottolineare che il calcolo è strettamente dipendente dal sistema studiato; quindi ogni configurazione che andremo ad analizzare avrà dei risultati differenti dalle altre.

Si è ipotizzato uno smorzamento di tipo proporzionale, definito da una matrice di smorzamento del tipo

C=α J+βK (35)

dove α e β sono due costanti.

Al fine di calcolare le frequenze proprie del sistema è lecito studiare il generico sistema libero (privo di smorzamenti). Scrivendo le equazioni in forma matriciale otteniamo la relazione

Jθ&&+Kθ =0 (36)

Si è ipotizzato una soluzione del tipo

t i

eω

che sostituita nella (36) porta ad un sistema algebrico omogeneo lineare in Θ e parametrico in ω :

(−ω2_{J+K )}⋅Θ

=0 (38)

questo sistema ammette soluzioni non tutte nulle se e solo se, definendo con

A= J-1 _{K (39)}

si ha che

det (A−ω2_{I)=0 (40)}

con I matrice identica. I valori di ω2

che soddisfano questa relazione si dicono autovalori della matrice A e rappresentano le frequenze proprie del sistema, che saranno tante quanti sono i gradi di libertà del sistema stesso. Imponendo alla pulsazione propria ω il valore generico ω_i nel sistema (38) è possibile calcolare il generico i-esimo modo principale di vibrare Θ , la cui deformata sarà definita a (i)

meno di una costante. Le frequenze proprie f del sistema libero si calcolano con la _i relazione π ω 2 i i f = (41) ) (i

Θ si dice autovettore della matrice A relativo all’i-esimo autovalore.

3.4.2 Analisi di Fourier

Una generica funzione periodica x

( )

( )

_∑

con

( )

∫

la quale è definita armonica fondamentale.

Lo spettro di una funzione periodica è evidentemente costituito da un certo numero (finito o infinito) di armoniche, poste a distanza f1 l’una dall’altra [7]. In Figura 3-2 è

mostrata a titolo di esempio, la scomposizione nel dominio del tempo e delle frequenze di una funzione x

( )

Figura 3-2 – Se x

( )

( )

3.4.3 Calcolo dei coefficienti di smorzamento

Tramite l’analisi delle pulsazioni proprie del sistema è possibile, con un procedimento algebrico ottenere una stima dei coefficienti di smorzamento da inserire nel modello [6].

Si supponga di aver posto il sistema nella forma espressa dall’equazione (38) e calcolato la matrice A tramite la relazione (39). e’ possibile a questo punto calcolare gli autovalori di A e gli autovettori Θ corrispondenti a ciascun autovalore. (i)

Si definisce Y la matrice modale del sistema, ovvero la matrice che ha come colonne gli n modi di vibrare (autovettori). Dunque sarà

Y =[Θ ,(1) Θ ,…,(2) Θ ] (n) ₍₄₄₎

E’ importante notare che gli autovettori presentano le seguenti proprietà

YiT J Yk= δ_ikµ_i (45)

YiT K Yk= δikωi µi

2

(46)

dove δ_ik è il delta di Kronecker, e si dicono ortogonali rispetto alle matrici di massa e di rigidezza.

Se composta da autovettori di questo tipo, la matrice Y assume la proprietà fondamentale di disaccoppiare le equazioni del moto, ovvero di scindere il sistema di n equazioni in altrettante equazioni indipendenti le une dalle altre, risolvibili separatamente. Ciò avviene diagonalizzando le matrici dei momenti d’inerzia J e di rigidezza K definite nel Paragrafo 3.3, tramite le relazioni

YT J Y= J* (47)

YT K Y= K* (48)

Dove J* e K* sono le nuove matrici dei momenti d’inerzia e di rigidezza, ora entrambe diagonali.

Si noti che nel caso di autovettori ortonormali, cioè “scalati” in modo che µ_i =1, la matrice J* diviene la matrice identica I e K*, che ora indichiamo con

Ω,

Si considera la trasformazione

dove a è un vettore, funzione del tempo, il cui generico elemento a_i

( )

Tramite il procedimento sopra indicato, in pratica si è effettuato un cambiamento di variabili. Le nuove coordinate si dicono principali.

Applicando tale trasformazione alla (34), moltiplicando a sinistra ogni membro per YT e tenendo conto delle proprietà di ortogonalità dei modi propri, si ottiene

Ia&&+YTCYa&+

Ω

Avendo supposto uno smorzamento di tipo proporzionale, vale a dire una matrice C con la seguente forma

C=αJ+βK (35)

Si ha che ogni vettore Yi è ortogonale alla matrice di smorzamento e la (50) si

trasforma in n sistemi ad un grado di libertà. Indicando con

YiT C Yk=δ_ik

(

)

Dalla (50) si ottiene, per ogni modo proprio

i i i i i i a a m a +_γ +_ω2 = & && (52)

dove m = Y_i iTM è la forza modale.

In analogia con un sistema ad un grado di libertà con smorzamento, per mettere in evidenza il rapporto di smorzamento modale ξ_i, la (52) può essere scritta in questo modo i i i i i i i a a m a + + 2 = 2ξω & ω && (53)

i i i ξω

γ =2 (54)

E’ da notare che per le (52) e (51) si può scrivere

YiT C Yi=γ_i =2ξ_iω_i =α+βω_i2 (55)

Dalla quale risulta che il rapporto di smorzamento modale è legato ad α β dalla relazione 2 2 i i i βω ω α ξ = + ₍₅₆₎

A questo punto, conoscendo due valori di ξ_i, si possono determinare α e β. Se sono disponibili più valori di ξ_i, è possibile ricavare α e β col metodo dei minimi quadrati [6].

Nel seguente capitolo si riportano i risultati delle analisi effettuate su tutti i modelli studiati, ottenuti seguendo i procedimenti sopra spiegati.