Antenna Azimuth con riflettore sagomato

(1)

Capitolo 8:

Antenna Azimuth con riflettore sagomato

8.1 Generalità

Anche nel caso dell’Antenna Azimuth, per ottenere un andamento del guadagno che si avvicina a quello richiesto dalle specifiche, è necessario sagomare la superficie del riflettore.

Nei paragrafi successivi vengono mostrati gli andamenti del guadagno ottenuti deformando la superficie del riflettore mediante i metodi descritti nel capitolo 2.

8.2 Deformazione mediante polinomi rettangolari

La deformazione della superficie è stata effettuata utilizzando sia un

algoritmo genetico binario che un algoritmo genetico reale.

Nelle figure 8.1, 8.2 e 8.3 riportiamo l’andamento del guadagno ottenuto mediante il GA binario.

Come possiamo notare dalle figure 8.1 e 8.2 anche dopo molte iterazioni non siamo riusciti a soddisfare, la richiesta di ottenere un guadagno max di 38 dB ma questo si è fermato intorno ai 37.3 dB

Per quanto riguarda invece l’andamento del guadagno ottenuto, questo poteva essere ritenuto molto simile, soprattutto nell’intorno del lobo principale, a quello richiesto dalle specifiche.

(2)

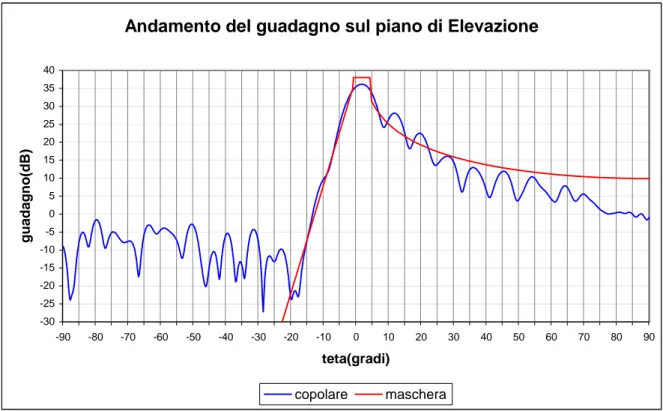
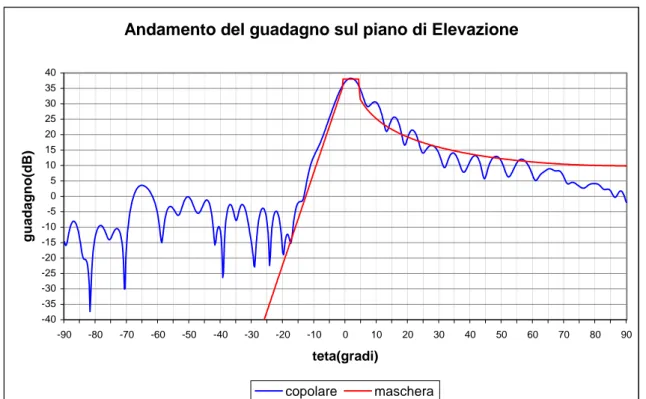
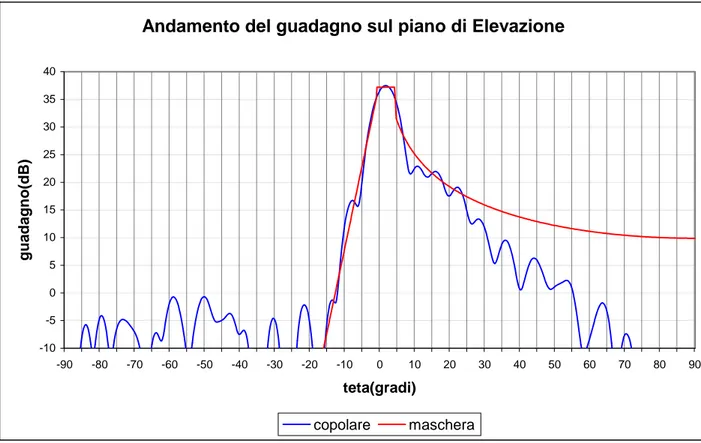
Infatti, l’andamento ottenuto sul piano di Elevazione (fig. 8.1) decresce di -3 dB ogni grado per la parte sotto l’orizzonte (ϑ ≤ 0) mentre, si avvicina ad un andamento a 2

cosec per la parte sopra l’orizzonte )

0 (ϑ ≥ .

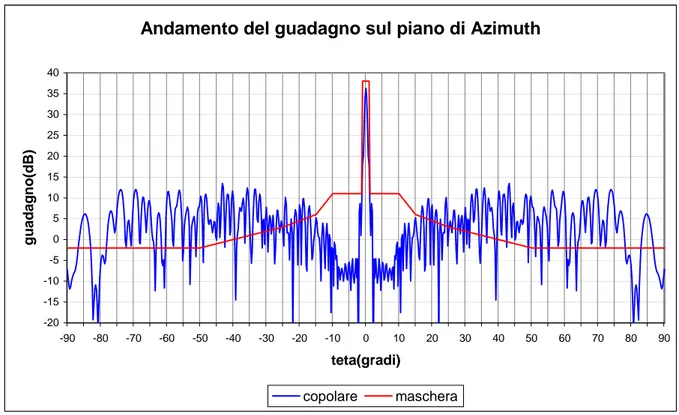
Sul piano di Azimuth invece otteniamo un lobo principale stretto e lobi secondari che si trovano al di sotto della maschera.

Andamento del guadagno sul piano di Elevazione

-30 -25 -20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) guadag no( dB ) copolare maschera

Figura 8.1: Andamento del guadagno della componente copolare sul piano di Elevazione (piano H) con riflettore sagomato mediante polinomi rettangolari e GA binario.

(3)

Andamento del guadagno sul piano di Azimuth -20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) guadag no(dB) copolare maschera

Figura 8.2: Andamento del guadagno della componente copolare sul piano di Azimuth (piano E) con riflettore sagomato mediante polinomi rettangolari e GA binario.

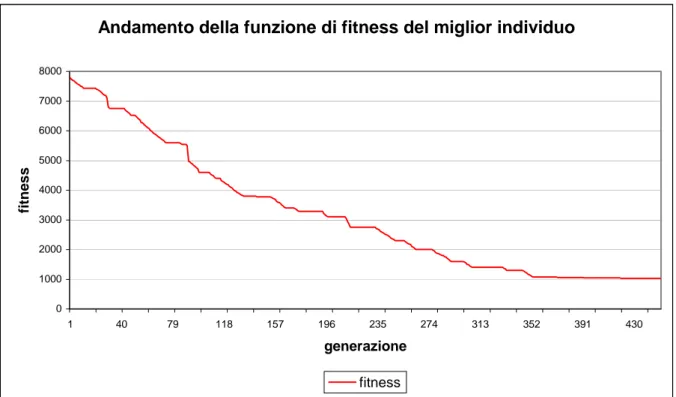
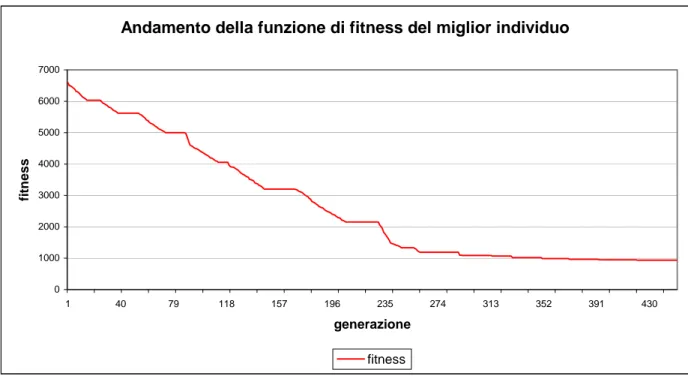
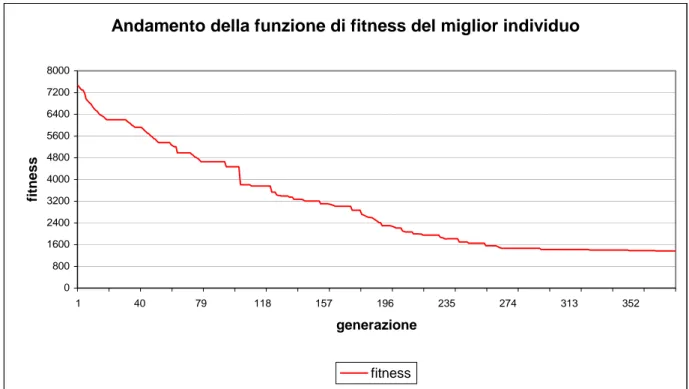
In figura 8.4 riportiamo l’andamento della funzione di fitness del miglior individuo di ogni generazione per circa 450 generazioni, come possiamo notare arrivati nei dintorni della generazione 350 non si è più verificato un miglioramento significativo del valore di fitness. Ciò lascia presupporre che anche continuando il processo di ottimizzazione non si sarebbero ottenuti risultati migliori.

(4)

Andamento della funzione di fitness del miglior individuo 0 1000 2000 3000 4000 5000 6000 7000 8000 1 40 79 118 157 196 235 274 313 352 391 430 generazione fitnes s fitness

Figura 8.4: Andamento del valore della funzione di fitness del miglior individuo di ogni generazione nel caso di GA binario e deformazioni mediante polinomi rettangolari.

Gli andamenti ottenuti mediante il GA reale, sono riportati nelle figure 8.5, 8.6 e 8.7.

(5)

Andamento del guadagno sul piano di Elevazione -20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) guadag no(dB) copolare maschera

Figura 8.5: Andamento del guadagno della componente copolare sul piano di Elevazione (piano H) con riflettore sagomato mediante polinomi rettangolari e GA reale.

Andamento del guadagno sul piano di Elevazione

-20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) gua da gno( d B ) copolare maschera

Figura 8.6: Andamento del guadagno della componente copolare sul piano di Azimuth (piano E) con riflettore sagomato mediante polinomi rettangolari e GA reale.

(6)

Anche in questo caso l’andamento del guadagno ottenuto, soprattutto nell’intorno del lobo principale, risulta su entrambi i piani soddisfacente. Tuttavia pur ottimizzando mediante il GA reale, non siamo riusciti a realizzare un guadagno di 38 dB.

Questo viene confermato dall’ andamento della funzione di fitness del miglior individuo di ogni generazione, mostrato in figura 8.8, osservando il quale si può notare che arrivati nell’intorno della generazione 300 non si verifica più un miglioramento del fitness.

Andamento della funzione di fitness del miglior individuo

0 1000 2000 3000 4000 5000 6000 7000 1 40 79 118 157 196 235 274 313 352 391 430 generazione fitn e s s fitness

Figura 8.8: Andamento del valore della funzione di fitness del miglior individuo di ogni generazione nel caso di GA reale e deformazione mediante polinomi rettangolari.

(7)

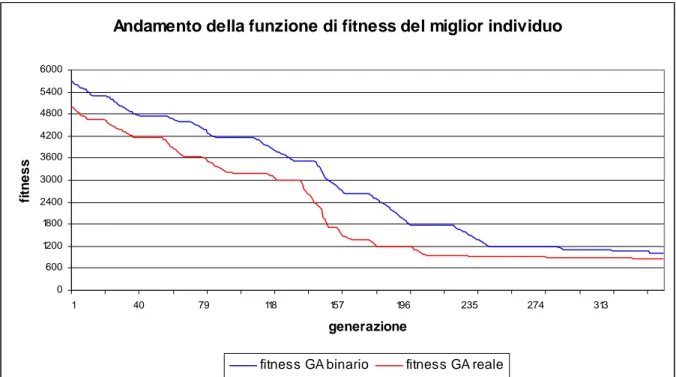
Per completezza mostriamo in figura 8.9 un confronto tra l’andamento del fitness del miglior individuo di ogni generazione del GA binario e del GA reale per circa 400 generazioni , naturalmente il confronto è stato effettuato a parità di condizioni operative.

Come possiamo notare per entrambi i metodi di ottimizzazione arrivati nell’ intorno della generazione 350, otteniamo un valore del fitness molto simile. Questo conferma che, nell’ambito del numero di generazioni considerato ( circa 400 ), nessuno dei due metodi di ottimizzazione può essere considerato migliore dell’altro.

0 600 1200 1800 2400 3000 3600 4200 4800 5400 6000 1 40 79 118 157 196 235 274 313 generazione fi tn e s s

fitness GA binario fitness GA reale

Figura 8.9: Andamento del valore della funzione di fitness del miglior individuo di ogni generazione nel caso di GA binario e di GA reale e deformazione mediante polinomi

(8)

Visto che, sia mediante il GA binario che mediante il GA reale, non abbiamo ottenuto un guadagno max di 38 dB, si è pensato di risolvere il problema aumentando la superficie del riflettore che viene illuminata dal feed.

Abbiamo quindi considerato un bordo ellittico avente un asse minore disposto lungo l’asse x pari a 430 mm, ed un asse maggiore disposto lungo l’asse y sempre di 3800 mm.

Nelle figure 8.10, 8.11 e 8.12 riportiamo l’andamento del guadagno ottenuto ottimizzando mediante GA binario.

Come possiamo notare, aumentando la superficie illuminata dal feed siamo riusciti ad ottenere un guadagno max di 38 dB come richiesto dalle specifiche.

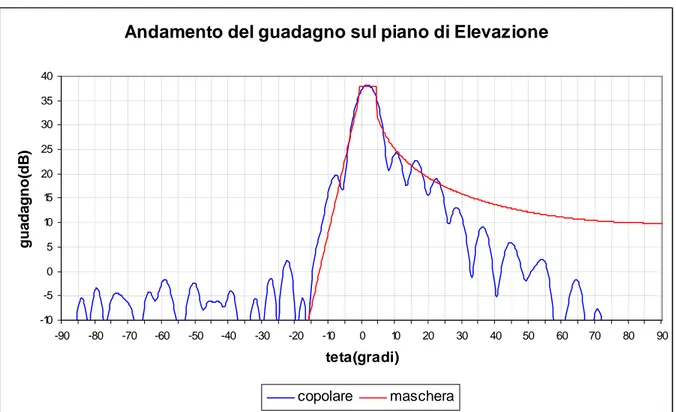
Per quanto riguarda gli andamenti del guadagno ottenuti, questi possono essere ritenuti soddisfacenti sia sul piano di Elevazione (fig. 8.10) che sul piano di Azimuth (fig 8.11).

(9)

Andamento del guadagno sul piano di Elevazione -40 -35 -30 -25 -20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) guadagno(dB) copolare maschera

Figura 8.10: Andamento del guadagno della componente copolare sul piano di Elevazione (piano H) con riflettore sagomato mediante polinomi rettangolari e GA binario.

Andamento del guadagno sul piano di Azimuth

-10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) gu a d a gno( dB ) copolare maschera

Figura 8.11: Andamento del guadagno della componente copolare sul piano di Azimuth (piano E) con riflettore sagomato mediante polinomi rettangolari e GA binario.

(10)

8.3 Deformazione mediante polinomi di Zernike

Anche in questo caso la deformazione della superficie è stata effettuata sia utilizzando un algoritmo genetico binario che un algoritmo genetico

reale.

Come possiamo notare sul piano di Elevazione (fig. 8.13), otteniamo un andamento del guadagno che può essere ritenuto soddisfacente per la parte sotto l’orizzonte (ϑ ≤ 0), mentre si osserva un certo allontanamento dall’andamento richiesto per la parte sopra l’orizzonte

) 0

(ϑ ≥ . Per quanto riguarda il valore max del guadagno, in questo caso abbiamo ottenuto i 38 dB richiesti senza che sia stato necessario aumentare le dimensioni del riflettore.

In figura 8.16 riportiamo l’andamento della funzione di fitness del miglior individuo di ogni generazione. Come possiamo notare una volta giunti nell’intorno della generazione 250 non si osserva più un miglioramento significativo del fitness, questo lascia presupporre che anche se si fosse continuato il processo di ottimizzazione l’andamento del guadagno non si sarebbe ulteriormente avvicinato all’andamento a

2

(11)

Andamento del guadagno sul piano di Elevazione -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) gua da gno( dB ) copolare maschera

Figura 8.13: Andamento del guadagno della componente copolare sul piano di Elevazione (piano H) con riflettore sagomato mediante polinomi di Zernike e GA binario.

-20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) gua da g no( dB) copolare maschera

Figura 8.14: Andamento del guadagno della componente copolare sul piano di Azimuth (piano E) con riflettore sagomato mediante polinomi di Zernike GA binario.

(12)

Andamento della funzione di fitness del miglior individuo 0 800 1600 2400 3200 4000 4800 5600 6400 7200 8000 1 40 79 118 157 196 235 274 313 352 generazione fi tn ess fitness

Figura 8.16: Andamento del valore della funzione di fitness del miglior individuo di ogni generazione nel caso di GA binario e deformazione mediante polinomi rettangolari.

Nelle figure 8.17, 8.18 e 8.19 riportiamo invece l’andamento del guadagno ottenuto mediante il GA reale.

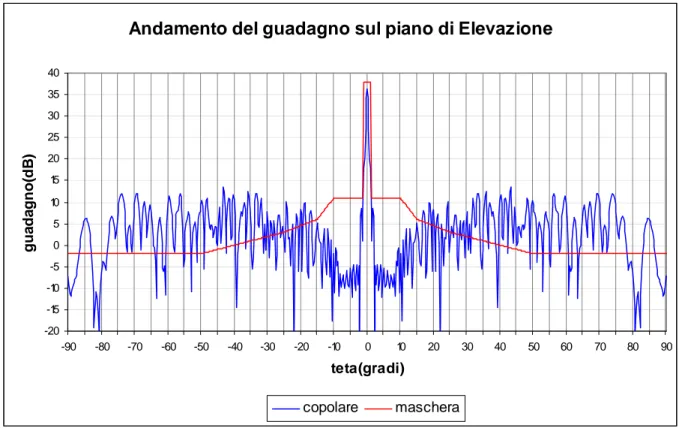
Come possiamo notare, mediante il GA reale, è notevolmente migliorato l’andamento del guadagno sul piano di Elevazione (fig. 8.17) per la zona sopra l’orizzonte (ϑ ≥ 0).

Per quanto riguarda l’andamento sul piano di Azimuth, otteniamo un lobo principale stretto e dei lobi secondari, che nell’intorno del lobo principale, si trovano al disotto della maschera.

(13)

Andamento del guadagno sul piano di Elevazione -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) gua da gno(dB) copolare maschera

Figura 8.17: Andamento del guadagno della componente copolare sul piano di Elevazione (piano H) con riflettore sagomato mediante polinomi di Zernike e GA reale.

Andamento del guadagno piano di Azimuth

-20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) gua dagno( d B ) copolare maschera

Figura 8.18: Andamento del guadagno della componente copolare sul piano di Azimuth (piano E) con riflettore sagomato mediante polinomi di Zernike e GA reale.

(14)

Possiamo quindi affermare che, nel caso di deformazione mediante polinomi di Zernike, l’ottimizzazione mediante GA reale ha fornito risultati migliori.

Questo è evidenziato anche dal diagramma 8.20, nel quale viene confrontato l’andamento del fitness dell’individuo migliore del GA binario e del GA reale per circa 400 generazioni. Come per i casi precedenti il confronto è stato effettuato a parità di condizioni operative.

0 700 1400 2100 2800 3500 4200 4900 5600 6300 7000 1 40 79 118 157 196 235 274 313 352 391 430 generazione fitn ess

Figura 8.20: Andamento del valore della funzione di fitness del miglior individuo di ogni generazione nel caso di GA binario e di GA reale e deformazione mediante polinomi di

(15)

8.4 Deformazione mediante funzioni B-Splines

Mostriamo, infine, i risultati ottenuti deformando mediante le funzioni B-Splines.

Come nei due casi precedenti la deformazione della superficie è stata effettuata sia utilizzando un algoritmo genetico binario che un algoritmo

genetico reale.

Per quanto riguarda l’andamento del guadagno sul piano di Elevazione (fig. 8.17), si ottiene un andamento accettabile per la parte sotto l’orizzonte (ϑ ≤ 0) mentre, sopra l’orizzonte (ϑ ≥ 0) si discosta da quello richiesto.

L’andamento del guadagno sul piano di Azimuth (fig. 8.22) presenta un lobo principale molto stretto e lobi secondari che, nell’intorno del lobo principale, si trovano al di sotto della maschera.

Questo è il miglior andamento che siamo riusciti ad ottenere, ciò si deduce osservando il valore della funzione di fitness del miglior individuo di ogni generazione mostrato in figura 8.24. Infatti, una volta giunti nell’intorno della generazione 250 non si osserva più un miglioramento significativo del fitness.

(16)

Andamento del guadagno sul piano di Elevazione -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) guadag no(dB) copolare maschera

Figura 8.21: Andamento del guadagno della componente copolare sul piano di Elevazione (piano H) con riflettore sagomato mediante funzioni B-Splines GA binario.

-20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) guadagno( dB ) copolare maschera

Figura 8.22: Andamento del guadagno della componente copolare sul piano di Azimuth (piano E) con riflettore sagomato mediante funzioni B-Splines e GA reale.

(17)

Andamento della funzione di fitness del miglior individuo 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 1 40 79 118 157 196 235 274 313 352 391 generazione fitnes s fitness

Figura 8.24: Andamento del valore della funzione di fitness del miglior individuo di ogni generazione nel caso di GA binario e deformazione mediante funzioni B-Splines.

Nelle figure 8.25, 8.26 e 8.27 riportiamo invece l’andamento del guadagno ottenuto mediante il GA reale.

Come possiamo notare, mediante il GA reale, si ottiene un notevole miglioramento dell’andamento del guadagno su entrambi i piani.

Infatti, sul piano di Elevazione il guadagno per la parte sopra l’orizzonte si avvicina maggiormente all’andamento a 2

cosec mentre, sul piano di Azimuth si riescono ad ottenere i 38 dB del guadagno max richiesto.

Quindi, anche in questo caso si sono ottenuti risultati migliori ottimizzando la deformazione mediante il GA reale.

(18)

Andamento del guadagno sul Piano di Elevazione -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) guadagno(dB) copolare maschera

Figura 8.25: Andamento del guadagno della componente copolare sul piano di Elevazione (piano H) con riflettore sagomato mediante funzioni B- Splines e GA reale.

Andamento del guadagno piano di Azimuth

-20 -15 -10 -5 0 5 10 15 20 25 30 35 40 -90 -80 -70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 teta(gradi) guadag no(dB) copolare maschera

Figura 8.26: Andamento del guadagno della componente copolare sul piano di Azimuth (piano E) con riflettore sagomato mediante funzioni B-Splines e GA reale.

(19)

Come per i casi precedenti in figura 8.28 viene mostrato, sempre a parità di condizioni operative, un confronto dell’andamento del fitness dell’individuo migliore del GA binario e del GA reale per circa 400 generazioni.

Possiamo notare come mediante il GA reale sia possibile raggiungere un valore del fitness più basso rispetto al GA binario.

0 1000 2000 3000 4000 5000 6000 7000 8000 1 40 79 118 157 196 235 274 313 352 391 generazione fitn ess

Figura 8.28: Andamento del valore della funzione di fitness del miglior individuo di ogni

generazione nel caso di GA binario e di GA reale e deformazioni mediante

funzioni B-Splines.

8.5 Confronto tra le varie tecniche di deformazione

Dai risultati presentati nei paragrafi precedenti, si può notare che il processo di sintesi che ha fornito i risultati migliori (relativamente all’andamento della funzione di fitness) è il metodo basato sulla deformazione tramite polinomi di Zernike con GA reale.

(20)

Va osservato inoltre, che il valore max di 38 dB richiesto dalle

specifiche è stato ottenuto con i due metodi di Zernike e funzioni B-Splines senza aver deformato il bordo ellittico come è invece stato

necessario fare nel caso di deformazione con polinomi rettangolari.

A parità di condizioni operative, così come illustrato nel paragrafo 7.5., abbiamo riportato in fig 8.29 un confronto dell’andamento della funzione di fitness ottenuto applicando i metodi di deformazione mediante polinomi di Zernike e funzioni B-Splines.

0 1000 2000 3000 4000 5000 6000 7000 1 40 79 118 157 196 235 274 313 352 391 generazione fitn e s s

fitness " Zernike " fitness " B-Splines "

Figura 8.29: Confronto tra i metodi migliori.

Riportiamo infine, nelle figure 8.30, 8.31, 8.32, 8.33, 8.34 e 8.35 i tagli della superficie dell’antenna che nei metodi di deformazione analizzati in precedenza ha fornito i migliori risultati.

(21)

Taglio superficie antenna sul piano di Elevazione 0 5 10 15 20 25 30 35 100 140 180 220 260 300 340 380 420 x (mm) z (m m )

paraboloide superficie deformata

Figura 8.30: Taglio superficie sul piano di Elevazione ottenuto mediante deformazione con

polinomi di Zernike e GA reale.

Taglio superficie antenna sul piano di Azimuth

0 50 100 150 200 250 300 350 400 450 500 550 600 -1900 -1700 -1500 -1300 -1100 -900 -700 -500 -300 -100 100 300 500 700 900 1100 1300 1500 1700 1900 y (mm) z ( mm)

Figura 8.31: Taglio superficie sul piano di Azimuth ottenuto mediante deformazione con

(22)

Taglio superficie antenna sul piano di Elevazione 0 3 6 9 12 15 18 21 24 27 30 33 36 100 140 180 220 260 300 340 380 420 x (mm) z ( m m )

Figura 8.32: Taglio superficie sul piano di Elevazione ottenuto mediante deformazione con

funzioni B-Splines e GA reale.

-50 0 50 100 150 200 250 300 350 400 450 500 550 600 650 -1900 -1700 -1500 -1300 -1100 -900 -700 -500 -300 -100 100 300 500 700 900 1100 1300 1500 1700 1900 y (mm) z ( mm)

Figura 8.33: Taglio superficie sul piano di Azimuth ottenuto mediante deformazione con

(23)

Taglio superficie antenna piano di Elevazione 0 5 10 15 20 25 30 35 100 140 180 220 260 300 340 380 420 460 500 x (mm) z ( mm)

Figura 8.34: Taglio superficie (con bordo ellittico maggiorato) sul piano di Elevazione ottenuto mediante deformazione con polinomi rettangolari e GA binario.

0 50 100 150 200 250 300 350 400 450 500 550 600 -1900 -1700 -1500 -1300 -1100 -900 -700 -500 -300 -100 100 300 500 700 900 1100 1300 1500 1700 1900 y (mm) z (m m )

Figura 8.34: Taglio superficie (con bordo ellittico maggiorato) sul piano di Azimuth ottenuto mediante deformazione con polinomi rettangolari e GA binario.