Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin

(1)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin

Appendice D Approfondimenti sulla funzione di

ottimizzazione lsqnonlin

Questa appendice chiarisce le modalità di ottimizzazione adoperate dalla funzione lsqnonlin al fine di comprendere al meglio il significato degli output visualizzati sullo schermo ad ogni iterazione e alla fine del processo identificativo. Per questo il primo dei due paragrafi dell’appendice definisce le metodologie di calcolo adoperate dall’ottimizzatore mentre il secondo gli output visualizzati sullo schermo.

D.1 Algoritmi di calcolo adoperati dalla funzione lsqnonlin

Molte volte, avendo modelli rappresentativi del sistema fisico che si vuole rappresentare, nasce l’esigenza di ottimizzare i parametri che vi compaiono al fine di migliorare l’andamento dei segnali simulati. Il miglioramento richiesto, nel caso di funzioni non lineari, viene ottenuto attraverso la funzione "lsqnonlin" dell’Optimization Toolbox di Matlab.

La funzione lsqnonlin consente di determinare la migliore approssimazione di funzioni non lineari con la tecnica dei minimi quadrati. In sintesi, data una funzione F(x,t):

( )

( ) ( )

(

) ( )

            φ − φ − φ − =             = m m 1 2 1 1 m 2 1 t ,t y ... t ,t y t ,t y f ... f f ,t F x x x x x x x (D.1.1)

in cui y(x,t) è l’output che deve inseguire con errore trascurabile il segnale Φ(t) per un vettore x e uno scalare t, i parametri x per i quali f_i

( )

x →0 sono quelli che minimizzano la

(2)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin funzione f

( )

x ottenuta come somma dei quadrati delle componenti di F(x,t), ossia:

[

f ( ) f ( ) f ( ) ... f ( )

]

2 1 min ) ( f min 2 m 2 3 2 2 2 1 n n x _x x x x x x + + + + = ℜ ∈ ℜ ∈ (D.1.2)

La funzione lsqnonlin determina i parametri del modello attraverso l’equazione (D.1.2) che in forma compatta può essere riscritta come:

) ( F ) ( F 2 1 ) ( f 2 1 min ) ( F 2 1 min ) ( f min T m 1 i 2 i n 2 2 n n x _x x _x x x x x ⋅ ⋅ = = =

∑

= ℜ ∈ ℜ ∈ ℜ ∈ (D.1.3)

Sebbene la funzione f(x) possa essere minimizzata usando la generica tecnica di minimizzazione non vincolata, attraverso il metodo della "discesa più ripida" (steepest descent) in cui la ricerca è compiuta in una direzione −∇f x( ) (∇f x( ) è il gradiente della funzione obiettivo), certe caratteristiche del problema, come il gradiente e la matrice Hessiana, possono essere sfruttate per migliorare l’efficienza della procedura solutiva. Siano: • J(x) lo Jacobiano di F(x) in cui: j i ij x ) ( F ) ( J ∂ ∂ = x x (D.1.4)

• g(x) il vettore gradiente di f(x) definito come:

( )

f( ) F( ) F( ) 2 J( )T F( ) m 1 i i i x x x x x x g =∇ =

∑

⋅∇ = ⋅ ⋅ = (D.1.5)

• H(x) la matrice Hessiana di f(x) in cui:

j i 2 ij 2 ij x x ) ( f ) ( f ) ( H ∂ ⋅ ∂ ∂ = ∇ = x x x (D.1.6)

(3)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin allora la matrice Hessiana può essere riscritta come:

H(x) = 2 ·J(x)T ·J(x) + 2 · Q(x) (D.1.7)

avendo definito Q(x) come:

) ( H ) ( F ) ( Q _i m 1 i i x x x =

∑

⋅ = (D.1.8)

La matrice Q(x) tende a zero quando il residuo Fi(x) tende a zero e cioè quando xk,

valore assunto dal vettore dei parametri durante la k-esima iterazione, tende alla soluzione. Quando poi F x( ) tende a zero, un metodo molto efficace è quello di usare la direzione di Gauss-Newton come base per una procedura di ottimizzazione.

Gli algoritmi che possono essere usati dalla funzione lsqnonlin sono tre:

1. Gauss-Newton: algoritmo, più veloce tra i tre discussi, utilizzato esclusivamente quando la funzione residuo tenda a zero ;

2. Levenberg-Marquardt: utilizzato nel caso in cui non esistano coefficienti di vincolo; 3. Trust region: algoritmo usato specificatamente se esistono coefficienti di vincolo,

rappresenta un miglioramento dell’algoritmo di Levenberg-Marquardt. Riesce a risolvere problemi non lineari anche molto complessi ed è più efficiente di molti altri .

D.1.1 Metodo Gauss-Newton

Per spiegare il metodo di Gauss-Newton, algoritmo largamente usato nell’ottimizzazione ai minimi quadrati di funzioni non lineari, è necessario introdurre il metodo di Newton, formulato, in questa sede, al fine di risolvere un’equazione ad una incognita.

Supponiamo di voler calcolare con una buona approssimazione il numero che corrisponde alla 3 . Fare questo significa cercare il valorex_* che annulla l’equazione

3 x ) x (

f = 2 − partendo da un valore iniziale pari a x0, figura D.1.

Il valore di migliore stima x+ è ottenuto attraverso l’intersezione della retta tangente alla curva f(x) in x0 e l’asse x:

(4)

y

x

2

f(x) = x -3

-3

+

x

0

x

y

x

*

figura D.1 Ricerca del valore x_* che annulla la funzione f(x)=x2 −3.

x x

x₊ = ₀−∆ (D.1.9)

in cui si è indicato con ∆x lo step di Newton s ottenuto durante l’iterazione k-esima. N_k Attraverso la definizione di tangente si può dunque calcolare il valore x+:

) (x f ) f(x x x 0 0 0− _′ = + (D.1.10)

Il procedimento viene applicato identicamente fino al raggiungimento del valore x_* che annulla la funzione f(x) considerando come valore di partenza dell’iterazione k-esima, il valore x₊_k₋₁ determinato durante l’iterazione precedente.

Durante ogni iterazione k-esima può essere quindi costruito un modello locale della nostra funzione f(x) valutata in x_k, scritto come:

) x x ( ) x ( f ) x ( f M_k = _k + ′ _k ⋅ − _k (D.1.11)

sviluppo di Taylor della funzione in x_k arrestato ai termini di ordine superiore al primo. Il metodo di Newton, chiamato anche modello affine, può essere identicamente applicato ad un caso multivariabile utilizzando semplicemente la serie di Taylor arrestata al termine

(5)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin di ordine superiore al primo e ricordando che x, x_k sono ora dei vettori.

Il valore x_* per il quale F

( )

x_* =0 si può ora ricercare attraverso l’uso del modello affine, applicato durante ogni iterazione k-esima, ad F(x) in x_k, ossia:

) ( ) ( J ) ( F ) ( M_k x = x_k + x_k ⋅ x−x_k con M_k :ℜn →ℜm e m > n (D.1.12)

La soluzione del problema può essere equivalentemente ottenuta attraverso l’uso del metodo Gauss-Newton ossia come soluzione del problema lineare ai minimi quadrati su Mk come indicato di seguito:

) ( mˆ min ) ( ) ( J ) ( F 2 1 min M 2 1 min _k n 2 2 n 2 2 k n _x xk xk x xk _x x x∈ℜ ∈ℜ ∈ℜ = − ⋅ + = (D.1.13)

in cui (x−x_k) rappresenta dunque lo step sk, relativo all’iterazione k-esima, che permette

di determinare il valore x+ da cui partirà la successiva iterazione. In questo caso la

soluzione del problema (soluzione della minimizzazione del quadrato della norma due dello sviluppo di Taylor della F(x) arrestato al primo ordine), risulta:

( ) ( )

[

k k

]

( ) ( )

k k

k x x x x

x

x₊ = − J T⋅J −1⋅J T⋅F (D.1.14)

Il valore x+ che annulla la funzione durante l’iterazione k-esima poteva essere

direttamente ottenuto attraverso l’approssimazione:

( )

x

( )

x x x k n nf minm min ℜ ∈ ℜ ∈ ≅ (D.1.15)

con m_k

( )

x modello quadratico di f(x) in x_k

:

(

)

f( ) ( ) 2 1 ) ( ) ( f ) ( f ) ( m_k x = x_k +∇ x_k T⋅ x−x_k + x−x_k T⋅∇2 x_k ⋅ x−x_k (D.1.16) ossia:

(6)

[

J( ) J( ) Q( )

]

( ) ) ( 2 1 ) ( ) ( J ) ( F ) ( F ) ( F 2 1 ) ( m_k x = ⋅ x_k T⋅ x_k + x_k T⋅ x_k ⋅ x−x_k + ⋅ x−x_k T x_k T⋅ x_k + x_k ⋅ x−x_k (D.1.17)

coincidente con lo sviluppo di Taylor della f(x) arrestato ai termini di ordine superiore al secondo e calcolato in x_k . La minimizzazione di m_k

( )

x consiste nel risolvere il problema di Newton sulla derivata prima di m_k

( )

x ; la soluzione al problema in questo caso è:

( ) ( )

[

k k k

]

( ) ( )

k k

k x x x x x

x

x₊ = − J T ⋅J +Q( )−1⋅J T⋅F (D.1.18)

Come si vede, la soluzione ottenuta attraverso il metodo di Gauss-Newton, espressa nell’equazione (D.1.14), è uguale a quella di Newton applicata alla minimizzazione di

( )

x

k

m , equazione (D.1.18), a meno di Q(x), matrice che contiene i termini ∇2f(x). La soluzione di Newton-Gauss può essere dunque utilizzata in sostituzione di quella di Newton applicata alla minimizzazione di m_k

( )

x solo quando il termineQ x

( )

_* è nullo o piccolo rispetto agli altri termini e cioè solo quando i residui F_i

( )

x_* =0 sono nulli o quasi nulli, in caso contrario il metodo non risulta convergente.

D.1.2 Metodo di Levenberg-Marquardt

Il metodo di Levenberg-Marquardt adotta lo step che è soluzione del problema:

( ) ( ) (

)

₂ n x J F min x_k + x_k ⋅ x−x_k ℜ ∈ con x−xk 2 <δi (D.1.19)

e cioè la soluzione del set di equazioni lineari:

[

J( _k)T J( _k) λ_k I

]

1 J( _k)T F( _k)

k x x x x

x

x₊ = − ⋅ + ⋅ − ⋅ ⋅ (D.1.20)

in cui λk controlla sia il modulo che la direzione dello step k-esimo sk. Quando λk = 0 la direzione sk coincide con quella del metodo di Gauss-Newton. Come λk →∞ , sk tende ad

(7)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin ripida". In questo modo il metodo di Levenberg-Marquardt usa una direzione di ricerca intermedia tra quella ottenuta con il metodo di Gauss-Newton e quella steepest descent.

La principale problematica nell’uso dell’algoritmo di Levenberg-Marquardt è rappresentata dalla necessità di determinare una strategia di controllo del valore di λk ad ogni iterazione. Questo rappresenta il motivo per il quale esistono molte versioni di tale metodo, unicamente differenti per la strategia utilizzata nella valutazione di λk.

Il metodo usato nell’implementazione di Matlab è volto a stimare la non linearità di f(x) usando una predizione lineare della somma dei quadrati, indicata con f_p(x_k), e una stima del minimo attraverso interpolazione cubica, definita comef_k(x_*). In questo modo la dimensione di λk viene determinata ad ogni iterazione. La predizione lineare della somma dei quadrati è calcolata come:

) ( F ) ( J ) ( f_p x_k = x_k₋₁ ⋅s_k₋₁ + x_k₋₁ (D.1.21)

mentre il termine f_k(x_*) viene calcolato come interpolazione cubica dei punti f

( )

x_k e

(

xk−1

)

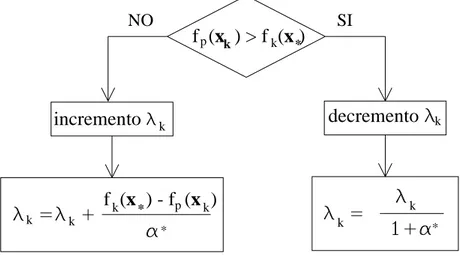
f . Un parametro sulla lunghezza dello step, α*, viene calcolato attraverso questa interpolazione; se f_p(x_k)>f_k(x_*) il parametro λk viene ridotto attraverso α*, altrimenti viene incrementato, come riportato nella figura D.2. La spiegazione di questo sta nel fatto che la differenza tra f_p(x_k) e f_k(x_*) rappresenta una misura della linearità del problema e dunque dell’efficienza del metodo di Gauss-Newton. Questo determina se usare una direzione di approccio steepest descent o Gauss-Newton.

*

decremento

* * p

f (

x ) - f (x )

p

incremento

*

f (

x ) > f (x )

NO SI k k k k k k k k k k

(8)

D.1.3 Metodo Trust Region

Per capire come opera l’algoritmo Trust Region si consideri dapprima il caso di minimizzazione non vincolata :

) ( f min x x con n ℜ ∈ x (D.1.22)

Supponiamo di essere nel punto x dello spazio ad n dimensioni e di volerci muovere in un punto in cui il valore della funzione è più basso. L’idea di base è quella di approssimare la funzione f(x) con una funzione q(x) più semplice, che approssima ragionevolmente bene il comportamento della funzione f(x) in un intorno N del punto x, chiamato trust region. Uno step di prova s viene calcolato per minimizzare o approssimativamente minimizzare la funzione in N. Così il problema definito nell’equazione (D.1.22) viene sostituito dal sottoproblema trust region definito come segue:

) ( q

min s

s con s∈N (D.1.23)

Nel caso in cui f

(

x+s

) ( )

<f x , si aggiorna il punto x con x+s altrimenti il punto rimane invariato e la regione N viene ristretta ripetendo il calcolo dello step di prova nella nuova regione.

In sintesi il problema di minimizzazione della f(x) consiste nel:

1. definire la trust region N in cui minimizzare correttamente f(x);

2. definire una funzione q(x) che approssimi al meglio f(x) nell’intorno N.

La funzione q(x) viene definita come lo sviluppo di Taylor della f(x) arrestata al termine di

secondo ordine; l’intorno N viene preso sferico o ellittico. Il sottoproblema trust region si riconduce dunque al problema:

      ⋅ + ⋅ ⋅ ⋅s s s g s T T H 2 1 min con D s⋅ ₂ ≤∆ (D.1.24)

(9)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin diagonale scalare, ∆ uno scalare positivo.

La soluzione di tale minimizzazione viene determinata facilmente dopo aver ristretto la trust region in un sottospazio bidimensionale S= s₁,s₂ .

Il toolbox assegna ad s1 la direzione del gradiente g e ad s2 o la direzione ottenuta

attraverso l’uso del Preconditioned Coniugate Gradient (PCG) applicato al problema :

g s₂ =−

⋅

H (D.1.25)

o la direzione della curvatura negativa:

0 H T_⋅ _⋅ _< 2 2 s s (D.1.26)

Il metodo del Preconditioned Coniugate Gradient è un approccio molto usato per risolvere sistemi di equazioni lineari simmetrici definiti positivi come quelli rappresentati nell’equazione (D.1.25). L’approccio iterativo richiede la capacità di calcolare il prodotto matrice per vettore H·v dove v è un vettore arbitrario. La matrice simmetrica definita

positiva M è il precondizionato di H (si definisce matrice simmetrica se M = MT e definita positiva se vT⋅M⋅v >0 ∀v≠0∈ℜn o in maniera equivalente se gli autovalori sono positivi ), cioè M = C2 dove C−1⋅H⋅C−1 è la matrice ben condizionata ([7]).

Il toolbox di ottimizzazione risolve dunque problemi di minimizzazione non vincolata attraverso l’uso della trust region ripetendo i seguenti quattro passi fino al raggiungimento della convergenza :

• determinazione del sottospazio bidimensionale S;

• risoluzione del problema definito nell’equazione (D.1.24) al fine di determinare lo step di prova s;

• se f(x+s) < f(x) ⇒ x = x + s;

• adattamento di ∆ nel caso f(x+s) > f(x).

Si analizzi ora il caso di minimizzazione con vincoli di bordo definita di seguito:

) ( f min n x x∈ℜ con l≤x≤u (D.1.27)

(10)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin dove l è il vettore limite inferiore, u il vettore limite superiore. Due tecniche vengono utilizzate per portare a convergenza la soluzione:

1. approssimazione di Newton modificata rispetto a quella utilizzata per il caso non vincolato e utilizzata per la valutazione di s2 del sottospazio bidimensionaleS= s1,s2 ;

2. metodo delle riflessioni usato per incrementare la dimensione dello step.

Il toolbox assegna ad s2, mediante l’uso della tecnica chiamata step di Newton modificato a

scalare, la direzione dello step sk ottenuto come soluzione del sistema lineare (D.1.28) :

g

sN ˆ

D

Mˆ ⋅ ⋅ =− (D.1.28)

in cui all’iterazione k-esima Mˆ e gˆ sono definiti come di seguito:

g v g g _k _⋅      = ⋅ = −1 ₂1 diag D ˆ (D.1.29) v 1 1 J ) ( diag D H D Mˆ = − ⋅ ⋅ − + g ⋅ (D.1.30)

in cui Jv rappresenta lo jacobiano di v .

La matrice D è rappresentata invece mediante la (D.1.31):

      = 2 1 diag ) ( D x v_k (D.1.31)

dove il vettore v(x) è definito come segue per 1≤ i ≤ n: • v_i = x_i −u_i se g_i <0 e u_i <∞;

• v_i =x_i −l_i se g_i ≥0 e l_i >−∞; • v_i =−1 se g_i <0 e u_i =∞; • v_i =1 se g_i ≥0 e l_i =−∞.

(11)

D.2 Output della funzione lsqnonlin

Come già annunciato, la struttura del programma è tale da permettere di confrontare iterativamente i dati sperimentali delle velocità angolari della ruota e del tamburo, con quelli ottenuti dalla simulazione del modello in funzione del valore attuale dei parametri. In base al risultato di tale confronto il programma adatta ad ogni passo successivo il valore di tutti i parametri, procedendo iterativamente fino ad ottenere la migliore risposta possibile.

Il programma è stato realizzato in modo tale che durante e a fine identificazione vengano visualizzati sullo schermo degli output capaci di dare sufficienti informazioni sullo stato della minimizzazione.

La sintassi adottata nei programmi di identificazione, relativa alla funzione lsqnonlin, è :

[x, resnorm, residual, exitflag, output] = lsqnonlin (@fun,x0,lb,ub,options)

in cui gli argomenti dell’output, visualizzati a fine identificazione, restituiscono :

• x: vettore dei parametri i cui valori risolvono il problema della minimizzazione definito nell’equazione (D.1.3);

• resnorm: quadrato della norma due della funzione di costo calcolata in x_*, ossia

) x ( f ) x ( F _* 2₂ = _* ;

• residual: funzione dei residui F

( )

x_* :

• exitflag: numero intero corrispondente alla condizione di uscita dal ciclo di iterazione, ossia:

0 = il numero di iterazioni supera il valore specificato in option.MaxIter oppure il numero di valutazioni della funzione supera il valore definito in option.FunEvals. 1 = la funzione converge ad un valore;

2 = x varia meno della tolleranza specificata in TolX;

3 = f(x) varia meno della tolleranza specificata in TolFun;

•

output: struttura contenente informazioni circa l’ottimizzazione quali ad esempio il metodo adottato dalla funzione lsqnonlin per minimizzare la f(x), il numero di iterazioni effettuate, etc..

(12)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin • fun: funzione in cui è descritta la funzione di costo F(x) di cui verrà minimizzata la

somma dei quadrati delle componenti, chiamata nel caso specifico LocalCostFcn; • x0: vettore di partenza per la determinazione del vettore x;

• lb, ub: vettori limiti inferiore e superiore dell’intervallo entro il quale si deve trovare x, ossia lb ≤ x ≤ ub ;

• options: struttura che definisce le opzioni di ottimizzazione, settate attraverso la funzione optimset. Nel caso in esame la struttura options è stata definita in modo tale da visualizzare ad ogni iterazione lo stato della minimizzazione. Inoltre definisce i campi di tolleranza sulla funzione calcolata in x e sul valore della stessa x rispettivamente in 10−7 e 10−6, ossia:

options = optimset (‘Display’,’iter’,’TolFun’,1e-7,’TolX’,1e-6)

Settando l’opzione Dispay su iter, ad ogni iterazione, sul display viene visualizzata una riga che definisce lo stato della minimizzazione al ciclo k-esimo:

Norm of First-order

Iteration Func-count f(x) step optimality CG-iterations 0 2 0.0915282 0 1.23 0

in cui:

• Iteration: numero dell’iterazione in corso;

• Func-count: numero cumulativo di valutazioni della funzione, pari al numero di parametri da identificare aumentato di una unità. In generale dà un’indicazione circa il

costo della minimizzazione della funzione; • f(x): valore della funzione calcolato in x;

• Norm of step: norma dello step durante la k-esima iterazione;

• First order optimality: norma infinito del gradiente attuale, dipende dall’algoritmo. Per gli algoritmi di larga scala (Trust Region), First order optimality è la norma infinito di

v·g dove v è il vettore definito nella minimizzazione attraverso trust region con vincoli

di bordo mentre g è il gradiente di f(x):

_i _i n i 1 g v max ≤ ≤ ∞ = ⋅g v (D.2.1)

(13)

Appendice D Approfondimenti sulla funzione di ottimizzazione lsqnonlin • CG iteration: numero di iterazioni effettuate dal gradiente coniugato per determinare la direzione s₂ del sottospazio bidimensionale S = s₁,s₂ , durante il ciclo k-esimo della minimizzazione.

In conclusione si riporta il listato totale, relativo all’identificazione del parametro x

s

K_µ per il test1 con α=1, costituito dalle righe di output visualizzate ad ogni iterazione e gli output visualizzati a fine identificazione. In particolare si può notare il messaggio atto a spiegare la modalità di fine identificazione, supportato dal valore assunto dal parametro exitflag, e il valore P del parametro identificato.

Norm of First-order

Iteration Func-count f(x) step optimality CG-iterations 0 2 0.0915282 1.23 1 4 0.0202118 0.167989 0.103 1 2 6 0.0127609 0.0702033 0.0114 1 3 8 0.0126273 0.0112441 0.00062 1 4 10 0.0126269 0.000643767 2.75e-005 1 5 12 0.0126269 2.85732e-005 1.15e-006 1

Optimization terminated: relative function value changing by less than OPTIONS.TolFun. P = 8.0218

resnorm = 0.0126 residual = […] exitflag = 3

output = firstorderopt: 1.1502e-006 iterations: 5

funcCount: 12

cgiterations: 5 algorithm: [1x43 char]