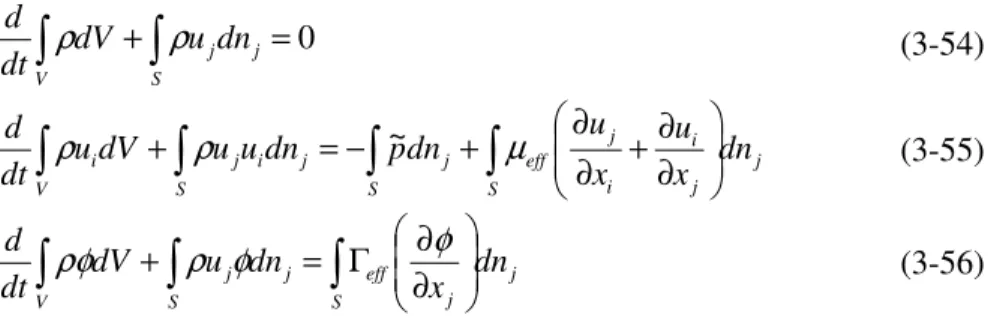Capitolo 3

Capitolo 3

Fondamenti di fluidodinamica

computazionale

3.1 Introduzione

La fluidodinamica computazionale (CFD) risolve problemi termofluidodinamici tramite codici di calcolo sviluppati per risolvere in maniera approssimata (modello numerico) il sistema di equazioni che definisce il problema in studio (modello matematico). Tipicamente, i problemi di interesse industriale, (riguardanti flussi laminari o turbolenti, comprimibili od incomprimibili in geometrie complesse con vari tipi di trasferimento di calore) richiedono notevoli risorse di calcolo per poter essere risolti con un livello di accuratezza adeguato. Ciò ha limitato fino a tempi recenti l’uso della CFD, ma l’attuale disponibilità a costi ridotti di calcolatori sempre più potenti e veloci permette di affrontare la risoluzione di problemi sempre più complessi in termini di dominio di calcolo o di modelli fisici.

I moti di fluidi sono governati da un set di equazioni di bilancio, che esprimono la conservazione della massa, della quantità di moto e dell’energia; inoltre devono essere presenti un numero variabile di equazioni aggiuntive che governano eventuali fenomeni particolari presenti nel flusso, quali la turbolenza, la combustione, la cavitazione, il flusso bifase e molti altri. Queste formano un sistema di equazioni accoppiate non lineari alle differenze parziali (PDEs).

L’approccio CFD si occupa di questo, le equazioni differenziali sono sostituite da un sistema di equazioni algebriche risolto in maniera iterativa . La

soluzione ottenuta è un’approssimazione della soluzione esatta (si calcola il valore delle differenti incognite in molteplici punti del dominio di calcolo).

Nel presente capitolo si introducono rapidamente le principali caratteristiche delle tecniche CFD, facendo particolare attenzione a quelle utilizzate nel presente lavoro di tesi.

3.2 Equazioni di bilancio

Le equazioni di bilancio, insieme alle condizioni al contorno ed a quelle iniziali, definiscono il problema termofluidodinamico, e costituiscono il punto di partenza degli studi di CFD. Dato il ruolo basilare che ricoprono nel presente lavoro, si ritiene importante riportarle insieme alle principali ipotesi semplificative adottate.

3.2.1 Equazione di conservazione della massa

L’equazione di conservazione della massa, detta anche equazione di continuità, è data dalla seguente relazione, ottenuta imponendo la conservazione della massa in un volume di controllo arbitrario e finito:

( )

t +∇⋅ =

∂

∂ρ _ρ

(3-1)

dove S rappresenta una eventuale sorgente di massa (nello studio effettuato questa non è presente). La formula vale sia nel caso di fluidi comprimibili che incomprimibili. Nel caso in studio, la densità del fluido è costante nello spazio e nel tempo, per cui si annulla il primo termine a primo membro e l’equazione precedente diventa:

0 = ∂ ∂ i i x u (3-2)

Si osserva, comunque, che è comunemente adottata l’assunzione che un fluido, seppur comprimibile, si può considerare incomprimibile (ρ =cost) se si trova ad una condizione di moto tale che il suo numero di Mach è inferiore a 0,3.

3.2.2 Equazione di conservazione della quantità di moto

L’equazione di conservazione della quantità di moto nella sua forma integrale è data da:

Ω Ω Ω + − = + Ω uu n dS n dS pi n dS g d d u dt d i S j ij S j ij S j j i i ρ τ ρ ρ (3-3)

La cui corrispondente forma differenziale, rispettivamente in forma Lagrangiana conservativa e non conservativa, è data da:

( )

₍

₎

dove p è la pressione statica, τ_ij rappresenta la componente del tensore degli sforzi viscosi, ossia la componente deviatorica del tensore di Cauchy (σ =τ − pI), g_i è la forza di gravità, che è stata assunta come unica forza di massa agente sul fluido. La seconda equazione può essere ottenuta dalla prima in combinazione con l’equazione di continuità (3-1).

A questo punto si rende necessaria l’introduzione di una equazione costitutiva che leghi il tensore degli sforzi al campo di moto, ciò può essere fatto introducendo alcune ipotesi sul comportamento viscoso del fluido. In molti casi di

interesse pratico, compreso il presente lavoro, si può assumere che un fluido abbia un comportamento di tipo Newtoniano, il che implica l’assunzione della seguente equazione costitutiva nel caso di flusso laminare:

ij i i j i i j ij x u x u x u δ µ µ µ τ ∂ ∂ − ′ + ∂ ∂ + ∂ ∂ = 3 2 (3-6)

dove δij è il simbolo di Kronecker, µ è la viscosità dinamica e µ’ è la viscosità di

bulk, la quale è zero per un gas monoatomico, molto piccola per fluidi densi, ed è abitualmente trascurata.

Introducendo tale relazione nell’equazione di conservazione della quantità di moto espressa in forma conservativa otteniamo l’equazione di Navier-Stokes, nella quale non è più presente il tensore degli sforzi viscosi, dato che le sue componenti sono state espresse come funzioni delle derivate delle componenti di velocità:

( )

(

)

Essendo, nel caso in studio, il fluido incomprimibile, l’equazione costitutiva assume la forma semplificata seguente:

∂ ∂ + ∂ ∂ = j i i j ij x u x u (3-8)

e l’equazione di Navier-Stokes diventa:

( )

(

)

una ulteriore semplificazione si può ottenere considerando la viscosità costante:

( )

(

)

Quando sia la gravità che la densità sono costanti è d’uso comune includere il termine gravitazionale all’interno del gradiente di pressione, il che è equivalente a considerare la pressione di testa al posto di quella statica, quindi si definisce:

gz p p = +ρ

~ _(3-11)

dove z indica la coordinata in direzione opposta a quella di azione della forza gravitazionale, quindi l’equazione di Navier-Stokes diventa:

( )

(

)

Se la densità varia con la temperatura, solitamente se ne tiene conto solo nel termine gravitazionale, che viene suddiviso in due contributi secondo la forma seguente:

(

)

(

)

(

)

dove T0 è la temperatura di riferimento corrispondente alla pressione di

riferimento p0 e β è il coefficiente di espansività termica. Questa ipotesi è nota

con il nome di approssimazione di Boussinesq, la quale introduce errori di notevole entità se le variazioni di temperature sono grandi. Ciò può essere evitato solo prendendo in considerazione la variazione di temperatura anche nei termini convettivo e non-stazionario, ed inoltre assumendo un modello più accurato di quello lineare rappresentato dall’equazione (3-14).

3.2.3 Equazione di conservazione dell’energia

L’equazione di conservazione dell’energia può essere scritta in termini di temperatura nel seguente modo:

( )

( )

dove cp è il calore specifico a pressione costante, 'q' è il flusso termico e q''' è la

generazione interna di calore. Il secondo termine del lato destra rappresenta il lavoro compiuto dal tensore degli sforzi viscosi, chiamato dissipazione viscosa. Il flusso termico può essere espresso tramite la legge di Fourier:

T

q''=−λ∇ (3-16)

questa è una legge costitutiva che, se introdotta nell’equazione di bilancio, induce la presenza di un termine diffusivo. C’è un’importante analogia tra questa e la relazione costitutiva dei fluidi Newtoniani (3-6): la diffusione sia della quantità di moto che del calore sono governate dai gradienti di velocità e temperatura rispettivamente.

In molti casi di interesse, possono essere introdotte le seguenti ipotesi:

• le variazioni di energia potenziale e cinetica possono ritenersi trascurabili • il lavoro compiuto dalle forze viscose può ritenersi trascurabile

• non si ha generazione interna di calore e l’equazione assume la forma semplificata:

(

)

(

)

dove cv è il calore specifico a volume costante e λ è la conduttività termica del

se si assume anche che siano costanti ed uniformi, l’equazione si semplifica nella seguente forma:

( )

(

)

dove Pr indica il numero di Prandtl, definito come segue:

α ν λ µ = ⋅ = Cp Pr (3-19)

cioè è il rapporto tra la diffusività della quantità di moto e la diffusività termica.

3.2.4 Equazione di conservazione di uno scalare

Nel caso in cui si abbia il trasporto di un generico scalare nel fluido, l’equazione che ne descrive la conservazione è la seguente:

( )

( )

dove φ è lo scalare trasportato, Γ è il coefficiente di diffusione e Sφ è l’eventuale

sorgente volumetrica di generazione dello scalare. Se quest’ultima non è presente l’equazione diventa:

( )

( )

che è formalmente identica alla (3-18), dove la temperatura T è sostituita dallo scalare φ ed il numero di Prandtl dal numero di Schmidt, definito come segue:

Γ = µ

Sc (3-22)

Quindi se i numeri di Prandtl e Schmidt sono uguali allora le soluzioni delle due equazioni di trasporto sono simili. Questo permette di poter usare la temperatura come “tracciante” dello scalare passivo, se si risolve l’equazione dell’energia, oppure il viceversa se si considera l’equazione (3-21).

3.3 La turbolenza

Tutti i flussi che si incontrano nella pratica ingegneristica, oltre un certo numero di Reynolds (Re=UL dove U e L sono rispettivamente la velocità e la dimensione caratteristica, mentre è la viscosità cinematica), diventano instabili, o meglio, turbolenti. Lo studio fluidodinamica deve contemplare la presenza della turbolenza, essendo un fenomeno fisico che ha importanti ricadute sul campo di velocità, di temperatura e sulla altre variabili del problema.

3.3.1 Descrizione fisica

I flussi turbolenti sono fenomeni molto complessi, caratterizzati dalle seguenti proprietà:

• sono altamente non-stazionari, ed il modo in cui le variabili fisiche dipendono dal tempo appare completamente casuale;

• sono altamente tridimensionali, ed il campo di moto istantaneo fluttua rapidamente nelle tre dimensioni;

• sono sempre presenti un certo numero di strutture chiamate vortici, caratterizzati da intensi moti rotatori locali. Lo stiramento dei vortici è uno dei principali meccanismi responsabili dell’incremento della turbolenza;

• sono coinvolti un ampio range di scale di grandezza, infatti la dimensione caratteristica dei vortici varia da quella dei contorni geometrici del flusso a scale microscopiche;

• sono coinvolte un ampio range di scale temporali, infatti si va dal periodo della più rapida delle fluttuazioni alla vita media del vortice più grande; • l’energia cinetica viene trasferita dalle grandi strutture a quelle piccole in

un processo “a cascata”;

• la turbolenza è sempre dissipativa, dato che l’energia che raggiunge le scale più piccole viene convertita in energia termica attraverso processi irreversibili;

• da un punto di vista macroscopico, la turbolenza è caratterizzata da un notevole incremento della diffusività di tutte le quantità trasportate, come la quantità di moto e l’energia. Ciò comporta un mescolamento molto più efficace rispetto al flusso laminare, ed anche un aumento delle forze di attrito;

• la turbolenza è un processo continuo, nel senso che anche la più piccola lunghezza caratteristica è grande rispetto alla scala molecolare, quindi le equazioni di conservazione mantengono la loro validità e contengono (virtualmente) tutta la fisica del flusso turbolento;

3.3.2 Metodo “Direct Numerical Simulation” (DNS)

L’approccio più intuitivo al problema della simulazione numerica di un flusso turbolento consiste nel tentare di risolvere le equazioni di conservazione nella loro forma completa, ottenendo così il valore delle variabili incognite in funzione del tempo e dello spazio. Così facendo non si ha alcuna perdita di informazioni sull’evolvere delle strutture turbolente. Questo modo di risolvere il flusso turbolento è noto con il nome di “Direct Numerical Simulation” (DNS).

Attualmente la DNS è una delle sfide più ambiziose per le tecniche di risoluzione numerica di problemi fluidodinamici. Infatti la discretizzazione

spaziale e temporale del dominio devono essere sufficientemente raffinate da permettere la soluzione della più piccola struttura, ma devono essere sufficientemente grandi da poter contenere anche la più grande delle strutture turbolente. Per la maggior parte dei problemi di interesse ingegneristico, il numero di celle richieste per l’approccio DNS è proibitivo già per semplici casi studio se comparato alle risorse di calcolo reperibili ad un costo contenuto. Infatti, il numero di nodi richiesti per un dato volume aumenta rapidamente con il numero di Reynolds turbolento; le tecniche DNS sono attualmente applicabili solo a flussi con basso numero di Reynolds utilizzando calcolatori disposti in parallelo con tempi di calcolo dell’ordine di settimane.

Consideriamo, ad esempio, un flusso incomprimibile turbolento in un canale di altezza H; valgono le relazioni seguenti per il numero di nodi ed il

timestep, ricavate da Wilcox [11]:

(

)

queste relazioni si trovano in accordo con gli esperimenti svolti da Laufer (per

ReH = 12300, 30800 e 61600) e da Comte-Bellot (per ReH = 230000), i cui

risultati sono riportati in Tabella 3-1:

ReH Reττττ NDNS Timesteps

12300 360 6.7x106 ₃₂₀₀₀

30800 800 4.0x107 47000 61600 1450 1.5x108 ₆₃₀₀₀

230000 4650 2.1x109 114000 Tab. 3-1: costi computazionali di un’analisi DNS

3.3.3 Metodo “Large Eddy Simulation” (LES)

Per tentare di ridurre le risorse di calcolo necessarie a risolvere i flussi turbolenti, è stato sviluppato un approccio semplificato rispetto al DNS, il “Large

Eddy Simulation” (LES). In questo metodo si applica un filtro spaziale alle equazioni di conservazione, in modo da simulare soltanto i vortici di più grandi dimensioni, mentre quelli più piccoli vengono modellati nelle equazioni.

L’idea su cui si basa l’approccio LES è che le strutture più grandi siano le maggiori responsabili del trasporto delle grandezze, e che siano anche le più direttamente influenzate dalle condizioni al contorno. D’altro canto, le piccole strutture sono meno efficaci nel trasporto delle grandezze, e sono quasi uniformemente distribuite nel flusso; ciò rende relativamente semplice una loro modellazione. Così facendo si diminuisce notevolmente la richiesta di risorse di calcolo rispetto alla DNS. Una prima stima della diminuzione delle richieste computazionali può essere fatta utilizzando la seguente correlazione fornita da Wilcox: DNS LES N N ≈ 4 1 Re 4 . 0 τ (3-25)

La separazione tra le grandi e le piccole scale di grandezza si ottiene tramite un’operazione di filtraggio che permette di conservare solamente le componenti delle grandezze dovute alle grandi scale; si usano operatori del tipo:

( )

( ) ( )

Q = , ′ ′ ′ (3-26)

dove G

( )

(

)

Un’altra possibilità è il “volume-average box filter”:

(

)

questo è uno dei filtri più semplici, ed equivale ad applicare una media spaziale su

un cubo di lato xi. La sua implementazione numerica è sensibilmente

semplificata se xi è uguale alla dimensione della discretizzazione spaziale

applicata. In questo caso l’operazione di filtraggio è implicitamente svolta integrando sul volume di controllo le equazioni di conservazione mediate.

In aggiunta al tipo di filtro utilizzato, devono essere definiti dei modelli per le piccole strutture. Uno dei più usati è quello proposto da Smagorinsky, basato sull’aggiunta di un contributo all’equazione di conservazione della quantità di moto. Uno dei punti deboli di questo modello, ma più in generale di tutti i modelli LES, è la difficoltà nel tenere conto dell’anisotropia della turbolenza dei piccoli vortici in prossimità delle pareti. Nonostante ciò il modello di Smagorinsky è quello che ha ottenuto il maggior successo, anche perché, prevedendo una sufficiente produzione e dissipazione, riesce a stabilizzare il calcolo.

Se è richiesta una maggiore accuratezza, può essere utilizzata una delle varianti “dinamiche” del modello di Smagorinsky, che ricalcolano la costante del modello ad ogni timestep, ottenendo una riduzione dell’eccesso di dissipazione stimato.

3.3.4 Metodo “Reynolds Averaged Navier-Stokes Equations” (RANS)

Il metodo più usato per risolvere i flussi turbolenti è il metodo “Reynolds

Averaged Navier-Stokes Equations” (RANS), che riduce notevolmente le risorse

di calcolo necessarie. Basato sullo studio statistico del moto, questo approccio parte dalla definizione delle variabili come somma di due componenti; per la generica grandezza Q si ha, indicando con Q la componente media e con q quella fluttuante:

q Q

Q = + (3-29)

La componente media è ottenuta come media su un intervallo di tempo sufficientemente grande rispetto alle fluttuazioni turbolente, ma piccolo rispetto alla scala temporale di risoluzione delle equazioni:

∆ + − ∆ = t t t Qdt t Q 1 (3-30)

applicando questo approccio alle equazioni di trasporto otteniamo:

0 ) ( = ⋅ ∇ + ∂ ∂ U t ρ ρ _(3-31) ) ( ) ( U U u u t U _{+∇⋅ × =∇⋅ − ×} ∂ ∂ρ _{ρ τ ρ} (3-32) ) ( ) (ρ φ φ ρ φ ρφ _{U u} t +∇⋅ =∇⋅ Γ∇ − ∂ ∂ _(3-33)

in cui per brevità si è mantenuta identica la simbologia delle differenti grandezze, omettendo la barra con cui precedentemente si sono indicate le componenti medie. Queste equazioni prendono il nome di Reynolds Averaged Navier-Stokes Equations (RANS). Si può notare come l’equazione di continuità non sia stata alterata nella sua forma, mentre quelle del trasporto della quantità di moto e dello scalare presentano termini aggiuntivi (la tensione di Reynolds ρu×u ed il flusso

di Reynolds ρuφ). Questi rispecchiano il fatto che il trasporto convettivo dovuto alle fluttuazioni turbolente della velocità produce un incremento del mescolamento in aggiunta a quello prodotto dalle fluttuazioni termiche a livello molecolare.

L’equazione dell’energia diventa:

t p T h u h U t h tot tot ∂ ∂ = ∇ − + ⋅ ∇ + ∂ ∂ρ _{(ρ ρ λ ) (3-34)}

dove l’entalpia totale media è data da:

2 2 2 1 2 1 u U h htot = + + (3-35)

dove i primi due termini costituiscono l’entalpia totale del flusso medio, mentre il terzo termine rappresenta il contributo dell’energia cinetica turbolenta, che indicheremo con k.

Per ottenere la chiusura del problema così formulato, sono necessari modelli che descrivano la tensione di Reynolds ed il flusso di Reynolds in base alle altre grandezze. Uno di questi è il modello di Boussinesq [11], che relaziona la tensione di Reynolds al gradiente di velocità:

( )

dove µ_t è la viscosità turbolenta, assunta come una quantità scalare isotropica, cosa che non è strettamente vera. In letteratura sono disponibili molte altre relazioni. Da alcune loro combinazioni hanno origine diversi modelli di turbolenza. Sfortunatamente non esiste un unico modello turbolento di validità generale. La scelta del modello turbolento dipende da considerazioni sulla fisica contenuta dal flusso, sulla pratica confermata per una specifica classe di problemi,

sul livello di accuratezza richiesta, sulle risorse di calcolo disponibili e sul tempo disponibile per la simulazione.

Di seguito vengono fornite brevi descrizioni dei principali modelli implementati nel codice ANSYS CFX 10.0.

3.3.5 Modelli “k - ” Modello “Standard k - ”

Il modello “Standard k - ” [12] si basa su equazioni derivate da considerazioni fenomenologiche ed empiriche; k indica l’energia cinetica turbolenta, mentre il tasso di dissipazione, cioè la velocità di dissipazione delle fluttuazioni di velocità. Le equazioni di conservazione della massa e della quantità di moto diventano:

( )

(

)

(

)

(

)

dove B è la somma delle forze di massa, µ_eff è la viscosità effettiva, mentre p′ è la pressione modificata; queste variabili sono definite come segue:

k p p ρ 3 2 + = ′ (3-39) t eff µ µ µ = + (3-40)

dove µt è la viscosità turbolenta; questo modello assume che essa sia funzione di

k ed secondo la formulazione seguente:

ε ρ µ µ 2 k C t = (3-41)

dove la costante vale C_µ =0.09.

I valori di k ed vengono calcolati risolvendo le loro equazioni di trasporto:

( )

₍

₎

( )

₍

₎

₍

₎

dove le costanti valgono σk =1,σε =1.3,Cε1 =1.44 e Cε2 =1.92; mentre Pk è

la produzione di turbolenza dovuta alle forze di galleggiamento ed alle azioni viscose e vale:

( )

(

)

(

)

nel caso di fluidi incomprimibili il secondo termine del secondo membro può essere trascurato. Il coefficiente moltiplicativo della viscosità turbolenta può essere regolato, il suo valore prefissato è 3 (come si può vedere dall’equazione), ciò è dovuto all’assunzione di “frozen stress” che è stata fatta per impedire che i valori di k ed diventino troppo grandi.

Il termine P_kb indica la produzione di turbolenza dovuta ai fenomeni di galleggiamento a causa della forza gravitazionale, è modellato come segue:

ρ ρ µ _⋅∇ − = g P t kb (3-45)

Concludendo, il modello “Standard k - ” prevede la soluzione di due equazioni di trasporto separate per determinare indipendentemente la velocità turbolenta e la scala di lunghezza. Ciò offre un buon compromesso tra robustezza di calcolo ed accuratezza computazionale per un ampio campo di flussi turbolenti, il che spiega la sua popolarità nella simulazione di flussi industriali.

Modello “Renormalization Groupk - ” (RNG)

Il modello “RNG k - ” [13] fu ricavato usando una rigorosa tecnica statistica chiamata appunto “renormalization group theory”. Esso è simile nella forma al modello “Standard k – ”, ma include le seguenti raffinatezze:

• il modello “RNG k - ” ha un termine addizionale nella sua equazione in che migliora l’accuratezza per flussi forzati;

• la teoria RNG provvede una formula analitica per il numero di Prandtl turbolento, mentre il modello “k- standard” utilizza valori costanti stabiliti dall’utente;

• mentre il modello “Standard k – ” è valido per alti numeri di Reynolds, la teoria RNG tiene conto degli effetti dei bassi numeri di Reynolds. L’effettivo uso di questa caratteristica dipende, comunque, da un appropriato trattamento della regione vicino la parete.

Queste caratteristiche rendono il modello “RNG k - ” più accurato e affidabile per una più ampia classe di flussi rispetto allo “Standard k - ”.

3.3.6 Modelli “k - ” Modello “Standardk - ”

Il modello “Standard k - ” [10] in CFX è basato sul modello di Wilcox, ed incorpora modifiche per gli effetti dei bassi numeri di Reynolds, della comprimibilità e della diffusione del flusso di taglio.

Le equazioni di conservazione della massa e della quantità di moto sono le stesse del modello “Standard k - ”, mentre per la viscosità turbolenta vale la relazione :

ω ρ

mentre il modello di Wilcox fornisce le due equazioni di trasporto perl’energia cinetica turbolenta k e per la frequenza di dissipazione turbolenta :

( )

₍

₎

( )

₍

₎

dove le costanti valgono σk =2, σω =2, β =0.075, β′=0.09 ed α =5 9;

mentre Pk è la produzione di turbolenza dovuta alle forze di galleggiamento ed

alle azioni viscose e viene calcolata come nel modello “Standardk - ”.

Modello “Baselinek - ” (BSL)

Il principale problema del modello “Standard k - ” è l’eccessiva sensibilità alla condizione di flusso libero. Inoltre le soluzioni ottenute sono fortemente dipendenti dai valori imposti ad in ingresso. Per evitare questo problema, Menter [14] ha sviluppato un modello in cui vicino alle pareti viene utilizzato il modello k - , mentre altrove il modello k - ; la transizione tra i due avviene per mezzo di una funzione apposita. Per far ciò il modello k - viene riformulato in termini di k - , e quindi moltiplicato per una funzione di transizione 1-F1 . Il modello k - viene moltiplicato per F1 e sommato al

precedente. La funzione F1 assume il valore 1 alla parete e 0 all’esterno dello

strato limite. Così facendo si ottiene il modello BLS, che alla parete risolve le equazione del k - standard, mentre all’interno del flusso quelle del modello k -

Modello “Shear Stress Transport” (SST)

Il modello SST è stato sviluppato per fornire una maggiore accuratezza nel predire la separazione del flusso sotto gradienti di pressione avversi, per ottenere questo risultato:

• nell’equazione di trasporto di è presente un termine differenziale per la diffusione trasversale;

• la definizione della viscosità turbolenta è modificata per modellare il trasporto della tensione di taglio turbolenta;

• le costanti del modello hanno differenti valori rispetto al modello standard. Queste caratteristiche rendono il modello SST più accurato e affidabile per una classe più vasta di flussi rispetto agli altri modelli k - .

3.3.7 Modelli “Reynolds Stress”

I modelli “Reynolds Stress” [16,17] sono i più elaborati di cui dispone il codice CFX. Abbandonando l’ipotesi di isotropia fatta nei modelli precedenti, questi modelli chiudono le equazioni di Navier-Stokes mediate alla Reynolds risolvendo l’equazioni di trasporto per tutte le componenti del tensore delle tensioni di Reynolds insieme ad una equazione per il rateo di dissipazione. Questo significa che per flussi bidimensionali sono richieste quattro equazioni di trasporto addizionali e per flussi tridimensionali devono essere risolte sette equazioni di trasporto addizionali.

Poiché i modelli “Reynolds Stress” predicono gli effetti della curvatura delle linee di corrente, del moto vorticoso, della rotazione e dei rapidi cambiamenti nel rateo di deformazione in un modo più rigoroso dei modelli ad una e due equazioni, hanno un maggior potenziale per fornire predizioni accurate per fluidi complessi. Comunque, la fedeltà delle predizioni fornite è ancora limitata dalle assunzioni fatte nelle equazioni di trasporto per le tensioni di Reynolds, e dalla risorse computazionali disponibili. La modellazione dei termini delle forze di pressione e del rapporto di dissipazione è particolarmente complessa

e spesso può comprometterne l’accuratezza. Uno degli elementi più fragili dei modelli consiste nella funzione di correlazione tra pressione e deformazione.

I modelli “Reynolds Stress” non sempre producono risultati con livelli di accuratezza molto superiori di quelli dei modelli più semplici, così da giustificare i maggiori costi di calcolo. Comunque il loro uso è d’obbligo quando le caratteristiche d’interresse del fluido sono il risultato dell’anisotropia delle tensioni di Reynolds. Tra di essi ci sono flussi con elevati moti vorticosi all’interno di combustori, passaggi di flussi rotanti e tensioni prodotte da flussi secondari nei condotti.

Modello “Reynolds Stress” (RSM)

E’ basato sull’equazione di trasporto del tasso di dissipazione . In CFX sono implementate due differenti espressioni di questa equazione in base alla modellazione dei coefficienti di diffusione: una variante prevede la loro formulazione anisotropa, mentre nell’altra la formulazione è isotropa.

Nel codice sono implementate tre varianti generali del modello:

• Launder, Reece e Rodi - Isotropisation of Production [17] (LRR-IP)

• Launder, Reece e Rodi - Quasi-Isotropic [17] (LRR-QI)

• Speziale, Sarkar e Gatski [18] (SSG).

Queste risolvono le medesime equazioni di trasporto delle componenti del tensore degli sforzi di Reynolds, ma con differenti valori delle costanti, ed una diversa funzione di correlazione tra pressione e deformazione.

Modello “ Reynolds Stress” (SMC - )

Il modello “ Reynolds Stress” è basato sull’equazione di trasporto della frequenza e consente una modellazione più accurata degli effetti di parete. In questo modello il legame tra pressione e deformazione è implementato con una differente formulazione.

Modello “Baseline Reynolds Stress”

L’approccio è identico a quello del modello BSL: è definita una funzione di transizione tra il modello “SMC - ” ed il modello RSM (basato sul trasporto del tasso di dissipazione ) riformulato in termini di . Questa permette il passaggio da un modello all’altro al variare della distanza dalla parete.

3.3.8 La legge alla parete

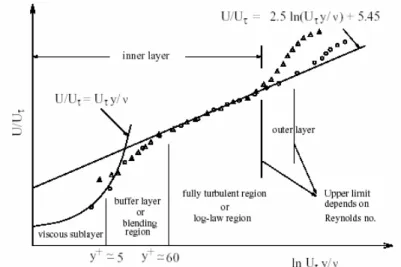
Un altro strumento ingegneristico ben consolidato è la legge della parete, con la quale si predice l’influenza sul campo di velocità, e su tutti i parametri turbolenti, della presenza di una superficie solida a contatto con il flusso. Da un punto di vista fenomenologico, uno strato limite turbolento può essere suddiviso in tre regioni: “viscous sublayer”, “log layer” e “defect layer” (vedi Figura 3.1Fig. 3.).

Nella prima regione, chiamata “viscous sublayer”, dominano gli effetti molecolari, mentre le tensioni turbolente sono trascurabili. Nella “log layer” la distanza dalla parete è tale che le tensioni viscose possono ritenersi piccole rispetto a quelle turbolente. Nella “defect layer” dominano gli effetti inerziali.

Fig. 3.1: strato limite turbolento

Si definiscono le seguenti quantità:

ρ τ_ω τ = u velocità di taglio τ u U u+ ₌ t _{velocità adimensionale} µ ρu_τ y

y+ = ∆ _{distanza adimensionale dalla parete}

dove Ut è la velocità tangente alla parete ad una distanza y da essa.

Nella “viscous sublayer” il profilo di velocità è approssimativamente proporzionale alla distanza adimensionale dalla parete:

+ + _{= y}

u (3-49)

Per grandi valori di _y+ _{(“log layer”) esso tende alla legge della parete, che}

( )

κ (3-50)

dove è la costante di Von Karman e C è una costante dimensionale che dipende dalla rugosità superficiale della parete (per un fluido incomprimibile oltre il piano dello strato di contorno, senza gradienti di pressione, l’esperienza stabilisce

41 0,

≈ e C ≈5,0).

Quando si entra nella “defect layer” il profilo si allontana dalla legge logaritmica. La “log layer” si trova tipicamente tra y+=30 e y=0,1 (dove è lo

spessore dello strato turbolento).

Da queste considerazioni nasce l’idea di modellare il flusso alla parete con la “wall function”, in pratica vengono utilizzate formule semi-empiriche per descrivere il flusso all’interno dello strato limite. L’uso della “wall function” evita la necessità di modificare i modelli turbolenti sviluppati per flussi non confinati per tenere in conto della presenza di una parete. Si osserva che questo approccio fornisce risultati tanto più accurati quanto più semplici sono i casi in studio (per esempio un canale piano), mentre sono meno accurati quelli relativi ad effetti di ricircoli, pareti curve, ecc.

Nel codice CFX sono implementati tre modelli per la “wall function”: • “Standard Wall Function”, che è stato appena descritto;

• “Scalable Wall Function”, che utilizza una diversa definizione di u+ _per

evitare problemi di instabilità dell’equazione (3-50) nel caso di separazione del flusso; inoltre permette un infittimento arbitrario della discretizzazione spaziale prossima alla parete indipendentemente dal numero di Reynolds;

• “Automatic Near-Wall Treatment”, che cambia automaticamente la formulazione alla parete in base alla raffinatezza della griglia ed al numero di Reynolds; per ottenere ciò calcola il valore di definendo una funzione di transizione tra il trattamento alla parete tramite “Wall Function” ed il modello “Standard k - ”.

Il principale limite della formulazione della legge alla parete sta nel fatto che i risultati ottenuti sono dipendenti dalla discretizzazione spaziale della zona in prossimità di questa [19].

3.4 Discretizzazione

Soluzioni analitiche delle equazioni di conservazione esistono solo per flussi estremamente semplici sotto condizioni ideali particolarmente restrittive. Per ottenere soluzioni di flussi reali deve essere usato un approccio numerico che si basa sulla sostituzione delle equazioni di campo con la loro approssimazione algebrica. Le equazioni così ottenute vengono integrate su ciascun elemento in cui è stato precedentemente suddiviso il dominio. Il sistema algebrico così ottenuto può essere risolto usando uno schema di discretizzazione numerica.

3.4.1 Discretizzazione numerica

Consideriamo le seguenti equazioni di conservazione di massa, quantità di moto e scalare passivo di un flusso generico espresse in coordinate Cartesiane:

( )

( )

(

)

( )

( )

Integrando queste equazioni sul volume di controllo, ed applicando il teorema della divergenza di Gauss per convertire alcuni integrali di volume in integrali di

0 = + S j j V dn u dV dt d _{ρ ρ} (3-54) j S j i i j eff S j S j i j V i _x dn u x u dn p dn u u dV u dt d ∂ ∂ + ∂ ∂ + − = + ρ µ ρ ~ (3-55) j S j eff S j j V dn x dn u dV dt d ∂ ∂ Γ = + ρ φ φ ρφ (3-56)

dove dn indica la componente Cartesiana differenziale della normale esterna alla j

superficie. Le precedenti equazioni sono valide per volumi di controllo che non si deformano nel tempo, altrimenti la loro formulazione avrebbe richiesto altre procedure.

Il codice ANSYS CFX si basa sulla tecnica dei volumi finiti. Le equazioni di conservazione sono integrate sui volumi di controllo in modo da imporre la conservazione delle grandezze in senso discreto su ciascuno di essi. Nella Figura 3.2 è mostrato un volume finito per un caso bidimensionale. Tutte le variabili e le proprietà del fluido sono computate nel nodo.

Fig. 3.2: volume finito

Per poter risolvere numericamente le equazioni di bilancio, è necessario riformularle in termini discreti. Considerando una singola cella di un dominio bidimensionale (vedi Figura 3.3), i flussi superficiali sono calcolati in maniera discreta nei punti di integrazione, definiti come i punti medi dei segmenti che congiungono il baricentro della cella con i punti medi dei lati.

Fig. 3.3: cella del dominio

3.4.2 Schemi di discretizzazione numerica

Teoricamente è possibile formulare un numero illimitato di schemi numerici. Dal punto di vista applicativo quelli più impiegati sono meno di una decina. Di seguito sono brevemente illustrati i metodi numerici implementati nel codice CFX, facendo riferimento ad un semplice caso monodimensionale.

“Upwind Differencing Scheme”

Il valore nodale di una generica variabile viene calcolato in base al valore che essa assume nel nodo immediatamente a monte:

up ip φ

φ = (3-57)

dove ip indica il punto di integrazione. Questo è uno schema del primo ordine, è numericamente stabile e garantisce l’assenza di fenomeni non-fisici nella soluzione, ma è soggetto a diffusione numerica (vedi paragrafo 3.4.4).

“Numerical Advection Correction Scheme”

Questo schema modifica la formula (3-57) introducendo un termine che tiene conto del gradiente della grandezza considerata, formalmente si ha:

t

up

ip =φ +β∇φ⋅

φ (3-58)

dove t è il vettore che va dal nodo a monte al nodo di integrazione, mentre β è un coefficiente da fissare in un intervallo compreso tra 0 e 1; per β =0 lo schema si riduce al precedente “Upwind Differencing Scheme”, mentre quandoβ =1 lo schema è formalmente del secondo ordine. La quantità β∇φ⋅t, chiamata

Numerical Advection Correction, può essere vista come un flusso anti-diffusivo

aggiunto allo schema “Upwind”. Questo schema ha lo svantaggio di essere meno robusto ed ha la possibilità di mostrare fenomeni non-fisici nella soluzione.

“High Resolution Scheme”

Questo schema utilizza la medesima formula del precedente (3-58), con la differenza che il coefficiente β viene calcolato localmente per ogni nodo, cercando di fargli assumere il valore più vicino possibile ad 1 senza violare i principi di vincolo. La formulazione di β è basata su quella fornita da Barth e Jesperson [20]. Per le grandezze vettoriali, come ad esempio la velocità, il coefficiente viene calcolato indipendentemente per ciascuna delle componenti del vettore. Lo “High Resolution Scheme” ha un’accuratezza superiore ai due precedenti.

3.4.3 Errori di discretizzazione

Tutti gli schemi di discretizzazione numerica sono “portatori” di errori. Alcuni sono dovuti al troncamento di termini addizionali nelle espansioni in serie, mentre altri sono il risultato dell’ordine di differenziazione usato nell’approssimazione. Questi errori possono essere notevolmente ridotti da una comprensione maggiore sulle modalità della loro insorgenza e propagazione.

Diffusione numerica

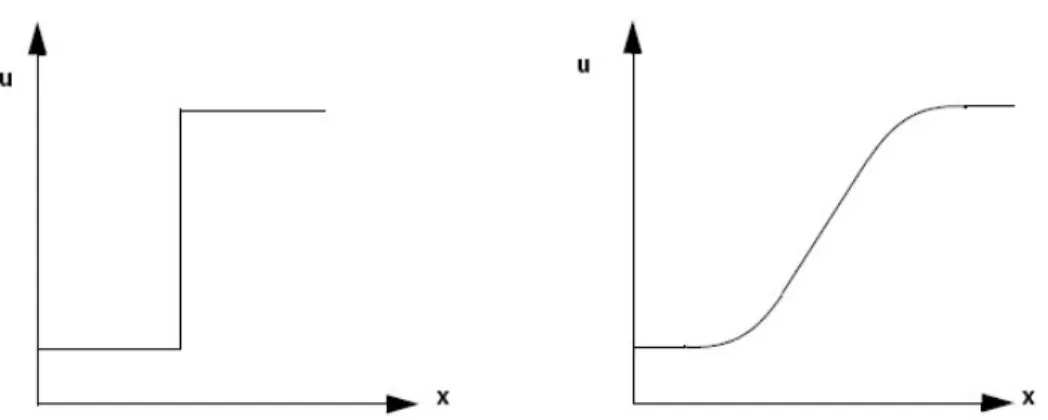
Solitamente la diffusione numerica si manifesta quando il termine convettivo delle equazioni di trasporto viene discretizzato utilizzando uno schema di ordine dispari, come lo “Upwind Differencing Scheme”. Questo effetto si manifesta quando il flusso non è allineato con una delle direzioni principali della discretizzazione spaziale, cioè quando la direzione del flusso è obliqua rispetto alle facce delle celle. In questo caso, in presenza di variazioni localizzate delle grandezze del flusso, (come ad esempio funzioni a gradino) lo schema di discretizzazione numerica non riesce a “catturare” il fenomeno; il risultato che si ottiene è una variazione graduale della grandezza considerata. In pratica il gradiente si riduce, e la variazione della grandezza viene distribuita su un tratto più ampio. Questo fenomeno è comunemente chiamato “gradient smearing”, che letteralmente significa “spalmaggio del gradiente”, ed è illustrato in Figura 3.4.

Fig. 3.4: visualizzazione della diffusione numerica

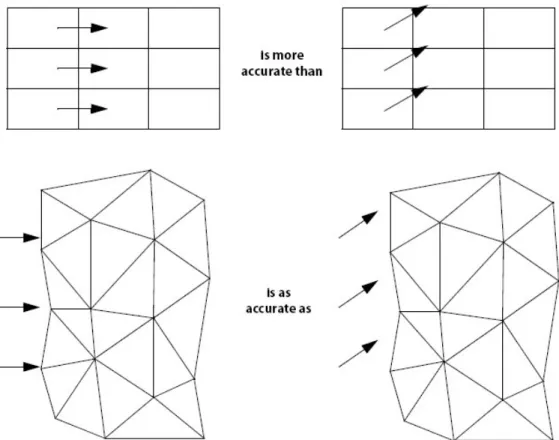
L’effetto varia in ragione dell’allineamento delle celle con la direzione del flusso, quindi è dipendente dalla forma delle celle. Utilizzando celle di forma esaedrica è relativamente facile ottenere soluzioni accurate per problemi semplici in cui la direzione del flusso è nota e fissa, mentre in casi di ricircolo o di flusso non stazionario la diffusione numerica limita l’accuratezza della soluzione. Ciò non vale per le celle di forma tetraedrica, infatti non si ha una direzione preferenziale per l’abbattimento degli effetti della diffusione numerica in quanto tutte le possibili direzioni del flusso sono ugualmente non allineate con le celle (vide Figura 3.5).

Fig. 3.5: differenti casi di allineamento del flusso con le celle

Quindi l’uso di celle tetraedriche non aggiunge inaccuratezza nelle aree con ricircoli o direzioni variabili del flusso.

Dispersione numerica

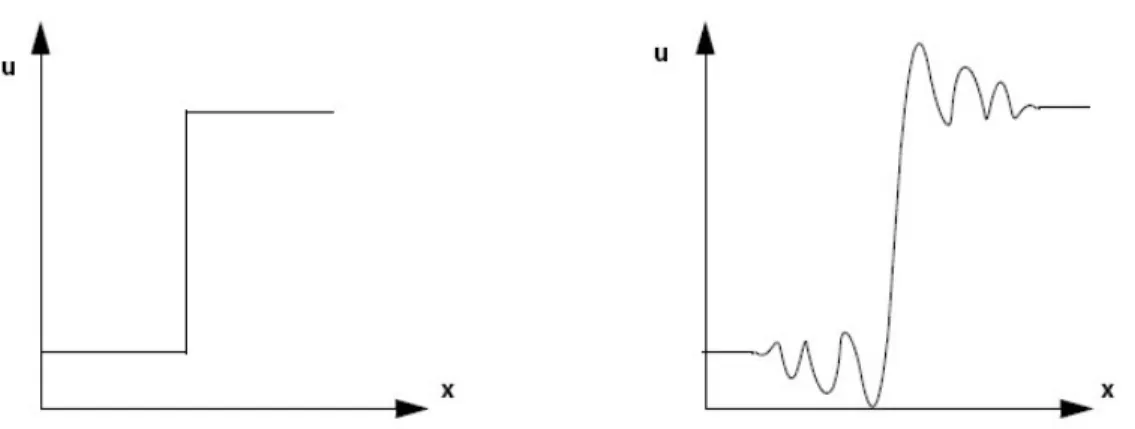
Solitamente la dispersione numerica si manifesta quando il termine convettivo delle equazioni di trasporto viene discretizzato utilizzando uno schema di ordine pari, come lo “Numerical Advection Correction Scheme” con β =1. Questo effetto si manifesta quando il flusso presenta variazioni localizzate delle grandezze (come ad esempio funzioni a gradino). Lo schema di discretizzazione numerica riesce a “catturare” il fenomeno, ma la soluzione esibisce delle oscillazioni immediatamente a monte ed a valle della variazione, come mostrato

Fig. 3.6: visualizzazione della dispersione numerica

Errori di Rhie-Chow

Nel codice CFX è implementato lo schema di interpolazione di Rhie-Chow [21] per calcolare pressione e velocità nel medesimo nodo della discretizzazione spaziale. E’ noto che per alcune tipologie di flusso in combinazione con discretizzazioni spaziali grossolane, lo schema introduce nella soluzione degli errori non trascurabili. Ciò si verifica ad esempio nel caso di flussi rotazionali bilanciati dal gradiente di pressione, oppure per flussi stazionari con sorgenti di quantità di moto bilanciate dal gradiente di pressione. In entrambi i casi le velocità diventato nulle in un particolare sistema di riferimento, rotazionale nel primo e stazionario nel secondo. Questa è la causa del problema che, senza entrare nel dettaglio, produce un errore che si riduce raffinando la discretizzazione spaziale (ad esempio riducendo la dimensione delle celle di un fattore 2, l’errore si riduce di un fattore 8).

Ricapitolando, l’errore di Rhie-Chow non rappresenta un problema per flussi generici, ma può produrre effetti allarmanti in circostanze specifiche; tuttavia può essere reso arbitrariamente piccolo raffinando la discretizzazione spaziale.

3.4.4 Gestione delle interfacce

Si definisce interfaccia la superficie di connessione tra più sottodomini. Nel codice CFX sono implementate tre metodi per la gestione delle interfacce, il 1

to 1 ,il Genereal Grid Interface (GGI) ed il Multiple Frame of Reference (MFR).

Il 1 to 1 è applicabile quando la superficie di interfaccia ha discretizzazioni identiche nei sottodomini che connette; le celle sovrapposte sono identiche e tutti i flussi superficiali sono mantenuti nell’attraversamento dell’interfaccia.

Il GGI è basato su un algoritmo che permette di ottenere connessioni con discretizzazioni differenti anche nel caso in cui le superfici dei due lati dell’interfaccia non siano fisicamente coincidenti. L’algoritmo si basa sulla definizione di superfici di controllo da utilizzare per il calcolo conservativo dei flussi. La numerica ed il trattamento dei flussi sulle superfici di controllo sono implementati in modo da ottenere la massima robustezza ed una buona accuratezza. Infatti i flussi di interfaccia sono trattati in modo completamente implicito, e sono conservativi per quanto riguarda la massa, la quantità di moto, l’energia, gli scalari e tutte le altre grandezze. Ciò significa che la robustezza e la velocità di convergenza del calcolo complessivo non sono penalizzati dalle interfacce GGI.

Il MFR permette la gestione delle interfacce nel caso in cui si abbiano rotazioni relative tra domini. L’algoritmo è basato sul GGI, e non si ritiene necessario fornire qui ulteriori informazioni su questo metodo.

Nell’analisi effettuata è stato utilizzato il modello 1 to 1 ove possibile, altrove è stato usato il GGI, ad esempio nelle interfacce tra discretizzazioni esaedriche e tetraedriche.