2 Instabilità fluidodinamiche di cavitazione: stato dell’arte

dell’arte

I

I

N

N

S

S

T

T

A

A

B

B

I

I

L

L

I

I

T

T

A

A

’

’

F

F

L

L

U

U

I

I

D

D

O

O

D

D

I

I

N

N

A

A

M

M

I

I

C

C

H

H

E

E

D

D

I

I

C

C

A

A

V

V

I

I

T

T

A

A

Z

Z

I

I

O

O

N

N

E

E

:

:

S

S

T

T

A

A

T

T

O

O

D

D

E

E

L

L

L

L

’

’

A

A

R

R

T

T

E

E

In questo capitolo viene analizzato lo stato dell’arte sulle instabilità fluidodinamiche indotte dalla cavitazione che si manifestano nelle turbopompe ad alte prestazioni. In particolare verrà inizialmente fornito un elenco delle instabilità tipiche delle turbomacchine seguendo una delle molteplici classificazioni riportate in letteratura [1]. Il seguito del capitolo si può considerare suddiviso in due parti: nella prima vengono fornite diversi tipi di analisi teoriche che hanno portato alla scoperta continua di nuovi tipi di instabilità, mentre nella seconda viene mostrato come le stesse instabilità scoperte mediante le suddette analisi teoriche, siano state individuate sperimentalmente sia nei principali centri di ricerca internazionali (principalmente in quelli giapponesi), sia nel laboratorio presente in ALTA S.p.A.

2.1 Introduzione

Nelle turbomacchine per uso spaziale la necessità di disporre di velocità di rotazione e di densità di potenza sempre più elevate ed al tempo stesso l’esigenza fondamentale di limitare i pesi, hanno aumentato la possibilità, anche in assenza di fenomeni di cavitazione, di avere fallimenti strutturali causati dai fenomeni di instabilità.

Data la complessità e la varietà di questi fenomeni, che sono ancora oggi oggetto di studio in diverse attività di ricerca, la letteratura [1] ha individuato un sistema di classificazione che divide le possibili forme di oscillazione del flusso nelle turbomacchine in tre differenti categorie all’interno delle quali si possono distinguere un certo numero di fenomeni.

Elenchiamo, quindi, tali fenomeni di instabilità: ¾ Oscillazioni globali del flusso

Sono fenomeni vibratori che coinvolgono oscillazioni del flusso su larga scala,

quali:

ƒ “Stallo rotante” e “Cavitazione rotante”

Tali fenomeni possono emergere se alla macchina è richiesto di funzionare ad angoli di incidenza elevati, vicini al valore dell’angolo per cui le pale possono subire lo stallo. Spesso succede che lo stallo si manifesti inizialmente su un ristretto numero di pale adiacenti e che questa “cella stallata” si propaghi circonferenzialmente ad una velocità pari ad una frazione della velocità di rotazione della macchina. Questo tipo di fenomeno è tipicamente osservato nelle macchine che possiedono un elevato numero di pale, come i compressori, ma è stato individuato anche nelle pompe centrifughe. Quando la macchina opera in regime cavitante il fenomeno si presenta con degli aspetti particolari e viene riferito come stallo rotante con cavitazione. Un fenomeno diverso, denominato cavitazione rotante, prevede che una o due pale presentino una maggiore o minore estensione di cavitazione con la formazione di un disturbo che propaga in direzione circonferenziale, come avviene per lo stallo rotante, anche se a velocità supersincrona.

ƒ “Surge” ed “auto-oscillazione”

Il “surge” si manifesta nelle macchine che lavorano in una condizione di carico sulle pale elevato, condizione che tipicamente coincide con la zona in cui la curva di prestazione (Φ,Ψ) ha pendenza positiva. Questa è una instabilità di sistema alla quale cioè contribuiscono tutti i componenti del sistema di pompaggio. Si verificano quindi oscillazioni di pressione e di portata attraverso l’intero impianto. Quando è presente anche la cavitazione il fenomeno viene chiamato auto-oscillazione1 e può avvenire anche in zone a pendenza negativa.

1

Tale fenomeno è stato rinominato, in tempi recenti, surge di cavitazione (cavitation surge). Poiché si pensa che tale denominazione sia più appropriata per il fenomeno, nel seguito verrà sempre indicato con il nome di surge di cavitazione.

ƒ “Cavitazione parziale” e “ Supercavitazione ”

Tali eventi possono divenire instabili se la lunghezza della paletta è paragonabile alla lunghezza della cavità; in queste condizioni la cavità collassa vicino al bordo di uscita. Un tale fenomeno può portare a violente oscillazioni su tutta la lunghezza della cavità .

ƒ “Line Resonance”

I fenomeni di risonanza avvengono quando una delle frequenze di passaggio delle pale della turbomacchina coincide con uno dei modi acustici della linea di aspirazione o di quella di scarico. Le oscillazioni di pressione associate a questi fenomeni di risonanza possono essere molto dannose.

ƒ “Rumore di cavitazione”

Il rumore di cavitazione può a volte raggiungere livelli sufficienti a causare la risonanza con le frequenze di vibrazione delle strutture.

ƒ Oscillazioni “POGO”

Tale forma di instabilità è causata dal fatto che nella maggior parte dei casi non si ha a che fare con sistemi immobili ma con macchine che sono soggette a forti accelerazioni. Un esempio di tale tipo di instabilità si ha in un razzo a propellente liquido, in cui le vibrazioni longitudinali del razzo provocano oscillazioni di pressione e di flusso all’interno dei serbatoi e nei tubi di ingresso; tali eventi, accoppiandosi con oscillazioni della pompa (“cavitation surge”), causano fluttuazioni della spinta e del veicolo in senso longitudinale. ¾ Oscillazioni locali del flusso

I principali tipi di problemi causati da oscillazioni locali del flusso e da vibrazioni delle palette sono:

ƒ “Flutter di paletta ”

Come nel caso dei profili alari ci sono circostanze in cui una pala può cominciare a vibrare in conseguenza delle particolari condizioni del flusso (angolo di incidenza, velocità), della rigidezza della pala e del sistema di supporto.

ƒ “Eccitazione di paletta”

Tale fenomeno si può presentare se esistono delle interazioni rotore-statore. Questi effetti sono particolarmente importanti per le pale di uno statore che si trovi a valle di un rotore e viceversa: le scie che si staccano dalle pale a monte possono provocare vibrazioni importanti alla frequenza di passaggio delle pale o un suo multiplo. L’eccitazione della pala può essere anche dovuta al distacco di vortici od oscillazioni di zone cavitate.

¾ Forze radiali e rotodinamiche

Le componenti perpendicolari all’asse di rotazione possono causare diversi tipi di problemi:

ƒ “Forze radiali”

Dovute alla non uniformità circonferenziale nel flusso in ingresso o nella voluta. Anche quelle stazionarie rispetto all’alloggiamento possono creare effetti di vibrazione dannosi sia per l’albero che per i cuscinetti.

ƒ “Forze rotodinamiche”

Sono il risultato del movimento eccentrico dell’asse di rotazione dell’albero della girante. Esse possono provocare una riduzione della velocità critica dell’albero e quindi un calo delle prestazioni (riduzione della velocità operativa raggiungibile dalla macchina).

E’ importante osservare che la maggior parte dei fenomeni che causano seri problemi di vibrazioni nelle turbomacchine coinvolgono interazioni tra due o più dei suddetti fenomeni: tra questi fenomeni di risonanza, quello più spesso riconosciuto è l’interazione tra le frequenze di passaggio delle pale e i modi acustici della linea di aspirazione o di scarico; comunque un gran numero di fenomeni simili si possono trovare in letteratura. Un metodo per individuare la natura del fenomeno vibratorio di una turbomacchina è quello di esaminare le frequenze tipiche a cui si manifesta e la variazione di queste con la velocità di rotazione. Ciascuna delle instabilità sopradescritte è contraddistinta da frequenze dominanti diverse e, per alcune di esse, la frequenza dipende dalla velocità di rotazione. Nella tabella successiva sono riportate le frequenze tipiche di vibrazione dei vari fenomeni oscillatori osservati sperimentalmente nelle turbomacchine.

TIPO DI INSTABILITA’ CAMPO DI FREQUENZA

Surge Sistema-dipendente , 3 ÷10 Hz nei

compressori

Auto-oscillazione Sistema-dipendente, (0.1÷0.4) Ω

Stallo rotante (0.5÷0.7) Ω

Stallo nel diffusore (0.05÷0.25) Ω Cavitazione rotante (1.1÷1.2) Ω Cavitazione parziale oscillante < Ω

Distacco dei vortici Frequenza naturale di distacco Rumore di cavitazione 1÷20 kHz

Forze radiali frazione di Ω

Vibrazioni rotodinamiche frazione di Ω(quando ci si avvicina alla velocità critica)

Flutter di paletta Frequenza naturale della paletta nel fluido

2.2 Le instabilità fluidodinamiche di cavitazione

Tra le varie forme di instabilità menzionate nella sezione precedente, due sono quelle strettamente legate alla presenza di fenomeni di cavitazione: surge di cavitazione e cavitazione rotante. In generale si può affermare [2] che queste sono le due categorie in cui possono essere suddivise tutte le instabilità di cavitazione in quanto, all’interno di queste, ci sono poi diversi modi di instabilità che saranno descritti nel seguito del capitolo.

Nel corso degli anni sono stati introdotti in letteratura diversi metodi di analisi della stabilità di flussi cavitanti nelle turbomacchine, grazie ai quali sono state chiarite le caratteristiche (principalmente in termini di frequenza e di condizioni di “onset”) delle varie forme di instabilità osservate sperimentalmente di volta in volta.

In particolare tre tipi di analisi verranno descritte nei prossimi paragrafi. Innanzi tutto verrà mostrata in dettaglio un’analisi di tipo unidimensionale [3] con cui sono state definitivamente chiarite le caratteristiche principali di quattro tipi di instabilità: stallo rotante, surge, cavitazione rotante e surge di cavitazione. Infine verranno mostrati due tipi di analisi bidimensionali la prima delle quali [4] presenta un modello di cavità chiuso sulla superficie della pala con cui sono stati individuati vari modi di instabilità. L’ultima analisi di seguito mostrata [5] presenta invece un modello di cavità con scia, sviluppato per la comprensione di un particolare tipo di instabilità che, a differenza delle altre, è associata con il degrado delle prestazioni della turbomacchina dovuto alla cavitazione.

2.3 Analisi di stabilità unidimensionale

Diversi sono i lavori in letteratura in cui viene utilizzato questo tipo di analisi (vedi per esempio [2], [3], [6]). La presente trattazione segue il lavoro di Tsujimoto et al. [3], nel quale sono esaminate, contemporaneamente, quattro tipi di instabilità: surge, surge di cavitazione, stallo rotante e cavitazione rotante.

In tale analisi viene utilizzato il modello semplificato mostrato in Figura 2.1. Esso è formato da un condotto d’aspirazione, una turbomacchina e un condotto di scarico. Nel modello sono presenti quattro stazioni: flusso a monte della pompa (1), cavitazione all’ingresso nella pompa (2), prevalenza della pompa (3), flusso a valle della pompa (4). Oltre all’ipotesi di piccole perturbazioni (fatta in quanto ci si concentra solo sui criteri di innesco dei vari tipi di instabilità), vengono fatte anche le seguenti ipotesi:

• I flussi a monte e a valle della pompa sono considerati unidimensionali per le instabilità di surge e surge di cavitazione e bidimensionali per le instabilità di stallo rotante e cavitazione rotante.

• Gli effetti viscosi sono considerati sottoforma di perdite. • Flusso nella pompa perfettamente guidato.

Figura 2.1 – Modello semplificato per l’analisi unidimensionale [3]

Si andrà ora ad analizzare il flusso nelle varie stazioni. In particolare, per quanto riguarda il flusso a monte della pompa si farà una distinzione tra il caso in cui si trattano le instabilità unidimensionali (surge e surge di cavitazione) e quello in cui si trattano le instabilità bidimensionali (stallo rotante e cavitazione rotante). Per quanto riguarda, invece, il flusso a valle della pompa, ci sarà una trattazione diversa a seconda del tipo di instabilità trattata.

2.3.1 Flusso a monte della pompa

Instabilità bidimensionali (stallo rotante e cavitazione rotante)

Con riferimento alla Figura 2.2, consideriamo un flusso bidimensionale. Supponiamo che la lunghezza del condotto di aspirazione (L) sia molto maggiore della lunghezza d’onda dei disturbi ( ). Supponiamo di avere un flusso assiale con velocità uniforme

U

in direzione

s

x

e pale rotanti a velocità costante

U

_T in direzione y. Se supponiamo che il flusso a monte della pompa sia irrotazionale, allora i disturbi prodotti dalle instabilità del flusso possono essere espressi mediante un potenziale di velocità che supponiamo di tipo periodico in direzione y e esponenziale in direzione

x

:

(2.1)

(

s 2

)

u₁exp 2 j nt y exp 2 x s s

π

φ

=

π

π

⎛_⎜ − ⎞_⎟ ⎛_⎜ ⎝ ⎠ ⎝ ⎞ ⎟ ⎠

dove ,

s n

e

j sono la lunghezza d’onda in direzione

y

, la frequenza e l’unità

immaginaria rispettivamente. Di conseguenza, le velocità u e in direzione

v

x e

sono date dalla

y (2.2) 1 1

2

exp 2

exp

2

exp 2

exp

y

u U

U u

j nt

x

x

s

y

v

ju

j nt

x

y

s

φ

_π

π

φ

_π

π

⎧

_{= +}

∂

_{= +}

⎛

₋

⎞

⎛

⎪

_∂

⎜

_⎝

⎟

_⎠

⎜

_⎝

⎪

⎨

∂

⎛

⎞

⎛

⎞

⎪

₌

_{= −}

₋

⎜

⎟

⎜

⎟

⎪

_∂

_⎝

_⎠

_⎝

_⎠

⎩

s

s

⎞

⎟

⎠

Figura 2.2 – Schema del flusso a monte della turbomacchina [3]

L’equazione linearizzata della quantità di moto può essere scritta come:

1

u

u

U

t

x

ρ

p

x

∂

₊

∂

_{= −}

∂

∂

∂

∂

(2.3)

Sostituendo le (2.2) nella (2.3) e integrando rispetto a x si trova, quindi, il

seguente campo di pressione fluttuante:

(

)

1 1 2 1 exp 2 y exp p U jk u j nt s s

π

δ

= −

ρ

+

π

⎛_⎜ − ⎞_⎟ ⎛_⎜ ⎝ ⎠ ⎝ x ⎞ ⎟ ⎠ (2.4)

dove

k sn U

=

è la frequenza ridotta adimensionale. In generale è complesso e può essere espresso da . Usando per quest’ultima espressione, si ricavano le seguenti relazioni

k

R

k k

=

+

jk

_I

k

(

1

)

exp 2

exp

2

exp 2

tan

I R R P R T R T R

y

U

U

j nt

k t

j

k t

s

s

s

V

Uk

U k

U k

π

π

π

β

φ

⎧

⎛

₋

⎞

₌

⎛

₋

⎞

⎛

₋

⎞

⎪

⎜

_⎝

⎟

_⎠

⎜

_⎝

⎟

_⎠

⎜

⎟

⎝

⎠

⎨

⎪

_≡

₌

₌

⎩

y

Uk

In queste espressioni le quantità

kR tan

β e rappresentano rispettivamente la

₁

velocità di propagazione in direzione

adimensionalizzata e lo smorzamento,

mentre

I

k

y

φ è il coefficiente di flusso (da non confondere con il potenziale di

velocità precedentemente introdotto). Quindi, in conclusione, se è data la velocità

fluttuante

nel flusso a monte della turbomacchina, l’intero campo

fluidodinamico fluttuante è determinato dalle (2.2) e (2.4).

1

u

Instabilità unidimensionali (surge e surge di cavitazione)

Con riferimento alla Figura 2.3 consideriamo, in questo caso, un flusso unidimensionale da uno spazio a pressione costante (

δ

p=0) verso una turbomacchina attraverso un condotto di lunghezza L. Le velocità del fluido sono date, in questo caso, dalle seguenti relazioni: (2.5) 1

exp 2

0

u U u

jnt

v

π

= +

⎧

⎨

₌

⎩

Figura 2.3 – Flusso unidimensionale nel condotto d’aspirazione

Applicando il teorema di Bernoulli tra il serbatoio e la stazione 0, si trova la seguente relazione per la fluttuazione di pressione nella stazione 0:

0 1

exp 2

p

Uu

jnt

δ

= −

ρ

π

Integrando l’equazione della quantità di moto tra le stazioni 0 e 1 si ha

( )(

)

1 1

2

π

jnLu

exp 2

π

jnt

= −

1

ρ δ

p

−

δ

p

₀

Dalle due relazioni precedenti si trova, quindi, la fluttuazione di pressione nella stazione 1 che è data dalla relazione

(2.6)

δ

p

1

= −

ρ

U

(

1

+

jk u

L

)

1

exp 2

π

j

nt

dove

k

_L

=

2

π

nL U

è la frequenza ridotta. Quindi, data l’ampiezza della fluttuazione di velocità all’ingresso della pompa ( ), l’intero campo fluidodinamico fluttuante può essere descritto tramite le (2.5) e (2.6).

1

u

2.3.2 Cavitazione all’ingresso della pompa

La Figura 2.4 mostra il triangolo di velocità del flusso all’ingresso della girante, la cavitazione e il flusso nel canale tra le pale. Il volume della cavità su ogni pala ( ) può essere adimensionalizzato utilizzando la spaziatura tra le pale ( );si ha dunque

c

V

h

(2.7) a

(

σ α

₁, ₁

)

=V_c

(

h2×1

)

In condizioni quasi-stazionarie, come indicato nella (2.7), il volume della cavità adimensionalizzato può essere considerato funzione dell’angolo di incidenza (

α

1) e del numero di cavtazione (

σ

₁). Quest’ultimo è definito come

1 1 2 1 2 v p p W

σ

ρ

− = (2.8)

dove

p

1,

p

v e sono la pressione in ingresso, la pressione di vapore e la velocità

relativa rispettivamente. Di conseguenza il disturbo del volume della cavità sarà dato dalla seguente relazione:

1

W

2 1 1 1 1 1 1 1 1 c a a V h W p W p

σ

σ

1

δ

δ

δ

δ

σ

α

⎡ ∂ ⎛∂ ∂ ⎞ ∂ ⎤ = _{⎢ ⎜} + _⎟+ _⎥ ∂ _⎝∂ ∂ _⎠ ∂ ⎣

α

⎦ (2.9)

Utilizzando poi il triangolo delle velocità di Figura 2.4 per legare le deviazioni

δ

W

₁ e 1

δα

con le deviazioni

δ

u

₁ e

δ

v

₁ (vedi Appendice A), la (2.9) può essere scritta nella seguente forma: 2 1 1 1 2 3 2 c

u

v

p

V

h F

F

F

U

U

U

δ

δ

δ

δ

ρ

1

⎡

⎛

⎞

⎛

⎞

⎛

⎞

⎤

=

_⎢

_⎜

_⎟

+

_⎜

_⎟

+

_⎜

_⎥

⎝

⎠

⎝

⎠

⎝

⎠

⎟

⎣

⎦

(2.10) dove 2 1 1 1 2 2 1 1 2 3 1 1 1

2 cos

sin

cos

2 sin

cos

cos

2cos

F

K

F

K

F

K

a

M

a

K

σ

β

β

β

₁ 1

M

M

σ

β

β

β

β

α

σ

⎧

=

−

⎪ = −

−

⎪

⎪

_{= −}

⎪

∂

⎨

⎪

_∂

⎪

⎪

₋

∂

⎪

_∂

⎩

(2.11)

I parametri M e K sono due importanti parametri caratteristici della cavitazione che prendono rispettivamente il nome di fattore di guadagno di flusso di massa (mass flow

gain factor) e capacità di cavitazione (cavitation compliance).

Applicando l’equazione di continuità al canale tra le pale si ha

(

2 1

)

**

h u

u

Vc

t

δ

−

δ

=

∂

∂

δ

(2.12)

dove

∂ ∂

*

t

* rappresenta la derivata temporale in un sistema di riferimento solidale alla girante che può essere espresso (vedi dimostrazione nell’Appendice A) dalle seguenti relazioni nei casi bidimensionale e unidimensionale rispettivamente:

(

)

* 1 *

2

ta

U

j

k

t

π

s

n

β

∂

=

−

∂

* * L

U

j

k

t

L

∂

₌

∂

Utilizzando queste ultime espressioni e la (2.10), l’equazione di continuità assume le seguenti forme (nei casi bidimensionale e unidimensioale rispettivamente)

(2.13)

u

₂

u

₁

2

j

h

(

k

tan

₁

)

U F

₁

u

1

F

₂

v

1

F

_{3 2}

s

U

U

δ

δ

δ

δ

δ

π

β

ρ

1

p

U

⎡

⎛

⎞

⎛

⎞

⎛

⎞

⎤

−

=

−

_⎢

_⎜

_⎟

+

_⎜

_⎟

+

_⎜

_⎟

_⎥

⎝

⎠

⎝

⎠

⎝

⎠

⎣

⎦

(2.14)

u

₂

u

₁

j k U F

h

_{L 1}

u

1

F

₃ 1₂

L

U

U

δ

δ

δ

δ

ρ

p

⎡

⎛

⎞

⎛

⎞

⎤

−

=

_⎢

_⎜

_⎟

+

_⎜

_⎟

_⎥

⎝

⎠

⎝

⎠

⎣

⎦

2.3.3 Prevalenza della turbomacchina

Si suppone che tutta la cavitazione sia concentrata nel volume a monte del passaggio delle pale. Quindi, il flusso nella girante viene considerato a singola fase e incomprimibile. Dato che le instabilità indagate avvengono a numeri di cavitazione maggiori rispetto a quello per cui si ha il degrado delle prestazioni della turbomacchina, l’effetto della cavitazione sulla prevalenza non viene, in questo caso, considerato.

c

V

L’equanzione di Bernoulli non stazionaria per il flusso nella girante è dato dalla seguente relazione: (2.15) 2 1

1

(

₁2 ₂2

)

(

_{2 1}

)

2

p

p

W

W

t

φ φ

ρ

∗ ∗

−

∂

=

−

−

−

∂

Se si indica con

β

∗ l’angolo di pala medio (

β

∗ =

(

β

₁∗+

β

₂∗

)

2), la differenza di potenziale di velocità può essere approssimata tramite la seguente espressione:

2 2 2 1 1

cos

s

u l

W ds

φ φ

β

∗

− =

_∫

≅

La perdita di pressione totale nella girante può essere sintetizzata tramite due coefficienti: la perdita idraulica nel passaggio tra le pale (

ζ

_Q) e la perdita per incidenza all’ingresso (

ζ

_S). La perdita di pressione totale è data, dunque, da

(

)

2 2 1 t Q S

p

U

u

V

ζ

δ

ζ

ρ

Δ

₌

₊

_{+ Δ}

Sostituendo queste ultime due relazioni nella (2.15) e linearizzando si ottiene la differenza tra le fluttuazioni di pressione a monte e a valle della girante sia per fluttuazioni unidimensionali che per fluttuazioni bidimensionali:

(2.16)

(

)

(

)

2 1 1 1 2 1 2 2 2 2 2 2 1 2 1 1 (tan ) cos 1

per fluttuazioni unidimensionali cos

2

tan per fluttuazioni bidimensionali cos u v L p p u v u L L U U U U l u jk L U l u j k s U

δ

δ

δ

_β

δ

δ

ρ

β

δ

β

π

_β

δ

β

∗ ∗ ∗ − _{= − − − − −} ⎧ ⎪⎪ − ⎨ ⎪ ₋ ⎪⎩

2.3.4 Flusso a valle della turbomacchina

Surge

Per l’analisi dell’instabilità denominata surge, supponiamo che la turbomacchina sia direttamente collegata a un serbatoio e che il flusso in uscita dal serbatoio venga poi scaricato verso un ambiente a pressione costante (

δ

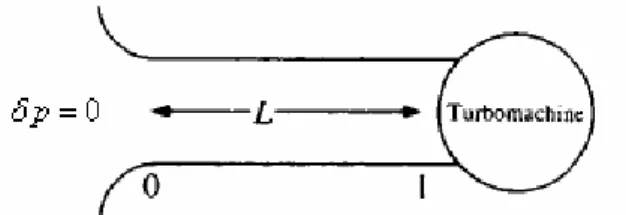
p=0) tramite una valvola (vedi Figura 2.5).

Figura 2.5 – Sistema a valle della turbomacchina nel caso del surge [3]

Applicando l’equazione di continuità al serbatoio, si trova la differenza tra le fluttuazioni di velocità a monte e valle di esso:

2 2 3 L d p U u u C Cj k p dt L 2

δ

δ

−

δ

= =

δ

(2.17)

dove C è la cosiddetta capacità del serbatoio.

Se si assume poi che la valvola abbia una caratteristica del tipo 2 2 3

p

u

R

U

U

δ

δ

ρ

=

(2.18)

dove R è la resistenza della valvola, sostituendo tale caratteristica nella (2.17) si trova il seguente legame tra le fluttuazioni di velocità e le fluttuazioni di pressione a valle della turbomacchina: 2 2 2 2 1 L u p B jk U R U

δ

_φ

δ

ρ

⎛ ⎞ =_⎜ + _⎟ ⎝ ⎠ 2 (2.19) dove

B

=

(

ρ

C L U

)

_T è il cosiddetto fattore di Greitzer.

Bisogna a questo punto mettere insieme tutti i modelli visti sinora. Siccome, per ora, si sta trattando il caso del surge, consideriamo il caso in cui non c’è cavitazione all’ingresso della pompa. Ciò implica che i coefficienti ed nella (2.14) sono entrambi nulli e l’equazione di continuità si riduce alla seguente relazione:

1

F

F

₃

1

u

u

2

Sostituendo ora le (2.5), (2.6), (2.19) e (2.20) nella (2.16) si ottiene la seguente equazione

( )

2 2

(

) (

)

2 1 2 1 1 1 1 1 1 L L u cos cos L l jk L jk u R B

φ

jk

β

∗

β

∗ L

δ

⎡ ⎤ + + − − + + = ⎢ ₊ ⎥ ⎣ ⎦ 0

Perché quest’equazione abbia soluzioni non banali, il termine tra parentesi quadre deve essere zero. Si ha dunque un’equazione caratteristicadel tipo

(2.21) akL2 +bjkL + =c 0

dove i coefficienti ,

a

b

e

c

sono dati dalle seguenti relazioni:

(2.22) 2 2 2 2 2 2 2 2 1 1 cos 1 1 1 1 cos cos 1 1 1 cos u u l a B L l b B L L R c L R

φ

β

φ

β

β

β

∗ ∗ ∗ ∗ ⎧ _{⎡ ⎤} ⎪ = _⎢ + _⎥ ⎪ ⎣ ⎦ ⎪ _{⎡ ⎤} ⎛ ⎞ ⎛ ⎞ ⎪ = − + + + ⎨ ⎢⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦ ⎪ ⎪ _{⎡ ⎛ ⎞⎤} ⎪ _{= − +⎢ ⎜ + ⎟⎥} ⎪ _{⎣ ⎝ ⎠⎦} ⎩ ⎥

La (2.21) è un’equazione quadratica in

jk

_L a coefficienti reali. Ammette, pertanto, due soluzioni del tipo

L R

k

= ± +

k

j

k

_I

dove e sono rispettivamente la frequenza e lo smorzamento. Considerando le condizioni di stabilità neutra ( ) si trova la seguente frequenza:

R

k

k

I

0

b

=

(2.23)

( )

(

)

(

)

2 2 1 1 1 cos 1 1 2 2 1 cos u L R L U n k L CL l L

β

π

π

ρ

β

∗ ∗ + + = = +

Per la condizione di stabilità neutra si ha poi

(

)

2 2 2 2

1

cos

1

cos

u

l L

L

B

R

β

β

φ

∗ ∗

+

+

= −

Introducendo la seguente definizione del coefficiente di prevalenza della turbomacchina (con cui si adimensionalizza la differenza tra pressione statica in uscita e pressione totale in ingresso), il primo termine di questa relazione può essere riscritto nella seguente forma

(2.24) 2 1 2 2 2 1 1 cos t t ts u T p p L U s

ψ

ψ

ρ

β

∗

φ

− ∂ ⇒ + = −

φ

∂

Pertanto la condizione di onset (

k

I

< ) del surge è data da

0

(2.25)

(

₂

)

1

cos

ts

l L

B R

β

ψ

φ

φ

∗

+

∂

≥

∂

Dalla (2.25) si vede che il surge avviene solo in quelle zone della curva

caratteristica della pompa (curva

φ ψ

−

ts) con pendenza maggiore di un determinato

Da un punto di vista fisico, il surge può essere spiegato (vedi per esempio [1]) facendo riferimento alla Figura 2.6 in cui la caratteristica stazionaria della pompa, curva (Φ,Ψ), è rappresentata insieme alla caratteristica stazionaria del resto del sistema.

Figura 2.6 – Esempi di turbomacchina con caratteristica stabile (A) e instabile (B) [1]

In condizioni stazionarie l’incremento di pressione attraverso la pompa deve eguagliare la caduta attraverso il resto del sistema, nelle stesse condizioni di portata, per cui il punto di lavoro è individuato dal punto O. Supponiamo quindi che avvenga una escursione dalle condizioni di equilibrio, ad esempio un piccolo decremento della portata. La pompa A, come appare chiaro in figura, avrà un incremento di prevalenza maggiore rispetto alla diminuzione di prevalenza nel resto del sistema a causa della diversa pendenza delle due curve; la portata tenderà perciò a risalire nuovamente riportando il sistema nelle condizioni iniziali.

La caratteristica della pompa A è detta quasi-staticamente stabile perché tende a riportare il sistema al punto di equilibrio O mentre il contrario succede per la pompa B che ha una caratteristica quasi-staticamente instabile. Questo tipo di instabilità avviene spesso nei compressori multistadio in cui si verifica un’oscillazione di pressione e portata nota come

surge di compressore. Surge di cavitazione

Come si è appena visto, perché avvenga il fenomeno del surge “convenzionale” è essenziale la presenza di componenti con una certa capacità a monte o a valle della girante. Nel caso del surge di cavitazione, invece, ciò non è necessario in quanto è proprio la cavitazione che fornisce la necessaria capacità.

In questo caso consideriamo un flusso in cui non ci sono fluttuazioni di portata a valle della turbomacchina (

δ

u

2

=

0

) che equivale a considerare il caso in cui si ha o un condotto molto lungo, o una grande resistenza a valle della pompa.

Con questa ipotesi, sostituendo le (2.5) e (2.6) nella (2.14), si ottiene la seguente equazione:

(

)

{

1

(

)

3

}

(

1

)

1 jk h L F_L 1 jk F_L

δ

u U

⎡ + − + ⎤

⎣ ⎦ =0

Escludendo la soluzione banale, si ottiene, quindi, la seguente equazione caratteristica:

(

)

{

1

(

)

3

}

Anche in questo caso, l’equazione caratteristica è quadratica in

jk

L e ha coefficienti reali.

Agendo, quindi, come nel caso del surge, si ottiene il seguente valore della frequenza: (2.27) 3 1

1

1

2

2

2 sin

2

T L

U

U

L

U

n

k

L

L

hF

KLh

π

π

π

β

=

=

−

=

Da questa espressione si vede che la frequenza del surge di cavitazione è proporzionale alla velocità di rotazione della pompa a differenza del surge “convenzionale” per cui la frequenza è funzione solo delle caratteristiche del condotto di aspirazione.

La condizione di innesco è invece la seguente:

(2.28)

F

₁

=

F

₃

⇒

M

≥

2 1

(

+

σ φ

)

K

Dalla (2.28) si vede che M e K sono due parametri chiave per la determinazione delle caratteristiche di stabilità del sistema. Poiché, generalmente, il volume della cavità cresce all’aumentare dell’angolo di incidenza, M assume valori positivi e ciò tende a promuovere l’instabilità. L’effetto destabilizzante di M può essere fisicamente spiegato come segue: se si ha un aumento di portata, allora l’angolo di incidenza diminuisce; siccome M è positivo, allora, anche il volume della cavità diminuisce. Pertanto la portata tende ad aumentare ulteriormente in modo tale da riempire il volume non più occupato dalla cavità.

Anche K è positivo, in quanto il volume della cavità decresce all’aumentare del numero di cavitazione. Ciò, a differenza di prima, va a favore della stabilità: se la portata aumenta, la pressione in ingresso diminuisce (per il teorema di Bernoulli) e, siccome , il volume della cavità aumenta provocando una diminuzione di portata. Pertanto, il criterio (2.28) indica che il surge di cavitazione appare quando l’effetto destabilizzante di

0

K

>

M è più forte dell’effetto stabilizzante di K.

Un ultima osservazione importante per quanto riguarda il surge di cavitazione è che esso avviene indipendentemente dalla forma della curva caratteristica della pompa (curva

ts

φ ψ

−

) e quindi, a differenza del surge convenzionale, può avvenire anche in condizioni di progetto.

Stallo rotante

In questo caso si assume, per semplicità, che a valle della turbomacchina ci sia un pozzo a pressione costante (quindi si ha

δ

p

₂

=

0

). Non essendoci cavitazione, anche in questo caso l’equazione di continuità assume la forma (2.20).

Con tali ipotesi e sostituendo le (2.2) e (2.4) nella (2.16) si trova un’equazione del tipo (2.29)

[

a

+

jk

]

(

δ

u U

₁

)

=

0

dove è un opportuno coefficiente complesso [3].

a

L’equazione caratteristica è, quindi, lineare in . Risolvendo l’equazione si trovano le seguenti espressioni per la parte immaginaria ( ) e la parte reale ( ) di rispettivamente

k

I

2

1 cos

1

1 2

cos

1 2

cos

u t I

L

k

l s

l s

β

ψ

s

φ

π

β

π

∗ ∗ ∗

+

∂

=

= −

+

+

β φ

∂

(

)

1

2

1

1

tan

1 2

cos

S P R T

V

k

U

l s

ζ

φ φ

β

π

β

∗ ∗

−

=

= −

+

(2.30)

La condizione di innesco (

k

_I

<

0

) è data dunque da

0

ts

ψ

φ

∂

>

∂

(2.31)

Questa condizione indica che lo stallo rotante avviene se il coefficiente di prevalenza della pompa (calcolato usando la pressione statica all’uscita e la pressione totale in ingresso) ha, nel piano

φ ψ

−

ts, pendenza positiva. Inoltre, confrontando questa con la

(2.25), è chiaro che è più facile che avvenga lo stallo rotante che non il surge.

Dalla (2.29), essendo il coefficiente di flusso (

φ

=cot

β

₁) generalmente minore del coefficiente

φ

∗( cot

β

1

∗

= ), si vede che

V U

_{P T}

<

1

. Il che implica che la regione di stallo propaga in direzione circonferenziale con velocità angolare minore rispetto a quella di rotazione della turbomacchina.

Per quanto riguarda la spiegazione fisica del fenomeno, Emmons et al. [7] sono stati i primi a fornirla in maniera coerente: per spiegarla si può fare riferimento alla Figura 2.7.

Figura 2.7 – Schema per la spiegazione dello stallo rotante [1]

Supponiamo che la schiera di Figura 2.7 rappresenti un set di palette (un rotore o uno statore) che opera in condizioni di elevata incidenza e supponiamo inoltre, per esempio, di avere lo stallo sulla pala B. Questo genera una scia separata e, di conseguenza, provoca un aumento del bloccaggio del flusso nel passaggio tra le pale B e A. Tutto ciò provoca una deviazione del flusso come indicato in figura che porta ad un aumento di incidenza sulla pala A e, contemporaneamente, ad una diminuzione di incidenza sulla pala C. Quindi la pala A tende a stallare, mentre lo stallo sulla pala C (se presente) tende a scomparire. Conseguentemente si può affermare che la cella di stallo tende a muoversi

verso l’alto in figura. La cella di stallo, che naturalmente può comprendere anche un numero di pale superiore a uno, ruota quindi intorno all’asse di rotazione della macchina ed è per questo che il fenomeno prende il nome di stallo rotante.

Cavitazione rotante

Così come nel caso del surge di cavitazione, supponiamo che non ci siano fluttuazioni di velocità a valle della pompa. Con tale ipotesi e sostituendo le (2.2) e (2.4) nella (2.13), si ottiene la seguente equazione:

(2.32)

⎡

_⎣

1 2

+

π

j h s k

( )

(

−

tan

β

₁

)

{

F

₁

−

jF

₂

− +

(

1

jk F

)

₃

}

⎤

_⎦

(

δ

u U

₁

)

=

0

L’equazione caratteristica sarà dunque quadratica in . La condizione di innesco è data quindi da

k

(2.33)

M

≥

2 1

(

+

σ φ

)

K

che è identica alla condizione di innesco del surge di cavitazione. La cavitazione rotante può essere, quindi, spiegata in maniera analoga al surge di cavitazione: l’unica differenza sta nel fatto che bisogna considerare un aumento di portata ad una specifica posizione circonferenziale. Come il surge di cavitazione, anche la cavitazione rotante può avvenire in condizioni di disegno indipendentemente dalla forma della curva caratteristica della pompa e questa è una delle caratteristiche principali che differenzia la cavitazione rotante dallo stallo rotante.

Prendendo la parte reale dell’equazione caratteristica, si ha la seguente equazione per :

k

(

)

2 1 3 3

tan

2

F

s

k

k

F

h

β

π

⎛

⎞

−

_⎜

+

_⎟

= −

⎝

⎠

F

Se si utilizza la relazione V U_{P T} =k tan

β

₁ e le espressioni di ed , questa equazione può essere riscritta nella seguente forma:

2

F

F

₃

(2.34)

(

V U_{P T} −1

)

{

V U_{P T} +

(

σ

+M

φ

2K

)

}

=

( )

s h

(

4

π

K sin2

β

₁

)

Questa equazione ha due soluzioni con le seguenti caratteristiche:

(

)

(

)

2

(

1

)

1

2

P T P T

V U

V U

σ

M

φ

K

>

< −

+

Questo vuol dire che la cavitazione rotante presenta due modi: uno che propaga con velocità angolare maggiore di quella della pompa e l’altro che propaga nella direzione opposta a quella di rotazione della pompa. Questi due modi sono noti con il nome di cavitazione rotante nello stesso verso (forward rotating cavitation) e cavitazione rotante in verso opposto rispetto al rotore (backward rotating cavitation). Come vedremo nei prossimi paragrafi, il primo di questi modi (che nel seguito verrà indicato col nome di cavitazione “convenzionale”) è stato osservato sperimentalmente già all’inizio degli anni ‘80 [8], mentre il secondo (che sarà invece indicato con il nome di cavitazione “controrotante”) è stato osservato sperimentalmente solo nella seconda metà degli anni ‘90 [9].

2.3.5 Presenza contemporanea delle diverse instabilità

Nella trattazione fin qui svolta, le diverse instabilità sono state analizzate tutte in maniera indipendente. In questo paragrafo verrà fatto un accenno alla possibilità di una coesistenza delle suddette instabilità. In particolare saranno brevemente descritti due casi: coesistenza di stallo rotante e cavitazione rotante e coesistenza di surge e surge di cavitazione.

Stallo rotante e cavitazione rotante

Nell’analisi dello stallo rotante, si è fatta l’ipotesi di assenza di fenomeni di cavitazione, quindi si è utilizzata la forma (2.20) dell’equazione di continuità. Per studiare la possibile coesistenza di stallo rotante e cavitazione rotante bisogna utilizzare, invece, la forma (2.13) dell’equazione di continuità.

In questo modo, si può dimostrare [3] che l’equazione caratteristica è di terzo grado in . Risolvendo tale equazione si trovano tre soluzioni per la parte reale di

k

con le seguenti caratteristiche:

k

(

)

{

}

(

)

{

}

(

)

{

}

1 1 1 2 1 2 3 1 3 Re tan 1 Re tan 0 Re tan 1 P T P T P T V U k V U k V U k

β

β

β

= > = < = <

Oltre a quelle appena mostrate, le tre soluzioni hanno anche le seguenti caratteristiche: 1. I valori di e sono molto vicini a quelli ottenuti dalla (2.34), quindi

rappresentano i due modi di cavitazione rotante visti in precedenza. Mentre il valore di è molto vicino a quello ottenuto dalla (2.29), quindi rappresenta lo stallo rotante.

1

k

k

₂

3

k

2. Il valore di

k

₃ dipende dal coefficiente di flusso (

φ

) e dai coefficienti di perdita (

ζ

_Q e

ζ

_S), mentre tali parametri influenzano poco le altre due soluzioni.

3. I parametri M e K influenzano in maniera sostanziale le soluzioni e , ma non .

1

k

k

₂

3

k

Quindi le tre radici possono coesistere, oppure manifestarsi in maniera indipendente. In particolare in passato da Murai [10] e più recentemente nei laboratori di ALTA s.p.a. ([11] e [12]) è stato osservato sperimentalmente lo stallo rotante con cavitazione.

Surge e surge di cavitazione

Anche questo caso può essere analizzando usando la forma (2.14) dell’equazione di continuità nell’analisi del surge. Così facendo si trova un’equazione biquadratica a coefficienti reali in

jk

_L. Pertanto si hanno due tipi di soluzioni complesse coniugate del tipo che hanno caratteristiche molto simili a quelle che si trovano nei casi separati di surge e surge di cavitazione. Quindi è possibile anche la coesistenza di questi tipi di instabilità.

1,2 1,2

L

Per concludere, si riassumono i principali risultati di questo tipo di analisi nelle Tabelle 2.2 e 2.3.

Tabella 2.2 – Cause delle instabilità delle turbomacchine [3]

Tabella 2.3 – Condizioni di “onset” e frequenze delle instabilità delle turbomacchine [3]

2.4 Analisi di stabilità bidimensionale con cavità chiusa

L’analisi unidimensionale descritta nel paragrafo precedente teneva conto solo delle fluttuazioni del volume della cavità. In questo paragrafo viene invece descritta un’analisi di stabilità bidimensionale che prevede un modello di cavità chiusa sulla superficie della pala.

Il modello [4] è rappresentato dalla schiera di Figura 2.8. Per semplicità si assume che il condotto a valle della schiera abbia lunghezza infinita e che, in tale condotto non ci siano fluttuazioni di velocità (

δ

u

₂

=

0

). Il condotto di aspirazione è, invece, di lunghezza L ed è connesso a uno spazio a pressione costante (

δ

p

1

=

0

).

Supponiamo di avere piccole perturbazioni con dipendenza dal tempo del tipo ej tω , dove

R

j

I

ω ω

=

+

ω

è la frequenza complessa che deve essere determinata dall’analisi. Il disturbo di velocità è rappresentato da una distribuzione di sorgenti (

q s

( )

₁ ) nella regione della cavità, e dalle distribuzioni di vortici

γ

1

( )

s

1 e

γ

2

( )

s

2 sulle pale e

γ ξ

t

( )

a valle

Figura 2.8 – Modello per l’analisi di stabilità bidimensionale [4]

Si considerano poi, le intensità delle singolarità e la lunghezza della cavità come somma di una componente stazionaria e una non stazionaria.

Le condizioni al contorno del problema sono le seguenti:

1. La pressione della cavità deve essere uguale alla pressione di vapore del liquido. 2. La componente normale di velocità sulla superficie bagnata della pala deve essere

nulla.

3. La cavità si chiude al bordo d’uscita (mobile) della cavità stessa (modello di cavità chiusa).

4. La differenza di pressione al bordo d’uscita della pala deve essere nulla (condizione di Kutta).

5. Pressione totale costante lungo la linea AB e fluttuazioni di velocità nulle a valle della schiera.

Specificando le intensità delle singolarità in punti discreti ( ) come incognite, le condizioni al contorno si traducono in un sistema di equazioni lineari nelle suddette incognite. In particolare, se si separano le incognite in una componente stazionaria e una non stazionaria, la parte stazionaria delle condizioni al contorno è del tipo

i j S

( )

{ }

2

j s s j S

q U

A l

U

α

γ

α

σ α

⎧

⎫

⎪

_{⎪ =}

⎡

_{⎤ ⎨}

_⎬

⎣

⎦

⎪

⎪

⎩

⎭

B

che è un sistema non omogeneo di equazioni lineari. Grazie a tale sistema, si può dimostrare che la componente stazionaria della lunghezza della cavità normalizzata con lo spazio tra le pale (

l h

_s ) è funzione solo di

σ α

2

.

Invece, la componente non stazionaria delle condizioni al contorno da luogo a un sistema di equazioni lineari omogeneo del tipo:

(

,

)

{

0

j u s j s

q

A l

l

ω

γ

⎧ ⎫

⎪ ⎪

=

⎡

_{⎤ ⎨ ⎬}

⎣

⎦

⎪ ⎪

⎩ ⎭

}

Imponendo che tale sistema abbia soluzioni non banali, si trova la seguente equazione caratteristica

(

)

dalla quale si possono determinare i vari valori di

ω

caratteristici delle instabilità del sistema. In particolare si vede che, date la geometria e le condizioni di flusso, i diversi valori di

ω

e quindi i diversi modi di instabilità sono funzione di

l h

_s (ovvero, per quanto detto in precedenza, di

σ α

2

). Tale parametro, quindi, influenza le condizioni di innesco delle instabilità nelle turbomacchine.

Come si è detto in precedenza, risolvendo il sistema ottenuto prendendo la componente stazionaria delle condizioni al contorno, si trova che la lunghezza stazionaria della cavità dipende solo da

σ α

2

. Nel grafico in alto di Figura 2.9a viene mostrata la variazione di

s

l h

in funzione di

σ α

2

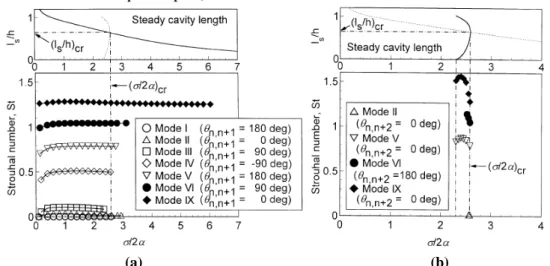
ottenuta dall’analisi assumendo cavità di lunghezza uguale sulle diverse pale nel caso di periodicità del flusso su quattro pale (che corrisponde al caso di un induttore a quattro pale).

(a) (b)

Figura 2.9 – Lunghezza stazionaria della cavità (grafici in alto) e numero di Strouhal (grafici in

basso) in funzione di

σ α

2

per un induttore a quattro pale (

C h

=

2

,

β

=80°,

1000

L C

=

) [4]

Nel momento in cui è stata effettuata tale analisi, era ben nota, da risultati sperimentali, l’esistenza della cavitazione alternata di pala (alternate blade cavitation) negli induttori con un numero pari di pale in cui la lunghezza delle cavità è diversa in maniera alternata sulle diverse pale. L’analisi è stata quindi effettuata anche per questo tipo di flusso assumendo cavità di lunghezza diversa in maniera alternata sulle quattro pale e la variazione di

l h

s in funzione di

σ α

2

ottenuta con tale ipotesi è mostrata nel grafico

in alto di Figura 2.9b.

Come si vede da questa figura, la cavitazione alternata di pala si sviluppa quando la lunghezza stazionaria della cavità supera il 65% dello spazio tra le pale. Ciò può essere spiegato facendo riferimento alla Figura 2.10, in cui viene mostrato il campo di velocità attorno alla cavità per tre tipologie di flussi cavitanti. In particolare si osserva un’inclinazione del flusso verso la superficie della pala in corrispondenza del bordo d’uscita della cavità. Quando la lunghezza della cavità supera il 65% dello spazio tra le pale, questa regione interagisce con la pala successiva, provocando su questa una diminuzione di incidenza e quindi una diminuzione della lunghezza della cavità.

Figura 2.10 – Campo di velocità attorno alle cavità per tre diverse tipologie di flussi cavitanti [4]

Tornando ai risultati dell’analisi, la soluzione della componente non stazionaria delle condizioni al contorno porta ai risultati mostrati nei grafici in basso di Figura 2.9 in cui i numeri di Strouhal (definito come

St

=

ω

_{R s}

l

2

π

U

) di diversi modi instabili (ovvero tali che

ω

_I

<

0

) sono plottati in funzione di

σ α

2

. Vediamo ora più in dettaglio le caratteristiche di questi modi instabili osservando che il simbolo

θ

_{n n, +1} indica la differenza di fase tra i disturbi su una pala e quella successiva calcolata dall’analisi. Il modo I (Figura 2.9a) ha un numero di Strouhal, e quindi una frequenza, pari a 0 e una differenza di fase di 180°. Esso corrisponde alla transizione da cavità di lunghezza uguale a cavitazione alternata, infatti compare a partire da un valore di

l h

_s pari a 0.65 (dimostrando che una maggiore lunghezza della cavità nel caso di cavitazione “uguale” è instabile), mentre non compare nel grafico di Figura 2.9b (dimostrando che, invece, nel caso di cavitazione alternata è stabile).

Il modo II è un modo di oscillazione di tipo assiale (

θ

_{n n, +1}=0) e ha una frequenza ben correlata con 1 L. Pertanto questo modo rappresenta il surge di cavitazione predetto anche dall’analisi unidimensionale. E’ importante sottolineare il fatto che questo modo di instabilità è l’unico dipendente dal sistema.

Anche il modo IX è un modo di oscillazione di tipo assiale (

θ

_{n n, +1} =0). A differenza del modo II, però, presenta una frequenza maggiore e, pertanto, è stato denominato surge di cavitazione di ordine superiore (higher order surge mode oscillation). Altra differenza con il modo II è che, in questo caso, la frequenza non dipende né dal sistema, né dalla geometria della schiera, infatti esso si manifesta anche nel caso di un singolo profilo [13]. A differenza di tutti gli altri modi, questo comincia ad apparire per valori di

σ α

2

molto maggiori.

I modi dal III al VI sono, invece, vari modi di cavitazione rotante (

θ

n n, +1 ≠0). Il disturbo nel caso del modo III ruota con velocità angolare maggiore rispetto a quella del rotore. Esso è dunque la cavitazione rotante convenzionale (forward rotating cavitation) già predetta dall’analisi unidimensionale.

Il modo IV rappresenta un modo di cavitazione rotante a una cella che propaga in direzione opposta a quella di rotazione del rotore (

θ

_{n n, +1} = − °90 ) e rappresenta, pertanto, la cavitazione controrotante (backward rotating cavitation) anch’esso già predetto dall’analisi unidimensionale.

Il modo V (

θ

n n_, +₁ =180°) rappresenta cavitazione rotante a due celle.

Il modo VI rappresenta anch’esso cavitazione rotante a una cella (

θ

n n_, +₁ =90°). A

differenza del modo III, però, ha una velocità di propagazione maggiore e, pertanto, è stato denominato cavitazione rotante di ordine superiore (higher order rotating

cavitation).

Come si è detto in precedenza, tutti i modi, tranne il modo IX, appaiono quando la lunghezza stazionaria della cavità supera il 65% dello spazio tra le pale; quindi si pensa che tutti questi modi siano causati dall’interazione del flusso in corrispondenza del bordo d’uscita della cavità con il bordo d’attacco della pala successiva. Il modo IX avviene, invece, per cavità molto più corte e di ciò non è stata ancora data alcuna spiegazione fisica.

Grazie a questo tipo di analisi sono stati dunque predetti vari tipi di instabilità di cavitazione “nuovi” rispetto a quelli già predetti mediante l’analisi unidimensionale. Sebbene tali modi siano meno frequenti rispetto a surge di cavitazione e cavitazione rotante convenzionale, essi, come vedremo più avanti, sono stati comunque osservati sperimentalmente. Essi sono comunque molto importanti in quanto, essendo caratterizzati da alte frequenze, possono andare in risonanza con i modi di vibrazione delle pale e, quindi, avere conseguenze molto dannose per la turbomacchina.

2.5 Analisi di stabilità bidimensionale con cavità aperta

L’ultimo tipo di analisi descritto, come è già stato accennato in precedenza, è un’analisi bidimensionale con modello di cavità “aperta” [5]. Tale tipo di analisi è stata effettuata per descrivere in maniera teorica un nuovo tipo di instabilità osservato sperimentalmente a cui, per i motivi che saranno spiegati nel prossimo paragrafo, è stato dato il nome di bloccaggio rotante (rotating choke). Dal momento che tale fenomeno è associato al degrado delle prestazioni della macchina dovuto alla cavitazione (cavitation breakdown), il modello usato per descrivere tale fenomeno deve poter simulare il breakdown della macchina. Siccome il modello con cavità chiusa non può simulare tale fenomeno, è stato introdotto il modello di cavità con scia mostrato in Figura 2.11.

Il flusso è suddiviso in un flusso turbolento interno dietro alla cavità e in un flusso esterno non viscoso.

La scia della cavità è suddivisa in tre regioni. La prima è la regione di mescolamento (mixing region) in cui il profilo di velocità nella scia comincia a svilupparsi e la densità cambia in maniera graduale a causa della ricircolazione del flusso. La seconda è la zona vicino alla scia (near cavity wake) in cui il profilo di velocità cambia in funzione del gradiente di pressione esterno. La terza è la scia a valle della pala (far wake) che inizia dal bordo d’uscita delle pale e che si sviluppa in funzione del flusso a valle. Le condizioni di interazione tra flusso viscoso e non viscoso nella seconda zona rendono possibile il calcolo della forma del contorno del flusso non viscoso e, quindi, di calcolare sia la componente stazionaria che quella non stazionaria del flusso.

L’analisi di stabilità è, quindi, simile a quella vista nel paragrafo precedente: ci si riduce a un problema agli autovalori con cui si calcolano le frequenze e le caratteristiche di innesco dei vari modi di instabilità.

La Figura 2.12 mostra la curva

ψ σ

− predetta dal modello. Sulle curve viene mostrato anche lo sviluppo della cavitazione rotante (simboli vuoti) e quello del bloccaggio rotante (simboli pieni): è evidente che il bloccaggio rotante avviene ai bassi valori di

σ

.

Figura 2.12 – Prestazioni della schiera in regime cavitante [5]

In Figura 2.13 viene mostrato, invece, il rapporto di velocità di propagazione in funzione di

σ

: il bloccaggio rotante ruota a una velocità angolare pari a circa la metà della velocità angolare della schiera.

Infine, per quanto riguarda le condizioni di innesco del fenomeno, in Figura 2.14 viene mostrato sia la lunghezza stazionaria della cavità (calcolata col modello del paragrafo precedente), sia la somma della lunghezza della cavità e della lunghezza della zona di mescolamento (calcolata con il presente modello) in funzione di

σ α

2

. Le barre presenti in figura rappresentano gli intervalli in cui avvengono la cavitazione rotante e il bloccaggio rotante nei due modelli. Si vede, in particolare, che nel modello con cavità con scia, la cavitazione rotante si sviluppa quando la somma delle suddette lunghezze supera il 65% dello spazio tra le pale, risultato in accordo con quello che si ottiene dal modello con cavità chiusa. Il bloccaggio rotante, invece, si sviluppa quando supera il 150% dello spazio tra le pale e , quindi, a numeri di cavitazione più bassi.

c m

l

+

l

Figura 2.13 – Rapporto di velocità di propagazione per la cavitazione rotante e per il bloccaggio

rotante [5]

Figura 2.14 – Lunghezza della cavità (modello chiuso) e lunghezza totale di cavità e regione di

mescolamento in funzione di

σ α

2

[5]

2.6 Osservazioni sperimentali dei fenomeni di instabilità

Oltre alle analisi teoriche viste nei paragrafi precedenti sviluppate nel corso degli anni, sono stati effettuati diversi lavori sperimentali nei quali sono stati osservati la maggior parte dei fenomeni di instabilità finora menzionati. In questo paragrafo vengono, quindi, analizzati alcuni di questi lavori, con particolare attenzione rivolta a quelli svolti nei laboratori giapponesi nell’ambito dello sviluppo della turbopompa dell’ossigeno liquido del motore LE-7 montato sul lanciatore giapponese H-II.

Surge di cavitazione

Il surge di cavitazione (o auto-oscillazione) è un fenomeno noto, come la cavitazione rotante, da diversi anni. Esso è stato osservato sia dai ricercatori americani durante lo

sviluppo della turbopompa dell’ossigeno liquido del motore principale dello space shuttle [1], sia da quelli giapponesi ([14], [15].

Cavitazione rotante convenzionale

Per quanto riguarda la cavitazione rotante convenzionale (forward rotating cavitation), i primi a osservarla furono Kamijo e alcuni suoi collaboratori [16] nel 1977. In particolare essi riconobbero, sia attraverso semplici osservazioni, sia attraverso un’analisi delle fluttuazioni di pressione, le seguenti caratteristiche della cavitazione rotante:

1. In un certo range di coefficienti di flusso e di numeri di cavitazione, la regione cavitante propaga da una pala all’altra nella direzione di rotazione della pompa, quindi la velocità di propagazione è maggiore della velocità di rotazione del rotore.

2. La frequenza delle fluttuazioni di pressione in ingresso è in accordo con quella di propagazione della cavità. Tali frequenze sono invece poco significative all’uscita, quindi la cavitazione rotante è un fenomeno legato alle condizioni del flusso in ingresso.

Già prima di Kamijo, Rosemann [17] nei suoi studi eseguiti nel 1965 osservò delle vibrazioni supersincrone dell’albero (riconosciute, solo in tempi recenti, come conseguenza della cavitazione rotante) che avvenivano per valori di

σ

pari a 2÷3 volte il valore di breakdown.

Dopo i primi studi, effettuati a cavallo del 1980, il gruppo di Kamijo nel 1994 [19] fu il primo a riportare un quadro chiaro dei vari fenomeni di instabilità con uno studio effettuato su un induttore a tre pale sia grazie allo studio delle fluttuazioni di pressione, sia grazie all’uso di una telecamera ad alta velocità. In particolare, dallo studio delle fluttuazioni di pressione in ingresso, fu evidente la presenza della cavitazione rotante, la quale, secondo l’analisi delle vibrazioni dell’albero della pompa, provocò anche la vibrazione dell’albero alla stessa frequenza.

La cavitazione rotante convenzionale è stata riscontrata anche in successivi studi svolti nei laboratori giapponesi. In particolare Hashimoto et al. [14] nel 1997, effettuando l’analisi delle fluttuazioni di pressione in ingresso su un induttore a tre pale, trovarono i risultati mostrati in Figura 2.15. Nello spettro è facilmente distinguibile la frequenza

2

138 Hz

c

ω

=

di poco superiore alla frequenza di rotazione del rotore (

ω

_S

=

117 Hz

). Tale frequenza può essere classificata come cavitazione rotante convenzionale per i seguenti motivi:

1. Il rapporto di velocità di propagazione è tipico della cavitazione rotante.

2. Nello spettro sono presenti anche le frequenze

ω

_c2

−

ω

_S e

3

(

ω

_c2

−

ω

_S

)

dovute a interazioni non lineari tra la rotazione dell’induttore e la cavitazione rotante stessa. Il fatto che queste frequenze compaiono con il segno meno suggerisce che i due fenomeni interagenti sono corotanti (in quanto rappresenta la frequenza di rotazione del fenomeno nel sistema di riferimento solidale all’induttore).

3. Da un’analisi fatta mediante una videocamera ad alta velocità (vedi Figura 2.16) si vede chiaramente che il fenomeno ruota nella stessa direzione di rotazione dell’induttore.

Figura 2.15 – Spettro delle fluttuazioni di pressione in ingresso per un induttore a tre pale [14]

Figura 2.16 – Fluttuazioni dell’area della cavità presente su ogni pala [14]

Sempre nel 1997, Tsujimoto et al. [9] osservarono, tra l’altro, un fenomeno rotante a singola cella con rapporto di velocità di propagazione di

1.1

classificato come cavitazione rotante in seguito all’analisi delle fluttuazioni delle cavità sulle pale fatta mediante una telecamera ad alta velocità.

1.3

∼

Oltre che su induttori a tre pale, la cavitazione rotante è stata osservata, nei laboratori giapponesi, anche su induttori a quattro pale (vedi per esempio [15]).

Cavitazione controrotante

La cavitazione controrotante fu osservata per la prima volta nel già citato lavoro di Hashimoto et al. [14]. Infatti, nello spettro di Figura 2.15 è evidenziata la frequenza

1

159 Hz

c

ω

=

(

1.36Ω

) classificata come cavitazione rotante all’indietro sia perché nella parte dello spettro non presente in figura compaiono le frequenze

ω

c₁

+

ω

S e

(

1

3

ω

_c

+

ω

_S

)

, sia perché tale condizione è in miglior accordo con i dati sulla lunghezza delle cavità sulle pale ottenuti tramite la telecamera ad alta velocità.

Un esempio di cavitazione rotante all’indietro su un induttore a quattro pale è documentato anche in [4]. Tale fenomeno ha un rapporto di velocità di propagazione di

.

1.95

−