CAPITOLO 2
Algoritmo di Deskewing
2.1 Introduzione
L’analisi dell’algoritmo di Deskewing è stata sviluppata realizzando un implementazione software del sistema con l’ausilio dei tool offerti da Matlab. In questo modo ne è stata testata la funzionalità sia nel caso ideale che nel caso in cui sia presente un certo mismatch circuitale. In particolare sono stati simulati i due algoritmi di correzione, Bisezione e Differenziale al Nonio facendone un’analisi statistica. Sono state in seguito valutate le curve di valor medio dello skew residuo al termine della correzione con l’algoritmo di Bisezione e dello skew al termine della correzione differenziale al variare della deviazione standard dovuta al mismatch circuitale. Infine sono state ricavate le curve di deviazione standard dell’errore in funzione dello sfasamento da recuperare per entrambi gli algoritmi al variare del mismatch circuitale. Osserviamo che i valori dello skew residuo ottenuti sia nell’implementazione software, sia nelle simulazioni hardware sono estremamente piccoli (dell’ordine del decimo di picosecondo). Purtroppo questi valori sono ottenibili solo in simulazione in quanto in un sistema reale intervengono errori di mismatch circuitale che peggiorano le prestazioni ottenibili in simulazione. Tali errori di mismatch nei componenti può essere limitato utilizzando particolari tecniche nel progetto del layout ma un mismatch residuo significativo non può essere evitato e l’errore introdotto da tale mismatch può essere anche maggiore della risoluzione raggiunta dal nostro algoritmo,
soprattutto nella tecnologia a nostra disposizione che è superata rispetto a quelle usate per i circuiti integrati in cui le tecniche di Deskewing trovano applicazione. Facciamo notare tuttavia che il dimensionamento delle capacità per la regolazione del ritardo è puramente dimostrativo e può essere scelto in fase di progetto in funzione dell’applicazione e della tecnologia utilizzata. Il metodo proposto è invece valido per tutte le tecnologie e applicazioni.
2.2 Scelta degli algoritmi per la correzione
Il range di recupero previsto per il Deskewer realizzato in questo lavoro di tesi è di 200 ps. Considerata l’ampiezza di tale range in relazione alla piccolissima risoluzione da raggiungere si è pensato di spezzare la correzione in due parti: una correzione grossolana e una correzione fine.
2.2.1 Algoritmo di Bisezione.
La correzione grossolana è stata realizzata implementando un algoritmo di bisezione doppio in modo che con solo sette pesi è possibile coprire l’intero intervallo di recupero. La (2.1) mostra l’implementazione software dell’algoritmo di approssimazioni successive: ) . ... 2 2 ( 2 0 2 0 0 1 0 1 b b b B n B n n B n τ + τ + +τ − − − − (2.1) con n=7 e τ0B = 0.9 ps
dove n è il numero di pesi, τ0B è il ritardo elementare di Bisezione e (bn-1...b0) rappresentano la configurazione di bit della parola digitale da produrre per impostare il ritardo desiderato.
Infatti con un numero di pesi pari a sette e un ritardo elementare di bisezione pari a 0.9 ps la somma del ritardo introdotto quando tutti i pesi sono inseriti è pari a 114.3 ps che moltiplicato per due fornisce 228.6 ps sufficienti a
coprire l’intero intervallo da correggere. La moltiplicazione per due è dovuta al fatto che l’algoritmo di Bisezione è implementato su entrambe le linee di ritardo. Sulla linea che produce il segnale in anticipo vengono inseriti i pesi secondo l’algoritmo di approssimazioni successive (SAR). Sulla linea che produce il segnale in ritardo, i pesi vengono tolti (su questa linea, una volta rilevata la polarità dello sfasamento, procediamo all’accensione di tutti i pesi) secondo lo stesso algoritmo citato prima. La correzione grossolana ha una durata di sette cicli di clock e termina mantenendo lo stesso segno dello sfasamento tra i due segnali prima della correzione. La Figura 2.1 mostra i due fronti del segnale di clock prima e dopo la correzione con il metodo del SAR. In particolare la Figura 2.1 (a) evidenzia come l’algoritmo di correzione venga implementato sui due segnali mentre la Figura 2.1 (b) mostra come al termine del recupero la polarità dello skew residuo risulti essere perfettamente uguale alla polarità dello skew iniziale.
C _
Clk_2 Clk_2
lk_1 Clk 1
Skew Skew Residuo
(a) (b)
2.2.2 Algoritmo Del Nonio (Vernier)
Per la correzione fine la soluzione proposta in questa tesi prevede una correzione differenziale in cui i pesi introdotti durante il recupero differiscono per
ogni linea e i pesi sono calibrati in modo tale che τ0D (ritardo elementare
differenziale) introduca un ritardo pari a 2 ps e τ0D + ∆ introduca un ritardo
pari a 2.2 ps. La scelta del valore dei due ritardi non è stringente, importante è che differiscano di un ∆ prefissato. La nostra scelta è caduta su un ∆ di 0.2 ps poichè con soli dieci pesi possiamo recuperare uno skew residuo di 2 ps. Ad ogni passo viene inserito un ritardo τ0D su linea_1 e τ0D + ∆ su linea_2. Poichè linea_1 produce il segnale in ritardo e linea_2 quello in anticipo ad ogni inserimento recuperiamo uno sfasamento tra i due segnali di 0.2 ps pari proprio a ∆ .
La Figura 2.2 mostra la configurazione degli elementi di ritardo differenziale su ciascuna linea con il metodo del Nonio.
Ritardi_Differenziali_Introdotti_Da_Linea_1
τ0D τ0D τ0D ………. τ0D τ0D
Ritardi_Differenziali_Introdotti_Da_Linea_2
τ0D +∆ τ0D+∆ τ0D +∆ ………. τ0D +∆ τ0D +∆
Figura 2.2 Configurazione degli elementi di ritardo differenziale con il metodo del nonio.
quindi la risoluzione con cui operiamo la correzione differenziale con il metodo del Nonio è di 0.2 ps. Passo successivo nello sviluppo degli algoritmi è stato quello di verificarne la funzionalità mediante l’ausilio del linguaggio di programmazione Matlab.
2.3 Implementazione software del Deskewer mediante
utilizzo di Matlab.
Matlab è un linguaggio di programmazione potente e nello stesso tempo un ambiente computazionale interattivo. In questo ambiente di sviluppo è possibile realizzare file che contengono codici Matlab definiti M-file. Questi file sono editabili con un qualsiasi editor di testo. Questi possono essere usati come un comando o una funzione Matlab. Ci sono due generi di M-file:
Script: non accettano argomenti di ingresso o argomenti di uscita. Questi operano su dati presenti nel workspace cioè l’area di memoria accessibile dal prompt di Matlab.
Function: possono accettare argomenti di ingresso e argomenti di uscita. Una variabile interna è locale alla funzione.
in questa tesi si è scelto di utilizzare gli Script per testare la funzionalità del sistema sia nel caso ideale che in quello non ideale grazie alla possibilità di utilizzare le funzioni statistiche offerte dal tool.
Quando si richiama uno script, Matlab esegue semplicemente i comandi presenti nel file. Gli Script possono operare su dati esistenti nel workspace, o possono creare dati nuovi su cui operare. Sebbene gli script non forniscono dati di output,qualsiasi variabile che loro creano rimane nel workspace per essere usata in calcoli susseguenti. Inoltre gli script possono produrre dei grafici usando funzioni apposite.
Matlab offre la possibilità di utilizzare strutture di controllo del flusso quali if statement, for loop, while loop etc. Con la prima è possibile eseguire un gruppo di operazioni se l’espressione logica o aritmetica valutata dal costrutto if ha prodotto un risultato vero. Mentre il costrutto for ci permette di ripetere un certo numero di volte un gruppo di operazioni. Le potenzialità offerte da questo
tool ci hanno permesso di fare un modello software del sistema in grado di emularne il funzionamento.
2.4 Caso Ideale
La descrizione mediante utilizzo di Script Matlab è stata divisa in due sezioni. La prima descrive la correzione grossolana con il metodo delle approssimazioni successive (SAR). La seconda descrive la correzione Differenziale con il metodo del Nonio (Vernier). Stessa gerarchia è stata successivamente mantenuta nella realizzazione semicustom del controllore digitale per l’implementazione dei due algoritmi di correzione. È stato innanzi tutto definito un vettore di sette elementi contenenti i pesi da inserire durante la correzione:
v =[ 57.6 28.8 14.4 7.2 3.6 1.8 0.9 ];
successivamente sono stati definiti due vettori maschera: b =[0 0 0 0 0 0 0 ];
c =[1 1 1 1 1 1 1 ];
con l’ausilio delle proprietà del prodotto scalare tra vettori, dello statement if e della possibilità di modificare ogni singolo elemento dei vettori indicandone il numero dell’elemento stesso, abbiamo implementato l’algoritmo SAR. Il vettore c applicato alla linea che produce il segnale di clock in ritardo, permette di disinserire gli elementi di ritardo, mentre il vettore b applicato alla linea che produce il segnale in anticipo ci permette di inserire gli elementi di ritardo. Questa strategia ci permette di applicare il metodo di bisezione in maniera duale su entrambe le linee di ritardo. I pesi che vengono inseriti crescono con la potenza
del due. Per inserire ad esempio il ritardo corrispondente all’elemento più significativo del vettore v basta settare l’elemento sei del vettore b con l’istruzione:
b(1) = 1 ;
Questa istruzione produce il vettore:
b =[1 0 0 0 0 0 0];
Effettuando il prodotto scalare tra il vettore b e il vettore v degli elementi di ritardo con l’istruzione:
v*b.’;
produciamo uno scalare del valore di 57.6 ps che possiamo sommare al segnale che percorre la linea su cui è stato inserito quel quanto temporale producendo un ritardo di propagazione nel segnale di clock. Contemporaneamente sull’altra linea verrà tolto il peso più significativo settando l’elemento sei del vettore c con l’istruzione:
c(1) = 0;
la quale produce il vettore:
c =[0 1 1 1 1 1 1];
effettuando il prodotto scalare tra il vettore c e il vettore v degli elementi di ritardo con l’istruzione:
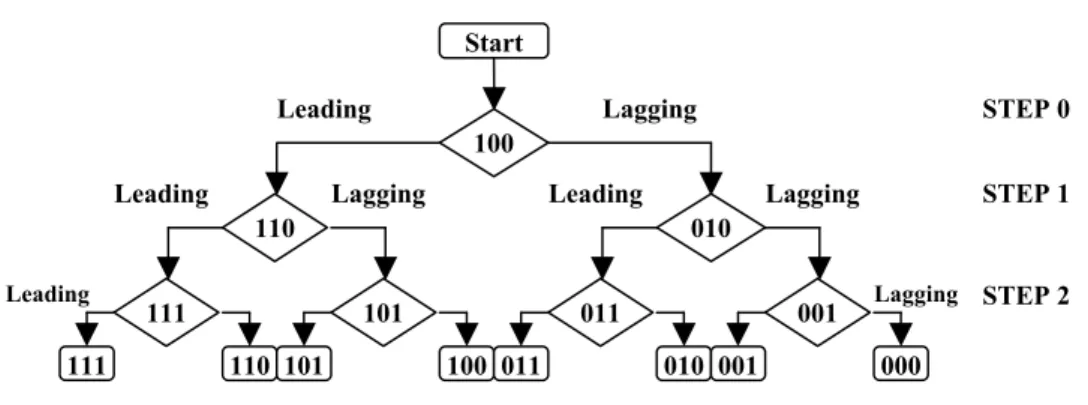
produciamo uno scalare del valore di 56.7 ps pari al ritardo totale introdotto da tutti gli elementi di ritardo per la correzione di tipo SAR (114.3 ps ) decurtato del peso più significativo pari a 57.6 ps. Si procede così in maniera esaustiva fino al termine dell’algoritmo. Nella Figura 2.3 viene mostrato il diagramma di flusso dell’algoritmo SAR implementato nella nostra descrizione, che per semplicità di lettura è riferito ad un registro a soli tre bit, mentre nella nostra realizzazione il registro è di sette bit.
Lagging Lagging Lagging Lagging Leading Leading Leading Leading 000 001 010 011 100 101 110 111 001 011 101 111 010 110 100 Start STEP 0 STEP 1 STEP 2
Figura 2.3 Diagramma di Flusso Algoritmo SAR.
La Figura 2.4 mostra come è stato realizzato lo step 0 e lo step 1 nello script Matlab. Nel segmento di codice mostrato in figura è possibile notare la presenza di una variabile skew a cui assegniamo lo sfasamento presente tra i due segnali. Questa variabile si aggiorna ad ogni step eseguito fornendo al termine il valore dello skew residuo. Le due variabili cka e ckb rappresentano i due segnali di clock che viaggiano su due percorsi di diversa lunghezza e che pilotano celle il cui carico capacitivo può differire in maniera considerevole. Sotto queste condizioni tra i due segnali è presente uno sfasamento del quale si tiene conto attraverso la variabile skew accennata precedentemente. Lo statement if ci ha permesso di descrivere correttamente il flusso dell’algoritmo SAR. In base al risultato prodotto dal controllo sulla condizione di anticipo tra i segnali
l’algoritmo decide la corretta configurazione dei quanti temporali. La variabile
cka1 contiene il valore di un offset la cui utilità verrà descritta in dettaglio nel seguito. . . . b=[0 0 0 0 0 0 0]; c=[1 1 1 1 1 1 1]; d=c; echo off cka1=v*d.' ; b(1)=1; c(1)=0; cka=cka1+v*b.'; ckb=skew+v*c.';
if cka>ckb b(1)=0 ; c(1)=1 ; else b(1)=1; c(1)=0; end; b(2)=1; c(2)=0; cka=cka1+v*b.'; ckb=skew+v*c.'; . . .
Figura 2.4 Segmento di codice Matlab correzione algoritmo SAR.
Per realizzare correttamente la doppia bisezione è stato necessario sommare un offset pari al ritardo totale introdotto dalla linea quando tutti i pesi della bisezione sono inseriti. Tale ritardo, come detto in precedenza, è di 114.3 ps. L’offset deve essere inserito sulla linea che presenta tutti gli elementi di ritardo per la bisezione disinseriti. L’offset è stato definito con le istruzioni:
d =c; v*d.’;
la presenza di questo ritardo fisso è fondamentale per l’applicazione del doppio algoritmo SAR in quanto l’accensione dei pesi per la bisezione sulla linea che produce il segnale di sincronismo in ritardo, senza inserire un ritardo della stessa quantità sulla linea che produce il segnale di sincronismo in anticipo modificherebbe il reale sfasamento esistente tra i due segnali falsando la misura effettiva dello shew tra i due.
Terminata la prima correzione con l’algoritmo SAR siamo passati alla correzione dello Skew residuo applicando l’algoritmo differenziale con il metodo del Nonio. Valutato tale residuo, questo è stato usato come variabile di ingresso per lo script che implementa la correzione differenziale. In questo codice Matlab abbiamo definito due vettori di dieci elementi contenenti quanti temporali che differiscono tra loro di 0.2 ps:
linea_1 =[2.2 2.2 2.2 2.2 2.2 2.2 2.2 2.2 2.2 2.2]; linea_2 =[2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0];
ad ogni step viene inserito in maniera simmetrica un elemento di ritardo su ciascuna linea. Il quanto temporale minore è inserito sulla linea che produce il segnale di clock che si trova in ritardo, (ckb nella nostra simulazione) mentre il quanto temporale maggiore sulla linea che produce il segnale di clock in anticipo rispetto al precedente (cka nella nostra simulazione). L’algoritmo funziona correttamente anche invertendo la configurazione dello sfasamento tra i due segnali essendo perfettamente simmetrico rispetto ai segnali di ingresso. Nella
Figura 2.5 riportiamo i primi due step della correzione differenziale al Nonio. Innanzi tutto sono state definite due costanti a cui è stata assegnata ad una il riferimento (cka1) e all’altra lo skew residuo (ckb2) valutato precedentemente. Assegniamo queste due costanti alle variabili cka e ckb che verranno modificate ad ogni step dopo l’inserimento dei quanti temporali. I quanti temporali con il
metodo differenziale al Nonio vengono inseriti in modo termometrico. L’inserzione di un quanto temporale è discriminata dal verificarsi della condizione contenuta nello statement if. La correzione termina quando si ha inversione di segno nello sfasamento tra i due segnali.
. . . cka1 =0; ckb2 =residuo; cka=cka1; ckb=ckb2;
if cka<ckb cka=cka1 + linea_1 * [1 0 0 0 0 0 0 0 0 0].’; ckb=ckb2 + linea_2 * [1 0 0 0 0 0 0 0 0 0].’;
else cka=cka;ckb=ckb;end; skew=cka-ckb;
if cka<ckb cka=cka1 + linea_1 * [1 1 0 0 0 0 0 0 0 0].’; ckb=ckb2 + linea_2 * [1 1 0 0 0 0 0 0 0 0].’;
else cka=cka;ckb=ckb;end; skew=cka-ckb;
. .
Figura 2.5 Segmento codice Matlab correzione differenziale al nonio.
2.5 Caso non ideale: analisi statistica del deskewer con
Matlab.
Verificata la funzionalità degli algoritmi di Deskewing nel caso ideale si è passati a testarne il corretto funzionamento in presenza di un errore dovuto al
mismatch circuitale. Di tale mismatch a livello di descrizione come codice Matlab si è tenuto conto introducendo su ogni ogni peso un errore con distribuzione di probabilità gaussiana. Per introdurre tale errore è stata usata la funzione randn resa disponibile dal tool di sviluppo. Questa funzione ci ha permesso di generare un numero casuale e, con distribuzione di probabilità gaussiana a media m nulla e varianza v prefissata. La corretta sintassi di questa funzione è:
e =sqrt(v)*randn(nr,nc) + m
I campi nr e nc permettono di generare una matrice o un vettore di numeri casuali con distribuzione di probabilità gaussiana in quanto rappresentano il numero di elementi per riga e per colonna. Nell’analisi statistica effettuata questo campo è posto ad uno poichè si è interessati a produrre uno scalare. Tale scalare è stato sommato al peso che costituisce il quanto temporale. Per la correzione con il metodo di bisezione il vettore dei quanti temporali si modifica nel seguente modo:
[57.6 + e 28.8 + e 14.4 + e 7.2 + e 3.6 + e 1.8 +e 0.9 + e]
per la correzione con il metodo differenziale al Nonio i due vettori contenenti i quanti temporali sono stati così modificati:
linea_1 =[2.2+e 2.2+e 2.2+e 2.2+e 2.2+e 2.2+e 2.2+e 2.2+e 2.2+e 2.2+e]; linea_2 =[2.0+e 2.0+e 2.0+e 2.0+e 2.0+e 2.0+e 2.0+e 2.0+e 2.0+e 2.0+e];
L’analisi statistica è stata condotta su un campione di 100 prove. Nell’analisi dell’algoritmo di Bisezione per ogni prova la variabile skew variava in un range compreso tra 60 ps e 200 ps generando un vettore di 140 elementi contenenti lo skew residuo relativo ad ogni valore di sfasamento iniziale compreso nel range citato prima. Il valore minimo di tale intervallo non è stringente. Questi è stato scelto per limitare il numero di elementi del vettore degli skew residui in modo da ridurre i tempi di simulazione. È stato verificato che l’algoritmo di Bisezione
funziona correttamente anche con skew iniziali di lunga inferiori ai 60 ps menzionati. Mediante l’utilizzo della funzione max offerta dal tool è stato possibile valutare il valore massimo tra gli elementi che costituiscono il vettore degli skew residui. Dunque il valore massimo tra questi elementi non rappresenta altro che il massimo skew residuo ottenibile applicando l’algoritmo di Bisezione analizzando tutto il range di interesse. Tutto ciò è stato ripetuto per tutte e 100 le prove. Alla termine delle 100 prove avevamo a disposizione un vettore di 100 elementi contenenti gli skew residui massimi con distribuzione di probabilità gaussiana valutati in ogni singola prova. Su questo vettore è stato effettuato il calcolo di media. Questo calcolo è stato ripetuto per ogni valore della Deviazione Standard, la quale variava in un intervallo compreso tra lo 0 e il 10%. La funzione Matlab che calcola la media di una sequenza di numeri casuali è mean(x) dove x è la sequenza di numeri casuali con la distribuzione menzionata in precedenza e con una prefissata Deviazione Standard s. A tal proposito si ricorda che vale la relazione:
s =sqrt(v)
dove v, come detto in precedenza, è la varianza. Si ricordi inoltre che se i numeri casuali x sono generati da una distribuzione di probabilità, i valori stimati m e v approssimano media e varianza vere all’aumentare del numero di realizzazioni (lunghezza del vettore x). Noto il vettore media, contenente il valor medio per ciascuna deviazione standard dovuta al mismatch circuitale è stato possibile graficare l’andamento del valor medio dello skew residuo al variare dell’errore dovuto al mismatch. Ottenuto lo skew residuo al termine dell’applicazione dell’algoritmo di Bisezione in presenza di errore dovuto al mismatch si è passati all’analisi statistica dell’algoritmo Differenziale al Nonio. Tale residuo è stato utilizzato come variabile di ingresso per lo Script che realizza la suddetta correzione. Sempre utilizzando la funzione randn abbiamo generato uno numero casuale, con distribuzione di probabilità gaussiana a media nulla e deviazione standard variabile. Il numero così generato è stato sommato ad ogni singolo peso
per la correzione Differenziale al Nonio. Per ogni valore di Deviazione Standard sono state realizzate 100 prove. Di ogni realizzazione ne è stato calcolato il valor medio e successivamente è stato valutato il grafico della variazione del valor medio dello skew residuo al termine della correzione Differenziale al Nonio al variare dell’errore percentuale dovuto al mismatch circuitale.
2.5.1 Algoritmo di Bisezione
Come descritto in precedenza grazie alle funzioni offerte da Matlab è stato possibile condurre un’analisi in presenza di mismatch ed è stato quindi possibile fornire una descrizione statistica degli algoritmi di correzione. Sono stati ricavati i massimi degli skew residui in una realizzazione di 100 prove analizzando tutto il range dello skew da correggere con deviazione standard dovuta al mismatch del processo tecnologico variabile in un intervallo 0-10%.
0 10 20 30 40 50 60 70 80 90 100 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 1.9 1.95 2 Numero di Realizzazioni S kew M as si m o R es iduo ( ps )
Skew Residui Massimi con Deviazione Standard del 3%
Skew Massimo Residuo
Skew Massimo Residuo in assenza di mismatch Valor Medio Skew Residuo
La Figura 2.6 mostra i 100 campioni relativi agli skew massimi residui ottenuti analizzando tutto il range di correzione, il valor medio dello skew residuo quando l’errore di mismatch è del 3% e infine il valore ideale dello skew residuo in assenza di mismatch. Il valor medio misurato in questa realizzazione è di 1.7884 ps, il massimo skew residuo è di 1.938 ps mentre il minimo skew residuo risulta essere di 1.5896 ps. Il risultato è pienamente verificato andando a leggere in corrispondenza di una deviazione standard del 3% il valor medio graficato in
Figura 2.8.
Di seguito riportiamo solo una tabella come mostrato in Figura 2.7 in cui vengono indicati i valor medi dello skew residuo ottenuti variando la deviazione standard del mismatch in un intervallo compreso tra 1% e 7% visto che come mostrato in Figura 2.8 ha poco senso spingersi oltre visto che il valor medio è maggiore di 2 ps.
Valor Medio Skew Residuo Deviazione Standard del Mismatch
1.7793 ps 1% 1.7897 ps 2% 1.7884 ps 3% 1.7936 ps 4% 1.7836 ps 5% 1.7899 ps 6% 1.9539 ps 7% Figura 2.7
Si ricorda infatti che con l’algoritmo Differenziale al Nonio per ottenere la correzione dello skew residuo con risoluzione piccolissima questi deve essere inferiore a 2 ps.
La Figura 2.8 mostra quindi l’andamento del valor medio dello skew residuo in funzione della deviazione standard dovuta al mismatch circuitale al termine della correzione con il metodo di Bisezione.
0 1 2 3 4 5 6 7 8 9 10 1.5 2 2.5 3 3.5 4
Deviazione Standard Mismatch Processo (%)
V al or M edi o S kew R es idu o (ps )
Valor Medio Skew Residuo
Figura 2.8
Concludendo dal grafico di Figura 2.8 è possibile notare come il valor medio dello skew residuo dopo la correzione con il metodo di Bisezione si mantenga sotto i 2 ps per errori inferiori al 7%. Risultato importante poiché per la
correzione fine con il metodo Differenziale al Nonio possiamo recuperare al più 2 ps visto che i pesi utilizzati sono dieci e differiscono di 0.2 ps.
2.5.2 Algoritmo Differenziale al Nonio
Analogamente a quanto realizzato per l’altro algoritmo, noto il residuo dello skew la termine del correzione con il metodo di Bisezione su una realizzazione di 100 prove è stata ricavata la curva di valor medio dello skew corretto con il metodo Differenziale al Nonio al variare della deviazione standard dovuta al mismatch del processo tecnologico. In Figura 2.9 vengono mostrati i 100 campioni dello skew corretto al termine della correzione Differenziale al Nonio calcolati con una deviazione standard dovuta al mismatch del processo tecnologico del 3%. 0 10 20 30 40 50 60 70 80 90 100 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 Numero di Realizzazioni Sk ew (p s)
Skew al termine della correzione Differenziale al Nonio su 100 Prove Skew
Valor Medio Skew
Da questa realizzazione è stato misurato un valor medio pari a 0.0964 ps il massimo valore di skew rilevato è di 0.2595 ps. Dalla misura ottenuta si nota come lo Skew è stato ridotto a valori dell’ordine del decimo di pico secondo partendo da volori di sfasamento del segnale di sincronismo dell’ordine del centinaio di pico secondi. Ricordiamo inoltre che lo skew residuo al termine dell’algoritmo di Bisezione era dell’ordine del pico secondo. Succesivamente per osservare il comportamento del valor medio al variare del mismatch si è fatto variare per ogni realizzazione di 100 prove la Deviazione Standard in un intervallo compreso tra lo 0-10%. Il risultato di questa misura è mostrato in Figura 2.10 da cui è possibile notare come in un intervallo compreso tra 0-10% lo skew in valore assoluto si mantenga nell’ordine della decimo di pico secondo. Inizia a aumentare in valore assoluto per valori di Deviazione Standard superiori al 9% pur restando ancora inferiore al decimo di pico secondo.
0 1 2 3 4 5 6 7 8 9 10 -0.08 -0.06 -0.04 -0.02 0 0.02 0.04 0.06 0.08 0.1 Deviazione Standard (%) V al or M edi o S kew C orr et to ( ps )
Valor Medio Skew dopo correzione Differenziale al Nonio in presenza di mismatch Valor Medio Skew Corretto
I risultati ottenuti hanno messo in evidenza come il mismatch circuitale si faccia sentire in maniera meno pesante sui pesi utilizzati per la correzione Differenziale al Nonio che su quelli utilizzati per la correzione con il metodo di Bisezione.
2.5.3 Deviazione Standard dello skew residuo
Su ogni singola realizzazione di 100 prove per l’algoritmo di Bisezione al variare dell’errore dovuto al mismatch del processo tecnologico utilizzando le funzione mean e std rese disponibili dal tool Matlab ne sono stati misurati Valor Medio e Deviazione Standard. I valori misurati sono riassunti nella tabella mostrata in Figura 2.11. Queste grandezze statistiche, visto che per la correzione con il metodo di Bisezione l’intervallo di errore che garantisce uno skew residuo inferiore al 2% era compreso tra lo 0-6%, come mostrato in Figura 2.8, sono state misurate per questi valori di errore.
Valor Medio Deviazione Standard Errore Mismatch
1.7793 ps 0.0358 ps 1% 1.7897 ps 0.0405 ps 2% 1.7884 ps 0.0585 ps 3% 1.7936 ps 0.0878 ps 4% 1.7836 ps 0.1149 ps 5% 1.7899 ps 0.1136 ps 6% Figura 2.11
Note queste grandezze è stato realizzato uno Script Matlab che interpolava con legge gaussiana i dati presenti in tabella fornendo le curve di errore al variare del mismatch, mostrate in Figura 2.12.
1.4 1.5 1.6 1.7 1.8 1.9 2 2.1 2.2 0 2 4 6 8 10 12 Valor Medio (ps) N um e ro d i R e al iz za zi on i
Densitá di probabilitá dello skew residuo
m=1.7793;std=0.0358 m=1.7897;std=0.0405 m=1.7884;std=0.0585 m=1.7936;std=0.0878 m=1.7836;std=0.1149 m=1.7899;std=0.1136 Figura 2.12
In Figura 2.12 si nota come all’aumentare dell’errore dovuto al processo tecnologico la deviazione standard intorno al valor medio aumenti. Analogamente per la correzione con il metodo differenziale al Nonio sono state ricavate al variare dell’errore dovuto al mismatch, le distribuzioni dello skew residuo per questo algoritmo. La tabella indicata in Figura 2.13 mostra valor medio e deviazione standard per ogni realizzazione di 100 prove per i diversi valori della deviazione standard dell’errore dovuto al mismatch in un intervallo pari a 0-10%.
Valor Medio Deviazione Standard Errore Mismatch 0.0934 ps 0.0717 ps 1% 0.1039 ps 0.0616 ps 2% 0.1108 ps 0.0684 ps 3% 0.1000 ps 0.0749 ps 4% 0.1106 ps 0.0854 ps 5% 0.1044 ps 0.0879 ps 6% 0.0807 ps 0.1309 ps 7% 0.0947 ps 0.1578 ps 8% 0.0306 ps 0.2128 ps 9% 0.0672 ps 0.2072 ps 10% Figura 2.13
Mentre la Figura 2.14 mostra le curve di deviazione standard in funzione dello skew residuo al variare dell’errore dovuto al processo tecnologico. Nella stessa figura è possibile osservare come al crescere dell’errore dovuto al mismatch circuitale la deviazione intorno al valor medio dello skew corretto aumenti pur restando confinato intorno a valori dell’ordine del decimo di picosecondo e per alcune realizzazioni addirittura dell’ordine del centesimo di picosecondo.
-0.60 -0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1 2 3 4 5 6 7 Valor Medio (ps) N um er o d i R eal iz za zi on i
Densitá di probabilitá errore residuo
Err=1% Err=2% Err=3% Err=4% Err=5% Err=6% Err=7% Err=8% Err=9% Err=10% Figura 2.14
Gli Script Matlab utilizzati per l’analisi statistica dell’algoritmo di Deskewing sono allegati nell’Appendice A in fondo alla tesi.