Capitolo 3

Analisi piezoresistiva di una trave sottoposta a

torsione.

3.1

Introduzione al programma di simulazione ad

elementi finiti ANSYS

.

Le molle di sostegno contenute nei dispositivi descritti nel capitolo 2 sono sollecitate a torsione ed è possibile studiare il loro comportamento attraverso un programma di simulazione ad elementi finiti: si è scelto il programma ANSYS, perché, fra quelli a disposizione, è l’unico che permette di simulare il comportamento piezoresistivo dei materiali..

Il programma ANSYS permette di simulare strutture meccaniche, elettriche, magnetiche ed elettromeccaniche.

Per interagire con esso (dal menu principale oppure con un apposito linguaggio di programmazione) è necessario inserire tutte le specifiche di progetto, che ovviamente dipendono dal tipo di struttura che si intende analizzare e dal particolare problema, collegato a tale struttura, che si vuole risolvere.

Il programma permette di creare la geometria del dispositivo che si vuole analizzare: si possono, perciò, definire i volumi che formano il solido (se si lavora in 3 dimensioni), le superfici che delimitano tali volumi e le linee che circoscrivono le superfici. ANSYS crea, inoltre, dei “punti chiave” (keypoints), che corrispondono ai vertici di ogni volume.

Il programma accetta una serie di variabili in ingresso (ad esempio, le forze applicate) e restituisce, in maniera grafica e numerica, le variabili di uscita (ad esempio, gli stress e gli strain prodotti dalle forze applicate).

Data l’impossibilità di risolvere punto per punto le equazioni che legano le variabili di ingresso a quelle di uscita, ANSYS fa una discretizzazione del solido, dividendolo con una griglia in volumi più piccoli; la griglia viene definita “mesh”.

Questo processo di frazionamento aggiunge due nuove unità geometriche: il nodo e l’elemento. I nodi sono i punti di intersezione fra due o più linee della griglia, mentre gli elementi sono i singoli sottovolumi, i cui vertici sono i nodi; in corrispondenza di ogni nodo, ANSYS risolve le equazioni e restituisce i valori calcolati.

Si possono generare, attraverso la griglia, elementi di forma tetraedrica, oppure esaedrica; scegliere elementi tetraedrici permette di infittire la griglia nelle zone critiche del campione (dove, ad esempio, le quantità variano più rapidamente nello spazio). Con elementi esaedrici, le maglie della griglia sono più regolari, quindi il modello è più facile da analizzare, tuttavia non è possibile eseguire l’operazione di affinamento descritta prima. Se la forma del solido è regolare, è pertanto consigliabile utilizzare elementi esaedrici; se, invece, sono presenti forme irregolari, discontinuità fra volumi adiacenti, o qualsiasi altra caratteristica geometrica che richiede un’operazione di meshing più accurata, è necessario ricorrere all’uso di elementi tetraedrici.

Tutte le operazioni descritte fino ad ora fanno parte di un ambiente di programmazione di ANSYS, definito “Preprocessore” (Preprocessor); all’interno di esso si devono specificare anche il tipo di materiale e le sue proprietà fisiche.

Successivamente, si applicano le sollecitazioni elettriche e meccaniche e si lancia la simulazione vera e propria, all’interno di un altro ambiente di ANSYS, definito “Soluzione” (Solution). È necessario indicare anche il tipo di analisi che si vuole affrontare: ad esempio, si può scegliere di risolvere il problema in maniera statica, oppure osservare un transitorio, o cercare le frequenze di risonanza del campione.

Dopo aver terminato la simulazione, è necessario rivedere i risultati ottenuti: a questo scopo si fa uso di un terzo ambiente di programmazione, chiamato “Postprocessore”

(Postprocessor). In questo ambiente si può scegliere, ad esempio, di riportare su un grafico oppure di scrivere su una lista o su una tabella le risposte del solido alle sollecitazioni subite: ad ogni nodo (o elemento) viene associata una serie di quantità fisiche che corrispondono ai valori delle variabili di uscita, calcolati da ANSYS, nel punto del solido corrispondente al nodo (elemento) stesso.

Dopo aver introdotto il funzionamento di ANSYS, e prima di discutere i risultati delle simulazioni svolte, è necessario parlare brevemente della fisica che regola la torsione delle travi.

3.2

Nozioni teoriche sulla torsione delle travi.

Si riporta la definizione di trave [12]:

Si definisce trave un solido generato da una figura piana, il cui baricentro si sposta seguendo una curva spaziale, detta linea d’asse (più semplicemente, “asse”). Il piano della figura rimane, punto per punto, ortogonale alla curva, che viene supposta continua e a debole curvatura. Tale figura piana viene definita “sezione della trave”. In questo progetto, si considera che l’asse della trave sia rettilineo e che essa sia incastrata ad una estremo.

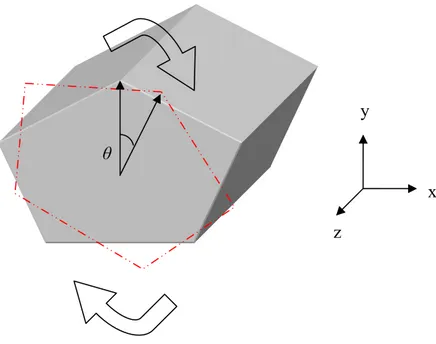
Si immagini, dunque, di applicare un momento torsionale alla sezione che si trova in corrispondenza di un estremo della trave (si faccia riferimento alla figura 3.1) e bloccare l’altro estremo: lo sforzo di tensione subito sarà trasmesso alle sezioni interne, a partire da quella più esterna che subisce torsione.

FIGURA 3.1: Schema di una trave a torsione, con sezione generica.

Se il materiale è omogeneo e il volume non presenta buchi al suo interno, sono vere le seguenti affermazioni:

• In generale, una sezione si deforma, in seguito ad una torsione applicata1_.

• A parità di angolo di torsione θ , gli stress di taglio τ_xz e τ_yz sono funzioni solo di

x ed y: sono costanti, cioè, al variare dell’asse z.

• Su una generica sezione della trave, a parità di coordinata (x, y ), gli stress di taglio variano proporzionalmente con θ .

• La teoria dell’elasticità mostra che lo stress di taglio agli angoli della sezione è nullo [4].

• I massimi valori di tensione e deformazione non si trovano in corrispondenza della massima distanza dall’asse di rotazione [4].

Il momento torcente può essere espresso in due modi: si può scegliere di esprimerlo con gli stress τ_xz e τ_yz, oppure in funzione di θ . Il primo modo è complicato da

1 _{Questo concetto non è valido per travi a sezione circolare.}

θ

y

x z

trattare, dal punto di vista analitico, poiché gli stress di taglio, in funzione di x ed y,

sono sviluppi in serie di Fourier2 . Pertanto si procede discutendo la relazione che c’è fra il momento e l’angolo θ , mentre si rimandano alla consultazione dell’appendice A eventuali approfondimenti sul primo modo.

3.2.1 Relazione fra il momento torcente e l’angolo di torsione

valide seguenti affermazioni [4]:

i tensione e deformazione di taglio si hanno in corrispondenza del centro del lato più lungo della sezione rettangolare.

Si consideri un parallelepipedo rettangolo omogeneo, in altre parole una trave a ezione rettangolare, a cui è applicata una coppia di forze che generano una torsione,

In questa tesi sono analizzate travi con sezione rettangolare, per le quali sono le

• I massimi valori d

• I valori di tensione e deformazione di taglio sono nulli agli angoli e nel centro della sezione rettangolare.

• I valori di tensione e deformazione all’interno della sezione variano in maniera non lineare.

s

come illustrato nella figura 3.2 [15]:

y

FIGURA 3.2

Si consideri, inoltre, che il solido abbia comportamento elastico ed una costante elastica torsionale k_θ: ad essa è applicato un momento torcente M perpendicolare alla

sezione della trave, cioè diretto lungo l’asse z.

Si considera il modello della trave a torsione incastrata ad un estremo; si veda la figura 3.3 [12]: z x Asse di rotazione della trave: per semplicità, sarà chiamato “asse della trave”

FIGURA 3.3: Rappresentazione schematica del modello citato.

Si riporta la relazione, ricavata per mezzo della teoria dell’elasticità, fra il momento

M applicato alla trave e l’angolo θ di torsione [12]:

2 2 1 d dz GJ dz θ = ⋅dM , (3.1)

dove G è il modulo di taglio e è il fattore di rigidezza torsionale [16] ed è funzione

dei parametri geometrici della sezione della trave:

J 3 3 2 2 1 3 h h l J f t h l ⎛ ⎞ = _{⎜ ⎟}⋅ + ⎝ ⎠ h f t ⎛ ⎞ ⎜ ⎟

⎝ ⎠ è una funzione tabulata del rapporto

h t

⎛ ⎞ ⎜ ⎟

⎝ ⎠, dove h e l sono i lati del rettangolo che forma la sezione.

( )

(

)

₍

₎

∑

Si continua l’analisi, integrando la (3.1); poiché M è costante con z (si faccia riferimento all’appendice A), si ricava la seguente uguaglianza:

M GJ dz d _{= ⋅} 0 1 θ (3.2)

Integrando la (3.2) su tutta la lunghezza della molla, si ottiene il valore dell’angolo in corrispondenza dell’estremo libero (dove si applica la forza che genera il momento):

M GJ l 0 = θ (3.3)

Dove l è la lunghezza della trave.

Si è ottenuta, dunque, una relazione che lega il momento torcente all’angolo di torsione, attraverso una quantità che viene definita “costante elastica torsionale”:

θ θ k M = , (3.4) dove k GJ l

Osservazioni:

È stato detto che gli stress di taglio crescono proporzionalmente al crescere dell’angolo di torsione; osservando la (3.4), si vede che lo stesso angolo è proporzionale al momento applicato M . Dalle due affermazioni fatte, si deduce che esiste una relazione di proporzionalità anche fra gli stress di taglio ed il momento.

3.3 Simulazioni con ANSYS di travi a torsione.

Dopo aver introdotto alcune nozioni sulla fisica che regola la torsione delle travi a sezione rettangolare, si prosegue lo studio mostrando i risultati ottenuti con le simulazioni di ANSYS; dall’analisi dei risultati, poi, si cercherà di ottenere una relazione fra la variazione di resistenza della trave sottoposta a torsione e l’angolo θ. In particolare, si dimostrerà la validità della relazione introdotta nel capitolo 1:

2

R αθ

∆ =

Si cercherà, inoltre, di ricavare un’espressione per il parametro α .

Il testo del file che contiene tutti i comandi relativi alle simulazioni descritte in questo capitolo è contenuto nell’appendice A. Si rimanda pertanto a tale appendice un eventuale approfondimento sul codice sorgente delle simulazioni.

3.3.1 Geometria e caratteristiche della struttura.

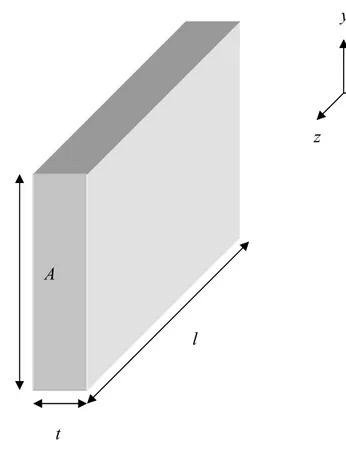
La trave in questione è un parallelepipedo rettangolo con lunghezza l = 25 µm, altezza h = 4 µm, spessore t = 0.6 µm.

y

x z

FIGURA 3.4: Si nota la sezione A=ht.

Si crea, quindi, tale geometria con il programma ANSYS.

Poiché si esegue uno studio di tipo piezoresistivo, è necessario specificare al programma che il materiale utilizzato ha proprietà piezoresistive. ANSYS mette a disposizione una gamma di tipi di elementi, ciascuno dei quali ha particolari caratteristiche: in questo progetto si sceglie il tipo di elemento chiamato SOLID226, che può avere le seguenti proprietà:

• Strutturali-termiche • Piezoresistive • Piezoelettriche • Termoelettriche • Strutturali-termoelettriche • Termiche-piezoelettriche A h l t

Si attribuisce al solido il codice 101, con il quale si specifica che l’elemento è piezoresistivo (a questo proposito, si veda l’appendice A, che contiene i file sorgente delle simulazioni).

Il passo successivo è l’inserimento dei gradi di libertà, ossia delle variabili di uscita del sistema: gli spostamenti ux, uy, uz, la tensione e la corrente.

Le altre quantità necessarie per il progetto (ad esempio, gli stress ed i campi elettrici) sono ricavate dal programma, a partire dai gradi di libertà.

Si inseriscono, poi, i valori delle proprietà del materiale:

• Costanti elastiche, in termini di modulo di Young e coefficiente di Poisson.

• Matrice dei coefficienti di piezoresistività. • Resistività.

È necessario fare una precisazione:

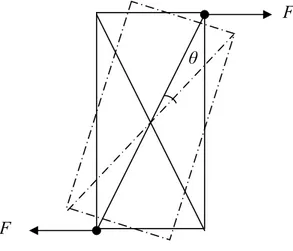
Il momento torcente viene applicato attraverso una coppia di forze uguali ed opposte, che agiscono su due spigoli della faccia libera del solido (figura 3.5):

F

θ

F

FIGURA 3.5: Schema della coppia torcente applicata.

Se le forze fossero applicate direttamente agli spigoli, provocherebbero un’eccessiva deformazione della faccia e delle zone in corrispondenza degli angoli, diversamente da quanto avviene nella realtà: si ricordi che, nel dispositivo completo, la molla è adiacente ad un diaframma, attuata elettrostaticamente per mezzo di una tensione.

Per rendere più realistico il modello, si inserisce un blocco rigido, contiguo alla faccia

A libera (si ricordi che l’altro estremo della trave è bloccato), ai cui spigoli sarà applicata la coppia di forze, come in figura 3.7. Tale blocco non esiste fisicamente, serve solo per trasmettere la rotazione alla trave vera e propria, senza deformare eccessivamente la faccia A.

La figura 3.6 mostra la geometria del solido, formato dai due blocchi descritti sopra:

FIGURA 3.6: Il blocco rigido, di 1 µm di spessore, è evidenziato in rosso.

Gli spigoli ai quali si applica la coppia corrispondono, dal punto di vita del linguaggio di ANSYS, ai due punti di coordinate (0,h,0) e (0,0,t); tali punti coincidono con due punti chiave della geometria (si veda la definizione di punto chiave di ANSYS, nel paragrafo 3.1).

Il materiale usato è silicio-germanio, per il quale è impossibile reperire i valori dei coefficienti di piezoresistività: si è scelto, pertanto, di utilizzare i coefficienti del silicio: 11 1 11 11 1 12 11 1 44 102.2 10 53.4 10 13.6 10 Pa Pa Pa π π π − − − − − − ⎫ = − ⋅ ⎪ = ⋅ _⎬ ⎪ = − ⋅ _⎭

Le altre quantità sono quelle del silicio-germanio: si consulti, a questo proposito, il capitolo 2. La resistività è isotropa: 5 10 x y z m ρ ₌ρ ₌ρ ₌ − _{Ω ⋅ Resistività}

Il materiale è isotropo; di conseguenza, si ha un solo valore del modulo di Young e del coefficiente di Poisson:

9 146 10 x y z E =E =E = ⋅ Pa ' E Modulo di Young ' 6 , , 10 , , x y z x y z

E = ⋅ Modulo di Young del blocco rigido 0.23

xy yz xz

ν =ν =ν = Coefficiente di Poisson

A questo punto, si crea la mesh: per la particolare semplicità e simmetria del solido, è consigliabile utilizzare una griglia di tipo esaedrico, con elementi di forma cubica. Per quanto riguarda la dimensione di ciascun elemento, attribuire 0.2 µm di lunghezza al lato del cubo costituisce un buon compromesso fra la precisione del modello e la necessità di fare uso di una griglia non troppo fitta (perché, altrimenti, le simulazioni impiegherebbero troppo tempo).

La misura di tipo piezoresistivo si fa nel modo seguente:

Si applica una corrente che attraversa la trave in direzione z e si rileva la tensione nella stessa direzione, ossia fra un capo e l’altro della trave; successivamente, si ripete la stessa operazione per diversi valori di torsione applicata.

È necessario che i valori di tensione siano uguali in tutti i punti di ciascuna superficie su cui si va a leggere tale quantità; dal punto di vista del linguaggio di programmazione, questa operazione si chiama coupling: si sceglie un sottoinsieme di nodi del modello, ad esempio quelli che formano la faccia bloccata, si sceglie una quantità fisica associata a tali nodi (in questo caso, la tensione) e si pone la

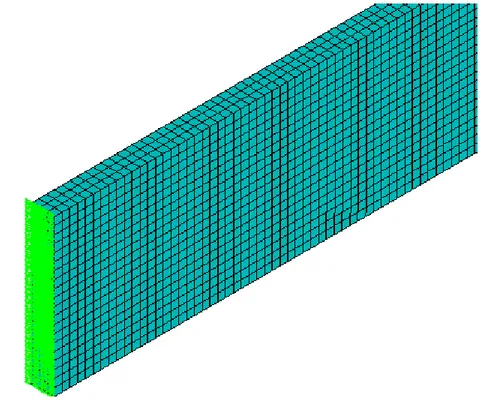
condizione che tutti i nodi considerati contengano lo stesso valore, per la quantità suddetta (si osservi la figura 3.7).

FIGURA 3.7: Operazione di coupling con ANSYS. L’immagine mostra una delle due facce su cui si rileva la differenza di potenziale: l’estremo bloccato. Lo strato verde rappresenta l’insieme dei nodi che formano la faccia; con il coupling si stabilisce che tali nodi contengano lo stesso valore di tensione. L’altra faccia è il confine fra il resistore vero e proprio ed il blocco rigido su cui si applica la torsione; su tale superficie si fissa il riferimento di tensione, che è pari a 0 Volt. Si fissa, inoltre, la condizione che il blocco rigido non sia attraversato da corrente e che la tensione ai suoi capi sia nulla.

3.3.2 Applicazione di una corrente e lettura della tensione

A questo punto, applica una corrente I₀ =10 mA e si incastra la trave all’estremo opposto al blocco rigido. La corrente va dall’estremo bloccato a quello libero, dove si applica la torsione.

Si prosegue lanciando la soluzione, senza torsioni applicate, per calcolare il valore della resistenza a riposo.

Successivamente, si entra nel postprocessore e si osservano i risultati: ANSYS permette di visualizzare una lista dei valori delle tensioni, in ogni singolo nodo della struttura (lo si può fare, in modo analogo, per ogni altra variabile di uscita).

Si definisce (tensione a riposo) la differenza di potenziale fra i due estremi della trave ed il suo valore si ottiene leggendo i nodi rappresentati in figura 3.7:

0 V 04166667 . 1 0 = V V Pertanto: 166667 . 104 0 0 0 = _I = V R Ω

Si noti che il valore della resistenza contiene 6 cifre decimali: questo non è stato fatto per appesantire i calcoli; più avanti, infatti, ci si accorgerà che la variazione R∆ assume valori dell’ordine di qualche , pertanto si è scelto di considerare le cifre significative che arrivano fino al centesimo di mΩ.

Si calcola il valore analitico della resistenza a riposo R_o, per verificare la correttezza della simulazione: 104.1666667 o l R A ρ = = Ω Il risultato è corretto.

3.3.3 Applicazione di un momento torcente

Si procede applicando alcuni valori di torsione al blocco rigido.

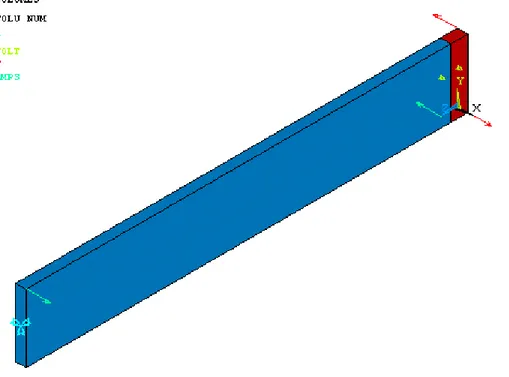
La figura 3.8 rappresenta il modello completo, con le sollecitazioni applicate:

• Le frecce rosse sono i vettori delle forze, uguali in modulo, che agiscono sul blocco rigido, provocando la torsione.

• Le frecce verdi rappresentano la corrente, che va da sinistra verso destra. • Il simbolo celeste in basso a sinistra indica che la faccia è bloccata.

• Gli altri due simboli in verde chiaro indicano che si è applicato il riferimento di tensione agli estremi del blocco rigido.

FIGURA 3.8: Rappresentazione grafica ottenuta.

Si lancia la simulazione, per i seguenti valori di forza F: 5, 7.5, 10 e 20 µN.. Successivamente, si elaborano nel seguente modo i risultati ottenuti:

Variazione di resistenza:

Si definisce la tensione misurata ai capi del resistore, dopo aver applicato una torsione.

'

V

Si calcola il nuovo valore di resistenza _{R come:} ' ' ' o V R I =

Si ricava, infine, la variazione di resistenza R∆ come:

' o

R R R

∆ = − (3.5)

Valutazione dell’angolo di torsione

Si può ricavare una stima dell’angolo θ di torsione, facendo uso dei risultati relativi ai valori degli spostamenti , u_x u_y, . u_z

Si consideri la sezione della trave a cui è applicata la torsione: questa subisce una rotazione di un angolo θ. FIGURA 3.9 sum u uuur r θ r` O t/2 P P` h/2 y x z

Si osservi la figura 3.9: ci troviamo in corrispondenza dell’ascissa z=0, pertanto la faccia ruota, ma non si deforma, perché appartiene al blocco rigido.

Il punto d’incontro delle diagonali del rettangolo si trova nell’origine del sistema cartesiano e viene identificato con il punto O.

Sia P il punto corrispondente ad uno spigolo della faccia, come rappresentato in figura: tale punto, in seguito alla torsione, si sposta nel punto P` e la distanza r che lo collega all’origine diventa r`; l’angolo compreso fra le direzioni di r e di r` è proprio l’angolo θ di torsione.

Il vettore uuuur_sum=u x u y u_xˆ+ _yˆ+ _zzˆ è la somma degli spostamenti nelle tre direzioni dello spazio e rappresenta lo spostamento totale del punto P.

Per i valori di torsione applicata, che generano angoli relativamente piccoli (dell’ordine di 10-2 rad), si possono formulare le seguenti ipotesi:

• senθ ≅θ

• u_z →0. Questo significa che la sezione ruota nel piano xy. • r r≅ `

Il vettore uuuur_sum può essere assimilato ad un arco di circonferenza di raggio r.

Pertanto, u_sum è la lunghezza dell’arco che sottende l’angolo θ, che può essere ricavato nel modo seguente:

r u_sum

≅

θ (3.6)

Con le relazioni (3.5) e (3.6) si può ora ricavare la variazione di resistenza ed il corrispondente angolo, per qualsiasi valore di torsione applicata, osservando i risultati delle simulazioni con ANSYS.

Analisi dei risultati: si applica una forza F= 5 µN

Dopo aver lanciato la simulazione della trave sottoposta ad una coppia di forze F del valore di 5 µN , si riportano e si discutono alcuni grafici, contenenti i risultati del modello.

Si inizia con l’andamento della tensione lungo l’asse della trave (figura 3.10): si nota il blocco rigido (in blu), che si trova a tensione nulla, e l’estremo incastrato (in rosso), dove andiamo a leggere il valore che determina la e quindi la _V' _{∆ . R}

ANSYS permette di leggere i risultati in diversi modi, fra i quali c’è lo strumento del grafico a colori, o plot (riportato sotto), e la lista numerica di valori, che non è qui riportata.

FIGURA 3.10:

Poiché il numero di cifre decimali deve essere tale da fissare, sul valore della resistenza, una precisione dell’ordine del centesimo di mΩ, tre cifre non sono sufficienti; si è ricavato un valore con precisione adeguata, consultando la lista dei valori delle tensioni, che ha prodotto il seguente risultato:

04160517 . 1 ' ₌ V V Dalla (3.9) si ricava: ' 6.15 mΩ o o V V R I − ∆ = ≅ −

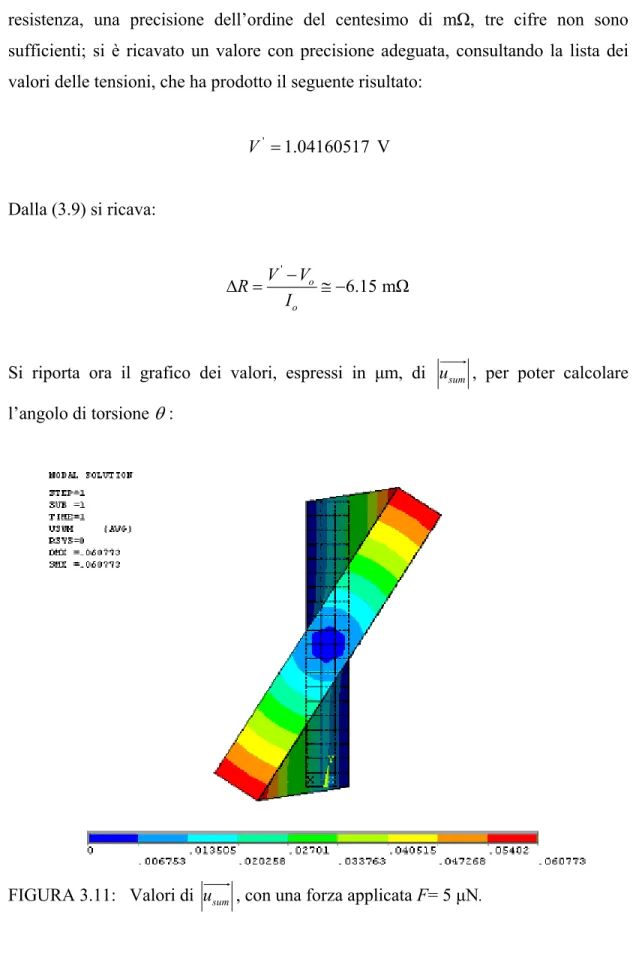
Si riporta ora il grafico dei valori, espressi in µm, di u_sum , per poter calcolare l’angolo di torsione θ:

Si ottiene: 0.060773 sum uuuur ≅ µm Dalla (3.6), poiché 1 2 2 _2.0223 2

r≅ h + ≅t µm, si ottiene il valore dell’angolo di torsione:

0.0150 rad 0.871

θ ≅ ≅ °

Sono state lanciate simulazioni relative agli altri valori di forza: F= 7.5, 10 e 20 µN. I risultati ottenuti sono riportati nella tabella 3.1:

F [µN] 5 7.5 10 20 ' V [V] 1.04160517 1.04152812 1.04141996 1.04066818 R ∆ [mΩ] -6.15 -13.855 -24.671 -99.85 sum u [µm] 0.060773 0.091159 0.121545 0.24309 θ [rad] 0.0301 0.0451 0.0601 0.120 α Ω₂ rad ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ -6.788 -6.812 -6.830 -6.934 TABELLA 3.1

Si osserva quanto già accennato nel capitolo 1: la variazione di resistenza cresce in maniera quadratica con la coppia di forze applicate e con l’angolo di torsione. Si può scrivere la seguente legge:

2

R αθ

dove α si misura in ₂ rad Ω ⎡ ⎢⎣ ⎦ ⎤

⎥ ed è funzione del tipo di materiale osservato e dei suoi parametri geometrici. Sono stati calcolati i valori approssimati di α sostituendo nella (3.7) gli angoli di torsione e le corrispondenti variazioni di resistenza (si veda la tabella 3.1).

Si è calcolato, infine, il valore analitico di kθ, verificando che fosse simile a quello

ricavato dai risultati delle simulazioni. Si è detto che k GJ l θ = , dove:

(

)

⎥ , valore analitico della costante della molla.

Il momento M può essere calcolato come: M =Fh, dove F è la forza applicata (7.5, 10 e 20 µN). Poiché, dalla (3.4), M =k_θθ, si uguagliano le due espressioni e si ottiene:

' Fh

k_θ

θ

= , dove θ si ricava dalle simulazioni.

È stato ricavato il valore di _k'

θ per tutti i valori di forza e si è ottenuto:

' _{6.64 10} 9 kθ ≅ ⋅ − N×m rad ⎡ ⎤ ⎢ ⎥ ⎣ ⎦

Si osserva che _k'

θ (ricavato dai risultati delle simulazioni) è molto simile al valore

analitico k_θ.

3.4 Conclusioni.

Dopo aver introdotto il funzionamento del programma di simulazione Ansys, in questo capitolo è stata affrontata l’analisi delle simulazioni di una trave sottoposta a torsione, in termini di comportamento piezoresistivo.

Dall’osservazione dei risultati restituiti dal programma, per diversi valori della coppia di forze, è stata ricavata una relazione fra la variazione di resistenza del solido e l’angolo di torsione. Si è inoltre scoperto che esiste un legame quadratico fra le due quantità: lo scopo del prossimo capitolo sarà proprio dimostrare la validità di tale andamento quadratico.