145
6
Procedura di riduzione dei dati
delle prove Rotodinamiche discrete
Prima della presentazione dei risultati della campagna sperimentale sull’induttore DAPROT3 sulle forze rotodinamiche indotte dal fluido, in questo capitolo verrà presentato nel dettaglio il principio di funzionamento del dinamometro rotante che rappresenta l’elemento fondamentale dell’apparato sperimentale per l’analisi rotodinamica e verrà approfondita la procedura che ha permesso tale indagine. Di questa procedura verrà descritta la dettagliata analisi matematico-fisica del fenomeno che ha portato alla progettazione dell’esperimento, in seguito verranno descritte le prove che compongono la procedura.Il Dinamometro
6.1
Lo strumento utilizzato per la misura delle forze che agiscono sulla girante durante il suo funzionamento viene chiamato Dinamometro rotante. Questo dispositivo è formato fa due piastre circolari connesse mediante quattro barrette di sezione quadrata.
146
Sulla superficie di ogni barretta sono incollati degli estensimetri a semiconduttore, i quali, sfruttando l’effetto piezoresistivo che trasforma la deformazione subita in una variazione di resistenza elettrica, consentono di misurare le forze agenti sull’induttore.
Figura 6-2 Dinamometro con estensimetri
Figura 6-3 dettaglio degli estensimetri posti sulla barretta
In tutto sono stati impiegati 40 estensimetri da 500 Ω prodotti dalla BLH, suddivisi sulle barrette secondo lo schema riportato di seguito. Su questa figura viene anche riportato il sistema di riferimento impiegato nello studio del dinamometro (sistema dinamometrico).
147
Figura 6-4 Disposizione degli estensimetri
Ogni estensimetro è stato identificato da una sigla del tipo
R
ijk, dove i indica la barretta su cui si trova l’estensimetro,j
la faccia e k la posizione su quest’ultima. La numerazione delle barrette viene effettuata in senso orario a partire da quella posizionata lungo l’asse positivo delle x, mentre la numerazione della faccia, sempre a partire da quella posizionata sull’asse positivo delle x, viene effettuata in senso antiorario. Infine, k0 indica che l’estensimetro è posizionato a metà barretta, k1 che si trova a un quarto della lunghezza e k2 che si trova a tre quarti della lunghezza.Il dinamometro può essere sottoposto a quattro tipi di condizioni di carico: Forza normale
Forza di taglio Momento flettente Momento torcente
Ma tutte e quattro queste condizioni di carico possono essere ricondotte all’applicazione di una forza di taglio e/o di una forza normale in corrispondenza dell’incastro semplice.
6.1.1 Analisi dei carichi agenti sul dinamometro
Dal momento che il dinamometro può essere schematizzato come 2 piastre rigide a cui sono vincolate le quattro barrette deformabili, per l’analisi dei carichi basterà considerare gli effetti delle forze esterne sulle barrette. Queste verranno schematizzate come delle travi di lunghezza l con un vincolo di incastro fisso su di un lato e con un vincolo di incastro semplice sull’altro.
148
Sollecitazione normale nella sezione della barretta
Figura 6-5 Caso di sollecitazione l’ungo l’asse longitudinale della barretta
Con questa condizione di carico la deformazione della barretta lungo l’asse z è costante e pari a z F EAz
. Nel caso in cui un estensimetro abbia la direzione principale coincidente con l’asse z risentirà di una deformazione pari a
z, mentre se è disposto ortogonalmente di deformerà di una quantità pari a
z, dove
è il modulo di Poisson.Sollecitazione sulla barretta con forza di taglio lungo y
Figura 6-6 Caso di sollecitazione con forza di taglio lungo y
Indicando con u lo spostamento assiale della sezione, con v lo spostamento lungo l’asse y e con
la rotazione della sezione, dall’equazione della linea elastica, con opportune condizioni al bordo si ottiene il momento flettente all’interno del materiale:1 2
x y y
M F z F l (6.1)
Dalla combinazione della formula di Navier e della relazione tra sollecitazione e deformazione, si ricava la deformazione della barretta:
x z x
M
y
EJ
(6.2)Dove E (197 GPa) è il modulo di Young del materiale (acciaio AISI 630 H 1025) e Jx è il momento di inerzia rispetto ad x. FZ z y x Fy z y x
149
Sollecitazione sulla barretta con forza di taglio lungo x
Figura 6-7 Caso di sollecitazione con forza di taglio lungo x
Similmente al caso precedente, si trova che il momento flettente all’interno del materiale è:
1 2
y x x
M F z F l (6.3)
E la deformazione della barretta è:
y z y M x EJ
(6.4)Dove
J
yè il momento di inerzia rispetto a y.6.1.2 Modalità di collegamento degli estensimetri
Gli estensimetri sono collegati tra loro in modo da formare dieci ponti di Wheatstone.
Figura 6-8 Ponte di Wheatstone
Grazie a questa configurazione, siamo in grado di associare alla deformazione subita dagli estensimetri una variazione di tensione VCD, molto più facile da misurare.
Per ottenere tale relazione si anno le seguenti considerazioni: R1R2 R3 R4 R
VCD 0 all’equilibrio (nessuna deformazione presente);
1 2 x R R .
Applicando i principi di Kirchhoff al ponte si ha:
F
xz
x
150 1 2 3 4
1
4
CDV
R
R
R
R
E
R
(6.5)Adesso consideriamo la relazione tra la deformazione e variazione di resistenza tipica di un estensimetro
1
FR
G
R
(6.6)Dove GF (155) è il fattore di guadagno e combiniamola con l’equazione (6.5) per ottenere
1 2 3 4
4 CD F V G E
(6.7)L’acquisizione della tensione di sbilanciamento del ponte, quindi, permette di risalire alle forze agenti sul dinamometro.
Ognuno dei dieci ponti è compensato in temperatura, sia nei confronti delle deformazioni apparenti, dovute a variazioni di resistività o a diversa dilatazione termica, sia nei confronti del coefficiente d’amplificazione GF
T . Questo è possibile grazie alla particolare disposizione degli estensimetri e all’aggiunta di una resistenza che compensa le variazioni di GF con la temperatura.Procedura Teorica Discreta
6.2
Dopo aver spiegato l’elemento fisico principale per la misurazione delle forze, e ricordando i principi della rotodinamica illustrati nel capitolo 3, si illustra il principio teorico dell’acquisizione delle forze.
L’assunzione fondamentale nella procedura di riduzione dei dati che si riferisce alle prove discrete è la costanza sia della velocità di rotazione , (motore primario), sia della velocita di whirl,
(motore secondario).In questo caso, il vettore forza istantanea F può essere espresso come la somma della forza stazionaria F0 (che non dipende dalla presenza del moto di whirl) e una forza non stazionaria legata al vettore delle perturbazioni
mediante la matrice rotodinamica
A , nel modo seguente 0 0 0 0 cos( ) sin( ) X X XX XY Y Y YX YY F t F A A F t F A A
(6.8)Dove
0 è l’anomalia dell’eccentricità all’instante iniziale di acquisizione t0.La relazione tra le forze nel sistema di riferimento rotante, Fx ed Fy ,e le forze nel sistema assoluto del laboratorio possono essere espresse come
0 0 0 0
( )
( ) cos(
)
( ) sin(
)
( )
( ) sin(
)
( ) cos(
)
X x y Y x yF t
F t
t
F t
t
F t
F t
t
F t
t
(6.9)Dove 0 rappresenta la posizione angolare dell’asse rotante x rispetto all’asse X nel sistema
151 y
F , e le componenti delle forze stazionarie F0 X e F0Y , e la matrice rotodinamica
A siottiene combinando le precedenti equazioni (6.8) e.(6.9)
0 0 0 0 0
0 0 0 0 0
( ) cos(
)
( ) sin(
)
cos(
)
sin(
)
( ) sin(
)
( ) cos(
)
cos(
)
sin(
)
x y X XX XY x y Y YX YY
F t
t
F t
t
F
A
t
A
t
F t
t
F t
t
F
A
t
A
t
(6.10)Si può notare che le componenti delle forze nel sistema di riferimento assoluto, F tX( ) e F tY( ) , sono composte rispettivamente da un termine costante,F0 X e F0Y, e da altri due termini lineari nelle componenti costanti della matrice rotodinamica
A ma che sono funzioni sinusoidali nel tempo con periodo uguale a quello di whirl,
2
(6.11)Questa proprietà può essere usata per valutare le forze radiali nel sistema di riferimento assoluto. Infatti, seno e coseno sono funzioni tali che il loro integrale è nullo se l’intervallo di integrazione è uguale, o multiplo intero, del proprio periodo.
Inoltre, moltiplicando le componenti delle forze nel sistema di riferimento assoluto, rispettivamente, per cos(
t 0) e sin(
t 0), ed integrando in un intervallo multiplo del periodo di whirl, è possibile ottenere le quattro componenti della matrice rotodinamica
A . infatti, una costante, come sono F0 X e F0Y, moltiplicata per una funzione sinusoidale in un tale intervallo danno un risultato uguale zero. La stessa cosa avviene per i termini che contengono0 0
sin(
t ) cos(
t ) ,mentre i soli termini che rimangono non nulli sono quelli con2
0
sin (
t
)
ecos (
2
t
0)
.La valutazione numerica di questi integrali può essere fatta mediante l’utilizzo di alcune formule di quadratura, la regola di Simpson o la regola del trapezio. Storicamente, questi integrali possono essere valutati usando l’analisi di Fourier e , in particolare, l’espansione in serie di Fourier delle forze laterali misurate dal dinamometro. Infatti, se sia
0 che 0 sono uguali azero, le componenti delle forze laterali e della matrice rotodinamica possono essere direttamente correlate con l’espansione in serie di Fourier di F tx( ) e
F t
y( )
. Per questo motivo è utile definire il periodo di riferimento fondamentale che dovrà essere multiplo intero sia del periodo di whirl che del periodo di rotazione della girante,T 2
: 2 2 c J I T
con I J
(6.12)Dove I e J rappresentano gli interi per cui dobbiamo moltiplicare, rispettivamente, i periodi di whirl e di rotazione per ottenere il periodo di riferimento fondamentale. In questa maniera, leggiamo da diversi cicli di riferimento (
N
cyc) che possono essere consistentemente accumulati e mediati (fornendo un processo di filtraggio del rumore molto efficiente). Le forze quindi possono essere risolte all’interno di diversi sistemi di riferimento. Di conseguenza, l’intervallo di integrazione, T, viene definito comecyc c
152
Nelle equazioni seguenti, verrà mostrata una generalizzazione della risoluzione del caso nel quale sia
0 che 0siano diversi da zero, insieme alla valutazione degli integrali mediantel’analisi di Fourier.
Le componenti della forza stazionaria sono ottenute mediando ciascuna equazione nel tempo
0 0 0 0 0 0 0 0 0
1
( ) cos(
)
( ) sin(
)
1
cos(
)
( ) cos(
)
( ) sin(
)
sin(
)
( ) sin(
)
( ) cos(
)
T X x y T x y x yF
F t
t
F t
t
dt
T
t
F t
F t
t
F t
F t
dt
T
(6.14) 0 0 0 0 0 0 0 0 01
( ) sin(
)
( ) cos(
)
1
cos(
)
( ) sin(
)
( ) cos(
)
sin(
)
( ) cos(
)
( ) sin(
)
T Y x y T x y x yF
F t
t
F t
t
dt
T
t
F t
F t
t
F t
F t
dt
T
(6.15)Gli elementi della matrice AXX e AYX vengono ottenuti integrando l’equazione nel modo seguente
0 0 2 cos( ) T t dt T
:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2( ) cos( ) cos( ) ( ) sin( ) cos( )
cos ( ) cos( ) ( ) sin( )
sin ( ) sin( ) ( ) cos( )
1 2 1
2 cos ( ) cos( ) ( ) sin(
T XX x y x y x y x y A F t t t F t t t dt T t F t F t t F t F t T t F t F t
0 0 0 0 0 0 0 )sin ( ) sin( ) ( ) cos( )
T x y dt t F t F t
(6.16)
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2( ) sin( ) cos( ) ( ) cos( ) cos( )
cos ( ) sin( ) ( ) cos( )
sin ( ) cos( ) ( ) sin( )
1 2 1
2 cos ( ) sin( ) ( ) cos(
T YX x y x y x y x y A F t t t F t t t dt T t F t F t t F t F t T t F t F t
0 0 0 0 0 0 0 )sin ( ) cos( ) ( ) sin( )
T x y dt t F t F t
(6.17)153
0 0 2 sin( ) T t dt T
:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2( ) cos( ) sin( ) ( ) sin( ) sin( )
cos ( ) sin( ) ( ) cos( )
sin ( ) cos( ) ( ) sin( )
1 2 1
2 cos ( ) sin( ) ( ) cos(
T XY x y x y x y x y A F t t t F t t t dt T t F t F t t F t F t T t F t F t
0 0 0 0 0 0 0 )sin ( ) cos( ) ( ) sin( )
T x y dt t F t F t
(6.18)
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2( ) sin( ) sin( ) ( ) cos( ) sin( )
cos ( ) cos( ) ( ) sin( )
sin ( ) sin( ) ( ) cos( )
1 2 1
2 cos ( ) cos( ) ( ) sin(
T YY x y x y x y x y A F t t t F t t t dt T t F t F t t F t F t T t F t F t
0 0 0 0 0 0 0 )sin ( ) sin( ) ( ) cos( )
T x y dt t F t F t
(6.19)Come spiegato in precedenza, la valutazione numerica di questi integrali può essere fatta usando delle formule di quadratura, come la regola di Simpson o la regola del trapezio. Inoltre, gli integrali possono essere calcolati con l’analisi di Fourier. Dalla definizioni delle forze seguenti:
10 0 0 20 0 0 1 0 0 0 0 2 0 0 0 0 1 0 0 0 0 2 0 0 ( ) ( ) cos ( ) sin ( ) ( ) sin ( ) cos ( ) ( ) cos( ) ( ) sin( ) ( ) ( ) sin( ) ( ) cos( ) ( ) ( ) cos( ) ( ) sin( ) ( ) ( ) sin( ) ( ) co x y x y x y x y x y x y F t F t F t F t F t F t F t F t F t F t F t F t F t F t F t F t F t F t
s( 0
0) (6.20)Ciascun termine delle equazioni (6.20) è un componente dell’espansione in serie di Fourier delle forze precedenti, con frequenza fondamentale pari a
J
. A titolo di esempio, l’ultimo termine di AXX
diventa
2 2 2 0 0 2 1 1 2 1 ( ) sin ( ) sin 2 2 2 T T J I S F t t dt F t J I t F T
T J
(6.21)Dove il pedice si riferisce alle componenti in seno o coseno, mentre all’apice abbiamo il numero dell’armonica della frequenza fondamentale,
J
. Infine, le equazioni possono essere scritte154
0 10 20 0 10 20 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 J J X C s J J Y S C J I J I J I J I XX C S C S J I J I J I J I XY S C S S J I J I J I J I YX S C S C J I J I J I J I YY C S C S F F F F F F A F F F F A F F F F A F F F F A F F F F
(6.22)L’estrazione sperimentale delle forze indotte dal fluido ad un fissato valore del rapporto di whirl e di condizioni operative, richiede l’esecuzione di due prove identiche, una in aria ed una in acqua. La sottrazione delle forze dalla prima prova alla seconda fornisce le forze indotte dal fluido. Infine separatamente si tolgono anche le forze dovute alla spinta idrostatica della parte rotante. 0 0 0 0 0 0 w a X X X w a Y Y Y buoyancy w a XX XX XX w a XY XY XY w a YX YX YX w a YY YY YY F F F F F F F A A A A A A A A A A A A (6.23)
Dove per w si intende la prova in acqua e per a si intende quella in aria.
I Momenti stazionari e non stazionari che si sviluppano dal moto di whirl possono essere espressi, nel sistema stazionario, nello stesso modo delle forze F. L’espressione di M0 e di
Bin termini di momenti laterali M tx( ) e
M t
y( )
sono simili a quelli precedenti , mentre l’effetto della spinta idrostatica influenza M0 X.0 0 0 0 0 0 w a X X X buoyancy w a Y Y Y w a XX XX XX w a XY XY XY w a YX YX YX w a YY YY YY M M M M M M M B B B B B B B B B B B B (6.24)
Le forze stazionarie e non stazionarie si ottengono mediante l’integrazione su 250 periodi completi (
N
cyc) della frequenza fondamentale di riferimento (Tc ). L’integrazione è stata sviluppata utilizzando le componenti dell’espansione in serie di Fourier. È stato anche verificato che i risultati numerici ottenuti con l’analisi di Fourier coincidono con la valutazione numerica degli integrali eseguita con le formule di quadratura.155
Le forze ed i momenti sono stati normalizzati come segue:
* 0 0 2 3 * 2 2 * 0 0 2 4 * 2 3 a T R R a T a T R R a T F F c r F F c r M M c r M M c r
(6.25)Dove
è la densità del fluido, ca è la lunghezza assiale della palla dell’induttore,
è il raggio dell’orbita circolare di whirl, è la velocità di rotazione dell’induttore ed rT è il raggio di estremità della paletta.6.2.1 Gli angoli Ω
0e ω
0Come si nota dalla procedura di riduzione descritta nel paragrafo precedente, risultano di fondamentale importanza gli angoli 0 e
0, definiti rispettivamente come l’angolo tra l’asse x del sistema dinamometrico e l’asse X del sistema assoluto all’istante iniziale (cioè nell’istante in cui cominci l’acquisizione dei dati), e come l’angolo tra il vettore eccentricità
e l’asse X del sistema di riferimento assoluto all’istante iniziale. La procedura attuale di calcolo dei due angoli è il perfezionamento di quella discussa da L. Pecorari [1].La misura degli angoli viene fatta tramite 2 lettori di tacca o lettori di contrasto digitali descritti in precedenza.
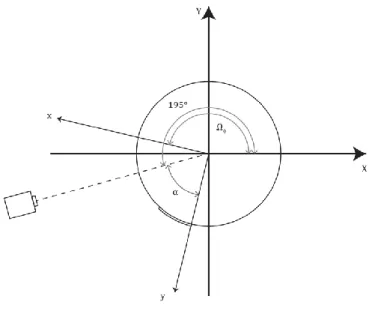
Come indicato in Figura 6-9 l’angolo 0 è dato da:
156
0
195 90 (6.26)
Dove
è l’angolo tra la tacca ed il sensore di contrasto. La tacca è stata incollata in maniera da coincidere con l’asse y del sistema di riferimento dinamometrico. Il valore invece di 195° dipende unicamente dal montaggio e rappresenta l’angolo tra il sistema ottico e l’asse X del sistema di riferimento assoluto.Nella Figura 6-10 viene definito invece l’angolo
0Figura 6-10 Rappresentazione schematica dell’angolo iniziale ω0 e del lettore di tacca secondario
0 170
(6.27)Dove
è l’angolo tra il sensore di contrasto e la tacca, incollata sull’accoppiamento scanalato in modo da coincidere col dente di riferimento, 170° è l’angolo dovuto al montaggio tra il sensore e l’asse X del sistema di riferimento assoluto, mentre
è l’angolo tra il vettore eccentricità e la tacca.6.2.2 La forma del segnale
Tutti i segnali che andremo ad analizzare, dal momento che vengono estrapolati dal sistema di riferimento rotante, possono essere visti come segnali sinusoidali. Facendo ad esempio lo studio sulla forza in x
( ) cos( ) sin( ) cos( )
x i xm i i i
F t F
t
c a
t b
t c (6.28) Dove ti i t è il tempo discretizzato. È possibile quindi confrontare il segnale del dinamometro con le incognite dell’equazione(6.28),Fxm , e c.157
2
2 2 1 11
1
( )
sin
cos
N N x i xi i i xi i iF t
F
a
t
b
t
c F
N
N
(6.29)Sia minimo, troviamo un sistema lineare di tre equazioni in tre incognite la cui soluzione fornisce a ,
b
e c:
2 1 2 1 1 1 1 2 1 2sin(
)
cos(
)
sin(
)
sin (
)
sin(
) cos(
)
sin(
)
sin(
)
0
sin(
)
cos(
)
cos(
)
sin(
) cos(
)
cos (
)
cos(
N i i xi i i N N N N i i i i xi i i i i i N i i xi i i i i i
a
t
b
t
c
F
t
a
a
t
b
t
t
c
t
F
t
a
t
b
t
c
F
t
b
a
t
t
b
t
c
t
1 1 1 1 2 1 1 1 1)
cos(
)
0
sin(
)
cos(
)
sin(
)
cos(
)
0
N N N N i xi i i i i i N i i xi i N N N i i xi i i iF
t
a
t
b
t
c
F
c
a
t
b
t
cN
F
(6.30)Da queste si ottengono le incognite cercate mediante le seguenti espressioni
2 2
arctan
xmF
a
b
a
b
c
c
(6.31)Procedura Sperimentale discreta
6.3
La procedura sperimentale utilizzata per la riduzione dei dati è stata sviluppata nel corso di diverse campagne sperimentali su induttori e pompe centrifughe. Questa procedura oltre a fornire i risultati delle forze rotodinamiche indotte dal fluido, è stata anche sviluppata in modo da renderla robusta agli errori che, inevitabilmente, affliggono tutte le campagne sperimentali. Tramite programmazione in ambiente Matlab, i dati provenienti dalle diverse prove sperimentali vengono accuratamente processati e filtrati, in modo da enfatizzare i parametri significativi per gli studi. Le prove stesse sono progettate in modo che certi parametri abbiano un effetto preponderante durante la prova permettendone una corretta estrapolazione. Le varie prove sperimentali, insieme alle caratteristiche tecniche di ciascuna prova, vengono riassunte nella Tabella 6-1 seguente.
158
Tabella 6-1 Tabulazione schematica delle prove sperimentali per l’induttore DAPROT3 nome prova velocità di rotazione del motore primario Ω= [rpm] velocità di rotazione del motore secondario ω=[rpm] durata in [s] campioni al secondo campioni
totali Risultati Ottenuti Peso della girante
Offset_Fx Offset_Fy Offset_Fz Offset_Mx Offset_My Offset_Mz angolo ϑ Fx Fy Fz Mx My Mz angolo δ eccentricità ε -1800 Fx_aria *18 prove -1600 Fy_aria*18 prove -1400 Fz_aria*18 -1200 Mx_aria*18 prove -1000 My_aria*18 prove -800 Mz_aria*18 prove -600 Axx_aria *18 prove -400 Axy_aria*18 prove -200 Ayx_aria*18 prove 200 Ayy_aria*18 prove 400 Bxx_aria*18 prove 600 Bxy_aria*18 prove 800 Byx_aria*18 prove 1000 Byy_aria*18 prove 1200 FN_aria*18 prove 1400 FT_aria*18 prove 1600 1800 Fy_buoyancy Mx_buoyancy -1800 Fx_acqua*18 prove -1600 Fy_acqua*18 prove -1400 Fz_acqua*18 prove -1200 Mx_acqua*18 prove -1000 My_acqua*18 prove -800 Mz_acqua*18 prove -600 Axx_acqua*18 prove -400 Axy_acqua*18 prove -200 Ayx_acqua*18 prove 200 Ayy_acqua*18 prove 400 Bxx_acqua*18 prove 600 Bxy_acqua*18 prove 800 Byx_acqua*18 prove 1000 Byy_acqua*18 prove 1200 FN_acqua*18 prove 1400 FT_acqua*18 prove 1600 1800 600000 PROVA ROTODINAMICA DISCRETA ACQUA 2000 120 5000 600000 OFFSET ACQUA 2 0 120 5000 PROVA ROTODINAMICA DISCRETA ARIA 2000 120 5000 600000 25000
procedura per la riduzione delle forze rotodinamiche
OFFSET ARIA 2 0 120 5000 600000
159
Figura 6-11 Diagramma di flusso dello svolgimento delle prove nel tempo (dall’alto al basso) e con la dipendenza dalle prove svolte in precedenza
6.3.1 La prova Offset
La prova denominata offset ha più di una funzione:
pulire la misurazione della prova dall’errore fisso che la scheda elettronica di acquisizione introduce nei dati
Eseguire una misurazione del peso della girante
Correggere il valore della posizione angolare del lettore di tacca posto sull’albero motore primario.
L’apparato sperimentale registra 5000 campioni al secondo per una durata complessiva della prova di 120 secondi e la prova viene eseguita in aria. Nella prova Offset l’unico motore interessato è quello principale,, mentre il moto di whirl è nullo (
0
). La velocità di rotazione del motore primario è di 2 rpm. Il valore di tale velocità è tenuto così basso per limitare l’entità delle forze centrifughe agenti sul dinamometro e fare in modo che l’unica forza con valore apprezzabile sia quella dovuta al peso (Figura 6-12)160
Figura 6-12 Rappresentazione schematica della prova Offset
Dal momento che i ponti estensimetrici montati sul dinamometro misurano le forze e i momenti nel sistema rotante, i risultati teorici che ci aspettiamo avranno una forma sinusoidale con valore massimo, nel caso delle forze F tx( ) e
F t
y( )
che dipende dalla forza peso.Usando la procedura descritta al paragrafo (6.2.2) il programma matlab offset estrapola una matrice che contiene i valori c di tutte le componenti presi in esame ed il valore
F
y (che rappresenta il peso del dispositivo), e salva tali valori in un file che verrà utilizzato nei programmi seguenti. Il file contiene i valori seguenti:_ _ _ _ _ _ x y x y z z Y offset F offset F offset M offset M offset M offset F F (6.32)
Dove gli offset rappresentano gli errori fissi di misura dovuti all’acquisizione dei dati. Il programma offset inoltre ha il compito di correggere la misurazione sull’angolo dovuta al montaggio del lettore ottico. Il valore di 195° è solo un valore approssimativo, in quanto il montaggio non permette l’assoluta certezza della precisione della misura. Tramite un algoritmo è possibile correlare il picco della forza misurata dal dinamometro (che la teoria ci dice essere il punto in cui
F
y, per esempio, è massimo, cioè che in quell’istanteF
yè allineato con la forza peso e con la verticale) e il punto di passaggio della tacca sotto il sensore ottico (Figura 6-13).161
Figura 6-13 Andamento della forza Fy in N e il passaggio del lettore di tacca adimensionale
Il t , rappresentato in figura, consente di calcolare la posizione angolare del lettore di tacca dal momento che la velocità angolare di rotazione è fissata.
Questa correlazione ci permette una correzione dell’angolo inizialmente assegnato con una misurazione molto più accurata. Anche questo angolo viene in seguito aggiunto al file di salvataggio.
Come abbiamo visto in precedenza la precisione degli angoli è fondamentale per il corretto svolgimento della procedura di riduzione delle forze. Un errore fatto in questa fase della sperimentazione si ripercuoterebbe su tutte le misure che verranno eseguite in seguito. Da qui l’importanza della prova di offset che verrà utilizzata in ogni programma successivo per correggerne le letture dei segnali.
Il programma offset in linguaggio matlab viene mostrato in appendice.
6.3.2 La prova Eccentricità
Una volta eseguita la prova offset, per lo studio delle forze rotodinamiche è necessario conoscere la posizione corretta del vettore eccentricità
. Questa operazione viene eseguita da un altro programma, il programma Eccentricità. Il programma eccentricità, a differenza dell’offset, interessa solo il motore secondario,
, mentre il motore primario rimane fermo,0
. La velocita di whirl è di 1000 rpm e la prova è composta da 5000 campioni al secondo per 5 secondi ed anche questa prova viene eseguita in aria.In questo caso, dal momento che le velocità in gioco non sono trascurabili, gli effetti delle azioni centrifughe diventano apprezzabili, e combinandole con l’azione della forza peso, sempre presente, è possibile ricavare la posizione del vettore eccentricità.
0 20 40 60 80 100 120 -60 -40 -20 0 20 40 60 DAPROT3 OFFSET tempo (s) F y ( N ) F y lettore di tacca Δt
162
Figura 6-14 Rappresentazione schematica della prova Eccentricità
La combinazione dei due effetti avviene tenendo conto che, nel suo moto lungo la circonferenza di whirl, l’orientazione degli assi del sistema solidale col dinamometro rimangono costanti,
0
, mentre il vettore eccentricità
ruota con velocità angolare pari a
1000
rpm. Indipendentemente dall’orientazione del sistema solidale e, a causa della presenza costante della forza peso, la forza risultanteFR definita come:R N peso
F F F (6.33)
dove FN rappresenta la forza normale alla traiettoria di whirl dovuta alle azioni centrifughe 2 N F m
(6.34) e Fpeso peso F mg (6.35)assumerà il valore massimo quando allineata e concorde con la forza di gravità. Infatti:
2 max
R
F
m
mg
(6.36)Una volta ottenuto l’andamento di FR, che può essere calcolata mediante la semplice espressione
2 2
R x y
F
F
F
(6.37)Si possono legare quindi il valore massimo FRmax con la lettura del sensore ottico posto sul
motore secondario, come vengono rappresentate nella figura seguente (Figura 6-15) mediante la relazione sul tempo, come per la prova offset.
163
Figura 6-15 Andamento di FR in N e del lettore di tacca secondario adimensionale
In questo modo si ottiene l’angolo tra il vettore eccentricità
e la tacca sull’albero secondario, cioè, come definito nel paragrafo 6.2.1, l’angolo
, cioè l’angolo che il vettore eccentricità percorre tra il picco della forza FR ed il passaggio della tacca sotto il sensore ottico.Questo angolo viene poi salvato in un file .mat che verrà utilizzato nei programmi successivi. Anche del programma eccentricità viene mostrato il codice in appendice.
Errore nel valore dell’eccentricità
A causa di possibili errori dovuti al montaggio causati principalmente dal fatto che l’induttore, o la pompa centrifuga, sono delle masse sospese, può succedere che il centro di massa del dispositivo, sia leggermente disallineato con l’asse effettivo di rotazione. Dal momento che l’eccentricità viene calcolata per via sperimentale, questo tipo di errore aggiunge un vettore eccentricità ulteriore, di cui però noi non possiamo conoscerne ne l’intensità ne la direzione.
1 1.02 1.04 1.06 1.08 1.1 1.12 1.14 1.16 1.18 1.2 0 50 100 150 DAPROT3 eccentricità tempo (s) F ( N ) F
lettore di tacca secondario
164
Figura 6-16 Rappresentazione schematica dell’errore dovuto al disallineamento del centro di massa
Durante questa campagna sperimentale, il confronto dei risultati di prove simili ha mostrato alcune incongruenze con i risultati attesi, costringendo il team di ricerca a valutarne le possibili cause e a progettare una procedura per la correzione, perlomeno parziale, di tale errore.
Per valutare l’effettiva intensità del vettore
massa mostrato nella Figura 6-16 si esegue un’ulteriore prova.Questa prova è molto simile alla prova di offset, ma differisce da questa per la velocità di rotazione del motore. Facendo girare il motore primario ad una velocità di
1000
rpm, le componenti dovute alle azioni centrifughe2 centrifuga massa
F M
(6.38)diventano rilevanti, e facendo un confronto con la prova offset, è possibile ricavare il valore di massa
.Una volta conosciuta l’intensità di tale disallineamento, l’attenzione passa alla correzione angolare.
Come mostrato in Figura 6-16, la differenza sostanziale tra caso ideale e quello reale, consiste nella presenza o meno della forza tangenziale FT. Nel caso ideale, la forza F avrebbe componenti solo in direzione radiale, quindi
_ ideale N ideale
F
F
(6.39)La presenza dell’eccentricità
massa fa si che la Fmisurata non sia allineata sulla direzione radiale, ma si scompone nelle due componenti radiali e tangenziali rispettivamente,F
N misurata_ e165
_ T misurata
F
. Questo disallineamento di un angolo
tra le due forze Fideale ed Fmisurata è uguale al disallineamento che c’è tra i vettori eccentricità
ideale ed
misurato, e poiché il nostro programma matlab calcola sia la forza tangenziale che quella normale, tramite considerazioni trigonometriche è possibile trovare il valore di
_ _ arctan T misurata N misurata F F
(6.40)E correggere quindi la misurazione.
6.3.3 La prova Rotodinamica Discreta in aria
Una volta eseguite le due prove precedenti che forniscono i parametri fondamentali per il settaggio dell’apparato sperimentale, si passa alla prova Rotodinamica Discreta. Questa è una prova che viene ripetuta per ogni singolo rapporto di whirl di interesse.
Come per la prova offset precedente, la durata della prova è di 120 secondi ed il numero di campioni al secondo è di 5000. La velocità di rotazione del motore primario,, è di 2000 rpm fissata per tutte le prove. Per quanto riguarda invece la velocità del motore secondario, questa verrà fissata per una singola prova, ma varierà da prova a prova. Per quanto riguarda l’attività sperimentale oggetto di questa tesi, le prove Rotodinamiche discrete in aria da svolgersi saranno 18, 9 per quanto riguarda i rapporti di whirl negativi (da -0.1 a -0.9) e 9 per quelli positivi (da 0.1 a 0.9).
Figura 6-17 Rappresentazione schematica della prova Rotodinamica discreta
A titolo di esempio, per eseguire la prova rotodinamica discreta a rapporto di whirl pari a -0.4, l’apparato sperimentale verrà impostato con velocità del primario
2000
rpm e velocità del secondario
800
rpm.166
Il programma matlab Rotodinamica discreta in aria è stato progettato per trasformare le forze misurate durante la prova e fornirci un valore medio di tali forze. La difficoltà principale di tale procedura, non risiede solamente nell’accuratezza con cui misuriamo gli angoli su ciascun albero rotante, ma come si intuisce dalla procedura teorica spiegata nel paragrafo 6.2.1, nell’accuratezza con cui misuriamo le posizioni relative che hanno i due angoli. L’algoritmo contenuto nel programma ci consente la possibilità di avere un unico programma utile per il calcolo degli angoli iniziali, indipendentemente dal verso di rotazione del motore secondario. Una volta trovati gli angoli e le loro posizioni relative, è possibile sviluppare la procedura teorica per l’integrazione delle relazioni al paragrafo 6.2 e trovare le forze agenti sulla girante.
Le forze trovate, 0 0 0 0 a a X X a a Y Y a a XX XX a a XY XY a a YX YX a a YY YY
F
M
F
M
A
B
A
B
A
B
A
B
(6.41)Dove l’apice a si riferisce alle prove in aria. Insieme alle forze FN e FT che vengono calcolate mediante le relazioni
1
2
1
2
a a a N XX YY a a a T XY YXF
A
A
F
A
A
(6.42)Verranno poi salvate in un file nominato col rapporto di whirl, e le utilizzeremo nell’ultimo passo della procedura.
Come metodo di controllo della prova, viene utilizzato l’andamento della forza
F
Na al variare del rapporto di whirl. Infatti la forza normale, dal momento che rappresenta la componente centrifuga del moto, al variare del rapporto di whirl dovrebbe assumere un andamento di tipo parabolico (Figura 6-18), proporzionale alla massa della giranteM
girante2 a
N girante
F M
(6.43)167
Figura 6-18 Plottaggio dei dati reali in aria (rosso) e andamento ideale (verde)
6.3.4 La prova Offset in Acqua
Una volta archiviati i dati delle prove eseguite in aria, vengono eseguite le prove in acqua. La prova offset in acqua tuttavia, pur formalmente eseguita allo stesso modo, cioè 5000 campioni al secondo per 120 secondi a 2 rpm, non ha lo stesso scopo di quella in aria, ma è necessaria per tenere conto di un altro fenomeno fisico: calcolare la spinta idrostatica.
Figura 6-19 Rappresentazione schematica della spinta idrostatica
La spinta idrostatica, o come chiamata nei capitoli precedenti usando il termine inglese
buoyancy, viene misurata facendo una semplice sottrazione tra il valore di
F
ya e quello che viene misurato dalla prova offset in acqua wy F -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 250
FORZA NORMALE PROVE IN ARIA DAPROT3
/ F N ( N ) F N discreta F N ideale
168 w a buoyancy y y
F F F (6.44)
Stessa cosa per il momento
M
buoyancyw a buoyancy x x
M M M (6.45)
Questi due termini verranno poi salvati in un file e richiamati al momento del calcolo delle forze. La prova offset in acqua, generalmente, viene ripetuta ogni volta che si effettua una serie di nuove prove, in modo che i risultati che si ottengono abbiano, il più possibile, le stesse condizioni fisiche.
6.3.5 Prova Rotodinamica discreta in acqua
Identicamente a quanto fatto per la prova rotodinamica discreta in aria, le stesse prove vengono ripetute in acqua. Otteniamo quindi le stesse 14 componenti
0 0 0 0 w w X X w w Y Y w w XX XX w w XY XY w w YX YX w w YY YY w w N T
F
M
F
M
A
B
A
B
A
B
A
B
F
F
(6.46)per i 18 rapporti di whirl calcolati in precedenza con l’apice w che indica le prove in acqua (vedi paragrafo 6.3.3).
6.3.6 La prova Rotodinamica Main
La prova Rotodinamica Main è il programma matlab che raccoglie tutti i dati estrapolati dalle prove precedenti e li mette insieme per eseguire la riduzione dei forze rotodinamiche agenti sulla girante. La funzione principale è quella di calcolare le Forze , Momenti e componenti delle matrici
A e
B tramite la procedura descritta nelle equazioni (6.23) e (6.24) una volta eseguiti i calcoli, il programma eseguirà un plottaggio di tutte le 14 componenti calcolate0 0 0 0 X X Y Y XX XX XY XY YX YX YY YY N T
F
M
F
M
A
B
A
B
A
B
A
B
F
F
(6.47)169
in funzione del rapporto di whirl. Tale plottaggio ha la funzione, oltre che dare il valore di tali componenti, di mostrare anche (tramite opportune colorazioni) le zone dove le forze producono azioni stabilizzanti o destabilizzanti.
Come già accennato nel capitolo 3, infatti, la rotodinamica è lo studio delle forze non stazionarie normali e tangenziali. I loro effetti, se stabilizzanti o destabilizzanti, nel loro moto di whirl sono definiti in base all’orientazione delle componenti normali (FN) e tangenziali (FT) della forza rotodinamica (FR ), e se queste tendono ad incrementare l’eccentricità del moto di whirl o a sostenere la rotazione, rispettivamente. Come mostrato nella Figura 6-20 e nella Figura 6-21 la componente normale è destabilizzante quando diretta verso l’esterno, mentre la componente tangenziale è destabilizzante quando diretta nella stessa direzione del moto di whirl.
Figura 6-20 Scomposizione Schematica della Forza Rotodinamica e delle sue componenti normale e tangenziale sull’orbita di whirl (rapporto di whirl positivo)
170
Figura 6-21 Scomposizione Schematica della Forza Rotodinamica e delle sue componenti normale e tangenziale sull’orbita di whirl (rapporto di whirl negativo)
Le stesse figure mostrano, mediante aree colorate, le regioni di stabilità per il rapporto di whirl positivo (Figura 6-20) e negativo (Figura 6-21).
171
Risultati sperimentali
6.4
In questo capitolo vengono riportati i risultati della campagna sperimentale effettuata sull’induttore DAPROT3 con l’obiettivo di analizzare le forze rotodinamiche agenti su tale induttore nel caso in cui questo si trovi forzato a ruotare con una certa eccentricità pari a
0.00113
m al variare del numero di Eulero
, scegliendo 3 valori, 0.778, 0.100 e 0.080 che rappresentano rispettivamente le condizioni non cavitanti, debolmente cavitanti e cavitanti.Per non appesantire la trattazione qui di seguito verranno presentati solo alcuni risultati, mentre i rimanenti verranno presentati in appendice. Tra i valori di interesse si presentano i risultati degli andamenti delle componenti normali e tangenziali delle forze rotodinamiche, FN e FT, adimensionalizzate e non adimensionalizzate. In entrambi i casi le forze verranno mostrate in funzione del rapporto di whirl
.Per gli induttori, le forze FN e FT vengono adimensionalizzate cosi: * 2 3 2 * 2 3 2 N N L a T T T L a T
F
F
c
R
F
F
c
R
(6.48)172
Figura 6-22 Andamento della Forza Normale adimensionale in funzione del rapporto di whirl
Figura 6-23 andamento della Forza Normale in funzione del rapporto di whirl
FORZA NORMALE ADIMENSIONALE DAPROT3
/ F N * -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -20 -10 0 10 20 30 40 F N* Destabilizzante F N* Stabilizzante F N* , = 0.778 , = 0.065 , T = 20°C F N* , = 0.100 , = 0.065 , T = 20°C F N* , = 0.080 , = 0.065 , T = 20°C
FORZA NORMALE DAPROT3
/ F N ( N ) -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -100 -50 0 50 100 150 200 F N Destabilizzante F N Stabilizzante F N , = 0.778 , = 0.065 , T = 20°C F N , = 0.100 , = 0.065 , T = 20°C F N , = 0.080 , = 0.065 , T = 20°C
173
Figura 6-24 Andamento della Forza Tangenziale adimensionale in funzione del rapporto di whirl
Figura 6-25 Andamento della Forza Tangenziale in funzione del rapporto di whirl
Come accennato al capitolo precedente, per questi tipi di componenti è stato possibile indicare con colori diversi le regioni che mostrano un comportamento stabile (colore verde) o instabile (colore rosso). Osservando le figure precedenti è possibile notare:
FORZA TANGENZIALE ADIMENSIONALE DAPROT3
/ F T * -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -20 -10 0 10 20 30 40 F T* Destabilizzante F T* Stabilizzante F T* , = 0.778 , = 0.065 , T = 20°C F T* , = 0.100 , = 0.065 , T = 20°C F T* , = 0.080 , = 0.065 , T = 20°C
FORZA TANGENZIALE DAPROT3
/ F T ( N ) -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -100 -50 0 50 100 150 200 F T Destabilizzante F T Stabilizzante F T , = 0.778 , = 0.065 , T = 20°C F T , = 0.100 , = 0.065 , T = 20°C F T , = 0.080 , = 0.065 , T = 20°C
174
L’andamento della componente normale è all’incirca quadratico per
negativo con discostamenti apprezzabili tra i risultati dei tre valori del numero di Eulero solo ad alti rapporti di whirl, mentre l’andamento quadratico non viene seguito per
positivo, e si presenta un picco per tutti i valori di
intorno a
0.3
fortemente stabilizzante. L’andamento della componente tangenziale si presenta pressoché costante per rapporti
negativi con una tendenza ad aumentare leggermente dopo
0.5
, mentre per
positivi abbiamo più attraversamenti ai bassi valori del rapporto di whirl ed una tendenza a portarsi nella zona stabile dopo valori di
0.6
. Per FN una diminuzione del coefficiente di flusso, in generale porta verso condizioni meno stabili, con differenze tra
che si amplificano per alti valori di
sia positivi che negativi. Per FT al diminuire del coefficiente di flusso, pur mantenendosi nella regione stabile per
negativi, diminuisce l’intensità della forza stabilizzante, mentre per
positivi tende a mantenersi più a lungo nella regione instabile aumentando l’intensità della forza.Dopo aver mostrato le forze rotodinamiche sul sistema rotante si mostreranno gli stessi risultati ma sul sistema assoluto, solidale al laboratorio. In particolare, anziché mostrare FN ed FT, si mostreranno
F
0* ed F0 insieme con il grafico dell’angolo in gradi sessadecimali compreso tra la forza F0 e l’asse X assoluto.0
F verrà adimensionalizzata come segue:
* 0 0 2 3 2 L a T
F
F
c
R
(6.49)175
Figura 6-26 Andamento della spinta radiale adimensionale in funzione del rapporto di whirl
Figura 6-27 Andamento della spinta radiale in funzione del rapporto di whirl
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
0 5 10 15
F0 PROVE DAPROT3 adimensionale
/ F 0 * F 0* , = 0.778 , = 0.065 , T = 20°C F 0* , = 0.100 , = 0.065 , T = 20°C F 0* , = 0.080 , = 0.065 , T = 20°C -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 5 10 15 20 25 30 F0 PROVE DAPROT3 / F 0 ( N ) F 0 , = 0.778 , = 0.065 , T = 20°C F 0 , = 0.100 , = 0.065 , T = 20°C F 0 , = 0.080 , = 0.065 , T = 20°C
176
Figura 6-28 angolo della forza radiale misurato rispetto all’asse X
Dalle figure qui sopra si nota come per coefficienti di flusso alti il modulo della spinta radiale abbia un andamento più uniforme e costante al variare del rapporto di whirl, mentre per i valori di
più bassi ha un andamento molto più variato.-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -150 -100 -50 0 50 100 150 200 F0 PROVE DAPROT3 / a n g o lo [ d e g ] F 0* , = 0.778 , = 0.065 , T = 20°C F 0* , = 0.100 , = 0.065 , T = 20°C F 0* , = 0.080 , = 0.065 , T = 20°C
177
Bibliografia
6.5
[1] L.Pecorari, Studio delle prestazioni cavitanti e delle forze rotodinamiche su induttori per uso spaziale, Tesi di Laurea in Ingegneria Aerospaziale, Università di Pisa,2008-2009
[2] L. Torre, A. Pasini, A. Cervone, L. Pecorari, A. Milani e L. d’Agostino, Rotordynamic Forces on a Three Bladed Inducer, ALTA S.p.A.
[3] A. Bhattacharyya, Internal Flows and Force Matrices in Axial Flow Inducers ,Ph.D. Thesis, California Institute of Technology,1994.
[4] A. Pasini, L. Torre, A. Cervone e L. d’Agostino, Rotordynamic Forces on four bladed inducer, ALTA S.p.A.
[5] C.E. Brennen, Hydrodynamics of Pumps, Oxford University Press, 1994
[6] L.d’Agostino, et al, A Reduced Order Model for Preliminary Design and Performance Prediction of Tapered Inducers, 12th Int. Symp. On Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, Haway, USA, 2008
[7] L.d’Agostino, et al, A Reduced Order Model for Preliminary Design and Performance Prediction of Tapered Inducers: Comparison with Numerical Simulations, AIAA Paper 5119, 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conf. and Exhibit, CT, USA, 2008
[8] L.d’Agostino, et al, The Different Role of Cavitation on Rotordynamics Whirl Forces in Axial Inducers and Centrifugal Impellers, CISM Courses and Lectures No. 496, Int Centre for Mechanical Sciences, Springer, Vien and New York, 2007






![Tabella 6-1 Tabulazione schematica delle prove sperimentali per l’induttore DAPROT3 nome provavelocità di rotazione del motore primario Ω= [rpm]velocità di rotazione del motore secondario ω=[rpm]durata in [s]campioni al secondocampioni](https://thumb-eu.123doks.com/thumbv2/123dokorg/7619929.116086/14.892.123.751.101.1094/tabulazione-schematica-sperimentali-provavelocità-velocità-rotazione-secondario-secondocampioni.webp)

