CAPITOLO 5

CAPITOLO 5

ANALISI NUMERICA AGLI ELEMENTI FINITI

Le indagini sul comportamento meccanico della trave hanno preso le mosse dalla de-finizione di alcuni modelli numerici sviluppati con il metodo degli elementi finiti allo sco-po di simulare e prevedere la rissco-posta della struttura sottosco-posta ad azioni di carattere sia statico che dinamico e di valutarne le caratteristiche di stabilità, resistenza e duttilità .

L’analisi numerica del prototipo TVT  si è proposta di approfondire i risultati ottenu-ti con il modello TVT α [11], evidenziando dapprima le parottenu-ticolarità della risposta mecca-nica del nuovo prototipo nel proprio piano ed approfondendo successivamente il problema della stabilità fuori dal piano.

Le variazioni rispetto al modello precedente, che ha costituito un buon punto di par-tenza per l’analisi, sono state rivolte principalmente al miglioramento delle proprietà degli elementi di contatto acciaio-vetro, la cui influenza sulla rigidezza della struttura è essenzia-le, come si mostrerà nel seguito. È stata inoltre determinata la rigidezza trasversale da at-tribuire ai nodi al fine di sopprimere il vincolo di planarità8, calibrandola su un modello tridimensionale locale e sono state definite condizioni di vincolo più accurate che tengono conto della non linearità indotta dalla differenza di schema statico tra la fase di presolleci-tazione e la fase di esercizio.

Considerato il ruolo chiave giocato dalla pretensione delle funi, è apparso naturale ri-volgere l’attenzione ai pro ed ai contro di una presollecitazione elevata, sia nei confronti della rigidezza globale della trave che della stabilità locale dei pannelli di vetro.

Infine l’esperienza acquisita con la campagna sperimentale sul primo prototipo di tra-ve TVT, che atra-veva mostrato in fase di prova notevoli deformazioni trastra-versali, ha messo in guardia contro il fenomeno dell’instabilità flessotorsionale ed ha condotto alla progettazio-ne di un nuovo sistema di controvento la cui efficacia è stata valutata attraverso analisi non

8

Il modello FEM della trave TVT  era un modello piano sviluppato in una fase preliminare della ri-cerca, parallelamente alla costruzione del primo prototipo, con il quale si volevano ottenere informazioni sul-la risposta delsul-la trave ad azioni verticali, trascurando eventuali spostamenti trasversali dei nodi.

lineari su modelli numerici ai quali sono state attribuite imperfezioni di carattere geometri-co e meccanigeometri-co.

Prima di passare ad una descrizione più approfondita delle caratteristiche dei modelli e dei risultati delle analisi si ritiene utile offrire una breve introduzione ai concetti base dell’analisi di instabilità lineare ed dell’analisi statica non lineare che costituiscono il nu-cleo delle indagini descritte in questo capitolo.

5.1 Analisi non lineare

5.1.1 Metodi numerici di analisi strutturale: calcolo matriciale

In questo paragrafo si intende fornire una brevissima introduzione ai metodi di calcolo matriciale che sono alla base del calcolo strutturale automatico, al fine di meglio compren-dere le considerazioni svolte nel seguito del capitolo. Una trattazione più approfondita può essere trovata in [24] e [5].

Il metodo della matrice di rigidezza è certamente il più diffuso per l’analisi di strutture complesse e dotate di molti gradi di libertà.

Noti i carichi applicati e le proprietà degli elementi che costituiscono la struttura, ven-gono calcolate dapprima le matrici di rigidezza dei singoli elementi e successivamente vie-ne assemblata la matrice globale di rigidezza. A questo punto vievie-ne risolto il sistema di equazioni di equilibrio e viene determinato il vettore degli spostamenti nodali. Le caratteri-stiche della sollecitazione vengono infine determinate a partire dagli spostamenti nodali at-traverso i legami costitutivi.

Convenendo di indicare le matrici tra parentesi graffe ed i vettori tra parentesi quadre, il sistema di equazioni di equilibrio può essere scritto:

𝐾𝑒 𝑥 = 𝑝

dove:

𝐾_𝑒 è la matrice elastica di rigidezza;

𝑥 è il vettore degli spostamenti nodali (incognito); 𝑝 è il vettore dei carichi nodali.

Premoltiplicando per la matrice inversa si ottiene: 𝑥 = 𝐾𝑒 −1 𝑝

Si osserva che la matrice di rigidezza deve essere definita positiva e che qualora nel corso dell’analisi dovesse generarsi una matrice singolare il solutore non potendo più in-vertirla sarebbe costretto ad arrestarsi.

In ambito lineare e per elementi unidimensionali i termini della matrice di rigidezza possono essere calcolati con la teoria tecnica delle travi imponendo una alla volta delle di-storsioni all’elemento e calcolando le azioni all’estremità dell’asta.

Ciascuna colonna della matrice 𝐾 coincide quindi con il vettore delle forze nodali da applicare sull’elemento per ottenere una deformazione unitaria associata al corrispondente grado di libertà mentre le altre componenti di distorsione sono nulle.

Per un’asta prismatica si ha:

𝐾_𝑒 = 𝐸𝐴 𝑙 0 12𝐸𝐽 𝑙3 𝑠𝑖𝑚𝑚. 0 6𝐸𝐽 𝑙2 4𝐸𝐽 𝑙 −𝐸𝐴 𝑙 0 0 𝐸𝐴 𝑙 0 −12𝐸𝐽 𝑙3 − 6𝐸𝐽 𝑙2 0 12𝐸𝐽 𝑙3 0 6𝐸𝐽 𝑙2 2𝐸𝐽 𝑙 0 − 6𝐸𝐽 𝑙2 4𝐸𝐽 𝑙

Per un mezzo continuo, invece si ricorre al metodo degli elementi finiti (FEM) che consiste in una approssimazione del campo di spostamenti ottenuta suddividendo il mezzo in elementi all’interno dei quali la funzione di forma 𝜙 (che in generale può rappresentare diverse grandezze fisiche: tensioni, deformazioni, energia potenziale, temperatura, ecc.) è continua ed è generalmente rappresentata da un polinomio.

Per un elemento triangolare una funzione appropriata è del tipo: 𝜙 = 𝑎₁+ 𝑎₂ 𝑥 + 𝑎₃ 𝑦

Le costanti 𝑎₁, 𝑎₂, 𝑎₃ possono essere espresse in funzione dei valo-ri 𝜙₁, 𝜙₂, 𝜙₃ che assume la funzione 𝜙 nei tre vertici.

Per un elemento quadrangolare ad otto nodi ci sono otto costanti 𝑎_𝑖 e la funzione di forma può rappre-sentare una superficie parabolica.

funzione 𝜙 deve essere continua (compatibilità) ma può presentare dei salti (jumps) nelle proprie derivate.

Scelto il tipo di elemento finito e quindi le funzioni di forma, la matrice delle rigidez-ze viene calcolata con procedimento analogo a quello accennato per le aste prismatiche.

Si osserva a questo punto che per strutture che mostrano un comportamento elastico lineare i termini della matrice di rigidezza sono costanti e la soluzione può essere ottenuta risolvendo un sistema di equazioni algebriche lineari, mentre nei casi in cui la rigidezza di-penda dal livello dei carichi applicati e dalla storia di carico (comportamento non lineare) si ricorre a procedimenti iterativi molto onerosi in termini di tempo di calcolo, la cui con-vergenza è questione estremamente delicata.

5.1.2 Non linearità

Le cause del comportamento non lineare di una struttura possono essere raggruppate in tre categorie principali [38]:

 Cambiamento di stato (tensione-compressione);  Non linearità del materiale;

 Non linearità geometriche.

Alla prima categoria appartengono gli elementi il cui comportamento dipende dallo stato di tensione o compressione cui sono sottoposti, come i cavi o gli elementi di contatto. Cambiamenti di stato possono essere determinati dai carichi applicati o da cause esterne come un cambiamento di schema statico in fase di costruzione.

Altra causa molto comune di non linearità è costituita dalla relazione tensione-deformazione caratteristica del materiale. Diversi fattori possono influenzare il legame co-stitutivo di un materiale, inclusa la storia di carico (comportamento elasto-plastico), condi-zioni ambientali (ad esempio la temperatura) oppure la durata di applicazione del carico (come nel caso della risposta viscosa).

La terza causa di non linearità è costituita dai cambiamenti nella configurazione geo-metrica indotti da grandi spostamenti o grandi rotazioni che possono causare ridistribuzioni degli sforzi da membranali a flessionali e

viceversa. In questi casi si pone anche la questione della direzione di applicazione del carico che può rimanere costante co-me nel caso delle forze legate alla gravità oppure può seguire la deformazione degli elementi.

Fanno parte della categoria delle non linearità geometriche anche gli effetti indotti, in presenza di piccole deformazioni, dallo stato di tensione (stress stiffening, detto anche

ometric stiffening o incremental stiffening). Questi effetti devono essere considerati nelle

strutture snelle, con rigidezza flessionale molto piccola rispetto alla rigidezza assiale, come i cavi, le aste sottili ed i gusci.

È infatti esperienza comune che un cavo sottoposto ad una grande forza di trazione manifesti una aumentata rigidezza laterale mentre in una barra molto lunga sottoposta a compressione la rigidezza laterale si riduca e che un piccolo carico trasversale può causar-ne l’instabilità. Le forze di traziocausar-ne in questi casi si oppongono alla rotaziocausar-ne dei nodi, mentre le forze di compressione la favoriscono.

L’effetto di irrigidimento (o di riduzione della rigidezza) è messo in conto attraverso l’introduzione di una matrice di rigidezza addizionale, denominata matrice geometrica di rigidezza 𝐾𝑔 .

Un semplice esempio tratto da [37] può chiarire il ruolo della matrice di rigidezza ge-ometrica.

Si consideri il cavo sottoposto ad uno stato iniziale di trazione, sul quale vengano ap-plicati gli spostamenti trasversali 𝑣𝑖 e 𝑣𝑗 alle estremità. Si fa l’ipotesi di spostamenti piccoli

che non cambiano la tensione nel cavo. Per garantire l’equilibrio nella configurazione de-formata si devono sviluppare le forze addizionali 𝐹𝑖 ed 𝐹𝑗.

Le equazioni di equilibrio alla rotazione attorno al punto j ed alla traslazione trasver-sale possono essere scritte:

𝐹𝑖 = 𝑁 𝐿 (𝑣𝑖− 𝑣𝑗) 𝐹𝑗 = −𝐹𝑖 da cui: 𝐹𝑖 𝐹_𝑗 = 𝑁 𝐿 1 −1 −1 1 𝑣_𝑖 𝑣_𝑗

cioè:

𝐹_𝑔 = 𝐾_𝑔 𝑣

È il caso di notare che la matrice geometrica 𝐾𝑔 non è funzione delle proprietà

mec-caniche dell’elemento, ma solo della lunghezza e della forza di trazione, da qui i termini “geometric” o “stress stiffness matrix” che la distinguono dalla matrice di rigidezza elastica (descritta nel paragrafo precedente).

Naturalmente la matrice geometrica esiste per tutte le strutture, ma viene considerata solo se non trascurabile rispetto alla matrice di rigidezza elastica.

Per un’asta generica dotata anche di gradi di libertà rotazionali nei nodi la matrice ge-ometrica scritta nel riferimento locale è la seguente:

𝐾𝑔 = 𝑁 𝑙 0 0 6 5 𝑠𝑖𝑚𝑚. 0 𝑙 10 2 15𝑙2 0 0 0 0 0 −6 5 − 𝑙 10 0 6 5 0 𝑙 10 − 𝑙2 30 0 − 𝑙 10 2 15𝑙2

La matrice globale di rigidezza di un’asta è data dalla somma della matrice geometrica e della matrice elastica e si può quindi scrivere:

𝐾_𝑒 + 𝐾𝑔 𝑥 = 𝑝

Si osserva che per sforzi di compressione i termini della matrice geometrica sono ne-gativi e si oppongono ai termini della matrice di rigidezza elastica, quindi valori elevati della compressione possono condurre ad una matrice non definita positiva (cioè ad una si-tuazione simile a quella causata da condizioni di vincolo non sufficienti); fisicamente ciò corrisponde all’insorgere di fenomeni di instabilità nella struttura.

Quindi il carico critico può essere calcolato aggiungendo un moltiplicatore incognito alla matrice geometrica e risolvendo un problema agli autovalori.

5.1.3 Metodi di calcolo incrementale

Nei casi in cui le equazioni di equilibrio non sono più lineari, si può ottenere una solu-zione approssimata suddividendo il carico applicato in una serie di piccoli incrementi

nell’ambito dei quali l’errore commesso trascurando le non linearità sia sufficientemente contenuto [24].

In pratica la soluzione di un problema non lineare viene trasformata nella ripetuta so-luzione di problemi lineari: a ciascun passo si assume come configurazione iniziale quella calcolata al passo precedente.

Siano:

∆𝐹 1 il primo incremento di carico;

𝛼 0 il vettore degli spostamenti nodali che definisce la configurazione iniziale

(vettore nullo se la configurazione iniziale è quella scarica);

𝐾𝑒 0 la matrice di rigidezza elastica calcolata nella configurazione iniziale;

𝐾_{𝑔 0} la matrice di rigidezza geometrica calcolata nella configurazione iniziale; Si effettua un primo calcolo lineare risolvendo il sistema:

𝐾𝑒+𝐾𝑔 ₀ ∆𝛼 1 = ∆𝐹 1

Si calcolano gli incrementi di spostamento nodale ∆𝛼 ₁ ed attraverso il legame costi-tutivo si possono determinare gli incrementi delle azioni interne ∆𝑆 ₁.

Si calcola quindi per ciascuna asta la nuova matrice di rigidezza e si assembla la ma-trice globale relativa allo stato 1.

A questo punto si applica il secondo incremento di carico ∆𝐹 ₂ e si risolve il sistema: 𝐾_𝑒+𝐾_{𝑔 1} ∆𝛼 ₂ = ∆𝐹 ₂

e si procede fino all’ultimo incremento ∆𝐹 _𝑛.

Gli spostamenti nodali e le azioni interne complessivi sono dati da: 𝛼 = 𝛼 0+ ∆𝛼 1+ ∆𝛼 2+ ⋯ + ∆𝛼 𝑛

𝑆 = 𝑆 0+ ∆𝑆 1+ ∆𝑆 2+ ⋯ + ∆𝑆 𝑛

Il procedimento che viene applicato più frequentemente nella pratica è quello che cor-risponde al metodo di Newton-Raphson per la ricerca degli zeri di una funzione di una o più variabili.

Per il primo incremento di carico si procede , come precedentemente descritto, risol-vendo il sistema lineare:

𝐾𝑒+𝐾𝑔 ₀ ∆𝛼 1,1 = ∆𝐹 1

Dove il primo pedice ricorda che si sta operando nel primo incremento di carico ed il secondo numera l’iterazione.

Si calcolano quindi gli incrementi degli spostamenti nodali ∆𝛼 1,1 e gli spostamenti

𝛼 _1,1 = 𝛼 ₀+ ∆𝛼 _1,1

Si risale ai valori delle azioni in ciascuna asta 𝑆 1,1 e sommando le

a-zioni delle varie aste che concorrono in un nodo si ottengono le forze nodali 𝐹 1,1 , che sono in equilibrio nella

configurazione 𝑎 1,1, ma che in

gene-rale non sono uguali a quelle che si so-no applicate. La differenza tra le forze applicate e quelle calcolate all’i-esimo passo prende il nome di vettore degli

squilibri nodali:

∆𝐹 _1,1 = ∆𝐹 ₁− 𝐹 _1,1

L’iterazione successiva consiste nell’applicare ai nodi gli squilibri nodali risolvendo nuovamente il sistema lineare:

𝐾𝑒+𝐾𝑔 _1,1 ∆𝛼 1,2 = ∆𝐹 1,1

cioè si sta compiendo un secondo calcolo lineare all’interno del primo incremento di carico. La matrice delle rigidezze usata per calcolare ∆𝛼 1,2 è calcolata nella

configura-zione ottenuta con la prima iteraconfigura-zione.

Le iterazioni continuano finché gli squilibri nodali diventano sufficientemente piccoli rispetto a ∆𝐹 1. Successivamente si opera in modo analogo per il secondo incremento di

carico ∆𝐹 ₂, ripetendo una serie di iterazioni fino alla convergenza.

Una variante di questo metodo consiste nel mantenere costante la matrice delle rigidez-ze all’interno di ciascun incremento di carico (figura 5.2, procedimento di Newton-Raphson

modificato). Questa soluzione pur rallentando

la convergenza comporta un risparmio di oneri di calcolo perché per ogni incremento la matri-ce delle rigidezze viene fattorizzata una volta sola.

Il codice di calcolo usato per i modelli TVT (Straus7) consente di scegliere le modali-tà di aggiornamento della matrice delle rigi-dezze e per ogni incremento effettua un controllo di convergenza sia sulle forze che

su-Figura 5.2: procedimento di Newton-Raphson modificato. La rigidezza è costante all’interno di ciascun incremento di carico.

Figura 5.1: algoritmo di Newton-Raphson per la solu-zione iterativa di un problema non lineare.

gli spostamenti generalizzati dei nodi.

5.2 Analisi di stabilità

Esistono due tecniche per condurre analisi di stabilità sulle strutture: analisi di stabilità lineare (linear o eigenvalue buckling analysis) ed analisi non lineari.

5.2.1 Analisi di stabilità lineare

Come accennato nei paragrafi precedenti, l’instabilità della struttura può essere vista come la conseguenza della riduzione di rigidezza della struttura causata da forze membra-nali di compressione crescenti fino al punto in cui la rigidezza si riduce a zero per alcuni modi di deformazione fisicamente possibili [5].

A monte c’è quindi l’ipotesi di esistenza di un punto di biforcazione dell’equilibrio e-lastico, in corrispondenza del quale più di una configurazione è possibile. Il punto di bifor-cazione, però può esistere solo se la struttura è priva di imperfezioni, mentre le strutture reali manifestano instabilità progressiva, raggiungendo gradualmente un punto limite oltre il quale piccoli incrementi dei carichi applicati causano la divergenza degli spostamenti.

Il valore del carico critico ottenuto con l’analisi lineare è quindi il limite superiore cui tenderebbe la struttura reale se le imperfezioni (geometriche, dei vincoli e del carico) fos-sero assenti ed è quindi una stima a sfavore di sicurezza.

Tuttavia l’analisi è utile perché oltre alla stima dei carichi che causano instabilità può fornire le configurazioni instabili assunte dalla struttura e quindi la distribuzione più sfavo-revole delle imperfezioni da assegnare in una analisi non lineare per innescare l’instabilità. Per quanto riguarda l’analisi, l’effetto di riduzione della rigidezza può essere messo in conto attraverso la matrice geometrica di rigidezza 𝐾𝑔 .

In un punto di biforcazione, se avviene uno spostamento 𝑑𝑥 dalla configurazione di riferimento 𝑥 , il carico non cambia (due configurazioni molto prossime sono entrambe configurazioni di equilibrio), cioè:

𝐾_𝑒+𝐾_𝑔 𝑑𝑥 = 0

Il procedimento che si segue si divide in due fasi: inizialmente si applica alla struttura un vettore di carichi di riferimento 𝐹 𝑟𝑒𝑓 con cui si conduce una normale analisi statica

lineare (o non lineare) e si determinano gli sforzi membranali necessari per generare la ma-trice geometrica 𝐾_{𝑔 𝑟𝑒𝑓}; poi si fa l’ipotesi che un incremento di carico ottenuto moltipli-cando il vettore dei carichi per un coefficiente 𝜆 produca un incremento di intensità del campo di tensioni (e quindi dei coefficienti della matrice 𝐾_𝑔 ) ma non una variazione della distribuzione delle tensioni.

Si ha quindi: 𝐾_𝑔 = 𝜆 𝐾_𝑔

𝑟𝑒𝑓 quando 𝐹 = 𝜆 𝐹 𝑟𝑒𝑓

Poiché il carico esterno non cambia in seguito ad uno spostamento di instabilità infini-tesimo, si ha:

𝐾𝑒 + 𝜆𝑐𝑟 𝐾𝑔 _𝑟𝑒𝑓 𝑥 = 𝐾𝑒 + 𝜆𝑐𝑟 𝐾𝑔 _𝑟𝑒𝑓 𝑥 + 𝑑𝑥 = 𝜆𝑐𝑟 𝐹 𝑟𝑒𝑓

da cui:

𝐾𝑒 + 𝜆𝑐𝑟 𝐾𝑔 _𝑟𝑒𝑓 𝑑𝑥 = 0

Si deve quindi risolvere questo problema agli autovalori per determinare il valore del carico critico 𝐹 _cr = λ_cr 𝐹 _𝑟𝑒𝑓 e la forma del corrispondente modo di instabilità (autovet-tore 𝑑𝑥 ).

5.2.2 Analisi di stabilità non lineare

Per strutture caratterizzate da elementi fortemente non lineari come i cavi o gli ele-menti di contatto e quando si cercano informazioni sul comportamento della struttura cessivo all’instabilità occorre eseguire delle analisi statiche non lineari introducendo carichi gradualmente crescenti [39] [38]. In questo modo si possono anche tracciare i dia-grammi carico-spostamento seguendo la risposta della struttura oltre il carico critico, fino al collasso.

In questi casi l’analisi lineare può essere utile solo in una fase preliminare per deter-minare la forma delle imperfezioni da asse-gnare alla struttura. Si osserva infatti che qualora la forma iniziale della struttura non avesse alcuna componente di un certo modo di instabilità, l’analisi non lineare non be in grado di cogliere il corrispondente ca-rico critico. Occorre quindi introdurre una perturbazione iniziale che forzi la struttura a seguire un certo percorso di deformazione (in particolare è importante non perdere il primo e più piccolo valore del carico critico). La figura 5.4 mostra alcuni possibili diagrammi carico-spostamento. Il percorso primario non è generalmente seguito quando il carico supera il valore corrispondente al punto di biforcazione (post-buckling state). Una pendenza positiva indica che la struttura ha delle risorse post-critiche e che malgrado subisca grandi deformazioni, è ancora in grado di incassare incrementi di carico. Vi-ceversa se la pendenza del ramo secondario è negativa, si dice che la struttura è sensibile alle imperfezioni (imperfection sensitive) perché il carico di collasso è fortemente in-fluenzato dalla presenza di difetti anche pic-coli.

Figura 5.4: possibili andamenti della curva cari-co-spostamento e comportamento post-critico. Le strutture reali (curva tratteggiata) a causa della inevitabile presenza delle imperfezioni, seguono fin dall’inizio una curva che si stacca dal percor-so primario e non manifestano alcun punto di bi-forcazione.

Figura 5.4:diagramma carico spostamento per una struttura sensibile alle imperfezioni. Il cari-co limite determinato cari-con una analisi non lineare è molto inferiore al carico critico elastico

5.3 Trave TVT: descrizione dei modelli

Per ottenere una approssimazione proporzionata alla complessità delle analisi svolte ed alla scala dei problemi affrontati, sono stati definiti quattro distinti modelli:

 il modello TVT 1 è un modello globale piano, sviluppato per analizzare la ri-sposta meccanica della struttura prescindendo da possibili fenomeni di instabili-tà e per studiare l’effetto del grado di presollecitazione delle funi sulla rigidezza globale;

 il modello TVT 2 è un modello locale tridimensionale, comprendente una sola lastra di vetro con tre nodi metallici ai vertici, usato per studiare la stabilità del vetro sotto l’effetto della pretensione delle funi;

 il modello TVT 3 è un modello locale tridimensionale, comprendente un solo nodo metallico ed una sola lastra di vetro, usato per valutare la rigidezza tra-sversale del nodo;

 il modello TVT 4 è un modello globale tridimensionale, con nodi semplificati rispetto al modello TVT 1, sviluppato per superare i problemi di stabilità nu-merica sorti nelle analisi statiche non lineari per valori elevati del moltiplicatore dei carichi esterni.

5.3.1 Modello TVT β1

In considerazione della simmetria dello schema geometrico, delle condizioni di vinco-lo e delle condizioni di carico, nel modelvinco-lo TVT β1 è stato rappresentato sovinco-lo uno dei due piani che costituiscono la trave. Definendo inoltre opportune condizioni di vincolo si è po-tuto ridurre ulteriormente la dimensione del modello: ai punti appartenenti all’asse di sim-metria sono stati imposti spostamenti longitudinali nulli ed in definitiva è stato modellato solo un quarto della trave.

Poiché nell’analisi di questo modello non si sono considerati fenomeni di instabilità, sono stati soppressi tutti i gradi di libertà esterni al piano della struttura (a tutti i nodi sono stati imposti spostamenti nulli in direzione ortogonale al piano medio e rotazioni nulle in-torno agli assi contenuti nel piano stesso).

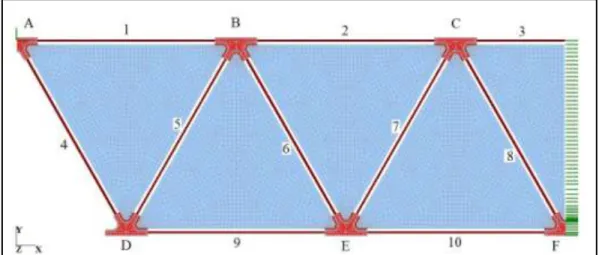
La figura 5.5 mostra il modello agli elementi finiti TVT β1 con le condizioni di vinco-lo imposte dalla simmetria della deformazione; accanto a ciascun elemento è riportata l’etichetta con la quale funi e nodi metallici verranno di seguito identificati.

Figura 5.5: modello TVT β1 con etichette delle aste e dei nodi.

Vetro

Le lastre di vetro sono state modellate con elementi shell disposti in una mesh a qua-drilateri prevalenti (cioè composta prevalentemente da elementi quadrangolari a quattro nodi [39]) opportunamente infittita in prossimità del contatto con i nodi metallici e simme-trica rispetto alle tre bisettrici. Il legame costitutivo del materiale è elastico lineare isotro-po, con modulo di Young pari a 70˙000 N/mm2. Lo spessore è pari alla somma degli spessori delle lastre che compongono i pannelli stratificati. La Tabella 5.1 riassume le pro-prietà meccaniche e geometriche di questi elementi.

Modulo di Young E

[N/mm2_]

Coefficiente di Pois-son 

Spessore h [mm] Tipo di legame -

70˙000 0,21 10 lineare

Tabella 5.1: proprietà degli elementi shell.

Funi metalliche

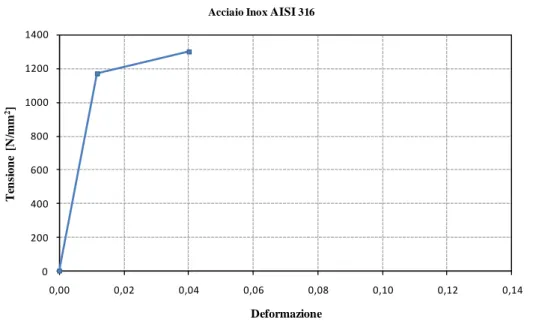
Le funi metalliche sono state divise in due sottoinsiemi. Quelle che durante la storia di carico risulteranno certamente tese (aste 4, 9 e 10 nella figura 5.5) sono state modellate con elementi truss ai quali è stato attribuito il legame costitutivo non lineare elastico-incrudente riportato in figura 5.6.

Invece le funi che per effetto dei carichi applicati potrebbero detendersi (aste 1, 2, 3, 5, 6, 7 ed 8 nella figura 5.5) sono state schematizzate con elementi truss reagenti solo a tra-zione, caratterizzati da un legame costitutivo lineare con modulo di Young pari a 100˙000

N/mm2.

Per tutte le funi, l’area netta della sezione trasversale è pari a 15,42 mm2 e corrisponde ad un diametro nominale di 6 mm.

Le proprietà degli elementi che rappresentano le funi sono riassunte nella Tabella 5.2.

Elemento (Figura 5.5)

Modulo di Young E [N/mm2]

Area [mm2] Tipo di legame - Segno possibile della reazione

4 - 9 - 10 100˙000 15,42 Vedi figura 5.6 Trazione e

Com-pressione

1 - 2 - 3 - 5 - 6 - 7 - 8 100˙000 15,42 Lineare Trazione

Tabella 5.2: proprietà degli elementi truss.

Figura 5.6: diagramma tensione-deformazione delle funi di acciaio.

Il carico di rottura delle funi è pari a 20 kN, tuttavia alle estremità, nei campi dove so-no presenti i capicorda (tutte le funi ad eccezione delle aste 1, 2, 10) la resistenza è limitata a 16 kN dal carico di rottura dei terminali metallici.

Nodi metallici

In analogia con gli elementi in vetro, per i nodi metallici è stata adottata una mesh a quadrilateri prevalenti costituita da elementi shell a quattro nodi, infittiti in prossimità del contatto al fine di avere lo stesso numero di nodi sul bordo del vetro e dell’acciaio.

Essendo il modello TVT β1 vincolato a rimanere nel piano, la rigidezza trasversale dei nodi non è stata presa in considerazione.

0 200 400 600 800 1000 1200 1400 0,00 0,02 0,04 0,06 0,08 0,10 0,12 0,14 Te n si on e [N /mm 2] Deformazione

Modulo di Young E [MPa]

Coefficiente di Poisson

 Spessore h [mm] Tipo di legame -

200˙000 0,25 18 lineare

Tabella 5.3: proprietà degli elementi shell dei nodi metallici.

Figura. 5.7: dettaglio della mesh del nodo e degli elementi di contatto acciaio-vetro. Particolare cura è stata posta nella creazione di una mesh simmetrica e di elementi di contatto perfettamente ortogonali alle superfici.

Contatto acciaio-vetro

Considerando che il contatto fra i nodi metallici e le lastre di vetro contribuisce in ma-niera decisiva a caratterizzare il comportamento meccanico della trave, si è posta molta cu-ra nella modellazione di questi elementi.

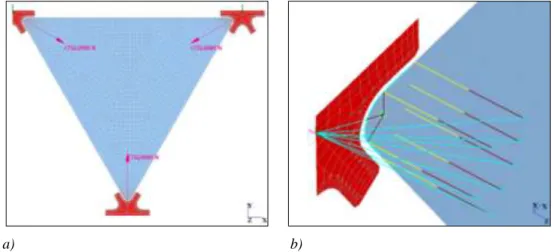
a) b)

Figura 5.8: configurazione deformata degli elementi di contatto collegati direttamente al nodo metallico (a) oppure accoppiati con vincoli interni scorrevoli lungo la superficie di contatto (b). Nel secondo caso si ottie-ne una rappresentazioottie-ne più accurata dello stato di tensioottie-ne ottie-nel vetro e si migliora notevolmente la conver-genza della soluzione per valori elevati dei carichi applicati.

Per riprodurre la condizione di vincolo unila-terale reagente solo a compressione sono stati usati elementi non lineari di tipo cutoff bar, dotati di ri-gidezza equivalente a quella dello strato di allumi-nio interposto fra acciaio e vetro e non reagenti a trazione (figura. 5.7). Tali elementi sono stati di-sposti perpendicolarmente al bordo della lastra e sono stati accoppiati con vincoli interni scorrevoli lungo la superficie di contatto, in modo tale da mantenersi ad essa ortogonali anche durante la de-formazione e non risultare tesi per effetto della semplice rotazione del vetro nel nodo metallico. La figura 5.8 mostra due configurazioni deformate de-gli elementi di contatto, con e senza questi vincoli scorrevoli.

Condizioni di vincolo

Per quanto riguarda le condizioni di vincolo, occorre considerare che in fase di mon-taggio la trave è libera di accorciarsi per effetto della presollecitazione delle funi, mentre quando viene posizionata sugli appoggi definitivi e sottoposta ai carichi esterni, il vincolo è costituito da due appoggi fissi.

Questa non linearità del vincolo è stata riprodotta applicando nel nodo A un appoggio scorrevole che a sua volta è collegato ad un punto fisso attraverso un elemento non lineare (point contact - zero gap) che reagisce solo dopo che il nodo ha compiuto uno spostamento orizzontale pari a quello indotto dalla pretensione delle funi.

Riassumendo, il modello TVT 1 è composto da:

 6750 elementi plate per il vetro;

 1590 elementi plate per i nodi metallici;  3 elementi truss per le funi tese;

 7 elementi cutoff bar per le altre funi;  554 elementi cutoff bar per il contatto

 1 elemento point contact di tipo zero gap per il vincolo non lineare. I carichi applicati sono costituiti da:

 peso proprio strutturale;

Point Contact – Zero Gap

Figura 5.9: condizioni di vincolo non line-ari.

 presollecitazione delle funi; al valore di riferimento, pari ad 1 kN, è stato appli-cato il moltipliappli-catore 

;

 carichi esterni variabili applicati ai nodi B e C (figura 5.5); il valore di riferi-mento è pari a 1 kN; tale valore è stato amplificato nel corso delle analisi appli-cando il moltiplicatore di carico ;

5.3.2 Modello TVT β2

Il modello TVT β2 è stato usato per scegliere il valore da assegnare alla forza di pre-tensione delle funi in relazione a possibili fenomeni di instabilità delle lastre di vetro. Il modello è composto da un unico pannello triangolare di vetro, estratto dal modello β1, e dai tre nodi metallici ai vertici. Essendo stata rimossa la condizione di spostamenti nulli in direzione trasversale, è stato necessario introdurre un sistema di link rigidi e di aste elasti-che elasti-che riproducesse la rigidezza trasversale del nodo (figura 5.10). Questa configurazione è uguale a quella usata nel modello β4 e verrà descritta più dettagliatamente nel paragrafo ad esso dedicato. La rigidezza è stata calibrata con il modello F.E. locale del nodo (TVT β3).

9

Si osserva che il valore della pretensione effettivamente applicato nel modello è leggermente superio-re rispetto a quello che si vuole imporsuperio-re nella struttura (1 kN), e dipende dalla posizione della fune. Infatti, per effetto della pretensione, la trave si contrae ed i nodi si avvicinano determinando una caduta di tensione proporzionale alla rigidezza degli elementi di contrasto. Questo effetto non si manifesta nella struttura reale perché mediante la chiave dinamometrica si impone direttamente la tensione nella fune.

a) b)

Figura 5.10: modello TVT β2 (a) e dettaglio del nodo (b), gli elementi di colore rosso sono aste di tipo beam la cui rigidezza è stata calibrata con il modello TVT 3, gli elementi di colore giallo sono link di tipo master-slave che impongono uguali spostamenti trasversali (direzione z) lasciando liberi i gradi di libertà nel piano xy.

5.3.3 Modello TVT β3

Per determinare la rigidezza trasversale del nodo, è stata istituita un’equivalenza fra un modello locale e dettagliato (TVT β3a) ed un modello semplificato (TVT β3b) che è stato poi inserito nel modello globale.

Nel modello β3a, i nodi metallici sono modellati con elementi solidi (brick) ed il pan-nello di vetro con elementi shell. Il contatto trasversale fra vetro e nodo è modellato con elementi cutoff bar reagenti solo a compressione, disposti su entrambi i lati del vetro e ad esso ortogonali.

Figura 5.11: modello TVT β3a nella prima condizione di carico.

Il modello TVT β3b è costituito da un numero molto inferiore di elementi ed è stato successivamente inserito nel modello globale per contenere i tempi di calcolo pur mante-nendo una schematizzazione sufficientemente dettagliata della realtà fisica.

I nodi metallici sono rappresentati da elementi shell e la rigidezza trasversale è fornita da elementi elastici ortogonali al vetro e ad esso collegati tramite elementi link di tipo

master-slave che impongono uguali spostamenti in direzione trasversale (asse z) lasciando

liberi gli altri gradi di libertà. Lo schema è lo stesso usato anche nel modello β2 e mostrato nella figura 5.10b.

L’uguaglianza fra i modelli β3a e β3b è definita in termini di spostamenti per tre di-stinte condizioni di carico. La prima condizione riproduce la flessione del pannello intorno ad un asse ortogonale alla bisettrice del vetro, la seconda aggiunge alla flessione il taglio e la terza condizione rappresenta la torsione del pannello intorno alla sua bisettrice.

5.3.4 Modello TVT β4

Il modello TVT β4 è il più completo e consente di studiare il comportamento globale della trave, mettendo in conto anche eventuali fenomeni di instabilità locale e globale e la presenza di imperfezioni sia geometriche (difetto di planarità della trave) che meccaniche

a) b)

Figura 5.13: terza condizione di carico, equivalenza fra i modelli TVT β3a e β3b; a) condizione di carico (modello β3a)

b) deformata (modello β3b).

a) b)

Figura 5.12: seconda condizione di carico, equivalenza fra i modelli TVT β3a e β3b; a) condizione di carico (modello β3a);

(diversa rigidezza trasversale dei nodi ed efficacia del controvento superiore nei confronti della stabilità flessotorsionale).

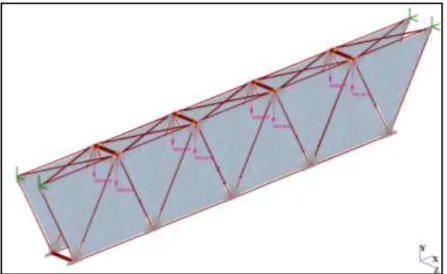
Figura 5.14: Modello TVT β4.

Rispetto al modello TVT β1, è stato rimosso il vincolo di planarità della deformazione e la trave è stata considerata nella sua interezza al fine di cogliere sia le configurazioni de-formate simmetriche che quelle antisimmetriche.

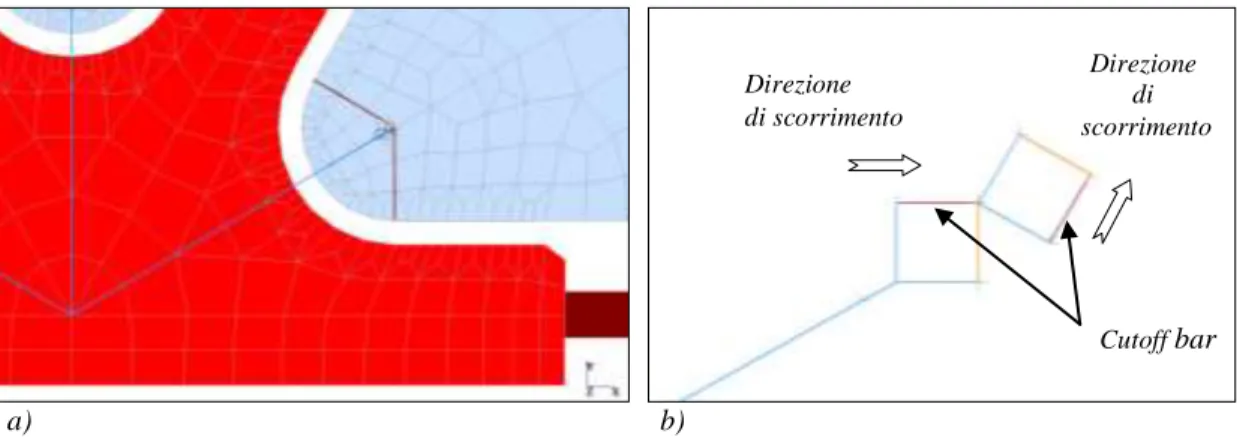
Il contatto acciaio-vetro, che nel modello TVT β1 era diffuso su tutta la superficie me-tallica che accoglieva il vetro, è stato semplificato, concentrando la non linearità del con-tatto in due soli elementi resistenti unicamente a compressione (cutoff bar) e paralleli alle due possibili direzioni di scorrimento di ciascun nodo. Per evitare singolarità della matrice delle rigidezze, gli spostamenti nella direzione ortogonale alle superfici di scorrimento so-no stati impediti con opportuni vincoli interni ed i due elementi soso-no stati posti in serie (figura 5.15b). In questo modo quando un pannello di vetro raggiunge la decompressione in una delle due direzioni (parallela alle funi di parete o ai correnti) è libero di staccarsi dal nodo metallico senza trasferire sforzi di trazione. Il collegamento tra questo dispositivo ed il pannello di vetro è costituito da tre aste inestensibili e dotate di una rigidezza flessionale che riproduce la resistenza offerta dal nodo alla rotazione relativa acciaio-vetro nel piano della trave. La rigidezza di queste aste è stata scelta in modo tale da minimizzare la diffe-renza fra i diagrammi carico-spostamento ottenuti con il modello β1 e con il modello β4.

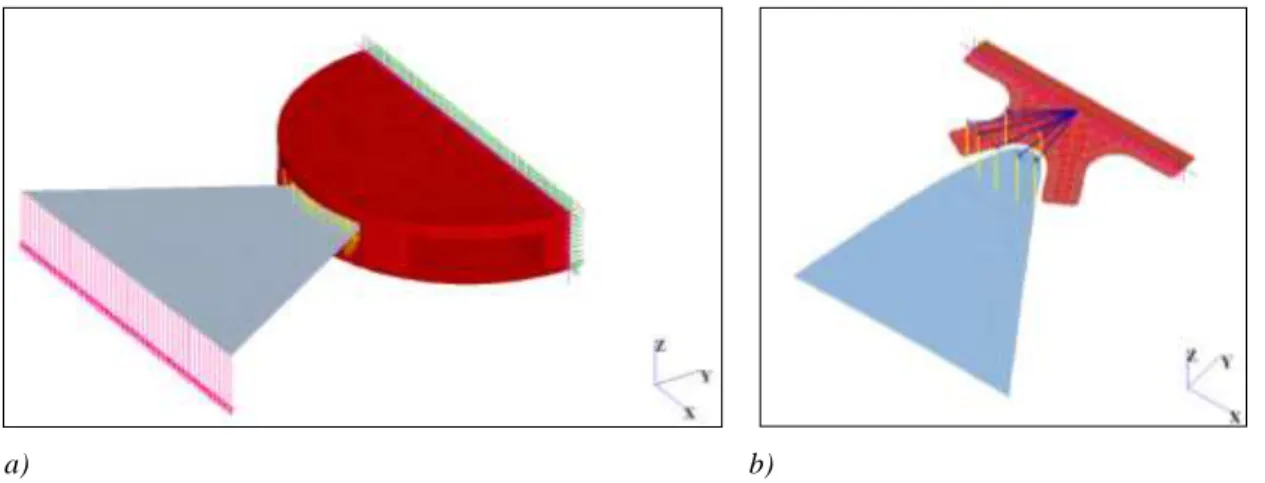
a) b)

Figura 5.15: configurazione semplificata del nodo (a) e dettaglio degli elementi non lineari (b).

La rigidezza trasversale del nodo è fornita dal dispositivo già descritto per i modelli TVT β2 e β3b.

5.4 Risultati numerici

Sul modello TVT β1 sono state condotte analisi statiche non lineari considerando la forza di pretensione delle funi, il peso proprio strutturale ed i carichi esterni applicati nei nodi del corrente superiore attraverso step successivi di carico fino al raggiungimento della crisi della struttura. Le analisi sono state ripetute per diversi valori della forza di pretensio-ne iniziale.

n. Azione LC Valore [N]

p.p. Peso proprio -

Lc 1 Pretensione delle funi 1˙000

Lc 2 Forze Fi verticali applicate ad ogni nodo 1˙000 Tabella 5.4: carichi elementari.

Load Case p.p. Lc 1 Lc2 Step 1 0,0  0,0 Step 2 1,0  0,0 Step 3 1,0  _0,5 Cutoff bar Direzione di scorrimento Direzione di scorrimento

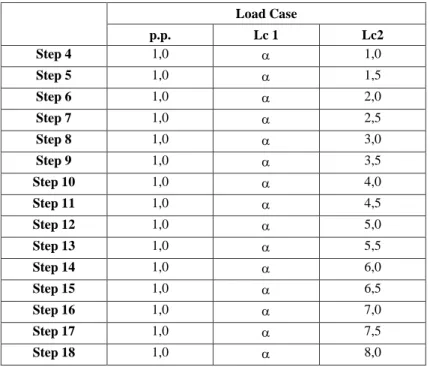
Load Case p.p. Lc 1 Lc2 Step 4 1,0  1,0 Step 5 1,0  1,5 Step 6 1,0  2,0 Step 7 1,0  2,5 Step 8 1,0  3,0 Step 9 1,0  3,5 Step 10 1,0  4,0 Step 11 1,0  4,5 Step 12 1,0  5,0 Step 13 1,0  5,5 Step 14 1,0  6,0 Step 15 1,0  6,5 Step 16 1,0  7,0 Step 17 1,0  7,5 Step 18 1,0  8,0

Tabella 5.5: moltiplicatori di carico (il valore  del moltiplicatore della preten-sione delle funi è costante per ogni analisi ed è compreso fra 2 e 12)

Sul modello TVT β2 sono state eseguite analisi di instabilità elastica per biforcazione dell’equilibrio ed analisi di instabilità progressiva, condotte mediante analisi statiche non lineari a partire da una configurazione geometrica iniziale imperfetta. Il valore dell’incurvamento che caratterizza la configurazione iniziale è pari alla massima imperfe-zione ammessa dalle norme europee EN 12377 [47] per vetri temperati chimicamente, am-plificata attraverso un coefficiente di sicurezza pari ad 1,50.

I modelli TVT β3a e β3b sono stati sottoposi ad analisi statiche non lineari per deter-minare il valore della rigidezza trasversale dei nodi da introdurre nel modello locale TVT

β2 e nel modello globale TVT β4.

Sul modello TVT β4 sono state effettuate analisi di stabilità lineare ed analisi di insta-bilità progressiva, innescata da imperfezioni geometriche iniziali. La configurazione inizia-le è stata ricavata dalinizia-le prime due forme modali (una simmetrica e l’altra antisimmetrica) dell’analisi di instabilità lineare. Le analisi sono state ripetute per diverse ampiezze dell’imperfezione iniziale, per diversi valori della rigidezza trasversale dei nodi e per di-verse configurazioni del controvento superiore.

5.4.2 Comportamento meccanico nel piano

L’analisi statica non lineare del modello TVT β1 ha condotto a risultati analoghi a quelli ottenuti in precedenza per il modello TVT α, confermando la validità

dell’interpretazione della risposta meccanica illustrata nel capitolo 4 . Le principali diffe-renze riguardano i valori del carico corrispondente alla decompressione del corrente infe-riore e del carico di collasso. Tali differenze sono dovute oltre che alle diverse dimensioni del prototipo, all’uso di funi spiroidali (dotate di scarsa rigidezza, ma di elevatissima resi-stenza) al posto delle barre usate nel prototipo α ed alla scelta di un valore sensibilmente maggiore per la pretensione iniziale delle funi.

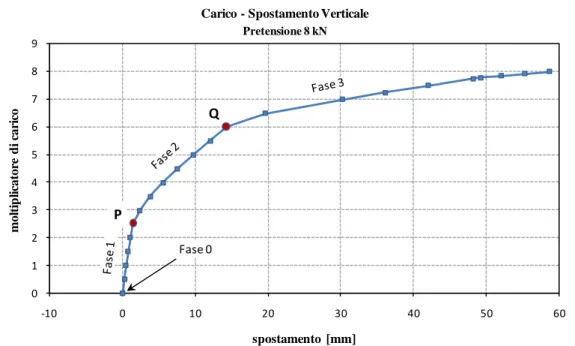
La il grafico riportato nella figura 5.16 consente di ripercorrere il comportamento del-la trave in termini di deformazioni, al crescere dei carichi applicati: inizialmente viene ap-plicata la pretensione delle funi (assemblaggio della trave), successivamente si applica il peso proprio strutturale (posizionamento della trave sugli appoggi) ed infine i nodi del cor-rente superiore vengono caricati progressivamente secondo gli incrementi definiti nella Tabella 5.5 (fase di carico progressivo).

Figura 5.16: diagramma dello spostamento verticale del nodo C in funzione del moltiplica-tore dei carichi esterni.

Il grafico evidenzia l’evoluzione della risposta meccanica attraverso tre fasi caratteriz-zate da valori sensibilmente diversi della rigidezza globale (intesa come rapporto fra la va-riazione di carico applicato ed il relativo spostamento).

Fase 0: pretensione delle funi e posizionamento sugli appoggi.

La trave subisce una contrazione per effetto della pretensione ed una debolissima in-flessione per effetto del peso proprio. Dal punto di vista tensionale si osserva una

compres-0 1 2 3 4 5 6 7 8 9 -10 0 10 20 30 40 50 60 mol ti p li cat or e d i c ar ic o spostamento [mm] Carico - Spostamento Verticale

Pretensione 8 kN

P

Q

sione quasi isotropa dei pannelli di vetro (figura 5.17). Si osserva una compressione mag-giore lungo i bordi dei pannelli posti in prossimità delle funi perimetrali rispetto ai bordi interni alla trave. Questa differenza è dovuta al fatto che pur avendo tutte le funi lo stesso valore della pretensione, quelli perimetrali sono contrastati da un solo pannello di vetro, mentre quelli interni agiscono su due pannelli, caricandone ciascuno con metà della propria forza assiale.

Figura 5.17: tensioni principali di compressione in fase 0, step 2.

Fase 1: carichi di esercizio.

Con l’applicazione dei carichi sui nodi del corrente inferiore, si osserva una diminu-zione della tensione di compressione nella parte inferiore dei pannelli di vetro ed un au-mento piuttosto modesto della tensione di trazione nelle funi inferiori. La fase 1 termina nel punto P, corrispondente alla decompressione del corrente inferiore ed al distacco del vetro dai nodi metallici.

Per un valore della pretensione delle funi pari ad 8 kN, il punto P viene raggiunto con un moltiplicatore dei carichi pari a 2,5. Ciò significa che la trave mantiene una rigidezza elevata per carichi applicati inferiori a 2,5 kN per ogni nodo, equivalenti ad un carico per unità di lunghezza pari a:

    P mi 7,6 / p kN m i dove:

Pi = 1000 N è il carico applicato in ciascun nodo;

 = 2,5 è il moltiplicatore dei carichi corrispondente alla decompressione;

i = 66 cm è l’interasse dei nodi.

Il carico totale applicato è quindi pari a:

25

tot

P   p L kN

dove:

L = 3,3 m è la lunghezza della trave.

In questa configurazione (punto P) il tiro nelle funi inferiori è aumentato appena del 6,6% rispetto al valore iniziale. Osservando la figura 5.18, si nota infatti che il tiro delle funi aumenta significativamente solo dopo aver superato la fase 1.

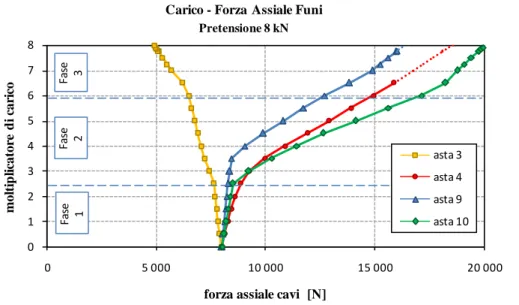
Figura 5.18: diagramma del tiro nelle funi in funzione del moltiplicatore dei carichi esterni.

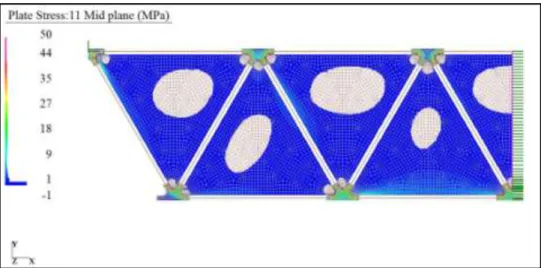
Nelle seguenti figure sono riportate le tensioni principali massime e minime relative al raggiungimento del carico di decompressione. Si nota la formazione di puntoni nel vetro in prossimità del corrente superiore e delle funi diagonali ascendenti verso la mezzeria e la decompressione delle zone prossime alle funi discendenti ed al corrente inferiore. Gli sfor-zi massimi calcolati nei pannelli di vetro risultano ampiamente sopportabili dal materiale (i valori fanno riferimento ad una pretensione iniziale di 8 kN).

0 1 2 3 4 5 6 7 8 0 5 000 10 000 15 000 20 000 mol ti p li cato re d i c ar ic o

forza assiale cavi [N] Carico - Forza Assiale Funi

Pretensione 8 kN asta 3 asta 4 asta 9 asta 10 Fa se ₁ Fa se ₂ Fa se ₃

Figura 5.19: tensioni principali massime (trazione) in fase 1, step 7 (σmax=25 N/mm 2

).

Figura 5.20: tensioni principali minime (compressione) in fase 1, step 7 (σmin=-144 N/mm2).

Fase 2: decompressione del corrente inferiore.

La fase 2 corrisponde al tratto PQ del diagramma riportato nella figura 5.16. In segui-to al superamensegui-to del carico di decompressione, si osserva una sensibile diminuzione della rigidezza globale (il valore del rapporto fra incremento dei carichi e deformazione si riduce dell’85% rispetto alla fase 1).

In questa fase l’allungamento delle funi inferiori è tale che i pannelli di vetro si distac-cano parzialmente dai nodi metallici e non riescono più a trasferire sforzi orizzontali. La sezione resistente è costituita dalla parte superiore dei pannelli di vetro (compressa) e dalle funi tese.

Come si può vedere nella figura 5.18, in fase 2 si assiste ad un marcato incremento della tensione nelle funi inferiori, fino al raggiungimento della tensione di snervamento (punto Q).

Figura 5.21: tensioni principali massime (trazione) in fase 2, step 14 (σmax=38 N/mm2).

Figura 5.22: tensioni principali minime (compressione) in fase 2, step 14 (σmin=-309 N/mm2).

Anche in fase 2 le tensioni principali nel vetro si mantengono al di sotto della resi-stenza del materiale (valutata secondo prEN13474-3 [41] ). Nella parte superiore del pan-nello più esterno si nota una diminuzione delle tensioni di compressione dovuta alla condizione di vincolo di appoggio non scorrevole (figura 5.22).

Nella parte inferiore dei pannelli con vertice rivolto verso l’alto, si manifestano delle tensioni di trazione che equilibrano le tensioni di compressione che fluiscono dai nodi su cui viene applicato il carico verso il basso e non possono essere trasferite ai pannelli adia-centi perché il contatto è venuto meno. Si riconosce in questi pannelli la formazione di due puntoni discendenti ed un tirante orizzontale, più evidente nel pannello prossimo alla mez-zeria che è il primo a decomprimersi (figure 5.21 e 5.22).

Fase 3: snervamento delle funi.

L’ultimo ramo del diagramma carico-deformazione (figura 5.16) corrisponde al supe-ramento della tensione convenzionale di snervamento delle funi. Come mostra la figura 5.18, l’analisi prosegue per effetto dell’incrudimento dell’acciaio fino al collasso, che può avvenire a causa della rottura di uno dei capicorda dell’asta 4 (carico ultimo pari a 16 kN) oppure, in caso di sovraresistenza dei terminali, per il raggiungimento del carico ultimo nell’asta 10 (che essendo priva di capicorda ha una resistenza di 20 kN).

Naturalmente alla base di questi scenari di rottura c’è l’ipotesi di un bloccaggio effi-cace delle funi anche nei nodi intermedi (in particolare nel nodo E).

Figura 5.23 tensioni principali massime (trazione) in fase 3, step 18 (σmax=67 N/mm2).

Figura 5.24 tensioni principali minime (compressione) in fase 3, step 18 (σmin=-621 N/mm 2

5.4.3 Influenza della pretensione delle funi

L'analisi statica non lineare è stata ripetuta per diversi valori della forza di pretensione

NP, per valutare gli effetti di questo parametro sulla risposta meccanica della trave, al fine

di scegliere il valore più vantaggioso sia in termini di rigidezza che di resistenza. Dall'esa-me dei diagrammi delle deformazioni e della forza normale nelle funi si sono potute trarre importanti considerazioni.

Nella figura 5.25 sono riportate le curve carico-spostamento del nodo C al variare del parametro NP.

All'aumentare della forza di pretensione si osserva un aumento dell’estensione della

fase 1, nella quale la risposta è pressoché elastica lineare. Il punto P, corrispondente alla

decompressione completa del corrente inferiore, si manifesta per valori del moltiplicatore gradualmente crescenti da 0,5 a 4. Il punto Q, invece, che segna l’inizio dello snervamento delle funi corrisponde sempre a valori del moltiplicatore prossimi a 6.

La pendenza dei tre segmenti che costituiscono le curve resta invariata, quindi la rigi-dezza nelle tre fasi è indipendente da NP, mentre gli spostamenti sono complessivamente

minori all'aumentare della pretensione, con differenze più marcate per la fase 2 e per la

fa-se 3: passando da 2 a 12 kN di pretensione, lo spostamento ultimo si riduce del 52%.

La figura 5.26 mostra il legame tra moltiplicatore dei carichi e tiro nelle funi del cor-rente inferiore all'aumentare della forza di pretensione. Anche in questo caso i tre segmenti che costituiscono le curve sono paralleli e l'estensione della fase 1, in cui l'aumento di ten-sione nelle funi è molto contenuto, cresce proporzionalmente al parametro NP. E’

impor-tante notare che nel tratto terminale tutte le curve sono molto vicine.

Ciò significa che il valore della presollecitazione ha effetti sul comportamento struttu-rale in fase di esercizio, ma non condiziona la resistenza ultima della trave: la crisi si mani-festa per valori molto simili dei carichi applicati. Quindi partire da un livello elevato di pretensione riduce le deformazioni senza avvicinare la crisi per snervamento delle funi.

Naturalmente, però la presollecitazione deve essere compatibile con la stabilità locale del vetro.

Figura 5.25: diagramma dello spostamento verticale del punto C in funzione del moltiplicatore dei carichi, per diversi valori del parametro Np.

Figura 5.26: diagramma della forza assiale nelle funi del corrente inferiore in funzione del moltiplicatore dei carichi, per diversi valori del parametro Np.

5.4.4 Stabilità locale dei pannelli di vetro

I risultati delle analisi di instabilità lineare svolte sul modello locale TVT β2 hanno fornito indicazioni preliminari sul valore critico della forza di pretensione delle funi. Nella

0 1 2 3 4 5 6 7 8 9 -10 0 10 20 30 40 50 60 70 80 90 mol ti p li cato re c ar ic h i es te rn i spostamento [mm] Carico - Spostamento Verticale

Np = 2 kN Np = 4 kN Np = 6 kN Np = 8 kN Np = 10 kN Np = 12 kN P Q 0 1 2 3 4 5 6 7 8 9 0 2 000 4 000 6 000 8 000 10 000 12 000 14 000 16 000 18 000 20 000 m ol ti p li cator e car ic h i es te rn i forza assiale [N] Carico - Forza Assiale Funi

Corrente Inferiore Np = 2 kN Np = 4 kN Np = 6 kN Np = 8 kN Np = 10 kN Np = 12 kN

figura 5.27 sono rappresentate le prime tre forme instabili del pannello di vetro con i relati-vi moltiplicatori critici di carico.

Si osserva che il valore critico del tiro delle funi che provoca l’instabilità del pannello per biforcazione dell’equilibrio elastico è pari a 14 kN.

A questo punto occorre notare che il carico critico, nella struttura reale, è influenzato da molti fattori, che vengono trascurati nell'analisi di instabilità lineare, nella quale la strut-tura è considerata perfetta. Di conseguenza il carico critico calcolato è sempre sovrastimato rispetto a quello effettivo. Le imperfezioni geometriche e di carico, sempre presenti nelle strutture reali, causano la scomparsa del punto di biforcazione. Al crescere dei carichi ap-plicati, la struttura comincia a deformarsi fin dall'inizio ed il valore degli spostamenti si amplifica progressivamente fino al punto in cui il fenomeno diverge. Questo comporta-mento può essere colto eseguendo un’analisi statica non lineare geometrica e mettendo in conto una configurazione iniziale non perfetta.

L’imperfezione iniziale è costituita da una configurazione deformata proporzionale al-la prima forma modale instabile. L’entità dell’incurvamento è stata scelta considerando il valore massimo ammesso dalle norme europee EN12337 [47] per vetri temperati chimica-mente (0,003 mm/mm) ed amplificando ulteriorchimica-mente questo valore attraverso l’applicazione di un coefficiente di sicurezza pari a 1,50.

a) b) c)

Figura 5.27: forme instabili di un pannello di vetro compresso a) 1° modo: λ=14,05

b) 2° modo: λ=33,15 c) 3° modo: λ=33,17

Figura 5.28: diagramma dello spostamento trasversale del baricentro in funzione della pretensione delle funi.

Figura 5.29: diagramma della massima tensione principale di trazione in funzione della pretensione delle funi (la linea tratteggiata rossa indica la resistenza secondo prEN13474-3).

Osservando i diagrammi dello spostamento del baricentro del pannello (figura 5.28) e della massima tensione principale di trazione (figura 5.29) in funzione della pretensione delle funi, si riconosce l’andamento tipico dei fenomeni di instabilità progressiva, caratte-rizzato da una rapida diminuzione di rigidezza.

Il valore limite della pretensione deve essere tale da non indurre nel vetro tensioni su-periori alla resistenza di calcolo del materiale. secondo prEN13474-3 [41], per vetro tem-perato chimicamente e per carichi di lunga durata, la tensione limite è pari a 95 N/mm2 (vedi paragrafo 3.2.6). 0 2 4 6 8 10 12 14 0 2 4 6 8 10 p re te n si on e f u n i [k N ] spostamento [mm] Spostamento Baricentro 0 2 4 6 8 10 12 14 0 20 40 60 80 100 120 p re te n si on e f u n i [k N ] tensione [N/mm2_]

E’ però anche opportuno che in un intorno del valore di pretensione scelto, la struttura manifesti una rigidezza residua sufficiente. Per individuare il punto in cui la diminuzione di rigidezza è tale che il fenomeno di instabilità può essere considerato in atto, le curve so-no state approssimate con delle poligonali (tali che la distanza curva-segmento sia inferiore rispettivamente al 5% dello spostamento ultimo e del 5% della tensione limite di calcolo) e si è scelta la pretensione corrispondente al primo vertice della poligonale.

Il valore di pretensione compatibile con entrambi i criteri di resistenza e rigidezza pre-cedentemente descritti è pari a:

8 P

N  kN

A questo punto occorre considerare che l’instabilità locale del pannello deve essere scongiurata anche nella fase di esercizio della trave e non solo in fase di presollecitazione.

Disponendo nel modello globale (TVT β4) dei pannelli di vetro con imperfezioni ini-ziali uguali a quella considerata nel modello locale (TVT β2) ci si accorge che la deforma-zione trasversale dovuta alla pretensione delle funi e le relative tensioni di tradeforma-zione tendono a diminuire nel corso della fase di carico della trave. Questo fenomeno si manifesta sia per configurazioni che favoriscono la rotazione dei nodi (incurvamento locale alternato rispetto al piano medio, come nella figura 5.30) sia per configurazioni che la impediscono (incur-vamento locale sempre dello stesso segno).

Figura 5.30: diminuzione delle inflessioni trasversali dei pannelli nel passaggio dalla “fase 0” alla “fase 2”.

Questo fenomeno può essere spiegato notando che all’incremento dei carichi applicati corrisponde un aumento della compressione in alcune zone del pannello ed una diminuzio-ne in altre zodiminuzio-ne. Inoltre la condiziodiminuzio-ne di vincolo non scorrevole, produce un effetto catena-ria che riduce le compressioni nel corrente superiore. Complessivamente ciò si traduce in una distensione dei pannelli di vetro.

5.4.5 Stabilità flessotorsionale della trave

Il tema della stabilità flessotorsionale è particolarmente importante per una struttura leggera e snella come quella in esame. La necessità di garantire una stabilità autonoma ri-sulta tanto più evidente se si pensa che la trave in vetro farà certamente parte di una struttu-ra con analoghe castruttu-ratteristiche di tstruttu-rasparenza e leggerezza, che difficilmente potrà svolgere una funzione stabilizzante. Si è pensato quindi di introdurre un elemento di controvento superiore che collega le due pareti costituenti la trave e fornisce rigidezza trasversale ai correnti superiori.

L’analisi è stata condotta inizialmente sulla struttura considerata priva di imperfezioni. Questa sottoposta a carichi crescenti manifesta instabilità per biforcazione dell’equilibrio. Successivamente è stata eseguita una analisi statica non lineare per tener conto della inevi-tabile presenza di imperfezioni.

Seguendo le indicazioni dell’eurocodice 3 (EN1993-1-1 § 5.3 [45] ) gli effetti di im-perfezioni quali mancanza di verticalità, mancanza di rettilineità, mancanza di planarità ed inevitabili giochi ed eccentricità nei nodi, sono stati considerati introducendo nel modello delle imperfezioni geometriche equivalenti, la cui forma è derivata dai modi di instabilità elastica globale della struttura. Sono state considerate due forme modali, caratterizzate ri-spettivamente da una deformata simmetrica (1° modo) ed una antisimmetrica (2° modo).

Le analisi sono state ripetute per diversi valori dell’imperfezione geometrica iniziale, per diversi schemi di controvento e per diversi valori della rigidezza trasversale degli ele-mento di contatto acciaio-vetro.

Le figure 5.31 e 5.32 mostrano le prime due forme modali ricavate dall’analisi di in-stabilità elastica lineare. I moltiplicatori critici sono riferiti a carichi applicati di 1 kN per ogni nodo del corrente superiore.

Figura 5.32: 2° modo di instabilità lineare (λ=25).

Si osserva che il valore del carico critico, pur non essendo molto significativo conside-rando che questa analisi trascura tutte le non linearità, è superiore al valore del carico che provoca il collasso per superamento della resistenza delle funi.

La generazione delle imperfezioni in una struttura realizzata attraverso la composizio-ne di tanti elementi distinti è un problema estremamente delicato. In particolare il difetto più evidente che si è riscontrato nel prototipo è costituito dal non perfetto allineamento dei due piani vetrati che compongono la trave e conseguentemente dalla non perfetta ortogona-lità dei montanti del controvento rispetto ai nodi metallici. Al fine di ottenere delle defor-mate che rispecchiassero le effettive imperfezioni presenti [1], per questa analisi è stato adottato un controvento tipo Vierendeel con incastro non perfetto dei montanti sui nodi. Sono stati applicati end release rotazionali parziali per ottenere delle deformate che presen-tassero rotazioni dei montanti del controvento superiore rispetto ai nodi piuttosto che in-flessioni dei montanti stessi.

Il risultato principale di questa analisi è quindi costituito dalle configurazioni defor-mate da adottare come imperfezione iniziale per l’analisi non lineare.

Prima di esporre i risultati dell’analisi statica non lineare si riporta una descrizione schematica dei parametri che sono stati presi in considerazione.

Il primo parametro è costituito dall’ampiezza dell’imperfezione iniziale. Sono stati considerati quattro diversi valori: L/100, L/200, L/300, L/400. La lunghezza libera di in-flessione, L, corrisponde alla distanza fra i flessi della linea d’asse della trave nel modo di instabilità considerato.

Il secondo parametro (al quale sono state assegnate le etichette 1A, 1B, 1C, 1D) è co-stituito dalla rigidezza trasversale dei nodi metallici, definita attraverso la rigidezza assiale delle aste trasversali mostrate nella figura 5.10b (configurazione locale del nodo).

L’etichetta 1A corrisponde alla rigidezza trasversale calcolata con il modello TVT β3, le altre etichette corrispondono a valori di rigidezza inferiori.

Il terzo parametro (etichette 2A, 2B, 2C , 2D, 2E) si riferisce al controvento superiore e corrisponde a diversi schemi ed a diversi valori della rigidezza dei nodi.

Etichetta Rigidezza Trasversale Nodo (Rig. Assiale Aste Trasversali)

[N/mm] Schema Statico Controvento Rigidezza Rotazionale Nodi Controvento [Nmm/rad] 1A 7600 1B 3800 1C 1900 1D 950 2A Vierendeel ∞ 2B Vierendeel 10.000.000 2C Vierendeel 5.000.000 2D Vierendeel 2.500.000 2E Reticolare a Croci di S. Andrea 0

Tabella 5.6: caratteristiche ed etichette dei parametri dei modelli sottoposti ad analisi sta-tica non lineare.

I grafici ottenuti dalle analisi non lineari parametriche sulla struttura con imperfezioni simmetriche sono riportati nelle figure 5.33, 5.34 e 5.35.

Figura 5.33: andamento dello spostamento trasversale del nodo C (appartenente al corrente superiore) in funzione del moltiplicatore dei carichi applicati, al variare dell’ampiezza della imperfezione geometrica iniziale (simmetrica), a parità di rigidezza trasversale ed a parità di rigidezza del controvento superiore.

La prima considerazione che si può fare è che anche per imperfezioni iniziali di note-vole entità, gli spostamenti trasversali sono piuttosto contenuti (figura 5.33). Si osserva che le imperfezioni riscontrate sul prototipo costruito in laboratorio sono state inferiori ad 1 mm, quindi molto minori dell’imperfezione L/100 applicata al modello numerico che cor-risponde ad un incurvamento (distanza massima dell’asse effettivo della trave dal segmen-to congiungente gli appoggi) pari a 33 mm.

La figura 5.34 mostra l’influenza della rigidezza dei nodi sullo spostamento trasversa-le del corrente superiore. Confrontando la curva 1A con la curva 1B, a fronte di un dimez-zamento della rigidezza si osserva un aumento della deformazione ultima del 19%. Lo stesso confronto effettuato sulle curve 1B-1C ed 1C-1D mostra incrementi della deformzione ultima rispettivamente del 14% e del 9%. Quindi passando da una curva a quella a-diacente a variazioni costanti di rigidezza (riduzione del 50%) segue un aumento della deformabilità che è progressivamente meno importante. Ciò significa che la struttura non è molto sensibile alla rigidezza trasversale dei nodi.

Rigidezze troppo basse hanno però un effetto negativo sulla stabilità locale dei pannel-li di vetro. 0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 mol ti p li cat or e car ic h i es te rn i spostamento [mm] Carico - Spostamento Trasversale

(Imperfezione Simmetrica)

L/400 - 1A - 2A

L/300 - 1A - 2A

L/200 - 1A - 2A

Figura 5.34: andamento dello spostamento trasversale del nodo C (appartenente al corrente superiore) in funzione del moltiplicatore dei carichi applicati, al variare della rigidezza tra-sversale dei nodi metallici, a parità di ampiezza dell’imperfezione geometrica (simmetrica) ed a parità di rigidezza del controvento superiore.

Figura 5.35: andamento dello spostamento trasversale del nodo C (appartenente al corren-te superiore) in funzione del moltiplicatore dei carichi applicati, al variare della rigidezza e dello scema statico del controvento superiore, a parità di ampiezza dell’imperfezione ge-ometrica (simmetrica) ed a parità di rigidezza trasversale dei nodi metallici.

0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 mol ti p li cat or e car ic h i es te rn i spostamento [mm] Carico - Spostamento Trasversale

(Imperfezione Simmetrica) L/300 - 1A - 2A L/300 - 1B - 2A L/300 - 1C - 2A L/300 - 1D - 2A 0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 mol ti p li cat or e car ic h i es te rn i spostamento [mm] Carico - Spostamento Trasversale

(Imperfezione Simmetrica) L/300 - 1A - 2A L/300 - 1A - 2B L/300 - 1A - 2C L/300 - 1A - 2D L/300 - 1A - 2E

La successiva analisi parametrica ha coinvolto la rigidezza del controvento superiore. Valgono le stesse considerazioni svolte per la rigidezza trasversale dei nodi: valori decre-scenti della rigidezza hanno effetti progressivamente meno importanti. Confrontando le curve 2B-2C e 2C-2D, ad una riduzione del 50% della rigidezza di incastro dei montanti dello schema Vierendeel corrisponde un aumento della deformazione trasversale ultima ri-spettivamente dell’ 8% e del 6%.

Passando invece dallo schema Vierendeel allo schema reticolare a croci di S. Andrea si ottiene un notevole effetto stabilizzante. La deformazione trasversale ultima è pari ad appena 5,2 mm. Il vantaggio nell’inserimento di aste diagonali di controvento è tale che l’instabilità locale dei pannelli di vetro precede lo sbandamento globale del corrente supe-riore della trave.

Considerazioni analoghe valgono per le analisi svolte a partire da configurazioni de-formate iniziali antisimmetriche. I grafici ad esse relativi sono riportati nelle seguenti figu-re. Rispetto ai casi precedenti si nota una generale diminuzione degli spostamenti ultimi, mentre le variazioni percentuali di spostamento tra le curve corrispondenti a diversi para-metri sono più accentuate.

Figura 5.36: andamento dello spostamento trasversale del nodo C (appartenente al corren-te superiore) in funzione del moltiplicatore dei carichi applicati, al variare dell’ampiezza della imperfezione geometrica iniziale (antisimmetrica), a parità di rigidezza trasversale ed a parità di rigidezza del controvento superiore.

0 1 2 3 4 5 6 7 8 9 0 2 4 6 8 10 12 14 16 18 mol ti p li cat or e car ic h i es te rn i spostamento [mm] Carico - Spostamento Trasversale

(Imperfezione Antisimmetrica)

L/400 - 1A - 2A

L/300 - 1A - 2A

L/200 - 1A - 2A

Figura 5.37: andamento dello spostamento trasversale del nodo C (appartenente al corrente superiore) in funzione del moltiplicatore dei carichi applicati, al variare della rigidezza tra-sversale dei nodi metallici, a parità di ampiezza dell’imperfezione geometrica (antisimmetrica) ed a parità di rigidezza del controvento superiore.

Figura 5.38: andamento dello spostamento trasversale del nodo C (appartenente al corrente superiore) in funzione del moltiplicatore dei carichi applicati, al variare della rigidezza e dello

0 1 2 3 4 5 6 7 8 9 0 2 4 6 8 10 12 14 16 18 mol ti p li cat or e car ic h i es te rn i spostamento [mm] Carico - Spostamento Trasversale

(Imperfezione Antisimmetrica) L/300 - 1A - 2A L/300 - 1B - 2A L/300 - 1C - 2A L/300 - 1D - 2A 0 1 2 3 4 5 6 7 8 9 0 2 4 6 8 10 12 14 16 18 mol ti p li cat or e car ic h i es te rn i spostamento [mm] Carico - Spostamento Trasversale

(Imperfezione Antisimmetrica) L/300 - 1A - 2A L/300 - 1A - 2B L/300 - 1A - 2C L/300 - 1A - 2D L/300 - 1A - 2E

scema statico del controvento superiore, a parità di ampiezza dell’imperfezione geometrica (antisimmetrica) ed a parità di rigidezza trasversale dei nodi metallici.