Capitolo 4 Ottimizzazione

Ottimizzazione

4.1 Modello di ottimizzazione

Il nostro obiettivo, come è noto, è quello di ottenere una configurazione di equilibrio della vela, sotto l’effetto di un sistema di carichi applicati nei nodi della griglia, che discretezza il problema. La ricerca della configurazione può essere affrontato ricorrendo a tecniche di ottimizzazione, che consentono di valutare un insieme di variabili di progetto tali da minimizzare o massimizzare una funzione obiettivo. Nel caso generale la soluzione è vincolata al rispetto di alcune condizioni, dipendenti dal problema specifico: si parla pertanto di ricerca di minimo o massimo vincolato. Il problema generale di ottimizzazione si può rappresentare nella forma:

Dove la f(x) rappresenta la funzione obiettivo da minimizzare, x l’insieme delle variabili di progetto e Gi(x) le equazioni di vincolo nella forma sia di equazioni che disequazioni.

La ricerca della configurazione di equilibrio sotto l’effetto di carichi assegnati, è stata affrontata scegliendo come funzione obiettivo il lavoro delle forze esterne e determinando la configurazione che massimizzasse la funzione in presenza solo di vincoli geometrici del tipo Gi(x) = 0. Dovendo ricondurre il problema alla ricerca di minimo nella forma sopra illustrata, la f(x) effettivamente usata è il lavoro delle forze esterne cambiato di segno. Un aspetto importante in tale processo è costituito dalla discretizzazione del problema, ovvero:

• la rappresentazione della superficie con una griglia di elementi-aste incernierate tra di loro .

• l’assegnazione di forze nei nodi di tale griglia.

• la definizione della funzione obiettivo in termini di spostamenti e carichi associati ai nodi. ) ( 2 ( ) ( ) ) ( ) 1 ( n i n p n i n i = + ⋅r ⋅G X + _λ λ

L’ipotesi di schematizzare il comportamento della vela con aste rigide inestensibili e trascurare la rigidezza a flessione della struttura [1], implica che al lavoro delle forze esterne contribuisce soltanto lo spostamento dei nodi, calcolati imponendo che la lunghezza delle aste resti costante. Questa condizione, nella forma Gi(x) = Li –L0i = 0, dove L0i è la lunghezza assegnata alla i-esima asta nella configurazione di partenza, costituisce un insieme di vincoli del problema. Un altro insieme è determinato dalle condizioni geometriche al contorno relative agli estremi delle aste appartenenti ai bordi della vela, che possono rimanere fissi o muoversi su superfici particolari. Il primo caso si riferisce alla condizione di vela inferita, ad esempio lungo l’albero o uno strallo, al vincolo dei punti di mura e penna o a un’ipotesi di lavoro per trascurare le deformazioni di un lato libero della vela. Il secondo caso invece, è quello del vincolo della bugna collegata alla scotta, quando sia libera di muoversi su una superficie sferica il cui raggio è fissato dalla lunghezza della scotta ed il centro definito dalla posizione del bozzello in assi-barca.

La ricerca di minimo può essere affrontata con diverse tecniche. È possibile scomporre il problema nella ricerca di una successione di minimi non vincolati, convergente al minimo globale della funzione obiettivo originale.

Questo approccio, noto anche come SUMT (Sequential Unconstrained Minimization Techniques), determina i minimi di una nuova funzione obiettivo F, definita secondo il metodo scelto dei moltiplicatori di Lagrange:

Si introduce un vettore dei moltiplicatori di Lagrange λ di dimensione pari al numero dei vincoli ed un coefficiente di penalizzazione rp.

La soluzione del singolo problema di ricerca di minimo locale, rappresenta il punto di partenza per la ricerca successiva. Ad ogni ricerca (n+1) corrisponde un aggiornamento dei moltiplicatori di Lagrange e del coefficiente di penalizzazione rp≤ rpmax:

[

]

(

)

∑

⋅

+

⋅

+

=

f

x

G

x

r

G

x

r

x

F

)

(

)

(

)

(

)

,

,

(

λ

λ

max se max max ) 1 ( ) 1 ( ) 1 ( ) ( ) 1 ( p n p p n p p n p n p n p r r r r r r se r r > = < ⋅ = + + + + _γ

dove γ è un coefficiente uguale a 3, come consigliato in [2].

Gli stessi parametri vengono inizializzati assegnando a rp un valore iniziale piccolo e costruendo il vettore dei moltiplicatori di Lagrange con le due possibili scelte [2]:

oppure

La successione di minimi locali converge al minimo globale della funzione obiettivo originale.

Questi minimi locali sono valutati con il metodo della metrica variabile, un metodo del primo ordine, implementato secondo le indicazioni di [2] e che si applica a problemi non vincolati. Esso rappresenta il metodo più efficiente della sua categoria e un’alternativa valida a tecniche più complesse, quali i metodi del secondo ordine (SQP). Si è ritenuto inutile sviluppare una metodologia del secondo ordine anche perché accessibile agli utenti che dispongano del pacchetto accessorio OPTIMIZATION TOOLBOX di MATLAB. Si è provveduto comunque ad impostare il programma per consentire l’uso di tali opzioni, se disponibili. me 1, i , 0 ) 0 ( _{= =} i λ me 1, i 0 ) ( ) ( se , 1 0 ) ( ) ( se , 1 ) 0 ( ) 0 ( ) 0 ( ) 0 ( ) 0 ( ) 0 ( = > ∇ • ∇ − = < ∇ • ∇ = per X f X G X f X G i i λ λ

4.2 Schema generale da implementare

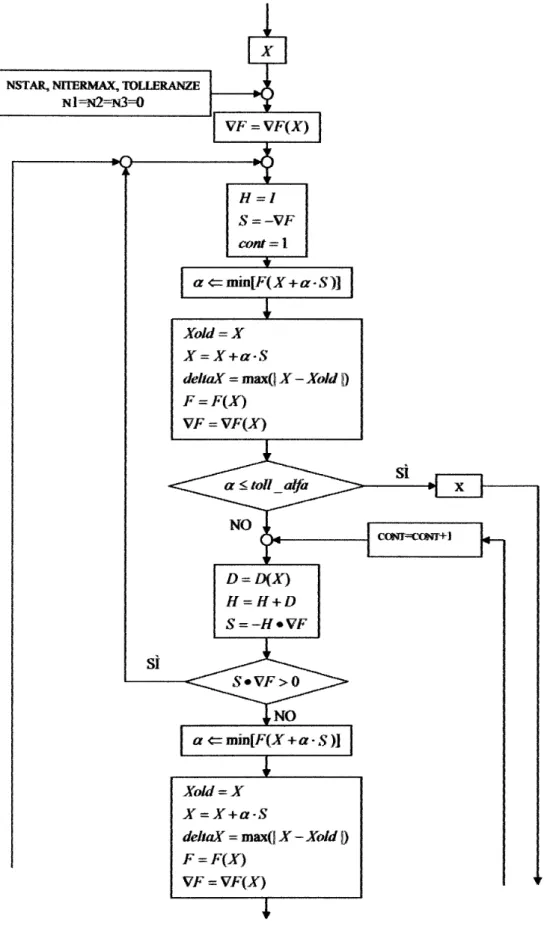
La parte relativa al calcolo della deformata è stata organizzata secondo il diagramma di flusso di seguito rappresentato. Si è evidenziata la struttura ciclica della tecnica SUMT. La configurazione X(0) rappresenta quella fornita dal velaio o la soluzione ottenuta all’iterazione precedente dal loop di calcolo. Per essa si sono calcolate le pressioni ed è stata poi assunta come condizione di lancio per la ricerca della configurazione deformata.

Come criteri di convergenza della procedura iterativa SUMT si assumono le seguenti condizioni:

• |f(X(n+1)_{) – f( X}(n)_{)| < TolFun; massima variazione ammissibile della funzione} obiettivo originale (lavoro delle forze esterne cambiato di segno) calcolata tra due iterazioni successive del ciclo SUMT.

• |Gi (X(n+1))| < TolCon, ( i = 1, me); massima violazione ammissibile dei vincoli.

4.3 Rappresentazione delle coordinate dei nodi

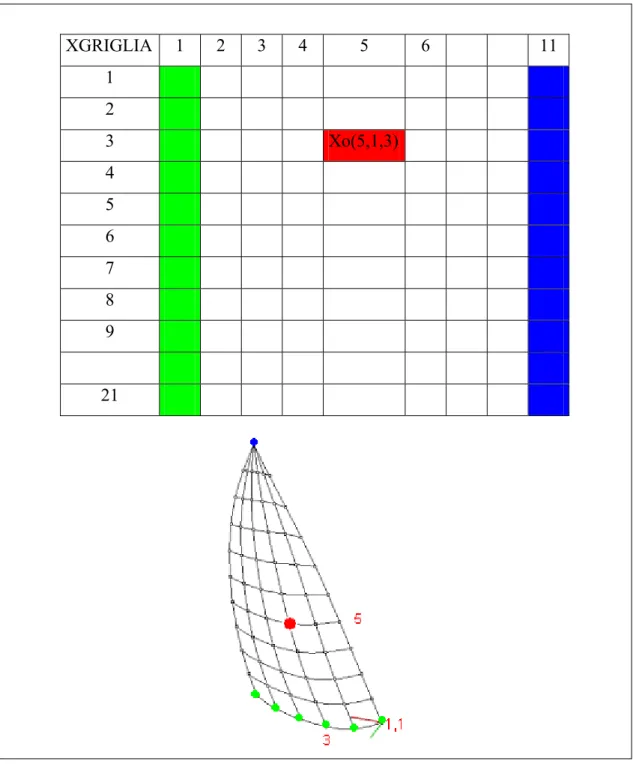
Quando si parla di griglia, ci si riferisce ad una rappresentazione come in figura 4.2. La notazione matriciale, come si è detto, prevede tre matrici, ognuna delle quali raccoglie una delle tre coordinate di tutti i nodi. Naturalmente è necessario suddividere la penna, pensandola come tanti punti coincidenti quante sono le linee verticali della griglia. Ogni colonna contiene una coordinata dei punti appartenenti alla stessa linea orizzontale, cominciando dal punto sulla ralinga. Per una griglia di 6 linee verticali e 11 orizzontali, ad esempio, il punto della matrice associato al nodo evidenziato in rosso occupa la posizione (3,5), cioè appartiene alla colonna 5 ed alla riga 3. Le coordinate complete del nodo sono [x,y,z] = [ Xgriglia(3,5), Ygriglia(3,5), Zgriglia(3,5)], estratte da tre matrici distinte.

In giallo si sono evidenziati i nodi della base, in blu quelli della penna. La prima riga corrisponde alla ralinga mentre l’ultima alla balumina.

Per trattare più efficacemente le coordinate dei nodi si sono raccolte le tre matrici in una sola. Con un ciclo for si passa alla nuova notazione x0 o xnew, indicando con x0 la matrice della configurazione per la quale si sono calcolate le pressioni, ovvero l’input iniziale del ciclo SUMT, mentre con xnew la soluzione delle successive iterazioni del ciclo SUMT.

for indlv=1:nlv % tutti i nodi strutturali

x0(:,:,indlv) = [xgriglia(indlv,:).' ygriglia(indlv,:).' zgriglia(indlv,:).'];

end

(l’apice indica l’operazione di trasposizione, nlv il numero di righe verticali della griglia).

XGRIGLIA 1 2 3 4 5 6 11 1 2 3 Xo(5,1,3) 4 5 6 7 8 9 21

Figura -4.2 Corrispondenza tra nodi e posizione nelle matrici

La struttura di x0 e xnew è assimilabile a un insieme di tante matrici sovrapposte quante sono le linee verticali della griglia. Ognuna di queste matrici, individuata dal terzo indice di x0 o xnew, è costituita da tre colonne, una per ogni coordinata, e tante righe quanti sono i nodi della linea verticale. Per analogia con la rappresentazione precedente risulta che il nodo evidenziato in rosso appartiene al livello 3 di x0 e alla riga 5, contando i nodi a partire dalla base:

X0(:,:,3) x y z 1

2 3 4

5 Xgriglia(3,5) Ygriglia(3,5) Zgriglia(3,5)

6 7 8 9 10 11

Figura –4.3 Rappresentazione con una matrice a più livelli

A seconda delle necessità si è adottata ora l’una ora l’altra rappresentazione della griglia. Questa notazione è anche quella usata per scrivere la funzione obiettivo che valuta il lavoro cambiato di segno delle forze esterne, associato al passaggio dalla configurazione x0 a quella xnew della generica iterazione del ciclo SUMT. Questa operazione è affidata alla funzione F_work, che esegue l’operazione

(

)

(

∑∑

)

(con nlh e nlv si indica il numero delle linee orizzontali e verticali della griglia, con (nx,

ny, nz)i,j il versore normale alla superficie nel generico nodo, con Pi,j il carico applicato

corrispondente, con segno positivo se concorde alla normale orientata da sopravento verso il sottovento).

4.4 Assegnazione dei carichi

La metodologia per passare dalla distribuzione di pressione associata alla mesh aerodinamica alle forze nei nodi della griglia strutturale, è la stessa utilizzata in [3]. Alcuni aspetti vengono qui riassunti per chiarezza, con le rappresentazioni originali di [3], gentilmente concesse. Le seguenti fasi sono realizzate con la function loads2.m, adattando la routine loads.m sviluppata dall’autore di [3] alla procedura iterativa:

1. la prima operazione è quella di caricare in MATLAB i file .dat delle pressioni relative alla faccia sopravento e sottovento, filtrando i dati in base al numero massimo di valori che si vogliono utilizzare. Si lancia la function limita_dati.m. 2. ci si assicura che l’ordine dei nodi della mesh aerodinamica, come è stato salvato nei

file .dat da FLUENT, sia lo stesso per le due facce della vela.

3. si esegue la differenza tra i valori di pressione statica relativi alla superficie sopravento e quelli sottovento, ottenendo per ogni nodo della mesh aerodinamica la differenza di pressione che contribuisce a generare i carichi sentiti dalla vela.

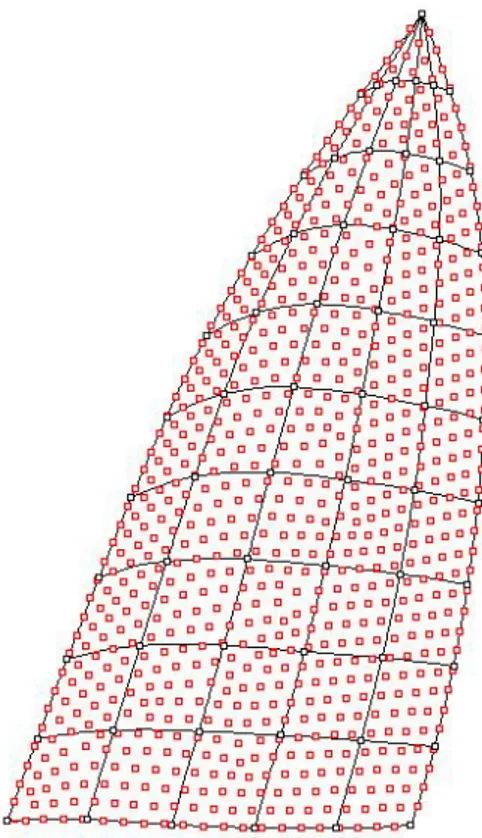
4. La griglia aerodinamica possiede un numero di nodi assai più elevato della griglia strutturale, come evidenziato dalla figura 4.4. I nodi strutturali sono rappresentati insieme ad alcuni di quelli della mesh generata in GAMBIT.

Figura -4.4 Esempio di sovrapposizione tra i nodi CFD (in rosso) e quelli della griglia strutturale 5. Per ogni vertice delle aste rigide è necessario stabilire un’area d’influenza,

associando ad ogni nodo solo l’effetto delle pressioni che agiscono dentro tale area. La superficie della vela viene ripartita tra i nodi della griglia strutturale, aggiungendo dei punti intermedi sulle aste e collegandoli tra di loro. Gli schemi della fig. 4.5 illustrano gli aspetti principali, ovvero come i nodi originali generino due nuovi nodi ciascuno, suddividendo i quadrangoli originali in due parti.

Questa condizione rappresenta il punto di partenza per creare altri nodi e dividere ulteriormente i pannelli. L’alternanza dei colori, nell’effetto finale, evidenzia meglio l’assegnazione delle aree di influenza ai vari nodi della griglia strutturale. Si nota subito come ai nodi disposti sui lati della vela corrispondano aree più piccole. Si tralasciano qui i particolari relativi alle notazioni matriciali, per i quali si rimanda a [3]. La stessa metodologia può essere utilizzata per stimare l’area della vela quando non la si conosca. A tale scopo si è scritta la routine calcolo_area.m. 6. L’operazione più corretta per assegnare ad un nodo strutturale una forza, sarebbe

quella di integrare tutti i valori di pressione del lato sopravento e di quello sottovento che cadono all’interno dell’area di influenza relativa. Si è preferito, invece, adottare un criterio semplificativo e considerare la differenza di pressione tra le due facce uniforme su tutta l’area di influenza. Ad essa si è poi assegnato il valore relativo al punto più vicino al nodo tra quelli della stessa area di influenza.

In condizioni di uso corretto della vela, la distribuzione di pressione è tale da non indurre difformità apprezzabili tra i due metodi. Una differenza potrebbe rilevarsi solo nel caso di un’area d’influenza interessata da una condizione mista, ovvero con tratti in cui la differenza di pressione agisca nel verso concorde a quello della normale alla superficie, e tratti in cui accada il contrario. La stima generata dal criterio scelto assegnerebbe al nodo una forza coerente con la differenza di pressione registrata nelle sue immediate vicinanze, e non quella che tenesse conto di un bilancio effettivo tra i due contributi di segno opposto. Il prodotto della differenza di pressione così scelta per l’area di influenza del nodo, stabilisce la forza che agisce sul nodo della griglia strutturale.

7. La direzione della forza, associata al generico nodo è quella della normale alla superficie, valutata nel nodo stesso. La normale si intende orientata dal lato sopravento verso il sottovento ed il segno della differenza di pressione è coerente con tale scelta. Le componenti delle normali alla superficie nei nodi sono valutate con il comando surfnorm disponibile in MATLAB.

8. la matrice P delle forze è costruita in modo tale che la prima riga contenga i carichi associati ai nodi della base, ordinati dall’angolo di mura verso quello di scotta; l’ultima riga i carichi associati alla penna, scomposti nei contributi delle aree dei singoli triangoli in cui gli elementi quadrangolari degenerano in prossimità della penna.

[

]

(

)

∑

⋅

+

⋅

+

=

f

x

G

x

r

G

x

r

x

F

)

(

)

(

)

(

)

,

,

(

λ

λ

4.5 Minimo non condizionato della funzione

pseudo-obiettivo F(X,

λ, rp): variable metric method

All’interno della procedura iterativa SUMT della figura 4.1 un aspetto importante è rappresentato dalla ricerca di minimo non vincolato in Rn della funzione obiettivo modificata

Anche questa ricerca particolare è sviluppata in modo iterativo, con l’ obiettivo è ottenere la matrice xnew, avente la struttura descritta precedentemente e relativa alla posizione dei nodi della griglia strutturale che minimizzano la funzione associata a dei precisi valori del fattore di penalizzazione rp e del vettore λ. Aggiornando questi ultimi, si ottiene una successione di matrici xnew, che converge alla soluzione cercata: la deformata finale della vela sotto carico.

Il metodo utilizzato per la ricerca del minimo non condizionato, come tutti i metodi del primo ordine, utilizza il gradiente della funzione F(X, λ, rp) per decidere in quale direzione cercare il minimo. La peculiarità del metodo sta nelle informazioni che vengono utilizzate per costruire questa strategia, e come esso costruisce di volta in volta il vettore

n

S∈ℜ che indica la direzione in cui cercare il minimo locale. Il diagramma di flusso della

procedura VARIABLE METRIC METHOD è stato, nella rappresentazione, suddiviso in due

parti: nella figura 4.6 relativa alla strategia di ricerca, e nella figura 4.7 che descrive il percorso decisionale attraverso l’applicazione di molteplici criteri di convergenza.

L’input del problema è costituito dalla configurazione di lancio, se si è alla prima applicazione del metodo, o la matrice xnew calcolata al passo SUMT precedente.

Nelle espressioni si è eliminata la dipendenza formale da rp e λ, perché essi si ritengono assegnati e costanti. Ciò che si modifica è la matrice X delle soluzioni provvisorie. La configurazione caricata costituisce il punto di partenza. Si illustrano di seguito le varie fasi.

1. La direzione di ricerca del minimo viene inizializzata nel modo più semplice, scegliendo di muoversi sulla superficie F(X) proprio secondo la “maggiore pendenza” S=-grad(F). Il gradiente viene rappresentato come un vettore colonna, le cui componenti sono le derivate parziali di F(X) rispetto alle coordinate dei nodi della griglia. È necessario stabilire un ordine con cui eseguire le derivate. Si è scelto di ordinare le variabili di derivazione immaginando di partire dall’angolo di mura, di scorrere lungo la ralinga fino alla penna e poi di ricominciare partendo dalla base e salendo sulla seconda linea verticale della griglia. Prima di passare al nodo successivo si esauriscono le derivate di F(X) rispetto ad x, y, z del nodo selezionato. 2. una volta noto il punto di partenza e la direzione di ricerca, il metodo risolve un

problema di ricerca di minimo monodimensionale, calcolando la variabile α che corrisponde ad un minimo locale della superficie F(X) nella direzione scelta. Tale punto, espresso come (X+α*S), rappresenta il punto di partenza per una successiva ricerca. Si aggiornano i valori di F, grad(F) e si valuta la massima variazione delle componenti di X passando dal primo al secondo punto di Rn. La ricerca di minimo monodimensionale è realizzata con il comando fminbnd di MATLAB, applicato alla function aug_lagrange_di_alfa.m.

3. se α è inferiore ad una tolleranza fissata, la ricerca si ritiene terminata ed il punto costituisce la soluzione cercata.

4. se si prosegue è necessario aggiornare la direzione di ricerca. A tale scopo si utilizza una matrice H, che alla prima iterazione coincide con l’identità, poi viene modificata aggiungendo un matrice simmetrica D, che contiene informazioni sul nuovo punto di partenza e quello precedente. Le possibili relazioni si possono trovare in [2] e [4], ed esse sono state usate nel file VMM_sumt.m nelle due forme più note: la forma BFGS e quella DFP, distinte nella loro espressione rispettivamente per il valore θ = 1 e θ = 0 di un parametro interno. La particolarità di D è quella di garantire che H sia sempre definita positiva e rappresenti un’approssimazione dell’inversa della matrice Hessiana 2 ( ).

X F

∇

5. prima di proseguire si esegue una verifica sul valore F =∇F X ⋅S

∂ ∂ ) ( ) ( α α . Se tale valore fosse positivo, esso rappresenterebbe un’indicazione di cattivo condizionamento del problema. In tal caso è necessario eseguire un restart della procedura, ponendo H = I allo scopo di limitare la propagazione dell’errore accumulato.

6. si esegue una ricerca di minimo monodimensionale in α, posizionandosi in un nuovo punto X=X+α*S di minimo locale di F.

7. si applicano i criteri di convergenza (fig. 4.7). Essi sono sostanzialmente i seguenti: a. |F(Xn+1)−F(Xn)|<TolFun

b. max(|Xn+1 −Xn |)<TolSol

c. ∇F(X)<TolGrad

La routine decidi_break_3cc.m è in grado di riconoscere diverse eventualità e restituire al programma dei parametri sulla base dei quali decidere un percorso: il numero di volte consecutive che un criterio è stato soddisfatto (rispettivamente N1, N2, N3 per a, b, c), e un valore indicato come codice. Se un criterio viene soddisfatto più volte consecutivamente il parametro n corrispondente si aggiorna, ma non appena il criterio non è soddisfatto il parametro viene azzerato. La variabile codice assume invece tre valori:

• codice = 1, si sono esaurite le iterazioni a disposizione, la procedura si interrompe all’ultima soluzione X trovata.

• codice = 2, un criterio è stato soddisfatto un numero di volte consecutive pari a Nstar. Può accadere infatti che un criterio soddisfi rapidamente la condizione imposta, mentre un altro converga più lentamente o addirittura oscilli senza soddisfare la tolleranza imposta. In tal modo si evita di continuare a calcolare soluzioni che si sono stabilizzate ma non possono soddisfare la precisione richiesta.

• Codice = 0, nessuno dei due casi precedenti si è verificato.

8. la combinazione codic = 0 AND N1>0 AND N2>0 AND N3>0 significa che allo stato attuale tutti i criteri sono stati soddisfatti almeno una volta. Se questo si verifica per la prima volta, si effettua un restart, ovvero si ripete la procedura inizializzando la matrice H con la matrice identità, per verificare che il risultato non sia l’effetto della propagazione dell’errore. Se tale condizione si verifica per due volte consecutive, si ritiene di avere trovato la soluzione e si esporta la configurazione X nel processo SUMT.

9. se il punto 8 non è soddisfatto si danno altre due condizioni:

a. La prima consiste nel verificare che la funzione di cui si sta cercando il minimo effettivamente decresca tra due iterazioni successive. In caso contrario, si esegue un restart, interrompendo l’aggiornamento della matrice H che viene inizializzata con la matrice identità.

b. Si verifica che le iterazioni attivate dopo l’ultimo restart non superino un valore limite stabilito a priori ed indicato con Nrestart.

Una struttura delle verifiche così articolata è stata sviluppata per contenere l’errore numerico e per gestire tutte quelle situazioni che potrebbero aumentare inutilmente il tempo di calcolo. Sempre per limitare l’errore si è proceduto a definire esplicitamente la funzione , dopo aver definito in forma esplicita anche le equazioni di vincolo G(X) associate a tutte le condizioni al contorno possibili per una vela. Un’alternativa è rappresentata dal metodo delle differenze finite, sconsigliato sia in [2] che [4] quando le funzioni derivate sono facilmente ricavabili, proprio per non introdurre una causa di errore.

) (X

F

∇

Durante l’esecuzione del programma, ogni iterazione della procedura generale SUMT è caratterizzata da un numero variabile di ripetizioni del metodo appena descritto per la ricerca di minimo incondizionato. Per ciascuna di esse vengono visualizzati su una stessa riga i valori relativi a:

• Numero iterazione • α

• F(X)

• i tre criteri di convergenza sopra descritti nei punti 7.a, 7.b, 7.c • ∇F(X)⋅S

Quando l’applicazione del metodo della metrica variabile converge vengono riassunti i valori più importanti. L’intera storia di calcolo può essere analizzata nel file storia_calcolo_gennaker.txt che viene salvato ad ogni applicazione della procedura di analisi della deformata nel loop di calcolo principale.

Le funzioni f(X) e F(X), i vincoli e i relativi gradienti, sono valutati con function dedicate: • f_work.m • vincoli_miei.m • grad_vincoli_def.m • aug_lagrange • grad_auglm

ITERAZIONE DEL LOOP DI CALCOLO PRINCIPALE: 1 griglia per il calcolo della deformata:

linee orizzontali: 11 linee verticali : 11

VINCOLO GEOMETRICO DELLA VELA:

VELA TRIANGOLARE: ANGOLI DI PENNA, MURA E SCOTTA VINCOLATI: VINCOLO GEOMETRICO PER L'ANGOLO DI SCOTTA:

ANGOLO DI SCOTTA VINCOLATO A MUOVERSI SULLA SFERA CENTRATA NEL PUNTO DI SCOTTA COORDINATE DEL PUNTO DI SCOTTA IN ASSI BARCA E LUNGHEZZA SCOTTA:

x= 4800.000 (mm) y= 1600.000 (mm) z= 500.000 (mm) Lscotta= 1200.000 CARICHI NEI NODI (N):

4.37 6.03 4.65 3.81 3.46 3.12 2.62 2.29 2.04 1.88 1.06 7.81 12.16 10.67 9.18 8.17 7.06 6.11 5.43 4.86 4.33 1.91 6.89 10.58 10.18 9.68 8.52 7.14 6.17 5.48 4.88 4.28 1.87 6.89 10.09 9.46 9.31 8.54 7.22 6.20 5.48 4.85 4.34 1.91 7.08 9.77 8.66 8.39 8.13 7.19 6.14 5.44 4.89 4.33 1.78 6.96 8.80 7.59 7.30 7.29 6.78 5.98 5.33 4.73 4.26 1.78 5.97 7.51 6.43 6.14 6.23 6.11 5.70 5.14 4.55 4.14 1.77 5.11 6.61 5.47 5.24 5.29 5.32 5.21 4.85 4.41 3.90 1.73 3.93 5.52 4.68 4.36 4.21 4.13 4.00 3.79 3.55 3.25 1.47 2.17 3.45 3.03 2.73 2.53 2.43 2.30 2.20 2.08 1.98 0.94 0.28 0.55 0.55 0.54 0.53 0.53 0.52 0.51 0.50 0.49 0.25 TOLLERANZE SCELTE: TolFun = 2 (N*mm) TolCon = 0.01 (mm) TolGrad = 0.1 (N) TolSol = 0.01 (mm) TolAlfa = 1e-006 max iter.= 500 NStar = 150 Nrestart= 100

INITIAL PENALTY PARAMETER RP = 0.4 RP MASSIMO = 1e+005

COEFF. GAMMA PER L'AGGIORNAMENTO DI RP E LAMBDA = 3.0

---- SEQUENTIAL UNCONSTRAINED MINIMIZATION TECHNIQUES ----

---

ITERAZIONE SUMT N°: 1

---

---- VARIABLE METRIC METHOD CON TETA = 1 AL PASSO SUMT N°: 1 ---- iter min_alfa F_pseudo_ob c1=F_new-F_old c2=delta_x c3=|max(grad(F))| SLOPE

0 ***** 143917.43 0.00e+000 0.00e+000 420.43 DATI INIZIALI 1 276.89392 63151.98 -8.08e+004 2.77e+002 212.23 S = -grad(F) 2 196.94745 36102.23 -2.70e+004 1.97e+002 144.19 -275.18 3 133.95222 20440.37 -1.57e+004 1.34e+002 100.57 -235.60 4 105.31741 7398.48 -1.30e+004 1.05e+002 81.37 -248.05 5 98.15655 -4495.98 -1.19e+004 9.82e+001 73.65 -243.15 6 82.36752 -15237.10 -1.07e+004 8.24e+001 57.06 -261.61 7 89.84736 -26996.08 -1.18e+004 8.98e+001 41.16 -259.79

166 0.01006 -345863.45 -3.74e-004 1.01e-002 0.00 -0.07 167 0.01218 -345863.45 -3.72e-004 1.22e-002 0.00 -0.06 168 0.00955 -345863.45 -3.10e-004 9.55e-003 0.00 -0.06

169 0.00225 -345863.45 -1.38e-004 2.25e-003 0.00 S = -grad(F) 170 0.00357 -345863.45 -1.43e-004 3.57e-003 0.00 -0.08

DA MIN_VAR_METRIC : CRITERI DI CONVERGENZA SODDISFATTI

---

RISULTATI PARZIALI SUMT ---

numero iterazione = 1

lavoro_new = -511817.0233 (N*mm) (lavoro_new - lavoro_old) = -511817.0233 (N*mm) massima violazione vincoli = 236.3738 (mm) max(abs(xxnew-xxold)) = 0.0035716 (mm) max(|grad_F_lagrangiana|) = 0.0027816 (N) --- --- ITERAZIONE SUMT N°: 2 ---

---- VARIABLE METRIC METHOD CON TETA = 1 AL PASSO SUMT N°: 2 ---- iter min_alfa F_pseudo_ob. c1=F_new-F_old c2=delta_x c3=|max(grad(F))| SLOPE

0 ***** 293424.16 0.00e+000 0.00e+000 33.69 DATI INIZIALI 1 260.61772 178408.84 -1.15e+005 2.61e+002 97.76 S = -grad(F) 2 67.02256 144259.67 -3.41e+004 6.70e+001 78.40 -1018.27 3 72.33129 109930.58 -3.43e+004 7.23e+001 79.39 -948.82 4 71.57318 77042.08 -3.29e+004 7.16e+001 123.69 -915.60 5 67.80441 47333.45 -2.97e+004 6.78e+001 104.78 -872.40 6 61.81299 19634.27 -2.77e+004 6.18e+001 124.47 -892.08 7 45.27788 362.33 -1.93e+004 4.53e+001 105.14 -849.78 8 41.26500 -14837.65 -1.52e+004 4.13e+001 100.54 -736.60 9 40.15544 -28969.39 -1.41e+004 4.02e+001 72.01 -704.58 10 23.67820 -36205.82 -7.24e+003 2.37e+001 47.33 -611.61 11 32.97695 -44417.03 -8.21e+003 3.30e+001 45.10 -498.15 12 25.52885 -49540.87 -5.12e+003 2.55e+001 43.65 -401.72 13 28.91953 -54562.78 -5.02e+003 2.89e+001 53.60 -347.55 14 29.90895 -59552.97 -4.99e+003 2.99e+001 55.58 -334.37 15 50.16811 -68149.35 -8.60e+003 5.02e+001 44.29 -343.74 16 51.84633 -77867.84 -9.72e+003 5.18e+001 56.91 -375.39 17 20.46746 -82504.16 -4.64e+003 2.05e+001 41.04 -454.20 18 23.65482 -86901.50 -4.40e+003 2.37e+001 30.94 -372.98

Si nota come per ottenere la convergenza della prima iterazione del ciclo SUMT (fig. 4.1), sia stato necessario applicare 170 volte la ricerca di minimo monodimensionale secondo lo schema del metodo della metrica variabile (fig. 4.6 e 4.7).

La configurazione trovata non rispetta i criteri di convergenza sulla funzione obiettivo originale non modificata (-1* lavoro delle forze esterne) e sulla violazione dei vincoli, perciò la procedura SUMT attiva una seconda volta la ricerca di una soluzione.

4.6 Scelta dei vincoli

Le scelte disponibili per simulare le condizioni di vincolo della vela sono selezionabili dall’interfaccia grafica relativa alla definizione del calcolo strutturale e prevedono i seguenti casi:

• Ralinga e base non deformabili. • Ralinga non deformabile e:

o Base libera e angolo di scotta fisso

o Base libera e angolo di scotta mobile ma vincolato sulla superficie sferica definita da:

Posizione bozzello in assi barca Lunghezza della scotta

• Bugne vincolate. Penna e mura fisse e: o Angolo di scotta fisso

o Angolo di scotta mobile ma vincolato su superficie sferica definita da: Posizione bozzello

Lunghezza scotta

Quando si vincola un intero lato della vela le equazioni di vincolo sono lineari e stabiliscono che le tre coordinate di ogni nodo siano costanti. Da questa condizione si ottiene anche il rispetto dell’inestensibilità delle aste appartenenti al bordo, vincolo che non può essere aggiunto esplicitamente per evitare la ridondanza delle condizioni ed un numero di equazioni (F(X) e vincoli G(X)) superiore alle incognite (coordinate [x y z] di tutti i nodi). Nel caso dell’angolo di scotta libero di muoversi su una superficie sferica, l’equazione è una sola e non lineare, ed impone che la distanza tra la bugna ed il bozzello resti costante ed uguale alla lunghezza di scotta assegnata.

4.7 Bibliografia

[1] T. Charvet, F. Hauville, S. Huberson, Numerical evaluation of the

flow over sails in real sailing conditions, Journal of Wind

Engineering and Industrial Aerodynamics 63 (1996) 111 - 129

[2] G. N. Vanderplaats, Numerical Optimization Techniques For

Engineering Design, McGraw Hill Book Company,1984

[3] M. Scarponi, Progettazione di vele per imbarcazioni da diporto (2003), Tesi di laurea in Ingegneria Meccanica, Università degli Studi di Perugia

[4] M. Minoux, Mathematical Programming. Theory and Algorithms,

John Whiley And Sons, 1986

[5] Matlab 6 Reference Guide, The MathWorks Inc., Natick (MA),