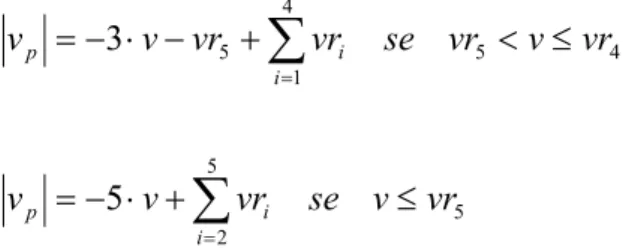IV.2
Andamento della potenza spesa in funzione della velocità della
capsula e del numero di zampe
Ci sono alcune considerazioni piuttosto importanti che devono essere fatte per l’ottimizzazione del moto della capsula.
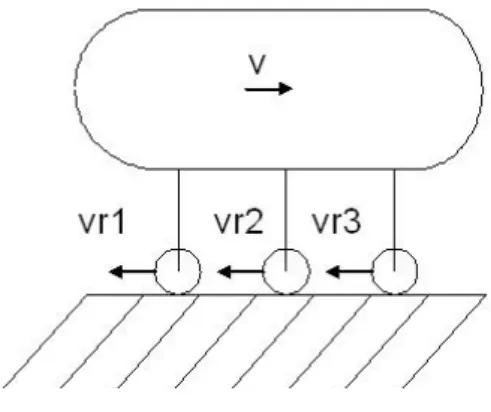
Il dispositivo sia in movimento con velocità pari a v su un supporto.
Si vuole capire come varia la potenza totale spesa dal sistema endoscopico in funzione del numero N di zampe e di v. Si indica con vri la velocità relativa dell’i-esima articolazione rispetto alla superficie di appoggio.
Capsula con due zampe:
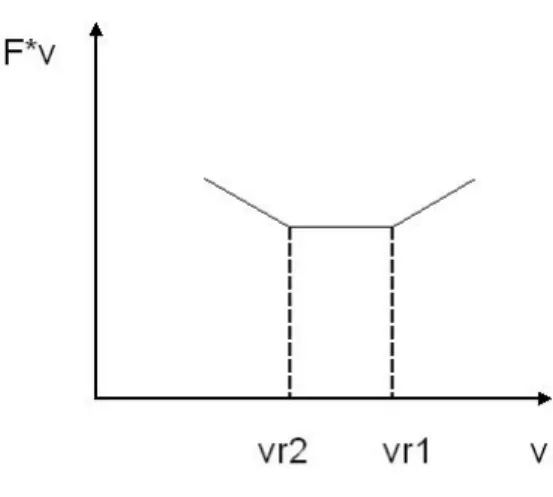
Fig. IV.2 Capsula a due zampe
Senza perdere di generalità sia vr1>vr2.
Se F è la forza che permette il moto del meccanismo la potenza complessiva necessaria può essere scritta nella forma:
2 2 1 1 v F v F v F⋅ p = ⋅ + ⋅
2 2 1 1 vr v v vr v v − = − =
E dato che F può essere ritenuta una costante:
2 1 1 2 2 1 1 2 1 2 2 vr v se vr vr v v vr v vr se vr vr v vr v se vr vr v v p p p < + + ⋅ − = ≤ ≤ − = > − − ⋅ =
I risultati sopra scritti permettono di tracciare il seguente grafico:
Fig. IV.3 Andamento della potenza in funzione di v con 2 zampe
Esiste cioè una zona, quella compresa tra vr1 e vr2, nella quale il dispositivo si porta a lavorare in una configurazione di dispendio minimo per il moto.
Il ragionamento è esattamente analogo al precedente salvo per il fatto che devono essere presi in considerazione anche i termini relativi ad una terza zampa:
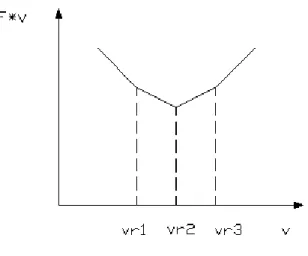
Fig. IV.4 Capsula a tre zampe
Ancora senza perdere di generalità si suppone vr1>vr2>vr3.
Le equazioni che governano il problema in questione in questo caso sono:
3 3 2 1 2 3 3 2 1 1 2 3 2 1 1 3 2 1 3 3 2 2 1 1 3 3 vr v se vr vr vr v v vr v vr se vr vr vr v v vr v vr se vr vr vr v v vr v se vr vr vr v v v F v F v F v F p p p p p ≤ + + + ⋅ − = ≤ < − + + − = ≤ < − − + = > − − − ⋅ = ⋅ + ⋅ + ⋅ = ⋅
Fig. IV.5 Andamento della potenza in funzione di v con 3 zampe
Anche in questo caso le forze sono supposte costanti.
Il sistema a tre zampe ha un minimo in corrispondenza della velocità vr2.
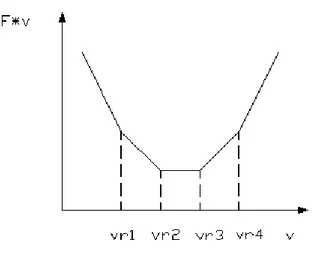
Capsula con quattro zampe: Posto vr1> vr2> vr3> vr4 si ha: 4 4 1 3 4 3 1 1 2 3 4 3 2 1 1 2 4 2 1 1 4 1 4 4 3 3 2 2 1 1 4 2 2 4 vr v se v vr v vr v vr se vr vr v v vr v vr se vr vr v vr v vr se vr vr v v vr v se vr v v v F v F v F v F v F i i p i i p i i i i p i i p i i p p ≤ ⋅ − = ≤ < + − ⋅ − = ≤ < − = ≤ < − + ⋅ = > − ⋅ = ⋅ + ⋅ + ⋅ + ⋅ = ⋅
∑
∑
∑
∑
∑
∑
= = = = = =Per un andamento complessivo che supponendo le forze costanti dà:
Fig. IV.6 Andamento della potenza in funzione di v con 4 zampe
Ricompare la zone di minimo, questa volta tra le velocità relative vr2 e vr3.
Capsula con 5 zampe:
Posto vr1> vr2> vr3> vr4> vr5 si ha: 3 4 5 4 3 1 2 3 5 3 2 1 1 2 5 2 1 1 5 1 5 1 3 5 vr v vr se vr vr v v vr v vr se vr vr vr v v vr v vr se vr vr v v vr v se vr v v v F v F i i i i p i i p i i p i i p i i i p ≤ < − + − = ≤ < − + + = ≤ < − + ⋅ = > − ⋅ = ⋅ = ⋅
∑
∑
∑
∑
∑
∑
= = = = = =5 5 2 4 5 4 1 5 5 3 vr v se vr v v vr v vr se vr vr v v i i p i i p ≤ + ⋅ − = ≤ < + − ⋅ − =
∑
∑
= =Per un andamento complessivo che supponendo le forze costanti dà:
Fig. IV.7 Andamento della potenza in funzione di v con 5 zampe
Il minimo si ha in corrispondenza della velocità vr3.
A questo punto si può quindi generalizzare il ragionamento osservando che esistono due possibili situazioni. La prima è relativa ad un numero pari di zampe, la seconda ovviamente ad uno dispari.
Capsula con N pari zampe:
Si fanno le solite ipotesi, cioè vr1>vr2>….>vrN e forze costanti:
∑
= ⋅ = ⋅ N i i i p F v v F 1(
)
( ) N N i i p N N N N i i N i i p N i i p N i i p vr v se vr v N v vr v vr se vr vr v vr v vr se vr vr v N v vr v se vr v N v ≤ + ⋅ − = ≤ ≤ − = ≤ ≤ + − ⋅ − = > − ⋅ =∑
∑
∑
∑
∑
= + + = = = = 1 1 2 / 2 / 1 2 / 2 / 1 1 2 2 1 1 1 ... ... 2Da cui si può costruire il diagramma:
Fig. IV.8 Andamento della potenza in funzione di v con N pari zampe
Da cui la possibilità di concludere che esiste una zona di potenza minima compresa tra i valori di v che vanno da vr(N/2-1) a vr(N/2).
Si fanno le solite ipotesi, cioè vr1>vr2>….>vrN e forze costanti:
(
)
( ) N N i i p N N N N i i N i i p N i i p N i i p N i i i p vr v se vr v N v vr v vr se vr vr v v vr v vr se vr vr v N v vr v se vr v N v v F v F ≤ + ⋅ − = ≤ ≤ − + = ≤ ≤ + − ⋅ − = > − ⋅ = ⋅ = ⋅∑
∑
∑
∑
∑
∑
= + + = = = = = 1 1 2 / 2 / 1 2 / 2 / 1 1 2 2 1 1 1 1 ... ... 2Da cui si può costruire il diagramma:
Da cui la possibilità di concludere che esiste un minimo per v pari a vr(N/2).
Si noti inoltre che diagramma sopra riportato per N sufficientemente grande può essere approssimato con buona precisione con una parabola.