CAPITOLO 5
STRUMENTI DI GEOSTATISTICA PER L’AIUTO ALLE
DECISIONI
5.1 INTRODUZIONE
In un processo di aiuto alle decisioni multicriteri di tipo territoriale, dove il ruolo della componente spaziale è fondamentale, sia per la costruzione e la standardizzazione delle mappe dei criteri di valutazione, che per la rappresentazione geografica delle alternative decisionali, il supporto della geostatistica risulta ormai essenziale.
Nella maggior parte dei problemi decisionali reali che interessano la pianificazione del territorio, gli strati informativi (map layers), che devono essere elaborati tramite una specifica regola decisionale multicriteri, difficilmente sono disponibili in forma “completa ed esaustiva” (in termini di estensione geografica, formato, livello di disaggregazione, grado di accuratezza e di aggiornamento etc) per essere direttamente processati tramite una procedura a criteri multipli.
Diventa, pertanto, cruciale la conoscenza di metodi di analisi spaziale e di geostatistica, sia univariata che multivariata, i cui aspetti fondamentali vengono descritti nel presente capitolo, proprio nell’ottica di individuare tecniche capaci di supportare un processo di valutazione a criteri multipli di tipo territoriale.
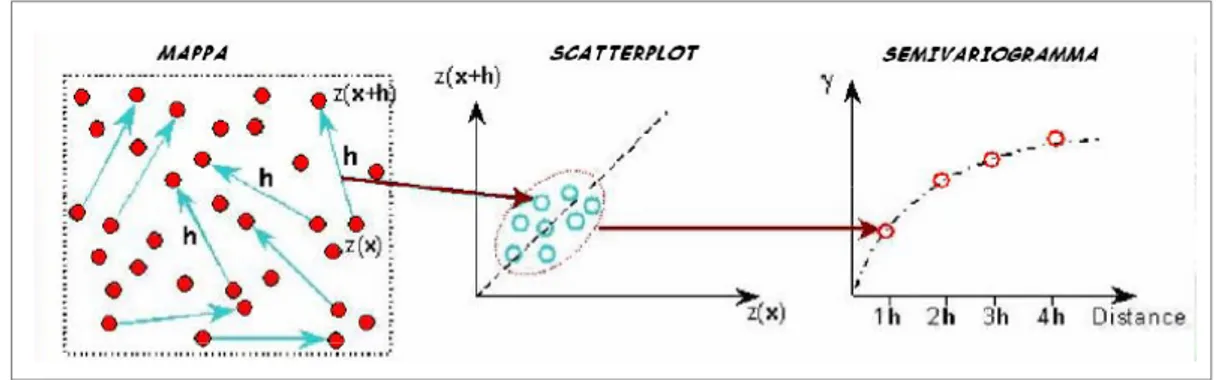
La prima parte del presente capitolo è, quindi, incentrata sullo studio dei metodi di analisi univariata in cui il focus dell’indagine è rivolto all’approfondimento di tecniche capaci di misurare la distribuzione territoriale delle informazioni campionate (ad esempio tramite opportune misure di densità) e di analizzare la struttura dei dati in termini di autocorrelazione spaziale. Quest’ultima può essere, infatti, quantificata mediante opportuni indici (sia globali che locali), descritta tramite grafici adeguati (ad esempio il variogramma) e modellata per mezzo di specifiche funzioni matematiche che consentono un processo di interpolazione più robusto ed adeguato (ad esempio il Kriging) capace di stimare, su tutto il territorio dell’area di studio, la distribuzione spaziale di ogni variabile e di calibrare la stima sulla base delle informazioni contenute nei punti di misura.
La seconda parte del capitolo approfondisce, invece, alcuni aspetti salienti relativi all’analisi geostatistica di tipo multivariato che, in un processo di analisi multicriteri spaziale, si rende necessaria allorché si voglia investigare il grado di correlazione spaziale fra i “criterion maps”. Questa analisi è finalizzata a comprendere se sia possibile individuare un set di criteri, fra loro indipendenti, capaci di sintetizzare la maggior parte della varianza del dataset iniziale ed a determinare aree spazialmente omogenee (cluster spaziali multivariati) sulla base della distribuzione territoriale dei valori congiuntamente assunti dal set dei criteri.
5.2 ANALISI GEOSTATISTICA UNIVARIATA
5.2.1 Autocorrelazione Spaziale
L’autocorrelazione spaziale è il termine tecnico che esprime il concetto secondo cui
oggetti spazialmente vicini hanno una maggiore probabilità di avere proprietà simili rispetto ad elementi fra loro distanti. In sostanza l’autocorrelazione spaziale misura
quanto oggetti spazialmente vicini siano fra loro simili (figura 5.1).
Molti fenomeni territoriali possono essere descritti in termini di caratteristiche locali simili di un evento che varia nello spazio: le città sono concentrazioni di popolazione ed all’interno di un aggregato urbano si possono individuare attività residenziali, economiche o distinguere zone di diversità sociale. Anche da un punto di vista ambientale, variabili quali il clima, le condizioni atmosferiche o la morfologia di un territorio rappresentano pattern (strutture) di omogeneità spaziale; ma fino a che limite si estende tale omogeneità spaziale e come è possibile misurala?
Figura 5.1 Autocorrelazione spaziale: a) raggio dell’intorno, b) variazione del fenomeno con la distanza
Aumentando il grado di approfondimento dell’analisi si può dire che ogni set di dati spaziali possiede, con buona probabilità, distanze o lunghezze “caratteristiche”all’ interno delle quali individuare la proprietà di “self-correlazione” o meglio di autocorrelazione. In generale, in base alla “prima legge della geografia” di Tobler secondo cui:
“Everything is related to everything else, but near things are more related than distant things”(Tobler, 1970).
l’autocorrelazione ha maggiore probabilità di verificarsi e di essere pronunciata a brevi distanze. L’analisi dell’ autocorrelazione spaziale fra i dati territoriali e lo studio della localizzazione delle porzioni di territorio dove tale fenomeno si manifesta con maggiore forza sono aspetti di fondamentale importanza per la comprensione di un fenomeno territoriale. L’esistenza dell’autocorrelazione spaziale aumenta la complessità dell’analisi del fenomeno, innanzitutto perché si assume implicitamente che la distribuzione spaziale degli elementi non sia completamente “random”, il che impedisce l’applicazione di statistiche di tipo convenzionale. Gli usuali parametri di stima statistica, basati sull’assunzione che il campione abbia distribuzione assolutamente casuale, quando
applicati a dati di tipo spaziale possono essere influenzati dai valori prevalenti (dovuti all’autocorrelazione) assunti dai dati campionati nella regione di studio.
Un altro elemento di riflessione è legato al fatto che l’ autocorrelazione spaziale introduce
ridondanza nei dati e pertanto all’ aggiunta di informazioni addizionali non consegue un
incremento sostanziale di conoscenza strutturata del fenomeno in esame.
Per questo motivo a monte di qualsiasi modellazione del processo vengono effettuate misure diagnostiche di autocorrelazione quali la costruzione degli indici di Moran e Geary o l’analisi variografica, come descritto in dettaglio nei paragrafi seguenti.
Nello studio dell’autocorrelazione ci sono, in generale, tre possibilità: autocorrelazione positiva, negativa o nulla.
Si parla di autocorrelazione spaziale positiva o attrazione quando valori simili di una variabile tendono a raggrupparsi in prossimità l’uno dell’altro (formazione di clusters), viceversa, si parla di autocorrelazione spaziale negativa o repulsione quando valori simili di una variabile tendono ad essere dispersi sul territorio.
Il concetto di autocorrelazione nulla è equivalente invece a quello di indipendenza: gli eventi di una distribuzione si dicono infatti indipendenti se tra loro non sussiste alcun tipo di relazione spaziale che condiziona la posizione degli eventi stessi, pertanto le osservazioni variano in modo casuale nello spazio.
La descrizione e la modellazione di pattern di variazione del fenomeno nella regione di studio considerata, cioè l’analisi della struttura di autocorrelazione può essere condotta considerando due tipologie di variazione spaziale: di primo e di secondo ordine.
Si parla di variazioni spaziali del primo ordine quando le osservazioni nell’area di studio variano in funzione dei cambiamenti delle proprietà globali della porzione di territorio in esame (es: dimensione dell’aggregato urbano, densità della popolazione, concentrazione di attività industriali o commerciali etc.), mentre le variazioni spaziali del secondo ordine sono riconducibili principalmente ad interazioni di tipo locale fra le osservazioni (es: la concentrazione di specifiche attività commerciali sarà maggiore in prossimità di nuclei urbani storici etc.). Molti scienziati, afferenti al campo della geografia quantitativa e della pianificazione territoriale, hanno sviluppato approcci analitici allo studio dell’autocorrelazione con la volontà di fornire della basi più oggettive per decidere la presenza o meno di pattern spaziali ed, in caso affermativo, con l’intento di studiarne la natura e le radici, elementi necessari per la comprensione della struttura del territorio in esame.
Il concetto di autocorrelazione spaziale può essere applicato a qualsiasi tipologia di dato spaziale (punti, linee, poligoni) anche se la letteratura fornisce strumenti di analisi più facilmente applicabili ad informazioni territoriali aventi struttura geometrica puntuale o areale . In entrambi i casi si assume che la variabile di cui si voglia studiare il pattern (es: densità di popolazione, produzione di rifiuti, quota del territorio, qualità dell’aria, tipo
di uso del suolo etc.) sia memorizzata come attributo alfanumerico (field) del dato di primitiva geometrica puntuale oppure poligonale.
5.2.2 Point Pattern Analysis
L’analisi denominata “Point Pattern” comprende una varietà di metodi e tecniche usate per analizzare le proprietà delle distribuzioni dei punti al fine di studiare come determinati eventi siano disposti sul territorio.
Un “point pattern” consiste in un insieme di eventi puntuali localizzati spazialmente in una data regione di studio (O’Sullivan ed Unwin, 2003); ciascun evento rappresenta una singola istanza del fenomeno di interesse (es: localizzazioni di immobili, di crimini, di rilevamenti archeologici, di incidenti, di servizi alla popolazione etc).
La disposizione dei punti nello spazio può essere ricondotta ad una delle seguenti tipologie: casuale quando la posizione di ogni punto è indipendente dalle altre, regolare quando i punti sono distribuiti uniformemente nello spazio, raggruppata quando i punti sono concentrati in determinate zone dello spazio (clusters).
Il focus della Point Pattern Analysis è rivolto quindi ad individuare e descrivere se i punti corrispondenti agli eventi analizzati si distribuiscono secondo un determinato “pattern” spaziale in modo da testare se vi sia o meno una concentrazione di eventi, cioè un “clustering”, in specifiche porzioni dell’area di studio.
Per analizzare e descrivere il pattern spaziale che gli eventi puntuali descrivono nel territorio si fa riferimento ad una varietà di metodi che possono essere ricondotti a quattro famiglie principali :
Misure o statistiche di tipo descrittivo che forniscono una descrizione di sintesi della
distribuzione spaziale dei punti;
Metodi basati sulla densità in cui si esaminano le variazioni di intensità del processo nello spazio, cioè gli effetti del primo ordine in cui la posizione assoluta dei punti è determinante nell’analisi;
Metodi basati sulla distanza in cui si misurano gli effetti del secondo ordine dove è importante studiare l’interazione fra la posizione dei punti che dipende dalla distanza relativa.
Metodi basati su distribuzioni statistiche
Si analizzano in maggiore dettaglio le principali tecniche appartenenti a ciascun gruppo sopra identificato.
5.2.2.1 Analisi basate su statistiche centrografiche di tipo descrittivo
Queste tecniche forniscono una descrizione sintetica della distribuzione nello spazio dei punti S= (s1, s2, …si….sn) nella regione di interesse A di area a in cui ricade la numerosità
Ciascun evento “i” è individuato da un vettore si, ovvero dalle sue coordinate xi e yi che
sono le uniche informazioni strettamente necessarie per l’analisi del pattern, mentre opzionale è l’assegnazione ai punti di attributi aggiuntivi, quali il peso wi, che rappresenta
l’importanza relativa di ciascun evento, oppure l’intensità ii che indica la magnitudo del
fenomeno in esame.
Questa classe di semplici indici per la descrizione delle caratteristiche generali della distribuzione e delle sue proprietà del primo ordine è, di fatto, l’equivalente bidimensionale dei momenti di base di una distribuzione statistica monodimensionale: media, deviazione standard, indice di asimmetria.
In primo luogo può essere calcolato il cento medio (mean center) o centro di gravità del point pattern:
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
µ
µ
=
∑
=1∑
=1n
y
,
n
x
)
,
(
s
n i i n i i y x [5.1]Quindi
s
è il punto le cui coordinate sono la media delle corrispondenti coordinate degli eventi del pattern, mentre per tener conto di un eventuale peso wi associato agli eventi,può essere calcolato un centro di gravità pesato:
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
µ
µ
=
∑
=1∑
=1n
y
w
,
n
x
w
)
,
(
s
n i i i n i i i y x w [5.2]È possibile poi calcolare la deviazione standard
σ
del pattern che misura la dispersione del pattern rispetto ai valori medi di xi ed yi:⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
1
−
µ
−
1
−
µ
−
=
σ
σ
=
σ
∑
=1∑
=1,
)
n
(
)
x
(
,
)
n
(
)
x
(
)
,
(
n i i x n i i x y x [5.3]Viene poi computata la distanza standard del dataset puntuale che fornisce una misura di quanto dispersi siano gli eventi rispetto al centro medio della distribuzione.
n
)
y
(
)
x
(
d
n i i x i y∑
=1 2 2+
−
µ
µ
−
=
[5.4]Le misure di distanza standard e centro medio possono essere impiegate simultaneamente per plottare un cerchio di sintesi (summary circle) del point pattern che sarà centrato in
s
ed avrà raggio d.Elaborazioni più complesse sulle coordinate degli eventi possono essere effettuate computando la distanza standard separatamente per ciascun asse : in questo caso sarà possibile plottare un’ellisse di sintesi del point pattern che avrà centro nel centro di gravità dei punti e semiassi pari alle distanze standard lungo ciascun asse. Attraverso questa misura è possibile studiare se una distribuzione è più dispersa in una direzione piuttosto che in un’altra, sia cioè se presenta un’anisotropia di cui vengono espressi il grado e la direzione .
5.2.2.2 Misure basate sulla densità
Gli approcci basati sulla densità caratterizzano la distribuzione spaziale dei punti in termini di proprietà del primo ordine: stimano cioè il modo con cui l’intensità del fenomeno varia nella regione di studio.
È possibile innanzitutto determinare un densità semplice detta anche Densità
Complessiva del point pattern attraverso la seguente espressione:
a
)
A
S
(
n
a
n
)
s
(
=
=
°
∈
λ
[5.5]dove n°(S∈ A) è il numero degli eventi del pattern S che ricadono nella regione di studio A di area a. Un aspetto critico di questa misura risiede nella sensitività connessa alla definizione dell’area di studio all’interno della quale contare gli eventi.
Quando la distribuzione dei punti è sostanzialmente omogenea il valore di λ rimane piuttosto stabile dato che, all’aumentare dell’area a, aumenterà in proporzione anche il numero dei punti che cadono al suo interno; viceversa questo aspetto diventa assai problematico quando la distribuzione dei punti non è omogenea e lo sforzo è rivolto al calcolo di una densità locale (figura 5.2).
Figura 5.2 Misure di densità locale al variare della definizione dell’area di studio (O’Sullivan e Unwin, 2003).
Una maniera più articolata per calcolare l’intensità di un fenomeno puntuale è quello di computare il numero di eventi del pattern che ricadono in un set di elementi regolari, generalmente celle di dimensione quadrata, dette “quadrats” aventi una dimensione fissa. Tali metodi detti Quadrat Counts Methods misurano la densità del fenomeno in relazione alla distribuzione di frequenza osservata, cioè in base al modo in cui la densità dei punti stessi varia nell’area studiata. In pratica si tratta di creare un istogramma di frequenza bidimensionale relativo alla distribuzione di frequenza dei dati osservati (Bailey e Gatrell, 1995).
Il calcolo della densità in ciascuna cella può essere fatto o attraverso un censimento esaustivo dei quadrats che in questo caso ricopriranno completamente l’area di studio (griglia regolare), oppure posizionando in maniera random i quadrats nell’area in esame (“moving window”) ed andando poi a calcolare il numero degli eventi che accadono in ogni quadrat. In entrambi i casi il risultato dell’analisi è rappresentato dalla determinazione, per ogni cella, del numero degli eventi di ciascun quadrat e dalla conversione di questo conteggio in una misura di intensità dividendolo per l’area di ciascuna cella. (figura 5.3). Il risultato finale dà indicazioni su come e se l’intensità del processo λ(s) varia nell’area di studio A.
Figura 5.3 Due metodi di quadrat counts: census esaustivo (sinistra) e campionamento random (destra) (O’Sullivan e Unwin, 2003).
I metodi di quadrat analysis di tipo “esaustivo” sono più largamente impiegati nelle analisi di tipo territoriale perché possono essere facilmente integrati con altri strati informativi (rasters) la cui primitiva geometrica è rappresentata da un pixel quadrato. Anche in questo caso l’aspetto critico dell’analisi risiede nella scelta della dimensione della cella: grandi quadrats comportano una descrizione più grossolana del fenomeno, mentre, se la dimensione del quadrat viene ridotta eccessivamente, le celle possono contenere pochi eventi o addirittura nessuno ed in tal caso il conteggio risulta essere poco significativo per la descrizione della variabilità del pattern.
La naturale estensione del metodo del quadrat counting che produce stime locali della densità del pattern è rappresentata dai metodi di Kernel Density Estimation (KDE) la cui
idea di base è quella di associare una densità ad ogni punto dello spazio, non soltanto ai punti in cui avviene l’evento; viene creato, perciò, un istogramma di frequenza “smussato” (smooth) relativo alla distribuzione di frequenza dei dati osservati (Bailey e Gatrell, 1995). La densità viene stimata contando il numero di eventi in una regione, detta kernel, centrata in corrispondenza del punto p dove vuole essere fatta la stima. Il metodo più semplice di calcolo della densità kernel, detto “naive method” (O’Sullivan e Unwin, 2003), considera il cerchio centrato in corrispondenza del punto p dove vuole essere fatta la stima che viene computata come segue:
2 π ∈ ° = λ r )] r , p ( C S [ n ) p ( ˆ [5.6]
dove il numeratore indica il numero dei punti del pattern S appartenenti a C(p,r), cioè al cerchio di raggio r centrato nel punto p di interesse (figura 5.4).
Figura 5.4 Densità di tipo Kernel secondo il metodo “naive”.
Attraverso questa analisi è possibile convertire un pattern di punti discreti in una mappa di densità di tipo continuo che può essere trattata come una superficie di cui estrarre linee isometriche (contour line) e per questo motivo è una delle trasformazioni più usate nelle analisi basate su GIS. Infatti una mappa di densità kernel permette di individuare i punti di maggiore intensità del fenomeno esaminato (“hot spots”) e consente di unire un’informazione di base di tipo puntuale con gli altri elementi geografici distribuiti sul territorio.
La scelta del raggio r del kernel, detto “bandwith”, influenza fortemente la superficie della densità stimata, infatti, se il raggio cresce, il cerchio C(p,r) va ad approssimare la dimensione dell’intera area di studio rendendo la stima abbastanza omogenea e vicina alla densità media dell’intero pattern. Quando invece il bandwith è piccolo la superficie di densità di kernel è fortemente focalizzata sugli eventi individuali con la densità che tende a zero in corrispondenza delle zone più lontane dagli eventi. Per questo motivo la scelta del bandwith, che viene spesso effettuata per approssimazioni successive fino ad arrivare
p
ad una soddisfacente superficie di densità stimata, è determinata dal contesto del caso di studio. Se ad esempio gli eventi rappresentano i punti di innesco di un incendio, il raggio di influenza può essere connesso ai tempi di risposta dei mezzi di soccorso.
A fianco della semplice stima della densità espressa dall’equazione [5.6] esistono misure più sofisticate basate sulla costruzione di una funzione kernel (kernel function) che pesa in maniera più forte i punti più vicini agli eventi rispetto alle zone più lontane. Attraverso la funzione di kernel density si produce una superficie curva smussata il cui valore è più alto in corrispondenza del punto generico s di posizione p, raggiunge lo zero ad una distanza pari al bandwith e racchiude un volume equivalente al numero totale degli eventi n del pattern che ricadono nel kernel.
Se p indica la posizione in A del generico punto ed S=(s1, s2,...sn) sono le posizioni degli
n eventi osservati, allora la densità λ(p) può essere stimata dalla seguente funzione:
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ τ − τ 1 δ 1 = λ
∑
1 = 2 τ τ (p) k (p s) ) p ( ˆ n i i [5.7] dove k() è la funzione di densità di probabilità bivariata ritenuta idonea per il caso in esame. Tale funzione è detta appunto kernel e risulta simmetrica rispetto all’origine. Il parametro τ >0 è il bandwith che determina la misura dello “smussamento” (smoothing) nella stima di densità ed è, essenzialmente, il raggio del disco centrato in p all’interno del quale i punti si contribuiscono in modo significativo alla stima ˆλ )(p τ.Il fattore du ) u p ( k ) p ( A ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ τ − τ 1 = δτ
∫
2 [5.8]è un fattore di correzione di bordo (“edge correction”): il volume al di sotto della funzione kernel deve essere centrato sul punto p che giace all’interno della regione di studio A. Per ogni kernel k() e raggio di influenza τ, la densità stimata. può essere computata ed il risultato analizzato su ogni punto p di una griglia che ricopre l’area di studio in modo da avere una rappresentazione visiva della variazione dell’intensità sull’intero territorio esaminato.
τ
λ )(p ˆ
Una tipica scelta per la funzione k() è la quartic kernel definita come segue:
⎪⎩ ⎪ ⎨ ⎧ 0 1 ≤ − 1 π 3 = 2 altrimenti u u per u) u ( k(u) T T [5.9]
Utilizzando la precedente espressione ed ignorando il fattore di correzione di bordo, la stima della densità diventa:
2 2 2 τ ≤ 2 τ ⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ τ − 1 πτ 3 = λ
∑
i hi h (p) ˆ [5.10]dove hi è la distanza fra il punto p e gli eventi osservati aventi posizione si e la
sommatoria è estesa su tutti i valori di hi che ricadono all’interno della regione di
influenza di raggio τ e centro p.
Una sezione della funzione quartic kernel, radialmente simmetrica, centrata in p e di raggio τ, mostra che il massimo valore è raggiunto in corrispondenza di p (τ=0), è pari a 3/πτ2 e va smussandosi progressivamente a zero in corrispondenza di τ (figura 5.5).
La computazione di una funzione di densità di tipo kernel su una griglia che riveste l’intera regione di studio, può essere visualizzata come una funzione che esamina ogni punto p della griglia: quando le distanze da ciascun evento osservato si ricadono nella
regione di influenza di p, cioè nel raggio τ, l’intensità del fenomeno viene misurata e contribuisce alla stima della densità complessiva di p in modo proporzionale alla vicinanza di tal eventi al punto della griglia considerato (figura 5.6).
Figura 5.5 Sezione di una funzione quartic kernel (Bailey e Gatrell, 1995)
Figura 5.6 Stima di densità kernel di un point pattern (Bailey e Gatrell, 1995) Qualsiasi sia la scelta della funzione k(), l’effetto dovuto all’incremento del bandwith τ è quello di “stirare” intorno a p la regione all’interno della quale gli eventi osservati contribuiscono alla stima della densità puntuale.
Un’altra importante evoluzione delle tecniche di KDE è quella che consente di attribuire un peso agli eventi (si ) che ricadono nella regione di influenza di raggio τ. Supponiamo
che gli eventi distribuiti sul territorio e visualizzati tramite una primitiva geometrica puntuale rappresentino delle aziende: in tal caso è possibile considerare uno specifico attributo, ad esempio il numero degli impiegati, che permette, nel calcolo della superficie di densità, di contare differentemente gli eventi osservati, dando maggiore importanza a quelli cui corrisponde un più alto valore dell’attributo. Nello specifico esempio delle imprese, il risultato fornirà una misura dell’intensità del fenomeno che tiene conto sia della distribuzione geografica degli eventi, ma anche di attributi alfanumerici (numero di addetti) di fondamentale importanza nell’analisi territoriale del fenomeno.
5.2.2.3 Misure basate sulla Distanza
Per la comprensione dei fenomeni territoriali rappresentabili attraverso punti, un’alternativa alle misure basate sulla stima della densità è quella di analizzare le distanza fra gli eventi o fra i punti del point pattern in modo da ricavare informazioni utili sulle proprietà locali, o di secondo ordine, della distribuzione stessa che dipendono dalle caratteristiche della zona piuttosto che dall’andamento generale della distribuzione. Il metodo più semplice per misurare le distanze relative è quello dei “vicini più prossimi” detto appunto “Nearest-Neighbor Distance” in cui l’interesse è rivolto al calcolo sia della distanza evento-evento cioè fra ciascuna coppia di eventi (s1, s2, sn) più vicini scelti in
maniera random, sia della distanza punto-evento valutata fra un punto qualsiasi dell’area di studio (p1, p2, pm) ed il nearest neighbor degli eventi osservati (siNN).
Tutti i metodi basati sulle distanze nearest-neighbor forniscono informazioni riguardo all’interazione fra gli elementi puntuali ad un scala fisica di ridotte dimensioni, per questo motivo vengono considerate solamente distanze fra elementi di ridotta entità (proprietà del secondo ordine).
La distanza fra due qualsiasi eventi (si ed sj) che ricadono nell’area di studio viene
calcolata con il teorema di Pitagora.
Se indichiamo con dmin(si) la distanza fra ogni evento osservato si e l’evento sj più vicino,
cioè dmin(si) = min[d(si, sj)] = min [dij] è possibile calcolare la distanza media di nearest
neighbor (NND) come segue:
n ) s ( d d n i min i min
∑
1 = = [5.11]Tale distanza viene spesso rapportata ad una distanza media di un ugual numero di eventi distribuiti in modo random nella regione di studio costruendo un indice di nearest
⎪ ⎩ ⎪ ⎨ ⎧ 5 0 = = n / A , d d d NNI ran ran min [5.12]
Il termine al denominatore della [5.12] rappresenta infatti il valore atteso della distanza minima fra gli n eventi quando si considerano distribuiti in maniera puramente casuale. Ciò significa che, quando NNI assume valore minore di uno, la distanza media osservata è inferiore rispetto a quella attesa, gli eventi sono cioè più vicini di quanto ci saremmo aspettati con una distribuzione random, il contrario accade quando l’indice è maggiore di uno.
Per non perdere molta dell’informazione contenuta nei dati, come avviene impiegando le misure sintetiche sopra esplicate, sono state elaborate funzioni capaci di tener conto della distanza relativa fra gli elementi puntuali distribuiti sul territorio: tali misure considerano la distribuzione di frequenza cumulata delle distanze di nearest neighbor fra gli elementi. In particolare la funzione G(d) è la distribuzione di frequenza cumulata delle distanze fra gli eventi (si) più vicini all’interno pattern:
n ] d ) s ( d [ n ) d ( G = ° min i ≤ [5.13]
Il valore della funzione G rivela, ad ogni specifica distanza d fra gli eventi si (i=1,2,…n),
quante sono, in percentuale, tutte le distanze di nearest neighbour del pattern che risultano minori o uguali a d.
La forma di questa funzione di frequenza cumulata rivela molto sul modo con cui gli eventi sono distribuiti spazialmente nel point pattern: se essi sono posizionati in modo da costituire dei clusters, allora la funzione G(d) si impenna rapidamente a brevi distanze, mentre se sono distribuiti uniformemente allora G(d) cresce lentamente fino alla distanza in corrispondenza della quale la pendenza aumenta perché coinvolge la maggior parte degli eventi.
La funzione F(d) viene costruita in modo analogo a G(d), ma invece di accumulare la frazione delle distanze di nearest neighbour fra gli eventi del pattern, vengono selezionati in modo random i punti che ricoprono l’area di studio e la minima distanza fra questi e ciascun evento del pattern viene computata. La funzione F(d) è la distribuzione di frequenza cumulata di queste distanze punto-evento.
Indicando con [p1, p2….pm] il set degli m punti selezionati casualmente nella regione di
studio, la funzione F(d) può essere formalizzata come segue:
m ] d ) S , p ( d [ n ) d ( F = ° min i ≤
[5.14]
dove dmin(pi,S) è la minima distanza fra i punti pi ed ogni evento nel point pattern S.
È importante notare la differenza fra le due funzioni sopra esplicate, infatti il loro andamento è molto diverso a seconda che gli eventi siano disposti in modo uniforme o tendano a raggrupparsi in clusters.
Mentre G(d) fornisce informazioni riguardo a quanto vicini siano gli eventi nel pattern, F(d) indica quanto lontani tali eventi siano da punti scelti arbitrariamente nell’area di studio. In generale (figura 5.7):
se gli eventi formano dei clusters in zone marginali dell’area di studio, allora la pendenza di G(d) sarà elevata a quelle brevi distanze che separano la maggior parte degli eventi dai loro vicini più prossimi, mentre F(d) crescerà lentamente con il progredire della distanza perché, essendo buona parte della regione di studio vuota, la distanze di nearest neighbour fra punti casuali ed eventi risulterà comunque elevata.
se invece la distribuzione degli eventi è più omogenea, G(d) crescerà lentamente per poi impennarsi bruscamente ad una distanza critica che separa la maggior parte dei nearest neighbor; F(d) invece crescerà da subito molto velocemente, in quanto punti casuali tenderanno ad essere piuttosto vicini ad eventi uniformemente distribuiti.
Figura 5.7 Confronto fra G(d) ed F(d) al variare della distribuzione dei dati: a) distribuzione raggruppata, b) distribuzione omogenea (O’Sullivan e Unwin, 2003).
Sia la funzione F(d) che la funzione G(d) si basano sulle distanze di nearest neighbour per ogni evento o punto del pattern: questo può tuttavia costituire un ostacolo alla piena comprensione del fenomeno spaziale specialmente quando i dati sono fortemente raggruppati e di conseguenza le distanze fra i vicini più prossimi sono molto ridotte rispetto alle altre distanze del pattern. Per questo motivo sono state introdotte misure (Ripley, 1976) che non considerano solamente le più piccole scale del pattern, ma tengono conto di tutte le distanze fra gli eventi S.
La funzione che tiene conto della dipendenza spaziale fra i punti del pattern in corrispondenza di un più ampio range di distanze fra gli elementi puntuali è la funzione K
il cui significato può essere compreso immaginando di tracciare, per ogni evento, un cerchio di raggio d centrato sul punto.
La funzione di K-Order Nearest Neighbour amplia la logica del NNI confrontando non solo le minime distanze tra gli eventi con le distanze “casuali” attese, ma, in successione anche le distanze tra ogni evento ed il secondo evento più prossimo, il terzo più prossimo e così via.
Calcolando la media degli altri eventi che cadono in ciascun cerchio relativo all’evento si e
dividendo poi per la densità totale dell’area di studio λ [5.5] si determina la funzione K(d) che, al variare del raggio d, può essere così formalizzata:
∑
∑
1 = 1 = = ⋅ 1 ° ∈ λ ∈ ° = ni i n i i n[S C(s,d)] n n a n )] d , s ( C S [ n ) d ( K [5.15]dove C(si,d) è il cerchio di raggio d e centro nell’evento si.
La funzione K(d) assume andamenti diversi a seconda della distribuzione spaziale dei dati (figura 5.8). Per pattern fortemente raggruppati la funzione K(d) cresce progressivamente fino ad un limite inferiore di distanze (lower end) che corrisponde alla dimensione del cluster, mentre il limite superiore (top end) è connesso alla distanza di separazione del pattern. Quando la distribuzione dei punti è più omogenea la funzione k(d) cresce proporzionalmente con la distanza d.
Figura 5.8 Andamento qualitativo della funzione K(d) al variare della distribuzione dei dati (O’Sullivan e Unwin, 2003).
Le informazioni che la funzione K fornisce nell’analisi di point pattern sono molteplici: innanzitutto misura la distribuzione di frequenza delle distanze fra gli elementi osservati per diverse scale territoriali, considera la posizione degli eventi di cui calcola la distanza a tutti i livelli non solo rispetto al nearest neighbour. Un aspetto critico di tutte le misure basate sulla distanza (funzioni G, F, K) è legato alla presenza, nell’analisi, di effetti di bordo che si presentano soprattutto quando il numero degli elementi puntuali nell’area di
studio è ridotto. In tal caso infatti, vicino al bordo, le distanze fra gli elementi più prossimi (evento-evento, evento-punto) è in genere elevata, anche se ciascuno di essi può avere un nearest neighbour, immediatamente fuori dall’area, a distanza nettamente inferiore. Un modo per ridurre questo effetto è quello di estendere l’analisi ad una zona di “guardia” (guard zone) costruita individuando un buffer intorno all’area di studio: i punti che ricadono in tale zona-buffer sono computati nel calcolo di G, F, K, ma non sono considerati parte del pattern.
5.2.2.4 Metodi di stima basati su distribuzioni statistiche
Questi metodi studiano la disposizione dei punti in esame attraverso un confronto tra la distribuzione di punti osservata (misurabile attraverso le tecniche descritte nei paragrafi precedenti) ed una distribuzione teorica generata da processi statistico-matematici e/o da simulazioni software. L’obiettivo è quello di comprendere se il pattern osservato può essere la realizzazione di un processo spaziale descritto attraverso distribuzioni statistiche più o meno complesse. La veridicità di tale ipotesi viene verificata attraverso opportuni test statistici. La distribuzione statistica dei punti campionati può essere determinata analiticamente, assumendo che il processo spaziale sia di tipo random indipendente (Indipendent Random Process, IRP) oppure di completa casualità spaziale (Complete Spatial Randomness, CSR). Quando non è possibile dare una formulazione del processo di tipo analitico possono essere effettuate simulazioni al computer per generare sintetiche distribuzioni dei dati campionati. (figura 5.9).
5.2.3 Indici
di
Autocorrelazione Spaziale
5.2.3.1 Indicatori globali di autocorrelazione: Moran e Geary
Gli indici di autocorrelazione sono finalizzati a verificare l’esistenza di particolari relazioni tra gli eventi considerati, ad esempio l’esistenza e la localizzazione di clusters.
Ciò che rende importante questo tipo di analisi risiede nella possibilità di analizzare e quantificare se le caratteristiche di un evento territoriale risultino spazialmente correlate, cioè se non siano distribuite in maniera indipendente tra loro, ma tendano a concentrarsi in alcune zone.
Alcuni degli indici di autocorrelazione spaziale più utilizzati nelle analisi territoriali vengono di seguito descritti.
a. INDICE DI MORAN (I)
∑ ∑
∑ ∑
∑
=1 =1 1 = =1 1 = 2 − − − = n i n J ij n i n j ij i j n i i w ) y y )( y y ( w ) y y ( n I [5.16]Il termine che sta al numeratore della seconda frazione,
∑ ∑
=1 =1 − −n i
n
j wij(yi y)(yj y) [5.17] rappresenta la covarianza: infatti, essendo i e j due unità territoriali della regione di studio A, il prodotto delle differenze fra i valori assunti dalla variabile y nelle due zone (yi
ed yj) rispetto alla media dell’intera distribuzione (y¯), rappresenta la misura con cui essi
variano insieme. Se entrambi i valori yi ed yj giacciono sopra o sotto la media (ambedue
dalla stessa parte), tale prodotto è positivo, altrimenti negativo ed il risultato finale dipende quindi da quanto essi, congiuntamente, siano vicini al valor medio di y sull’intera regione di studio.
La covarianza è moltiplicata per un peso, infatti i termini wij sono gli elementi di una
matrice W detta matrice di adiacenza: in generale se le zone i e j sono fra loro adiacenti allora wij è pari ad 1, altrimenti assume valore nullo.
Il divisore della seconda frazione dell’equazione [5.16], cioè
∑ ∑
=1 =1 n in
J wij [5.18]
tiene conto del numero di adiacenze complessive fra le zone territoriali in cui suddivisa l’area di studio, mentre il moltiplicatore
∑
=1 2 − n i (yi y) n [5.19]rappresenta la varianza dell’intero dataset e viene inserito nel calcolo dell’indice di Moran per assicurare che valori alti di I non siano semplicemente dovuti ad un’alta variabilità di y.
Analogamente ai coefficienti di correlazione non spaziale, se l’indice di Moran è positivo indica un’autocorrelazione positiva, se invece è negativo indica un’autocorrelazione
inversa. In generale il campo di variazione di I non è strettamente compreso fra –1 e +1,
come nei casi di convenzionale correlazione non spaziale, tuttavia volendo forzare il range nell’intervallo [-1, +1] è opportuno inserire un appropriato coefficiente di correzione (Bailey e Gatrell, 1995):
2 1 n 1 i 2 i n 1 i 2 n 1 j ij i j n 1 i n 1 J ij (y y) ) y )(y y (y w w n I ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ≤
∑
∑ ∑
∑ ∑
= = = = = [5.20] b. INDICE DI GEARY (C)Un’alternativa all’indice di Moran è l’indice di Geary C (Contiguity Ratio), simile ad I, la cui formula è:
∑ ∑
∑ ∑
∑
= = = = = − − − = n 1 i n 1 J ij n 1 i n 1 j 2 j i ij n 1 i 2 i 2 w ) y (y w ) y (y 1) (n C [5.21]Il primo termine della [5.21], vale a dire:
∑
= − − n 1 i 2 i y) (y 1) (n [5.22]è la varianza dell’’intero dataset che costituisce il fattore di normalizzazione dei valori numerici della variabile territoriale y.
Il numeratore del secondo termine della [5.21], cioè
∑ ∑
= = − n 1 i n 1 j 2 j i ij(y y ) w [5.23]è sempre positivo ed è elevato quando è alta la differenza fra i valori della variabile y in zone adiacenti; il termine 2
∑ ∑
ni=1 nJ=1wijconsente poi di normalizzare tale numeratore in base al numero delle adiacenze presenti nell’area di studio.Quando l’indice di Geary C assume valore pari ad 1 significa che non c’è autocorrelazione fra i valori della variabile in esame, quando è compreso fra 0 ed 1 indica un’autocorrelazione positiva, mentre quando assume valori maggiori di 1 indica un’autocorrelazione negativa. Questo è dovuto al fatto che il termine riportato nell’equazione [5.23] è sempre positivo, ma ha valore tanto più piccolo quanto più vicini sono i valori assunti dalla variabile y nelle zone adiacenti i e j. Il range di variazione di C può essere convertito nell’intervallo [-1, +1] sottraendo +1 al valore dell’indice.
È possibile comparare i valori misurati degli indici di Moran e Geary con quelli attesi ipotizzando una distribuzione aleatoria della variabile y, in modo da valutare sia la possibilità di modellare la variabile in esame tramite una distribuzione statistica nota, sia la presenza valori inusuali nei dati osservati.
Un’importante variazione che può essere apportata nel calcolo degli indici di Moran e Geary risiede nella possibilità di computare in maniera diversa la matrice W delle adiacenze andando ad esplorare come la struttura di autocorrelazione del data-set vari al variare del concetto di adiacenza.
Tale assunzione risulta poi necessaria quando, anziché valutare l’adiacenza fra poligoni, si vogliano computare gli indici di correlazione su dati di tipo puntuale dove non è possibile considerare il concetto di adiacenza in modo diretto.
In generale infatti gli elementi della matrice W assumono valore booleani appartenenti all’intervallo 0-1: [5.24] ⎩ ⎨ ⎧ = altrimenti 0 adiacenti j i, 1 wij
È possibile invece considerare come pesi i valori proporzionali alla distanza dij fra la zona
i e la zona j, oppure fra il punto i ed il punto j:
wij = dijz, z<0 [5.25]
Quando la distanza fra gli elementi i e j assume un valore maggiore di una distanza critica d, allora tali zone (o punti) non possono più essere considerati dei neighbours ed il termine della matrice di adiacenza assume valore nullo:
[5.26] 0 < ⎪⎩ ⎪ ⎨ ⎧ > < = z d d 0 d d d w ij ij z ij ij
Un altro modo per pesare le zone adiacenti è quello basato sulla lunghezza della zona di bordo adiacente. In questo caso: i ij ij l l w = [5.27]
dove li è la lunghezza del bordo del poligono esimo ed lij è la lunghezza del bordo del
poligono i adiacente al poligono j.
È inoltre possibile valutare gli elementi della matrice W combinando sia la distanza che la lunghezza del bordo di adiacenza:
0 < ⎪ ⎩ ⎪ ⎨ ⎧ > < = z d d 0 d d d l l w ij ij z ij i ij ij [5.28]
Infine, una variazione nella calcolo dei pesi wij della matrice delle adiacenze che merita
particolare interesse è quella denominata “adiacenza sfasata” (lagged adjacency) che anziché utilizzare la matrice W delle adiacenze, computata con uno dei metodi sopra descritti, considera le adiacenze in corrispondenza dei vari “lag”, cioè di distanze progressive fra gli elementi del dataset. L’idea di fondo del metodo è quella di considerare non solamente le zone immediatamente adiacenti ma di analizzare se e come avviene l’autocorrelazione a differenti lags.
Si valuta l’autocorrelazione fra gli elementi spaziali in funzione di distanze progressive, cioè dello sfasamento: per elementi vicini al lag 2, cioè al passo 2, si costruisce una matrice delle adiacenze W(2) i cui elementi sono w
ij(2), per elementi adiacenti al lag 3, cioè
al passo 3, si costruisce una matrice delle adiacenze W(3) i cui elementi sono w
ij(3) e così
via.
È possibile quindi determinare le misure degli indici di autocorrelazione per differenti lags e quindi plottare in un grafico il grado di autocorrelazione fra gli elementi spaziali al variare del lag considerato: questo tipo di approccio è molto vicino all’analisi di tipo variografico che verrà discussa nei prossimi capitoli.
5.2.3.2 Indicatori locali di associazione spaziale (LISA)
Gli indicatori di autocorrelazione spaziale analizzati nel paragrafo precedente sono misure statistiche di tipo globale che permettono di stabilire se ed in quali proporzioni la configurazione complessiva del dataset spaziale risulti autocorrelata, mentre nessuna informazione viene fornita riguardo alla localizzazione dei processi di interazione evidenziati dall’analisi.
Per questo motivo vengono costruiti degli indicatori locali di associazione spaziale, detti LISA (“Local Indicators of Spatial Association”) che permettono di capire dove, nella regione esaminata, siano presenti dei comportamenti anomali.
Tali indici costituiscono infatti misure disaggregate di autocorrelazione spaziale capaci di descrivere il grado di somiglianza o dissomiglianza degli elementi areali della zona di studio rispetto ai corrispondenti neighbors.
Il primo indice denominato G, costruito da Getis ed Ord (1992), esprime il valore dell’attributo y nella regione i-esima (yi) come frazione del valore totale che la variabile
in esame y assume nell’intera regione di studio:
∑
∑
1 = ≠ = n i i j i i ij i y y w G [5.29]dove wij sono gli elementi della matrice di adiacenza W.
Un’alternativa alla misura data dall’indicatore G è fornita da Anselin (1995) che mostra la possibilità di decomporre gli indici di Moran (I) e di Geary (C) in corrispondenti misure locali di autocorrelazione.
Per la computazione dell’indice di Moran locale vengono considerati gli “z-scores” di ciascuna zona i-esima e lo “z-score” medio delle zone circostanti:
∑
≠ − − = j i j ij i i s ) y (y w s ) y (y I [5.30]Ricordando infatti che lo z-score nella regione i-esima può essere espresso come rapporto il cui numeratore è la differenza del valore della variabile y nelle regione e la media dell’intera distribuzione ed il denominatore è rappresentato dalla deviazione standard s dell’intero dataset:
s ) y (y z i i = − [5.31]
allora l’indice di Moran locale può essere espresso in forma sintetica come segue:
∑
≠ = j i j ij i i z w z I [5.32]Con considerazioni analoghe la forma locale dell’indice di Geary C (contiguity ratio) può essere espresso come segue:
2 ≠
∑
− = w (y y ) C j i j i ij i [5.33]Gli indicatori locali di associazione spaziale possono essere visti come funzioni locali di analisi statistica e possono essere rappresentati graficamente attraverso mappe georeferenziate, strumento molto importante di analisi esplorativa della struttura spaziale soprattutto quando la dimensione del dataset assume grandi proporzioni.
Quando la struttura del dato areale è di tipo raster la cui primitiva geometrica è costituita da pixel quadrati che ricoprono l’intera regione in esame, è possibile costruire e rappresentare su mappa misure locali di autocorrelazione facendo riferimento ad indici focali di map algebra (Tomlin, 1990).
5.2.4 Interpolazione
Spaziale
Il processo di interpolazione spaziale può essere definito come quell’insieme di tecniche capaci di predire il valore scalare di una variabile spaziale in tutti i punti del territorio, dove tale valore è sconosciuto, a partire da misure conosciute del valore della variabile in punti di campionamento di posizione nota, detti punti di controllo.
L’utilità della procedura di interpolazione nel trattamento dei dati geografici risiede nella possibilità di convertire i dati, acquisiti sotto forma di osservazioni in punti sparsi, in funzioni matematiche continue in modo da confrontare ed integrare il modello di distribuzione spaziale, costruito a partire dalle osservazioni della variabile in esame nell’area di studio considerata, con i modelli spaziali derivanti da altre entità/variabili territorialmente distribuite.
I dati utilizzati per l’interpolazione possono essere:
di tipo hard (hard data): rappresentano le misure relative ad un campionamento sparso di un qualsiasi fenomeno territoriale di interesse;
di tipo soft (soft information): costituiscono l’insieme di informazioni sul processo fisico o in generale sul fenomeno considerato. In molti casi, infatti, il processo fisico è poco conosciuto o comunque molto complesso da modellare ed è quindi necessario introdurre semplificazioni ed ipotesi riguardanti la variabilità spaziale e la stazionarietà dell’attributo considerato.
I metodi di interpolazione spaziale possono essere classificati in vario modo a seconda se si voglia porre l’accento sulla dimensione dell’area dove viene applicata la procedura interpolante oppure sulla natura analitica del processo di interpolazione.
Una prima classificazione, quindi, distingue le tecniche di interpolazione in metodi globali
e metodi locali.
I Metodi Globali usano tutti i dati disponibili per ottenere predizioni nell’intera area di interesse. Sono in generale utilizzati non per l’interpolazione diretta, ma al fine di esaminare e possibilmente rimuovere gli effetti di una eventuale variazione globale causata da un trend o dalla presenza di varie classi, che possono indicare che l’area in esame può avere differenti valori medi. Una volta esaminato l’andamento globale, è possibile passare all’interpolazione locale dei residui. I metodi di interpolazione globale più largamente utilizzati sono:
- la Classificazione mediante uso di informazioni esterne - l’Interpolazione Polinomiale (trend surface)
I metodi di classificazione utilizzano delle “soft information” (es: uso del suolo, aree amministrative etc.) per suddividere l’area di studio in regioni che possano essere caratterizzate dai momenti statici (media, varianza) degli attributi misurati all’interno delle regioni stesse. Le predizioni sono effettuate utilizzando metodi di analisi di varianza di cui il più semplice, detto ANOVA (ANalysis Of VAriance), può essere così formalizzato:
ε α µ )
Z(x0 = + k + [5.34]
dove Z(x0) è il valore dell’attributo nella posizione x0,
µ
è la media generale suldominio di interesse,
α
k è la deviazione tra la mediaµ
e la media dell’unità k-esima ed ε è l’errore residuo (rumore). Il modello assume che la distribuzione dell’attributo in esame nella classe k sia di tipo normale, con valor medio pari a (µ+α
k) stimato a partire da un insieme di campioni ipotizzati spazialmente indipendenti. Una misura della bontà della classificazione è data dal rapporto fra la varianza dell’intero campione (σ
t2) e la varianza all’interno della classe k (σ
k2): minore è tale rapporto (detto varianza relativa), migliore è la classificazione. La significatività della classificazione può essere verificata mediante test statistico basato sulla F di Fisher.I metodi di interpolazione polinomiale descrivono invece l’andamento della variabile territoriale in esame attraverso la costruzione di una superficie (trend-surface) che consente di studiare l’andamento generale del fenomeno. L’analisi delle deviazioni dal trend può essere eseguita generando e studiando la carta dei residui. La precisione con cui la superficie segue l’andamento del fenomeno dipende dal grado del polinomio utilizzato e dalla variabilità della superficie reale (campioni). La variabile territoriale in esame, di cui sono campionate le osservazioni Zi, viene quindi interpolata con un polinomio di grado n di cui devono
essere stimati (generalmente con il metodo dei minimi quadrati) i coefficienti che sono in numero variabile a seconda del grado del polinomio interpolante (3 per un polinomio del primo ordine, 6 per uno di secondo ordine, 10 per uno di terzo ordine etc.). In ogni caso il numero delle osservazioni deve essere superiore rispetto al numero dei parametri da stimare. Il metodo della trend surface analysis verrà descritto in maggiore dettaglio nei paragrafi successivi.
I Metodi Locali, a differenza di quelli globali, non partono dal presupposto che esista una struttura spaziale globale del dataset e non attribuiscono le variazioni locali sui dati ad un rumore casuale e non strutturato (random noise), ma al contrario utilizzano l’informazione locale dei punti campionati più vicini al punto da interpolare con l’obiettivo di modellare proprio la variazione locale della variabile in esame. Questi metodi operano all’interno di una piccola zona nei dintorni del punto da interpolare, in modo da assicurare che la stima sia eseguita solo a partire dai punti nelle immediate vicinanze.
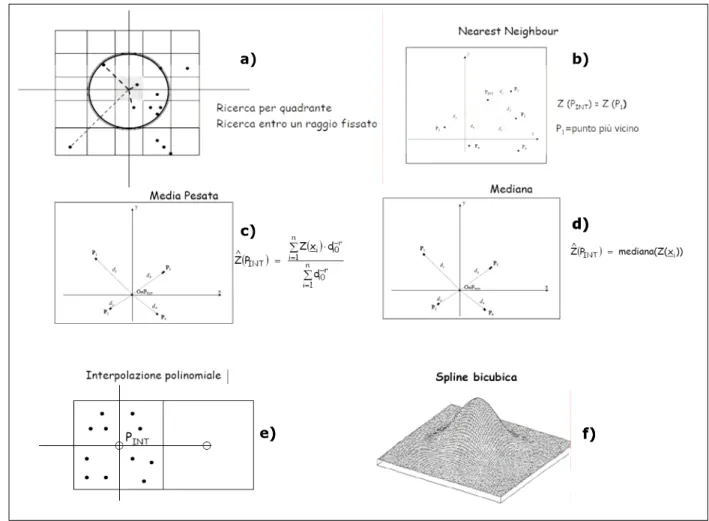
Per effettuare l’interpolazione bisogna, quindi, definire un’area di ricerca o di “prossimità” (figura 5.10, a) nei dintorni del punto dove deve essere calcolata l’interpolazione: tale area deve essere scelta in modo tale da comprendere un sufficiente numero di punti di controllo. È necessario, poi, scegliere una funzione matematica per la modellazione della variazione locale della variabile territoriale a
partire dai dati campionati. Infine, per rendere in processo continuo su tutta l’area di studio, è opportuno valutare il risultato dello step precedente su una griglia regolare che ricopre l’intera area di studio e reiterare il processo finché i valori di tutti i punti della griglia prescelta siano stati calcolati. Alla famiglia dei metodi locali appartengono(figura 5.10):
- Interpolazioni che comportano l’attribuzione al punto incognito del valore di
nearest neighbor, o di altre semplici statistiche (media pesata, mediana)
calcolate a partire dai punti di misura che ricadono all’interno della zona di prossimità;
- Interpolazioni polinomiali locali in cui i punti considerati per l’interpolazione sono quelli che cadono nell’intorno del punto da interpolare (PINT);
- Interpolazioni con funzioni di spline bicubiche in cui vengono utilizzate funzioni matematiche capaci di interpolare i punti di controllo attraverso superfici curve “smussate”. In generale le spline vengono utilizzate in tutte quelle situazioni dove l’approssimazione polinomiale sull’intero intervallo non è soddisfacente. Ovviamente nelle regioni distanti dai punti di controllo i valori interpolati possono sono affetti da elevata incertezza.
a) b) c) d) e) f) a) b) c) d) e) f)
Figura 5.10 Metodi locali di interpolazione statistica:a) area di prossimità, b) nearest neighbor, c) media, d) mediana, e) polinomi locali, f) spline bicubiche
Un altro modo di classificare le tipologie di interpolazione spaziale fa riferimento alla natura del processo di interpolazione effettuando una distinzione fra metodi deterministici
e metodi stocastici.
I Metodi Deterministici assumono che i dati rilevati nei punti di controllo siano esatti e che possa essere impiegata una procedura matematica per effettuare l’interpolazione. Dati quindi i valori della variabile territoriale in esame nei punti campionati e stabilita la funzione matematica interpolante di cui vengono computati i parametri, il risultato dell’interpolazione risulta univocamente
determinato. È possibile modificare i parametri della funzione o la funzione stessa,
ma il risultato è sempre verificabile e ripetibile. Questo tipo di approccio non consente quindi di controllare l’attendibilità della stima al di fuori dei punti di misura, né consente di quantificare l’errore di stima.
I Metodi Stocastici partono invece dal presupposto che le osservazioni della variabile in esame possano essere descritte in termini di processo casuale (random process) (figura 5.11) e che l’interpolazione sia possibile attraverso tecniche statistiche. Queste tecniche presuppongono infatti che la variazione spaziale del valore di una variabile territoriale sia, molto spesso, così irregolare da essere difficilmente modellabile tramite una semplice funzione matematica. Questi metodi inoltre forniscono stime probabilistiche sulla qualità dell’interpolazione e possono guidare l’interpolazione stessa facendo in modo da aumentare la precisione dei risultati. Con i metodi stocastici è quindi possibile sia controllare
l’attendibilità del processo interpolante anche al di fuori dei punti di misura sia
quantificare l’errore di stima.
Nei successivi paragrafi vengono analizzati in maggiore dettaglio le tecniche di interpolazione afferenti sia alla famiglia dei metodi deterministici cha a quella dei metodi stocastici.
5.2.4.1 Metodi Deterministici
I modelli di interpolazione spaziale di tipo deterministico ipotizzano che i dati misurati in corrispondenza dei punti di controllo siano esatti e che possa essere impiegata una funzione matematica, di cui calcolare i parametri, per effettuare l’interpolazione sul territorio in esame.
Il risultato del processo, cioè la stima, è univocamente determinato e dipende solamente dal valore dei dati di input e dalla loro distribuzione nello spazio: nessuna assunzione viene fatta sull’incertezza associata a tali valori. Di conseguenza non viene affrontato il problema della qualità dell’interpolazione e neppure della quantificazione dell’errore di stima.
Viene riportata una descrizione sintetica dei metodi di interpolazione spaziale maggiormente impiegati nelle analisi di tipo territoriale.
a. METODI BASATI SULLA TASSELLAZIONE
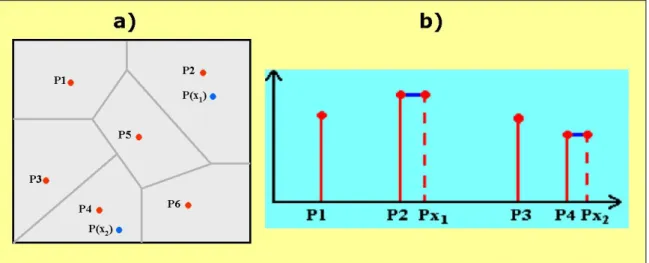
Uno dei più semplici metodi deterministici di interpolazione consiste nell’attribuire ai punti non campionati, in corrispondenza dei quali si vuole stimare il valore della variabile in esame, il valore corrispondente al punto campionato più vicino utilizzando dei poligoni di prossimità.
Dati n distinti punti di controllo disposti in piano, viene assegnato ad ogni punto xi della
regione di studio A una porzione di territorio corrispondente a quella parte di A la quale è più vicina ad xi che non a qualsiasi altro punto. Uno dei primi metodi di interpolazione
basati sulla costruzione dei poligoni di prossimità è denominato tassellazione di Voronoy
o di Diriclet ed i corrispondenti poligoni sono detti Poligoni di Thiessen (Thiessen, 1911).
Intorno ad ogni punto di grandezza nota viene costruito un poligono: tutti i punti interni al poligono sono i più vicini al punto di controllo che ha generato il poligono.
Secondo questa tecnica si assume che il valore di tutti i punti del territorio che appartengono al suddetto poligono abbiano uno stesso valore pari a quello a del punto di controllo (figura 5.12).
Le mappe di Voronoi creano dei poligoni attorno ai punti suddividendo in parti uguali le loro congiungenti (figura 5.13).
Figura 5.12 Poligoni di Thiessen: a) costruzione, b) interpolazione
Figura 5.13 Mappe di Voronoi
Il metodo dei poligoni di Thiessen, impiegato per la prima volta nel 1911 per stimare la distribuzione della pioggia in un dato territorio, è ancora oggi molto usato in idrologia proprio per la costruzione dei topoieti; in generale il suo utilizzo è limitato ai casi in cui si voglia modellare la distribuzione di una superficie partendo da dati puntuali di tipo categorico (es: tipo di vegetazione, uso del suolo etc.) ed assume una certa validità fintanto che le variazioni ambientali sono piuttosto graduali e soprattutto fino a quando la distanza fra i punti di controllo ed i punti stimati è ridotta (rete di campionamento fitta ed omogenea). Viceversa quando la distanza fra le osservazioni ed i punti interpolati è talmente elevata da presupporre variazioni nette di tutti gli attributi territoriali (es: quota, clima, esposizione, densità abitativa, dotazione infrastrutturale etc.), allora questo metodo perde di attendibilità.
Il metodo di tassellazione basato sulla costruzione dei poligoni di Thiessen non produce, inoltre, una campo di stima di tipo continuo perché in corrispondenza degli spigoli di ogni poligono c’è un salto equivalente alla differenza fra i valori che la variabile assume nei poligoni contigui (figura 5.14).
Figura 5.14 Poligoni di Thiessen: discontinuità dell’interpolazione
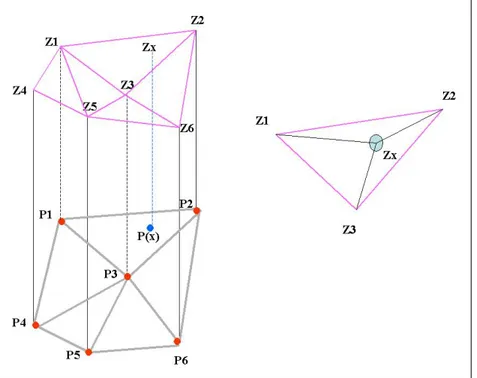
Un altro metodo di tasselazione ampiamente usato nella modellazione e la rappresentazione di dati territoriali è quello dei triangoli di Delaunay che consente di costruire un TIN (Triangulated Irregular Network).
Una triangolazione è definita di Delaunay quando il cerchio che circoscrive ciascun triangolo non contiene alcun punto di altri triangoli.
A partire dai punti osservati possono essere prodotte molte triangolazioni, ma quella di Delanuay è in genere preferibile perché i triangoli prodotti sono, per la maggior parte dei casi, equilateri.
Una volta creata la serie di triangoli (possibilmente equilateri) i cui vertici sono i punti di osservazione, è possibile costruire un modello di tipo TIN che consente di interpolare il valore incognito della variabile in esame (es: quota, pioggia, qualità atmosferica etc.) in ciascun punto che cade all’interno dei triangoli che formano la rete di triangolazione, attribuendo al punto incognito un valore proporzionale alla distanza fra i due punti osservati.
Un modello di interpolazione TIN può essere usato per interpolare il valore zx della
variabile da stimare in ogni punto interno alla triangolazione (figura 5.16) attribuendo un valore proporzionale all’area dei tre triangoli che hanno due vertici corrispondenti ai punti campionati in cui è nota la misura della variabile ed un terzo vertice corrispondente al punto da stimare.
Figura 5.16 Rappresentazione di una superficie interpolante TIN b. METODI DI MEDIA PESATA SULL’INVERSO DELLA DISTANZA (IDW)
Questi metodi di interpolazione appartengo alla famiglia degli “spatial moving average” e consistono nell’andare a calcolare misure statistiche, in genere una media pesata, prendendo come input i dati campionati più vicini al dato da stimare.
Nella previsione del valore della variabile nel punto incognito, piuttosto che valutare allo stesso modo tutti i punti appartenenti ad un intorno prefissato, si ipotizza di dare maggiore importanza, per il calcolo della media locale, a quelli più vicini al punto da interpolare: zˆ(x ) m w z(x) [5.35] i i ij j
∑
1 = =dove zˆ(xj) indica il valore stimato della variabile z nel punto xj e z(xi) è invece il valore
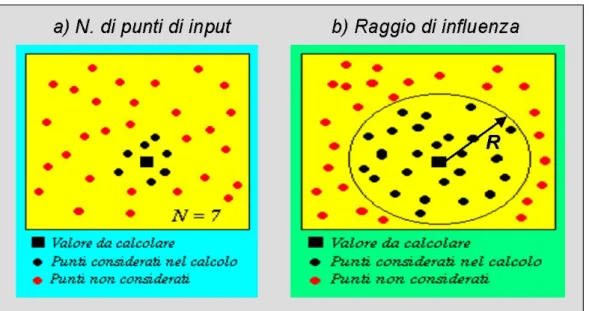
osservato negli m punti di controllo xi.che si trovano all’interno di un raggio prefissato. I
pesi wij assumeranno valore nullo al di fuori di tale raggio critico ed un valore
proporzionale all’inverso della distanza dai punti di controllo internamente all’area di pertinenza:
ij ij d
Assumendo che la somma dei pesi debba essere pari ad 1, l’espressione precedente diventa:
∑
=11 1 = m i ij ij ij d / d / w [5.37]Al crescere della distanza dij fra il punto da interpolare ed i punti di controllo, il peso dato
ai valori campionati diventa meno importante nel calcolo dell’interpolazione, mentre più il punto da interpolare è vicino al punto di controllo, più forte è la sua influenza nell’interpolazione.
Quando il punto da interpolare coincide con il punto osservato, il valore del peso, secondo la [5.37], risulta indeterminato, pertanto si assume che il punto incognito assuma valore pari a quello del punto di controllo (interpolatore esatto).
Con il metodo dell’IDW i punti da interpolare non possono assumere valori minori rispetto al valore minimo dei punti campionati, né superiori al massimo osservato perché la somma dei pesi varia fra 0 ed 1.
È possibile modificare il valore dell’interpolazione introducendo un’ulteriore parametro nel calcolo del valore stimato:
α 1 ∝ ij ij d w [5.38]
dove α è un parametro che, modificando la distanza, permette di variare il numero dei punti considerati nell’analisi ovvero il raggio di influenza dove estendere l’interpolazione (figura 5.17).
Figura 5.17 IDW: scelta dell’intorno a) selezione del numero dei punti, b) indicazione del raggio di influenza.
L’espressione completa che fornisce la stima IDW del punto incognito xj sulla base degli
⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ 1 =
∑
∑
1 = 1 = α α m i i m i ij ij j z(x) d / d / 1 ) (x zˆ [5.39]Valori del parametro α maggiori di 1 riducono l’influenza sull’interpolazione dei punti di controllo più distanti, dando luogo a mappe che presentano picchi più evidenti, mentre quando α è minore di 1 viene incrementata l’importanza dei punti osservati più distanti e la conseguente rappresentazione spaziale del processo di interpolazione dà luogo ad una mappa dai contorni più smussati.
c. METODI BASATI SULLA COSTRUZIONE DI CURVE SMUSSATE “SPLINES”
L’interpolatore di tipo “splines” stima i valori della variabile territoriale in esame nei punti di misura incogniti, utilizzando una funzione radiale matematica che minimizza la curvatura della superficie che meglio interpola i punti di controllo campionati.
Tali superficie presenta infatti delle linee isometriche (contours lines) che sono delle curve in due dimensioni, dalla forma più smussata possibile, capaci di effettuare il miglior fitting dei dati a disposizione.
Detto ∆ una decomposizione dell’ intervallo monodimensionale [a, b] in cui ricadono i punti di misura:
∆=a≡x0<x1<x2<……..x(M-1)<xM≡b [5.40]
si dice funzione spline di grado m≥1 relativa alla decomposizione ∆ una funzione s(x) soddisfacente le seguenti proprietà:
•
s(x) ristretto ad ogni intervallo [xk, xk+1] (k=0…..M-2), è un polinomio al più digrado m
•
la derivata di s(x) in ciascun intervallo è una funzione continua su tutto [a,b]. Ogni osservazione può essere quindi interpolata attraverso una combinazione lineare delle funzioni di spline che cadono nell’intervallo in cui si trova l’osservazione: ogni spline deve avere almeno un’osservazione nel suo supporto, quindi il passo della spilne deve essere maggiore della distanza minima fra le osservazioni.Nelle interpolazioni basate su funzioni spline, così come in quelle dove la funzione matematica è un unico polinomio, deve essere effettuata la stima dei parametri del modello. Un’interpolazione basata su poche splines produce una superficie morbida che media i valori osservati seguendone l’andamento nei punti di alta variabilità.
Un’interpolazione con tante splines è più accurata, ma comporta maggiori difficoltà nella stima dei coefficienti dei polinomi che risultano molto influenzati dai valori delle singole osservazioni soprattutto laddove è presente una scarsa densità di dati: la superficie interpolante può presentare, quindi, delle oscillazioni indesiderate.
5.2.4.2 Metodi Stocastici
I metodi di interpolazione spaziale di tipo stocastico partono dal presupposto che sia poco realistico stimare un fenomeno territoriale complesso attraverso rigorosi algoritmi matematici adducendo, a tal riguardo, le seguenti motivazioni:
Il valore misurato nei punti di controllo risulta comunque affetto da errori insiti nella procedura stessa di campionamento, perciò un certo grado di incertezza può essere associato alla misura dei dati osservati. Tali misure, inoltre, sono affette da una variabilità temporale che comporta un’ulteriore imprecisione nella determinazione di un valore unico di riferimento.
La scelta dei parametri del modello matematico di interpolazione si basa su una
conoscenza generale del fenomeno modellato e non sull’informazione del processo
territoriale nello specifico territorio in esame, informazione questa contenuta nei punti di controllo.
In un processo spaziale ciascuna delle n osservazioni della variabile territoriale in esame nel generico istante viene simbolicamente espressa come:
z(xi,tk) con i=1,2….n e k=1,2….m [5.41]
dove xi rappresentano le posizioni dei punti osservati nella regione A all’istante k.
La possibilità di collezionare un numero teoricamente infinito di campioni della variabile in esame, al variare della posizione dei punti di controllo nell’area di studio (dominio della variabile), comporta la definizione di una variabile regionalizzata (REV, Regionalized
Variable):
z(x) ∀x∈ A [5.42]
Pertanto il dataset {z(xi) i=1,2….n} può essere considerato come un insieme costituito da
un numero limitato di valori che la variabile regionalizzata può assumere nel dominio A denominato “supporto”: ciascun valore misurato (campione) della variabile regionalizzata z(x) su A viene detto valore regionalizzato.
Un nuovo punto di vista viene introdotto nell’approccio di tipo statistico secondo cui ciascun valore regionalizzato della variabile è considerato come il risultato di un qualche processo di tipo casuale. Questo processo può essere definito in termini formali come
variabile casuale Z(xi) di cui i valori campionati z(xi) ne rappresentano
un’estrazione/sorteggio (draw). In ciascun punto xi del dominio A il meccanismo aleatorio
che genera i valori z(xi) può essere differente, perciò Z(xi) può avere, a priori, proprietà
diverse in ogni punto dell’area di studio.
I valori che la variabile assume nel dominio A possono anche essere visti come un’ estrazione/sorteggio da un insieme infinito di variabili aleatorie (una variabile casuale per ogni punto del dominio): tale famiglia di variabili random è denominata funzione aleatoria
o random (RAF, Random Function):
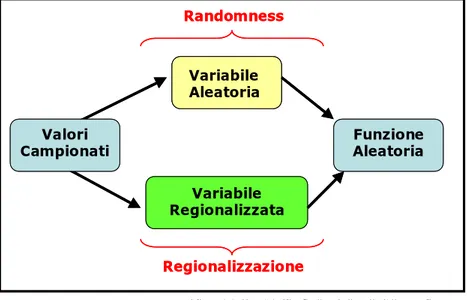
Valori Campionati Variabile Aleatoria Variabile Regionalizzata Funzione Aleatoria Randomness Regionalizzazione Valori Campionati Variabile Aleatoria Variabile Aleatoria Variabile Regionalizzata Funzione Aleatoria Randomness Regionalizzazione
Figura 5.18 Il modello della funzione aleatoria
La figura 5.18mostra come il modello di costruzione di una funzione aleatoria, capace di descrivere il fenomeno territoriale da studiare, possa essere visto da due differenti angolazioni. Il primo aspetto considera i dati campionati nei punti di controllo come originati da un mero processo fisico (spazio bidimensionale e tempo) ed ipotizza che la loro relazione dipenda esclusivamente dalla relativa posizione nelle regione di studio: tali punti sono il risultato di un processo di regionalizzazione (Kanevski e Maignan, 2006). Il secondo aspetto considera invece i punti campionati come il risultato di un processo stocastico: le osservazioni corrispondono a valori assunti da una variabile di natura aleatoria in quanto non modellabile in termini puramente deterministici.
In generale quindi, nei modelli di analisi dei fenomeni territoriali di tipo probabilistico/stocastico, si assume che una variabile regionalizzata z(x) sia la
realizzazione di una funzione aleatoria Z(x), cioè di una infinita famiglia di variabili
aleatorie (una per ogni punto dell’area di studio) (Wackernagel, 2002). Seguendo questo
approccio i valori campionati z(xi) in specifiche localizzazioni rappresentano i campioni di
una particolare realizzazione z(x) della variabile Z(x)(figura 5.19).
RAF (Random Function) REV (REgionalized Value) Z(x) Z(x0) z(x) z(x0) Il valore regionalizzato z(x0) è la realizzazione
della della variabile aleatoria Z(x0) RAF (Random Function) REV (REgionalized Value) Z(x) Z(x0) z(x) z(x0) RAF (Random Function) REV (REgionalized Value) Z(x) Z(x0) z(x) z(x0) Il valore regionalizzato z(x0) è la realizzazione
della della variabile aleatoria Z(x0)