ANALISI DELLA FASE DI PRETENSIONAMENTO DELLA CINGHIA

Capitolo 4

ANALISI DELLA FASE DI PRETENSIONAMENTO

DELLA CINGHIA

4.1 Introduzione

Nel paragrafo 3.6 sono state illustrate le motivazioni che hanno spinto allo sviluppo in questa sede di un modello matematico che riproduca la fase di assestamento della cinghia sulle pulegge, motivazioni che si possono riassumere essenzialmente nei seguenti punti:

o differenza misurata tra le tensioni teoriche nei rami della cinghia, calcolate secondo la teoria dell’elasticità e considerando il percorso di avvolgimento nominale, e quelle effettive misurate in condizioni di pulegge ferme;

o differenza tra i raggi di avvolgimento nominali e quelli effettivi, sempre misurati in a pulegge ferme.

Si rende necessario allora disporre di uno strumento che consenta di “correggere” le tensioni e i raggi di avvolgimento teorici in modo da ottenere dei parametri di ingresso attendibili per la successiva analisi dinamica della trasmissione.

Nel fare ciò si sono seguite due strade diverse, che si differenziano tra loro per l’approccio al problema e per il tipo di risultati forniti.

Un primo modello statico sviluppato prevede l’analisi di un tratto infinitesimo della cinghia, considerata come se fosse un corpo continuo, e la conseguente imposizione dell’equilibrio in direzione radiale e tangenziale. Questo comporta l’abbandono della logica di modellazione “a parametri concentrati”, tuttavia consente di scrivere una relazione che leghi la tensione teorica iniziale nella cinghia, calcolabile per via elementare tramite le equazioni della elasticità lineare, con la penetrazione radiale che la cinghia subisce in fase di montaggio e,

successivamente, di trovare una relazione univoca tra la tensione iniziale teorica e quella effettiva. Questo relazione può essere esplicitata attraverso diagrammi che rappresentano l’andamento della tensione effettiva in funzione di quella teorica iniziale, una volta note le caratteristiche geometriche della trasmissione e i parametri di rigidezza della cinghia.

La seconda via seguita, indipendente dal modello continuo accennato in precedenza, consiste nello sviluppo anche per l’analisi statica di un modello a parametri concentrati che simuli la condizione iniziale e quella finale dopo il montaggio e che dia anche dei riscontri sui risultati calcolati con il modello analitico. L’obiettivo che si vuole raggiungere è valutare il valore corretto della tensione nella cinghia e il raggio di assestamento raggiunti attraverso due modelli indipendenti tra loro.

La risoluzione per via numerica di questo secondo modello a parametri concentrati ha richiesto una sua implementazione nell’ambiente di simulazione SIMULINK® 5.0, mentre la risoluzione del modello continuo è stata ottenuta utilizzando le routine di soluzione di MATLAB® _6.5.

Nei paragrafi seguenti sono illustrati i dettagli matematici dei due modelli proposti e i risultati ottenuti, procedendo inoltre a confrontarli con le previsioni fornite da un modello multibody realizzato tramite codice commerciale Adams® in un precedente lavoro di tesi [12]

4.2 Modello continuo

Sfruttando la teoria dell’elasticità e considerando, come detto nel paragrafo precedente, la cinghia come un corpo continuo, si può scrivere la pretensione iniziale in funzione dei parametri geometrici della trasmissione e del materiale della cinghia; ricordando l’equazione (1.4) per il calcolo della lunghezza del percorso di avvolgimento teorico e indicando con L0 la

lunghezza della cinghia a riposo, la deformazione1 iniziale subito dopo il montaggio vale 1 0 0 0 _{= −} − = L L L L L ε _(4.1)

e quindi la tensione teorica iniziale è

EA L L EA T_{iniz ⎟⎟} ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = = 1 0 ε (4.2)

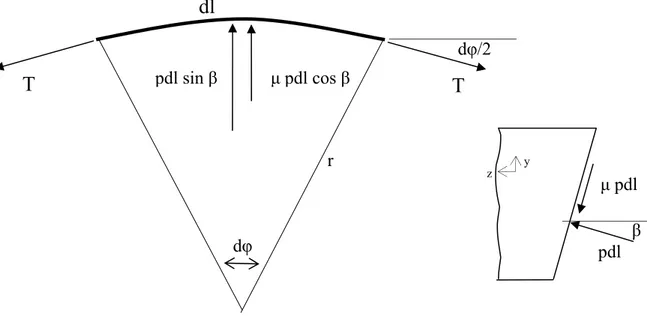
In figura 4.1 è rappresentato il tratto infinitesimo di lunghezza dl, posto alla quota r dall’asse e soggetto alla tensione T, alle pressioni sui fianchi p e all’attrito, che in questo caso ha esclusivamente direzione radiale. L’equazione di equilibrio in direzione radiale per l’elemento infinitesimo dl di cinghia può essere scritta come

0 cos 2 sin 2 2 2 + + ⋅ = − Tdϕ pdl β µ pdl β (4.3)

dl

T

T

Fig. 4.1 Equilibrio statico dell’elemento infinitesimo di cinghia da cui, ponendo dφ/dl = 1/r si ottiene l’equazione

) cos (sin 2 β+µ β = rp T (4.4)

Restano ora da definire i legami tra la forza di trazione T, la pressione sul fianco p e il raggio di avvolgimento r. Per quanto riguarda la pressione laterale sul fianco della cinghia, vale quanto esposto nel paragrafo 3.4, tenendo però presente che ora si has&=0.

Si ricava allora la relazione

e e l e e l s K R r K p= (sinβ) = (sinβ) ( ₀ − ) (4.5)

Il calcolo del legame tra forza di trazione e raggio di avvolgimento può essere condotto nel modo seguente: si immagini l’elemento di cinghia disposto ad una quota radiale r e soggetto ad una tensione T (figura 4.2); se ora si aumenta il raggio di avvolgimento alla quota (r+s) l’elemento di lunghezza dl subisce una deformazione circonferenziale

r dφ y z µ pdl β pdl

r s rd rd d s r = − + = ϕ ϕ ϕ ε ( ) (4.6)

In questa condizione la tensione nella cinghia risulta aumentata di una quantità

r s EA EA T = = ⋅ ∆ ε (4.7)

Se inizialmente, nella condizione r = R0, la tensione nella cinghia è Tiniz, la tensione T(r) può

essere scritta nella forma

r r R EA T r T T r T( )_{= iniz −∆} ( )_{= iniz − ⋅}( 0 − ) _(4.8) εdl

Fig. 4.2 Deformazione circonferenziale dell’elemento infinitesimo di cinghia Sostituendo ora nella equazione di equilibrio (4.4) le equazioni costitutive (4.5) e (4.8) si ottiene la relazione 0 ) )( cos (sin ) (sin 2 ) ( 0 0 − _{− + − =} ⋅ − K R r r r r R EA T e e l iniz β β µ β da cui ponendo ) cos (sin ) (sin 2 β β +µ β = e l K K

in definitiva si perviene alla equazione cercata

0 ) ( ) ( 0 0 − _{− − =} ⋅ − K R r r r r R EA T e iniz (4.9) r r + s dl T T T + ∆T T + ∆T dφ

Noto il valore della pretensione iniziale, calcolabile conoscendo i parametri geometrici della trasmissione e quelli costruttivi della cinghia, la risoluzione per via iterativa della equazione non lineare (4.9) permette di risalire al raggio di avvolgimento r su cui la cinghia si dispone dopo la fase di assestamento sulle pulegge e in seconda analisi, tramite la (4.8), alla tensione effettiva presente sui rami della cinghia in questa configurazione, dati entrambi indispensabili per il successivo studio dinamico.

Per l’analisi dei risultati e per uno studio di sensibilità del modello alla variazione di alcuni parametri fondamentali si rimanda al paragrafo 4.4.

4.3 Modello a parametri concentrati

Il modello a parametri concentrati è stato sviluppato principalmente con lo scopo di fornire una conferma dei valori calcolati con le relazioni (4.8) e (4.9) del modello continuo, attraverso un modello che seguisse la logica di modellazione adottata nel presente lavoro di tesi. Il modello a parametri concentrati offre inoltre la possibilità di visualizzare l’andamento temporale delle grandezze in esame a partire dal valore iniziale fino a quello finale di equilibrio

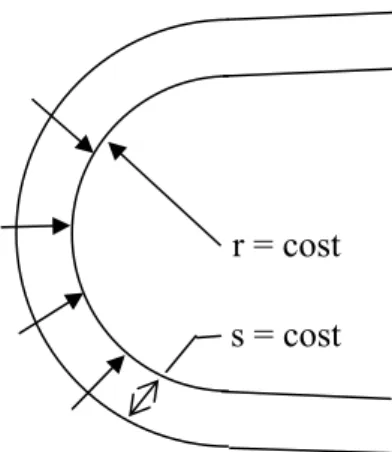
Prima di illustrare la trattazione matematica è necessario premettere alcune ipotesi alla base del modello. Innanzitutto si osservi che durante la fase di assestamento la cinghia non presenta grandi differenze nel raggio di avvolgimento all’interno dell’arco di contatto; si può perciò considerare che il raggio sia costante, come mostrato in figura 4.3. Inoltre ipotizzando che la tensione nella cinghia sia uniforme lungo tutto il percorso di avvolgimento, ci si convince subito che essa risulta perfettamente in equilibrio nella direzione tangenziale alla puleggia in ogni punto dell’arco di contatto.

r = cost s = cost

La modellazione della cinghia avviene secondo quanto già esposto nel paragrafo 3.2: in sostanza ogni tratto di cinghia di lunghezza stabilita viene schematizzato attraverso un elemento avente una certa massa concentrata in un punto. Gli elementi sono connessi tra loro tramite molle e smorzatori tangenziali di rigidezza opportune.

Per le ipotesi appena fatte, l’elemento di cinghia è in grado di muoversi unicamente in direzione radiale; la coordinata che si assume come indicativa del moto dell’elemento è dunque la penetrazione s(t) a partire dal raggio di avvolgimento nominale R0, mentre r(t) è il

raggio di avvolgimento effettivo su cui si sistema la cinghia. Vale la relazione )

( )

(t R₀ s t

r = − (4.11)

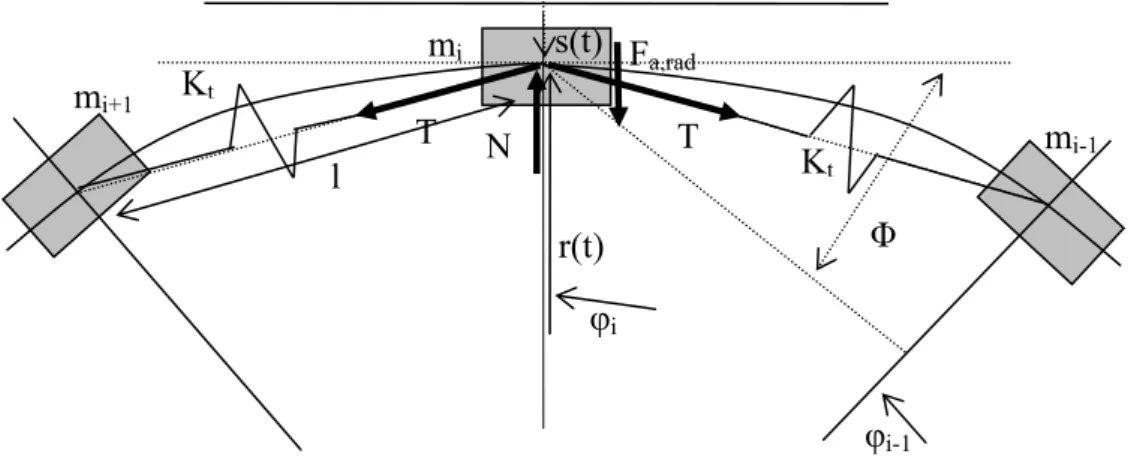
La coordinata angolare φi che individua la posizione angolare della massa viene considerata a

partire dal raggio che unisce il centro della puleggia con il punto di impatto del ramo rettilineo della cinghia sulla puleggia (figura 4.4).

Inoltre, dato che si è ipotizzato un moto esclusivamente radiale della massa, si ha che l’angolo formato dai raggi che individuano due masse consecutive è costante, ossia

Φ = = − = = − _{− −} 0 1 1) costante ( ) ( R l_iniz iniz i i i i ϕ ϕ ϕ ϕ _(4.12)

L’analisi può dunque essere condotta scrivendo una sola equazione relativa al moto radiale della massa i-esima, considerando tale massa rappresentativa del comportamento delle altre masse presenti nell’arco di contatto.

s(t) mi

Fig. 4.4 Sistema di riferimento e forze agenti sulla massa i-esima

Utilizzando il sistema di riferimento e i versi positivi indicati dalle frecce in figura 4.4, l’equazione di equilibrio può essere scritta nel modo seguente

r(t) φi-1 φi mi-1 mi+1 Fa,rad T _N T Kt Kt Φ l

rad a rad N F T s m_&&= − ± _{, (4.10)}

dove m è la massa dell’elemento di cinghia calcolata secondo la relazione (3.4), s è la penetrazione radiale a partire dal raggio di avvolgimento nominale, Trad è la componente della

tensione T in direzione radiale, N la componente delle forze di contatto sui fianchi e Fa,rad è la

forza di attrito coulombiano che si sviluppa durante l’incuneamento della cinghia nella gola della puleggia; il verso di Fa,rad è in ogni istante opposto a quello della velocità della massa

mi.

4.3.1 Tensione nella cinghia

Riferendosi ancora alla figura 4.4, si può valutare la tensione delle molle che rappresentano la rigidezza estensionale della cinghia. La lunghezza delle molle tangenziali di connessione tra gli elementi in una configurazione diversa da quella iniziale vale

Φ − = Φ =r (R₀ s) l (4.11)

mentre la forza di trazione esercitata dalla molla sulla massa mi è

[

]

K

T = _t − Φ− (4.12)

In definitiva la componente radiale delle due forze di trazione vale

[

]

mentre le due componenti tangenziali si equilibrano. 4.3.2 Forze di contatto

Per modellare il contatto tra cinghia e puleggia si utilizza la relazione non lineare del tipo p C p K F e _l l + & = (4.14)

già illustrata nel paragrafo 3.4; utilizzando i passaggi già esplicitati nel medesimo paragrafo si ottiene l’espressione della forza globale sui fianchi della cinghia agente in direzione radiale:

s C s K N e _c c + & = (4.15)

Lo smorzamento di contatto Cc è assunto proporzionale alla rigidezza di contatto Kc secondo

4.3.3 Attrito sui fianchi della cinghia

Anche per le forze di attrito in linea generale vale quanto già espresso nel paragrafo 3.5. Nel caso in esame tuttavia la forza di attrito non ha componenti tangenziali perché la velocità dell’elemento è diretta in senso esclusivamente radiale. In letteratura si trovano diverse espressioni del legame tra velocità di strisciamento e forza di attrito [8]; anche in questo caso però si è scelto di utilizzare un andamento del coefficiente di attrito costante al variare della velocità, essenzialmente per il fatto che, trattandosi di una analisi “quasi statica” ossia con piccole velocità radiali dell’elemento di cinghia, una modellazione più accurata dell’attrito avrebbe appesantito il modello senza garantire effettivamente una maggiore accuratezza della simulazione.

La forza di attrito sui fianchi dell’elemento di cinghia può essere espressa nel modo seguente )

(s sign F

F_a =−µ⋅ _{l &} (4.16)

Utilizzando la relazione (3.16), che si riporta per comodità β β sin 1 ) ( sin = + ⋅ = e c e c l K s C s N F _& (3.16 bis)

si trova che la componente radiale della forza di attrito vale

) ( ) ( sin cos cos , F N sign s N tg sign s

F_arad = _a =− ⋅ ⋅ _& =−µ ⋅ β⋅ _& β

β µ

β (4.17)

4.3.4 Riepilogo

L’equazione del moto della massa i-esima può essere scritta esplicitando l’espressione (4.10)

[

]

[

]

Le condizioni iniziali da fornire sono due, in quanto si tratta di una equazione differenziale ordinaria del secondo ordine:

0 ) 0 ( 0 ) 0 ( 0 ) 0 ( ) 0 ( ₁ = → = = → = s r s R r & & (4.19)

[

]

[

]

L’equazione scritta è una equazione differenziale del secondo ordine non omogenea a coefficienti costanti (per quanto detto nel paragrafo sull’attrito, anche µ si considera costante e variabile solo in segno a seconda del valore della velocità radiale dell’elemento).

Questa equazione è stata risolta in ambiente di simulazione SIMULINK® 5.0, utilizzando un algoritmo Runge-Kutta di ordine 4 a step di integrazione fisso; sono stati ottenuti gli andamenti del raggio di avvolgimento e, tramite la (4.12), della tensione nella cinghia in funzione del tempo illustrati nel paragrafo seguente.

L’implementazione del modello in ambiente SIMULINK® 5.0 è mostrata in dettaglio in Appendice A.

4.4 Analisi dei risultati e confronto con un modello multibody

I modelli illustrati nei paragrafi precedenti per descrivere la fase di assestamento della cinghia sulle pulegge sono stati utilizzati con lo scopo di ricavare informazioni utili alla successiva analisi dinamica delle trasmissioni CVT montate da Piaggio sui motori 200 cc e 500 cc.

Le condizioni iniziali imposte ad entrambi i modelli riguardano il raggio di avvolgimento iniziale, pari a quello nominale per il rapporto di trasmissione assegnato, e la tensione nella cinghia calcolata con la relazione (4.2).

Per quanto riguarda il valore del raggio di avvolgimento nominale non sussistono problemi nella sua determinazione, essendo un parametro di progetto fondamentale per la definizione della trasmissione; è fonte di incertezze invece il valore della tensione iniziale nella cinghia, che è legato alle caratteristiche geometriche della trasmissione, alle proprietà elastiche della cinghia e alla sua lunghezza a riposo.

Se si assumono fissate le caratteristiche geometriche quali raggi di avvolgimento e interasse della trasmissione e le caratteristiche elastiche della cinghia, il valore della pretensione dipende solo dalla sua lunghezza L0 (equazione (4.2)). Tuttavia tale valore non è noto a priori

con sufficiente accuratezza, per cui nell’analisi condotta si è provveduto a modificare per passi successivi tale valore fino a raggiungere il livello di tensione voluto nella cinghia.

Nella tabella 4.1 sono indicate le caratteristiche geometriche ed elastiche delle due trasmissioni analizzate, il valore della lunghezza a riposo della cinghia e la tensione teorica iniziale.

CVT 200

CVT 500

Raggio puleggia motrice 27.759 mm 41.10 mm

Raggio puleggia condotta 68.541 mm 89.34 mm

Interasse 244 mm 185 mm

Lunghezza percorso di avvolgimento teorico 797.37 mm 792.44 mm Lunghezza cinghia a riposo 794.985 mm 789.452 mm Rigidezza estensionale (EA) 700000 N 1050000 N

Tensione teorica iniziale 2102 N 2650 N

Tab. 4.1 Caratteristiche geometriche ed elastiche delle trasmissioni

4.4.1 Risultati del modello continuo

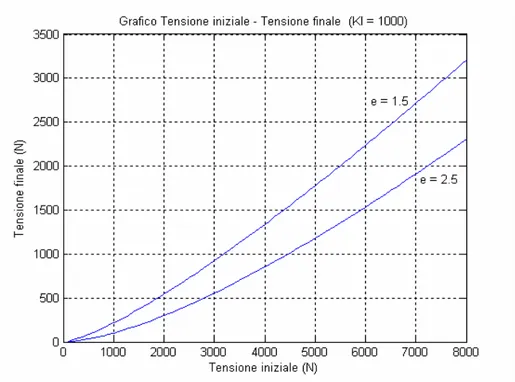
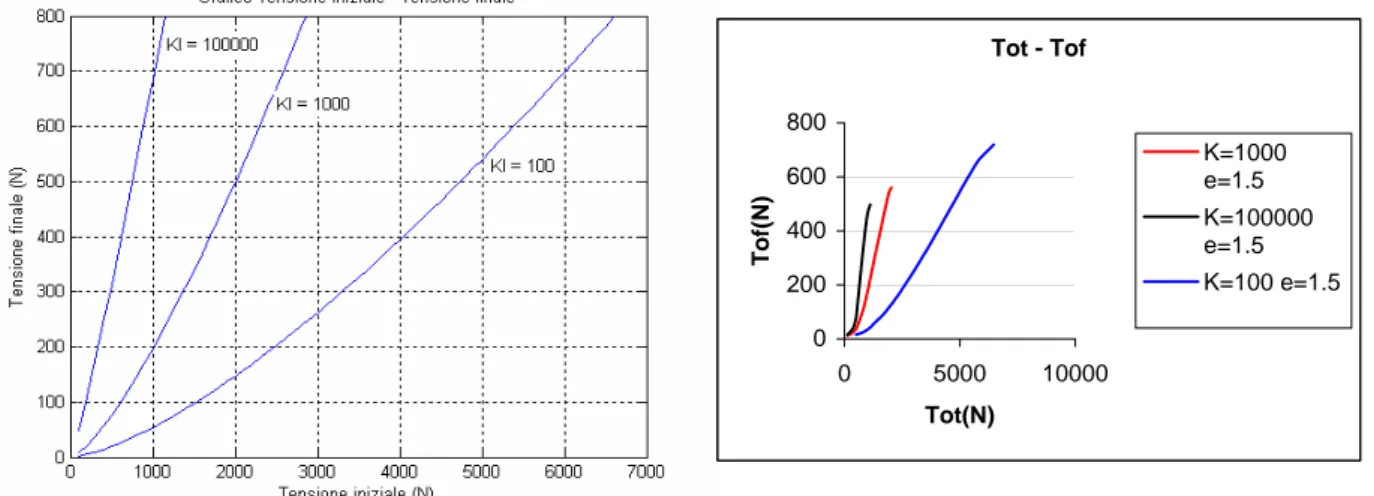
Le relazioni (4.8) e (4.9) possono essere rappresentate graficamente in funzione della tensione iniziale teorica, al variare dei parametri che definiscono il contatto tra cinghia e puleggia. Nelle figure 4.5 e 4.6 è mostrato il legame tra la tensione iniziale teorica e la tensione effettiva al variare dei parametri Kl e di e.

L’andamento generale riscontrato nelle curve prevede un primo breve tratto non lineare seguito da un secondo tratto in cui si ha un legame sostanzialmente lineare tra tensione iniziale e finale. All’aumentare della rigidezza del contatto, a parità di tensione iniziale, la cinghia penetra meno nella gola della puleggia, pertanto essa si assesta su raggi di avvolgimento maggiori; conseguentemente la tensione nella cinghia tende rimanere elevata. Questo si manifesta con un aumento della pendenza del tratto lineare della curva all’aumentare della rigidezza di contatto.

Fig. 4.5 Influenza della rigidezza di contatto sulla tensione finale

Fig. 4.6 Influenza dell’esponente e sulla tensione finale

Anche la variazione delle curve di tensione con l’esponente e risulta assai marcata; in particolare ad un aumento dell’esponente corrisponde una curva più “piatta” per tensioni iniziali prossime allo zero. Ciò è in accordo con la formulazione (4.5) della funzione di contatto: infatti indipendentemente dal valore della rigidezza di contatto, per piccole penetrazioni radiali (s < 1 mm) la curva con esponente maggiore sta sempre “sotto” quella con esponente minore.

In figura 4.7 sono invece riportati gli andamenti della penetrazione radiale nella gola della puleggia in funzione delle tensioni iniziali. In questo caso mentre da un lato permane la forte influenza della rigidezza di contatto, dall’altro si nota che l’effetto dell’esponente e è più piccolo rispetto a quello giocato nella determinazione della tensione finale.

Fig. 4.7 Penetrazione radiale in funzione della tensione iniziale

In figura 4.8 è riportato un confronto tra le curve che individuano la tensione finale nella cinghia ottenute con un modello multibody in Adams® e quelle ricavate dal modello continuo proposto in questa sezione, al variare della rigidezza di contatto e assumendo e = 1.5.

Tot - Tof 0 200 400 600 800 0 5000 10000 Tot(N) T o f(N) K=1000 e=1.5 K=100000 e=1.5 K=100 e=1.5

Fig. 4.8 Risultati del modello Adams®

Dalla figura si nota come entrambi i modelli rivelino l’andamento qualitativo già illustrato all’inizio di questo paragrafo, con il breve tratto iniziale non lineare seguito dal tratto lineare di ampiezza molto maggiore.

Nella tabella 4.2 sono invece confrontate le pendenze dei tratti lineari calcolate con il modello proposto e con il modello Adams®. Anche qui si può notare un buon accordo tra i dati a confronto, con scostamenti percentuali attorno al 6 % per rigidezze di contatto elevate, mentre si commette un errore più elevato con un valore di rigidezza più basso; tale errore resta comunque entro un limite accettabile se si considera la relativa semplicità del modello analitico proposto rispetto al modello multibody.

Pendenze del tratto lineare (e = 1.5) Modello analitico Modello Adams® ∆ %

Kt = 100 0.167 0.1503 11.1

Kt = 1000 0.389 0.365 6.5

Kt = 100000 0.879 0.835 5.2

Tab. 4.2 Pendenze del tratto lineare della curva Tiniz - Tfin

Il vantaggio rilevante del modello continuo rispetto al modello multibody è tuttavia quello di poter disporre esplicitamente delle relazioni (4.8) e (4.9) che legano univocamente tensione iniziale teorica e tensione finale, mentre nel modello Adams® le curve in figura 4.8 sono state ottenute per punti effettuando numerose simulazioni successive e variando i settaggi dei parametri.

Il risparmio in termini di tempo è evidente ed è in linea con l’obiettivo del presente lavoro di fornire uno strumento in grado di dare indicazioni per il calcolo della trasmissione in maniera rapida e con il grado di accuratezza richiesto nelle fasi di scelta di massima tra diverse soluzioni costruttive.

4.4.2 Risultati del modello a parametri concentrati

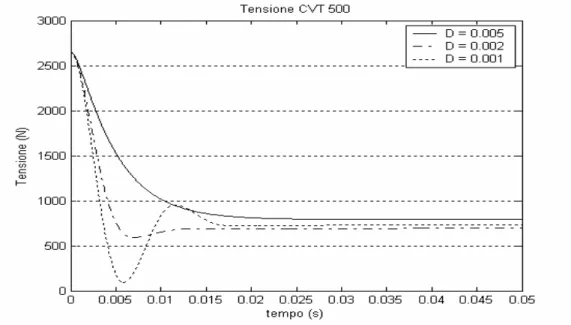
Una rappresentazione temporale di quanto avviene durante la fase di assestamento della cinghia è fornita dal modello a parametri concentrati implementato in ambiente Simulink®. Le figure 4.9 e 4.10 illustrano l’andamento della tensione e del raggio di avvolgimento sulla puleggia motrice del CVT 200, mentre le figure 4.11 e 4.12 si riferiscono a quanto accade sul CVT 500. Nei diagrammi riportati è chiaramente evidenziata la dipendenza dell’evoluzione temporale delle grandezze in esame dal rapporto di smorzamento di contatto D.

Fig. 4.9 Andamento della tensione nella cinghia del CVT 200

Fig. 4.11 Andamento della tensione nella cinghia del CVT 500

Fig. 4.12 Raggio di avvolgimento su puleggia motrice CVT 500

In tutti i casi analizzati la durata dell’assestamento della cinghia è stimabile attorno ai 15-20 ms, ma le simulazioni sono state effettuate considerando un tempo di 50 ms per verificare che non vi fossero comportamenti numerici anomali nel modello e che la configurazione di equilibrio raggiunta fosse effettivamente stabile.

Anche in questo caso i risultati del modello trovano piena conferma con quanto già disponibile in Adams®; a titolo di esempio si riporta in figura 4.13 un esempio di transitorio dinamico della fase di assestamento ricavato tramite il modello multibody.

Fig. 4.13 Tensione nella cinghia calcolata tramite modello Adams® --- D = 0.01 s; -- -- -- D = 0.001 s; - - - - D = 0.0001 s

Il tempo di assestamento calcolato in ambiente Adams® risulta essere attorno ai 20 ms, e comunque sempre inferiore ai 30 ms in tutte le analisi effettuate.

4.4.3 Confronto tra i modelli proposti

Nella tabella 4.3 si riassumono i risultati ottenuti tramite i due modelli definiti nel presente capitolo e che costituiscono dei dati di ingresso fondamentali per il modello dinamico descritto in dettaglio nel capitolo seguente.

CVT 200

CVT 500

Modello Continuo Simulink Continuo Simulink

Raggio effettivo puleggia

motrice (mm) 27.694 27.695 41.027 41.028 Raggio effettivo puleggia condotta (mm) 68.470 68.469 89.267 89.266 Rapporto di trasmissione effettivo 0.404 0.4596 Tensione effettiva (N) 481 474.5 803.3 791.5

Per quanto riguarda la trasmissione CVT 200, la penetrazione radiale subita dalla cinghia è dell’ordine dei 6 centesimi di mm per la puleggia motrice e dei 7 centesimi di mm per quella condotta; per il CVT 500 il valore si assesta attorno ai 0.07 mm per entrambe le pulegge. È stato calcolato anche il rapporto di trasmissione effettivo per entrambi i CVT: si nota che la variazione di τ è praticamente ininfluente in quanto la cinghia subisce uno spostamento radiale su entrambe le pulegge all’incirca della stessa entità.

Ad una variazione di lunghezza della cinghia dell’ordine di pochi decimi di mm è associata tuttavia una variazione di tensione consistente: il valore finale della tensione cala di circa il 70% nel CVT 500 e addirittura del 77 % nel CVT 200. Questo risultato è strettamente legato alla notevole rigidezza estensionale delle cinghie utilizzate, ed in particolare alla rigidezza delle fibre longitudinali di rinforzo, che conferiscono loro una grande resistenza a trazione e permettono la trasmissione di coppie elevate.

Nel modello continuo sono stati assunti quali parametri caratteristici del contatto i seguenti valori: Kl = 6000 N/mm2 ed e = 1.5; per quanto concerne le dimensioni di Kl si ricordi che tale

parametro lega una forza per unità di lunghezza (p) ad uno spostamento (s) come indicato nel paragrafo 4.2.

Nel modello a parametri concentrati invece si sono utilizzati i seguenti valori: Kc = 500000

N/mm ed e = 1.5; in questo caso Kc rappresenta una costante di proporzionalità tra una forza

ed uno spostamento.

I due modelli proposti forniscono in sostanza gli stessi risultati sia per quanto riguarda la tensione che per quanto concerne il raggio; l’errore nella valutazione della tensione iniziale è stimato attorno all’1.5 %, un valore che può essere ritenuto sufficientemente piccolo per considerare attendibili i risultati forniti. Si possono dunque ritenere ragionevolmente affidabili i valori calcolati, per poterli utilizzarli come dati di ingresso del modello completo.