CONSIDERAZIONI PRELIMINARI SUL MODELLO DI TRASMISSIONE SVILUPPATO

Capitolo 3

CONSIDERAZIONI PRELIMINARI SUL MODELLO DI

TRASMISSIONE SVILUPPATO

3.1 Generalità

Il modello a parametri concentrati scelto in questa sede per l’analisi della trasmissione CVT nasce dall’esigenza di avere uno strumento per quanto possibile semplice ma che al tempo stesso descriva quei fenomeni che nei modelli analitici classici non vengono in genere considerati, come ad esempio l’effetto delle forze di inerzia [3].

In linea teorica la realizzazione di un modello a parametri concentrati prevede la sostituzione delle caratteristiche di un corpo continuo, dotato di proprietà inerziali, elastiche e viscose distribuite, con una serie di elementi aventi masse, rigidezze e smorzamenti concentrati in punti ben definiti. Nel caso in esame il particolare adatto ad essere rappresentato tramite elementi a parametri concentrati è essenzialmente la cinghia, mentre le pulegge possono essere studiate come se fossero indeformabili in quanto in condizioni di esercizio esse subiscono delle deformazioni di entità molto inferiore rispetto a quelle della cinghia.

Il modello dinamico dell’intera trasmissione non si limita però alla sola discretizzazione della cinghia, ma deve prendere in considerazione tutti i fenomeni che influenzano il comportamento del CVT. Occorre allora implementare modelli di schematizzazione per quanto possibile accurati delle sue parti costituenti che sono:

• cinghia • pulegge

• attrito sui fianchi della cinghia

Per motivi di semplicità il modello sviluppato è bidimensionale ed è contenuto nel piano di simmetria longitudinale della trasmissione. Si sono dunque trascurati tutti quei fenomeni spaziali che possono verificarsi, come eventuali vibrazioni laterali della cinghia o configurazioni non simmetriche della cinghia stessa sulle pulegge.

Una ulteriore ipotesi che è stata formulata per il modello sviluppato in questo lavoro è quella di trascurare qualsiasi slittamento macroscopico tra cinghia e puleggia; ciò è giustificato dal fatto che il rapporto tra le velocità angolari della puleggia condotta e di quella motrice in un CVT in fase di funzionamento stazionario si mantiene all’incirca costante, fino a quando non si verifichino fenomeni di strisciamento della cinghia su tutto l’arco di contatto. Questa ipotesi non esclude tuttavia che localmente si abbiano dei microscorrimenti dovuti all’elasticità della cinghia stessa; sono proprio questi scorrimenti locali che originano le forze di attrito tra le pulegge e l’organo di trasmissione del moto.

La costruzione di un modello matematico normalmente avviene in più fasi secondo livelli crescenti di complessità: in un primo step si considerano solo gli aspetti fondamentali per la descrizione del comportamento del sistema. Nelle fasi successive si potrà procedere all’inserimento nel modello dei dettagli secondari che contribuiscono a renderlo sempre più accurato sebbene più oneroso da sviluppare.

Seguendo questa logica, nel presente lavoro di tesi si è preferito costruire un modello della cinghia che contenesse in primo luogo gli aspetti fondamentali di funzionamento, lasciando a ulteriori sviluppi futuri il compito di migliorarne l’accuratezza includendo aspetti qui trascurati.

Per fare ciò si è scelto di discretizzare soltanto quella parte di cinghia a contatto con le pulegge; nei due tratti rettilinei (ramo teso e ramo lento) il modello prevede la presenza di una sola molla estensionale di opportuna rigidezza. È stata poi trascurata l’influenza della rigidezza flessionale della cinghia, poiché, se i raggi di avvolgimento non sono troppo piccoli, essa non influenza sensibilmente le pressioni di contatto e le tensioni nella cinghia (cfr. [5]).

Inoltre la dinamica della trasmissione verrà studiata sia simulando una fase di partenza da fermo sia in condizioni di funzionamento stazionario, imponendo un andamento della velocità angolare alla puleggia motrice..

Nei paragrafi successivi saranno illustrati in dettaglio le ipotesi adottate, le semplificazioni effettuate e le relazioni fondamentali utilizzate nella modellizzazione di ciascuna delle componenti che costituiscono il modello della trasmissione CVT.

3.2 Discretizzazione della cinghia

Come è già stato accennato nel paragrafo introduttivo, si è scelto di modellare con elementi a parametri concentrati quella parte di cinghia all’interno dell’arco di contatto con le pulegge; la cinghia è stata dunque suddivisa in un numero prestabilito di elementi equidistanti tra loro, dotati di massa e connessi da elementi elastici e smorzanti che simulano le proprietà elastiche e viscose di ciascun tratto di cinghia, come mostrato in fig. 3.1.

s m,Ixx,Iyy,Izz egmenti y x elementi Kt Ct segmenti di cinghia elementi R1 Ramo teso Ramo lento Kspan

Fig. 3.1 Schema degli elementi e delle connessioni elastiche e smorzanti

Ogni elemento è assimilato ad un punto materiale (massa puntiforme) ed è vincolato a muoversi nel piano di simmetria longitudinale della trasmissione; possiede pertanto solo i due gradi di libertà relativi al moto piano.

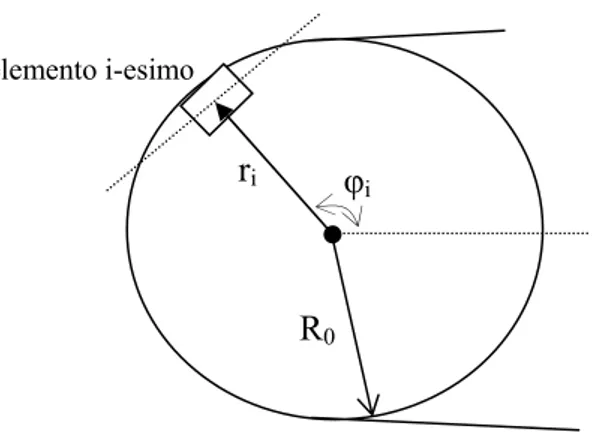
Il sistema di riferimento adottato per descrivere il moto di ciascun elemento è un riferimento in coordinate polari (r,φ) avente origine nel punto di intersezione tra l’asse di rotazione della puleggia e il piano su cui avviene il moto della cinghia. Dato che le pulegge sono due, sono anche due i sistemi di riferimento utilizzati; ciascun riferimento descrive il moto degli elementi a contatto con la rispettiva puleggia.

In definitiva il moto di ogni elemento è descritto

o dalla coordinata angolare φ misurata a partire dalla retta che unisce i centri delle pulegge e che individua la posizione dell’elemento all’interno dell’arco di contatto; o dalla distanza r dall’asse della puleggia che individua la posizione radiale del generico

elemento (fig. 3.2).

Gli elementi tuttavia non seguono il movimento di rotazione della cinghia attorno alle pulegge ma, oltre alle oscillazioni in direzione radiale, compiono esclusivamente delle oscillazioni tangenziali attorno alla loro posizione iniziale, mantenendosi quindi all’incirca nella posizione angolare di partenza; ne risulta una configurazione dinamica degli elementi

caratterizzata da piccole oscillazioni attorno ad una posizione di equilibrio stabile e da conseguenti variazioni della tensione nella cinghia.

ri _φi

elemento i-esimo

R0

Figura 3.2 Sistema di coordinate che descrive il moto dell’elemento

Questo comportamento del modello è giustificato dal fatto che, mentre una “particella” della cinghia compie materialmente un giro completo sul percorso di avvolgimento, l’andamento delle grandezze che caratterizzano il moto della cinghia è praticamente statico. In altri termini, se si adotta il punto di vista euleriano, ossia se si fissa un punto preciso dello spazio e si osserva l’andamento delle grandezze misurate in quel punto al passare del tempo, si trova che tali grandezze sono “quasi stazionarie” e variano considerevolmente solo cambiando la porzione dello spazio in esame.

Il numero totale di elementi che definiscono il modello può essere assegnato arbitrariamente, così come arbitraria è la ripartizione degli elementi tra puleggia motrice e condotta; tuttavia si osservi che, poiché ogni elemento ha due gradi di libertà, raddoppiando il numero complessivo di elementi si quadruplica il numero di equazioni necessarie per risolvere il problema. Occorre dunque cercare di avere un numero di elementi che costituisca un compromesso tra l’esigenza di una elevata accuratezza del modello e la sua rapidità di soluzione.

3.2.1 Calcolo delle caratteristiche elastiche e smorzanti degli elementi di cinghia

Le connessioni inserite tra due elementi comprendono una molla di rigidezza Kt che

schematizza la rigidezza estensionale della cinghia, e uno smorzatore viscoso di costante Ct

che tiene conto della isteresi del materiale e delle dissipazioni di energia che tendono a smorzare le vibrazioni longitudinali della cinghia. Tali elementi possono, in prima approssimazione, essere considerati lineari.

I rami rettilinei della cinghia vengono invece sostituiti (fig. 3.3) da una molla di costante Kspan

e da uno smorzatore viscoso di rigidezza Cspan (non rappresentato in figura) che collegano

l’elemento di ingresso sulla prima puleggia e quello di uscita sulla seconda nel ramo teso, e viceversa per il ramo lento.

Dalla teoria dei continui si ricava che la rigidezza a trazione di un tratto di un corpo continuo di lunghezza L si può esprimere come

L A E

K = ⋅ (3.1)

Fig. 3.3 Schema degli elementi del modello e rigidezze dei tratti rettilinei

dove E è il modulo elastico del corpo in esame ed A è l’area della sua sezione trasversale. Nel nostro caso, se si indica con l0 la distanza tra due masse puntiformi successive a cui sono

attaccati gli estremi delle molle, la costante Kt deve essere tale da riprodurre attraverso un solo

elemento l’elasticità del tratto di cinghia corrispondente; si deve allora necessariamente avere

0 l A E K K_t = = ⋅ _(3.2)

Come si vede dalla equazione (3.15) la costante Kt viene a dipendere, oltre che dalle proprietà

della cinghia, anche dalla lunghezza dell’elemento di cinghia e, dunque in ultima analisi, dal numero di elementi con cui la si discretizza.

Il valore dell’area della sezione trasversale è un dato di non facile attribuzione, a causa della presenza della dentellatura inferiore della cinghia e merita un discorso a parte nel paragrafo 3.2.2. R2 R1 Kspan Ramo teso Kspan Ramo lento

Per quanto riguarda i coefficienti di smorzamento, si fa l’ipotesi che essi siano proporzionali alle rigidezze, ossia tra gli elementi della matrice di rigidezza [K] e quelli della matrice di smorzamento [C] si abbia una relazione del tipo

[ ]

C =D⋅[K] (3.3)

Si parla allora in questi casi di smorzamento proporzionale (cfr. [8]).

Per quanto riguarda i valori da attribuire al fattore di smorzamento D sono state effettuate numerose prove sul modello variandone il valore e confrontando la risposta del sistema in modo da ottenere un valore realistico di tale parametro.

3.2.2 Definizione delle caratteristiche geometriche ed inerziali della sezione della cinghia

La sezione della cinghia viene considerata di materiale omogeneo, di spessore sottile e costante. In realtà la cinghia reale ha uno spessore non trascurabile, non è omogenea in quanto presenta dei rinforzi in materiale ad elevata rigidezza, ricoperti da gomma o materiale elastico avente le funzioni di protezione del rinforzo e di aderenza con i fianchi delle pulegge, e inoltre non è a sezione trasversale costante, come già illustrato nel paragrafo 1.3.

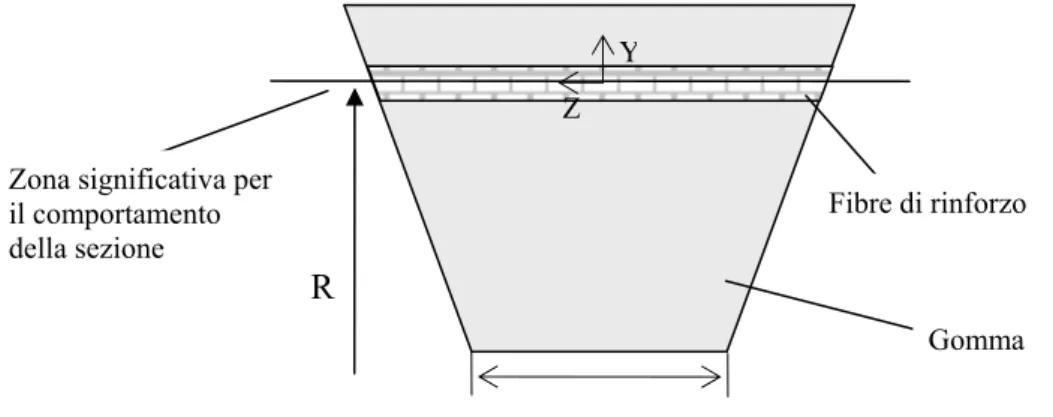
In questa sede si è scelto di considerare la zona del rinforzo come significativa del comportamento dell’intera sezione; ciò equivale ad assimilare la cinghia ad un nastro sottile posizionato sulle pulegge all’altezza delle fibre di rinforzo, come indicato nella fig. 3.4, e sul quale agiscono tutte le forze esterne comprese quelle di contatto con le pulegge. Tutti i raggi di avvolgimento indicati nel modello si riferiscono a questa quota.

Y

Fig. 3.4 Sezione della cinghia

Il valore A dell’area della sezione trasversale e il modulo di Young E sono, come detto, dati di difficile attribuzione. Tuttavia non sono interessanti i valori assunti singolarmente da questi

Z

Fibre di rinforzo Zona significativa per

il comportamento della sezione

R

due parametri, bensì il loro prodotto EA, che costituisce la rigidezza estensionale della cinghia. Perciò è possibile assumere un valore “comodo” dell’area A e calcolare poi di conseguenza un modulo di Young equivalente che fornisca lo stesso valore del prodotto EA. Si sceglie di calcolare A della cinghia di sezione omogenea come media aritmetica tra le sezioni di area massima della cinghia reale, in prossimità delle creste della dentellatura, e quelle di area minima, in corrispondenza degli incavi.

Il calcolo del modulo di Young equivalente può essere effettuato nel modo seguente: si consideri un tratto di cinghia di lunghezza l e costituito da una parte in gomma di sezione Ag e

modulo di Young Eg, e da un rinforzo in fibre di area complessiva Ar e modulo di Young Er

(figura 3.5).

Figura 3.5 Schema per il calcolo del modulo di Young equivalente

Applicando una forza F di trazione alle estremità del segmento si ha che questo si allunga di una quantità ∆l, mentre la parte in gomma e il rinforzo assorbono una quota della forza F proporzionalmente alla loro rigidezza.

Si ha allora r g r r r g g g F F F l E A F l E A F l + = ⋅ = ⋅ = ∆

Esplicitando Fg nella seconda relazione e sostituendolo nella prima, dopo alcuni passaggi si

ottiene la seguente l E A E A F F r r g g r ∆ + = da cui anche l Gomma Ag, Eg Rinforzo Ar, Er

F

_F

∆l/2

l E A E A F l r r g g ⋅ + = ∆ _(3.5)

Se ora si prende in considerazione un tratto di cinghia omogeneo di lunghezza l, sezione trasversale A = Ag+Ar, calcolata per quanto detto in precedenza come media tra le aree

minima e massima della sezione trasversale, e di modulo di Young E, affinché sotto l’azione di F questo tratto subisca lo stesso allungamento ∆l si deve avere, confrontando con la (3.5),

l E A E A F l EA F l r r g g ⋅ + = ⋅ = ∆ _(3.6)

Dalla (3.6) discende la relazione cercata

A E A E A A A E A E A E g g r r r g r r g g ₌ + + + = (3.7)

Il valore del modulo di Young calcolato con la (3.7) è quello da utilizzare poiché il modello illustrato in questa sede necessita di una cinghia di materiale omogeneo e di sezione costante. In questa analisi si è trascurato il contributo delle sollecitazioni di taglio; se si considera la struttura di una cinghia trapezoidale così come illustrata nel capitolo 1 e si tiene conto del fatto che essa reagisce prevalentemente a forze di trazione e, in misura minore, anche a sollecitazioni flessionali ma ha una rigidezza a taglio trascurabile rispetto alle precedenti, si comprende come una tale scelta risulti giustificata.

Ad ogni elemento è associata una propria massa m, mentre agli elementi elastici sono associate le grandezze strutturali di un tratto di cinghia in modo tale che l’insieme massa-elementi di connessione risulti globalmente equivalente al tratto di cinghia in esame.

La massa associata ad ogni elemento è data dalla relazione A

l

m=ρ⋅ ₀ ⋅ (3.4)

dove ρ è la densità media della cinghia, l0 è la lunghezza del tratto compreso tra due elementi

successivi e A l’area della sua sezione trasversale media in condizioni di assenza di carico.

3.3 Modellazione delle pulegge

Ogni puleggia è rappresentata da un unico corpo rigido, assimilabile ad un cilindro dotato di una gola a V su cui si avvolge la cinghia.

Per la definizione di ciascuna puleggia occorre assegnare il rispettivo raggio R caratteristico del rapporto di trasmissione in esame e il momento di inerzia attorno al suo asse di rotazione I. Il raggio R rappresenta anche la distanza nominale dall’asse a cui si dispone il nastro che rappresenta la cinghia in condizioni di assenza di carico, ossia quando non si ha tensione sui rami. Tuttavia in condizioni di esercizio la cinghia subisce uno spostamento radiale; allora tutte le forze che la cinghia esercita sulla puleggia possono considerarsi applicate ad una distanza dall’asse pari al raggio di avvolgimento R meno la penetrazione radiale della cinghia. Tali forze sono date dalla sommatoria, effettuata su tutti i segmenti presenti nell’arco di contatto con la cinghia, delle forze di contatto e di strisciamento che gli elementini esercitano sui fianchi inclinati delle due semipulegge. Se il CVT lavora in condizioni di rapporto di trasmissione costante, ossia se non è in fase di cambiata, si può ritenere che tali forze siano simmetriche rispetto al piano longitudinale della trasmissione.

In questa sede si assume sempre fissato il rapporto di trasmissione, lasciando a lavori futuri il compito di sviluppare un modello dinamico che simuli la fase di cambiata.

Inoltre viene assegnata la velocità angolare alla puleggia motrice, mentre sulla puleggia condotta viene applicata una coppia resistente costante, il cui valore va ricercato per tentativi fino a quando la sua velocità angolare si mantiene costantemente attorno ad un certo valore. La differenza tra tale valore “di equilibrio” della velocità angolare e quello calcolato teoricamente considerando il rapporto di trasmissione τ permette di stimare le perdite tra la velocità dell’albero di ingresso e quello di uscita alla ruota e, dunque, fornisce una prima stima del rendimento della trasmissione.

3.4 Modellazione del contatto cinghia – puleggia

La modellazione del contatto tra due corpi è una operazione delicata, che richiede una valutazione adeguata dei vantaggi e delle problematiche connesse ai vari metodi proposti in letteratura. In questa sede si è scelto di modellare il contatto tra cinghia e puleggia facendo ricorso a una relazione del tipo:

p C p K F e _l l ⋅ + ⋅ & = (3.8)

La forza di contatto è data da un termine elastico, avente costante Kl, e da un termine viscoso

di costante Cl che tiene conto della velocità di penetrazione dei due corpi e rappresenta quei

fenomeni di isteresi e smorzamento strutturale che si hanno nella cinghia. Per semplicità si è scelto di utilizzare un esponente di contatto e pari a 1.

In realtà nel presente modello, così come accade per la tecnica “Penalty”, si parla di penetrazione radiale “fittizia”, ossia si immagina che la forza di contatto derivi da una compenetrazione tra i due corpi a contatto tra loro. Dal punto di vista fisico ciò risulta molto intuitivo: i due corpi a contatto in realtà non subiscono nessuna penetrazione tra loro, ma essenzialmente una compressione delle superfici a contatto, e la forza di contatto risulta legata all’entità di tale compressione, secondo dei parametri che dipendono dalla natura dei corpi a contatto.

Anche per il problema del contatto occorre riportare la cinghia reale ad una cinghia equivalente a sezione costante e di spessore sottile. La riduzione della cinghia trapezoidale ad una cinghia piatta avviene nel modo di seguito illustrato.

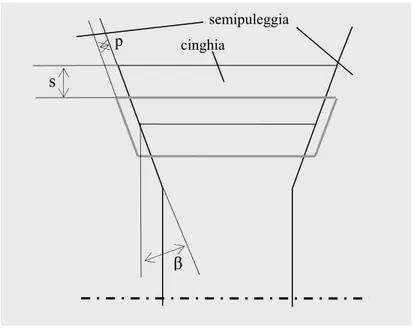
La penetrazione effettiva sui fianchi p è legata alla penetrazione radiale s della cinghia (figura 3.6) secondo la relazione seguente

β

sin ⋅ = s p

in cui compare anche l’angolo d’inclinazione del fianco della cinghia β.

p _cinghia

Fig. 3.6 Relazione tra spostamento radiale e penetrazione del segmento di cinghia Derivando rispetto al tempo la precedente relazione si ricava

β

sin ⋅ = s p_{& &}

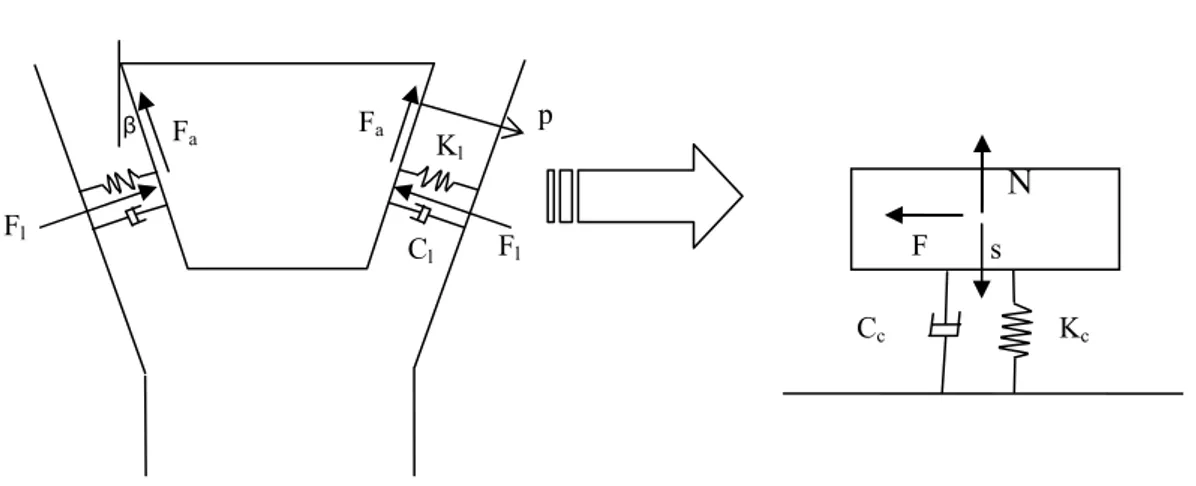
Riferendosi alla fig. 3.7, la forza sviluppata dall’elemento elastico sul fianco della cinghia vale e e l e l elast l K p K s F_, =2⋅ ⋅ =2⋅ ⋅ ⋅(sinβ) (3.9)

mentre quella dello smorzatore vale s

β

e e l e l damp l C p C s

F_, =2⋅ ⋅ _& =2⋅ ⋅_& ⋅(sinβ) (3.10)

Ponendo e=1 le componenti in direzione radiale delle due forze valgono rispettivamente 2 , ⋅sin(β)=2⋅ ⋅ ⋅(sinβ) =F K s N_{elast lelast l} (3.11) 2 , ⋅sin(β)=2⋅ ⋅ ⋅(sinβ) =F C s

N_{damp ldamp l} & (3.12)

Se ora per semplicità si pongono nelle (3.11) e (3.12) 2 ) (sin 2⋅ ⋅ β = _l c K K (3.13) 2 ) (sin 2⋅ ⋅ β = _l c C C (3.14)

l’espressione della forza di contatto radiale sulla cinghia “equivalente” si può scrivere come s

C s K

N = _c⋅ + _c⋅& (3.15)

Fig. 3.7 Passaggio dalla cinghia reale alla cinghia piatta “equivalente” mentre l’espressione della forza sul fianco della cinghia diventa

β β sin 1 ) ( sin = ⋅ + ⋅ ⋅ = N K s C s F_{l c c & (3.16)} Kc Kl Cl p Fa β _Fa N Fl _F l F s Cc

3.5 Modellazione dell’attrito

Tra i fianchi dell’elemento di cinghia e la gola della puleggia nascono, oltre alle forze di contatto normali, anche delle forze di attrito dirette in verso opposto alla velocità di strisciamento tra i due corpi e proporzionali alla forza di contatto normale al fianco della cinghia. In generale la velocità relativa tra cinghia e pulegge non è esclusivamente tangenziale ma presenta anche una componente in direzione radiale [3]. Dunque anche l’azione della forza di attrito si esplica nelle due direzioni radiale e tangenziale.

Tuttavia, se si considera che lo spostamento radiale della cinghia in condizioni di funzionamento è molto piccolo (si tratta in pratica di piccoli assestamenti), si comprende come molti autori scelgano di modellare l’attrito considerando la sola componente tangenziale e trascurando lo strisciamento radiale (cfr. [6]). Una ulteriore ipotesi che è ragionevole fare è quella di considerare in prima approssimazione il coefficiente di attrito indipendente dalla velocità di strisciamento ed uguale al suo valore statico; ciò perché, come chiarito nel paragrafo 3.1, si trascurano gli scorrimenti macroscopici globali che possono avere luogo tra cinghia e pulegge e dunque il valore della velocità relativa si mantiene su valori molto piccoli. In una cinghia trapezoidale il modulo della forza di attrito è proporzionale alla forza sul fianco:

l

F

F =µ⋅ (3.17)

dove µ è il coefficiente di attrito statico (o di primo distacco).

Se invece si considera la cinghia piatta equivalente, quello che si ricerca è un legame tra l’attrito e la componente radiale della forza di contatto. Allora il legame tra la forza normale e la forza di attrito agente su un elemento generico si ottiene sostituendo nella relazione precedente la (3.16): β µ sin N F = ⋅ _(3.18)

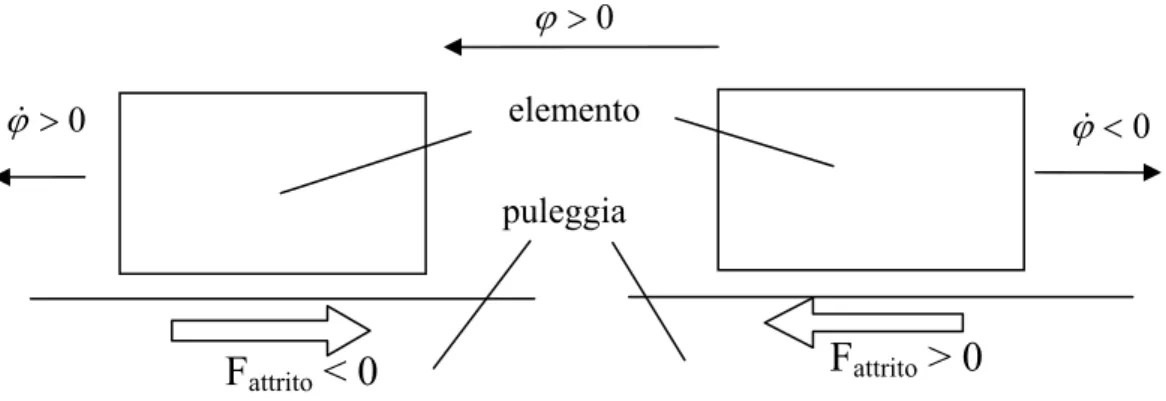
Il segno della forza di attrito è legato al verso dello scorrimento microscopico che si ha tra l’elemento e la puleggia; in particolare la forza di attrito è diretta in verso opposto a tale scorrimento (fig. 3.8).

Fig. 3.8 Verso dello scorrimento microscopico e della relativa forza di attrito

3.6 Problematiche relative alla pretensione iniziale nella cinghia

Il modello di CVT illustrato nei dettagli nel presente capitolo non risulta ancora completo poiché si è fin qui trascurato un fenomeno che avviene in fase di montaggio della cinghia sulle pulegge e che influenza fortemente il comportamento della intera trasmissione. Infatti durante l’operazione di avvolgimento nella gola la cinghia non si mantiene ad una quota radiale pari al raggio nominale previsto per il rapporto di trasmissione assegnato; essa si assesta invece su raggi di avvolgimento minori, modificando le tensioni nei rami rettilinei e lungo gli archi di contatto con le pulegge e influenzando in tal modo anche l’entità delle forze di attrito scambiate tra cinghia e puleggia.

Questo accade per il fatto che la cinghia, di lunghezza a riposo inferiore alla lunghezza del percorso teorico di avvolgimento sulle pulegge, dopo l’operazione di montaggio è soggetta ad un allungamento con conseguente pretensionamento. Ciò induce una situazione di non equilibro nella cinghia: la pretensione infatti non risulta equilibrata da alcuna forza, dal momento che alla quota di avvolgimento nominale la penetrazione dei segmenti di cinghia nella gola della puleggia è nulla, e nulle sono quindi anche le forze di contatto. La cinghia si dispone allora su un raggio di avvolgimento minore di quello teorico (figura 3.9) con due effetti: diminuiscono le tensioni effettive nei rami della cinghia e si sviluppano delle forze di contatto sui fianchi che equilibrano tali tensioni. In definitiva la cinghia, trovandosi in una condizione iniziale di non equilibrio, “reagisce” alla pretensione disponendosi su un raggio di avvolgimento minore in modo da raggiungere una condizione di equilibrio statico. L’entità di questo spostamento radiale e il valore della effettiva pretensione nella cinghia non sono calcolabili tramite le relazioni elementari introdotte nel paragrafo 1.4, tuttavia sono di

0 > ϕ_{& ϕ& <0}

F

attrito

< 0

F

attrito

> 0

elemento 0 > ϕ puleggia

fondamentale importanza per il funzionamento del modello, in ne quanto costituiscono la situazione di partenza. Tiniz Tfin p Tfin Tiniz

Fig. 3.9 Condizioni iniziale e finale della cinghia sulla puleggia

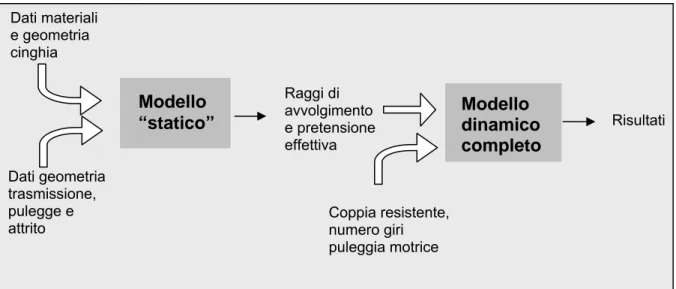
Si è scelto allora di costruire un secondo modello “statico” semplificato che riproduca esclusivamente la fase di assestamento della cinghia sulle pulegge; i risultati forniti da questo modello “preliminare” costituiscono i dati di ingresso per il modello dinamico completo. Il modello statico verrà illustrato nei dettagli nel capitolo successivo, mentre si rimanda al capitolo 5 per i dettagli matematici sul modello dinamico completo.

Per meglio chiarire il funzionamento e il legame tra i due modelli sviluppati si faccia riferimento allo schema in figura 3.10:

Dati materiali e geometria cinghia

Fig. 3.10 Legame tra il modello statico e il modello dinamico completo

Modello “statico” Dati geometria trasmissione, pulegge e attrito Raggi di avvolgimento e pretensione effettiva Modello dinamico completo Risultati Coppia resistente, numero giri puleggia motrice