Capitolo 5 Modello Pacejka-ESDU

(1)

Capitolo 5 – Modello Pacejka-ESDU

Capitolo 5

Modello Pacejka-ESDU

5.1 Introduzione

Attraverso il modello QSTM_08 e la successiva identificazione si è ottenuto, per la velocità angolare della ruota e del tamburo, un andamento molto prossimo a quello del segnale sperimentale, dal quale si discosta non più di qualche percento. Le simulazioni hanno dunque confermato la qualità del modello pur evidenziando il fatto che non sia in grado di approssimare il segnale nei primi istanti successivi all’applicazione del momento frenante. Questo comunque è dovuto al fatto che il modello non prevede l’analisi del transitorio che si instaura subito dopo che il sistema è stato forzato, essendo volto a definire essenzialmente la dinamica di lungo periodo quando i fenomeni transitori sono ormai estinti.

Malgrado il modello QSTM_08 approssimi molto bene i risultati sperimentali, esso tuttavia utilizza delle dipendenze tra le forze (frenante e di rotolamento) e i parametri dinamici del sistema non del tutto soddisfacenti. Infatti, in primo luogo utilizza un legame parabolico tra µ _b ed sx che fornisce risultati soddisfacenti nelle prove in esame – che sono caratterizzate dal fatto che si ha un sx quasi costante, in ogni prova, per la maggior parte del tempo – ma non rappresenta la realtà fisica del legame suddetto per valori qualunque di sx. In secondo luogo il modello è stato dedotto definendo la forza d’attrito di rotolamento come l’unica forza che dissipa energia nel corso della frenata. Questo ha comportato il fatto che nel modello non solo la forza frenante dipende da sx ma anche quella di rotolamento.

Nell’ottica di utilizzare un codice di identificazione per determinare i parametri del modello appare invece senz’altro più conveniente utilizzare per la forza d’attrito di

(2)

Capitolo 5 – Modello Pacejka-ESDU rotolamento il valore che si ottiene mediante formule di letteratura disponibili per puro rotolamento stazionario, concentrando nell’espressione della forza frenante tutti i parametri incogniti da determinare, in particolare la dipendenza da sx. Per quanto riguarda questa dipendenza la scelta più opportuna appare senz’altro quella di utilizzare la MagicFormula di Pacejka che, attraverso un numero relativamente basso di parametri, rappresenta bene la fisica del legame in questione, almeno per frenate stazionarie.

Riassumendo, nel nuovo modello si assume µ_roll =µ_roll₀, utilizzando la (2.55) per valutare

0 roll

µ , mentre per quanto riguarda la quota di forza frenante, nei prossimi paragrafi si sviluppa un modello specifico, basato sulle formule di Pacejka e su modelli di letteratura utili per tenere conto degli effetti legati alla non stazionarietà della frenata.

5.2 Formulazione del modello

5.2.1 La formula di Pacejka

In [9] e [10] viene proposta per la componente longitudinale, fissati il valore del carico normale e la velocità di avanzamento, la struttura così definita:

( )

x D sin

{

C arctan

[

B x E

(

B x arctan

(

B x

)

]

}

y = ⋅ ⋅ ⋅ − ⋅ ⋅ − ⋅ (5.1)

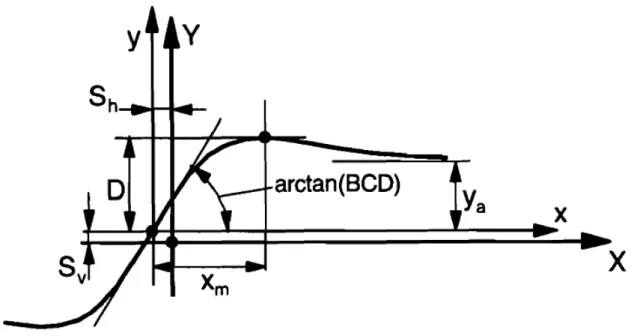
in cui, facendo riferimento alla figura 5.1, y è la componente longitudinale della forza tangenziale, x lo scorrimento pratico e B, C, D, E costanti definite come segue:

• CD BCD CD s F B x sx 0 b = ∂ ∂

= → : fattore di rigidezza (stiffness factor) (5.2)

•       π − = D y arcsen 2 2

C a : fattore di forma (shape factor) (5.3)

• max

b F

(3)

Capitolo 5 – Modello Pacejka-ESDU •

₍

₎

m m m Bx arctg Bx C 2 tg Bx E −       π −

= : fattore di curvatura (curvature factor) (5.5)

Il fattore di forma C controlla i limiti in cui varia l’argomento della funzione seno ed è il responsabile della forma della curva risultante poiché determina il rapporto tra il valore di picco e il valore della funzione per s_x →1. Tipicamente, per pneumatici automobilistici, il valore di C è compreso tra 1.55 e 1.75.

Il fattore di curvatura E è necessario poiché influenza la curvatura della funzione y

( )

x in un intorno delle condizioni di massimo, ma soprattutto il valore della x in cui la curva ha il picco. Tipicamente E assume valori negativi o, se positivi, comunque minori dell’unità per cui derivando la (5.1) si deduce che la funzione y

( )

x è in condizioni di massimo per un valore di x=x_m tale che sia:

(

)

(

)

[

]

2 x B arctan x B E x B arctg C⋅ ⋅ _m − ⋅ ⋅ _m − ⋅ _m = π (5.6)

da cui si deduce il legame (5.5) tra E e x_m .

(4)

Capitolo 5 – Modello Pacejka-ESDU La forma della curva e il numero di massimi e minimi relativi sono determinati dai valori di E e C. Se E<1 e 0 < C ≤ 1 si ha un andamento monotono crescente al valore asintotico

) 2 / C (

Dsen π . Se invece E < 1 ma 1 < C ≤ 2 si ha un massimo relativo per x =x_m con

D ) x (

y _m = ; è questo il caso più importante nelle applicazioni. Nel caso in cui sia E=1 si ha ancora un massimo per x =x_m con y(x_m)=D se Carctang(π/2)>π/2, altrimenti si ha un andamento monotono crescente [5]. Se E >1 si ha sempre almeno un massimo relativo, ma il numero di massimi e minimi relativi dipende dal valore assunto da C. Se

(

1+C2/2

)

<E

− la y"'(0)<0 per cui la curva ha, nel tratto iniziale, derivata seconda negativa, ossia parte con concavità verso il basso. Di solito si assume dunque 1<C<2 e

(

1+C2/2

)

<E<1

− , in modo che la curva di equazione (5.1) parta dall’origine degli assi

(

x = y=0

)

con concavità verso il basso, raggiunga un solo massimo relativo y(x_m)=D

portandosi poi ad un asintoto orizzontale. Inoltre la curva è antisimmetrica rispetto all’origine (funzione dispari) pertanto si ha sempre che y

( )

0 =0 e y′′

( )

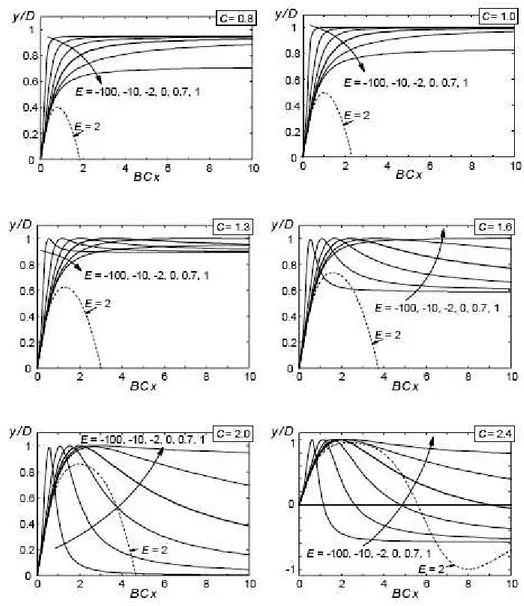
0 =0.

La figura 5.2 ([9]) illustra l’influenza dei parametri C ed E sulla funzione y. I diagrammi sono riportati normalizzando y attraverso il fattore di picco D e moltiplicando lo scorrimento x per BC in modo tale che il picco della curva e la pendenza nell’origine siano indipendenti dai parametri C ed E. Dalla figura è chiaramente visibile che per E>1 si ottengono delle curve non realistiche.

Il restante parametro B è utilizzato per fissare la pendenza nell’origine ed è quindi chiamato fattore di rigidezza. Ovviamente dato che B>0, C e D devono essere necessariamente dello stesso segno.

Per modellare la presenza della resistenza di rotolamento 0 roll

F , occorre permettere alla (5.1) di assumere un valore non nullo in corrispondenza della condizione x=0; questo si ottiene passando in un nuovo sistema di riferimento

(

O,X,Y

)

che rispetto al sistema precedente

(

o,x,y

)

è definito dalle:

( ) ( )

h v S x X S x y X Y − = + = (5.7)

risulta ovvio che

0 roll v F

(5)

Capitolo 5 – Modello Pacejka-ESDU

figura 5.2 Influenza dei fattori C ed E sulla funzione y.

Nel nostro caso, volendo descrivere solamente la forza F sarà sufficiente fare _b riferimento all’equazione (5.1) aggiungendo gli effetti del puro rotolamento, come già detto, attraverso la (2.55).

La formula così descritta è relativa ad un determinato carico e una precisa velocità di avanzamento. Spesso i parametri B, C, D, E vengono però resi dipendenti dal carico verticale secondo delle relazioni empiriche, ad esempio ([5],[9]):

z 2 z 1 z maxF (a F a )F D=µ = + (5.8)

(6)

Capitolo 5 – Modello Pacejka-ESDU espressioni possono essere:

(a5Fz) z 4 2 z 3 e F a F a D C B⋅ ⋅ = ⋅ +_⋅ ⋅ (5.10) 8 z 7 2 z 6 F a F a a E= ⋅ + ⋅ + (5.11)

in cui i coefficienti ai sono ottenibili dalla sperimentazione.

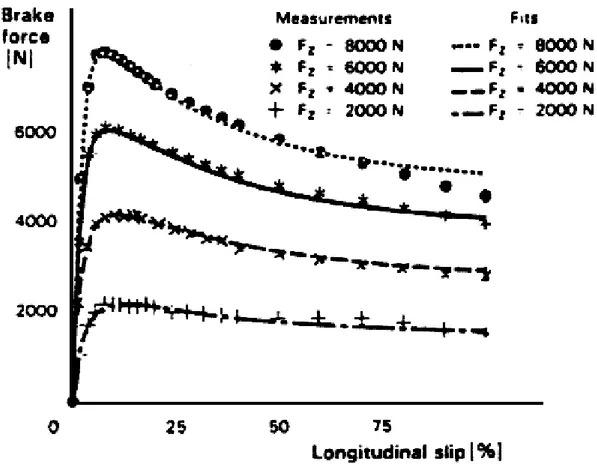
La figura 5.3 ([9]) illustra il confronto tra i dati sperimentali, registrati durante test a carichi verticali differenti, e le curve ottenute attraverso applicazione della Magic Formula; come si può notare la formula rappresenta molto bene l’andamento dei dati.

figura 5.3 Confronto dei dati sperimentali della F_b

( )

s_x , registrati durante test a carico verticale variabile, con le curve ottenute attraverso la Magic Formula.

(7)

5.2.2 Variazione dell’attrito con la velocità

La Magic formula non prende però in considerazione la variazione della velocità di avanzamento della ruota, parametro fondamentale nelle applicazioni aeronautiche. Infatti mentre i pneumatici montati su veicoli terrestri vengono testati a velocità costante, in quanto in tale ambito è fondamentale l’analisi delle forze longitudinali nella condizione di regime al fine di poter minimizzare i consumi, nelle applicazioni aeronautiche l’uso del pneumatico è fondamentale nelle fasi di taxing, di atterraggio e decollo durante le quali si assiste ad una variazione repentina della velocità. Inoltre già l’identificazione del modello QSTM_08 aveva evidenziato come la dipendenza esplicita della F dalla velocità di _b avanzamento non potesse essere annullata, in modo particolare per i test1 e 2, pena un pessimo inseguimento del segnale sperimentale con repentino bloccaggio della ruota e del tamburo.

Purtroppo, la variabilità della F in funzione della velocità di avanzamento, è quasi _b completamente assente in letteratura, solamente in [12] si trovano grafici relativi alle funzioni µ_max =f₁(V) e µ_skid/µ_max =f₂

( )

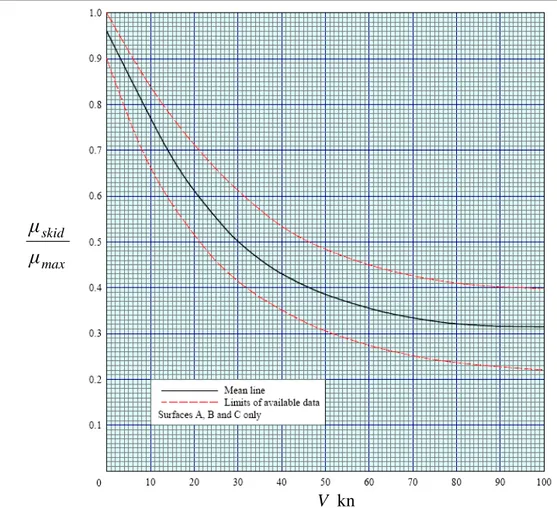
V , in cui µ_skid rappresenta il coefficiente di attrito per s_x =1 (notare come il parametro C sia funzione del rapporto µ_skid/µ_max ). Tali andamenti derivano da misure dirette della forza frenante sviluppata da aeroplani, veicoli stradali e macchine di prova. In particolare le misure del coefficiente massimo d’attrito vengono realizzate direttamente su pneumatici di velivoli in atterraggio oltre che su pneumatici automobilistici montati su macchine di prova. I valori del coefficiente d’attrito in condizioni di bloccaggio incipiente vengono invece registrati durante test realizzati mediante macchine di prova simulanti le condizioni d’atterraggio, in termini di carico e velocità, sulle quali vengono montati carrelli principali di velivoli. Le figure 1.1a e 5.4 illustrano tali dipendenze per manto stradale molto liscio per il quale la rugosità superficiale media è di 0.10÷0.15 mm, considerandola sufficientemente rappresentativa della rugosità che può caratterizzare un tamburo in acciaio. Le prove, da cui derivano le figure suddette, sono state svolte su pneumatici aeronautici alla pressione di gonfiaggio di 13.8 bar, sia su fondo asciutto che su fondo bagnato, utilizzando il carico verticale rappresentato in figura 5.5, in cui Vi rappresenta la velocità al momento dell’applicazione del momento frenante. Purtroppo la variabilità del carico verticale con la velocità di

(8)

V kn

figura 5.4 Curva µ_skid/µ_max =f₂

( )

V per manto stradale con rugosità superficiale media di 0.10÷0.15 mm per pneumatico aeronautico alla pressione di gonfiaggio p_i =13.8bar.

coincide con le modalità di prova dei test in nostro possesso, caratterizzati da carico costante. In ogni caso questo fatto non introduce un errore significativo nell’analisi che si sta conducendo in quanto il carico di figura 5.5 è sostanzialmente costante per velocità minori agli 80 m/s, velocità superiore a quella per la quale, nei test in nostro possesso, si inizia la frenata.

Come si può osservare dalla figura 1.1(a) il coefficiente di attrito massimo aumenta al diminuire della velocità per cui, a parità di carico verticale, la forza F sposta il suo _b massimo a valori sempre maggiori al diminuire della velocità. E’ da notare comunque come la pendenza della curva in questione sia molto bassa, dell’ordine di 10−3

[ ]

kn−1

(≈5.14⋅10−4

[ ]

m/s −1).

Per quanto riguarda la funzione x_m =f_m

( )

V non si conosce alcun tipo di informazione se non quella reperibile dalla figura 5.6, tratta da [13], secondo cui il valore di x_m sembra

max skid

µ

(9)

figura 5.5 Variazione con la velocità V di avanzamento del carico verticale applicato

sulla ruota.

spostarsi verso destra al diminuire della velocità. Inoltre le variazioni del coefficiente di attrito massimo e del coefficiente µ_skid, osservabili in figura 5.6, risultano concordi con le figure 1.1(a) e 5.4 tratte da [12].

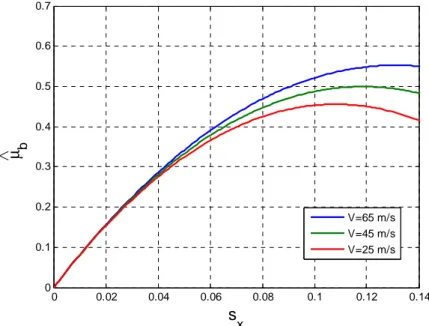
A fronte di questi andamenti, al fine di poter effettuare un raffronto che funga da conferma sulla correttezza delle strutture formulate, nel modello QSTM_08, per F e per il _b termine di F_roll funzione di s_x, si è diagrammata la variazione della forza Fˆ_b in funzione della velocità di avanzamento, figura 5.7, intendendo Fˆ_b come costituita da tutti i termini della forza longitudinale funzioni dello scorrimento pratico, ossia:

(

) (

)

x roll₀ b 2 x 2 x x s 2 x roll 0 roll b roll F 1 K s N K s K s sign(s )N F Fˆ F F= + =µ + + _µ + = + (5.12) da cui:

(

K s K s

)

sign(s )N N s K Fˆ_b =µ_roll₀ _roll _x2 + _µ_s_x _x + ₂ _x2 _x (5.13)

Il confronto tra le figure 5.6 e 5.7 evidenzia come attraverso il modello QSTM_08 si ottengano curve con andamenti opposti. Ossia, mentre nella figura 5.6, max

b

(10)

Capitolo 5 – Modello Pacejka-ESDU diminuire della velocità, spostandosi verso destra, nella figura 5.7 diminuisce al diminuire della velocità, spostandosi verso sinistra. Tale comportamento, in netta contrapposizione a quanto illustrato fino ad ora, evidenzia il fatto che, come già detto, il legame parabolico tra

b

ˆ

µ ed sx non rappresenta in modo soddisfacente la realtà fisica del problema.

figura 5.6 Andamento del coefficiente di attrito µ_b(s_x) al variare della velocità di avanzamento. 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 s x µ b V=65 m/s V=45 m/s V=25 m/s

figura 5.7 Andamento del coefficiente di attrito µˆ_b(s_x) al variare della velocità di avanzamento.

(11)

5.3 Identificazione del sistema ruota-tamburo

5.3.1 Modello di simulazione

Il nuovo modello, come introdotto nel paragrafo 5.1, è stato realizzato descrivendo la forza frenante mediante la formula di Pacejka modificata attraverso i modelli di letteratura proposti, in modo tale da tenere conto degli effetti legati alla non stazionarietà della frenata, non contemplati dalla Magic Formula. In effetti, non possedendo alcun diagramma circa le curve µ_max =f₁(V) e µ_skid/µ_max =f₂

( )

V relative ai carichi verticali dei test in nostro possesso, si è optato per degli andamenti che riprendessero almeno quelli osservati nelle figure 1.1(a) e 5.4.

In particolare l’andamento del coefficiente d’attrito massimo in funzione della velocità di avanzamento V è stato rappresentato attraverso una linearizzazione attorno alla condizione rappresentata dal carico nominale Nnom e dalla velocità massima Vmax per il pneumatico in

esame, ossia: max max V 0 0 N 0 max V V V ) N ( a N N N ) N ( a a ) V , N ( = + − + − µ (5.14)

in cui aN e aV rappresentano dei coefficienti adimensionali considerati negativi al fine di

ottenere un andamento per la µ_max decrescente all’aumentare del carico verticale e della velocità, congruentemente a quanto analizzato nel paragrafo 5.2.2.

La curva µ_skid/µ_max =f₂

( )

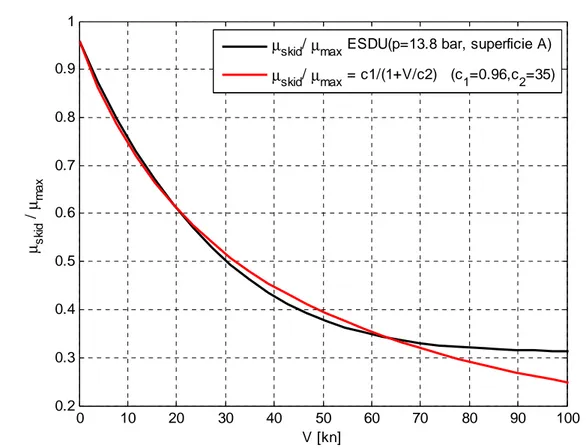
V viene rappresentata, in funzione del carico verticale applicato, mediante l’equazione:

) N ( c V 1 ) N ( c ) V , N ( 2 1 max skid + = µ µ (5.15)

in cui c1 e c2 sono dei coefficienti funzioni del carico verticale N. L’equazione (5.15)

(12)

Capitolo 5 – Modello Pacejka-ESDU 0 10 20 30 40 50 60 70 80 90 100 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 V [kn] µ ski d /µ m a x

µskid/ µmax ESDU(p=13.8 bar, superficie A)

µskid/ µmax = c1/(1+V/c2) (c1=0.96,c2=35)

figura 5.8 Variazione di µ_skid/µ_maxcon la velocità di avanzamento V.

per velocità inferiori ai 35 Kn, valore superiore a quello per il quale vengono iniziati i tre test in esame.

Un’ulteriore ipotesi adottata nel modello, conseguente della mancanza di informazioni a riguardo, consiste nell’aver supposto che s_x(F_bmax) rimanga costante al variare della velocità. Risulta chiaro come questa ipotesi si ripercuota nella validità generale del modello, evidenziando come ulteriori informazioni a proposito possano migliorare le risposte ottenute già largamente valide.

Il braccio della risultante della distribuzione di pressione è stato scomposto, anche in questo caso, nei due contributi

0 roll

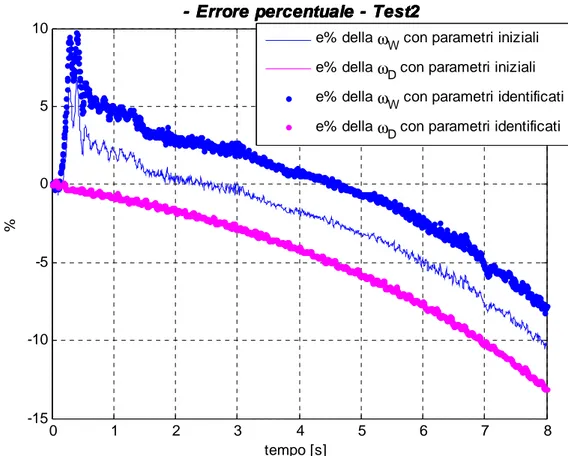
x e x dovuti, il primo al solo contributo di puro _b rotolamento stazionario della forza longitudinale, il secondo al solo contributo frenante. In questo modo si riesce a valutare separatamente l’effetto indotto dalle due forze, ed in particolare dal momento frenate, sulla posizione della risultante delle azioni di pressione. E’ da osservare come il contributo x sia fondamentale all’interno del modello e non si _b possa prescindere da esso. Infatti, annullare il valore di x comporta un eccessivo _b rallentamento sia della ruota che del tamburo come illustrato in figura 5.9. Questo è dovuto

(13)

Capitolo 5 – Modello Pacejka-ESDU 0 1 2 3 4 5 6 7 8 -15 -10 -5 0 5 10 tempo [s] %

- Errore percentuale - Test2 - Errore percentuale - Test2 - Errore percentuale - Test2 - Errore percentuale - Test2

e% della ω

W con parametri iniziali e% della ω_D con parametri iniziali e% della ω

W con parametri identificati e% della ω

D con parametri identificati

figura 5.9 Errore percentuale della velocità angolare della ruota e del tamburo, simulate

con i parametri iniziali e identificati per il test2 con α = 0.95, nell’ipotesi x_b =0.

al fatto che il braccio x_roll₀, anteriore alla congiungente degli assi di rotazione della ruota e del tamburo, determina un momento N

0 roll

x frenante, sia per la ruota che per il tamburo, di elevata entità. Considerare x non nullo comporta una ridistribuzione delle pressioni la cui _b risultante arretrata rispetto alla posizione relativa all’ipotesi x_b =0, dando luogo ad un momento frenante Nx di entità minore. E’ da notare che il valore assunto dal braccio x , e _b dunque l’arretramento della risultante della distribuzione di pressioni, è funzione non solo del momento frenante ma anche del carico verticale applicato alla ruota. Infatti, l’entità del momento frenante influenza x mediante il coefficiente di attrito frenato e il raggio di _b rotolamento frenato, mentre l’entità del carico verticale influenza, mediante la forza frenante, la posizione dell’orma dell’impronta relativamente alla congiungente gli assi della ruota e del tamburo.

I due contributi

0 roll

(14)

Capitolo 5 – Modello Pacejka-ESDU h x_roll₀ =µ_roll₀ (5.16)         − µ = h R K K h x_b _b ₁ ₂ eb (5.17)

in cui i due coefficienti correttivi K₁ e K₂ conglobano l’effetto della curvatura del tamburo, trascurata nell’equazione di

0 roll

x . In particolare gli andamenti appena espressi sono stati ritenuti il miglior compromesso tra quelli capaci di garantire una buona rappresentazione dei dati sperimentali con la massima semplicità. Infatti durante l’identificazione del modello è stata vagliata la rappresentazione del braccio x attraverso _b polinomi del secondo ordine in sx e V quale quella illustrata nell’equazione (5.18):

(

) (

)

2 x 2 6 5 4 x 2 3 2 1 b K K V K V s K K V K V s x = + + + + + (5.18) con rappresentazione di 0 roll

x mediante la (5.16). In tal caso si ottenevano velocità angolari simulate più distanti dai valori sperimentali rispetto a quelle ottenute attraverso le (5.16) e (5.17), con dinamiche corredate da andamenti anomali. Questo a causa dell’aver considerato per il braccio x una rappresentazione semplificata dell’equazione (2.32), realizzata, nelle incognite V ed sx, mediante uno sviluppo in serie di Taylor, arrestato ai termini superiori al secondo, nel punto sx=0. Infatti l’espressione completa del braccio x contempla non solo termini del secondo grado in sx, ma anche termini del quarto grado in V. Ovviamente, una rappresentazione semplificata quale quella delle equazioni (5.18) e (5.16) garantiva un numero minore di parametri da identificare (già in numero pari ad 12) rispetto alla formulazione completa perdendo però di precisione sul segnale inseguito.

Le equazioni (5.16) e (5.17) forniscono invece una rappresentazione esaustiva, sia in termini di semplicità del modello (i parametri sono ora solo otto) che in termini di rappresentatività dei dati sperimentali. Inoltre, mediante questa rappresentazione, si vuole dare una definizione del braccio x indipendente, almeno in maniera esplicita, dal raggio del tamburo. Infatti l’equazione (5.16) viene dedotta dall’equazione di moto della ruota in condizioni di moto stazionario su pista piana, mentre la (5.17) prende spunto dalla formulazione del braccio x mediante il modello energetico, sempre in condizioni di moto _b

(15)

Capitolo 5 – Modello Pacejka-ESDU su pista piana. Attraverso la (5.17) si è voluta definire, per il braccio x , una dipendenza _b lineare dalla distanza h e dal raggio di rotolamento frenato attraverso il coefficiente di attrito µ_b.

In sintesi il set di equazioni implementate nel modello Pacejka-ESDU risulta:

Equazioni del moto:

   − − = − − = ω Nx F V m T Nx Fh I D w w w & & (5.19) Forza di contatto: b 0 roll F F F= + (5.20) in cui: N F 0 roll roll =µ (5.21)

( )

{

[

(

)

]

}

(

)

                       −       π − = µ = =       µ µ π − = = ∂ ∂ = ⋅ − ⋅ ⋅ − ⋅ ⋅ ⋅ = → m m m max max b max skid 0 x s x b x x x x b Bx arctg Bx C 2 tg Bx E N ) V , N ( F D ) V , N ( arcsen 2 2 C CD BCD CD s F B s B arctan s B E s B arctan C sin D s F ) 26 . 5 ( ) 25 . 5 ( ) 24 . 5 ( ) 23 . 5 ( ) 22 . 5 (

(16)

Capitolo 5 – Modello Pacejka-ESDU Coefficienti di attrito:                  + = µ µ − + − + = µ       +       +               _δ + δ + = µ ) N ( c V 1 ) N ( c ) V , N ( V V V ) N ( a N N N ) N ( a a ) V , N ( V V C 1 V V C 1 R C R C C 2 1 max skid 0 0 V 0 0 N 0 max n max 2 rv 2 max 1 rv 2 0 2 rd 0 1 rd 0 rd 0 roll ) 29 . 5 ( ) 28 . 5 ( ) 27 . 5 (

braccio della risultante

        − µ + µ = h R ) N ( K ) N ( K h h x _roll₀ _b ₁ ₂ eb (5.30)

5.3.2 Programma per l’identificazione

Attraverso l’uso della funzione lsqnonlin si vogliono identificare tre dei quattro parametri che definiscono la forza frenante Fb e i due parametri K1, K2 che compaiono nell’equazione (5.17).

L’identificazione dei parametri che compaiono nell’equazione (5.22) viene svolta con l’ipotesi che il prodotto BCD, pendenza della curva nell’origine degli assi, possa essere considerata pari al prodotto K N

x s

µ . Tale ipotesi trova il suo fondamento in quanto già

ampiamente analizzato nel paragrafo 2.8 secondo cui, il coefficiente

x s

K_µ , pendenza nell’origine della curva µ_b =f(s_x), poteva essere ricavato mediante l’equazione:

) NR ( s T K * e xt t x s = µ (5.31)

(17)

Capitolo 5 – Modello Pacejka-ESDU Mediante questa assunzione, i coefficienti da identificare nell’equazione (5.22) si riducono a tre, ossia C, D, xm.

La determinazione dei parametri C e D viene fatta mediante l’identificazione dei coefficienti a0, aV, aN, c1, c2 presenti nelle funzioni µmax =f1(N,V), µskid/µmax =f2

(

N,V

)

descritte dalle equazioni (5.28) e (5.29).

L’identificazione del parametro xm, ascissa della Fbmax, si ritiene indispensabile dal

momento che il suo valore risulta funzione non solo della velocità di avanzamento bensì anche del carico verticale applicato. Una volta identificato xm, il valore di E viene simulato

tramite l’equazione (5.26).

Anche in questo caso, come per l’identificazione dei parametri presenti nelle strutture dei coefficienti µ_b e µ_roll del modello energetico, la struttura del programma è tale da permettere di confrontare iterativamente i dati sperimentali delle velocità angolari della ruota e del tamburo, con quelli ottenuti dalla simulazione del modello in funzione del valore attuale dei parametri. In base al risultato di tale confronto il programma adatta ad ogni passo successivo i valori di tutti i parametri, procedendo iterativamente fino ad ottenere la migliore risposta possibile.

L’identificazione è stata effettuata per tre diversi valori del peso α, pari a 0.95, 0.8, 0.5, e con tolleranze sulla funzione f(x) e sulla x pari a 10−5, valore considerato soddisfacente al fine di ottenere bassi valori per la funzione errore senza allungare troppo i tempi di identificazione già ragguardevoli. Da notare che la tolleranza sulla funzione errore, in tale modello, genera all’uscita del ciclo iterativo di identificazione, dei valori di f(x)

paragonabili, o minori, a quelli ottenuti tramite identificazione dei parametri nel modello energetico, nonostante, in tale modello, la tolleranza sulla funzione errore sia inferiore di due ordini di grandezza.

Il peso maggiore, all’interno della funzione di costo F è stata assegnato, analogamente a quanto fatto nell’identificazione dei parametri del modello QSTM_08, alla funzione F_ω_w, al fine di poter meglio evidenziare eventuali anomalie nelle forze, indotte dalla struttura del modello, maggiormente rilevabili sulla ruota a causa della sua bassa inerzia.

Il modello Simulink, adottato per l’identificazione degli otto parametri a0, aV, aN, c1, c2,

xm, K1, K2, è identico a quello relativo al modello QSTM_08, sia per quanto riguarda lo

(18)

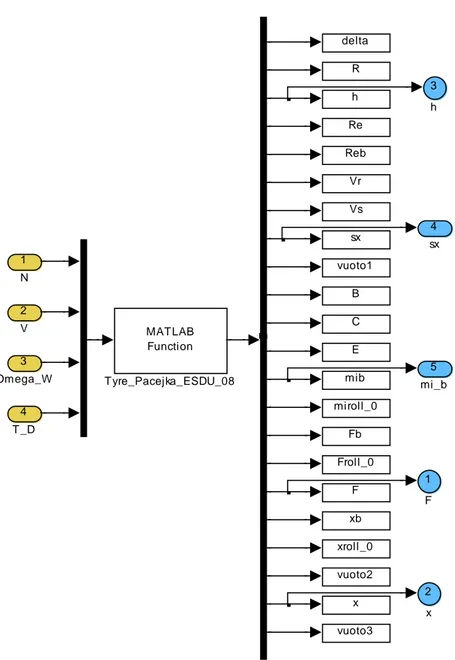
Capitolo 5 – Modello Pacejka-ESDU Pacejka-ESDU, risiede unicamente nel blocco Tyre Mechanics, illustrato in figura 5.9. Infatti in tale modello, i valori istantanei delle forze e del braccio della risultante della distribuzione di pressione vengono calcolati tramite la function Tyre_Pacejka_EDSU_08 (cfr. Appendice I) attraverso il set di equazioni (5.20)-(5.30).

5 mi_b 4 sx 3 h 2 x 1 F vuoto1 sx Vs Vr Reb Re h vuoto3 x vuoto2 xroll_0 R xb F Froll_0 Fb miroll_0 mib E C B delta MATLAB Function T yre_Pacejka_ESDU_08 Demux 4 T _D 3 Omega_W 2 V 1 N

(19)

5.3.3 Validazione del modello

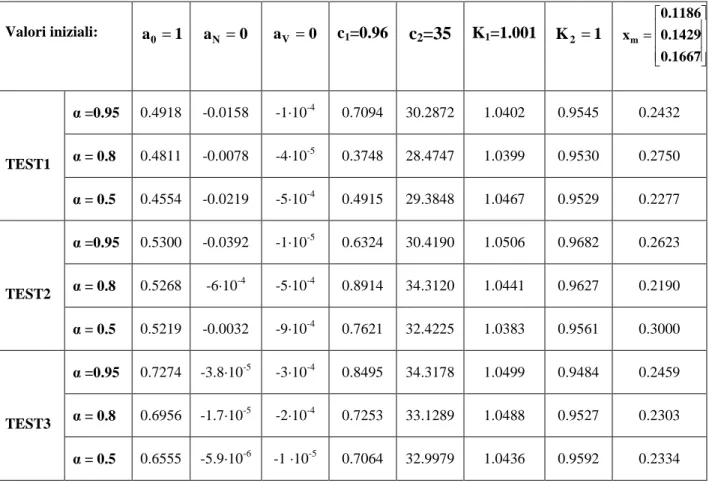
L’analisi della tabella 5.1, in cui sono riassunti i valori identificati dei parametri, permette di poter affermare che la dipendenza del coefficiente di attrito massimo dalla velocità di avanzamento è praticamente trascurabile, avendo identificato per il parametro aV un valore

mediamente dell’ordine di 10-4. Tale risultato era stato parzialmente già raggiunto mediante l’identificazione, nel modello energetico, dei parametri caratterizzanti la struttura del coefficiente d’attrito µ_b nell’ipotesi di dipendenza diretta dalla velocità nulla.

Al contrario, la dipendenza dal carico verticale assume dimensioni non trascurabili, pur avendo identificato per il coefficiente aN dei valori che oscillano tra 10-2 e 10-6. Infatti,

diversamente da quanto avviene per il contributo della velocità, il coefficiente aN, pur

essendo di piccola entità dev’essere moltiplicato per il termine

nom nom N N N− non trascurabile. Valori iniziali: _a ₁ 0 = aN =0 aV =0 c1=0.96 c2=35 K1=1.001 K₂ =1           = 0.1667 0.1429 0.1186 xm α =0.95 0.4918 -0.0158 -1·10-4 0.7094 30.2872 1.0402 0.9545 0.2432 α = 0.8 0.4811 -0.0078 -4·10-5 0.3748 28.4747 1.0399 0.9530 0.2750 TEST1 α = 0.5 0.4554 -0.0219 -5·10-4 0.4915 29.3848 1.0467 0.9529 0.2277 α =0.95 0.5300 -0.0392 -1·10-5 0.6324 30.4190 1.0506 0.9682 0.2623 α = 0.8 0.5268 -6·10-4 -5·10-4 0.8914 34.3120 1.0441 0.9627 0.2190 TEST2 α = 0.5 0.5219 -0.0032 -9·10-4 0.7621 32.4225 1.0383 0.9561 0.3000 α =0.95 0.7274 -3.8·10-5 -3·10-4 0.8495 34.3178 1.0499 0.9484 0.2459 α = 0.8 0.6956 -1.7·10-5 -2·10-4 0.7253 33.1289 1.0488 0.9527 0.2303 TEST3 α = 0.5 0.6555 -5.9·10-6 -1 ·10-5 0.7064 32.9979 1.0436 0.9592 0.2334

tabella 5.1 Riassunto dei valori numerici assunti dai parametri durante le diverse

(20)

Capitolo 5 – Modello Pacejka-ESDU In sintesi il coefficiente d’attrito massimo risulta dunque insensibile alle variazioni di velocità ma di entità diversa al variare del carico verticale, in particolare assume i valori di 0.47, 0.52, 0.69 rispettivamente per i test1, 2 e 3.

I valori identificati per i coefficienti K1 e K2 sono mediamente uguali a 1.04 e 0.95 nei tre

test. Il loro valore non può essere approssimato all’unità, dal momento che il valore del braccio xb è ottenuto attraverso sottrazione di quantità di entità rilevante, per cui piccole

variazioni hanno una notevole influenza sull’intero risultato.

Di seguito vengono anche riportano i grafici considerati più significativi nell’identificazione del modello Pacejka-ESDU. In Appendice H si riportano i risultati in modo completo.

Al fine di continuare il confronto dei risultati, gia avviato nei capitoli 4 e 5, nelle figure 5.10-5.16 si illustrano le velocità angolari della ruota e del tamburo per i tre test e gli errori percentuali relativamente all’intero periodo di simulazione.

0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 60 65 70 75 80 7 7.5 8 35 40 45 50 55 0 0.5 1 42 43 44 45 46 tempo [s] ω D [ ra d /s ] sperimentale parametri iniziali parametri identificati 4 4.5 5 26 28 30 32 34 tempo [s] 7 7.5 8 16 18 20 22 tempo [s]

figura 5.10 Ingrandimenti delle velocità angolari della ruota e del tamburo, identificazione

(21)

Capitolo 5 – Modello Pacejka-ESDU 0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 70 75 80 85 7 7.5 8 50 55 60 65 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale parametri iniziali parametri identificati 4 4.5 5 31 32 33 34 35 36 tempo [s] 7 7.5 8 23 24 25 26 27 28 tempo [s]

dei parametri per il test 2 con α = 0.8.

0 0.5 1 70 80 90 100 110 120 ωW [ ra d /s ] 4 4.5 5 90 92 94 96 98 7 7.5 8 80 82 84 86 88 90 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] sperimentale parametri iniziali parametri identificati 4 4.5 5 40 40.5 41 41.5 42 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 38.5 tempo [s]

(22)

C a p ito lo 5 – M o d el lo P a ce jk a -E S D U 1 7 9 fi g u ra 5 .1 3 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d ei p ar am et ri p er il t es t1 a l v ar ia re d el p es o α . 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 αααα=0.95 Test1 =0.95 Test1 =0.95 Test1 =0.95 Test1 tempo [s] e % 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 αααα=0.8 Test1 =0.8 Test1 =0.8 Test1 =0.8 Test1 tempo [s] 0 2 4 6 8 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 αααα=0.5 Test1 =0.5 Test1 =0.5 Test1=0.5 Test1 tempo [s] e% sulla ω

W con parametri identificati

(23)

C a p ito lo 5 – M o d el lo P a ce jk a -E S D 1 fi g u ra 5 .1 4 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u id en tif ic az io n e d ei p ar am et ri p er il t es t2 a l v ar ia re d el p es o α . 0 2 4 6 8 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 αααα =0.95 Test2 =0.95 Test2 =0.95 Test2 =0.95 Test2 tempo [s] e % 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 αααα =0.8 Test2 =0.8 Test2 =0.8 Test2=0.8 Test2 tempo [s] 0 2 4 6 8 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 tempo [s] α

ααα=0.5 Test2=0.5 Test2=0.5 Test2=0.5 Test2

e% sulla ω

(24)

figura 5.15 Errori percentuali per le velocità angolari della ruota e del tamburo,

identificazione dei parametri per il test3 al variare del peso α.

0 2 4 6 8 -5 0 5 1 0 1 5 2 0 2 5 3 0 3 5 αααα = 0 .9 5 T e s t3 = 0 .9 5 T e s t3 = 0 .9 5 T e s t3 = 0 .9 5 T e s t3 te m p o [ s ] e% 0 2 4 6 8 -5 0 5 1 0 1 5 2 0 2 5 3 0 3 5 αααα = 0 .8 T e s t3 = 0 .8 T e s t3 = 0 .8 T e s t3 = 0 .8 T e s t3 te m p o [ s ] 0 2 4 6 8 -5 0 5 1 0 1 5 2 0 2 5 3 0 3 5 αααα = 0 .5 T e s t3 = 0 .5 T e s t3 = 0 .5 T e s t3 = 0 .5 T e s t3 te m p o [ s ]

(25)

C a p ito lo 5 – M o d el lo P a ce jk a -E S D 1 fi g u ra 3 .2 8 In g ra n d im e n ti d eg li er ro ri p er ce n tu a li d el le v el o ci tà a n g o la ri d el la r u o ta e d ta m b u ro p er il te st 3 . 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 αααα =0.95 Test3 =0.95 Test3 =0.95 Test3=0.95 Test3 tempo [s] e % 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 αααα =0.8 Test3 =0.8 Test3 =0.8 Test3 =0.8 Test3 tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 αααα =0.5 Test3 =0.5 Test3 =0.5 Test3=0.5 Test3 tempo [s]

(26)

Capitolo 5 – Modello Pacejka-ESDU Ad ultimo, nelle figure 3.29-3.31, si illustrano le velocità angolari della ruota e del tamburo ottenute mediante simulazione del modello Pacejka-ESDU, realizzata utilizzando i valori di a0, aV, aN, c1, c2, xm, K1, K2 identificati con α=0.5, e dalla simulazione del modello

energetico, effettuata con i valori identificati, attraverso lo stesso valore di α, di K_µ_s_x, C , ₀

1

C e i valori originali dei restanti parametri. Si rimanda all’appendice H per un’analisi più approfondita dei grafici di confronto dei risultati ottenuti mediante i due modelli.

0 0.5 1 90 95 100 105 110 115 ω W [ ra d /s ] 4 4.5 5 64 66 68 70 72 74 7 7.5 8 38 40 42 44 46 48 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] 4 4.5 5 27 28 29 30 31 32 tempo [s] 7 7.5 8 16 17 18 19 20 21 tempo [s] dati sperimentali

parametri identificati con modello Pacejka-Esdu parametri identificati con modello energetico

figura 3.29 Test1 con α=0.5: confronto tra le velocità angolari della ruota e del tamburo

(27)

Capitolo 5 – Modello Pacejka-ESDU 0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 72 74 76 78 80 7 7.5 8 52 54 56 58 60 62 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] 4 4.5 5 31 32 33 34 35 tempo [s] 7 7.5 8 23 24 25 26 27 tempo [s] dati sperimentali

figura 3.30 Test2 con α=0.5: confronto tra le velocità angolari della ruota e del tamburo

simulate con il modello energetico e con il modello Pacejka-ESDU.

0 0.5 1 70 80 90 100 110 120 ωW [ ra d /s ] 4 4.5 5 90 91 92 93 94 7 7.5 8 81 82 83 84 85 86 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] 4 4.5 5 40 40.5 41 41.5 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 tempo [s] dati sperimentali

(28)

5.4 Identificazione del sistema ruota

5.4.1 Considerazioni preliminari

Nel paragrafo 5.3 l’identificazione dei parametri presenti nei coefficienti d’attrito, definiti dalle equazioni (5.28) e (5.29), è stata realizzata mediante il modello Pacejka-ESDU applicato al sistema ruota-tamburo. In questo modo i valori numerici da assegnare ai parametri vengono determinati come quelli che minimizzano la differenza tra la velocità angolare simulata e sperimentale sia per la ruota che per il tamburo. Attraverso il peso α si decide poi quale tra le curve sperimentali deve essere approssimata meglio.

In questo paragrafo invece l’identificazione dei parametri che caratterizzano le strutture della forza frenante e del braccio x viene realizzata per il sistema costituito dalla sola ruota, in analogia a quanto già realizzato per il modello energetico. Di conseguenza anche in questo caso, la velocità angolare del tamburo non costituisce più un segnale da inseguire bensì un nuova forzante al sistema.

5.4.2 Programma per l’identificazione

Lo schema d’assieme del modello Simulink denominato Pacejka_ESDU_Wheel_08, relativo alla sola ruota, e lo schema di secondo livello relativo al blocco Wheel Dynamics sono identici a quelli illustrati nelle figure 3.55 e 3.4 mentre lo schema di secondo livello relativo al blocco Tyre Mechanics è rappresentato in figura 3.31. Anche in questo caso, la velocità angolare della ruota calcolata nel blocco Wheel Dynamics, viene utilizzata, assieme al carico verticale N e alla velocità di avanzamento V, come dato di input ad una function, denominata tyre_Pacejka_ESDU_Wheel_08, la quale calcola, mediante il set di equazioni (5.19)÷(5.30), i valori istantanei della forza longitudinale, del braccio x e delle rispettive componenti. Evidentemente il set di equazioni implementato nella function tyre_Pacejka_ESDU_Wheel_08 non comprende la seconda delle (5.19) riferita all’equilibrio al momento del tamburo.

La struttura del programma è analoga a quella usato per l’identificazione del sistema ruota-tamburo e tale dunque da permettere di confrontare iterativamente i dati sperimentali della velocità angolare della ruota con quelli ottenuti dalla simulazione del modello in

(29)

Capitolo 5 – Modello Pacejka-ESDU 5 mib 4 sx 3 h 2 x 1 F MATLAB Function tyre_Pacejka_ESDU_Wheel_08 C sx Vs Vr Reb Re h B x R xroll_0 xb F Froll_0 Fb miroll_0 mib E delta Demux 3 Omega_W 2 V 1 N

figura 5.31 Modello Pacejka-ESDU_Wheel_08 Simulink: blocco Tyre Mechanics (II

livello).

funzione del valore attuale dei parametri. In base al risultato di tale confronto il programma adatta ad ogni passo successivo il valore di tutti i parametri, procedendo iterativamente fino ad ottenere la migliore risposta possibile.

(30)

5.4.3

Validazione del modello

In questo paragrafo vengono riportati i risultati relativi all’identificazione, mediante il modello Pacejka-ESDU_Wheel_08, degli otto parametri di a0, aV, aN, c1, c2, xm, K1, K2. I

parametri sono stati identificati mediante ottimizzazione della funzione di costo F, costituita unicamente dai residui della velocità angolare della ruota espressi come percentuale del relativo valore sperimentale, nell’intervallo temporale 2÷8 secondi. Nella tabella 5.2 vengono riportati nel dettaglio i valori numerici assegnati dall’ottimizzatore ai parametri nei tre test in esame.

Le figure 5.32, 5.33, 5.34 illustrano gli errori percentuali della velocità angolare della ruota, simulata mediante i valori identificati degli otto parametri, in percentuale del valore sperimentale per i tre test in esame. Dall’esame delle figure si nota come il modello Pacejka-ESDU, applicato alla sola ruota, fornisca dei risultati, in termini di errore percentuale, molto soddisfacenti. Per contro, un’analisi più approfondita degli andamenti temporali del braccio xb e del braccio x, figure 5.35, 5.36, 5.37, permette di affermare che il

modello non sia in grado, per tale sistema, di dare risultati fisicamente accettabili dal momento che i valori assunti a regime dal braccio x sono positivi e dunque non fisicamente giustificabili. In particolare i valori a regime sono pari a 0.04 m, 0.05 m, 0.5 m rispettivamente per il test1, test2 e test3, per il quale il valore di x supera abbondantemente il valore dell’impronta al suolo del pneumatico.

Per l’analisi dettagliata dei risultati del modello si rimanda al paragrafo H.3.3 dell’Appendice H.

tabella 5.2 Riassunto dei valori numerici assunti dai parametri durante le diverse

identificazioni. Valori iniziali: 1 a₀ = a_N =0 a_V =0 c₁ =0.96 c₂ =35 K1=1.001 K₂ =1           = 0.1667 0.1429 0.1186 x_m TEST1 0.9257 -2·10-5 -0.0015 0.9048 34.4536 1.1811 0.8466 0.1930 TEST2 0.9282 -5·10-5 -0.0015 0.9123 34.5719 1.1715 0.8433 0.2052 TEST3 1.8815 -1.088 -3·10-4 -1·10-4 33.1932 1.4545 0.6875 0.1501

(31)

Capitolo 5 – Modello Pacejka-ESDU 0 1 2 3 4 5 6 7 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 tempo [s] %

e% della ω_W con parametri identificati

figura 5.32 Test1: errori percentuali della velocità angolare della ruota, simulata mediante

i valori identificati per a0, aV, aN, c1, c2, xm, K1, K2.

0 1 2 3 4 5 6 7 8 -2 -1 0 1 2 3 4 tempo [s] %

e% della ω

(32)

Capitolo 5 – Modello Pacejka-ESDU 0 1 2 3 4 5 6 7 8 -5 0 5 10 15 20 25 30 35 tempo [s] %

e% della ω

i valori identificati per a0, aV, aN, c1, c2, xm, K1, K2.

0 1 2 3 4 5 6 7 8 3 4 5x 10 -3 x ro ll 0 [ m ] TEST1 0 1 2 3 4 5 6 7 8 0 0.02 0.04 0.06 x b [ m ] 0 1 2 3 4 5 6 7 8 0 0.02 0.04 0.06 tempo [s] x [ m ]

figura 5.35 Test1: andamenti temporali del braccio x e delle sue componenti ottenuti

mediante simulazione del modello Pacejka_ESDU_Wheel_08 attraverso l’uso dei valori identificati per a0, aV, aN, c1, c2, xm, K1, K2.

(33)

Capitolo 5 – Modello Pacejka-ESDU 0 1 2 3 4 5 6 7 8 3.5 4 4.5x 10 -3 x ro ll0 [ m ] TEST2 0 1 2 3 4 5 6 7 8 0 0.02 0.04 0.06 x b [ m ] 0 1 2 3 4 5 6 7 8 0 0.02 0.04 0.06 tempo [s] x [ m ]

figura 5.36 Test2: andamenti temporali del braccio x e delle sue componenti ottenuti

mediante simulazione del modello Pacejka_ESDU_Wheel_08 attraverso l’uso dei valori identificati per a0, aV, aN, c1, c2, xm, K1, K2. 0 1 2 3 4 5 6 7 8 3.8 4 4.2x 10 -3 x ro ll0 [ m ] 0 1 2 3 4 5 6 7 8 0 0.5 1 x b [ m ] 0 1 2 3 4 5 6 7 8 0 0.5 1 tempo [s] x [ m ]

figura 5.36 Test3: Andamenti temporali del braccio x e delle sue componenti ottenuti

mediante simulazione del modello Pacejka_ESDU_Wheel_08 attraverso l’uso dei valori identificati per a0, aV, aN, c1, c2, xm, K1, K2.