7
Ottimizzazione locale della traiettoria
7.1
Equazioni di perturbazione
Sono note dalla letteratura le equazioni di perturbazione dei 6 elementi or-bitali classici , a,e, i, Ω, ω, M in presenza di una forza esterna F (cfr. [7]). Si assume che l’entit`a della forza di disturbo sia molto minore della forza gravitazionale agente sul satellite a causa della terra (corpo primario). L’es-pressione di F `e dato dall’equazione (3.4), che, sostituita alle equazioni di perturbazione fornite dalla letteratura, fornisce (cfr. [10]):
da dt =
µmL
m I cos i(1 + e cos ν)
4 (7.1)
de dt =
µmL
m I cos i(cos ν + cos E)(1 + e cos ν)
3 (7.2) di dt = − µmL m I sin i cos 2u(1 + e cos ν)2 (7.3) dΩ dt = − µmL
m I sin u cos u(1 + e cos ν)
2 (7.4) dω dt = µmL m I cos i √
ν (2 sin ν + e cos ν sin ν + e sin u cos u) (1 + e cos ν)
3 (7.5)
dM
dt = n −
µmL
m (2 + e cos ν) sin ν cos i (1 + e cos ν)
`
E possibile rappresentare le precedenti equazioni in termini di parametri equinoziali, mediante le seguenti equazioni:
p = a(1 − e2) (7.7) ( f = e cos (ω + Ω) g = e cos (ω + Ω) (7.8) ( h = tan¡i 2 ¢ cos Ω k = tan¡i 2 ¢ sin Ω (7.9) L0 = Ω + ω + ν (7.10) s02 = 1 + h2+ k2 (7.11) w0 = 1 + f cos L0+ g sin L0 (7.12) τ =√h2+ k2 (7.13)
Da cui si ottengono le relazioni di variazione dei parametri equinoziali analoghe alle equazioni (7.1) ÷ (7.6):
dp dt = 2p w0 r p µT (7.14) df dt = r p µ ½ [(w0+ 1) cos L0+ f ] T w0 − (h sin L 0− k cos L0)gN w0 ¾ (7.15) dg dt = s p µ ½ [(w0+ 1) sin L0+ g] T w0 + (h sin L0 − k cos L0) f N w0 ¾ (7.16) dh dt = r p µ s2cos L0 2w0 N (7.17)
dk dt = r p µ s2sin L0 2w0 N (7.18) dL dt = √ µp µ w0 p ¶2 + r p µ (h sin L0− k cos L0) w0 N (7.19)
Dove le componenti delle accelerazioni del tether sono date da: R = 0 T = LIµm mr3 cos ¡ 2arctg√h2+ k2¢ N = −LIµm mr3 sin ¡
2arctg√h2+ k2¢(h cos L√0+k sin L0)
h2+k2
(7.20)
Data la maggiore comprensibilit`a dal punto di vista fisico, degli elemen-ti orbitali classici, si uelemen-tilizzeranno queselemen-ti ulelemen-timi nella risoluzione del nostro problema; nel corso del capitolo, si cercheranno le condizioni di ottimo lo-cale per l’equazione (7.1), ipotizzando inizialmente inclinazione ed eccentri-cit`a costanti, in seguito considerando anche le variazioni temporali di queste ultime.
7.2
Ottimizzazione locale con e ed i costanti
Se si mantengono costanti i due elementi orbitali e ed i, si ottengono le condizioni per cui il secondo membro della (7.1) diventa positivo:
(
cos i > 0 se i ∈ [0,90◦]
cos i < 0 se i ∈ (90◦,180◦]
Nel nostro caso si `e considerato :
i = 30◦ e = 0.716
Per i valori caratteristici del tether si sono utilizzati gli stessi valori gi`a uti-lizzati in precedenza e si `e proceduto scegliendo come legge di variazione temporale dell’anomalia vera, la seguente:
in cui ωtether `e la velocit`a angolare del tether e si ottiene:
ωtether =
2π
Ttether
in cui il periodo Ttether `e dato dalla:
Ttether = 2π
s
a3
µ
Si `e quindi proceduto in maniera indiretta, abbiamo cio`e integrato la (7.1) su un intervallo di tempo [t0,tf] = [0,60] h, mantenendo I costante ed
abbia-mo risolto rispetto alla corrente, l’equazione ottenuta sempre per valori del controllo L che vanno da 3000 a 11000 m. Tale procedura `e stata ripetuta per ottenere variazioni del semiasse maggiore pari a:
∆a = 200 300 400 500 km
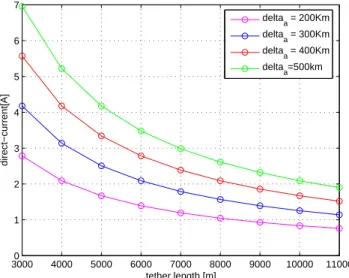
I risultati ottenuti sono riportati nella Figura (7.1) e nella Tabella (7.1):
30000 4000 5000 6000 7000 8000 9000 10000 11000 1 2 3 4 5 6 7 tether length [m] direct−current[A] delta a = 200Km deltaa = 300Km deltaa = 400Km delta a=500km
Figura 7.1: Variazione del valore della corrente al variare del parametro di controllo L
∆a [km] L=3000 m L=4000 m L=5000 m L=6000 m 200 2.7835 2.0877 1.6701 1.3918 300 4.1753 3.1315 2.5052 2.0877 400 5.5671 4.1753 3.3402 2.7835 500 6.9589 5.2191 4.1753 3.4794 L=7000 m L=8000 m L=9000 m L=10000 m L=11000 m 1.1929 1.0438 0.9278 0.8351 0.7591 1.7894 1.5657 1.3918 1.2526 1.1387 2.3859 2.0877 1.8557 1.6701 1.5183 2.3859 2.0877 1.8557 1.6701 1.5183
Tabella 7.1: Corrente I [Am] nel caso di ottimizzazione di dadt con e ed i costanti
7.3
Ottimizzazione locale con e ed i variabili
L’ipotesi semplificativa di mantenere costanti eccentricit`a e inclinazione ri-sulta poco realistica; essa infatti non tiene conto del fatto che tutti i sei elementi orbitali classici subiscono variazioni nel tempo a causa delle forze perturbative esterne. `E necessario quindi tenere di conto di queste ulteriori variazioni per determinare le condizioni di ottimo locali di da
dt. Si riportano
di seguito le equazioni di perturbazione di a, e ed i:
da dt =
µmagnL
m I cos i(1 + e cos ν)
4
de dt =
µmagnL
m I cos i(cos ν + cos E)(1 + e cos ν)
3 di dt = − µmagnL m I sin i cos 2u(1 + e cos ν)2
Dai risultati ottenuti per l’ottimizzazione a parametri costanti, si `e os-servato che tutte le correnti sono comprese tra 2.7 e 7 A; poich´e `e noto che il parametro di controllo varia tra 3000 e 11000 m, si `e deciso di utilizzare come nuovo controllo il prodotto della corrente con la lunghezza del tether (LI) e si `e scelto:
LI = 8000 ÷ 78000 m · Am
precedenti, partendo dalle seguenti condizioni iniziali: [a0,e0,i0] = [24568 m,0.05,30◦]
Ottenendo i seguenti risultati per le variazioni suddette di a, e ed i:
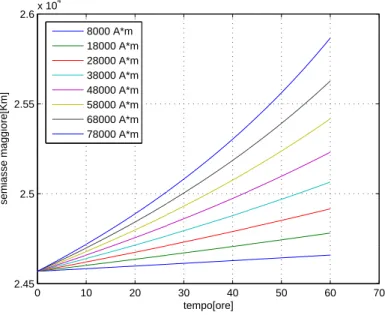
0 10 20 30 40 50 60 70 2.45 2.5 2.55 2.6x 10 4 tempo[ore] semiasse maggiore[Km] 8000 A*m 18000 A*m 28000 A*m 38000 A*m 48000 A*m 58000 A*m 68000 A*m 78000 A*m
Figura 7.2: Variazione del semiasse maggiore al variare del parametro di controllo
LI 0 10 20 30 40 50 60 70 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 tempo[ore] eccentricità 8000 A*m 18000 A*m 28000 A*m 38000 A*m 48000 A*m 58000 A*m 68000 A*m 78000 A*m
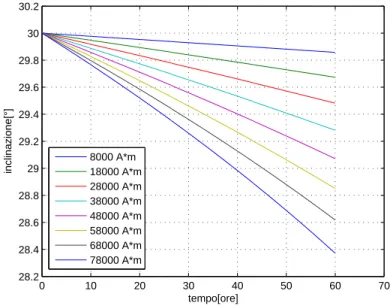
0 10 20 30 40 50 60 70 28.2 28.4 28.6 28.8 29 29.2 29.4 29.6 29.8 30 30.2 tempo[ore] inclinazione[°] 8000 A*m 18000 A*m 28000 A*m 38000 A*m 48000 A*m 58000 A*m 68000 A*m 78000 A*m
Figura 7.4: Variazione dell’inclinazione al variare del parametro di controllo LI
7.4
Considerazioni
In tutti e tre i grafici suddetti, si nota un progressivo miglioramento delle va-riazioni rispettivamente di a,e ed i con l’aumentare del parametro di control-lo. Dai risultati ottenuti nel paragrafo precedente, `e possibile scegliere il va-lore di ottimo di LI e quindi i valori di I e di L che massimizzano la variazione di da
dt. La massima variazione di dadt (vedi figura 7.2) si ottiene dal valore del
controllo LI seguente:
LI = 78000 m · Am
Tale valore del controllo, fra l’altro, `e anche quello che contemporaneamente massimizza la variazione di de
dt (cfr. fig. 7.3) che passa da un valore di 0.05
ad un valore di 0.34 in un intervallo di tempo di 60 ore; inoltre per lo stesso valore del controllo si ha una diminuzione dell’inclinazione da 30◦ a 28.37◦
(vedi fig.7.3). Occorre quindi scegliere le coppie di valori di L e di I che sod-disfano la condizione sul loro prodotto; tra tutte le coppie possibili, si sono scelte le seguenti:
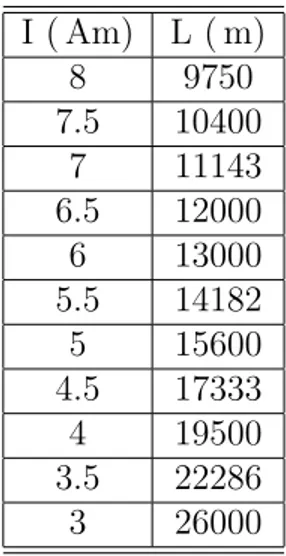
I ( Am) L ( m) 8 9750 7.5 10400 7 11143 6.5 12000 6 13000 5.5 14182 5 15600 4.5 17333 4 19500 3.5 22286 3 26000
Tabella 7.2: Coppie dei parametri di controllo I ed L
Nella Tabella (7.2) si sono riportate le coppie di parametri accettabili, quelle in cui cio`e si hanno tensioni non superiori a 10 Am e non inferiori a 3 Am, i valori limite che sono riportati in letteratura (cfr. [1]). Infatti, va-lori superiori a quelli dati, implicherebbero sistemi di generazioni di potenza non accessibili per questo tipo di applicazione, d’altra parte, valori inferiori, necessiterebbero di lunghezze del tether eccessive e quindi ingombri troppo elevati.
![Tabella 7.1: Corrente I [Am] nel caso di ottimizzazione di da dt con e ed i costanti](https://thumb-eu.123doks.com/thumbv2/123dokorg/7260474.81967/5.918.236.731.116.342/tabella-corrente-am-caso-ottimizzazione-dt-costanti.webp)