Capitolo IX Conclusioni e Sviluppi

(1)

-Capitolo IX- Conclusioni e Sviluppi

Capitolo IX Conclusioni e Sviluppi

Ricordiamo che obiettivo del lavoro era sviluppare e rendere disponibile per applicazione in ambito industriale una metodologia di indagine in grado di identificare i difetti presenti in un cuscinetto volvente. Ci si è inoltre posti l’obiettivo di individuare le tecniche più sensibili alle variazioni dello stato di salute dei cuscinetti e tra queste quelle che richiedono un minore carico computazionale.

Affinché la metodologia sviluppata fosse bene adattabile alla realtà industriale, si sono scelte tecniche di indagine che consentano misurazioni il meno intrusive possibile nei macchinari limitando le acquisizioni di segnale alla carcassa del supporto del cuscinetto in esame, in direzione ortogonale rispetto all’asse di rotazione dell’albero.

La scelta del tornio parallelo come banco prova è stata fatta tenendo anche conto dei seguenti aspetti fondamentali:

I. banco quanto più possibile simile alle macchine dell’ambiente industriale;

II. possibilità di effettuare un’estesa tipologia di prove con combinazione di più sorgenti di vibrazione;

III. semplicità e rapidità di montaggio/smontaggio della struttura e dei supporti dei cuscinetti;

IV. possibilità di regolazione della struttura e dei suoi componenti.

L’utilizzo di cuscinetti a rulli conici ha portato i seguenti vantaggi:

I. possibilità di eseguire rapidi montaggi/smontaggi per un controllo visivo/fotografico dello stato delle piste;

II. facilità nell’aumentare l’entità del danno prodotto tramite la penna a vibrazione; III. la capacità di sopportare gli elevati carichi assiali trasmessi dalla contropunta del

(2)

Quindi alla luce dell’intero lavoro svolto si possono trarre una serie di indicazioni in merito ai risultati ottenuti ed ai metodi che sono stati utilizzati per il monitoraggio ed il filtraggio di segnali di cuscinetti volventi con difetto su una pista di rotolamento.

♦ Si sottolineano i buoni risultati raggiunti nelle operazioni di filtraggio di segnali rappresentanti cuscinetti con difetto sulla pista di rotolamento esterna e fortemente contaminati da rumore esterno, con rapporti Noise/Signal con valori del 90% o superiori, le tecniche di filtraggio scelte hanno permesso di rimuovere il rumore e di individuare, o nel dominio del tempo o nel dominio delle frequenze, il segnale rappresentante il difetto o la sua frequenza caratteristica.

♦ Il metodo del RMS, per quanto riguarda risultati e applicabilità, ha il vantaggio di raccogliere tutta l’informazione in un unico valore, monitorando il livello globale di vibrazione; questo è però anche il suo limite principale perché se da un lato da una misura della gravità del difetto non ci da indicazioni sulla sua tipologia. Data la sua semplicità può essere utilizzato per definire i valori iniziali di soglia, normalmente fissati un 20 % superiori al livello di firma riscontrata a cuscinetti sani, e di allarme, in parallelo con i valori di soglia definiti sullo spettro. Non è però adatti a sviluppare una diagnosi sulla posizione dei difetti.

♦ L’utilizzo della trasformata di Hilbert, cuore del metodo dell’inviluppo spettrale, in combinazione con lo spettro delle frequenze delle vibrazioni, si è invece rivelato efficace per una facile identificazione, e riconoscimento del posizionamento, del danneggiamento dei cuscinetti.

Si è dimostrato possibile che anche alla presenza di forti rumori di disturbo provenienti dal sistema esterno, la tecnica è stata in grado di fornire risultati facilmente interpretabili e utili per una tempestiva manutenzione dei cuscinetti.

Alla presenza di danni di entità molto più piccoli di quelli analizzati, un possibile sviluppo del lavoro potrebbe essere la combinazione della tecnica della trasformata di Hilbert con un metodo per aumentare il rapporto segnale/rumore, ricorrendo ad esempio al metodo della media sincrona (Sinchronized Time Average), al fine di migliorare la possibilità di individuare precocemente il danneggiamento del cuscinetto e di stimare correttamente la sua posizione.

(3)

A priori non è stato necessario nessun accorgimento particolare per adattare la routine di MatLab della trasformata di Hilbert al nostro caso di demodulazione.

♦ Notevole è stato l’apporto fornito dalla tecnica del filtraggio adattivo che, anche in presenza di un altissimo rapporto rumore/segnale, è stato in grado di operare una pulizia del segnale dal rumore proveniente dalla macchina, permettendo una successiva individuazione del danno facendo ricorso alla visualizzazione dei risultati nel dominio delle frequenze.

Naturalmente questa tecnica può essere usata se e solo se in precedenza si è provveduto a creare un database con le “firme zero” della macchina in esame nelle varie condizioni di funzionamento ottimale.

Anche per questo metodo sarebbe interessante valutare la sua efficacia in presenza di un danno di grandezza molto inferiore, e quindi realmente “nascosto” dal rumore della macchina e non da rumore aggiunto artificialmente al segnale registrato.

♦ In quelle situazioni dove il filtraggio adattivo e la trasformata di Hilbert non sono stati di aiuto la situazione è stata risolta grazie al denoising tramite la decomposizione con l’uso delle Wavelet. Tale metodo in maniera semplice ha permesso di ritrovare nel dominio del tempo quelle periodicità tipiche di un difetto del cuscinetto. E questo risultato è stato raggiunto partendo da un segnale fortemente compromesso dalla presenza di rumore esterno, ma soprattutto da rumore generato internamente al cuscinetto stesso, prodotto dalla sua rotazione, e quindi significativamente connesso al segnale prodotto dal solo difetto.

Le scelte operate hanno riguardato solo la Wavelet madre da utilizzare e il livello di decomposizione a cui arrivare per poter ottenere i migliori risultati possibili.

E’ da notare come eccezion fatta per il valore di step scelto per trovare la convergenza del filtro adattivo, le altre due tecniche non hanno necessitato di settaggi particolari e accurati, scelti in relazione all’esperienza che si stava effettuando e analizzando, a dimostrazione di una loro grande versatilità ed adattabilità alle situazioni senza grandi interventi esterni da parte di operatori esperti.

(4)

-Appendice A- Densità Spettrale di Potenza

Appendice A Densità Spettrale di Potenza (PSD)

A.1.Definizione

In fisica, il segnale è generalmente associato ad una forma d’onda, onde elettromagnetiche, vibrazioni random, od onde acustiche. La densità spettrale dell’onda, quando moltiplicata per un appropriato fattore, fornisce la potenza trasportata dal segnale per unita di frequenza. Questo è noto come Densità Spettrale di Potenza o Distribuzione Spettrale di Potenza del segnale. L’unità di misura sono comunemente espresse in watts per hertz (W/Hz), oppure watts per nanometri (W/nm) per una misura della lunghezza d’onda del segnale invece che la sua frequenza.

A.2 Densità Spettrale di Potenza

Per segnali aleatori stazionari è possibile definire la Densità Spettrale di Potenza (Power Spectral Density), che descrive come la potenza di un segnale o di una serie temporale è distribuita rispetto alle frequenze del segnale stesso.

Può essere definita come il quadrato dei valori del segnale:

( )

P

=





s t





2 (A.1)

Essa è definita come il limite del valore atteso della trasformata di Fourier al quadrato per la lunghezza del segnale che tende a infinito

[ ]

N j j n N n N

S( e

)

lim E

x n e

N

ω − ω →∞ ₌₋





=





+







∑



2

1

2

1

(A.2)

(5)

Per teorema di Wiener-Khinchin la PSD (power spectral density), risulta essere la trasformata di Fourier della funzione di autocorrelazione, R( τ ) , del segnale se il segnale può essere considerato un processo stazionario casuale almeno in senso lato.

Questo risulta dalla formula,

f

S( f )

∞

R( )e

τ

−π τ

d

τ

−∞

=

_∫

2 oppure j _xx

[ ]

j n n

S( e

ω

)

r

n e

ω ∞ − =−∞

=

∑

(A.3)

La potenza del processo in una data banda di frequenza può essere calcolata per integrazione sia del campo delle frequenze positive che negative,

F F F F

P

S( f )df

−

S( f )df

−

=

_∫

1

+

_∫

1 2 2

(A.4)

La PSD di un segnale esiste se e solamente se il segnale è, in senso lato, considerato un processo stazionario, cioè si può considerare un processo stocastico durante il quale la distribuzione di probabilità ad un tempo fissato o per una fissata posizione è la stessa per tutti i tempi e posizioni misurabili del processo.

Inoltre se il segnale non è stazionario, almeno in senso lato, allora la funzione di autocorrelazione, R( τ ), deve essere una funzione a due variabili, così allora non esiste la PSD, ma esiste una tecnica simile che può comunque essere usata in questi casi per stimare la variazione temporale della densità spettrale.

La densità spettrale è usualmente stimata usando come tecnica del periodogramma la trasformata di Fourier; ma altre tecniche come il metodo di Welch , il metodo di Thompson e il calcolo della massima entropia possono essere usati.

A.3 Il Metodo di Welch

Riportiamo il solo metodo di Welch perché è stato quello maggiormente preso in considerazione durante l’analisi dei segnali registrati dei cuscinetti. Il metodo di Welch, basato sulla procedura di Barlett, va a dividere il set dei valori rappresentanti il segnale nel

(6)

tempo (valori campionati), in gruppi più piccoli di uguale grandezza e calcola un periodogramma, di ogni singolo gruppo di valori.

Il periodogramma è ottenuto applicando un finestramento al dominio del tempo dei dati, invece che sull’intero intervallo di registrazione, calcolando la trasformata discreta di Fourier in ogni sottogruppo, quindi viene calcolando il quadrato di tale segnale trasformato. Infine viene presentato il periodiogramma che va a riunire tutti i risultati dei singoli sottogruppi.

( )

k

( )

k

x

f

P

f

N

=

2

( )

K k k

P f

P

f

K

=

∑

1

1 (A.5)

Ma le funzioni di finestramento solitamente “soffrono” della maggiore influenza del valore centrale del gruppo di dati scelto rispetto ai valori più “esterni”. Per mitigare questo, che si traduce in una perdita di informazioni provenienti dal segnale, i vari gruppi di dati vengono sovrapposti a livello temporale, ad esempio il set n può andare a ricoprire fino al 25% del set n+1, e naturalmente essere a sua volta ricoperto al 25% dal set n-1.

A.4 Utilizzo

Nelle nostre prove si è usato il metodo di Welch con ricopertura del 50% totale di ogni sottogruppo di dati

Fondamentalmente il metodo non è esattamente una tecnica di filtraggio, perché al segnale originario non togliamo nulla, ma serve per rendere più chiari e leggibili i grafici provenienti dai dati registrati nei cuscinetti. Lo spettro finale o meglio, la stima della densità spettrale di potenza risulta più smooth, ma i picchi se ci sono e non sono troppo vicini tra di loro risultano più visibili.

Si riportano i risultati ottenuti con cuscinetti obliqui, a rulli e a rulli con danneggiamento.

A) Cuscinetti Obliqui a sfere

(7)

I diagrammi rappresentano lo spettro registrato durante la prova del 27/02/07 con il carico di 2,58 kN, alla massima velocità 2000 giri/min.

Periodogrammi ottenuti con il metodo di Welch, grandezza di ogni sotottogruppo di 20000 elementi su un set completo di 100000 elementi (tempo di campionamento tC di 100 kHz

per 1 sec di registrazione) ed effetto di ricopertura del 50%.

Figura A.1 Segnale nel Dominio del tempo

(8)

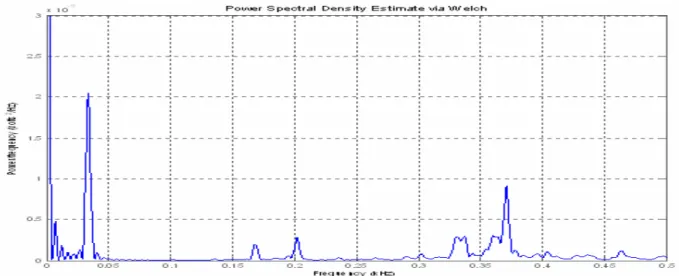
Figura A.3 PSD del cuscinetto obliquo sano

A) Cuscinetti a Rulli conici senza danneggiamento

Dalla registrazione effettuata il 19/03/07 con i cuscinetti a rulli nuovi e senza alcun danneggiamento, si noti come risultino essere molto più “silenziosi” dei cuscinetti a sfere obliqui

Velocità di rotazione di 2000 giri/min e carico applicato di 2,83 kN

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 -0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5

dominio nel tempo del segnale registrato

tempo sec

(9)

0 50 100 150 200 250 300 350 400 450 500 0

0.05 0.1

dominio delle frequenze del segnale

Hz

Figura A.5 FFT del cuscinetto a rulli integro

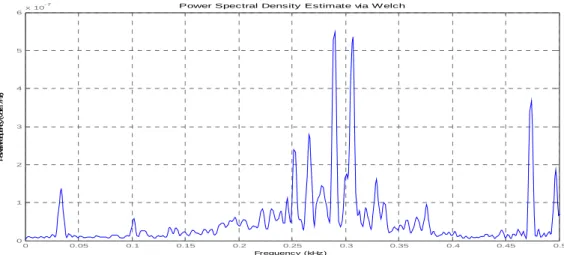
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0 1 2 3 4 5 6x 10 -7 Frequency (kHz) P o w e r/ fr e q u e n c y ( v o lts 2/H z )

Power Spectral Density Estimate via W elch

Figura A.6 PSD del cuscinetto a rulli integro B) Cuscinetto a rulli conici danneggiato

Dalla registrazione effettuata il 28/03/07 con i cuscinetti a rulli danneggiati con la penna a vibrazione.

(10)

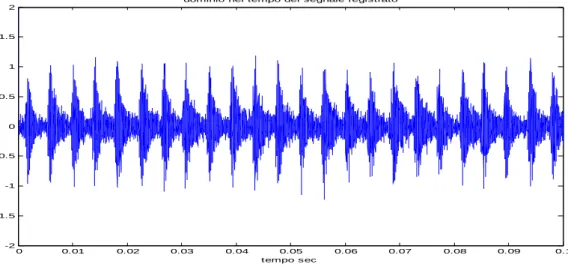
-Appendice A- Densità Spettrale di Potenza 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2

dominio nel tempo del segnale registrato

tempo sec

Figura A.7 Segnale nel Dominio del tempo

0 50 100 150 200 250 300 350 400 450 500 0 0.005 0.01 0.015 0.02 0.025

dominio delle frequenze del s egnale

Hz

(11)

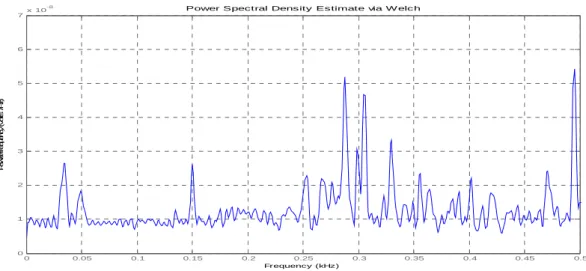
-Appendice A- Densità Spettrale di Potenza 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0 1 2 3 4 5 6 7x 10 -8 Frequency (kHz) P o w e r/ fr e q u e n c y ( v o lts 2/H z )

Power Spectral Density Estimate via W elch

Figura A.9 PSD del cuscinetto a rulli danneggiato

Da queste immagini risulta che, anche se migliorava la definizione dei picchi nei grafici, la PSD non poteva certo eliminare la modulazione che abbiamo in seguito scoperto affliggere il segnale registrato.

Infatti anche essa, come la normale FFT, non mostra sostanziali differenza nel campo delle frequenze tra cuscinetti sani e danneggiati, cosa che invece nel dominio del tempo risulta essere più che visibile.

(12)

-Appendice B- Elementi di Analisi dei dati

12

Appendice B Elementi di Analisi dei dati

B.1 Segnali analogici

Si dice segnale il modo di variare di una qualsiasi grandezza fisica in funzione del tempo. Ad esempio la pressione in un punto dello spazio (segnale sonoro), la differenza di potenziale tra due elettrodi (segnale elettrico), la velocità di un punto della crosta terrestre (segnale sismico), etc.

Un segnale si dice analogico quando è definito per qualsiasi istante di tempo e la grandezza in oggetto può assumere qualsiasi valore all’interno di un intervallo.

Estrarre da un segnale tutte le informazioni interessanti richiede tipicamente una quantità enorme di calcoli, che possono essere effettuati solamente da un calcolatore.

B.2 Segnali deterministici e segnali aleatori

Un segnale si dice deterministico se è possibile prevedere con precisione il suo valore ad un istante assegnato, ad esempio una sinusoide di frequenza e fase nota è un segnale deterministico.

Un segnale di dice aleatorio quando è possibile prevedere solamente la probabilità che il segnale assuma un certo valore ad un dato istante. Un segnale aleatorio è detto Gaussiano quando può essere definito completamente da due funzioni: la densità di probabilità e la funzione di correlazione.

• La prima dà la probabilità che il segnale assuma un valore dato;

(13)

13 I casi più importanti sono quelli in cui la distribuzione del segnale è gaussiana e quello in cui il valore del segnale ad un dato istante è completamente non correlato da quello ad istanti precedenti e successivi (rumore bianco).

B.3 Scheda di acquisizione

Per permettere ad un calcolatore di elaborare un segnale, bisogna dapprima convertirlo in un segnale di tipo elettrico, in questo modo è possibile inviare il segnale ad una scheda di acquisizione che trasforma il segnale in una tabella di numeri binari interi, gli unici in grado di essere elaborati dal calcolatore, che poi l’utente leggerà come numeri decimali, dopo una appropriata conversione.

Si rendono quindi necessarie due distinte operazioni sul segnale: la discretizzazione e la quantizzazione.

– La discretizzazione consiste nel misurare l’ampiezza del segnale ad intervalli di tempo fissati.

– La quantizzazione consiste nella trasformazione dei valori misurati in numeri interi binari.

B.4 Trasduttori

Un trasduttore è un sensore che fornisce ai morsetti di uscita una differenza di potenziale proporzionale alla grandezza che si intende misurare. Un esempio di trasduttore è un microfono (sensore di pressione), una termocoppia (sensore di temperatura), un fotodiodo (sensore di luminosità), etc.

Esistono anche sensori di posizione, di velocità, di forza (accelerometri), e di quasi tutte le grandezze fisiche soggette a misura. Caratteristiche importanti di un trasduttore sono l’ampiezza del segnale in uscita, la sensibilità, ovvero il minimo valore misurabile, la velocità di risposta, ovvero il tempo impiegato al sensore per fornire una risposta costante dopo una

(14)

14 brusca variazione della grandezza da misurare. Da quest’ultima caratteristica dipende la cosiddetta banda passante, ovvero la massima frequenza di variazione del segnale a cui il sensore è in grado di funzionare.

B.5 Segnale e rumore

Un trasduttore è uno strumento di misura: pertanto la tensione fornita sarà affetta da una piccola componente casuale, che porterà la misurazione a fluttuare intorno al valor medio. Si schematizza questo fenomeno considerando il segnale prodotto dal trasduttore come la somma di una parte proporzionale al segnale vero e proprio, che si intende misurare (o “segnale” tout-court), e da un segnale aleatorio. A quest’ultimo si da il nome di rumore.

Le cause delle fluttuazioni, o “sorgenti di rumore” sono molteplici, si va dalla temperatura (rumore termico) alla quantizzazione della carica dell’elettrone, ai campi elettrici presenti nelle vicinanze dell’apparecchio (ad esempio la linea a 50 Hz), alle vibrazioni meccaniche, etc.

Ulteriore rumore verrà introdotto quando il segnale prodotto dal trasduttore verrà trasportato lungo una linea elettrica, o amplificato, o comunque manipolato.

B.6 Discretizzazione

La discretizzazione consiste nel misurare l’ampiezza del segnale ad intervalli di tempo fissati. Sia ∆T l’intervallo di tempo tra due misure successive: la discretizzazione genera un vettore xn definito come:

(

n T

)

x

xn = ∆

È evidente che l’intervallo di tempo ∆T deve essere sufficientemente piccolo da riuscire ad individuare anche piccole variazioni de segnale.

L’inverso dell’intervallo ∆T si chiama frequenza di campionamento, o frequenza di sampling, e indica quante volte al secondo viene misurata l’ampiezza del segnale.

(15)

-Appendice B- Elementi di Analisi dei dati 15 T fs ∆ = 1 Esempio di discretizzazione. In questo caso, ∆T=5s, fs=1/5=0.2 Hz

B.7 Quantizzazione

La quantizzazione consiste nella trasformazione delle ampiezze misurate in numeri interi binari ad N bit.

Supponiamo che la scheda di acquisizione accetti in ingresso una tensione positiva al massimo di V0 volts. Il numero di combinazioni che si possono ottenere con N bit è dato da 2

N_{. Allora il}

modo più efficiente di convertire il segnale è di dividere l’intervallo V0 in 2

N _{fettine, ciascuna di}

spessore V0 /2 N

, ed assegnare ad ognuna di queste fettine un numero binario ad N bit. Quando il segnale cade in una di queste fettine, viene assegnata al numero binario corrispondente. In questo modo, si commette in ogni misura un errore pari al massimo a metà dello spessore della fettina, e quindi V0 /2

N+1_{. La minima variazione rilevabile del segnale in ingresso risulterà}

inoltre V0 /2 N _.

(16)

16 Esempio di quantizzazione

segnale a 3 bit, pari a 8 livelli distinti.

B.8 Condizionamento

Supponiamo che il trasduttore produca in uscita un segnale compreso tra un massimo Vmax ad un minimo Vmin. Visto che la precisione con cui viene quantizzato il segnale dipende

solo dalle caratteristiche della scheda, per ottenere la massima risoluzione è necessario che Vmax

e Vmin rientrino all’interno dell’intervallo accettato dalla scheda, e che vi si adattino al meglio. A

questo scopo è necessario amplificare o attenuare il segnale fornito dal trasduttore, ed eventualmente fornire una tensione aggiuntiva per evitare valori negativi.

Queste operazioni costituiscono l’esempio più semplice del cosiddetto condizionamento del segnale, che può prevedere anche un filtraggio, la sottrazione di una componente continua, etc.

Molte di queste operazioni vengono effettuate automaticamente dalla scheda di acquisizione stessa.

(17)

17

B.9 Da Analogico a digitale.

Il segnale che risulta dalla discretizzazione e dalla quantizzazione consiste essenzialmente in una sequenza di N combinazioni di 1 e 0, ed in questa forma può essere salvata in un supporto magnetico o trasmessa via cavo o via etere.

Un segnale di questo tipo è detto segnale digitale.

Il termine analogico e digitale si estende anche alle apparecchiature elettroniche, in base al tipo di segnale che sono in grado di elaborare. I vantaggi del digitale rispetto all’analogico sono molteplici: il più grosso è la robustezza al rumore, infatti un segnale composto da 1 e 0 può subire danneggiamenti fino a metà della propria ampiezza rimanendo sempre perfettamente ricostruibile inoltre i segnali digitali sono facilmente elaborabili tramite calcolatore, che permette di effettuare manipolazioni più sofisticate rispetto a quelle

eseguibili sui segnali analogici.

Tra gli svantaggi, si può annoverare la necessità di trasportare segnali rapidissimamente variabili, che implica tipicamente frequenze di trasmissione più alte, inoltre, a meno di prevedere meccanismi di correzione di errore (che esistono) un segnale digitale può risultare estremamente vulnerabile alla perdita di piccole porzioni di segnale.

(18)

18 Figura B.1 Percorso di un segnale

(19)

-Appendice C- Disegni tecnici del supporto

19

Appendice C Disegni tecnici del supporto

E’ riportato il complessivo del supporto realizzato e i particolari quotati dei componenti.

(20)

20

(21)

21

(22)

22

(23)

23

(24)

-Appendice D- I programmi sviluppati

24

Appendice D I programmi sviluppati

Sono riportati in questa sezione i testi integrali dei programmi sviluppati in ambiente MatLab e utilizzati in questo lavoro di ricerca

D.1 Il programma di Analisi dei dati

%Programma di Analisi per il monitoraggio dei dati provenienti da un cuscinetto volvente

%si fa uso dei metodi di filtraggio dello spectrum envelope con la trasformata di Hilbert, filtraggio %adattivo e decomposizione multilivello con le wavelet

clear; close all; clc

% segnale rumore di fondo prodotto dal tornio % Legge segnale ingresso del tornio

matrice=estrattore_file_bin_tornio; %generata matrice dal file dati registrati noise=matrice(:,1);

noise=10*(noise-mean(noise));

% Calcola lo spettro temporale del rumore tc=1/100000; %tempo di campionamento t=(0:tc:1-tc);

figure(1); plot(t,noise); axis([0 0.1 -2 2]);

title('dominio nel tempo del rumore'); xlabel('sec');

% Calcola lo spettro delle frequenze del rumore nel dominio delle frequenze K=400000; deltaf=100000/K; f=(0:deltaf:50000); Xs=fft(noise',K); Volume=max(abs(Xs)); Xs=Xs/Volume; figure(2); plot(f,abs(Xs(1:K/2+1))); axis([0 500 0 0.1]);

title('dominio delle frequenze del rumore'); xlabel('Hz');

(25)

25

% Legge segnale ingresso proveniente dall'accelerometro del supporto % cuscinetti

matrice=estrattore_file_bin; %generata matrice dal file dati registrati d=matrice(:,1); %d=desidered signal, il segnale del difetto+rumore di fondo d=d-mean(d);

% Calcola lo spettro nel tempo del segnale tc=1/100000; %tempo di campionamento t=(0:tc:1-tc);

figure(3); plot(t,d); axis([0 0.1 -2 2]);

title('dominio nel tempo del segnale del cuscinetto'); xlabel('tempo sec');

% Calcola lo spettro nel dominio delle frequenze del cuscinetto K=400000; deltaf=100000/K; f=(0:deltaf:50000); Xs=fft(d',K); Volume=max(abs(Xs)); Xs=Xs/Volume; figure(4); plot(f,abs(Xs(1:K/2+1))); axis([0 500 0 0.1]);

title('dominio delle frequenze del cuscinetto danneggiato'); xlabel('Hz');

% Ipotesi di registrazione con presenza di forte rumore coprente % Spettro nel tempo del segnale registrato

r=noise+d; r=r-mean(r); tc=1/100000; %tempo di campionamento t=(0:tc:1-tc); figure(5); plot(t,r); axis([0 0.1 -2 2]);

title('dominio nel tempo del segnale '); xlabel('tempo sec');

% Si calcola il rapporto rumore segnale N/S in db k=10*log10((sum(abs(noise).^2)/sum(abs(d).^2))); disp(k);

% Calcola lo spettro nel dominio delle frequenze del segnale registrato K=400000; deltaf=100000/K; f=(0:deltaf:50000); Xs=fft(r',K); Volume=max(abs(Xs)); Xs=Xs/Volume; figure(6); plot(f,abs(Xs(1:K/2+1))); axis([0 500 0 0.1]);

title('dominio delle frequenze del segnale'); xlabel('Hz');

(26)

26

% Trasformata di Hilbert per Demodulare il segnale z=hilbert(r);

v=r+imag(z); z=abs(v);

% FFT della trasformata di hilbert Zs=fft(z,K);

Volume=max(abs(Zs)); Zs=Zs/Volume; figure(7);

plot(f,abs(Zs(1:K/2+1))); axis([1 500 0 0.1]);

title('dominio delle frequenze del segnale di Hilbert'); xlabel('Hz');

%filtraggio adattivo per cercare di rimuovere gran parte del rumore che %affligge il segnale registrato

h = adaptfilt.nlms(256,0.5); h.ResetBeforeFiltering = 'off'; [y,e] = filter(h,noise,r); figure(8) plot(t,r,'b',t,e,'r'); axis([0 0.1 -2 2]); grid; xlabel('Time [sec]'); %ylabel('Voltage [mV]');

title('Convergence of Adaptive Noise Canceller');

% Trasformata di Hilbert per Demodulare il segnale filtrato z=hilbert(e); v=e+imag(z); z=abs(v); figure(9) plot(t,e,'r'); axis([0 0.1 -1 1]); grid; xlabel('time [sec]');

title('Segnale ottenuto dopo il filtro adattivo');

% FFT della trasformata di Hilbert del segnale filtrato Zs=fft(z,K);

% Filtraggio fine tramite le wavelet per cercare di rimuovere l'eventuale % rumore che ancora affligge il segnale filtrato

% Si usa come wavelet madre la db9 a vari livelli di decomposizione % decomposizione ad primo livello

s=e(1:99999); l_s=length(s);

(27)

-Appendice D- I programmi sviluppati 27 A1 = idwt(cA1,[],'db9',l_s); D1 = idwt([],cD1,'db9',l_s); figure(11); subplot(2,1,1);

plot(s);axis([0 10000 -2 2]); title('original signal') subplot(2,1,2);

plot(A1);axis([0 10000 -0.5 0.5]); title('Approximation A1') %decomposizione al secondo livello

[C,L] = wavedec(s,2,'db9'); A2 = wrcoef('a',C,L,'db9',2); figure(12);

subplot(2,1,1);plot(s);axis([0 10000 -2 2]);title('Original'); subplot(2,1,2);

plot(A2);axis([0 10000 -0.3 0.3]);title('Level 2 Approximation'); %decomposizione al terzo livello

[C,L] = wavedec(s,3,'db10'); A3 = wrcoef('a',C,L,'db10',3); figure(13);

subplot(2,1,1);plot(s);axis([0 10000 -2 2]);title('Original'); subplot(2,1,2);

plot(A3);axis([0 10000 -0.3 0.3]);title('Level 3 Approximation'); %Trasformata di Hilbert della decomposizione A3, del terzo livello A3=A3-mean(A3);

z=hilbert(A3); v=A3+imag(z); z=abs(v);

% FFT della trasformata di Hilbert Zs=fft(z,K);

% Facendo uso della wavelet madre bior2.8 si opera un denoising % direttamente al terzo livello sempre del segnale uscito dal filtraggio % adattivo

[thr,sorh,keepapp] = ddencmp('den','wv',s);

clean = wdencmp('gbl',C,L,'bior2.8',3,thr,sorh,keepapp); figure (15);

%subplot(2,1,1); plot(s);axis([0 10000 -2 2]); title('Original') %subplot(2,1,2); plot(clean);axis([0 10000 -0.3 0.3]); title('De-noised') clean=clean-mean(clean); z=hilbert(clean); v=A3+imag(z); z=abs(v);

(28)

28

% FFT della trasformata di Hilbert Zs=fft(z,K);

D.2 Programma di confronto: Hilbert vs Fourier

%Questi programma consente di visualizzare il segnale tramite la FFT del %segnale "grezzo" e con una FFT dopo che è stato demodulato con Hilbert % cosi da poter , con il loro confronto controllare se è presente una

% qualche modulazione di ampiezza

%il programma provvede anche ad eseguire il calcolo del RMS del segnale %entrante

clear; close all; clc % Legge segnale ingresso

matrice=estrattore_file_bin; %generata matrice dal file dati registrati x=matrice(:,1);

x=x-mean(x); N=length(x);

% Calcola lo spettro di x nel dominio del tempo tc=1/100000; %tempo di campionamento t=(0:tc:1-tc);

figure(1); plot(t,x);

axis([0 0.1 -0.3 0.3]);

title('dominio nel tempo del segnale registrato'); disp('Calcolo dello spettro nel tempo del segnale') K=400000; deltaf=100000/K; f=(0:deltaf:50000); Xs=fft(x,K); Volume=max(abs(Xs)); Xs=Xs/Volume; plot(f,abs(Xs(1:K/2+1))); axis([0 500 0 0.1]);

title('dominio delle frequenze del segnale'); xlabel('Hz');

% Trasformata di Hilbert per Demodulare z=hilbert(x);

v=x+imag(z); t=abs(v);

% FFT della trasformata di hilbert Zs=fft(t,K);

(29)

29

figure(6);

title('dominio delle frequenze del segnale demodulato con Hilbert'); xlabel('Hz');

figure(7);

title('dettaglio del segnale demodulato'); xlabel('Hz');

%Calcolo del RMS del segnale rms=norm(x)/sqrt(N); disp('rms1');disp(rms);

D.3 Il programma estrattore

%Questo programma legge i dati registrati dagli accelerometri e salvati dal labView in .bin e permette

%la lettura ed utilizzo in ambiente Matlab

function data = estrattore_file_bin (binary_data, sample_start, sample_end) % gear_ReadRawData extracts samples from binary data

%

% data = gear_ReadRawData(binary_data, samples) %

% binary_data = binary file containing the acquired data % sample_start = the beginning of the interval to extract % sample_end = the end of the interval to extract % data = matrix contatining the chosen samples, with % channel selected by the column

%

% Version: 1.1 % Date: 08/06/2006

[fid, msg] = fopen('dati_6_2000.bin', 'r', 'ieee-be'); if (fid == -1)

sprintf('Error: unable to open file %s', 'dati_B_2_720.bin'); error(msg);

end

if (~ strcmp(fgetl(fid), '[DAQCompressedBinaryFile]')) error('Error: cannot find header information.'); end

% read headers channel = 0;

c0 = zeros(1, 4); % scale coefficients c1 = zeros(1, 4); % scale coefficients while true

(30)

30

line = fgetl(fid); %disp(line); if (line == -1)

error('Error: end of file reached while searching for binary data.'); %elseif (strcmp(line, '[Task0]') || strcmp(line, '[Task1]'))

% channel = 0;

elseif (strcmp(line, '[Task0Channel0]')) channel = 1;

elseif (strcmp(line, '[Task0Channel1]')) channel = 2;

%elseif (strcmp(line, '[Task0Channel2]')) % channel = 3;

%elseif (strcmp(line, '[Task0Channel3]')) % channel = 4;

% elseif (strcmp(line, '[Task1Channel0]')) %channel = 5;

% elseif (strcmp(line, '[Task1Channel1]')) %channel = 6;

%elseif (strcmp(line, '[Task1Channel2]')) %channel = 7;

% elseif (strcmp(line, '[Task1Channel3]')) % channel = 4;

elseif (channel ~= 0 && strncmp(line, 'PolynomialScalingCoeffs=', 24) && length(line) >= 25) % store the scale coefficients

coeff = sscanf(line, 'PolynomialScalingCoeffs=%f;%f'); c0(channel) = coeff(1);

c1(channel) = coeff(2);

elseif (strcmp(line, 'Begin=Here')) % end of headers

break end end

offset = (0 - 1) * 2 * 2; % 2 channels with 2 bytes per channel samples = 99999 - 0 + 1;

if (fseek(fid, offset, 0) ~= 0)

error('Error: failed to retrieve data.'); end

tmp = double(zeros(1, samples*2)); data = double(zeros(samples, 2));

[tmp, count] = fread(fid, samples*2, 'int16=>double'); if (count < samples*2)

error('Error: failed to retrieve data.'); end

for ch=1:2

data(:, ch) = c0(ch) + tmp(ch:2:samples*2-2+ch) * c1(ch); end

(31)

31

if (fclose(fid) ~= 0)

error('Error: unable to close file.') end

return

D.3 Il periodogramma

%Programma che fa uso della PSD con il metodo di Welch, mostra anche il %segnale nel dominio del tempo e la sua FFT

clear; close all; clc

matrice=estrattore_file_bin; %generata matrice dal file dati registrati x=matrice(:,1);

N=length(x);

% Calcola lo spettro di x nel tempo tc=1/100000; %tempo di campionamento t=(0:tc:1-tc);

figure(1); plot(t,x); axis([0 1 -2 2]);

title('dominio nel tempo del segnale registrato'); xlabel('tempo sec');

% Calcolo dello spettro delle frequenze di x disp('Calcolo dello spettro del segnale') fs=N; K=N; f=(0:K/2); Xs=fft(x',K); Volume=max(abs(Xs)); Xs=Xs/Volume; figure(2); plot(f,abs(Xs(1:K/2+1))); axis([0 500 0 0.3]);

title('dominio delle frequenze del segnale'); xlabel('Hz'); M=mean(x); y=x-M; Hs = spectrum.welch('rectangular',20000,50) figure(3); psd(Hs,y,'Fs',fs,'NFFT',100000,'SpectrumType','onesided'); axis([0 0.5 -80 -40]); Hs = spectrum.welch('rectangular',20000,50) figure(4); psd(Hs,x,'Fs',fs,'NFFT',100000,'SpectrumType','onesided'); axis([0 0.5 -80 -40]); figure(6); pwelch(x,20000,10000,[],fs,'onesided'); axis([0 0.5 -100 -40]);

(32)

32

(33)