Capitolo 4 - Modelli analitici di previsione

Capitolo 4 - Modelli analitici di previsione

4.1 INTRODUZIONE

Il ruolo fondamentale della rugosità superficiale nei fenomeni di danneggiamento superficiale ha portato allo sviluppo di diversi modelli per la determinazione dell’area di contatto reale, della vera distribuzione di pressione e del conseguente campo di tensioni sub-superficiale.

Questi modelli possono essere suddivisi in due grandi categorie. La prima include le analisi che assumono la superficie rugosa reale come equivalente ad una superficie liscia su cui sono sovrapposte asperità di data geometria; Greenwood e Williamson (GW), Greenwood e Tripp, Onions e Archard, Chang sono alcuni studiosi che hanno seguito tale linea, che prevede il ricorso ad un approccio statistico sulla distribuzione dei picchi di asperità; sulla scia di tali considerazioni sono state sviluppati studi sempre più fini fino ad elaborare teorie sulla forma frattale della rugosità (Majumdar e Bushan). La seconda categoria di modelli include l’analisi del profilo di rugosità per la determinazione della distribuzione di pressione, dell’area di contatto e del campo di tensione sub-superficiale. In tale ottica si ricorre più frequentemente alla soluzione dell’equazione di pressione-deformazione elaborata da Flamant, nel caso di problemi bidimensionali, o alla corrispondente equazione di Boussinesq per modelli tridimensionali.

Nei prossimi paragrafi vengono proposti modelli di contatto tra superfici rugose a partire dall’analisi dell’interazione tra le singole asperità dei corpi in contatto, seguita da una parte analitica che mira a quantificare l’influenza della rugosità sulla distribuzione delle pressioni e quindi delle sollecitazioni. Vengono quindi forniti i fondamenti della teoria elastoidrodinamica, evidenziando i progressi degli studi e i parametri fondamentali su cui si basa oggi la problematica dei contatti lubrificati su scala micrometrica. L’interazione tra regime di lubrificazione e rugosità appare evidente sia nella trattazione analitica che trae spunto dagli studi condotti da D. Dowson [29], L. Chang [30], che adottano un’analisi di profilo della rugosità, sia nel modello semplificato ideato da F. Antoine e J.-M. Besson dell’azienda francese Eurocopter, specificatamente per la previsione del micropitting in ingranaggi cilindrici [47].

4.2 MECCANICA DEL CONTATTO

Le superfici reali presentano sempre un certo grado di rugosità, quindi se si considerano due solidi in contatto asciutto o con lubrificazione limite, questo avviene sicuramente vicino o sui picchi delle asperità, determinando un’area di contatto reale generalmente molto minore di quella apparente.

Un modello di contatto può essere realizzato in due passi principali:

I. Determinare le equazioni rappresentanti il contatto di una singola coppia di asperità, includendo: la deformazione elastica, elasto-plastica o, se , completamente plastica; gli effetti di adesione per contatti in scala nanometrica; la forza applicata, normale e/o tangenziale.

el pl ε ε >>

II. Poiché le superfici reali sono rugose è necessario combinare gli effetti dei contatti tra le numerose asperità. In molti casi è importante scegliere se trattare questi contatti come disaccoppiati o no [63].

4.2.1

Meccanica del contatto per una singola asperità

4.2.1.1 Contatto Hertziano

Si considerino due solidi portati in contatto tramite l’azione di forze esterne. Il contatto fra i due corpi avviene su aree molto piccole, ciascuna delle quali costituisce il risultato del

contatto di una singola asperità. E’ necessario legare la forza agente sulla singola asperità alla sua deformazione ed alla sua area di contatto. La teoria di Hertz, assume che:

E’ valido il modello meccanico dei continui (si considerano dimensioni molto maggiori di quelle dei grani e/o delle celle atomiche);

L’area di contatto è ellittica;

ogni solido è approssimato da un semi-spazio elastico caricato sul piano dell’area di contatto ellittica;

le dimensioni del contatto sono molto più piccole rispetto alle dimensioni dei due solidi ed ai raggi di curvatura delle superfici;

le deformazioni sono sufficientemente piccole per validare la linearità dell’elasticità; il contatto è senza attrito così che è trasmessa la sola pressione normale.

Nel caso del contatto tra superfici rugose, ogni asperità è sottoposta a pressioni molto elevate e quindi a deformazione plastiche, la teoria di Hertz non è più applicabile e la distribuzione della pressione non è più semi-ellittica ma presenta un aumento ai bordi dell’area di contatto che porta ad una distribuzione di pressione quasi uniforme.

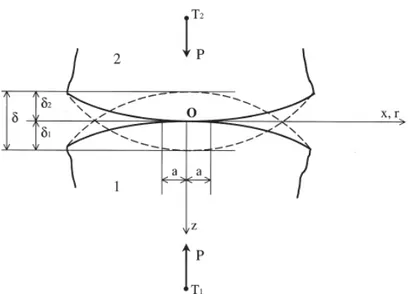
In Figura 4.1 sono rappresentati i due solidi in contatto ed il sistema di riferimento adottato per la soluzione del problema del contatto. Il punto di primo contatto è preso come origine del sistema di riferimento cartesiano in cui il piano x-y coincide con il piano tangente e l’asse z rivolto verso il basso. Durante la compressione dovuta al carico normale P, la distanza tra i punti T1 e T2 diminuisce della quantità δ =δ1+δ2, detta accostamento o interferenza.

Nel caso di solidi di rivoluzione premuti lungo l’asse di simmetria, l’area di contatto è circolare, e la soluzione è: 3 1 2 2 4 9       ⋅ ⋅ ⋅ = E R P δ (4.1) 3 1 2 3       ⋅ ⋅ ⋅ = E R P a (4.2) 3 1 2 3 2 0 2 3       ⋅ ⋅ ⋅ ⋅ = R E P p π (4.3) 2 2 2 1 2 1 1 1 2 E E E ν ν − + − = (4.4)

2 1 1 1 1 R R R = + (4.5)

dove p0 è la pressione massima del contatto, E ed R sono rispettivamente il modulo di

Young ed il raggio equivalenti dei due corpi.

Figura 4.1 – Contatto hertziano tra due solidi elastici non conformi.

Nel caso in cui, invece, il contatto è tra due cilindri con assi paralleli, si ha:

2 1 8       ⋅ ⋅ ′ ⋅ = E R P b π (4.6) 2 1 0 2      ⋅ ⋅ ⋅ ′ = R E P p π (4.7)

dove P’ _{è il carico applicato per unità di lunghezza.}

4.2.1.2 Contatti elasto-plastico e completamente plastico

La soluzione hertziana del contatto resta valida fino a che il carico applicato è tale da provocare l’inizio di una deformazione plastica. Secondo il criterio di Tresca della massima tensione tangenziale, la deformazione plastica ha inizio in un punto del corpo dove questa raggiunge un valore critico, dato dall’espressione:

{

₁ − ₂, ₂ − ₃, ₃ − ₁

}

=Y

max σ σ σ σ σ σ (4.7)

dove σ₁,σ₂,σ₃ sono le tensioni principali e Y è la tensione di snervamento ottenuta da una semplice prova a trazione monoassiale.

Secondo il criterio di von Mises lo snervamento avviene quando è l’energia di distorsione a raggiungere un valore critico, per cui lo snervamento ha inizio quando:

(

) (

) (

)

2 2 1 3 2 3 2 2 2 1−σ + σ −σ + σ −σ =2 Y⋅ σ (4.8)

La soluzione del contatto hertziano nel caso di due sfere, presenta il massimo della tensione tangenziale, per , ad una profondità di e di valore 0 . Quindi ambedue i criteri di Tresca e quello di von Mises predicono l’inizio dello snervamento, per il materiale con il valore minore del limite di snervamento, quando:

3 . 0 = ν 0.48⋅a .31⋅p₀

( )

p_{0 Y} = 601. ⋅Y (4.9) 2 3 2 ) 2 ( 2 . 21 E Y R P_Y = ⋅ ⋅ (4.10) 2 2 32 . 6 _      ⋅ ⋅ = E Y R Y δ (4.11)

Aumentando il carico aumenteranno anche le dimensioni della zona plasticizzata. Una soluzione analitica per il caso di completa plasticità, è stata ottenuta da Ishlinsky, il quale affermò che mentre il comportamento elasto-plastico avviene a:

Y

p_m = 071. ⋅ (4.12)

quello completamente plastico si ha a:

Y H

p_m = =2.8⋅ (4.13)

4.2.1.3 Contatti elastici non-Hertziani

Nei contatti Hertziani descritti precedentemente, è stata tacita l’assunzione che il contatto tra i corpi era non-conforme. La geometria locale dei contatti non-conformi può essere caratterizzata dal raggio di curvatura nei punti di contatto.

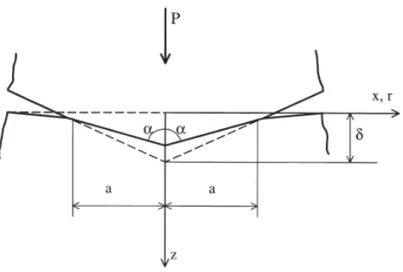
Se si prende il contatto di un cono con un semi-spazio elastico (Figura 4.2), questo non è un problema risolvibile con la teoria di Hertz.

Figura 4.2 – Contatto tra un cono ed un semi-spazio elastico.

Considerando quindi un contatto in cui i profili dei solidi non possono essere rappresentati da un polinomio di secondo grado, la distanza tra due corpi assial-simmetrici non deformati è data da:

( )

n n r A r h = ⋅ 2⋅ _(4.14)

dove n è un intero positivo.

La soluzione di Stuermann, dove i corpi sono modellati come semi-spazi elastici, fornisce:

1 2 4 2 1 + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ = ⋅+ n a n E A P n n n γ _(4.15) n n n a A _{⋅ ⋅} 2 = γ δ (4.16)

dove:

(

2 1

)

3 1 2 4 2 − ⋅ ⋅ ⋅ ⋅ ≡ n n n K K γ (4.17)

Per un problema di contatto bi-dimensionale, con una distanza iniziale h

( )

x , si ha:

( )

n n x A x h _{= ⋅} 2⋅ _(4.18) n n n a A E n P γ π_{⋅ ⋅ ⋅} ⋅ ⋅ = ′ 2 (4.19)

Dove è il carico per unità di lunghezza. Per n l’equazione sopra si riduce al contatto hertziano, mentre per valori di n grandi la distribuzione della tensione si avvicina a quella di un punzone piano con singolarità agli spigoli. Love e Sneddon hanno studiato il problema del cono utilizzando una tecnica diversa, determinando la relazione tra il raggio di contatto, la forza applicata e l’interferenza, ottenendo:

P′ =1

( )

α π cot 2 1_{⋅ ⋅} 2 _{⋅ ⋅} = a E P (4.20)

( )

α π δ cot 2 1_{⋅ ⋅ ⋅} = a (4.21)

La soluzione del contatto bi-dimensionale è stata fornita invece da Johnson [18]:

( )

α cot ⋅ ⋅ = ′ a E P (4.22)

4.2.1.4 Contatto in scala nanometrica – adesione

In scala nanometrica i corpi solidi possono ancora essere trattati come un continuo, ma gli effetti delle forze superficiali nelle immediate vicinanze della regione di contatto diventano importanti. La tensione adesiva è rappresentata tipicamente dal potenziale di Lennard-Jones:

( )

              −       ⋅ ⋅ ⋅ − = − − 9 0 3 0 0 3 8 z z z z z w z σ (4.23)

dove è la distanza di separazione tra i piani atomici, è la distanza di separazione di equilibrio, e è il lavoro dell’adesione dato, per esempio, dall’espressione:

z z₀ w 12 2 1 γ γ γ γ = + + ∆ = w (4.24)

dove , γ1 γ2, γ12 sono le energie superficiali corrispondenti.

Un modello della forza di adesione è stato sviluppato da Bradley per sfere rigide, che fornisce:               −       ⋅ ⋅ ⋅ ⋅ ⋅ − = − − 2 0 8 0 4 1 3 8 z z z z R w P π (4.25)

4.2.2

Modelli di contatto multi-asperità

I modelli convenzionali di superfici rugose possono essere classificati in base al completo disaccoppiamento (uncoupled multi-asperity model) o accoppiamento (coupled multi-asperity model) delle asperità superficiali [63].

Nel primo caso i modelli di rugosità superficiale sono caratterizzati da una serie di asperità con distribuzione statistica di parametri quali l’altezza o la curvatura dei picchi; l’effetto di ciascuna asperità è locale e quindi l’effetto risultante è cumulativo, ovvero è rappresentato dalla somma delle azioni delle singole asperità. I problemi di contatto tra multi-asperità accoppiate sono, invece, più complessi matematicamente in quanto le equazioni di elasticità devono essere risolte sull’intero dominio del contatto.

4.2.2.1 Modello di Greenwood e Williamson

Sono stati sviluppati diversi modelli statistici di contatto, tutti legati allo studio pionieristico di Greenwood e Williamson (1966). Questi modelli assumono determinate leggi di distribuzione delle altezze delle asperità e delle curvature (uncoupled multi-asperity model), e si basano sul calcolo della funzione probabilità per cui un picco, selezionato casualmente, entri in contatto con una superficie distante (Figura 4.3), che in generale è espressa dalla relazione: d

(

>

)

=

_∫

∞

( )

⋅ d

d z d g z dz

dove gd(z) è la funzione densità di probabilità delle altezze dei picchi.

Figura 4.3 – Superficie rugosa e corpo piano vicini al contatto.

Il modello di Greenwood e Williamson (GW) assume che, nel contatto tra una superficie rugosa e una superficie liscia:

− la rugosità superficiale è isotropica, ovvero le asperità sono distribuite uniformemente per unità di area con densità costante;

− le asperità sono emisferiche, tutte con ugual raggio di curvatura; − le altezze dei picchi di asperità seguono una distribuzione casuale; − non esiste alcuna interazione tra le asperità vicine.

L’area di contatto media tra le asperità risulta dunque:

(

) ( )

∫

∞ ⋅ ⋅ − ⋅ ⋅ ⋅ = = d d m N R z d g z dz A A π (4.27)

ed il carico totale applicato:

(

)

( )

∫

∞ ⋅ ⋅ − ⋅ ⋅ ⋅ ⋅ = d d z dz g d z R N E P 12 32 3 4 (4.28)

dove N individua il numero di asperità in contatto.

Le distribuzioni di altezze delle asperità considerate dal modello sono: − una distribuzione esponenziale:

( )

_z =_e− ,_z>0

g z

− una distribuzione Gaussiana:

( )

22 2 1 z d z e g ⋅ − ⋅ = π (4.30)

La distribuzione esponenziale porta ad una dipendenza lineare dell’area di contatto reale con il carico applicato, mentre quella Gaussiana ad un legame quasi lineare.

Il modello di Greenwood e Williamson introduce anche un indice di plasticità , dato da: ϕ

2 1       ⋅ = R H E σst ϕ (4.31)

dove è la deviazione standard della distribuzione delle altezze delle asperità, è la durezza del materiale.

st

σ H

L’indice di plasticità tiene conto della transizione da deformazione elastica a plastica; bassi valori di corrispondono a deformazioni elastiche. ϕ

Precedentemente al noto studio di Greenwood e Williamson, il modello di Zhuravlev (1940) assumeva una distribuzione delle altezze dei picchi di tipo lineare con asperità sferiche allineate:

( )

(

L z

)

z L L

z

g_d = 2₂ ⋅ − ,0< < (4.32)

e conduceva ad un legame tra carico e area effettiva del tipo:

11 10

P C

A= ⋅ (4.33)

dove C è una costante.

Greenwood e Tripp hanno esteso il modello di Zhuravlev per asperità non allineate e hanno dimostrato che il disallineamento porta ad una relazione proporzionale tra area di contatto e carico più vicina alla linearità, ovvero _A=C⋅P1213_.

Greenwood e Tripp hanno dimostrato, in particolare, che, come nel classico caso Hertziano, il contatto tra due superfici rugose può essere modellato dal contatto tra un piano e

una superficie rugosa. La superficie rugosa equivalente è caratterizzata da una curvatura dell’asperità che è somma delle curvature delle asperità delle due superfici rugose, eq. (4.5), e da una distribuzione di picchi con una deviazione standard data da:

2 2 2 1 p p p σ σ σ = + (4.34)

Nel caso di ipotesi di contatto elasto–plastico, il riferimento è costituito dal “modello profilometrico” di Abbot e Firestone. La deformazione di una superficie rugosa a contatto con un piano è considerata ottenuta dal troncamento della superficie rugosa in corrispondenza dell’intersezione con il piano. L’area di contatto reale, quindi, è l’intersezione geometrica della superficie piana con il profilo rugoso in analisi.

Un modello elasto-plastico basato sulla conservazione del volume dell’asperità durante la deformazione plastica è stato introdotto da Chang, Etsion e Bogy (CEB) [63]. L’area di contatto, la forza e l’interferenza per una singola asperità sono legate dalle seguenti relazioni:

c c R A δ δ δ δ δ π  >      − ⋅ ⋅ ⋅ = 2 , (4.35) H K A P= ⋅ ⋅ (4.36)

dove è l’interferenza critica all’inizio della deformazione plastica, è una costante che

lega la pressione media alla durezza . Per un valore dell’interferenza minore del valore critico, il contatto è elastico.

c

δ K

H

4.2.2.2 Approccio teorico per la stima della pressione di contatto media tra le asperità

Utilizzando dunque il modello di contatto di Greenwood e Williamson e il modello di contatto elasto-plastico CEB , è possibile stimare la pressione di contatto media tra le asperità [64], ed applicare l’analisi di Hamilton e Goodman per il calcolo della tensione massima principale di trazione sull’asperità. Il carico medio di contatto sulle asperità risulta pari a:

( )

t

n P

dove nt rappresenta il numero totale di contatti tra asperità e risulta pari a:

∫

∞ ⋅ − _⋅ ⋅ ⋅ ⋅ ⋅ = d z n t N A e dz n 0.5 2 2 1 π (4.38)

avendo indicato con l’area nominale del contatto. L’accostamento , combinando le equazioni (4.1) e (4.3), risulta equivalente a:

n A δ =z−d R E p ⋅       ⋅ = 2 max π δ (4.39)

e l’accostamento critico in cui ha inizio lo snervamento si ricava inserendo nella

relazione (4.39) l’uguaglianza c δ

( )

H

p_max δ = 60. ⋅ (4.40)

ricavabile dall’applicazione dei criteri di Tresca e von Mises (pmax

( )

δ rappresenta la

pressione massima hertziana per tutti i contatti tra le asperità). Il carico di contatto tra le asperità in corrispondenza di cui si verifica lo snervamento risulta:

( )

12 32 3 2 c y E R P δ = ⋅ ⋅ ⋅δ (4.41)

Se p

( )

δ >P_y

( )

δ , le asperità si deformano in modo elasto-plastico; in tali condizioni l’espressione dell’area di contatto elastico tra asperità non risulta valida, e dunque si può applicare il modello CEB espresso dall’equazione (4.35). Noti quindi

δ π⋅ ⋅ = ′ R A

( )

δ p e

( )

δ

A , è possibile determinare la pressione massima hertziana per tutti i contatti tra asperità:

( )

( )

_{( )}

δ δ δ A p p = ⋅ 2 3 max (4.42)

In base all’analisi condotta da Hamilton e Goodman per un contatto circolare di strisciamento, è possibile calcolare una delle tre tensioni principali, che è a trazione, ottenendo come valore massimo:

( )

σ1 max =K⋅pmax (4.43) dove:

(

) (

)

3 2 1 8 4 ν ν µ ⋅ + + − ⋅ = _attr K (4.44)

essendo µ_attr il coefficiente di attrito e il coefficiente di Poisson del materiale. ν

4.2.3

Modello di contatto tra superfici reali per l’analisi del micropitting

Al fine di studiare la deformazione di superfici rugose, si considera un corpo semi-infinito soggetto ad un carico concentrato nel punto w x=ξ (Figura 4.4).

Figura 4.4 – Deformazione di un corpo semi-infinito soggetto ad un carico di linea . w

La deformazione lungo l’asse di un punto sulla superficie è data dall’equazione di Flamant:

( )

x z z

(

x,0

)

( )

(

)

_      − − ⋅ ⋅ ⋅ − ⋅ = ∞ 2 1 ln 1 2 2 ξ π ν x d E w x z (4.45)

dove d è una distanza nel corpo per cui ∞ d∞ >>x.

Si considera ora un punto di riferimento arbitrario sulla superficie lontano dal punto di applicazione del carico . Quindi la deformazione calcolato rispetto a questo punto, è data da:

(

x_r,0

)

ξ = x d

( )

x

( ) ( ) ( )

(

)

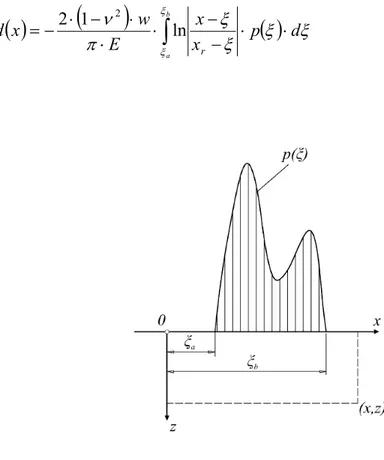
ξ ξ π ν − − ⋅ ⋅ ⋅ − ⋅ − = − = r r x x E w x z x z x d 2 1 ln 2 (4.46)

Se si sostituisce il carico con una pressione distribuita tra e (Figura 4.5), la deformazione si otterrà integrando l’eq. (4.46):

w p

( )

ξ ξ =ξ_a ξ =ξ_b

( )

(

)

( )

ξ ξ ξ ξ π ν ξ ξ d p x x E w x d b a r ⋅ ⋅ − − ⋅ ⋅ ⋅ − ⋅ − = 2 1

_∫

ln 2 (4.47)

Figura 4.5 – Corpo semi-infinito soggetto ad una pressione p

( )

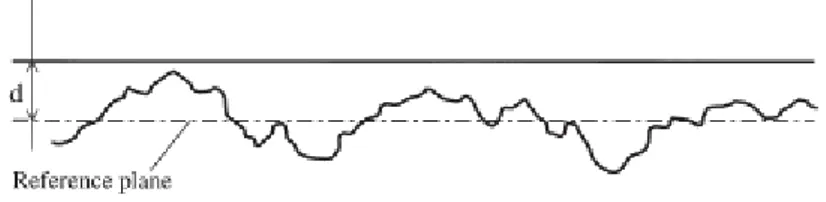
ξ .

Il contatto tra due cilindri con superfici rugose con picchi di rugosità, misurati a partire da un piano medio (reference plane) pari a e , possono essere sostituiti da un contatto equivalente di un cilindro rugoso, avente raggio di curvatura pari al raggio equivalente R (eq.

( )

x

4.34), un modulo di Young equivalente pari a E, una rugosità composta , con un piano

rigido completamente liscio:

( )

x h₀ b ⋅

( )

x h

( )

x h

( )

x h₀ = ₀₁ + ₀₂ (4.48)

( )

x h₀₁ ap h

, di h e sono positivi per o picchi e negativi per le valli [65]. La figura 4.6

mostra il cilindro equivalente pressato contro il piano rigido da una distanza di accostamento pari a .

( )

x

02 h0

( )

x

Figura 4.6 – Contatto tra un cilindro rugoso ed un piano rigido [65].

Un numero di picchi di asperità determinano sul piano rigido altrettanti segmenti di contatto di larghezza . A causa della rugosità, la larghezza di contatto 2 , che prende tutte le , da a , risulta diversa dalla larghezza 2 , prevista dalla teoria di Hertz.

n n ω i ω i ω ω₁ ⋅b_H

La larghezza di contatto reale ωc risulta dunque:

∑

= = n i i c 1 ω ω (4.49)

La deformazione elastica della superficie rugosa è dunque data dalla seguente equazione:

( ) ( ) ( )

x h x g x hap d = − + (4.50) dove:

( )

h

( )

x R x x g 2 ₀ 2⋅ − = (4.51)

e rappresenta la distanza del cilindro equivalente dal piano di riferimento in assenza di carico.

La pressione sviluppata può essere calcolata usando l’equazione di Flamant [65]:

( )

_∫

(

(

)

(

)

)

( )

= − = ⋅ ⋅ − − − ⋅ ⋅ − = 2 2 ln ln 4 L L r p d x x E x d ξ ξ ξ ξ ξ ξ π (4.52)

dove è una larghezza di controllo scelta in modo che L L> 2⋅b_H, dato che 2⋅b≠2⋅b_H. Le equazioni (4.50) e (4.52) consentono di determinare la distribuzione della pressione per un profilo di rugosità dato, se è nota la distanza di accostamento del piano h_ap.

Secondo il modello di deformazione elastico-perfettamente plastico assunto, le punte delle asperità si deformano elasticamente fino ad una pressione pari a , dove Y è la tensione di snervamento del materiale meno duro dei due corpi, e plasticamente se la pressione locale supera questo limite. Le condizioni al contorno delle equazioni (4.50) e (4.52) sono:

Y ⋅ 3

( )

c p

( )

c pξ >0,ξ∈ω ; ξ >0,ξ∉ω (4.53)

( )

x c h

( )

x c h =0,ξ∈ω ; >0,ξ∉ω (4.54)

( )

p

( )

if p

( )

Y pξ = ξ , _K ξ ≤3⋅ (4.55)

( )

Y if p

( )

Y

pξ =3⋅ , _K ξ >3⋅ (4.56)

( )

x g

( )

x hap x c

d =− + , ∈ω (4.57)

Una volta nota , è possibile determinare le componenti dello stress risultante in un punto attraverso le relazioni:

( )

ξ p

(

x,z

)

( ) (

)

(

)

[

]

∫

⋅ + − − ⋅ ⋅ ⋅ − = b a d z x x p z x ξ ξ ξ ξ ξ ξ π σ ₂ 2 2 2 2 (4.58)

( )

(

)

[

]

∫

⋅ + − ⋅ ⋅ − = b a d z x p z z ξ ξ ξ ξ ξ π σ ₂ 2 2 3 2 (4.59)

( ) (

)

(

)

[

]

∫

⋅ + − − ⋅ ⋅ ⋅ − = b a d z x x p z xz ξ ξ ξ ξ ξ ξ π τ ₂ 2 2 2 2 (4.60)

Applicando il criterio di von Mises, il massimo valore della tensione di taglio subsuperficiale τmax risulta pari a

2 2 max 2 xz z x σ _τ σ τ  +      − = (4.61)

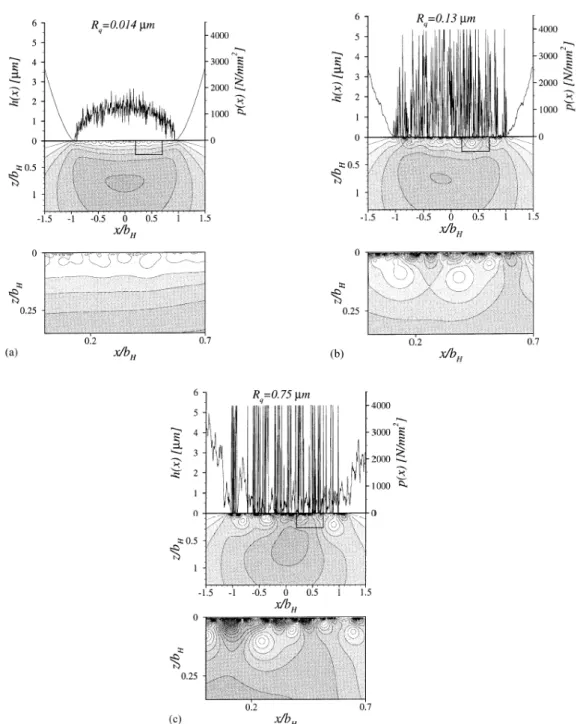
Nelle Figure 4.7 e 4.8 [65] sono illustrate la forma deformata, la distribuzione di pressione e il campo di tensione sub-superficiale risultante nel caso di un contatto tra due cilindri rispettivamente lisci e rugosi ad assi paralleli soggetti a carichi normali.

In particolare, la Figura 4.7 si riferisce al caso di un cilindro equivalente quasi perfettamente liscio (con rugosità quadratica media pari a ); il parametro b indica la semilarghezza di contatto hertziano, rappresenta la distanza di una superficie deformata misurata da un piano rigido di riferimento, individua la pressione di contatto, x e z sono le coordinate cartesiane di riferimento del contatto longitudinale e della profondità rispettivamente. m µ ⋅ 00013 . 0

)

H

( )

x h

(

x p

Figura 4.7 – Contatto tra cilindro liscio e piano rigido [65].

Le Figure 4.8 (a) ÷ (c) evidenziano i risultati che si ottengono da un’analisi tribologica del contatto al variare della rugosità quadratica media ( ). In Figura 4.8 (a) si nota che anche per valori di molto bassi ( 0 ), il campo di tensione sub-superficiale devia dal tipico andamento hertziano, mostrando picchi locali in corrispondenza delle asperità in contatto. L’area reale di contatto è pari al suo valore nominale; in tal caso tutte le asperità si deformano elasticamente. In Figura 4.8 (c), dove vale , il campo di tensione sub-superficiale non presenta alcuna somiglianza con l’andamento hertziano.

q R µ ⋅ q R .00013⋅µm q R 0.75 m

La posizione della massima tensione di taglio si sposta da una profondità pari a , come previsto dalla teoria di Hertz, ad una quota molto prossima alla superficie. In tale condizione, circa il dell’area di contatto nominale è deformata plasticamente, solo il 9 elasticamente; di conseguenza, il valore della massima tensione di taglio è indipendente dal carico imposto. L’area deformata plasticamente è dunque considerevole e non può essere trascurata quando il contatto è caratterizzato da elevate pressioni di Hertz, anche per superfici aventi rugosità composta molto inferiore a 0,75 µm.

H b ⋅ 78 . 0 % % 23

Figura 4.8 – Variazione della deformazione, della distribuzione di pressione e del campo di tensione

4.3 LUBRIFICAZIONE ELASTOIDRODINAMICA

4.3.1

Cenni storici

Nel 1916 Martin risolse il problema della lubrificazione, con fluido isoviscoso, del contatto non conforme fra cilindri rigidi (contatto di linea), ottenendo valori bassissimi dello spessore di meato, con la formula adimensionata:

W U

H = 94. ⋅ (4.62)

dove rappresenta lo spessore adimensionale del film, U la velocità adimensionale e W

il carico adimensionale per unità di lunghezza in un contatto lineare, ricavati dalle seguenti relazioni: H x R h H = _(4.63) x r R E u U ⋅ ⋅ = µ0 (4.64) L R E w W x⋅ ⋅ = (contatto di linea) (4.65) dove:

− h indica lo spessore del film [m]

− Rx indica il raggio di curvatura principale [m]:

x x x R R R _{1 2} 1 1 1 _{= +} (4.66)

− µ0 indica la viscosità in condizioni ambiente [Pa· s]

− E indica il modulo elastico equivalente [Pa]

− w indica il carico [N]

− L indica la lunghezza del cilindro per il contatto di linea [m]

Valori tipici dei parametri adimensionali U e sono rispettivamente 10 e 10 per ruote con dentatura ad evolvente con

W −10 −4

m N

w L ≈ 320000⋅ e v ⋅m s; quindi risulta dell’ordine di grandezza di 10 . Allo stesso modo, è tipicamente dell’ordine di

grandezza di 10 , dunque lo spessore minimo del film previsto dalla formula di Martin è usualmente dell’ordine di circa 10 , ovvero un centesimo di micron. Poiché le superfici dei denti degli ingranaggi presentano in genere una rugosità media nell’intervallo tra

, lo spessore specifico del meato risulterebbe molto minore di 1. A partire dal 1935 (Merrit), esperienze compiute soprattutto con macchine a dischi dimostrarono che la situazione reale era assai più favorevole (i solchi della rettifica erano ancora presenti sulle dentature anche dopo anni di servizio). E’ evidente come gli studi successivi si siano indirizzati alla comprensione di due fattori non analizzati dalla teoria di Martin, ovvero l’influenza della deformazione elastica dei solidi sulla forma della regione di concentrazione del carico e l’influenza dell’elevata pressione su caratteristiche del lubrificante quale la viscosità.

per ≈ 85 a R H 6 − m ⋅ −8 x R m ⋅ −2 m µ ⋅ ÷ 80. 4 . 0

4.3.1.1 Modello di Ertel e Grubin

Nel 1949 Grubin non ottenne una completa soluzione numerica del problema EHL, ma si servì di una serie di intuizioni relative alla forma del meato e dell’andamento della pressione che gli permisero di ottenere una valutazione sufficientemente realistica dell’altezza del meato nella zona centrale del contatto. Grubin condensò i risultati delle sue ricerche in una formula che consente una valutazione approssimata dello spessore del meato per contatti fortemente caricati, in funzione dei principali parametri operativi, sempre per il solo contatto di linea:

11 1 11 8 11 8 95 . 1 W G U H = ⋅ ⋅ (4.67) dove: E G=α⋅ (4.68)

e rappresenta il parametro adimensionale che prende in considerazione il tipo di materiale ed è l’esponente della formula di Barus: α

p

e ⋅

⋅ =_µ α

µ ₀ (4.69)

che esprime la variazione della viscosità in funzione della pressione.

4.3.1.2 Modello di Dowson e Higginson

Un nuovo approccio al problema elastoidrodinamico è stato introdotto da Dowson e Higginson nel 1959, i quali hanno sviluppato una tecnica risolutiva inversa in cui l’equazione di Reynolds è stata utilizzata non per calcolare il campo delle pressioni a partire da una data forma specifica del film, ma per calcolare la forma del film associata ad una data distribuzione di pressione. Questa procedura inversa ha permesso di ottenere forme di film lubrificante comparabili con le forme calcolate a partire dalla teoria dell’equazione di elasticità. La normale procedura iterativa, in particolare, è stata utilizzata per esaminare la regione di ingresso, mentre la procedura inversa è stata adottata nella regione centrale, ad alta pressione. Nel 1961 Dowson e Higginson hanno ottenuto la relazione che consente di calcolare lo spessore minimo del film:

13 . 0 7 . 0 6 . 0 6 . 1 W U G H = ⋅ ⋅ (4.70)

Lo sviluppo dei calcolatori numerici ha permesso di ottenere soluzioni sempre più accurate. Dowson, successivamente, ha corretto la formula originaria rendendola compatibile con le formule dell’analisi dimensionale:

13 . 0 7 . 0 54 . 0 65 . 2 W U G H = ⋅ ⋅ (4.71)

Anche questa soluzione, derivata semi-algebricalmente, è valida soltanto per il problema del contatto di linea.

4.3.1.3 Modello di Dowson e Hamrock

Nel 1977 Dowson e Hamrock hanno ottenuto una soluzione numerica completa del problema EHL del contatto tra due sfere, ricavandone una formula per lo spessore centrale e una per lo spessore minimo del meato da applicare a qualsiasi tipo di contatto [66]:

(

k

)

c e W U G H = ⋅ ⋅ ⋅ − ⋅ −0.73⋅ 067 . 0 67 . 0 53 . 0 61 . 0 1 69 . 2 (4.72)

(

_e k

)

W U G H = ⋅ ⋅ ⋅ − −0.68⋅ 073 . 0 68 . 0 49 . 0 min 3.63 1 (4.73) dove: 2 x R E w W ⋅ = (contatto ellittico) _(4.74) 64 . 0 03 . 1 _      ⋅ = x y R R k (parametro ellittico) (4.75)

4.3.2

Lubrificazione elastoidrodinamica nel contatto di linea

Come già visto nel §3, generalmente, la distribuzione di pressione in EHL è molto simile a quella del contatto Hertziano a secco, con le differenze che si hanno una crescita della pressione nella regione di ingresso ed un picco di pressione nella zona di uscita.

E’ dimostrato che aumentando la velocità o diminuendo il carico aumenta il picco di pressione e si sposta verso la regione di ingresso, mentre sotto elevati carichi, il picco di pressione tende a diminuire, fino anche a sparire, quindi il profilo della pressione tende a quello hertziano.

Sia la massima pressione hertziana che il picco di pressione sono parametri importanti nelle applicazioni di lubrificazione elastoidrodinamica; infatti, il secondo, può provocare elevate tensioni sub-superficiali, influenzando direttamente la vita a fatica dell’elemento meccanico.

Il valore del picco di pressione può essere determinato utilizzando l’espressione [66]:

391 . 0 275 . 0 185 . 0 648 . 0 W U G P_spike = ⋅ ⋅ ⋅ (4.76) dove: E p P= (pressione adimensionale) (4.77)

mentre la posizione è data da:

x

spike W U G R

x =_1.111⋅ 0.606⋅ −0.021⋅ 0.077⋅

4.3.3

Parametri influenzanti lo spessore del film EHL

4.3.3.1 Parametri operativi

Velocità superficiali dei corpi; mentre la velocità di rotolamento influenza come visto il parametro U (paragrafo 4.3.1), la velocità di strisciamento influenza il coefficiente d’attrito, le tensioni tangenziali e quindi la temperatura durante il contatto (vedi §7). Carico normale totale.

4.3.3.2 Caratteristiche dimensionali e del materiale

Modulo di Young dei due solidi, E1, E2; Modulo elastico equivalente:

Raggi di curvatura Rx1, Rx2, Ry1, Ry2;

Raggi di curvatura equivalenti in direzione x (Rx)ed y (Ry), vedi equazione (5.64); Raggio di curvatura totale:

y x R R R 1 1 1 _{= +} (4.79) Coefficienti di Poisson, ν1, ν2.

4.3.3.3 Viscosità e piezo-viscosità del lubrificante

Parlando di lubrificazione EHD, in cui vi sono variazioni di pressione dell’ordine di GPa si può utilizzare il modello esponenziale della piezoviscosità di Barus (4.69), semplice ma accurato solo per pressioni < 0.1 GPa, che risultano molto inferiori rispetto a quelle tipiche dei contatti hertziani.

Tuttavia per la valutazione del film di lubrificante l’uso di questo modello esponenziale non influenza negativamente, poiché lo spessore del film nella lubrificazione EHD dipende essenzialmente dal comportamento del lubrificante nella zona di ingresso del meato. Questo modello però è inutilizzabile per valutare la temperatura locale o il coefficiente di attrito.

Il valore di da introdurre nell’equazione di Barus è la derivata del logaritmo della relazione viscosità-pressione, calcolata a pressione ambiente:

0 0 0 0 0 ln = = ∂ ∂ = ∂ ∂ = = p p T p p µ µ µ µ α α _(4.80)

noto come modulo tangente, e dipendente in maniera non trascurabile dalla temperatura. Per migliorare a pressioni elevate si sostituisce al modulo tangente quello secante calcolato ad una pressione (= 0.07 GPa o = 0.1 GPa):

p e ⋅ ⋅ =_µ α µ ₀ S p

( )

0 ln 1 µ µ α α S S S p p = = _(4.81)

O utilizzare l’inverso della pressione isoviscosa asintotica p_∞:

∞ ∗ ₌ = p 1 α α _(4.82) dp p_∞ =

∫

∞ 0 0 µ µ (4.83) 0 µ α ⋅ attr

è un ottimo indice dell’attitudine del lubrificante a formare un film EHD. Nel caso si desideri conoscere la temperatura nel meato ed una valutazione del coefficiente d’attrito

bisogna utilizzare metodi più accurati. Roelands propose: µ         −         + ∞      = = ′ 1 1 0 0 Z p p µ µ µ µ µ (4.84) con _=63.1⋅10−6_{⋅Ns m}2 ∞ µ , p= 1960. ⋅GPa, z≠ f(T).

Volendo tener conto anche della temperatura il modello di Roelands può essere scritto:

            −           + + + ⋅         + ∞      = = ′ 1 1 1 1 1 0 0 0 S Z T TT T p p µ µ µ µ µ (4.85)

4.4 MODELLO SEMPLIFICATO PER LA PREVISIONE DEL

MICROPITTING

Il metodo semplificato per il calcolo del micropitting sulle ruote dentate, sviluppato da F. Antoine e J.-M. Besson dell’azienda francese Eurocopter [47], prende in considerazione tutti quei parametri che rappresentano i differenti fenomeni fisici che ne influenzano la formazione:

1. lo spessore del film di olio considerando l’influenza della pressione 2. la rugosità (modellizzazione semplificata con la curva di Abbot) 3. stima dell’effetto di plastificazione sulla rugosità

4. sovrapressioni sulla superficie di contatto considerando gli effetti combinati della rugosità e dello spessore del film di olio

I parametri principali presi in considerazione dal modello sviluppato dall’Eurocopter sono:

la geometria del contatto; il carico applicato; le velocità di rotazione; la viscosità dell’olio;

la rugosità (curva di Abbot); la durezza dei materiali in contatto;

le caratteristiche elastiche dei materiali (E, ν);

la resistenza allo snervamento e limite di durata a fatica di provini aventi le caratteristiche delle zone cementate.

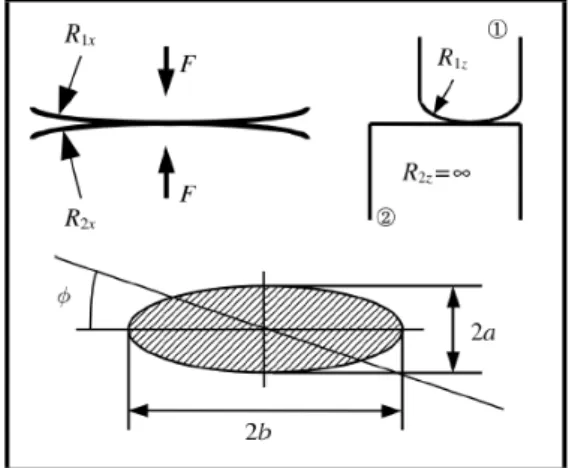
Il primo passo è quello di calcolare le dimensioni del contatto e la massima tensione di compressione secondo la teoria di Hertz applicata al contatto tra due cilindri con assi paralleli per un contatto di linea (Figura 4.9) ed al contatto tra due ellissoidi per un contatto di punto (Figura 4.10).

Figura 4.9 – Contatto hertziano cilindro-cilindro Figura 4.10 – Contatto hertziano ellittico

La massima pressione hertziana è data, per il contatto di linea, dalla formula:

L R E F P_Hertz ⋅ ⋅ ⋅ ⋅ = π 2 (4.86)

per il contatto di punto, da:

b a F P_Hertz ⋅ ⋅ ⋅ ⋅ = π 2 3 (4.87)

dove F rappresenta il carico applicato, L la lunghezza del contatto, a e b i semi-assi dell’ellisse di contatto, E e R rispettivamente il modulo ed il raggio equivalente (4.4, 4.5, 4.79) .

Per quanto riguarda il calcolo dello spessore del lubrificante, assegnati i valori del coefficiente piezo-viscoso e la viscosità dell’olio a pressione ambiente e ad una data temperatura, solitamente uguale ad 80 °C. Successivamente applicando la relazione di Grubin in forma dimensionata per il calcolo dello spessore del film di lubrificante al centro del contatto si ha: α µ₀

(

)

[

]

0.75 0.5 0.25 2 1 0 0 1.417 − ⋅ ⋅ + ⋅ ⋅ ⋅ = u u R b h α µ (4.88)

dove u1 e u2 sono le velocità lineari dei due solidi in corrispondenza del cerchio primitivo, sono cioè le velocità primitive periferiche (velocità di rotolamento puro), mentre R è il raggio

equivalente precedentemente calcolato per un contatto lineare o il raggio equivalente lungo la direzione x nel contatto di punto.

A questo punto si passa a determinare le condizioni operative caratterizzando la rugosità con la curva di Abbot-Firestone, che risulta essere una buona approssimazione del valor medio della stessa (paragrafo 3.3), calcolando il valore dell’altezza della rugosità, sommando il contributo di ambedue i solidi in contatto:

(

50%

)

2

(

50%

)

2⋅ ₁ + ⋅ ₂ ⋅

= δ δ

rug

h (4.89)

dove i due valori a destra nell’equazione rappresentano la profondità, riferendosi alla curva di Abbot-Firestone, a cui corrisponde un tasso di materiale superiore al 90 % (Figura 4.11), portando in questo modo a trascurare le valli più profonde (Figura 4.12).

Figura 4.11 – Curva di Abbot-Firestone Figura 4.12 – Profilo della rugosità

Per determinare quindi se il contatto è misto o idrodinamico si confrontano i valori delle altezze ricavate per la rugosità e per il film di lubrificante in questo modo:

se 1 0 > h h_rug il contatto è misto; se 1 0 < h h_rug il contatto è idrodinamico.

Il passo successivo è determinare la superficie plasticizzata e la profondità del profilo di rugosità plasticizzato. E’ noto che per il contatto tra una sfera ed un piano infinitamente liscio

(Figura 4.13) e con l’ipotesi di deformazione perfettamente plastica, vale la relazione di Ishlinsky, per cui la superficie deformata plasticamente è data dalla relazione:

p p Y F S ⋅ ≈ 3 (4.90)

Figura 4.13 – Area deformata plasticamente

dove F è il carico complessivo agente sui due solidi, mentre Y è una pseudo tensione di snervamento (MPa), poco superiore alla tensione di snervamento reale e legata alla durezza Vickers del materiale secondo la formula:

p

V

p H

Y ≈ 533. ⋅ _(4.91)

Per l’area totale di contatto si assumono: , per il contatto di linea;

L b S_T = 2⋅ ⋅

, per il contatto di punto.

b a S_T =π⋅ ⋅

La percentuale di area plasticizzata è data da:

100 % = ⋅ T p p S S S (4.92)

Nell’ipotesi che il profilo di rugosità misurato su ciascuna superficie è la stessa su ogni area di contatto, utilizzando sempre la curva di Abbot-Firestone è possibile ricavare la profondità

equivalente che rappresenta la profondità plasticizzata (Figura 4.14), introducendo nella stessa il risultato dell’equazione (4.92). Quindi si passa a calcolare, nuovamente, l’espressione dell’altezza somma dei profili di rugosità delle due superfici dopo la plasticizzazione, cioè dopo la fase di rodaggio (vedi anche paragrafo 3.3), verificando sempre la forma del contatto (misto o idrodinamico) con: r δ

(

)

2

(

) (

1 2 1 50% 2 50% 2 _{r r} rug h = ⋅δ + ⋅δ ⋅ − δ +δ

)

(4.93)

Figura 4.14 – Determinazione della profondità della plasticizzazione

A questo punto il modello passa alla determinazione della superficie di lavoro reale, ipotizzando che il lubrificante sia simmetricamente suddiviso rispetto alle due superfici di contatto. Si determina quindi, per ciascun solido in contatto, la profondità di lavoro reale che sopporta l’intero carico, secondo la relazione:

r tr h _δ δ = + 2 0 _(4.94)

ed utilizzando la curva di Abbot-Firestone determinare la superficie di lavoro reale (Figura 4.15).

Ricavato S_tr, il massimo valore della pressione agente su ciascun solido è dato, semplicemente, da: tr i S F p_max = _(4.95)

Figura 4.15 – Determinazione della superficie reale di lavoro

Naturalmente verrà scelto il maggiore tra i massimi dei due solidi, che risulteranno ambedue comunque maggiori dei valori ottenuti dalla teoria di Hertz riferita al contatto cilindro-cilindro.

La massima tensione tangenziale è data da:

π

τ i

i

p_max

max = (4.96)

Poiché vengono considerate solo le sollecitazioni di taglio e le stesse variano tra 0 e 3 , si considera la massima tensione possibile:

i

i max

max 3 τ

σ = ⋅ (4.97)

Noti il limite a fatica f del materiale indurito superficialmente (ottenuto mediante tests di fatica su provini induriti) ed il carico di snervamento, è possibile determinare l’insorgere o no del micropitting: se max _>1 f i σ ci sarà micropitting; se max _<1 f i σ