Capitolo 4
Modelli di motoveicolo
In questo capitolo verrà descritto il modo in cui sono stati formulati i vari modelli di motoveicolo e, di seguito, saranno mostrati i sistemi di equazioni che governano ognuno di essi.
4.1
Equazioni di Lagrange
Per ottenere le equazioni del moto del sistema, sono state utilizzate le Equazioni di Lagrange, nella seguente formulazione:
d dt µ ∂T ∂ ˙qi ¶ − ∂T ∂qi +∂U ∂qi = Qi (4.1) Dove:
• T è l’energia cinetica del sistema • U è l’energia potenziale del sistema
• qi è la generica i-esima coordinata lagrangiana
• Qi è la i-esima componente lagrangiana delle forze attive non
conser-vative
Nel caso di una schematizzazione di motoveicolo come quella proposta nel capitolo (2), si potrebbero utilizzare le seguenti coordinate lagrangiane1
: • xN
O e yNO rappresentano le coordinate assolute del punto N
1
i sistemi di riferimento ed i simboli utilizzati sono quelli definiti in (2.5).
4.1 Equazioni di Lagrange 44
• δ è l’angolo di sterzo • φ è l’angolo di rollio • ψ è l’angolo di imbardata
Nello studio di un sistema in cui l’angolo di imbardata assume grandi valori è preferibile sostituire le coordinate xN
O e yNO con la velocità di avanzamento
uN e quella laterale vN, definite in (2.8). Esse però non sono esprimibili
come derivate temporali di vere coordinate; è invalso l’uso di chiamarle quasi-coordinate.
4.1.1
Quasi-coordinate
In [20] è illustrato un metodo per modificare le equazioni di Lagrange, in modo da poterle utilizzare direttamente come quasi-coordinate. Più nello specifico, in [1] è reperibile un’applicazione di tale metodo alla dinamica del veicolo. Nel caso della schematizzazione di motoveicolo proposta, è sufficiente considerare le equazioni di Lagrange per le vere coordinate, ed introdurre il legame: " uN vN # = " cos ψ sin ψ − sin ψ cos ψ # " u0 v0 # Dove: vN = uNiN+ vNjN v0 = u0i0+ v0j0
Con notazione sintetica:
vN = Cv0
Anche per le componenti lagrangiane delle forze attive non conservative: " Qu Qv # = " cos ψ sin ψ − sin ψ cos ψ # " Qx Qy # = C " Qx Qy # Derivando, si ottiene: d dt µ ∂T ∂v0 ¶ = ˙CT ∂T ∂vN + CT d dt µ ∂T ∂vN ¶
4.2 Energia Cinetica 45
4.1.2
Equazioni
Tenendo presente quanto esposto in (4.1.1), si ottiene: Coordinata uN:
d dt µ ∂T ∂uN ¶ − ˙ψ ∂T ∂vN = Qu (4.2) Coordinata vN: d dt µ ∂T ∂vN ¶ + ˙ψ ∂T ∂uN = Qv (4.3) Coordinata δ: d dt µ ∂T ∂ ˙δ ¶ −∂T ∂δ + ∂U ∂δ = Qδ (4.4) Coordinata ψ: ∂T ∂ψ = ∂T ∂uN ∂uN ∂ψ + ∂T ∂vN ∂vN ∂ψ Siccome: ∂uN ∂ψ = vN ∂vN ∂ψ = − uN L’equazione per la coordinata ψ diventa:
d dt µ ∂T ∂ ˙ψ ¶ − vN ∂T ∂uN + uN ∂T ∂vN +∂U ∂ψ = Qψ (4.5) Coordinata φ: d dt µ ∂T ∂ ˙φ ¶ − ∂T ∂φ + ∂U ∂φ = Qφ (4.6)
4.2
Energia Cinetica
L’energia cinetica del sistema motoveicolo può essere considerata come somma di contributi; facendo riferimento a quanto esposto nelle sezioni (2.2), (2.5) e (2.8), si definisce:
T = Tt+ Trm+ Trf + Te+ Tw1+ Tw2 (4.7)
Dove:
• Tt è l’energia cinetica dovuta alla traslazione del corpo
4.2 Energia Cinetica 46
• Trf è l’energia cinetica dovuta alla rotazione dell’anteriore
• Te è l’energia cinetica dovuta alla rotazione del motore
• Tw1 è l’energia cinetica dovuta alla rotazione della ruota anteriore
• Tw2 è l’energia cinetica dovuta alla rotazione della ruota posteriore
Per la (2.24), che definisce la velocità di traslazione del baricentro G, si ha: Tt= 1 2m¡u 2 G+ v 2 G+ w 2 G¢ = = 1 2m h (uN + ˙ψh sin φ) 2 + (vN − ˙φh cos φ) 2 + ( ˙φh sin φ)2i (4.8)
Dove m è la massa totale del veicolo. Secondo la (2.25) che definisce la velocità di rotazione del baricentro G, si ha che:
Trm = 1 2¡Ixmp 2 + Iymq 2 + Izmr 2 − 2Izxmpr − 2Izymqr − 2Ixympq¢ = = 1 2 h Ixmφ˙ 2 + Iym( ˙ψ sin φ) 2 + Izm( ˙ψ cos φ) 2 − 2Izxmφ ˙˙ψ cos φ+ −2Izymψ˙ 2
sin φ cos φ − 2Ixymφ ˙˙ψ sin φ
i
(4.9)
Analogamente, considerando la relazione (2.34), che definisce la velocità di rotazione dell’anteriore, si ottiene:
Trf = 1 2¡Ixfp 2 P + Iyfq 2 P + Izfr 2 P − 2IzxfpPrP − 2IzyfqPrP+ −2IxyfpPqP) = = 1 2 h
Ixf( ˙φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ) 2
+ +Iyf(− ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ)
2
+ +Izf( ˙φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ)
2
+
−2Izxf( ˙φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ)( ˙φ sin ǫ+
+ ˙ψ cos φ cos ǫ + ˙δ) − 2Izyf( ˙φ sin ǫ + ˙ψ cos φ cos ǫ+
+ ˙δ)(− ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ)+ −2Ixyf( ˙φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ+
+ ˙ψ sin φ sin δ)(− ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ)i
4.2 Energia Cinetica 47
Utilizzando la relazione (2.31), che definisce la velocità di rotazione del sistema motore, si ottiene:
Te = 1 2¡Ixep 2 E+ Iyeq 2 E + Izer 2 E − 2IzxepErE− 2IzyeqErE+ −2IxyepEqE) = = 1 2 h Ixe( ˙φ) 2 + Iye( ˙ψ sin φ + uNτ ) 2 + Ize( ˙ψ cos φ) 2 + −2Izxeφ ˙˙ψ cos φ − 2Izye( ˙ψ sin φ + uNτ )( ˙ψ cos φ)+
−2Ixye( ˙φ)( ˙ψ sin φ + uNτ )
i
(4.11)
Utilizzando la relazione (2.28), che definisce la velocità di rotazione della ruota posteriore, si ottiene:
Tw2 = 1 2¡Ix2p 2 2+ Iy2q 2 2+ Iz2r 2 2 − 2Izx2p2r2− 2Izy2q2r2+ −2Ixy2p2q2) = = 1 2 h Ix2( ˙φ) 2 + Iy2( ˙ψ sin φ + uN/r2) 2 + Iz2( ˙ψ cos φ) 2 + −2Izx2φ ˙˙ψ cos φ − 2Izy2( ˙ψ sin φ + uN/r2)( ˙ψ cos φ)+
−2Ixy2( ˙φ)( ˙ψ sin φ + uN/r2)
i
(4.12)
Per determinare l’energia cinetica dovuta alla velocità di rotazione della ruota anteriore, si utilizza la relazione (2.37).
Tw1 = 1 2¡Ix1p 2 1+ Iy1q 2 1 + Iz1r 2 1 − 2Izx1p1r1− 2Izy1q1r1+ −2Ixy1p1q1) = = 1 2 h
Ix1( ˙φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ) 2
+ +Iy1(− ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ + uN/r1)
2
+ +Iz1( ˙φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ)
2
+
−2Izx1( ˙φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ)( ˙φ sin ǫ+
+ ˙ψ cos φ cos ǫ + ˙δ) − 2Izy1(− ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ+
+ ˙ψ sin φ cos δ + uN/r1)( ˙φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ)+
−2Ixy1( ˙φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ)
(− ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ + uN/r1)
i
4.3 Energia potenziale 48
Nel caso in cui l’angolo di sterzo possa ritenersi piccolo2
, alcuni termini costi-tuenti l’energia cinetica, in particolare quelli riguardanti l’anteriore, possono essere semplificati come di seguito:
Trf =
1 2 h
Ixf( ˙φ cos ǫ − ˙ψ cos φ sin ǫ + ˙ψ sin φδ) 2
+ +Iyf(− ˙φ cos ǫδ + ˙φ cos φ sin ǫδ + ˙ψ sin φ)
2
+ +Izf( ˙φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ)
2
+
−2Izxf( ˙φ cos ǫ − ˙ψ cos φ sin ǫ + ˙ψ sin φδ)( ˙φ sin ǫ+
+ ˙ψ cos φ cos ǫ + ˙δ) − 2Izyf( ˙φ sin ǫ + ˙ψ cos φ cos ǫ+
+ ˙δ)(− ˙φ cos ǫδ + ˙φ cos φ sin ǫδ + ˙ψ sin φ)+ −2Ixyf( ˙φ cos ǫ − ˙ψ cos φ sin ǫ+
+ ˙ψ sin φδ)(− ˙φ cos ǫδ + ˙φ cos φ sin ǫδ + ˙ψ sin φ)i
(4.14)
Tw1=
1 2 h
Ix1( ˙φ cos ǫ − ˙ψ cos φ sin ǫ + ˙ψ sin φδ) 2
+ +Iy1(− ˙φ cos ǫδ + ˙φ cos φ sin ǫδ + ˙ψ sin φ + uN/r1)
2
+ +Iz1( ˙φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ)
2
+
−2Izx1( ˙φ cos ǫ − ˙ψ cos φ sin ǫ + ˙ψ sin φδ)( ˙φ sin ǫ+
+ ˙ψ cos φ cos ǫ + ˙δ) − 2Izy1(− ˙φ cos ǫδ + ˙φ cos φ sin ǫδ+
+ ˙ψ sin φ + uN/r1)( ˙φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ)+
−2Ixy1( ˙φ cos ǫ − ˙ψ cos φ sin ǫ + ˙ψ sin φδ)
(− ˙φ cos ǫδ + ˙φ cos φ sin ǫδ + ˙ψ sin φ + uN/r1)
i
(4.15)
4.3
Energia potenziale
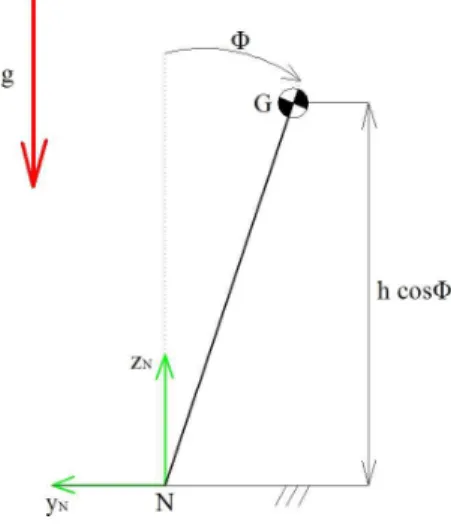
In Fig. 4.3 si vede il motoveicolo inclinato di un angolo φ. Esso è soggetto al campo gravitazionale g; ricordando che h rappresenta l’altezza del bari-centro, misurata sul piano mediano longitudinale del motoveicolo, si ha che l’energia potenziale è:
U = mgh cos φ (4.16)
2sin
4.4 Componenti delle forze attive 49
Figura 4.1: Energia potenziale
Nelle equazioni di Lagrange compaiono le derivate parziali dell’energia poten-ziale rispetto alle coordinate lagrangiane:
∂U ∂φ = − mgh sin φ ∂U ∂δ = 0 ∂U ∂ψ = 0 ∂U ∂uN = 0 ∂U ∂vN = 0
4.4
Componenti lagrangiane delle forze non
con-servative
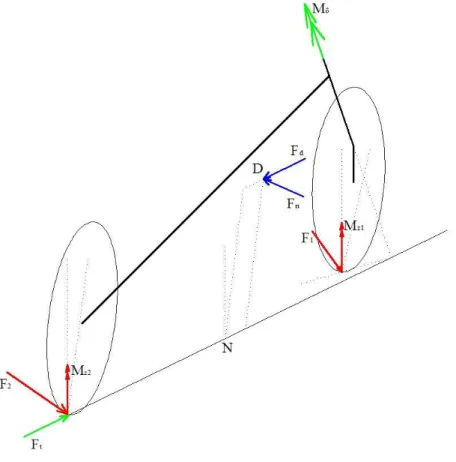
Le forze non conservative che agiscono sul sistema, che verranno prese in considerazione nello sviluppo del modello, sono quelle visibili in Fig. 4.2. Esse sono:
• F1 e Mz1 sono le azioni che derivano dal contatto del pneumatico
anteriore con il terreno durante il moto
• F2 e Mz2 sono le azioni che derivano dal contatto del pneumatico
4.4 Componenti delle forze attive 50
Figura 4.2: Forze attive non conservative • Fd è la forza di resistenza aerodinamica
• Fn è la forza di disturbo laterale, simulacro di raffiche di vento
• Mδ è la coppia esercitata dal pilota sul manubrio
• Ft è la forza di trazione esercitata nel punto di contatto a terra della
ruota posteriore, gestita dal pilota
4.4.1
Resistenza aerodinamica
Le azioni che derivano dall’interazione del motociclo con l’aria possono es-sere scomposte lungo varie direzioni di applicazione3
. Supponendo l’assenza di vento laterale, la forza aerodinamica può essere scomposta in una compo-nente verticale Fl(detta portanza) ed in una orizzontale Fd(detta resistenza)
4
3
Per una trattazione approfondita dei fenomeni aerodinamici si veda [21].
4
4.4 Componenti delle forze attive 51
ed in una componente laterale (detta devianza); quest’ultima è dovuta esclu-sivamente al moto di rollio del motoveicolo. La Fdviene chiamata resistenza
aerodinamica ed è l’unica che vale la pena prendere in considerazione in questo tipo di applicazione; infatti il lavoro compiuto dalle altre due compo-nenti è di entità trascurabile.
La resistenza aerodinamica si può esprimere come: Fd = 1 2ρSCxu 2 N (4.17) Dove:
• Cx è un coefficiente adimensionale, che viene chiamato coefficiente di
resistenza
• S è la sezione frontale del veicolo • ρ è la massa volumica dell’aria
• uN è la velocità longitudinale, precedentemente definita
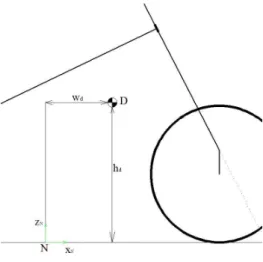
Figura 4.3: Punto di applicazione di Fd
La forza di resistenza aerodinamica è applicata nel punto D, detto centro di pressione, che nel sistema di riferimento (xN, yN, zN) ha le coordinate
(wd, 0, hd).
Nel medesimo punto, per comodità si applica anche la forza di disturbo laterale Fn, da non con fondere con la devianza precedentemente definita;
4.4 Componenti delle forze attive 52
infatti, la forza di disturbo laterale è un’azione che si introduce per saggiare la capacità del complesso pilota-motoveicolo di rispondere a disturbi laterali di tipo quasi impulsivo.
La velocità del punto D, espressa nel sistema di riferimento (xN, yN, zN),
si trova grazie alla formula fondamentale della cinematica piana: vd= vN + Ω ∧ ~N D Ã ud vd ! = Ã uN + ˙ψhdsin φ vN − ˙φhdcos φ + wdψ˙ ! (4.18)
4.4.2
Principio dei lavori virtuali
Per determinare le componenti lagrangiane delle forze attive non conser-vative, si utilizza il principio dei lavori virtuali. Tenendo presente quanto esposto in [22], la posizione del generico punto Pi appartenente al sistema
può essere espressa come: ~
OPi = ~OPi(q1, . . . , qn)
Dove q1, . . . , qn sono le n coordinate lagrangiane. Lo spostamento virtuale
del punto Pi vale:
∆Pi = n X j=1 ∂ ~OPi ∂qj ∆qj
Di conseguenza considerando la i-esima forza attiva non conservativa Fi, il
lavoro virtuale ad essa associato vale: ∆Wi = n X j=1 Ã Fi· ∂ ~OPi ∂qj ! ∆qj Considerando che n = 5: ∆W =X i ∆Wi = 5 X j=1 Qj∆qj (4.19)
Dove ∆qj rappresenta lo spostamento virtuale della coordinata j-esima e ∆W
è il lavoro virtuale totale. La relazione (4.19) può essere esplicitata, avendo precedentemente risolto i prodotti vari scalari:
∆W = F1cos δt∆y1− |F1sin δt| ∆x1+ Mz1(∆δt+ ∆ψ) +
+ Mδ∆δ − Fd∆xd+ Fn∆yd+ Mz2∆ψ + Ft∆x2+ F2∆y2
4.5 Modello semplificato 53
Gli spostamenti virtuali sono:
∆δt=Aδ∆δ + Bδ∆φ
∆y1 =∆y + a∆ψ + tc∆δt
∆x1 =∆x − δttc∆δt
∆xd=∆x + hdsin φ∆ψ
∆yd=∆y − hdcos φ∆φ + wd∆ψ
∆x2 =∆x
∆y2 =∆y − b∆ψ
(4.21)
Le espressioni (4.21) si ricavano da quelle delle velocità dei punti di appli-cazione delle forze, nelle direzioni volute. Per l’angolo di sterzo effettivo si fa riferimento alla (2.14), per il punto 1 si utilizzano le (2.45), per il punto 2 le (2.40), per il punto D le (4.18).
Con queste considerazioni se si ipotizza che gli angoli di sterzo rimangano piccoli5 , si ottiene: Qu = − |F1δt| − Fd+ Ft Qv = F1+ Fn+ F2 Qδ = F1tcAδ+ |F1δt| δttcAδ+ Mz1Aδ+ Mδ Qψ = F1a − Fdhdsin φ + Fnwd− F2b + Mz1+ Mz2 Qφ= + F1tcBδ+ |F1δt| δttcBδ+ Mz1Bδ− Fnhdcos φ (4.22)
4.5
Modello semplificato
In questa sezione verranno descritte le caratteristiche del modello più semplice di motoveicolo elaborato. Alcune ipotesi sono già state giustificate nei capitoli precedenti, mentre altre trovano sostegno in dati sperimentali, ricavati appositamente per il tipo di motoveicolo del quale si vuole riprodurre il comportamento, forniti dalla Ducati Motor.
5
Si estende questa ipotesi anche all’angolo di sterzo effettivo per quanto mostrato in (2.6.1).
4.5 Modello semplificato 54
4.5.1
Ipotesi
Lo schema di veicolo che si utilizza è quello a quattro corpi (ruota poste-riore, ruota anteposte-riore, mainframe e avantreno) proposto in (2.2); nel main-frame si include il pilota, collegato rigidamente. L’avantreno viene conside-rato rigido, trascurando la presenza della sospensione anteriore; questa sem-plificazione non comporta grandi errori, qualora si voglia riprodurre il compor-tamento del motociclo durante manovre ad ampio raggio di curvatura ed a velocità pressoché costante.
Si considerano le ruote lenticolari; secondo quanto descritto in (2.7), così facendo non si tengono in considerazione tre fenomeni e con le loro conseguenze:
• La variazione del punto di contatto a terra dovuta al moto di rollio • La variazione dell’altezza del baricentro a terra dovuta al moto di rollio • Il moto di beccheggio6
dovuto alla diversa sezione dei toroidi delle ruote, con rollio non nullo.
Si ipotizza di poter eguagliare l’angolo di sterzo effettivo δt a quello
impos-to δ. L’effetimpos-to di questa assunzione è illustraimpos-to in (2.6.1). In generale, si può asserire che questa semplificazione tende ad influire negativamente sulla veridicità dei valori della coppia di sterzo.
Si ipotizza di poter eguagliare l’angolo di rollio dell’anteriore γt a quello
del veicolo φ. L’effetto di questa assunzione è illustrato in (2.6.2). Con riferimento alla Fig. 2.3 si ipotizza che ef ≈ 0
7
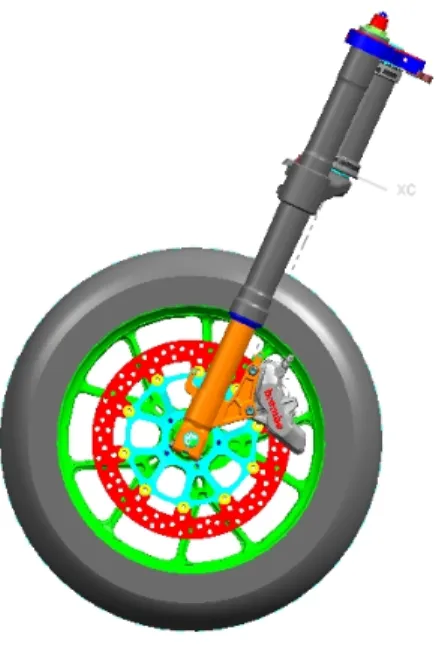
. E’ possibile sostenere questa ipotesi grazie al fatto che è diponibile un modello CAD 3D del mo-toveicolo, dal quale è immediato rilevare le proprietà di massa. In Fig. 4.4 è illustrato l’avantreno ed il relativo baricentro. Questa ipotesi semplifica notevolmente il calcolo delle velocità e non introduce praticamente alcun er-rore.
Si ipotizza di poter trascurare la presenza di organi rotanti solidali al
6
Si intende la rotazione attorno all’asse yG.
7
Si ricorda che ef è la distanza, misurata nel piano xN− zN con rollio nullo, fra l’asse
4.5 Modello semplificato 55
Figura 4.4: Avantreno CAD 3D del motociclo
mainframe (alberi del cambio, del motore, . . . ). In (2.8.3) è stata determina-ta la velocità di rodetermina-tazione di un albero motore di inerzia ridotdetermina-ta pari a quella delle parti rotanti del motore.
In (2.8.5) ed in (2.8.2) si sono ricavate le velocità di rotazione della ruo-ta anteriore e di quella posteriore in funzione delle coordinate lagrangiane. Vista la simmetria della ruota, nel sistema di riferimento (x2, y2, z2), si ha
che Ix2 = Iz2. Il vincolo fra il mainframe e la ruota posteriore lascia libera la
rotazione rispetto all’asse y2; visto che Ix2<< Ixm e Iz2 << Izm, si può
ipo-tizzare che Ix2= Iz2 ≈ 0. Inoltre, si ipotizza che la velocità di rotazione della
ruota posteriore attorno all’asse y2 sia Ω2y ≈ uN/r2. La stessa assunzione
viene fatta anche per la ruota anteriore, che, rispetto al sistema di riferimento (x1, y1, z1), ha momenti di inerzia Ix1, Iz1, Iy1, dei quali solo l’ultimo viene
considerato non nullo. Anche per l’anteriore si assume che Ω1y ≈ uN/r1.
Tenendo presente che nelle normali condizioni di utilizzo di un motociclo sportivo stradale, in manovre non troppo impegnative, l’angolo di sterzo ri-mane sotto i 10◦, si assume di poter utilizzare l’ipotesi dei piccoli angoli8
di sterzo.
Per il calcolo dell’angolo di deriva posteriore si utilizza quello ricavato nel
8
4.5 Modello semplificato 56
capitolo 2.9, espresso dalla relazione (2.41). Per l’angolo di deriva anteriore, si utilizza la versione espressa dalla relazione (2.44).
Vista la simmetria del veicolo rispetto al piano verticale longitudinale, si assume che i prodotti di inerzia Ixym e Izym siano nulli. Inoltre, si ipotizza
che i prodotti d’inerzia dell’anteriore Ixyf, Izyf e Izxm siano trascurabili. Per
l’anteriore si compie un ulteriore semplificazione, ponendo Ixf = Iyf = 0.
4.5.2
Energia cinetica
Grazie alle assunzioni appena descritte, le espressioni dell’energia cinetica esposte in (4.2) diventano: T = Tt+ Trm+ Trf + Te+ Tw1+ Tw2 (4.23) Dove: Tt = 1 2m h (uN + ˙ψh sin φ) 2 + (vN − ˙φh cos φ) 2 + ( ˙φh sin φ)2i , (4.24) Trm = 1 2 h Ixmφ˙ 2 + Iym( ˙ψ sin φ) 2 + Izm( ˙ψ cos φ) 2 + −2Izxmφ ˙˙ψ cos φ i , (4.25) Trf = 1
2Izf( ˙φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ)
2 , (4.26) Te = 0, (4.27) Tw1= 1 2 µ I1 r2 1 ¶ u2 N, (4.28) Tw2= 1 2 µ I2 r2 2 ¶ u2 N. (4.29)
4.5.3
Equazioni
Le equazioni di Lagrange descritte in (4.1) diventano: Coordinata uN: ˙uN = Qu m + vNψ − 2 ˙˙ φ ˙ψh cos φ − ψh sin φ 1 + 1 m ³ I1 r2 1 + I2 r2 2 ´ (4.30) Coordinata vN: ˙vN = Qv m + u ˙ψ · 1 + 1 m µ I1 r2 1 +I2 r2 2 ¶¸ −³ ˙φ2 + ˙ψ2´ h sin φ + ¨φh cos φ (4.31)
4.6 Modello complesso 57
Coordinata δ: ¨ δ = Qδ
Izf
+ ˙φ ˙ψ sin φ cos ǫ − ¨ψ cos φ cos ǫ − φ sin ǫ (4.32)
Coordinata φ: ¨
φ¡mh2
+ Ixm+ Izfsin 2
ǫ¢ = Qφ+ mgh sin φ − Izf˙δ ˙ψ sin φ cos ǫ+
− Izfδ sin ǫ − ¨¨ ψ cos φ (Izfsin ǫ cos ǫ − Izxm) +
+ mh cos φ³˙vN + uNψ˙ ´ + ¨ψ2 sin φ cos φ¡mh2 + Iym+ −Izm− Izfcos 2 ǫ¢ (4.33) Coordinata ψ: ¨ ψ£sin2 φ¡mh2 + Iym¢ + cos 2 φ (Izm+ Izfcos ǫ)¤ = Qψ+ + uNvN µ I1 r2 1 + I2 r2 2 ¶
+ Izf˙δ ˙φ sin φ cos ǫ − Izf¨δ cos φ cos ǫ+
+ (Izfsin ǫ cos ǫ − Izxm)³ ˙φ 2
sin φ − ¨φ cos φ´− ˙φ ˙ψ sin 2φ¡mh2
+ +Iym− Izm− Izfcos 2 ǫ¢ − mh sin φ³˙uN − vNψ˙ ´ (4.34)
4.5.4
Componenti lagrangiane delle forze attive non
con-servative
Tenendo conto delle ipotesi che reggono questo modello, le componenti lagrangiane delle forze attive non conservative risultano:
Qu = − |F1δ| − Fd+ Ft Qv = F1+ Fn+ F2 Qδ = Mz1cos ǫ + Mδ Qψ = F1a − Fdhdsin φ + Fnwd− F2b + Mz1+ Mz2 Qφ= − Fnhdcos φ (4.35)
4.6
Modello complesso
In questa sezione, in maniera analoga alla precedente, verranno descritte le caratteristiche del modello di motoveicolo più complesso elaborato.
4.6 Modello complesso 58
4.6.1
Ipotesi
In questa sezione verranno descritte solamente le ipotesi che differiscono da quelle elencate nella sezione (4.5.1).
Si introduce nel modello la differenza fra angolo di rollio del motociclo e quello dell’avantreno; l’espressione che esprime questo valore è stata ricavata in (2.6.2) e per comodità, si riporta di seguito:
γt = arcsin (sz) =
= arcsin (sin φ cos δ + cos φ sin δ sin ǫ)
Nella figura (4.5), sono rappresentati gli andamenti della differenza fra angolo di rollio anteriore γt e quello di rollio φ al variare rispettivamente dell’angolo
di sterzo imposto δ e dell’angolo di rollio φ, tenendo di volta in volta gli altri valori costanti. 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 −0.09 −0.08 −0.07 −0.06 −0.05 −0.04 −0.03 −0.02 −0.01 0 γt − φ (rad) δ (rad) φ=0° φ=10° φ=20° φ=30° φ=40° φ=50° 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 −0.09 −0.08 −0.07 −0.06 −0.05 −0.04 −0.03 −0.02 −0.01 0 γt − φ (rad) φ (rad) δ=0° δ=5° δ=10° Figura 4.5: (γt− φ)
Si introduce nel presente modello la relazione che esprime la differenza fra l’angolo di sterzo imposto δ e quello misurato sul piano stradale δt, analizzata
in (2.6.1). Questa espressione si riporta di seguito: δt = arctan µ −sx sy ¶ = = atan µ sin δ cos ǫ
cos φ cos δ − sin φ sin δ sin ǫ ¶
Nella Fig. 4.6, sono rappresentati gli andamenti della differenza fra angolo di sterzo effettivo δt e quello di sterzo δ al variare rispettivamente dell’angolo
4.6 Modello complesso 59 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 −0.02 0 0.02 0.04 0.06 0.08 0.1 δt − δ (rad) δ (rad) φ=0° φ=10° φ=20° φ=30° φ=40° φ=50° 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 −0.02 −0.01 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 ( δt − δ ) (rad) φ (rad) δ=5° δ=10° δ=0° Figura 4.6: (δt− δ)
valori costanti. In Fig. 2.14 si può osservare come il valore di φ influenzi l’andamento di δt al variare di δ; a parità di angolo di sterzo imposto,
all’au-mentare dell’angolo di rollio, la differenza (δt− δ) cambia di segno.
Per quanto concerne gli angoli di deriva, quello posteriore mantiene la forma espressa dalla (2.41); per l’anteriore, invece si utilizza la versione in cui si tiene conto dell’avancorsa, espressa dalla (2.46).
Si utilizzano le velocità di rotazione delle ruote ricavate in (2.8.5) ed in (2.8.2). Esse valgono: p1 q1 r1 = ˙
φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ − ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ + uN/r1
˙
φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ
p2 q2 r2 = ˙ φ ˙ ψ sin φ + uN/r2 ˙ ψ cos φ
In (2.8.3) è stata determinata la velocità di rotazione di un albero, consi-derato vincolato al mainframe mediante un coppia, che lascia libera sola-mente la rotazione attorno all’asse yE, del sistema di riferimento definito in
(2.5). Con quest’albero si vuole schematizzare la presenza degli organi rotan-ti del motore. Grazie alla disponibilità di misurazioni sperimentali effettuate dalla Ducati Motor, è stato possibile ricavare un momento di inerzia ridotto all’asse yE, di:
4.6 Modello complesso 60
• Distribuzione • Frizione • Cambio
4.6.2
Energia cinetica
Grazie alle assunzioni appena descritte, le espressioni dell’energia cinetica esposte in (4.2) diventano: T = Tt+ Trm+ Trf + Te+ Tw1+ Tw2 Dove: Tt= 1 2m h (uN + ˙ψh sin φ) 2 + (vN − ˙φh cos φ) 2 + ( ˙φh sin φ)2i (4.36) Trm = 1 2 h Ixmφ˙ 2 + Iym( ˙ψ sin φ) 2 + Izm( ˙ψ cos φ) 2 + −2Izxmφ ˙˙ψ cos φ i (4.37) Trf = 1
2Izf( ˙φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ)
2 (4.38) Te = 1 2IE³ ˙ψ sin φ + τ uN ´2 (4.39) Tw1 = 1 2I1 µ
−δ ˙φ cos ǫ + δ ˙ψ cos φ sin ǫ + ˙ψ sin φ +uN r1 ¶2 (4.40) Tw2= 1 2I2 µ ˙ ψ sin φ + uN r1 ¶2 (4.41)
4.6.3
Equazioni
Le equazioni di Lagrange descritte in (4.1) diventano: Coordinata uN: ˙uN = Qu + mvNψ − A˙ u− Bu− Cu m + I1 r2 1 + I2 r2 2 + IEτ 2 (4.42) dove: Au = ¨ψ sin φ µ mh + I1 r1 +I2 r2 + IEτ ¶
4.6 Modello complesso 61 Bu = ˙φ ˙ψ cos φ µ 2mh + I1 r1 +I2 r2 + IEτ ¶ Cu = I1 r1 ³
− ˙δ ˙φ cos ǫ − δ ¨φ cos ǫ + ˙δ ˙ψ cos φ sin ǫ+ +δ ¨ψ cos φ sin ǫ − δ ˙φ ˙ψ sin φ sin ǫ´
Coordinata vN: ˙vN = Qv m − I1 mr1 ³ δ ˙ψ2
cos φ sin ǫ − δ ˙ψ ˙φ cos ǫ´− ˙φ2
h sin φ+ + ¨φh cos φ − uNψ˙ m µ m + I1 r2 1 + I2 r2 2 + IEτ 2 ¶ + − ψ˙ 2 sin φ m µ mh + I1 r1 +I2 r2 + IEτ ¶ (4.43) Coordinata δ: ¨ δ = Qδ Izf + I1 Izf ³ δ ˙ψ2 cos2
ǫ − 2δ ˙ψ ˙φ cos φ sin ǫ cos ǫ+ − ˙φ ˙ψ sin φ cos ǫ − uN r1 ˙ φ cos ǫ + δ ˙ψ2 cos2 φ sin2 ǫ+ + ˙ψ2
sin φ cos φ sin ǫ + uN r1
˙
ψ cos φ sin ǫ ¶
+ + ˙φ ˙ψ sin φ cos ǫ − ¨ψ cos φ cos ǫ − ¨φ sin ǫ
(4.44) Coordinata φ: ¨ φ¡mh2 + Ixm+ Izfsin 2 ǫ + I1δ 2 cos2 ǫ¢ = Qφ+ mgh sin φ+ + I1φ ˙˙ψδ cos ǫAφ+ I1δ ˙ψ 2
sin ǫ cos 2φ + ˙ψuNBφ+
− Izf˙δ ˙ψ sin φ cos ǫ + ˙ψ 2
sin φ cos φCφ− Izfδ sin ǫ+¨
− B1φ− ¨ψDφ+ mh cos φ ³ ˙vN + uNψ˙ ´ (4.45) dove: B1φ= I1 h − ¨ψ cos ǫ¡δ sin φ + δ2
cos φ sin ǫ¢ + 2δ ˙δ cos ǫ³ ˙φ cos ǫ − ˙ψ cos φ sin ǫ´ + + ˙φ ˙ψδ cos ǫ (δ sin φ sin ǫ − cos φ) − ˙ψ ˙δ sin φ cos ǫ − ˙δuN
r1
cos ǫ − δ˙uN r1
cos ǫ ¸
Aφ= δ sin φ sin ǫ − cos φ
Bφ=
I1
r1
(cos φ − δ sin φ cos ǫ) + cos φµ I2 r2
+ IEτ
4.6 Modello complesso 62 Cφ= mh 2 + Iym− Izm− Izfcos 2 ǫ + I1¡1 − δ 2 sin2 ǫ¢ + I2+ IE
Dφ = cos φ (Izfsin ǫ cos ǫ − Izxm)
Coordinata ψ: ¨ ψAψ = − ˙ψ ˙φ sin 2φ¡mh 2 + Iym− Izm− Izfcos 2 ǫ + I2+ IE¢ + − mh sin φ³˙uN − vNψ˙ ´
− (Izfsin ǫ cos ǫ − Izxm)³ ¨φ cos φ+
− ˙φ2 sin φ´− uNφ cos φ˙ µ I2 r2 + IEτ ¶ − ˙uNsin φ µ I2 r2 + IEτ ¶ + + uNvN µ I1 r2 1 +I2 r2 2 + IEτ 2 ¶ − B1ψ− Izfδ cos φ cos ǫ+¨ + vNψ sin φ˙ µ I1 r1 + I2 r2 + IEτ ¶ + Izf˙δ ˙φ sin φ cos ǫ+ + vNδ I1 r1 ³
− ˙φ cos ǫ + ˙ψ cos φ sin ǫ´+ Qψ
(4.46) dove: Aψ = mh 2 sin2 φ + Iymsin 2 φ + Izmcos 2 φ + Izfcos 2 φ cos2 ǫ+ + I1£δ sin ǫ ¡sin 2φ + δ cos
2 φ sin ǫ¢ + sin2 ǫ¤ + + (I2+ IE) sin 2 φ B1ψ = I1 · uN r1
³ ˙φ cos φ + ˙δ cos φ sin ǫ − δ ˙φ sin φ sin ǫ´ + +˙uN
r1
(sin φ + δ cos φ sin ǫ) + 2δ ˙δ cos φ sin ǫ³ ˙ψ cos φ sin ǫ − ˙φ cos ǫ´+ + ˙φ ˙ψ sin 2φ¡1 − δ2
sin2
ǫ¢ − ¨φ¡δ sin φ cos ǫ + δ2
cos φ sin ǫ cos ǫ¢ + +δ ˙φ2
4.7 Modello intermedio 63
4.6.4
Componenti lagrangiane delle forze attive non
con-servative
Tenendo conto delle ipotesi che reggono questo modello, le componenti lagrangiane delle forze attive non conservative risultano:
Qu = − |F1δt| − Fd+ Ft Qv = F1+ Fn+ F2 Qδ = F1tcAδ+ |F1δt| δttcAδ+ Mz1Aδ+ Mδ Qψ = F1a − Fdhdsin φ + Fnwd− F2b + Mz1+ Mz2 Qφ= F1tcBδ+ |F1δt| δttcBδ+ Mz1Bδ− Fnhdcos φ (4.47)
4.7
Modello intermedio
In questa sezione verranno descritte le caratteristiche di un modello di motoveicolo simile al precedente, ma semplificato in alcune sue parti (angoli di deriva e componenti lagrangiane delle forze attive non conservative). Verranno utilizzati angoli di deriva forniti dalla seguente espressioni:
α2 = vn− b ˙ψ uN α1 = − δ′+ vn+ a ˙ψ + ˙δtc uN
Questa versione delle espressioni degli angoli di deriva, non tiene conto della differenza fra le derivate temporali dell’angolo di sterzo imposto e di quello effettivo; tuttavia risulta molto semplificata rispetto alle versioni complete. Per quanto concerne le equazioni di Lagrange, esse sono identiche a quelle ricavate in (4.6.3).
Le componenti lagrangiane delle forze attive non conservative sono: Qu = − |F1δt| − Fd+ Ft
Qv = F1+ Fn+ F2
Qδ = F1t cos φ + Mz1cos φ cos ǫ + Mδ
Qψ = F1a − Fdhdsin φ + Fnwd− F2b + Mz1+ Mz2
Qφ= − Fnhdcos φ
4.8 Calcolo della traiettoria 64
4.8
Calcolo della traiettoria
Con l’integrazione delle equazioni di lagrange mostrate in (4.1), non si hanno informazioni immediate circa la posizione9
del veicolo. Facendo riferimento ai sistemi di riferimento introdotti in (2.5):
" u0 v0 # = " ˙xN 0 ˙yN 0 # = " cos ψ − sin ψ sin ψ cos ψ # " uN vN # (4.49) Si sono trovate le velocità del punto N nel sistema di riferimento di assi suolo (x0, y0, z0). Mediante integrazione si ricava la posizione del mendesimo
punto: xN 0 (t) = x + Z t 0 ˙x0dt = x + Z t 0 (uNcos ψ − vNsin ψ) dt y0N(t) = y + Z t 0 ˙y0dt = y + Z t 0 (vNcos ψ + uNsin ψ) dt
L’angolo di imbardata ψ si ricava per integrazione: ψ(t) = ψ +
Z t
0
˙ ψ dt
I valori x, y e ψ sono quelli assunti dalle rispettive coordinate all’istante iniziale.
9