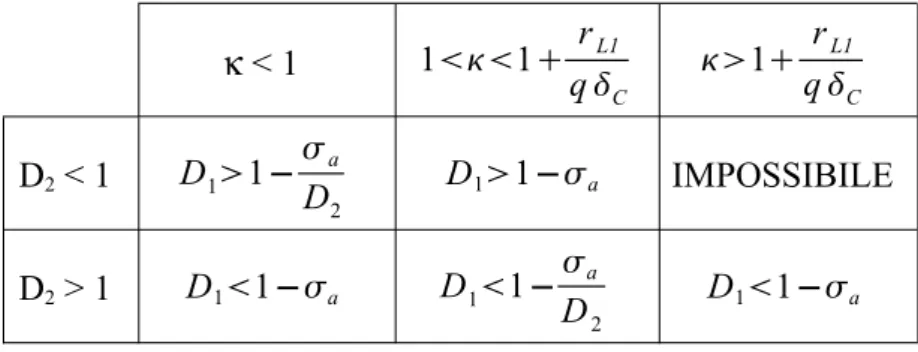Modelli di coesistenza ecologica tra diversi agenti patogeni

Capitolo 5

Modelli di coesistenza ecologica

tra diversi agenti patogeni

Una caratteristica rilevante dell'epidemiologia della meningite è rappresentata dalla coesistenza di batteri della stessa specie, ma estremamente diversi per caratteristiche antigeniche ed epidemiologiche, che competono per la colonizzazione del nasofaringe di individui umani. Se si esclude la possibilità di essere infettati contemporaneamente da più di un tipo di meningococco, la disponibilità di suscettibili è l'elemento che limita la diffusione della specie nella popolazione umana.

Come mostrato nel capitolo 4, la letteratura modellistica sul meningococco non affronta in modo diretto il problema di cosa giustifichi la coesistenza ecologica tra il meningococco e la lactamica, e tra serogruppi diversi di meningococchi.

Lo scopo di questo capitolo è studiare alcuni modelli per capire a quali aspetti della struttura dell'infezione è imputabile la coesistenza competitiva, e di conseguenza quali strutture del modello sono ammissibili per riprodurre verosimilmente i fenomeni di trasmissione e sviluppo della malattia.

I modelli su cui ci basiamo sono principalmente di tipo SIS, seguendo il suggerimento di Coen et al. e le indicazioni degli epidemiologi a proposito della scarsa immunità al carriage meningococcico. Per questo motivo riportiamo nella sezione 5.1 lo schema del modello SIS di base e ne riportiamo qualche proprietà aggiuntiva rispetto a quelle già mostrate nel capitolo 1.

Nella sezione 5.4 accenniamo in modo qualitativo ad alcuni modelli la cui struttura prevede un'immunità parziale al carriage.

5.1 Modello SIS semplice

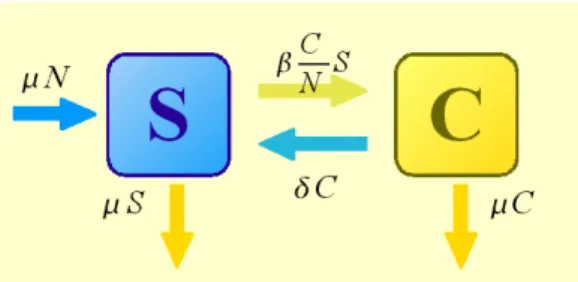
Il modello (figura 5.1) assume che i portatori di qualsiasi tipo di meningococco siano riuniti in un unico comparto omogeneo C, e che il carriage non induca nessun tipo di immunità a nuove infezioni. Le equazioni che descrivono questo modello sono:

˙S=N −S− SC ˙C= S−C ,

in cui C indica i carrier di qualsiasi tipo di meningococco. La quantità =C

N S rappresenta la

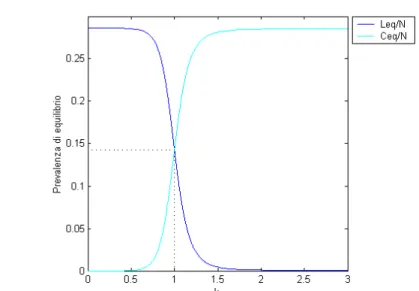
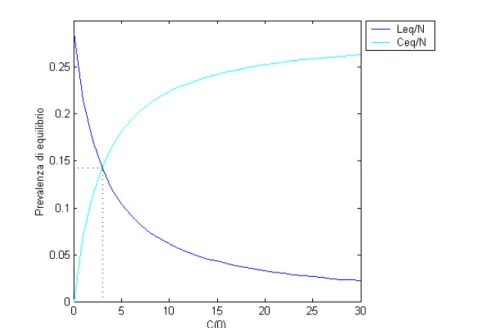
Questo modello è stato già approfonditamente studiato nel paragrafo 1.1.2, a cui si rimanda. In aggiunta a quanto già mostrato, si riportano qui solamente i grafici rappresentanti la frazione di infetti all'equilibrio rispetto al valore rispettivamente di δ e di R0 (che dipende linearmente da β). In

entrambi i grafici, mostrati in figura 5.2 e 5.3, si sono scelti i valori di β=3 e µ=0,1. Figura 5.1: Schema compartimentale SIS semplice

Figura 5.2: Andamento della prevalenza di equilibrio rispetto a γ in un modello SIS semplice (β=3 e µ=0,1)

5.2 Modello di competizione SIS semplice

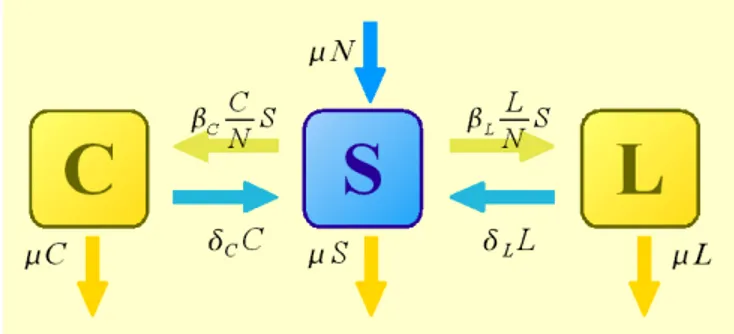
Il primo modello di competizione che introduciamo (figura 5.4) coincide sostanzialmente con quello assunto da Coen et al. (ma senza l'ipotesi di inibizione dovuto al carriage di Neisseria lactamica) e da Trotter et al., con la differenza che non è prevista una suddivisione in classi di età: tutti gli individui appartengono ad un unico gruppo omogeneo; C ed L indicano il numero di infetti relativi a due tipi epidemiologicamente diversi di meningococchi (in particolare si può pensare che C rappresenti il carrier di meningococco e L quello di lactamica).

Le equazioni che lo descrivono sono le seguenti: ˙S=N −S − 1 N  CCLL S LLCC ˙C=C N C S−C C ˙L=L N L S−L L

in cui C ed L rappresentano i carrier dei due tipi e sono già state esplicitate le forze di infezione relative ai due tipi. La domanda che ci poniamo è se questo modello ammette la coesistenza, cioé, in termini più precisi, se esistono degli stati di equilibrio stabile che prevedano valori di C ed L contemporaneamente non nulli; in tal caso, si vogliono determinare le condizioni che i parametri del modello devono rispettare per aversi tale situazione.

Studiamo i punti di equilibrio di questo sistema ponendo tutte le derivate uguali a zero:

(5.1) N −S −1 N CCLL S LLCC=0 C N C S−CC =0 L N L S−L L=0

e definiamo come di consueto R_0C= C C

e R_0L= L L

; dalla seconda e dalla terza equazione della (5.1), posto R_0C, R_0L1 (in quanto diversamente il tipo corrispondente scomparirebbe spontaneamente) si ottengono i seguenti equilibri:

(5.2a) C_eq=0, S_eq=N L L =N 1−_R1 0L  , L_eq=_RN 0L

(5.2b) L_eq=0, S_eq=NC C =N 1− 1 R_0C , Ceq= N R_0C

che si riconducono al caso banale in cui la competizione conduce all'esclusione di uno dei due ceppi e di conseguenza ad una dinamica SIS semplice come quella del modello 5.1.

Dalla seconda e terza equazione della (5.1), posto L_eq, C_eq≠0 , deve essere: (5.2c) S_eq=NL

L

=NC C

,

e dunque questo terzo equilibrio si può avere solo nel caso particolare in cui sia soddisfatta la seguente condizione:

R_0L= R0C .

Per R0L> R0C, il sistema tende verso l'equilibrio (5.2a), per R0L < R0C il sistema tende verso

l'equilibrio (5.2b).

I valori di equilibrio di C e di L non sono univocamente determinati nell'equilibrio (5.2c), in quanto sotto questa condizione la seconda e la terza equazione sono una multiplo dell'altra, e dunque linearmente dipendenti; le prevalenze di equilibrio, in particolare, dipendono dalle condizioni iniziali del sistema.

Il problema che stiamo affrontando si può ricondurre a un problema di competizione rispetto ad una risorsa esplicita, come proposto nella trattazione generale di Capelo [1], in cui la popolazione delle due specie è rappresentata dalle variabili x1 e x2:

˙x1=a1−a11x1−a12x2 x1

˙x2=a2−a21x1−a22x2 x2

Infatti, sostituendo l'espressione S = N – L – C nella seconda e terza equazione del sistema, risulta: ˙C=[C−C]−[ C N ]C −[ C N ] LC ˙L=[L−L]−[ L N ]L−[ L N ]C L ,

che coincide con quella generale di Capelo, dove:

a1=C−C a₂=L−L a11=a12= C N a₂₁=a22= L N .

Capelo mostra che questo problema generale può essere ricondotto a 13 possibili casi, dipendenti dai valori maggiore, minore o uguali a zero, di tre quantità H1 (che chiameremo HC), H2 (HL) e D,

così definite:

H₁=a1a22−a2a12

H₂=a2a11−a1a21

D=a11a22−a12a22

.

H_C=LC N  R0C R0C−1−R0L R0L−1 HL= LC N R0L R0L−1−R0C R0C−1=−HC D=0 .

Per HC > 0, necessariamente HL < 0 e in tal caso, secondo la trattazione di Capelo il sistema, che

ha invariabilmente D = 0, ha un solo equilibrio stabile, dato da C= a1

a11= N 1 –

1

R0C

e C = 0, che coincide con (5.2a); viceversa, per HC < 0, HL > 0 e l'equilibrio stabile coincide con (5.2b);

l'unico caso in cui si può avere una coesistenza stabile è per HC = HL = 0, cioè

R_0L R0L−1= R0C R0C−1 ,

che nei casi di interesse, cioè per RL, RC > 1, ha come unica soluzione positiva R0L = R0C

(esattamente la stessa condizione determinata in precedenza).

In questo caso particolare, l'analisi di Capelo permette di capire la dipendenza analitica del valore di equilibrio di C e di L dalle condizioni iniziali. Dal rapporto tra la seconda e la terza equazione differenziale del sistema, si ottiene l'equazione descrittiva delle traiettorie nello spazio C, L:

dC dL= C−C L−L C L= C L 1− 1 R_0C 1− 1 R0L  C L e quindi, essendo R0C = R0L, dC dL= C L C L .

La soluzione di questa equazione differenziale può essere ricavata banalmente per separazione di variabili, e risulta: C=C 0

[

]

Il punto di equilibrio sarà infine dato dall'intersezione di questa curva con la retta

C= N 1 – 1

R_0C ,

che si ottiene dalla condizione di equilibrio sulla terza equazione, sostituendo la condizione

S= N – C – L .

L'andamento di Ceq al variare di k o delle condizioni iniziali non è determinabile analiticamente

visto che l'intersezione tra le due curve fornisce un'equazione non lineare, ma si può determinare numericamente, ad esempio attraverso il metodo di Newton. I risultati di questi calcoli realizzati in Matlab forniscono le figure 5.5, 5.6 e 5.7.

Dalla figura 5.5 si nota che per k = 1 le due prevalenze di equilibrio sono esattamente identiche e pari a metà del valore di equilibrio che avrebbero avuto senza un competitore; inoltre, si vede che se uno dei due β è molto più grande dell'altro, l'equilibrio è molto simile a una competizione esclusiva (casi (a) e (b)) anche quando l'R0 dei due tipi è identico.

quando il rapporto tra gli infetti iniziali dei due comparti è a favore del ceppo con il β minore e vale poche unità.

L'andamento temporale delle prevalenze e della frazione di suscettibili a partire da uno stato in cui la popolazione è totalmente suscettibile, simulato con l'algoritmo ode45 di Matlab, mostra l'andamento tipico di un'epidemia SIS (figura 5.8).

Figura 5.6: Prevalenze di equilibrio per il modello di competizione SIS semplice al variare di L(0) e con N=106_{; C(0)=1; R0=1.4; k=1.1}

Figura 5.5: Prevalenze di equilibrio per il modello di competizione SIS semplice al variare di k e con N=106_{; C(0)=1; L(0)=1; R}

0=1.4; βL=1 (unità

Questo modello prevede la coesistenza tra i ceppi in competizione per la risorsa (il nasofaringe dei suscettibili nel caso del meningococco) solamente in un caso molto particolare di equilibrio esatto tra i due valori di R0 e con condizioni di trasmissibilità non eccessivamente diverse; nel mondo

reale, comunque, si dovrebbe tenere conto di una certa variabilità nel valore dei parametri che determinano gli R0, tra cui ad esempio la mortalità/natalità µ o il tasso medio di guarigione δ in uno

dei due ceppi. Per tenerne conto è stato simulato l'effetto di variazioni stocastiche di questi parametri, sommando al valore medio che garantisce l'equilibrio un segnale casuale con distribuzione gaussiana, integrato su una finestra mobile di ampiezza W e scalata in modo da ottenere variazioni del parametro entro un certo range. La finestra mobile ha lo scopo di eliminare le alte frequenze del segnale casuale, facendo sì che le variazioni dei parametri non possano essere

Figura 5.7: Prevalenze di equilibrio per il modello di competizione SIS semplice al variare di C(0) e conN=106_{; L(0)=1; R}

0=1.4; k=1.1

Figura 5.8: Andamento temporale del modello di competizione SIS semplice con N=106_{; C(0)=1; L(0)=1; R}

0=1.4; δC=1; δL=0.9; µ=0.01; di

istantaneamente compensate da un campione successivo uguale ed opposto ed introducendo una memoria pari all'ampiezza della finestra. La simulazione è stata effettuata mediante il metodo di Eulero con passo di integrazione pari a 0.5.

Inizialmente si è considerato l'effetto di una variazione della mortalità fino al 10% intorno al valore µ = 0,1 e con un'ampiezza di finestra W=2000. L'andamento temporale delle prevalenze (figura 5.9) mostra delle oscillazioni anche pronunciate, ma piuttosto piccole, considerando l'alto valore scelto per il valor medio di µ, per l'ampiezza delle variazioni e per la dimensione della finestra. Ciò è imputabile al fatto che la mortalità riduce o aumenta contemporaneamente gli R0 di

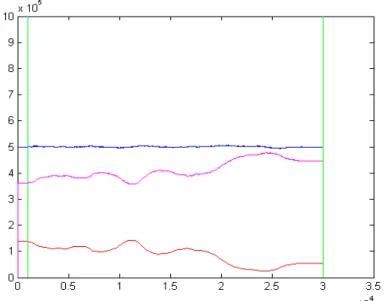
Figura 5.10: Evoluzione temporale del modello di competizione SIS semplice con variabilità stocastica di δC e N=106; µ=0.01; δL=0.9; R0=2;

C(0)=1; L(0)=1; C =1;

C MAX  C

= 0.5%; W=300. Figura 5.9: Evoluzione temporale del modello di competizione SIS semplice

con variabilità stocastica di µ e N=106_{; δ}

L=0.9; δC=1; R0=2;

C(0)=1; L(0)=1; _ = 0.1; MAX

entrambi i ceppi, seppur in misura diversa, e inoltre che la dipendenza dell'R0 da esso è blanda.

Quando però si considerano variazioni anche inferiori allo 0.5% rispetto al valore di uno dei due tassi medi di guarigione, ad esempio di δC, e con finestre di integrazione più strette (W=300

campioni), si possono osservare delle oscillazioni più marcate e anche delle inversioni di dominanza del ceppo, come mostrato in figura 5.10.

E' da notare come in entrambi i casi (e particolarmente nel secondo), le corrispondenti variazioni nella frazione di suscettibili siano del tutto trascurabili.

In conclusione, questo modello rientra nei modelli generali di competizione descritte da Capelo, ma con le ipotesi date sulla struttura porta inevitabilmente all'esclusione di uno dei due ceppi, eccetto che in condizioni estremamente particolari, che sembrano non potersi applicare al caso di Neisseria meningitidis o lactamica; tale equilibrio poco stabile potrebbe forse sussistere nella coesistenza di alcuni ceppi, e in tal caso il modello porterebbe a prevedere variazioni temporali delle prevalenze molto accentuate in conseguenza di piccole variazioni stocastiche sui parametri. L'esclusione dovuta a competizione potrebbe invece essere alla base della quasi totale dominanza del ceppo A nei casi endemici della fascia della meningite.

Esistono altri modelli di competizione all'interno dello schema individuato da Capelo, che porterebbero a una coesistenza dei ceppi meno sensibile alle variazioni dei parametri; è possibile che altri modelli con struttura simile possano essere ricondotti alla trattazione generale di Capelo e giustificare una coesistenza: per far ciò è necessario spezzare la simmetria tra i due gruppi che fa sì che il D risulti identicamente nullo; l'ipotesi di Coen sull'inibizione da Neisseria lactamica potrebbe esserne un esempio.

5.3 Altri modelli SIS di coesistenza competitiva

La letteratura disponibile sul tema della coesistenza competitiva nei modelli SIS si sofferma su diverse varianti di questo modello base, introducendo nelle dinamiche della malattia elementi quali:

• la mediazione di vettori non umani (Garnick, 1992);

• la possibilità di sovrainfezione (Levin e Pimentel, 1981; Hochberg e Holt, 1990);

• l'eterogeneità genetica nella popolazione ospite (Beck, 1984; Andreasen e Christiansen,

1993);

• la dipendenza della mortalità o della natalità dalla popolazione totale (Bremermann e Thieme,

1989; Andreasen e Pugliese, 1995);

• l'eterogeneità epidemiologica della popolazione ospite (Li, Ma, Blythe e Castillo-Chavez,

2003);

Nel caso della meningite meningococcica, è noto che non esistono altri modi di acquisire il batterio che per trasmissione diretta da un individuo umano ad un altro; la sovrainfezione è un evento molto raro nel caso dei meningococchi, come già rilevato da Stollenwerk et al., e l'eterogeneità di origine genetica, che Ancel Meyers et al. applicano nel primo dei due modelli between host, non è molto plausibile nel caso del carriage, mentre qualche ipotesi è stata avanzata relativamente a una predisposizione congenita all'acquisizione della malattia. Trascureremo perciò i modelli relativi a queste ipotesi, soffermandoci solo su quelli derivanti dalle ultime due assunzioni.

Rinunciando alla struttura SIS, si può giustificare la coesistenza attraverso le seguenti ipotesi, dimostrate nei modelli indicati tra parentesi:

• l'eterogeneità immunologica indotta nella popolazione ospite dall'eterogeneità stessa dei

patogeni (Wodarz, 2003);

• la possibilità che l'infezione con uno strain induca una cross-immunità anche parziale a strain

diversi (Castillo-Chavez et al., 1989; Andreasen, Lin e Levin, 1997; Gomes, Medley e Nokes, 2002);

• la strutturazione dei patogeni dovuta alla selezione naturale realizzata dalla risposta

immunitaria (Gupta et al., 1996; Gupta, Ferguson e Anderson, 1998). Di questi modelli daremo un breve accenno nella sezione 5.4.

5.3.1 Il modello di Andreasen e Pugliese

Andreasen e Pugliese [2] si sono soffermati su un modello di coesistenza competitiva tra due patogeni che si diffondono in una popolazione per cui la mortalità µ dipende dalla dimensione della popolazione stessa, N, secondo una funzione µ(N) strettamente crescente. Inoltre, i due patogeni influiscono sulla mortalità degli infetti aumentandola di un coefficiente ν dipendente dal tipo di patogeno.

Le equazioni del modello sono:

(5.3)

˙S=b N −N S−1S I−2S Y

˙I =1S I− N 1 I

˙Y =2S Y− N 2Y

,

essendo I ed Y il numero di infetti per i due patogeni, con N = S + I + Y. b indica il tasso di natalità, è assunto costante e pari a µ(K), dove K è la capacità di persistenza o carrying capacity,

cioè il massimo valore di equilibrio della dimensione della popolazione.

Per trovare le condizioni di coesistenza, è sufficiente imporre che all'equilibrio i valori di I ed Y siano positivi. Risulta, ponendo le derivate uguali a zero nella (5.3):

(5.4)

b N− N S −1S I−2S Y =0

1S I− N 1 I=0

2S Y − N 2 Y=0

con N , S , I e Y i valori all'equilibrio delle rispettive variabili.

Dalla seconda e terza equazione, essendo I e Y diversi da zero per ipotesi, deve essere contemporaneamente: (5.5) S= N1 1 S= N2 2 e dunque, elaborando:  N=12−21 2−1 ,

da cui sostituendo nella (5.5) si ottiene: (5.6) S=2−1

2−1

0 ;

dalla (5.6) deriva la prima condizione necessaria, e cioè che ν2 – ν1 deve avere lo stesso segno di

β2 – β1.

Considerando che

IY = N – S e che, dalla prima delle (5.4)

1I2Y=b



N

S −N , risolvendo il sistema rispetto ad I e Y , si ottiene:

(5.7) _I=b  N S −N−2 N – S 1−2 , (5.8) _Y=− b  N S −N−1 N – S 1−2 .

Posto 21 , dalla (5.7) si deve avere:

2S− N − N 2– b S 0 e dalla (5.8):  N 1− b S 1S − N 0 .

Tenendo conto che 2S− N =2 e 1S − N =1 , si ottiene:

(5.9) N 2–

b

(5.10) N 1–

b

S 1 .

Le condizioni (5.6), (5.9), (5.10) rappresentano le condizioni necessarie e sufficienti per l'equilibrio di coesistenza nel modello di Andreasen e Pugliese.

Inoltre, essendo 1=

 N1

S (per la prima delle (5.5) ), sostituendo nella (5.10), si ottiene:  N1– b N1– b

N

S 1 ,

da cui, infine:

 Nb

e dunque N < K, essendo µ(N) una funzione crescente di N e b = µ(K).

Si noti che i secondi membri delle (5.5) coincidono esattamente con l'inverso degli R0 dei due

patogeni, e che questi all'equilibrio devono essere necessariamente uguali per aversi coesistenza, esattamente come nel modello del paragrafo 5.2. Sebbene il modello di Andreasen e Pugliese ammetta una coesistenza su regioni relativamente ampie dello spazio dei parametri grazie all'introduzione della mortalità dipendente dalla densità, esso richiede ancora l'eguaglianza tra gli R0

dei due patogeni: i parametri che garantiscono la coesistenza sono quelli che regolano la popolazione di equilibrio su quei valori tali che i numeri di rimpiazzamento possono risultare uguali.

5.3.2 Modello SIS di coesistenza competitiva con gruppi di età

Il modello che si propone in questa sezione (figura 5.11) ricalca la struttura del modello proposto da Li, Ma, Blythe e Castillo Chavez [3], per la competizione di patogeni di malattie sessualmente trasmissibili; esso è sostanzialmente il modello di competizione SIS del paragrafo 5.2, in cui però la popolazione è suddivisa in due gruppi omogenei, che si distinguono per il comportamento sessuale; il mixing è considerato proporzionale con ai l'attività sociale del gruppo i.

Nel caso della meningite, la differenza epidemiologica rilevante non consiste tanto nel Figura 5.11: Schema compartimentale di un modello di coesistenza competitiva con gruppi di età

comportamento sociale, quanto nella differenza immunologica tra i bambini e gli adulti, e soprattutto nei diversi tipi di batteri che attaccano preferenzialmente queste due classi di età. Come già ampiamente evidenziato, in particolare dall'articolo di Coen et al., Neisseria lactamica è largamente diffuso nelle fasce di età inferiori ai 10 anni, mentre nelle età più avanzate diventano predominanti i meningococci patogeni. Rispetto al modello di Li et al., dunque, la struttura del modello si complica leggermente, dovendosi introdurre un trasferimento di individui dal gruppo 1 (quello dei bambini) al gruppo 2 (quello degli adulti); questa piccola variazione rende tuttavia molto più onerosi i passaggi algebrici che portano a determinare le condizioni di coesistenza tra i due tipi di batteri, in questo caso Neisseria lactamica (i cui carrier sono individuati dalla lettera L) e gli altri meningococci (carrier individuati dalla lettera C). E' da notare che analoghe differenze epidemiologiche rispetto all'età possono essere riscontrate anche tra due meningococci patogeni di serogruppo differente, come si evidenzia ad esempio dalla diversa distribuzione di età dei serogruppi B e C nei casi di notifica italiani, di cui si è già reso conto nel capitolo 3.

Un altra differenza importante, ma strutturalmente meno significativa, del modello qui proposto rispetto a quello di Li, Ma, Blythe e Castillo-Chavez, è che i βL e i βC sono diversi nei due gruppi di

età.

Tutta la trattazione di seguito riportata prende ampiamente spunto dalla tecnica utilizzata da Li et al. nella soluzione del sistema di equazioni all'equilibrio e nella determinazione delle condizioni di esistenza.

Si parte innanzitutto dalle equazioni del modello:

(5.11) ˙S1=−a1 L1a1L1L2a2L2 a₁N₁a2N2 C1a1C1C2a2C2 a₁N₁a2N2 S1L1L1C1C1b−1q S1; ˙ C₁=a1 C1a1C1C2a2C2 a₁N₁a2N2 S₁−C11qC1; ˙L1=a1 L1a1L1L2a2L2 a1N1a2N2 S1−L11q L1; ˙S₂=−a2 L1a1L1L2a2L2 a1N1a2N2 C1a1C1C2a2C2 a1N1a2N2  S2L2L2C2C2q S1−2S2; ˙ C₂=a2 C1a1C1C2a2C2 a₁N₁a2N2 S₂−C22C2q C1; ˙L2=a2 L1a1L1L2a2L2 a1N1a2N2 S₂−L22L2q L1; dove N₁=S1 L1C1; N2=S2 L2C2 .

Sommando tra loro le equazioni relative ai singoli gruppi risulta rispettivamente: ˙ N1=b−1q N1 ˙ N₂=q N1−2N2 , e pertanto all'equilibrio:

T₁=N_1eq= b 1q T2=  N2eq=b q 21q T=T₁T2= b2q 21q .

La nonlinearità del sistema può essere ridotta, studiando le equazioni semplificate che valgono una volta che la dinamica vitale si è assestata su un equilibrio, e cioè quando il termine al denominatore delle varie forze di infezione è diventato costante.

Se si pone: i= a_i a1T1a2T2 r_Ui=aiUi Ui=Uiiq , con U = C, L ed i = 1, 2,

e si esprimono i suscettibili dei due comparti come Si = Ti – Ci – Li, con i = 1, 2, il sistema viene

ridotto alle quattro equazioni indipendenti:

(5.12) ˙ C1=1T1– L1– C1rC1C1rC2C2−C1C1 ˙ C₂=2T2– L2– C2rC1C1rC2C2−C2C2q C1C2 ˙L1=1T1– L1– C1rL1L1rL2L2−L1L1 ˙L2=2T2– L2– C2rL1L1rL2L2−L2L2q  L1L2 .

Equilibrio disease-free e condizioni di invasione

Inizialmente studiamo la stabilità dell'equilibrio cosiddetto disease free, cioè che causa l'estinzione di entrambi gli agenti infettivi, dato dal vettore di stato [C1, C2, L1, L2] = [0, 0, 0, 0], studiando gli

autovalori della matrice jacobiana, data da:

J=

[

]

[

]

Essendo J una matrice a blocchi, si possono studiare gli autovalori dei singoli blocchi per valutare se l'equilibrio disease free è stabile o no.

Considerando che le matrici relative a C e ad L hanno la stessa struttura, è sufficiente trovare le condizioni per cui gli autovalori sono negativi per uno dei due blocchi, dopodiché si potranno estendendere le conclusioni all'altro blocco semplicemente cambiando tutti i pedici relativi al tipo di batterio (C o L).

Per il blocco relativo a C, QC risulta:

detQC=C1C2– q−C12T2rC2−C2– q 1T1rC1– q1T1rC2 ; se det(QC) > 0, si ha: (5.13) C1C2– qC12T2rC2C2– q1T1rC1q 1T1rC2 e dunque C1C2– qC12T2rC2 C1C2– qC2– q1T1rC1 ,

(5.13), i cui termini sono tutti positivi. Semplificando la prima disequazione per C1 e la seconda

per C2– q (termini positivi per definizione), si ottiene: 2T2rC2−C2– q0

1T1rC1−C10

,

pertanto i termini sulla diagonale di QC sono negativi, e di conseguenza anche la traccia. Poichè

per ipotesi det(QC) > 0, risulta infine che gli autovalori di QC sono negativi.

La condizione necessaria e sufficiente per la stabilità globale dell'equilibrio disease free è dunque che C1C2– q1− C12T2rC2−C2– q1T1rC1– q1T1rC2 C1C2– q 0 e cioè che: (5.14) 1−2T2 r_C2 C2– q −1T1 r_C1 C1 −q 1T1 r_C2 C2−qC1 0 ; Detti: (5.15) R_C1=1T1 r_C1 C1 RC2=2T2 r_C2 C2– q ,

la condizione disease free diventa:

R_C1RC2q R_C1R_C2 r_C12T2 1 . La quantità R_C=RC1RC2q R_C1R_C2 r_C12T2

è quindi il parametro che determina la possibilità di invasione da parte del tipo C e rappresenta dunque il numero di rimpiazzamento, conformemente alla definizione data nel capitolo 1. Si noti come RC1 e RC2 rappresentano i numeri di

rimpiazzamento che avrebbe il tipo C nei due gruppi se questi fossero del tutto indipendenti; l'accoppiamento dato dal passaggio di una frazione di individui q dal gruppo 1 al gruppo 2 nell'unità di tempo aumenta il numero di rimpiazzamento complessivo e dunque favorisce la probabilità che si abbia invasione.

Tutte le conclusioni ottenute possono essere estese al tipo L sostituendo il pedice C con il pedice L.

Equilibrio di coesistenza

A questo punto ci chiediamo se esistono delle condizioni che permettano l'esistenza di un equilibrio endemico che rappresenti la coesistenza tra i due tipi di agenti infettivi, in cui il vettore di stato all'equilibrio, [C1, C2, L1, L2], abbia tutti gli elementi strettamente positivi con C1L1≤T1

e C₂ L2≤T2 .

Ponendo le derivate uguali a zero, il sistema (5.11) diventa:

(5.15) 1T1– L1– C1rC1C1rC2C2=C1C1 1T1– L1– C1rL1L1rL2L2=L1L1 2T2– L2– C2rC1C1rC2C2=C2C2−q C1C2 2T2– L2– C2rL1L1rL2L2=L2L2−q L1L2 .

Dal rapporto tra la prima e la seconda equazione e tra la terza e la quarta (tutti i membri sono positivi per ipotesi) risulta:

(5.16) C1 L1 C1 L₁= rC1C1rC2C2 r_L1L₁rL2L2 C2C2– qC1C2 L2L2– q L1 L2 =rC1C1rC2C2 r_L1L₁rL2L2 ,

in cui, come si vede, i secondi membri sono identici. Ne deriva pertanto che: C1 L1 C1 L₁= C2C2– qC1C2 L2L2– q L1L2 , e, riordinando i termini: (5.17) L_L2 1 =C_C2 1 C2−q L2– q L1 C1 q L1 L2– q  1 L1 – 1 C1  . Riordinando la prima delle equazioni (5.16) risulta inoltre:

r_L1 L1 rL2 L1 L₂ L1 =rC1 C1 rC2 C1 C₂ C1 , da cui si ottiene: (5.18) L_L1 2 =L1 C1 rC1 r_L2 L1 C1 rC2 r_L2 C2 C₁– rL1 r_L2 Eguagliando la (5.17) e la (5.18) si ottiene: (5.19) C2 C₁ C2−q L2– q L1 C1 q L1 L2– q  1 L1 – 1 C1 =L1 C1 rC1 r_L2 L1 C1 rC2 r_L2 C2 C₁– rL1 r_L2 ,

che può essere risolta in funzione di C2

C1

con qualche laborioso passaggio.

Dividiamo ambo i membri per rC2

rL2 e poniamo: D2=  R_2L R2C= r_L2 L2−q rC2 C2−q , L=  rL2 L2– q e C=  rC2 C2−q , cosicché: D₂=L C . L'equazione (5.19) diventa: (5.20) D₂L1 C1 C2 C₁q L1 r_C2L 1 L1 – 1 C1 =L1 C1 C2 C₁– rL1 r_C2 L1 C1 rC1 r_C2 . Dividiamo per = L1 C1

e portiamo al primo membro tutti i termini contenenti il fattore C2

C1

al secondo membro i restanti: C2 C1 D2 – 1=_r1 C2rC1 – 1 rL1−q L 1 −1 ;

mettiamo in evidenza rC1 tra i primi due termini della sommatoria al secondo membro e definiamo:

D1=  R_1L R1C = r_L1 L1 rC1 C1 =1  r_L1 rC1 ;

contemporaneamente portiamo al secondo membro il termine (D2 – 1). Si ottiene infine:

(5.21) C2 C1 =rC1 rC2 1− D1–a  D2−1 =P_C , dove si è posto: a=  q L r_C1 1 −1 .

Sostituendo la formula (5.21) nella (5.18) si giunge all'analoga espressione:

(5.22) L2 L₁= r_L1 r_L2 1− 1 D₁−b 1 D₂−1 =P_L , dove: (5.23) b=q C r_L1−1= −a D₁D₂ .

L'espressione (5.22) rispetta la simmetria del problema, in quanto si può ottenere direttamente dalla (5.21) sostituendo i pedici C con i pedici L e invertendo le grandezze D1, D2 e κ (operazione

che corrisponde esattamente all'inversione dei pedici).

I valori di PC e PL appena definiti giocano, come si vedrà poco più avanti, un ruolo fondamentale

nel determinare le condizioni di coesistenza competitiva.

Condizione necessaria per la coesistenza è che tutti i valori di C1, C2, L1 ed L2 siano positivi;

pertanto, dovranno esserlo anche i rapporti (5.21) ed (5.22); ciò dà luogo alle seguenti condizioni:

per D2 > 1 (5.24) D11−a , (5.25) D1 1 1−b se b1 oppure per D2 < 1 (5.26) D11−a (5.27) D1 1 1−b se b1 .

Per σb > 1, cioè per 1

r_L1 qC

, il numeratore di PL è sempre negativo, e dunque bisogna che lo

sia anche il denominatore; pertanto in queste condizioni deve essere necessariamente D2 > 1.

Inoltre, utilizzando la relazione (5.23) all'interno della (5.25), si ottiene:

D₁1 a D₁D₂1  D1 a D₂1  D11− a D₂ ,

che domina la condizione (5.24) se σa < 0, cioè se κ > 1, in quanto ci siamo posti nella condizione

D2 > 0; per κ < 1 la condizione dominante è invece la (5.24).

Per D2 > 1 si ha D11−

a

D₂ ; in questo caso, se σa < 0, la condizione che prevale è la (5.26),

mentre la (5.27) è prevalente per σa > 0.

Ricapitolando, le condizioni, necessarie e non sufficienti, ottenute sin qui per la coesistenza sono:

κ < 1 11 rL1 qC 1 rL1 qC D2 < 1 D11− a D₂ D11−a IMPOSSIBILE D2 > 1 D11−a D11− a D₂ D11−a

Tabella 5.1: Condizioni necessarie per l'equilibrio di coesistenza

Per trovare le rimanenti condizioni, è necessario calcolare le espressioni di C1, C2, L1 ed L2, ed

imporre che siano tutte strettamente positive; per far ciò calcoliamo inizialmente il numero di suscettibili all'equilibrio in ciascun gruppo, dato da:

S₁=T₁– L₁– C₁ S2=



T2– L2– C2

,

che, usando la (5.15) e la (5.21) risulta:

S₁= C1

1rC1rC2PC

S₂=C2−q  PCq 2rC1rC2PC

.

Sostituendo l'espressione di PC e rielaborando, risulta:

(5.28) S₁= T1 RC1 D₂−1 D2−D1−a =T1 RL1 1 D₂−1 1 D2 − 1 D1 −b (5.29) S₂= T2 R_C21− D₂−1 D₂– D₁−a 1 – q C r_C1= T₂ R_L21− 1 D₂−1 1 D₂– 1 D₁−b 1−q L r_L1

Ancora una volta le due espressioni rispettano la simmetria del problema.

numeri di rimpiazzamento relativi ai due gruppi: (5.30) R_C1_D D2−1 2– D1−a R_C21− D2−1 D₂– D₁−a 1−qC r_C1 ;

si evidenzia ancora una volta come entrambi i numeri di rimpiazzamento potrebbero essere anche entrambi minori di 1, purché l'RC totale superi la soglia dell'invasione; la suddivisione in classi di

età in una situazione di competizione può permettere quindi che sia favorita la sopravvivenza di una popolazione batterica, anche se la sua trasmissibilità all'interno dei singoli gruppi non sarebbe sufficiente in assenza di suddivisione in gruppi.

Analoghe condizioni si possono ricavare per RL1 ed RL2 dalle (5.28 e 5.29), ma in ogni caso sono

sempre verificate se sono verificate le (5.30).

Una volta noti S1 ed S2, si può calcolare C1, C2, L1 ed L2 dal sistema:

S₁=T1– L1– C1

S₂=T2– L2– C2

,

tenendo conto che:

C₂=PCC1 L₂=PLL1 , risulta: C₁=T2−S2−PLT1– S1 PC– PL L₁=PCT1– S1−T2−S2 P_C−PL ;

Imponendo che entrambi siano positivi, si ottengono le condizioni: (5.31) P_CT1– S1T2– S2PLT1– S1

e

(5.32) P_LT1– S1T2– S2 PCT1– S1 ,

che aggiunte a quelle della tabella h1 costituiscono le condizioni necessarie e sufficienti per l'equilibrio di coesistenza. Queste condizioni non sono facilmente interpretabili dal punto di vista epidemiologico, né riconducibili a semplici espressioni dei parametri D1 e D2, e pertanto il loro

ruolo sarà mostrato nell'ambito di simulazioni al calcolatore. Altrettanto dicasi per le condizioni di stabilità del sistema intorno ai punti di equilibrio, che risultano estremamente complicate da determinare analiticamente.

La simulazione delle condizioni di stabilità prevede il calcolo automatico degli autovalori dello jacobiano al variare di βL1 e βL2 attraverso Matlab; la matrice jacobiana assume la forma:

J=

[

]

J11=1rC1 S1– C1−1rC2C2−C1 J22=−1rC2S1 J₁₃=−1rC1C1rC2C2 J21=−2rC1S2– q J₂₂=2rC2S2– C2−2rC1C1−C2– q J₂₄=−2rC1C1rC2C2 J31=−1rL1L1rL2L2 J₃₃=1rL1S1– L1−1rL2L2−L1 J₃₄=−1rL2S1 J₄₂=−2rL1L1rL2L2 J43=−2rL1S2– q J₄₄=2rL2S2– L2−2rL1L1−L2−q

e in cui C1, C2, L1, L2, S1, S2 sono i valori all'equilibrio, dati dalle formule individuate in questo

paragrafo e quindi a loro volta dipendenti da βL1 e βL2.

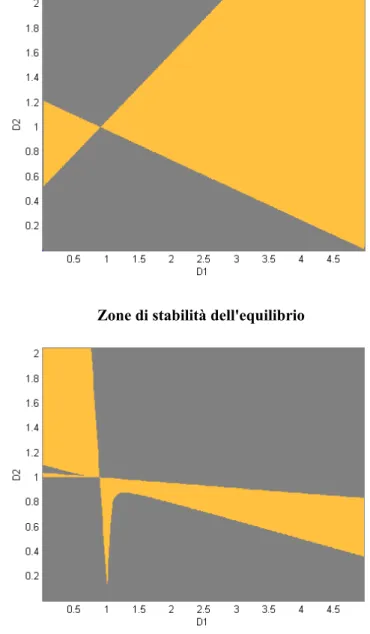
Si sono individuate, sulla base delle condizioni espresse della tabella 5.1 e di quelle indicate con (5.30), (5.31) e (5.32), le zone di esistenza possibile dell'equilibrio stabile per un modello avente i seguenti parametri (unità di misura arbitrarie):

b = 15000; q = 1/12; a1 = 2,5; a2 = 2; µ1 = 1/80; µ2 = 1/68; βC1 = 3,5; βC2 = 3; γC1 = 8; γC2 = 2,4; γL1 = 1,3; γL2 = 3,9;

e con βL1 variabile tra 0,001 e 3 e e βL2 tra 0,001 e 10, entrambi in 1000 passi. Esse sono state

contrassegnate con il colore arancione in un grafico avente in ascissa i valori di D1 e in ordinata

Zone in cui sono rispettate le condizioni di invasione ( (5.14) con il segno invertito)

Zone in cui sono rispettate le condizioni della tabella 5.1

Zone in cui sono rispettate le condizioni (5.31) e (5.32)

Zone di stabilità dell'equilibrio

Zone di equilibrio stabile per la coesistenza

Si noti che gli stati di equilibrio sono possibili solo quando D1 > 1 e D2 < 1 o viceversa: cioè, se

uno dei due tipi prevale sull'altro in un gruppo, la situazione deve essere invertita nell'altro gruppo. Non si può dunque avere coesistenza se un tipo ha un numero di rimpiazzamento maggiore in entrambi i gruppi. Questa situazione è rispettata nel caso di Neisseria lactamica e Neisseria meningitidis.

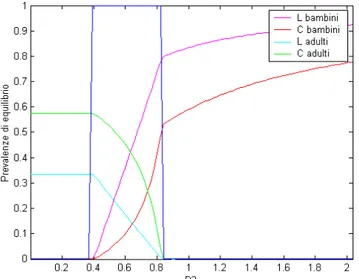
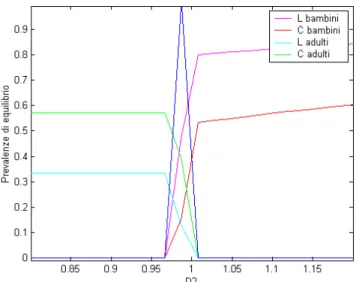
Per verificare che queste condizioni corrispondano effettivamente a degli equilibri di coesistenza, si sono eseguite diverse simulazioni del sistema con il metodo di integrazione numerica ode45 fissando un valore per βL1 e facendo variare βL2. Si sono riportati poi in un grafico i valori di

equilibrio di C1, C2, L1 ed L2 al variare di βL2 ed indicando contestualmente la finestra di valori di

questo parametro che portavano il sistema nella zona di equilibrio di coesistenza stabile. Questa operazione equivale a sezionare il grafico di figura 5.12 con una retta verticale passante per un certo D1, e ad individuare i valori di D2 corrispondenti che garantiscono la stabilità; si ricordi che c'é una

corrispondenza lineare tra D1 e βL1 e tra D2 e βL2. Il risultato che si dovrebbe ottenere è che per i

valori di βL2 che ammettono coesistenza, si abbiano valori di equilibrio non nulli per tutte le quattro

variabili di stato del sistema. Le figure seguenti mostrano che tale accordo sussiste per diversi valori di D1.

Figura 5.14: Prevalenze di equilibrio simulate e previste al variare di D e con D = 1,9803

Figura 5.13: Prevalenze di equilibrio simulate e previste al variare di D2 e con D1 = 4,9631

Il risultato che è stato trovato è un risultato innovativo nella letteratura dei modelli di meningite, in quanto mostra che la strutturazione della popolazione in gruppi di età può giustificare la coesistenza competitiva tra diversi agenti infettivi in un modello SIS, in cui il comparto dei suscettibili è la risorsa sulla quale insiste la competizione. Questo risultato dà via libera ad una parametrizzazione più realistica per valutare se la coesistenza possa sussistere nel caso di Neisseria lactamica e Neisseria meningitidis, e per studiare ulteriori implicazioni di questa struttura.

Figura 5.15: Prevalenze di equilibrio simulate e previste al variare di D2 e con D1 = = 0,9860 (dettaglio)

5.4 Modelli di coesistenza non SIS

Citiamo ora, per completezza, i rimanenti modelli focalizzati sulla coesistenza tra patogeni, elencati all'inizio della sezione 5.3. In tutti i modelli a cui accenneremo in questa sezione, è prevista una certa immunità, parziale o totale, specifica o cross-specifica, per giustificare la coesistenza e l'insorgenza di dinamiche complesse; pertanto tali modelli non rientrano nella categoria dei modelli SIS, per i quali è necessario che l'infetto, subito dopo la guarigione, torni immediatamente suscettibile ad una nuova infezione.

Eterogeneità immunologica indotta dalla popolazione

Un modello con eterogeneità immunologica indotta dall'infezione è stato proposto da Wodarz [4]: egli utilizza un modello a cascata in cui, una volta guariti dall'infezione con un ceppo, si è immuni a quel ceppo per un certo tempo, e si può essere infettati solo con l'altro. Dipendentemente dalla durata della protezione ('memoria immunologica'), può esistere coesistenza o meno: la coesistenza è più facile per durate dell'immunità maggiori, in quanto si riduce il livello di competizione tra i due patogeni, cosicché quello con R0 minore può persistere nella popolazione ospite.

L'ipotesi su cui si basa questo modello applicata al caso della meningite, cioè l'acquisizione di immunità parziale in conseguenza del carriage di meningococchi di un ceppo, è un argomento ancora molto controverso tra gli immunologi; gli studi di Goldschneider hanno mostrato che il carriage conferisce nella maggior parte dei casi livelli anticorpali adeguati a prevenire l'insorgenza della malattia, ma solo raramente impedisce la nuova acquisizione dell'infezione.

Immunità cross-specifica al carriage di altri meningococchi

Tra i modelli che tengono conto della sola immunità cross-specifica, quello forse più interessante è stato proposto da Andreasen, Lin e Levin [5] per l'influenza A, ma di validità estremamente generale. Essi suppongono l'esistenza di un numero finito n di ceppi, e tengono conto della storia di infezione dei suscettibili; ogni individuo è suscettibile solo ai ceppi con cui non è stato infettato, cioè l'immunità specifica è totale e dura per tutta la vita; ci possono pertanto essere 2n _{classi di}

suscettibili (una per ciascuna possibile storia infettiva) e n2n-1 _{classi di infetti. E' esclusa la}

possibilità di sovrainfezione, e si ipotizza che la cross-immunità consista in una riduzione della probabilità di trasmissione nei confronti di quegli strain considerati “simili”.

Attraverso una notazione compatta si riesce a determinare una condizione generale di tipo “a soglia” per la stabilità dell'equilibrio “disease-free”, cioè quello con tutti i comparti di infetti vuoti; tale condizione è sostanzialmente una generalizzazione della condizione R0 < 1 al caso con n ceppi,

ma in cui il numero di suscettibili è pesato per la suscettibilità relativa dipendente dalla cross-immunità ( ri

∑

con ri il numero di rimpiazzamento nel caso base, σi la probabilità di

acquisizione dello strain i, J l'appartenenza al comparto legata alla storia infettiva dell'individuo, K l'insieme di tutti i possibili strain). Inoltre, assumendo per semplicità che tutti gli R0 siano uguali, gli

autori individuano i diagrammi di biforcazione per n > 4, mostrando la possibilità di coesistenze stabili (già individuate in precedenza per n = 2 da Castillo-Chavez et al.) e oscillazioni nelle prevalenze relative dei ceppi (che invece sono legate alla presenza di un numero maggiore di strain).

Gomes, Medley e Nokes [6] formalizzano in modo più intuitivo il concetto di somiglianza tra ceppi attraverso l'utilizzo dello “spazio degli strain” (strain space); esso consiste in una rappresentazione geometrica della parentela genetica tra i ceppi, dalla quale si può desumere

immediatamente la relazione sulla cross-immunità, e che potrebbe permettere di considerare un modello con una varietà antigenica continua anzichè discreta.

L'induzione della cross-immunità nel caso della N. meningitidis è considerato da molti un elemento chiave dell'epidemiologia di questo batterio. Goldschneider (1969) mostra come circa i 2/3 degli individui colonizzati da N. lactamica acquisiscono livelli protettivi di anticorpi umorali contro i meningococci dei gruppi A, B e C; anche in questo caso, si tratta di immunità relativa alla malattia, che non è stata mostrata in modo altrettanto evidente anche rispetto al carriage. Goldschneider suggerisce comunque che il carriage ripetuto di meningococchi sia il responsabile della crescente immunità anche a nuove colonizzazioni, che fa diminuire rapidamente la prevalenza all'aumentare dell'età. Sia la coesistenza che le variazioni temporali nelle prevalenze relative dei vari ceppi sono fenomeni accertati per la meningite, e che i modelli alla Andreasen e colleghi potrebbero giustificare. Un problema notevole di questo tipo di modelli è la trattabilità, legata alla crescita esponenziale del numero di comparti necessari all'aumentare del numero di ceppi considerati.

Strutturazione della popolazione patogenica

Come mostrato in modo molto schematico nell'articolo di Gupta e Anderson [7], un fenomeno rilevante nella strutturazione della popolazione di molti patogeni è la risposta immunitaria dell'ospite, in quanto essa è focalizzata contro un numero limitato di antigeni.

Se l'antigene immunogenico è comune a tutta la popolazione batterica, il contatto con un qualsiasi strain renderà l'individuo immune a tutti i ceppi, favorendo la dominanza del ceppo maggiormente trasmissibile (quello con R0 maggiore) e quindi l'evoluzione di una popolazione monoclonale; se

invece si tratta di un antigene polimorfico, che può presentarsi in diverse forme al variare del ceppo, l'individuo sarà immune solo rispetto al ceppo del patogeno aggressore, e parzialmente a quelli che condividono l'antigene: il risultato della selezione legata all'immunità dell'ospite è una popolazione strutturata in diversi gruppi clonali in cui gli antigeni polimorfici si presentano in pattern non sovrapposti. La strutturazione della popolazione patogenica è molto importante nell'esito della competizione, in quanto determina, insieme alla cross-immunità, la frazione di suscettibili disponibile per ciascun ceppo e dunque l'equilibrio tra coesistenza ed esclusione.

L'articolo citato si basa su un modello di Gupta, Ferguson e Anderson (1998), che tiene conto della cross-immunità, distinguendo non una generica parentela tra gli strain fondata su un concetto astratto di distanza, ma la corrispondenza o meno dei siti polimorfici nel corredo antigenico. Anche in questo caso il modello considera una rimozione totale e definitiva per il ceppo con il quale si è stati infetti, una riduzione della forza di infezione per ceppi simili (cioè che condividono gli antigeni), ed R0 uguale per tutti i ceppi.

Il modello mostra, al variare del livello di cross-immunità, stati di coesistenza stabile senza strutturazione della popolazione batterica, o la dominanza di un insieme di ceppi con antigeni polimorfici non sovrapposti, o variazioni cicliche con periodicità sia di breve che di lungo periodo, o caoticità nell'evoluzione temporale della struttura.

Per la meningite l'origine della strutturazione batterica ha grande rilevanza nell'epidemiologia, date le notevoli variazioni geografiche e temporali nelle prevalenze dei vari serogruppi e la forte dipendenza della virulenza e del potenziale epidemico dal ceppo.

Riferimenti bibliografici

[1] Capelo A.C. (1989) Modelli matematici in biologia, Decibel, Padova.

[2] Andreasen, V., Pugliese A. (1995) Pathogen coexistence induced by density-dependent host mortality. J Theor Biol., 177(2), 159-65.

[3] Li J., Ma Z., Blythe S. P., Castillo-Chavez C. (2003) Coexistence of pathogens in sexually-transmitted disease models. J. Math. Biol., 47, 547–568.

[4] Wodarz D. (2003) Evolution of Immunological Memory and the Regulation of Competition between Pathogens. Current Biology, 13, 1648–1652.

[5] Andreasen V., Lin J., Levin S. A. (1997) The dynamics of cocirculating influenza strains conferring partial cross-immunity. J. Math. Biol., 35, 825–842.

[6] Gomes M. G. M., Medley G. F., Nokes D. J. (2002) On the determinants of population structure in antigenically diverse pathogens. Proc. R. Soc. Lond. B, 269, 227–233.

[7] Gupta S., Anderson R.M. (1999) Population Structure of Pathogens: The Role of Immune Selection. Parasitology Today, 15, 497-501.