Part I
Metodi e strumenti per l’analisi
dei sistemi dinamici
1
Problema di Cauchy,piano delle fasi per
sis-temi lineari autonomi,metodo di linearizzazione
di un sistema non lineare
1.1
Equazioni differenziali ordinarie del primo ordine
Definizione: Un’equazione differenziale è un’equazione che con-tiene una funzione incognita con alcune delle sue derivate(la funzione incognita e le sue derivate si intendono calcolate nello stesso punto). Esse si differenziano tra ordinarie e alle derivate parziali : le prime quando l’incognita è una funzione di una sola variabile,le seconde quando l’incognita è funzione di 2 o più variabili.
L’ordine massimo di derivazione che compare in un’equazione differenziale è detto l’ordine dell’equazione stessa.
La più generale forma di scrittura di un’equazione ordinaria di ordine n è la seguente:
F (t, x(t), x0(t), . . . ., x(n)(t)) = 0
dove F è una funzione di n + 2 variabili reali.
Le equazioni differenziali si presentano come validi strumenti di descrizione dei fenomeni più svariati della scienza : tutti i modelli presentati in questo lavoro sono descritti da sistemi di equazioni differenziali.
Lo studio di un fenomeno ha bisogno di una procedura per essere analizzato:
i) Rilevamento di dati sperimentali
ii) Interpretazione di tali dati e formulazione di leggi riguardanti
l’evoluzione del fenomeno
iii) Traduzione delle leggi in termini matematici:costruzione del
modello matematico
iv) Esame del modello allo scopo di trarne le informazioni che
si ritengono più utili.
Le equazioni differenziali del tipo x0 = f(t, x) sono equazioni dette in forma normale.
1.2
Problema di Cauchy:Teorema di esistenza e unicità .
Integrale generale
La più semplice equazione del primo ordine è:x0 = f(t)
Si deve quindi trovare l’insieme delle primitive di una data funzione. Se f è continua in un intervallo [a, b],una primitiva di f in questo
inter-vallo è data da:R
b
af (s) ds con soluzione x(t) =
Rb
af (s) ds +c dove c è una costante
arbi-traria.
Anche nel caso più elementare le soluzioni sono infinite.
Consideriamo ora l’equazione x0 = f(t, x) in cui il secondo membro è funzione delle due variabili t e x.
Definizione : Per soluzione di x0 = f(t, x) in un dato intervallo
(t1, t2) intendiamo una funzione x = x(t) in tale intervallo
differen-ziabile tale che x0(t) = f (t, x(t)) per ogni t appartenente a (t1, t2)
Definizione : L’integrale generale di x0 = f (t, x) è una famiglia di
funzioni x = §(t, c) dipendenti dal parametro c che rappresenta tutte ,a meno di un numero finito ,le possibili soluzioni dell’equazione.
Fissando nell’insieme delle soluzioni un determinato valore di c,si ottiene una soluzione particolare.
Altre possibili forme sono :
i)la forma implicita G(t, x, c) = 0 e
ii)quella parametrica x(ρ) = h(ρ, c) e t(ρ) = g(ρ, c) dove ρ è un
para-metro opportuno,variabile nell’intervallo (ρ0, ρ1).
Esempio:
l’equazione differenziale del primo ordine x0 = −t/x è risolvibile con il
metodo delle variabili separabili : xdx = −tdt
da cui integrando si ottiene x2/2 = −t2/2+c2/2 per cui la soluzione generale
è x2+ t2= c2.
Tale integrale generale non è altro che una famiglia di archi di cerchi con raggio variabile al variare di c.
D’altra parte la famiglia di cerchi può essere scritta con la sua formula para-metrica:
x(ρ) = c ∗ cos(ρ); t(ρ) = c ∗ sin(ρ)con ρ appartenente all’intervallo [0, 2π] . L’utilizzo delle equazioni differenziali come strumento per la costruzione di un modello matematico è affiancato dalla presenza di condizioni iniziali di rifer-imento che determinano la particolare evoluzione temporale delle variabili.
Definizione : Per problema di Cauchy relativo all’equazione x0=
f (t, x) si intende la ricerca di un integrale dell’equazione
soddis-facente una condizione iniziale del tipo x(t0) = x0.
Sia dal punto di vista pratico che da quello teorico risulta importante poter garantire l‘esistenza e l’unicità della soluzione del problema di Cauchy :il teo-rema che porta a questo risultato è dimostrato con l’utilizzo degli spazi metrici.
Theorem 1 : Esistenza e unicità per il problema di Cauchy
Indichiamo con R l’insieme {(t, x); t0−a ≤ t ≤ t0−a, x0−b ≤ x ≤ x0+b}con
a > 0 e b < +∞
Supponiamo che f (t, x) e df (t, x)
dx siano funzioni continue in R .
Allora esiste un σ > 0 tale che il problema di Cauchy x0= f (t, x), x(t
0) = x0
ha una e una sola soluzione x = x(t) definita in
[x0− σ, x0+ σ].
Osservazione 1:
Dalla dimostrazione emerge che σ=min(a, b/M )dove M è il massimo di |f(t, x)|.
Osservazione 2:
Conoscendo l’integrale generale x = φ(t, c) dell’ equazione x0 = f (t, x) si
possono calcolare gli integrali particolari in modo
tale da soddisfare la condizione iniziale x(t0) = x0scegliendo c affinché sia
x0= φ(t0, c) .
L’equazione x0 = f (t, x) e il relativo Problema di Cauchy hanno un preciso
significato geometrico :
supposto che f (t, x) sia definita in una regione di piano D , se (t0, x0)
ap-partiene a D ,l’equazione associa a tale punto
una direzione,più precisamente quella della retta passante per (t0, x0) e
avente come coefficiente angolare x0(t
0) = f (t0, x0) .
In altri termini l’equazione x0= f (t, x) determina in D un campo di direzioni
in modo che il grafico di una qualunque soluzione
è tangente in ogni suo punto alla direzione del campo.
1.2.1 Equazioni Lineari del 1◦ ordine
La più generale equazioni lineari del 1◦ordine è data da
x0+ p(t)x = q(t)
dove p e q sono funzioni continue nell’intervallo [a, b] .
La denominazione lineare sta ad indicare la relazione lineare tra x e x0.
Nel caso in cui q(t) = 0 l’equazione si dice omogenea . Per queste equazioni esiste sempre una soluzione data da
x(t) = e−Rp(t)dt{c +Rq(t)eRp(t)dtdt} con c costante arbitraria.
Dimostrazione : Consideriamo l’equazione x0+ p(t)x = q(t) ,
moltiplicando ambo i membri per eRp(t)dt otteniamo
eRp(t)dtx0+ eRp(t)dtp(t)x = eRp(t)dtq(t).
Il primo membro altro non è che la derivata della funzione
xeRp(t)dt=⇒ d(xe R p(t)dt) dt = e R p(t)dtq(t)
Da cui integrando si ottiene che
x(t) = e−Rp(t)dt{c +R(q(t)eRp(t)dt)dt}
c.v.d. Esempio1 :
p(t) = a, q(t) = 0 =⇒ x0 + ax = 0 con x(0) = 1
La soluzione generale è x(t) = Ke−at,soluzione particolare per la condizione
iniziale è x(t) = e−at
Esempio2 :
x0= (1/t) x + t2=⇒ p(t) = −1/t, q(t) = t2=⇒
x(t) = e−R(−1/t)dt{c +Rt2eR(−1/t)dtdt} =⇒ x(t) = ct + t3.
1.2.2 Equazione di Bernoulli
Un’equazione di Bernoulli ha la seguente forma:
x0 + p(t)x = q(t)xαcon α 6= 0, α 6= 1
dove p e q sono funzioni continue in [a, b] .
Si considera il fatto che se α > 0, x(t) = 0 è soluzione particolare dell’equazioni .
Escludendo tale soluzione si divide l’equazione per il termine xα=⇒ x−αx0+
p(t)x(1−α)= q(t)
Ponendo u = x(1−α)l’equazione diventa lineare
u = x(1−α)=⇒ u0+ (1 − α)p(t)u = q(t)(1 − α)
e può essere risolta con la formula dimostrata precedentemente ricordando
che da u = x(1−α) si ricava x = u1−a1 .
1.2.3 Equazione di Riccati
L’equazione di Riccati presenta la forma x0 = p(t)x + q(t)x2+ r(t) con p, q, r
funzioni continue in [a, b] e r(t) 6= 0 per escludere che l’equazione coincia con quella di Bernoulli.
Non ci sono metodi risolutivi per tale equazione ma se si riesce a conoscere
un integrale particolare x(t) = x∗
si può effettuare il seguente cambio di variabile
x = x∗ + 1/u rendendo l’equazione di Riccati lineare u(1) = −(p(t) +
2q(t)x∗)u − q(t)
Una volta trovata u si riconsidera la formula di trasformazione per deter-minare la x.
1.2.4 Equazione differenziale esatta Consideriamo l’equazione M (t, x) + N (t, x)x0= 0 oppure x0= −M(t, x)/N(t, x) con N (t, x) 6= 0
dove M ed N sono funzioni continue con le proprie derivate parziali prime nella regione di piano R = {∀(x, t)/ a < t < b , c < x < d}.
Il teorema di esistenza e unicità ci dà la certezza che nel rettangolo dei valori ammissibili per t e x esiste un’unica soluzione
per il problema di Cauchy con dato iniziale x(t0) = x0 .
L’equazione differenziale esatta è spesso espressa nella forma M (t, x)dt + N (t, x)dx = 0
Definizione: M (t, x)dt+N (t, x)dx = 0si dice esatta nel rettangolo R se esiste una funzionef = f (t, x)detta funzione potenziale tale
che df
dx = N and
df
dt = M, ∀(t, x) ∈ R.
Quindi due funzioni potenziali di una stessa equazione differiscono per una costante .
Se M (t, x)dt + N (t, x)dx = 0 è esatta allora possiamo riscrivere l’equazione
nella forma df = 0 dove f è una funzione potenziale.
Integrando questa nuova forma si ottiene l’integrale generale f (t, x) = c con c costante arbitraria (forma implicita).
Theorem 2 :
Se M e N sono funzioni continue con le loro derivate parziali prime in R = {∀(x, t)/ a < t < b , c < x < d}
allora l’equazione è esatta se e solo se dM
dx =
dN dt
La funzione potenziale che si annulla in un punto (t0, x0)) ∈ R è data dalle
seguenti formule: f (t, x) =Rtt 0M (s, x)ds + Rx x0N (t0, r)dr f (t, x) =Rtt 0M (s, x0)ds + Rx x0N (t, r)dr.
1.2.5 Le equazioni a variabili separabili
Sono delle equazioni differenziali esatte dove è possibile isolare le 2 variabili t e x :
Se
B(x) 6= 0 → x0 = A(t)B(x)
A(t)dt −B(x)1 dx = 0
che ne mostra l’esattezza con soluzione
Rt t0A(s, )ds − Rx x0 1 B(x)dr = c costante arbitraria
Poiché l’equazioni esatte non sono frequenti dato il forte vincolo che ne dà l’esattezza ci si è posto il problema di trovare
un fattore che moltiplicato per M e N rende l’equazione esatta:
tale fattore prende il nome di fattore integrante per l’equazione in ques-tione.
Dal punto di vista teorico è sempre possibile trovare un fattore integrante se l’equazione ammette un integrale
generale del tipo f (t, x) = c.
In tal caso risulta contemporaneamente che ∂f ∂xdx + ∂f ∂tdt = 0 e M (t, x)dt + N (t, x)dx = 0 → ∂f ∂x N (t, x) = ∂f ∂t M (t, x) Dato che ∂f ∂x = mN e ∂f ∂t = mM ,
dal punto di vista pratico la ricerca del fattore integrante risulta dalla con-dizione
∂(mN )
∂t =
∂(mM )
∂x .
1.3
Integrale generale,Integrale particolare ,Teorema di
esistenza e unicità,Inviluppo di una famiglia di curve
La dimostrazione del teorema di esistenza e unicità permette di dare una definizione di integrale generale più rigorosa.Definizione(integrale generale): Sia f = f (t, x) una funzione che soddisfi le ipotesi del teorema di esistenza e unicità nella regione D del piano (t, x).L’integrale generale dell’equazione x0 = f(t, x) è una famiglia di soluzioni contenenti una costante arbitraria a partire dalla quale si possono ottenere tutte le soluzioni soddisfacenti la
condizione iniziale x(t0) = x0 al variare di (t0, x0) in D.
Definizione(integrale singolare ):Gli integrali singolari sono soluzioni con punti che non soddisfano le ipotesi del teorema in nessun intorno.Come si può capire non si giunge alla conoscenza dell’integrale singolare attraverso quello generale particolarizzato da una costante arbitraria.
Definizione(inviluppo diuna famiglia di curve ) :Data una famiglia di curve y(t, x, c) = 0 si dice inviluppo della famiglia di curve una curva tale che ogni suo punto è tangente ad una di-versa curva della famiglia.
Se l’ integrale generale di un’equazione differenziale ammette inviluppo allora questo è un integrale singolare.
Per trovare l’inviluppo di una famiglia di curve basta eliminare c dalle equazioni
φ(t, x, c) = 0 e
∂φ(t, x, c)
∂c = 0
1.3.1 Dimostrazione del teorema di esistenza e unicità per il
prob-lema di Cauchy
Al fine di comprendere la seguente dimostrazione risulta utile dare alcune definizioni:
Definizione (Punto fisso) Un punto x è detto fisso per la
funzione F : X =⇒ X se risulta F (x) = x.I punti fissi per una fun-zione sono quelli che coincidono con la propria immagine: vengono lasciati invariati dalla trasformazione F .
Theorem 3 :Sia f una funzione reale di variabili reali,definita e continua in[0, 1]
e a valori in [0, 1],la funzione f ha allora un punto fisso.
La ricerca di un punto fisso equivale alla ricerca di un punto di intersezione del grafico con la retta y=x ed
infatti il teorema afferma che se una funzione è definita in un quadrato [0, 1],[0, 1]allora necessariamente avrà
un’ intersezione con la bisettrice che equivale a confermare l’esistenza del punto fisso per la funzione .
Definizione (Contrazione ) Una funzione F tra spazi metrici
F : (X, dx) =⇒ (Y, dy)si dice una contrazione di X in sé se esiste un
numero reale α ∈[0,1] tale che ∀ x1, x2∈ X risulta dy(F (x1), F (x2) <
αdx(x1, x2).
Definizione (iterata) Sia F un’applicazione dello spazio
met-rico X in sé: chiamiamo
iterata n-esima di F l’applicazione Fn di X in sé definita per
ricor-renza F1=F ; Fn+1= F Fn per n º 1.
Corollario:
Se Fh(iterata h-esima)è una contrazione ,allora F ha un unico punto fisso,inoltre
la successione{xn}definita
Teorema :
Indichiamo con R l’insieme {∀(t, x)/ t0−a ≤ t ≤ t0+a , x0−b ≤ x ≤ x0+b}
con a > 0 e b < +∞
Supposto che f (t, x) e ∂f
∂x(t, x) siano funzioni continue in R
Allora esiste un δ > 0tale che il problema di Cauchy
x0= f (t, x),
x(t0) = x0
ha una e una sola soluzione x = x(t)definita in[x0− δ, x0+ δ].
Dimostrazione:
Dimostrare il teorema equivale alla determinazione di una funzione x(t) definita e continua
nell’intervallo[x0− δ, x0+ δ], con δ opportunamente scelto ,soluzione della
seguente equazione integrale :
x(t) = x0+Rtt0f (s, x(s))ds
Infatti se x(t)è soluzione di questa equazione la condizione iniziale x(t0) = x0
è soddisfatta ,
inoltre l’equazione stessa implica che x è derivabile e che
x0(t) = f (t, x(t))
cioè x è soluzione di una famiglia di curve F (t, x(t), c) = 0.
Viceversa se x(t)è soluzione del problema di Cauchy ,integrando tra t0e t
l’equazione
x0(t) = f (t, x(t))
e tenendo conto della condizione iniziale, si ottiene proprio
x(t) = x0+Rtt0f (s, x(s))ds.
Per risolvere tale equazione integrale si usa il teorema sulle contrazioni.
Introduciamo lo spazio Y delle funzioni continue in [x0− δ, x0+ δ] a valori
in [x0− b, x0+ b]con 0 < δ ≤ a da scegliersi successivamente.
Se u e v ∈ Y ,definiamo la distanza tra u e v mediante la formula per t ∈
[t0− δ, t0+ δ]
d(u, v) = max|u(t) − v(t)|:
così facendo Y risulta uno spazio metrico completo .
∀ u ∈ Y poniamo T [u(t)] = x0 +
Rt
t0f (s, x(s))ds e notiamo che risolvere
l’equazione integrale equivale alla ricerca di un punto fisso per l’operatore T , ovvero per la definizione di punto fisso T x = x.
Per garantire l’esistenza e l’unicità di tale punto fisso si dimostra che se u ∈ Y =⇒ T u ∈ Y =⇒ T è una funzione dello spazio metrico Y in sè ;inoltre va dimostrato che una iterata di T è una contrazione in Y .
i)si dimostra che se u∈ Y e se δ è opportunamente scelto allora T u ∈ Y .
Chiaramente se u ∈ Y allora è continua in [to − δ, to + δ].
Denotiamo con M il massimo di |f(t, x)| in R . |T u(t) − x0| = |R t t0f (s, u(s))ds| ≤ Rt t0|f(s, u(s))|ds ≤ M|t − t0| ≤ Mδ
se si sceglie δ = b/M si ottiene che δ(T u, x0) ≤ b c.v.d.
ii)si dimostra che∃ n0/ T n0 è una contrazione di Y in sé.
SeK è il massimo di |∂f∂x| in R,applicando il teorema del valore medio di
Lagrange si può scrivere che
|f(t, u1) − f(t, u2)| = ∂x(t,u∂f 0)∗ |u1− u2| <= K|u1− u2| con u1< u0 < u2
Quindi |T u1(t) − T u2(t)| <= | Rt t0f (s, u1(s)) − f(s, u2(s))ds| <= | Rt t0K|u1(s) − u2(s)|ds| <= K|t − t0|d(u1, u2).
Per induzione si dimostra che
|Tnu 1(t) − Tnu2(t)| <= Kn|t − t0|nd(u1, u2)/n!con n >= 1 Infatti ,considerando t > t0 , |Tn+1u1(t) − Tn+1u2(t)| = |T (Tnu1(t)) − T (Tnu2(t)) ≤ R t t0|f(t, T nu 1) − f (t, Tnu2)|dt ≤R t t0K|T nu 1(s) − Tnu2(s)|ds,
utilizzando la suddetta ipotesi di ricorrenza si ricava
|Tn+1u 1(t)−Tn+1u2(t)| ≤ Kn+1/n!R t t0||s−t0| nd(u 1, u2)dt = Kn+[1/(n+ 1!)] ∗ |t − t0|n+1d(u1, u2)
Quindi l’ipotesi induttiva è dimostrata per n º 1 : questo implica che
d(Tnu
1, Tnu2) ≤ Knan/n! ∗ d(u1, u2).
Poiché il limite per n −→ ∞ di Knan/n! −→ 0,
allora esiste un n0 tale che Kn0an0/n! < 1 :
Tn0 è una contrazione di Y in sé e così il teorema risulta completamente
dimostrato. Osservazione :
L’ipotesi che ∂f /∂x sia continua in R ci è servita per dimostrare che Tn0è
una contrazione di Y in sé :
è possibile adottare un’ipotesi più generale ovvero
∃K > 0/∀(t, x1), (t, x2) in R risulta
|f(t, x1) − f(t, x2)| <= K|x1− x2|.
Una funzione soddisfacente tale ipotesi si chiama Lipschitziana nella vari-abile x,
uniformemente rispetto a x , K si chiama costante di Lipschitz.
1.4
Sistemi di equazioni differenziali ordinarie(equazioni
di ordine superiore al primo)
Definizioni e risultati di carattere generale
Un sistema dinamico, in evoluzione nel tempo, è definito da un vettore x(t) =
(x1(t), . . . , xn(t)) e governato da n equazioni del tipo:
La notazione vettoriale del sistema di equazioni differenziale del 1◦ordine è la seguente:
dx(t)/dt = f (t, x(t))dove f = (f1, ..., fn)
Definizione: Una soluzione di dx(t)
dt = f (t, x(t)) in un intervallo(t1, t2)
è un vettore x(t) le cui n componenti definite e differenziabili in
(t1,t2) soddisfano le equazioni del sistema .
Per tali sistemi chiamiamo Problema di Cauchy la ricerca di una soluzione x(t )che soddisfi l’equazione
dx(t)
dt = f (t, x(t))
e la condizione iniziale
x(t0) = x0con x0∈ Rn .
Le componenti di f sono funzioni delle n + 1 variabili
(t, x1(t), . . . , xn(t)).
Per il punto fissato
(t0, x0) = (t0, x01, x02, . . . , x0n)
indichiamo con
K la regione di piano (n + 1) dimensionale individuata dalle seguenti con-dizioni:
to− a <= t <= to+ a, x0j− b <= xj <= x0j + b, j = 1, 2, ..., n
Per n = 1 la regione sarà un rettangolo,per n = 2 sarà un parallelepipedo
etc,con centro nel punto(t0, x0).
Teorema :
Supponiamo che le componenti di f siano di classe C1(continue)in K rispetto
a x1, x2, x3, . . . , xn.
Allora esiste un δ > 0 tale che il problema di Cauchy dx(t)
dt = f (t, x(t)), x(t0) = x0,
ha una e una sola soluzione definita nell’intervallo
[to− δ, to+ δ].
Dalla dimostrazione possiamo precisare che δ º min(a, b/M)dove M = max(|f(t, x(t))|)al variare di(t, x)in K.
1.4.1 Riduzione di un’equazione di ordine n al primo ordine
Un’ equazione di ordine n del tipo
y(n)(t) = F (t, y(t), y(1)(t), y(2)(t), . . . , y((n
−1)(t))
può essere ricondotta ad un sistema di equazioni di ordine 1 : basta porre
y = y1, y(1) = y
2... =⇒ y2= y
(1)
1 , . . . , y(n−1)= yn,...,yn = y(1)n−1
ed osservare che l’equazione differenziale di ordine n è equivalente al sistema di equazioni differenziali di ordine 1
y1
Come conseguenza ricaviamo che i risultati ottenuti per i sistemi di n equazioni si trasferiscono direttamente
alle equazioni differenziali di ordine n:
vale il teorema di esistenza e unicità della soluzione per il problema di Cauchy che soddisfa le condizioni iniziali
y(t0) = y0, y1(t0) = y01, . . . ,
yn−1(t
0) = yn0−1.
Teorema :
Sia F di classe Cn−1nella regione K.
Esiste allora un δ >0 tale che il problema di Cauchy relativo all’equazione
y(n)(t) = F (t, y(t), y1(t), y2(t), . . . , yn−1(t))
sotto condizioni iniziali
y(t0) = y0, y1(t0) = y10, . . . , yn−1(t0) = yn0−1ammette una e una sola soluzione
nell’intervallo[t0− δ, t0+ δ].
1.4.2 Sistemi lineari di primo ordine in n equazioni e n incognite
Tale tipologia di sistemi ha la seguente forma matriciale
A(t)x(t) + b(t) = x0(t)
dove
A(t) è una matrice n × n e
b(t) il vettore dei termini noti ha dimensioni 1 × n mentre x(t),il vettore incognito ,ha dimensioni n × 1.
Proposizione:Se la matrice A(t)e il vettore b(t)sono continui in[a, b],
allora esiste un’unica soluzione definita in [a,b]del sistema che verifica le condizioni
iniziali del sistema x(t0) = η ∀t0∈ [a, b].
Tale proposizione risulta vera per il Teorema sulla riduzione di un’equazione differenziale di ordine n ad un
sistema di n equazioni del primo ordine .
Così che f (t, x) = A(t)x + b(t)e∂fj
∂xk
= ajk.
Le ipotesi del teorema valgono nella regione K data da a <= t <= b e η0
j
−b <= xj<= ξ0j+ b con b > 0qualunque.
Il teorema assicura l’esistenza di una soluzione xm del problema di Cauchy
definita in (t0− δ, t0+ δ)
con δdato da min(t0− a, b − t0) .
Bisogna dimostrare che la soluzione è definita in tutto [a, b].
Supposto che δ = t0− a allora xmè definito in[a, 2t0+ a]:
risolviamo ora il problema di Cauchy
x0= A(t)x + b
con la condizione iniziale
:per il teorema risulta che xm(t) è prolungabile fino al punto 2t0 − a + δ dove
δ = min(2t0− 2◦, b − 2t0+ a).
Se 2t0− a + δ = b la dimostrazione è conclusa,altrimenti bisogna ripetere il
fino ad ottenere il prolungamento della soluzione a b.
Proposizione : L’insieme delle soluzioni di un sistema di n equazioni in n incognite costituisce uno spazio vettoriale di dimensione n.
Quindi se le soluzioni del sistema sono linearmente indipendenti si parla di sistema fondamentale di soluzioni:
l’integrale generale sarà della forma φ(t) = c1φ1(t)+c2φ2(t)+. . .+cnφn(t)con
le c costanti arbitrarie.
Proposizione :L’integrale generale del sistema x0 = A(t)x + b si ottiene
ag-giungendo all’integrale generale del sistema omogeneo
associato una soluzione particolare del sistema non omogeneo.
Proposizione:Condizione necessaria e sufficiente affinché le n soluzioni costi-tuiscano un sistema fondamentale di
soluzioni è che det(φ1, . . . , φn) 6= 0 nell’intervallo [a, b].
1.4.3 Equazioni lineari di ordine n e lo spazio vettoriale delle soluzioni
Precedentemente abbiamo trasformato un’equazione lineare di ordine n in un sistema di n equazioni del primo ordine :
si può traslare questo concetto affermando che un’equazione
xn(t) = an−1xn−1(t) + an−2xn−2(t) + . . . + b(t)
è equivalente al sistema x0(t) = A(t)x(t) + b(t) dove
x(t) = (x1(t), x2(t), . . . , xn(t)), b(t) = (0, 0, 0, . . . , 0, b(t)) ed
A una matrice contenente i coefficienti dell’equazione nella prima riga e con n − 1 vettori di base di dimensione n.
Se b(t) = 0 allora l’equazione si dice omogenea.
Proposizione :Se le funzioni a0(t), a1(t), . . . , an−1(t)sono continue in [a, b] ,
esiste un’unica soluzione definita
in [a, b] dell’equazione soddisfacente le condizioni iniziali
x(t0) = x0, x1(t0) = x01, . . . , xn−1(t0) = xn0−1.
Proposizione:L’insieme delle soluzioni dell’equazione omogenea costituisce uno spazio vettoriale di dimenzione n.
Di conseguenza l’integrale generale sarà della forma
φ(t) = c1φ1(t) + c2φ2(t) + . . . + cnφn(t)
con le c costanti arbitrarie.
L’integrale generale dell’equazione non omogenea ha la forma
φno(t) = φ(t) + φm(t)
dove φ(t) è l’integrale generale della soluzione omogenea associata e
φm(t)è integrale particolare dell’equazione non
omogenea.
Proposizione :Condizione necessaria e sufficiente affinché n soluzioni φ1, . . . , φn
linearmente indipendenti è che
il determinante della matrice φ1 φ2 .. .. φn φ01 φ02 .. .. φ0n φ(2)1 φ(2)2 .. .. φ(2)n .. .. .. .. ... φ(n)1 .. .. .. φ(n)n 6= 0
sia diverso da zero in [a, b]:
tale determinante si chiama Wronskiano di φ1, . . . , φn ed
è indicato con wronsk(φ1, . . . , φn).
1.4.4 Equazioni lineari a coefficienti costanti. Stabilità
Equazioni omogenee ed integrale generale
Una generica equazione di ordine n a coefficienti costanti reali ha la seguente forma:
anxn(t) + an−1xn−1(t) + ... + a1x1(t) + a0x(t) = 0.
Ogni soluzione è definita su tutto l’asse reale, poichè i coefficienti sono costanti.
L’integrale generale è dato dalla combinazione lineare di n soluzioni φ1(t), . . . , φn(t)linearmente
indipendenti
φ(t) = c1φ1(t) + c2φ2(t) + . . . + cnφn(t)
con le c costanti arbitrarie.
Per trovare le n soluzioni linearmente indipendenti si usa l’equazione
carat-teristica associata all’equazione omogenea in questione P (λ) = anλn +
an−1λn−1+ ... + a1λ1+ a0= 0
Per il teorema fondamentale dell’algebra l’equazione caratteristica ha n radici ciascuna considerata con la sua molteplicità :
ad ogni radice reale λ di molteplicità k associamo le k funzioni
eλt, teλt, . . . , tk−1eλt.
Ad ogni coppia (a + ib, a − ib)
di radici complesse e coniugate di molteplicità h associamo le 2h funzioni:
eatcos(bt), teatcos(bt), . . . , th−1eatcos(bt) e eatsin(bt), teatsin(bt), . . . , th−1eatsin(bt).
Si ottengono complessivamente n funzioni dato che (teorema fondamentale dell’algebra)
la somma delle molteplicità di ogni radice è uguale al grado del polinomio.
Sull’origine di tali funzioni si può procedere intuitivamente osservando che
y0= ay
ha come soluzione
y(t) = Keat.
Si sostituisce dunque l’espressione nell’equazione ottenendo
eλtP (λ) = 0 :
eλt è soluzione dell’equazione se e solo se λ è radice del polinomio
Supposto che λ abbia molteplicità 2 ,oltre alla soluzione eλt,si può costruire un’altra soluzione pensando
al caso di 2 radici semplici λ e λ + εper ε −→ 0:
considerando il rapporto incrementale delle funzioni soluzioni per ε −→ 0,
limε−→0
(e(λ+ε)t− eλt)
ε = te
λt.
Se la molteplicità è superiore a 2 si procede sull’ultima soluzione alla stessa maniera.
Teorema:
Se le funzioni generate dagli autovalori sono tra loro linearmente indipendenti :
l’integrale generale è dato dalla loro combinazione lineare a coefficienti arbi-trari.
Nel caso in cui le radici λ1, λ2, . . . , λn diP (λ) sono tutte reali e distinte
l’integrale generale è dato dalla forma :
x(t) = c1eλ1t+ c2eλ2t+ . . . + cneλnt .
Per n = 2 l’equazione si presenta come :
a2x(2)(t) + a1x(1)(t) + a0x(t) = 0.
L’equazione caratteristica è P (λ) = a2λ2+ a1λ1+ a0= 0 da cui la soluzione
presenta tre possibili casi al variare del segno del discriminante ∆ > 0,∆ < 0, ∆ = 0
Caso1 : ∆>0 e le radici sono reali e distinte
x(t) = c1eλ1t+ c2eλ2t
Caso 2: ∆=0 e soluzioni coincidenti λ1= λ2= λ con molteplicità 2:
x(t) = (c1+ c2t)eλt.
Caso 3: ∆ < 0e soluzioni complesse e coniugate (a + ib, a − ib) :
x(t) = eat(c
1cos(bt) + c2sin(bt))
Dimostrazione:
Per il caso 1 basta verificare che x(t) è soluzione per diretta sostituzione e che le soluzioni siano linearmente
indipendenti come afferma il teorema precedente.
Nel secondo caso si deve dimostrare che eλt e teλt sono linearmente
indipendenti,ovvero basta dimostrare che
il wronskiano abbia determinante diverso da zero(infatti e2λt è sempre
di-verso da zero),
e che x(t) è soluzione lo si può verificare per sostituzione.
Nel terzo caso si procede alla stessa maniera:il wronskiano di (eatcos(bt), eatsin(bt))
ha un determinante pari a
1.4.5 Equazioni omogenee. Stabilità
Spesso l’utilizzo delle equazioni differenziali nelle applicazioni demografiche ,eco-nomiche o scientifiche,
più che conoscere l’integrale generale, tende alla conoscenza del comporta-mento asintotico della soluzione per t −→ +∞
Per le equazioni omogenee di ordine n x(t) = 0
è posizione di equilibrio . Definizione:
Il punto x(t) = 0 si dice dinamicamente e asintoticamente stabile per un’equazione differenziale omogenea
se ogni soluzione converge a zero per t −→ +∞.
Se è possibile calcolare tutte le radici dell’equazione caratteristica associata all’equazione ,
x(t) è asintoticamente stabile se soltanto se le radici reali sono negative e quelle complesse hanno parte reale negativa :infatti in tal caso le funzioni associate alle radici sono infinitesime.
Poiché non è sempre facile conoscere le n radici del polinomio caratteristico ci affideremo a dei criteri di stabilità
da usare senza risolvere l’equazione caratteristica.
Supposto an > 0 si può enunciare il criterio per le equazioni di 2◦ grado:
il punto di equilibio è asintoticamente o dinamicamente stabile se e solo se nell’equazione caratteristica
a2λ2+ a1λ + a0= 0
i tre coefficienti a2, a1, a0 sono tutti positivi
così che le radici reali risulteranno negative e quelle complesse a parte reale negativa.
Supponendo sempre che an > 0si può presentare il criterio di stabilità per le
equazioni di terzo grado :
il punto di equilibrio è asintoticamente stabile se e solo se l’equazione carat-teristica
a3λ3+ a2λ2+ a1λ + a0= 0
i 4 coefficienti a3, a2, a1, a0sono positivi
e
a1a2> a0a3.
Scrivendo l’equazione caratteristica come λ3+(a2/a3)λ2+(a1/a3)λ+(a0/a3) =
0
=⇒ λ3+ αλ2+ βλ + ψ = 0 :
la condizione a1a2> a0a3 si traduce in αβ > ψ.
Poiché α, β, ψ sono positive per la prima condizione lo studio delle radici del polinomio siffatto porta a 2 possibili casi:
i)tre radici reali negative o
Il primo caso è sicuramente di equilibrio dinamicamente stabile visto che le funzioni associate alle radici sono infinitesime .
Per il secondo caso la radice reale è negativa con funzione associata infin-itesima ,mentre per dimostrare che la parte reale dei complessi e coniugati è negativa si ricorre ad una proprietà delle radici di un polinomio di terzo grado:
λ1+ λ2+ λ3= 2α + λ1= −α < 0;
λ1λ2+ λ1λ3+ λ2λ3= 2αλ1+ a2+ b2= β > 0;
λ1λ2λ3= λ1(a2b2) = −ψ < 0
quindi a, b, c > 0.
Per la seconda condizione αβ > ψsi traduce in −(2α + λ1)(2αλ1+ a2+ b2) +
λ2(a2+ b2) > 0 =⇒ α < 0
Quindi in un polinomio di 3◦ grado
la somma delle radici è equivalente all’opposto del coefficiente del termine al secondo grado su quello al terzo,
il prodotto a 2 delle radici è uguale al coefficiente del termine al primo grado su quello al terzo ,
il prodotto a tre è uguale all’opposto del coefficiente del termine noto su quello al terzo.
Generalizzando si può dire che data l’equazione
anxn(t) + an−1xn−1(t) + ... + a1x1(t) + a0x(t) = 0
la somma delle radici è data da −an−1/an ,
la somma dei prodotti a due a due delle radici è data da an−2/an,
il prodotto delle radici è dato da (−1)na
0/an.
Teorema di Ruth-Hurwitz:(Criterio di stabilità per equazioni di grado n) Data la matrice
Ruth − Hurwitz matrix = an−1 an−3 an−5 ...0 an an−2 an−4 ...0 an−3 an−5 ... ...0 an−2 an−4 a2 a0
Il punto di equilibrio è stabile se e solo se tutti i minori principali della matrice di Ruth-Hurwitz sono positivi.
1.4.6 Equazioni non omogenee
Un’equazione non omogenea di ordine n ha la seguente forma
anxn(t) + an−1xn−1(t) + ... + a1x1(t) + a0x(t) = b(t).
In base a quanto detto prima, l’integrale generale dell’equazione non omo-genea è dato dalla somma dell’integrale
generale dell’equazione omogenea associata e di un integrale particolare di quella non omogenea in esame.
Per determinare l’integrale particolare dell’equazione non omogenea si pren-dono in esame dei casi particolari di b(t).
Proposizione :
Se b(t) è un polinomio di grado r ,esiste una soluzione dell’equazione non omogenea data da
dove q(t) è un polinomio di grado r se λ 6= 0 , oppure
data da tmq(t)se λ = 0 è soluzione dell’equazione caratteristica di
molteplic-ità m.
In pratica si considera un generico polinomio q(t) di grado r nel primo caso
,o tmq(t) nel secondo sostituendolo
nell’equazione per individuare i coefficienti mediante il principio di identità dei polinomi.
Proposizione :
Per b(t) = Reat
dove R è un polinomio di grado r.
Se a non è soluzione dell’equazione caratteristica,esiste un’unica soluzione data da
x(t) = Q(t) eat
dove Q(t) è un polinomio di grado r.
Se a è soluzione dell’equazione caratteristica di molteplicità m ,allora l’equazione non omogenea a una soluzione data da
x(t) = tmQ(t)eat.
Proposizione :
Per b(t) = Reatsin(bt)oppure b(t) = Reatcos(bt)
dove R è un polinomio di grado r .
Se a + ib non è soluzione dell’equazione caratteristica ,allora una soluzione particolare dell’equazione non omogenea è data da
x(t) = eat(Q(t)sin(bt) + S(t)cos(bt)) dove Q e S sono polinomi di grado r.
Se a + ibè soluzione dell’equazione caratteristica di molteplicità m allora una soluzione particolare dell’equazione
non omogenea è data da:
x(t) = tmeat(Q(t)sin(bt) + S(t)cos(bt)) dove Q e S sono polinomi di grado
r.
Proposizione :Principio di sovrapposizione delle soluzioni. Sia
xi(i = 1, 2, . . . , k)
una soluzione dell’equazione di ordine n non omogenea con b(t) = fi(t),
allora x1+ x2+ x3+ . . . + xkè soluzione dell’equazione
anx(n)(t)+an−1x(n−1)(t)+...+a1x(1)(t)+a0x(t) = f1(t)+f2(t)+. . . +fk(t).
1.4.7 Sistemi lineari a coefficienti costanti
Un qualunque sistema lineare può essere ridotto ,con l’introduzione di nuove variabili ,ad un sistema del primo ordine in forma normale.
In alcuni casi è preferibile ridurre il sistema ad un’equazione in un’unica incognita(metodo di eliminazione).
Sistemi in forma normale
Dato un sistema nella sua forma matriciale x0 = Ax
con i, , j = 1, 2, 3, . . . , n e
x = (x1, . . . , xn)T
si può applicare il metodo di sostituzione.
Se si è interessati alla stabilità asintotica ,si cerca una soluzione x = eλta,
dove a è un vettore a componenti non tutte nulle.
Sostituendo la soluzione nell’equazione del sistema, dato che x0 = λeλta,risulta
che Aa = λa ovvero (A − λI)a = 0.
Se questa equazione ha una soluzione per a 6= 0 deve essere det(A − λI) = 0, cioè λ è un autovalore di A e a è l’autovettore corrispondente.
Teorema
(Caso1)Se esistono λ1,λ2,λ3,. . . ,λn autovalori distinti l’integrale generale
del sistema si scrive
x(t) = c1x1(t) + c2x2(t) + . . . + cnxn(t)
dove xj(t) = eλjtxjcon xjautovettore corrispondente a λj, j = 1, 2, . . . , n.
(Caso2) Mentre se λj è un autovalore con molteplicità mj le soluzioni
cor-rispondenti sono
xj(t) = eλjt(g1(t), g2(t), . . . ., gn(t))
doveg1(t), g2(t), . . . ., gn(t) sono polinomi di gradomj− 1.
I coefficienti di questi polinomi si trovano per diretta sostituzione nel sistema e utilizzando il principio di identità.
In questo caso se gli autovalori distinti sono p < n le soluzioni sono
x(t) = c1x1(t) + c2x2(t) + . . . + cpxp(t)
dove le xj sono della forma xj(t) = eλjt(g1(t), g2(t), . . . ., gn(t)).
Caso particolare:Sistema di 2 equazioni
Dato il sistema lineare di 2 equazioni differenziali del primo ordine
x0
1(t) = ax1+ bx2
x0
2(t) = cx1+ dx2
A è la matrice dei coefficienti A=
·
a b
c d
¸
L’equazione caratteristica è un polinomio di 2◦ grado con coefficienti pari
all’opposto della traccia e al determinante:
λ2− (a + d)l + (ad − bc) = 0
I = a + d (tracciadiA) e ∆ = ad − bc(determinante di A) . Sono possibili 3 casi:
Caso1:
I2> 4∆
ovvero ci sono 2 autovalori reali e distinti per la matrice A.
A λ1 facciamo corrispondere l’autovettore
a = (a1, a2)
e
a λ2 l’autovettore
b = (b1, b2)
La soluzione generale è :
x1(t) = c1a1eλ1t+ c2b1eλ2t
con c1, c2costanti arbitrarie.
x2(t) = c1a2eλ1t+ c2b2eλ2t.
Caso2:
I2= 4∆
ovvero la matrice ha un solo autovalore con molteplicità 2. -Se esistono 2 autovettori linearmente indipendenti la soluzione è
x1(t) = c1eλt∩ x2(t) = c2eλt
-Se esiste un solo autovettore indipendente a = (a1, a2) la soluzione è:
x1(t) = c1a1eλt+ c2(a1t + k1)eλt
x2(t) = c1a2eλt+ c2(a2t + k2)eλt
con c1, c2costanti arbitrarie e k1, k2da determinarsi per diretta sostituzione.
Caso3:
I2< 4∆
ovvero la matrice A ha come soluzioni una coppia di complessi e coniugati
m1= λ1+ iλ2 e m2= λ1− iλ2
a cui corrispondono gli autovettori
(a1+ ia2, b1+ ib2) e (a1− ia2, b1− ib2)
per cui la soluzione è data da :
x1(t) = eλ1t[c1(−a1sin(λ2t) + a2cos(λ2t)) + c2(a2sin(λ2t) + a1cos(λ2t))]
x2(t) = eλ1t[c1(−b1sin(λ2t) + b2cos(λ2t)) + c2(b2sin(λ2t) + b1cos(λ2t))].
1.4.8 Stabilità
Per la stabilità del punto x = 0 si deve verificare che le parti reali di tutti gli autovalori di A siano negative:
nel caso di 2 equazioni tale condizione verificata per I < 0 e ∆ > 0,
ma nel caso di più di due equazioni non è facile sapere quali siano le
con-dizioni di stabilità dato che non è agevole sviluppare det(A − λId).
Per le matrici simmetriche valgono tali criteri di stabilità: Criterio1:
x = 0
è stabile se e solo se la matrice è definita negativa:una matrice negativa ha tutti gli autovalori negativi.
Criterio2 : x = 0
è stabile se i coefficienti della diagonale principale sono negativi e ,in valore assoluto, maggiori della somma dei valori
assoluti degli elementi della stessa riga o colonna. Per j = 1, 2, . . . , n
ajj < 0
|ajj| > |a1j| + |a2j| + |a3j| + . . . . + |anj|oppure
|ajj| > |aj1| + |aj2| + . . . . + |ajn|.
Criterio3 :
x = 0
sia stabile è che la somma degli elementi della diagonale sia minore di zero: se tale condizione non è verificata la soluzione sicuramente non è stabile ,ma se anche fosse verificata ,
con questo solo criterio non si può assicurare la stabilità di x = 0.
1.5
La tecnica del piano delle fasi per sistemi lineari
bidi-mensionali autonomi
Dato un sistema della forma dx/dt = F (x, y)
dy/dt = G(x, y)
doveF e G sono funzioni continue di classe C1 definite in tutto il piano.
Si parla di sistemi autonomi poiché la variabile indipendente tempo non compare esplicitamente nelle funzioni
che definiscono il problema.
Le informazioni che otterremo saranno di natura qualitativa ,dato che è impossibile risolvere il problema in maniera esplicita.
Tali informazioni riguarderanno il comportamento ,la forma e le proprietà della soluzione.
Una soluzione dell’equazione
x(1)= f (x)
ha la forma x = x(t)
e viene descritta graficamente nel piano (t, x):
quindi una soluzione del sistema suddetto dovrebbe essere definita nello spazio (t, x, y).
Il fatto che il sistema è autonomo permette di semplificare tale descrizione , considerando la proiezione di una curva soluzione(t, x(t), y(t)) nel piano (x, y) che chiameremo spazio delle fasi ,
dove t è un parametro e x(t), y(t)la coppia di equazioni parametriche di una curva nel piano x, y.
Tale curva prende il nome di caratteristica,traiettoria oppure orbita,del sis-tema .
Ad ogni traiettoria t è associato un verso di percorrenza:
nella regione di piano in cui F > 0,sarà anche dx/dt > 0 per cui il verso di percorrenza è nel senso delle x crescenti.
Definizione:
Un punto(x0, y0)tale che F (x0, y0) = G(x0, y0) = 0 si chiama punto di
equi-librio o punto critico del sistema.
Infatti per il punto critico(x0, y0),essendo una soluzione costante del sistema
,passa una traiettoria che sul piano delle fasi si riduce ad un unico punto(x0, y0).
Un punto critico si dice isolato se esiste un suo intorno che non contiene altri punti critici .
Consideriamo il sistema lineare autonomo di due equazioni differenziali del primo ordine
dx/dt = −x dy/dt = −y.
Tale sistema ha come soluzioni le funzioni
x(t) = c1e−t, y(t) = c2e−t:
l’andamento di tali curve, esponenziali nello spazio(t, x, y) e lineari nel piano
delle fasi(x, y),si svolge intorno al punto critico isolato (x0, y0) = (0, 0).
Oltre ai punti critici ,altre traiettorie notevoli sono i cicli ,traiettorie costi-tuite da una curva chiusa.
Queste soluzioni provengono da soluzioni periodiche ovvero soluzioni per le quali esiste un tempo T tale che
x(T + t) = x(t) e
y(T + t) = y(t)
(inoltre tali soluzioni sono sempre definite per ogni t). Proposizione:
Nell’intorno di ogni punto ordinario ,cioè non critico,al sistema
x(1)= F (x, y)
y(1)= G(x, y)
è associata l’equazione differenziale che si ottiene dividendo un’equazione del sistema per l’altra.
Conseguenza di tale operazione è l’eliminazione della variabile tempo:
dx/dy = F (x, y)/G(x, y) se F 6= 0
oppure
dy/dx = G(x, y)/F (x, y) se G 6= 0.
La famiglia di curve ad un parametro,soluzione dell’equazioni trovate , cor-risponde almeno localmente con quella
delle traiettorie del sistema.
Poiché però il tempo è stato eliminato dalle equazioni trovate non si può leggere il verso di percorrenza.
Conseguenza del teorema di esistenza e unicità di Cauchy è che per ogni punto del piano passa una e una sola caratteristica.
Il teorema di esistenza e unicità per i sistemi implica che per ogni punto(T, ε1, ε2)passa
una e una sola curva soluzione (t, x(t), y(t)).
Inoltre se una caratteristica tende ad un punto critico (x0, y0)per t −→
T − (risp.t −→ T +)
allora deve essere T = +∞(T = −∞) , ovvero la soluzione corrispondente deve essere definita in un intorno di +∞(−∞).
Dimostrazione:
Supponiamo che per assurdo T sia finito e che x(t), y(t) sia una traiettoria
tale chex(t) −→ x0ey(t) −→ y0per t −→ T − :
si può prolungare la curva soluzione corrispondente(t, x(t), y(t))definendox(T ) =
x0 e y(T ) = y0.
In questo modo si ottengono due curve (t, x(t), y(t)) e (T, x0, y0) passanti
si è chiaramente in contrasto con la conclusione affermata in precedenza riguardante l’unicità della curva soluzione passante per un determinato punto.
1.5.1 Sistemi lineari:classificazione dei punti critici e loro stabilità
Le fasi di studio di un sistema autonomo sono le seguenti:
i) individuare i punti critici
ii) studiare il comportamento delle traiettorie vicino ai punti critici
iii) esaminare la stabilità dei punti critici
iv) individuare le orbite periodiche
Tale analisi è facilmente attuabile per i sistemi lineari , dove si conosce la formula per l’integrale generale.
Consideriamo il sistema
x(1)= ax + by
y(1)= cx + dy
con la condizione che det(A) = ad − bc 6= 0 :
in questo modo l’unico punto critico del sistema è (x0, y0) = (0, 0).
La matrice del sistema è A = · a b c d ¸ L’equazione caratteristica è λ2− (a + d)λ + (ad − bc) = 0 con traccia(A) = I = (a + d) e det(A) = ∆ = ad − bc
dove λè la somma degli autovalori e ∆ il loro prodotto:
ritornando ai criteri di stabilità precedentemente trattati risulta che (0, 0)è un punto critico stabile se I < 0, ∆ > 0.
Individuati i punti critici si passa allo studio del comportamento delle trai-ettorie in vicinanza di tali punti.
Distinguiamo 3 casi e 6 categorie considerando la soluzione dell’equazione
caratteristica λ1,2= (I/2) ±
√
(I2−4∆)
2 .
CasoA:
Due radici reali e distinte λ1, λ2con 4∆ < I2
Distinguiamo due sottocasi: A1:
∆ > 0,allora per il teorema del segno di Cartesio ,si può affermare che le
radici λ1, λ2 hanno lo stesso segno.
A2 :
∆<0,allora le radici hanno segno diverso .
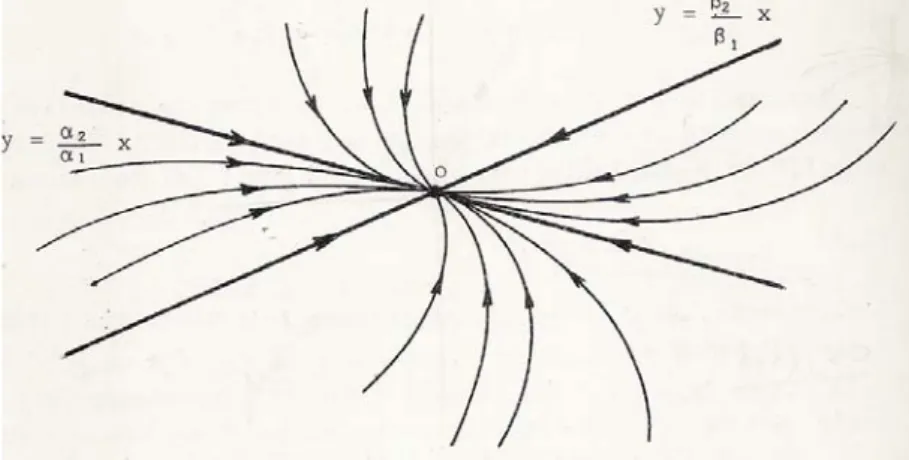
Esaminando il caso A1 e supposto che|λ1| < |λ2| ,a λ1corrisponde l’autovettore
Figure 1: Lo spazio delle fasi di un nodo stabile
La soluzione generale del sistema è in questo caso
x(t) = c1a1eλ1t+ c2b1eλ2t
y(t) = c1a2eλ1t+ c2b2eλ2t
con c1, c2costanti arbitrarie.
Se c1= 0e c26= 0
allora sarà
x(t) = c2b1eλ2t
y(t) = c2b2eλ2t:
dal loro rapporto ,eliminando così la variabile tempo (il sistema è autonomo ),si ottiene y(t)/x(t) = b2/b1 ovvero y = (b2/b1) x Se invece c16= 0e c2= 0 x(t) = c1a1eλ1t e y(t) = c1a2eλ1t:
procedendo allo stesso modo si ottiene
y(t)/x(t) = a2/a1
ovvero
y = (a2/a1)x.
Le equazioni delle semirette ritrovate sono delle traiettorie notevoli.
L’andamento delle altre soluzioni, c16= 0 e c26= 0,è soddisfatto dall’equazione
y(t)/x(t) = (c1a2eλ1t+c2b2eλ2t)/(c1a1eλ1t+c2b1eλ2t) =
(a2+ (c2/c1)b2e(λ1−λ2)t)
(a1+ (c2/c1)b1e(λ1−λ2)t)
Figure 2: Traiettorie per un nodo stabile sul piano delle fasi
Nel caso in cui λ2< λ1< 0
x(t) −→ 0 e y(t) −→ 0 per t −→ +∞ e inoltre y/x −→ a2/a1 poiché e(λ1−λ2)t−→ 0 per t −→ +∞.
Il punto di equilibrio asintotico(0, 0) è stabile e prende il nome di nodo a 2 tangenti .
Nel caso in cui 0 < λ1< λ2 la tangenza alla retta
y/x −→ a2/a1si ha per t −→ −∞
le freccie del grafico risultano invertite ed (0, 0) è un punto instabile di equilibrio dinamico.
Dalla figura si denota che y = (b2/b1)x è composta da tre traiettorie del
sistema :
l’origine(punto critico)e le due semirette uscenti dall’origine stessa. Analoghe conclusioni si ottengono per l’equazione
y = (a2/a1)x.
Per il caso A2,
∆ < 0 con radici che hanno segno diverso,supponiamo λ1< 0 < λ2.
Le semirette
y = (b2/b1)x
y = (a2/a1)x
sono ancora traiettorie ,ma analizzando le altre soluzioni, c16= 0e c26= 0,
y/x −→ a2/a1per t −→ −∞
Figure 3: Traiettorie sul piano delle fasi perr un punto di sella
y/x −→ b2/b1per t −→ +∞:
queste traiettorie quindi non tendono al’origine come per il nodo.
In questo caso il punto critico (0,0) prende il nome di colle ed è un punto di equilibrio dinamicamente instabile
Ecco come si presentano le traiettorie per il caso λ1 < 0 < λ2,con(0, 0)colle
instabile: Caso B :
4∆ = I2.In questo caso la soluzione dell’equazione caratteristica ci fornisce
un solo autovalore con molteplicità 2.
Esistono,anche in questo caso,2 sottocasi dovuti al fatto che non sempre esistono 2 autovettori indipendenti se λ ha molteplicità 2.
CasoB1 : Se b = c = 0 −→ 4ad = (a + d)2−→ (a − d)2 = 0 −→ a = d = λesistono 2 autovettori indipendenti. Il sistema diventa x0 = λx y0 = λy
che ha come soluzioni
x(t) = c1eλt
e
y(t) = c2eλt
Se c1= 0, c26= 0
allora
y(t)/x(t) = c2eλt/c1eλt−→ +∞ per c2 > 0(semiasse positivo delle ascisse)
e a −∞ per c2< 0(semiasse negativo delle x).
Figure 4: Piano delle fasi di un nodo a stella stabile
c16= 0,
allora
y(t)/x(t) = c2/c1.
La configurazione delle traiettorie nel caso B1 è di un nodo a stella stabile nel caso in cui λ è negativo,instabile per λ positivo.
Caso B2 :
se b2+ c26= 0 esiste un solo autovettore indipendente
A λ facciamo corrispondere l’autovettore(a1, a2) .
In questo caso la soluzione generale del sistema è data da
x(t) = c1a1eλt+ c2(a1t + k1)eλt
e
y(t) = c1a2eλt+ c2(a2t + k2)eλt
con k1, k2 opportuni e le c costanti arbitrarie.
Se c16= 0, c2= 0
y/x = a2/a1
che risultano traiettorie del sistema,
per le altre si osserva che y/x =⇒ a2/a1pert −→ +∞ se λ < 0,lo stesso
rapporto y/x −→ a2/a1per t −→ −∞ seλ > 0.
Il punto di equilibrio dinamico (0, 0) ,per il caso B2,prende il nome di nodo ad 1 tangente:
l’equilibrio sarà stabile con λ < 0(come nel caso mostrato dalla figura)o instabile se λ > 0
(il verso di percorrenza del grafico dovrebbe essere invertito in questo caso). Caso C :
Figure 5: Piano delle fasi per un nodo a 1 tangente
4∆ > I2 .In questo caso esistono 2 autovalori complessi e coniugati λ
1 =
u + iv e λ2= u − iv.
Anche per il caso C esistono i sottocasi C1 e C2 :
siamo nel caso C1 seλ = 0 −→ u = 0 : le soluzioni sono immaginari puri,mentre se λ 6= 0 (caso C2 ) il numero complesso ha anche parte reale u 6= 0.
Caso C1 :
Poiché λ=a + d = 0 −→ a = −d Il sistema può essere riscritto come
dy/dx = (cx − ay)
(ax + by) −→ (cx − ay)dx − (ax + by)dy = 0
che è un’equazione esatta : (cx − ay)/y = (−(ax + by))/x.
Per cui integrando si ottiene cx2− 4axy − by2= costante che è una famiglia
di ellissoidi
(curve chiuse=traiettorie periodiche centrate sull’equilibrio dinamico(0, 0)che prende il nome di centro).
Caso C2 :
La parte reale del numero complesso è diversa da zero Re(λ) 6= 0 −→
b2+ c26= 0
La soluzione generale è data,facendo corrispondere gli autovettori (a1 +
ia2, b1+ ib2)e (a1− ia2, b1− ib2), da
x(t) = eut[c1(−a1sin(vt) + a2cos(vt)) + c2(a2sin(vt) + a1cos(vt))]
y(t) = eut[c
1(−b1sin(vt) + b2cos(vt)) + c2(b2sin(vt) + b1cos(vt))]
da cui,dividendo per il cos(vt) risulta che
y(t)/x(t) = (c1b1+ c2b2− (c1b2+ c2b1)tg(vt))
(c1a1+ c2a2− c1a2+ c2a1)tg(vt)
Figure 6: Piano delle fasi per un centro
Figure 7: Piano delle fasi per un fuoco stabile
Se u < 0 allora le traiettorie tendono al punto critico (0, 0) per t−→+∞,se invece u > 0 allora le traiettorie tendono
a (0, 0)per t −→-∞,mentre il rapporto y/x non ha limite ed oscilla tra +∞ e -∞ sia per t −→ +∞,sia pert −→ −∞.
L’andamento delle traiettorie è una spirale,vortice o fuoco attorno al punto (0, 0) .
Nel grafico è mostrata una spirale che si avvolge sul punto d’equilibrio stabile (0, 0)dato che u < 0,
il verso di percorrenza è in senso opposto quando u > 0 con (0, 0)punto di equilibrio asintoticamente instabile.
Con l’analisi di quest’ultimo caso si conclude lo studio dei sistemi lineari bidimensionali autonomi di equazioni
Figure 8: Possibili traiettorie per un sistema lineare autonomo
differenziali del primo ordine.
Può comunque risultare utile un’immagine che considera tutti i risultati raggiunti.
1.6
Sistemi non lineari
1.6.1 Linearizzazione
La natura di gran parte dei fenomeni reali è di carattere non lineare,per cui anche il modello matematico corrispondente
sarà non lineare.
Si considera un sistema del tipo x0 = F (x, y)
y0 = G(x, y) con F e G funzioni non lineari
Per risolvere un sistema autonomo bidimensionale non lineare si può ricorrere ad un metodo di linearizzazione .
L’idea principale di tale tecnica è quella di considerare che se(0, 0) è un punto critico isolato ,si potrebbero sviluppare le funzioni F e G con la formula di Mac Laurin e scrivere il sistema come:
x0 = ax + by + o(x, y) y1 = cx + dy + o(x, y)
e o(x, y) è un termine di grado superiore o uguale a 2.
Se le (x, y)sono vicine all’origine ,i termini di secondo grado sono più piccoli rispetto a quelli di primo:
si può allora congetturare che i termini di grado superiore al primo sia trascurabili in modo che sia plausibile
pensare che il comportamento delle traiettorie ,in un intorno di (0, 0),del sistema non lineare sia simile a quello del sistema linearizzato associato:
x0= ax + by
y0= cx + dy.
Il sistema non lineare può essere in questo senso riscritto come: x0 = ax + by + f(x, y)
y0 = cx + dy + g(x, y)
dove f e g sono funzioni perturbanti il sistema lineare. Ipotesi: Ipotesi1: ad − bc 6= 0 Ipotesi2: f (x, y) p (x2+ y2)−→ 0, g(x, y) p (x2+ y2) −→ 0 per (x, y) −→ 0 Ipotesi3:
f (x, y) e g(x, y)sono funzioni continue con la loro derivata prima in un in-torno di (0, 0).
Date tali ipotesi si può affermare che queste sono certamente verificate se f e g sono polinomi di grado superiore o uguale al secondo e che il punto(0, 0)è un punto critico isolato.
Se delle tre valgono solo le prime due ipotesi, il punto (0, 0) è detto punto critico semplice,poiché non è garantito che
tale punto sia l’unico critico nel suo intorno ,dato che non si assicura la continuità delle funzioni e delle rispettive derivate prime .
L’ipotesi 2 assicura che ,se (x, y) −→ 0 allora f e g −→ 0(tendono a zero) più velocemente di un polinomio di primo grado .
Se il punto critico è diverso dall’origine ,può essere conveniente applicare una traslazione degli assi tramite un cambio di
variabile che porti il punto critico(x0,y0) all’origine dei nuovi assi:
X = x − x0
Y = y − y0 .
Effettuata la traslazione si possono usare tutti i risultati raggiunti per (0, 0). E’ possibile quindi analizzare il comportamento locale di un sistema non-lineare nell’intorno di un punto fisso tramite
l’approssimazione del sistema in uno lineare associato :l’approssimazione è fatta tramite l’esansione di Taylor che risulta
f (x) = f (xf) + 1!1 df (xf) dx (x − xf) + 1 2! d2f (x f) dx2 (x − xf) 2+ 1 3! d3f (x f) dx3 (x − xf)3+ ... +n!1 dnf (x f) dxn (x − xf) n
Il sistema si presenta quindi nella forma linearizzata come :
x0 = f(xf) + Jx=xf(x − xf)
1.6.2 Sistemi espressi in coordinate polari
Un’altra utile trasformazione del sistema è quella in coordinate polari dove
x = ρcos(θ), y = ρsin(θ)con ρ =p(x2+ y2.
In questo modo si comprende che ρ rappresenta la distanza euclidea dall’origine ,
mentre q è l’angolo che il vettore (x, y) forma con il semiasse positivo delle ascisse,
y/x = tg(θ).
Riscrivendo la seconda ipotesi per le coordinate polari risulta f (ρcosθ, ρsinθ) = o(ρ)
e
g(ρcosθ, rsinθ) = o(ρ) per
ρ −→ 0 Il sistema
x0 = ax + by + f(x, y) y0 = cx + dy + g(x, y)
si trasforma in due nuove funzioni incogniteρ(t)e θ(t):
dalla relazioneρ2= x2+ y2, derivando ambo i membri rispetto a t si ottiene
2ρρ(1)= 2xx(1)+ 2yy(1)−→ ρρ(1)= xx(1)+ yy(1),
mentre da y/x = tg(θ)si ottiene allo stesso modo (1+tg2θ)θ(1) =(y(1)x − yx(1))
x2 −→
(1 + (y2/x2))θ(1) = (y(1)x − yx(1))/x2−→ ρ2θ(1)= (y(1)x − yx(1)).
Sostituendo nel sistema x = ρcosθ, y = ρsin(θ) si ottengono le seguenti espressioni:
x0 = aρcos(θ) + bρsin(θ) + f(ρcos(θ), ρsin(θ)) y0 = cρcos(θ) + dρsin(θ) + g(ρcos(θ), ρsin(θ)).
La stabilità del punto critico (0, 0)è ora assicurata per ρ(t) −→ 0per t −→ +∞.
La funzione θ(t) esprime la direzione con cui le traiettorie arrivano all’origine (se vi arrivano):
se θ(t) −→ ±∞ la traiettoria gira infinite volte attorno l’origine(più precisa-mente in senso antiorario se θ(t) −→ +∞
e in senso orario per θ(t) −→ −∞ .
Quindi se ρ(t) −→ 0 e θ(t) −→ ±∞ il punto critico è una spirale.
Se invece θ(t) −→ θ0per t −→ +∞ la traiettoria nel tempo assume una
direzione definita,
1.6.3 Punti critici semplici Si considera il sistema
x0 = ax + by + f(x, y) y0 = cx + dy + g(x, y)
e si suppone che (0, 0)è un punto critico semplice.
i) (0, 0) è attrattore se esistono un δ e uno t0tali che ogni caratteristica
x(t), y(t), avente un punto all’interno
del cerchio di centro (0,0) e raggio δ, è definita per t > to(risp.t < to)e r(t) −→ 0per t −→ +∞(risp.t −→ −∞).
In altre parole la definizione vuole dire che l’origine è attrattore se ogni
caratteristica che passa sufficientemente vicino a (0, 0) vi tende
per t −→ ±∞.
ii) (0, 0) è un nodo se per il sistema è attrattore e se tutte le
caratteris-tiche che arrivano all’origine lo fanno con
una direzione definita:se tale direzione è uguale per tutte le caratter-istiche allora siamo di fronte ad un nodo ad 1 tangente,
se è la stessa per tutte tranne che per due allora si tratta di un nodo a 2 tangenti ,
se ogni semiretta uscente dall’origine è tangente ad una caratteristica il punto critico è un nodo a stella.
iii) (0,0) è un fuoco per il sistema se è attrattore e se |q(t)| −→ +∞ per
t −→ ±∞.
iv) (0,0) è un centro per il sistema se esiste una successione di orbite
chiuse{Gn}che contengono le successive
e l’origine e tali che ,per n −→ +∞, Gn si stringe intorno all’origine.
v) (0, 0) è un colle per il sistema se due caratteristiche arrivano a (0, 0)
per t −→ +∞,altre due arrivano per t −→ −∞,
mentre le altre hanno un andamento simile a quello lineare almeno in un intorno di (0,0).
Teorema
(Relazioni tra sistema non lineare e sistema lineare associato)
i) Se (0, 0) è attrattore per il sistema lineare
x0 = ax + by y0 = cx + dy
allora è attrattore anche per il sistema non lineare x0 = ax + by + f(x, y)
y0 = cx + dy + g(x, y)
ii) Se (0,0) è un colle , un fuoco , un nodo a 1 o 2 tangenti per il sistema
lineare allora (0,0) è dello stesso tipo per il sistema x0 = ax+by+f(x, y)
y0 = cx + dy + g(x, y).
La perturbazione di un nodo a stella o di un centro è più delicata dal punto di vista delle ipotesi per la particolarità
Per il nodo a stella l’ipotesi ii) va leggermente modificata per ottenere il seguente teorema:
a) Sia
f = o(ρ1+ε)
g = o(ρ1−ε)
per ρ>0 con ε>0 opportuno.
Se (0,0) è un nodo a stella per il sistema lineare allora lo è anche per il sistema
x0 = ax + by + f(x, y) y0 = cx + dy + g(x, y)
b) Se (0,0) è un centro per il sistema lineare allora potrebbe essere un
fuoco o un centro per il sistema non lineare .
1.7
Orbite chiuse .
1.7.1 Teoremi di Bendixon e Poincarè
Le orbite chiuse sono traiettorie generate da soluzioni periodiche. Se (0,0) è un centro,esso è circondato da infinite orbite chiuse. Nel caso di sistemi non lineari possono esistere orbite chiuse isolate . Esempio:
Consideriamo il sistema
x(1)= −y + x(1 − x2− y2)
y(1)= x + y(1 − x2− y2)
Per la trasformazione in coordinate polari consideriamo che
θ(1)(t) =(y (1)x − yx(1)) ρ2 , ρ(1)(t) = (xx(1)+ yy(1))/ρ, con x = ρcos(θ) e y = ρsin(θ): il sistema diventa θ(1)(t) = 1 ρ(1)(t) = ρ(t)(1 − ρ2(t))
che integrato porta a dire che
θ(t) = t + qo
e
ρ(t) = (1 + ρoe−2t)−1/2con θ
o, ρo costanti arbitrarie.
Se ρo= 0 allora ρ(t) = 1
con θ(t) = t + θo che rappresenta un cerchio con raggio uguale a 1 e centro
(0, 0):
si è così trovata un ‘orbita chiusa .
Figure 9: Traiettorie del sistema non lineare
mentre per t −→ +∞ =⇒ ρ(t) −→ 1 (quindi una spirale interna all’orbita
chiusa trovata si allontana dal centro (0,0) per avvicinarsi all’orbita trovata ).
Se ρo< 0allora le orbite sono definite solo per t > 1/2log|ρo|e r(t) −→ 1 per
t −→ +∞ .
In questo caso (0,0) è un fuoco.
In letteratura le orbite chiuse su cui si avvolgono a spirale orbite circostanti prendono il nome di cicli limite(limit cycle).
Un ciclo limite è stabile se le spirali si avvicinano al ciclo limite per t −→ +∞ sia dall’interno che dall’esterno,
semistabile se solo da una delle due parti ,instabile negli altri casi. Teoremi sull’esistenza dei cicli limite
Teorema 1:
Un’orbita chiusa contiene necessariamente un punto critico. Teorema di Bendixon:(Test Bendixon-Dulac)
Se (∂F
∂x+
∂G
∂y ) è sempre maggiore di zero o sempre minore di zero in una
regione D del piano x,y,
allora il sistema non può avere orbite chiuse in D . Teorema di Poincarè-Bendixon:
Sia D una regione del piano delle fasi che non contiene punti critici per il sistema
dx/dt = F (x, y) dy/dt = G(x, y).
Se x(t), y(t)è un’orbita che penetra in D e rimane in D per t −→ +∞(o per t −→ −∞) allora :
o x(t), y(t) è chiusa o si avvolge a spirale attorno ad un’orbita chiusa per
Figure 10: Stabilità di Liapunov e asintotica
1.7.2 Stabilità
Mentre per i sistemi lineari il punto (0,0) è asintoticamente stabile se ogni trai-ettoria tende all’origine per t −→ +∞
indipendentemente dalla condizione iniziale,tale indipendenza non è invece prerogativa dei sistemi non lineari.
Per la stabilità asintotica di sistemi non lineari bisogna distinguere tra sta-bilità asintotica globale e stasta-bilità asintotica locale.
Dato il sistema bidimensionale autonomo dx/dt = F (x, y) = ax + by + f (x, y) dy/dt = G(x, y) = cx + dy + g(x, y) ,
supponiamo che (0,0) sia un punto critico per il sistema . Definizione1 :
Il punto critico (0,0) si dice localmente asintoticamente stabile se esiste un δ tale che per ogni soluzione x(t), y(t)
che soddisfa le condizioni iniziali
x(to) = xo, y(to) = yo
con
x2+ y2< δ2 ,esistente per t > t0,(x(t), y(t)) −→ (0, 0) per t −→ +∞.
In altre parole (0,0) si dice localmente asintoticamente stabile se ogni punto che passa sufficientemente
vicino a (0,0) è tale che (x(t), y(t)) −→ (0, 0)per t −→ +∞.
Definizione 2 :
Il punto critico (0, 0) si dice globalmente asintoticamente stabile se per ogni soluzione x(t), y(t)
definita in un intorno di +∞,
si ha che (x(t), y(t)) −→ (0, 0) per t −→ +∞ ,indipendentemente da quanto sia vicina a (0, 0) all’istante iniziale.
La tecnica di linearizzazione permette di ottenere informazioni riguardanti la stabilità locale per un punto critico semplice
Figure 11: Sottospazio lineare invariante
di un sistema non lineare.
Teorema(sulla stabilità asintotica locale): Sia (0, 0)un punto critico semplice per il sistema dx/dt = F (x, y) = ax + by + f (x, y)
dy/dt = G(x, y) = cx + dy + g(x, y).
Se (0, 0) è asintoticamente stabile per il sistema linearizzato, allora è local-mente asintoticalocal-mente stabile per il sistema non lineare.
Teorema di Liapanov (sulla stabilità globale): Definizione:
Una funzione E = E(x, y)continua con le sue derivate prime in R2,si chiama
funzione di Liapanov per il sistema dx/dt = F (x, y) = ax + by + f (x, y)
dy/dt = G(x, y) = cx + dy + g(x, y) se soddisfa le seguenti proprietà:
i) E(x, y) >= 0, E(x, y) = 0se e solo sex = y = 0
ii) E(x, y) −→ +∞ se x −→ +∞ o y −→ +∞
iii) ∂E
∂xF +
∂E
∂yG < 0 per ogni (x, y) appartenente a R
2 .
Per la proprietà i) si può affermare che la funzione di Liapanov è definita positiva (come le funzioni distanza).
L’espressione ∂E ∂xF + ∂E ∂yG = ∂E ∂t = ∂E ∂xx 0+∂E ∂yy 0
rappresenta le variazioni di E lungo le traiettorie del sistema .
Il Teorema di Liapunov afferma che se (0,0) è un punto critico per il sistema non lineare
dx/dt = F (x, y) = ax + by + f (x, y) dy/dt = G(x, y) = cx + dy + g(x, y)
allora condizione necessaria e sufficiente affinché la soluzione sia globalmente asintoticamente stabile è che esista
Figure 12: Ciclo limite in un insieme compatto D
In altre parole sia D è una regione del piano delle fasi che non contiene punti critici:
se (x(t), y(t)) è una un’orbita che penetra in D e lì rimane per t−→ ±∞ allora (x(t), y(t)) o è un’orbita chiusa ,o si avvolge a spirale intorno ad un’orbita chiusa (limit cycle)per t−→ ±∞.
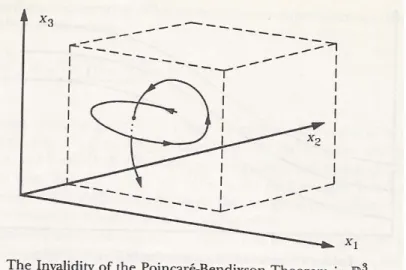
Il teorema di Liaponov non è valido per sistemi di dimensioni superiori a due :quando la dimensione è due il piano può essere diviso in una regione interna ed una esterna ,le traiettorie possibili nello spazio rendono concettualmente diverso il problema.
Il teorema di Poicarè-Bendixon non esclude l’esistenza di più cicli limite :determinare il numero di cicli limite esistenti non è possibile
con le conoscenze per problemi bidimensionali.
Esistono criteri per assicurare l’unicità del ciclo limite esistente tramite la "generalized Lienard Equation"
Figure 13: Invalidità del teorema di Liapunov in R3
Part II
Modelli dinamici introduttivi
2
Analisi dinamica per i modelli di Lotka-Volterra
e Anderson-May
2.1
Il modello di Lotka-Volterra(popolazioni conviventi con
predazione)
2.1.1 Introduzione
Il modello di Lotka-Volterra ci introduce ai processi biomatematici che legano popolazioni conviventi nello stesso ambiente:
per analizzare tale problema si assume che le popolazioni interagenti siano in un ambiente isolato .
Tale modello è esemplificativo dell’esistenza di orbite chiuse in dinamica :secondo il teorema di Hirsch-Smale
ogni traiettoria del sistema base Lotka -Volterra è un’orbita chiusa eccetto il punto fisso(c/d,a/b).
Conseguenza del teorema è che queste orbite chiuse bnon possono essere cicli -limite .
Nella presentazione base del sistemasi riscontra una periodicità delle flut-tuazioni del numero delle specie interagenti:
il sistema è in questo caso conservativo .
Un sistema conservativo è anche detto "area preserving"o "volume preserving "se la dimensione è maggiore di tre.
L’introduzione del principio di competizione tra specie muta i risultati di-namici :l’andamento temporale del numero
delle popolazioni conviventi presenta oscillazioni smorzate per determinati valori dei parametri :
il sistema diventa in tal senso è detto dissipativo,avviene cioè una contrazione dell’area racchiusa
dalle traiettorie-soluzioni .
2.1.2 Assunzioni
Si consideri un biosistema composto da due popolazioni x, y di cui una si ali-menta dell’altra :
d’ora in avanti x rappresenta la popolazione preda e y quella dei predatori . Devono essere poste ipotesi sull’interazione delle due specie affinché il mod-ello sia chiaramente descrittivo
del problema della predazione.
La prima ipotesi è che in assenza della popolazione dei predatori ,le prede crescono esponenzialmente al tasso