CAPITOLO 4: VERIFICA IDRAULICA DELLA RETE

80

CAPITOLO 4: VERIFICA IDRAULICA DELLA RETE

4.1 SOFTWARE PER SIMULAZIONI IDRAULICHE (HEC-RAS)

Il software per le simulazioni idrauliche adottato per il presente lavoro è l'HEC-RAS 3.1.3. Questo modello, sviluppato nel 2002 presso l'U.S. Army Corps of Engineers sul codice di calcolo UNET, gode oggi di una vasta diffusione grazie alle vaste potenzialità offerte. Proprio alla sua diffusione, incentivata da una distribuzione di tipo freeware, si deve la stima posta su un prodotto considerato ampiamente collaudato. HEC-RAS adotta una schematizzazione monodimensionale (variazioni graduali della sezione dell’alveo, limitata curvatura dei filetti liquidi, distribuzione di velocità pressoché uniforme nelle sezioni trasversali) su alveo assunto a fondo fisso sia per il moto permanente che per quello vario (non stazionario). A livello di schematizzazione di un bacino, HEC-RAS gestisce la modellazione di più tronchi fluviali con la rappresentazione delle confluenze secondo diversi approcci teorici (metodo dei momenti, metodo dell'energia) a seconda delle portate e delle angolazioni presenti nei singoli casi. A tale proposito, oltre al caricamento di una portata da una sezione di monte e nei pressi di un'immissione localizzata, è anche possibile gestire immissioni di portate distribuite (versamento dalle pendici).

L’interfaccia utente (Graphical User Interface GUI) permette un agevole inserimento di dati e una pronta analisi dei risultati e la possibilità di georefenziare le sezioni introdotte permette una intuitiva rappresentazione grafica dei risultati.

Il modello di moto permanente, costruito con il codice di calcolo HEC-RAS permette di valutare tutte le grandezze idrauliche di interesse per una corrente gradualmente variata in regime subcritico, supercritico o misto.

Tale codice è basato essenzialmente sull’integrazione, alle differenze finite, dell’equazione dell’energia di una corrente. Nella simulazione del moto vario il modello risolve le equazioni complete di de St. Venant utilizzando uno schema di risoluzione implicito alle differenze finite. Tale schema di calcolo è stato sviluppato per il moto vario in corrente subcritica.

Lo schema di risoluzione utilizza il metodo di Newton-Raphson iterativo per risolvere equazioni non lineari. Tale codice di calcolo, comunque, pur utilizzando

81

una soluzione linearizzata, per una corrente subcritica fornisce risultati affidabili e stabili, avendo l’accortezza di utilizzare intervalli di calcolo sufficientemente ridotti. Permette inoltre di simulare in modo efficace le singolarità introdotte nel modello: ponti, tratti tombinati, invasi in linea e in derivazione, sfioratori in linea, sfioratori laterali, luci a battente.

I limiti applicativi sono invece rappresentati dalla impossibilità di simulare l'inondazione di territori extra-alveo. Non è infatti supportato lo studio di fenomeni di trasferimento bidimensionale. Si deve qui notare che nella fase computazionale le sezioni sono assunte ortogonali alla direzione della corrente idrica.

Per il calcolo delle perdite di carico distribuite si utilizza l'equazione di Manning che risulta: 3 4 2 2 R n v Sf ⋅ = dove

Sf = perdita di carico distribuita per unità di percorso;

v = velocità media della corrente ;

n = coefficiente di scabrezza;

R = raggio idraulico della sezione (rapporto tra l'area liquida ed il contorno bagnato);

Considerando che in letteratura tecnica la portata della corrente liquida può essere rappresentata dalla seguente espressione:

2 1 f

S

K

Q

=

⋅

dove il termine K definito conveyance (esso misura l’attitudine di una data sezione a far defluire le portate) diviene, tenendo conto della formula di Manning e introducendo l’area A della sezione liquida

82 3 2 1 R A n K = ⋅ ⋅

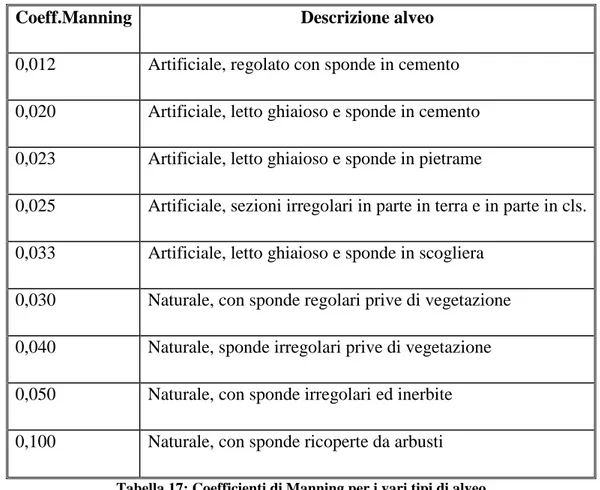
Per i valori dei coefficienti di Manning è di seguito riportata la Tabella 17 riassuntiva per i principali tipi d'alveo (V.T. Chow, D. Maidment, L.W. Mays - Applied Hydrology, McGraw-Hill).

Coeff.Manning Descrizione alveo

0,012 Artificiale, regolato con sponde in cemento

0,020 Artificiale, letto ghiaioso e sponde in cemento

0,023 Artificiale, letto ghiaioso e sponde in pietrame

0,025 Artificiale, sezioni irregolari in parte in terra e in parte in cls.

0,033 Artificiale, letto ghiaioso e sponde in scogliera

0,030 Naturale, con sponde regolari prive di vegetazione

0,040 Naturale, sponde irregolari prive di vegetazione

0,050 Naturale, con sponde irregolari ed inerbite

0,100 Naturale, con sponde ricoperte da arbusti

Tabella 17: Coefficienti di Manning per i vari tipi di alveo

Qui di seguito vengono descritte sommariamente le basi teoriche delle due procedure utilizzate .

4.1.1 MOTO PERMANENTE

La procedura di calcolo si basa sulla soluzione dell'equazione del moto permanente gradualmente variato con un metodo alle differenze finite. L’equazione differenziale del profilo liquido di una corrente in moto permanente gradualmente variato risulta la seguente:

83 f S ds dH ₌₋ con:

g

v

z

H

⋅

+

=

2

H = carico totale della corrente nella sezione generica di ascissa s misurato rispetto ad un riferimento orizzontale;

Sf = perdita di carico unitaria dovuta alle resistenze continue;

z = quota del pelo liquido misurato rispetto ad un riferimento orizzontale;

v = velocità media della corrente nella sezione generica di ascissa s;

g = accelerazione di gravità.

Passando alle differenze finite, tra due sezioni distanti Δs, l’equazione differenziale può essere scritta come:

s S H

H₂ − ₁ =− _fm ⋅∆

in cui:

H1 = carico totale della corrente nella sezione iniziale;

H2 = carico totale della corrente nella sezione finale;

Sfm = perdita di carico unitaria dovuta alle resistenze continue media tra le due sezioni.

Tenendo conto del legame esistente tra il carico totale e la componente potenziale e cinetica, indicando con i pedici 1 e 2 rispettivamente le grandezze relative alla sezione iniziale e quelle relative alla sezione finale l’equazione diviene:

84

0

2

2

2

⋅

∆

=

+

+

⋅

−

−

⋅

+

J

J

s

g

v

z

g

v

z

0

2

1

2

2

⋅

∆

=





















⋅

⋅

+

⋅

⋅

⋅

+

⋅

⋅

−

−

⋅

⋅

+

s

R

A

n

Q

R

A

n

Q

A

g

Q

z

A

g

Q

z

A1 = area liquida della corrente nella sezione iniziale;

A2 = area liquida della corrente nella sezione finale.

Essendo le caratteristiche geometriche di una data sezione funzione della sola altezza liquida, l’equazione permette di determinare la quota liquida nella sezione terminale di un tratto di corrente di lunghezza Δs una volta che sia nota la quota liquida in corrispondenza della sezione iniziale (condizione al contorno). L’equazione rappresenta quindi un’equazione non lineare in cui l’incognita è rappresentata dal valore z2 della quota liquida finale. Per la determinazione del profilo liquido relativo ad un dato tronco di un corso d’acqua, occorre suddividere tale tronco in una successione di tratti delimitati da sezioni di cui sia nota la geometria. Partendo quindi da una delle sezioni estreme, in cui deve essere noto il valore della quota liquida (condizione al contorno), l’applicazione reiterata dell’equazione permette di determinare le quote liquide nelle sezioni successive. Il modello permette la determinazione del profilo liquido secondo tre schemi di calcolo e precisamente: • Corrente lenta (subcritical flow)

• Corrente veloce (supercritical flow) • Corrente mista (mixed flow)

85

Il primo schema, che è applicabile quando la corrente è ovunque lenta e presenta quindi in tutte le sezioni di calcolo un’altezza liquida maggiore dell’altezza critica, richiede che la condizione al contorno sia posta in corrispondenza della sezione estrema di valle del tratto considerato. Il secondo schema, che è applicabile quando la corrente è ovunque veloce e presenta quindi in tutte le sezioni di calcolo un’altezza liquida minore dell’altezza critica, richiede che la condizione al contorno sia posta in corrispondenza della sezione estrema di monte del tratto considerato. Il terzo schema, deve essere utilizzato quando nel tratto in esame si possono verificare transizioni da un tipo di corrente all’altro, dando luogo ad una successione di tronchi con differenti caratteristiche di moto, che nel caso di transizione da corrente veloce a lenta porteranno alla formazione di risalti idraulici. Tale schema richiede che siano definite due diverse condizioni al contorno in corrispondenza delle due sezioni estreme (di monte e di valle) del tratto considerato. Nel caso di simulazioni in moto permanente sarà dunque sufficiente fornire il valore della portata in ingresso nella stazione di monte, eventuali cambiamenti della stessa dovuti a immissioni localizzate o distribuite, e le condizioni al contorno per le sezioni di chiusura del tronco in esame. Per la soluzione dell'equazione monodimensionale dell'energia le perdite di carico sono determinate, come detto in precedenza, tramite l'equazione di Manning e, corrispondenza di brusche variazioni di velocità dovute ad irregolarità d'alveo, tramite appositi coefficienti di espansione/contrazione. Irregolarità idrauliche (salti di fondo, confluenze, sbarramenti) nelle quali si viene a determinare un brusca variazione nel profilo del pelo libero della corrente, sono modellate attraverso la conservazione della spinta totale.

4.1.2 MOTO VARIO

Il solver di equazione a moto vario si è adattato al modello UNET (Barkau, 1992 e HEC, 1997). La componente di flusso instabile è stata sviluppata soprattutto per i calcoli di regime di flusso subcritico.

I calcoli idraulici per le sezioni trasversali, i ponticelli, i canali sotterranei ed altre strutture idrauliche che sono state sviluppate per la componente di flusso costante sono stati compresi nel modulo di flusso instabile.

86

I dispositivi speciali della componente di moto vario includono: Analisi della rottura della diga; argini che aprono un varco e che overtopping; Stazioni di pompaggio; funzionamenti della diga di navigazione; e reti di tubazioni pressurizzate.

4.2 SCHEMI IDRAULICI DI VERIFICA

Sul programma non è stata riportata la rete nella sua completezza ma solo i canali principali e precisamente gli stessi due tratti che sono stati schematizzati su HEC-HMS; infatti dai nodi introdotti in quest’ultimo programma è stato possibile reperire le portate da introdurre su HEC-RAS. Si è proceduto alla verifica idraulica della rete dei canali per il tempo di ritorno di ritorno pari a 25 anni (franco = 0.30 m).

4.2.1 ANALISI A MOTO PERMANENTE Il procedimento di lavoro è stato il seguente:

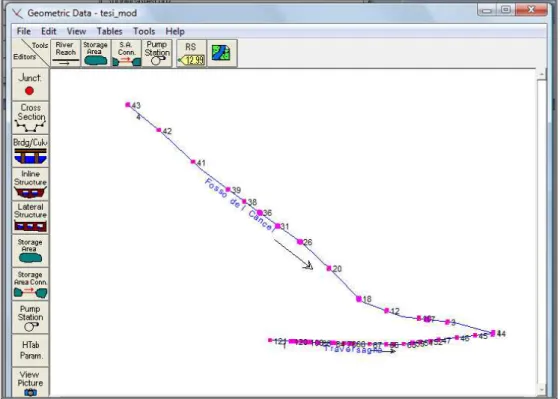
• creazione della ‘Geometry Data’ (Figura 31), con inserimento delle sezioni di progetto, della distanza della sezione considerata da quella di valle, del coefficiente di Manning e dei ‘Levees’, cioè dei margini (sia orizzontali che verticali) entro i quali può defluire l’acqua.

87

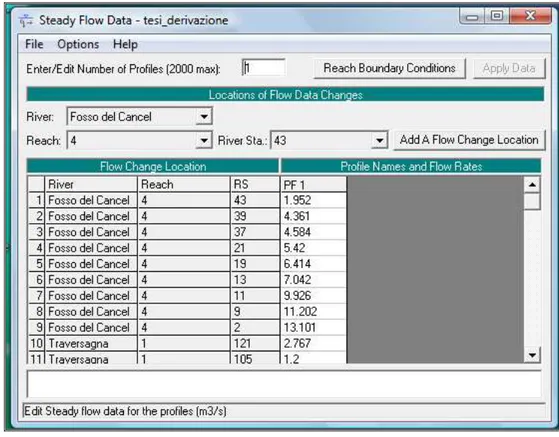
• immissione dei valori della portata nel file ‘Steady Flow Data’ (Figura 32). Dall’ immagine sottostante si vede che i cambiamenti di portata vengono inseriti in corrispondenza delle sezioni interessate. I valori della portata introdotti nei vari tratti sono pari ai picchi degli idrogrammi di piena ricavati precedentemente su HEC-HMS. Tale condizione sarà sicuramente la più gravosa, poiché considera in un certo istante che nei canali ci siano le portate massime. Da questa finestra devono essere fornite anche le condizioni al contorno, che per la rete studiata, essendo a debole pendenza e quindi comandata da valle, è stata introdotta l’altezza liquida nella sezione più a valle, cioè quella prossima all’impianto idrovoro. Tale altezza sarà pari alla quota liquida nella vasca di aspirazione, quota alla quale attacca la prima pompa e cioè pari a -3.2 m.

Figura 32:Steady Flow Data

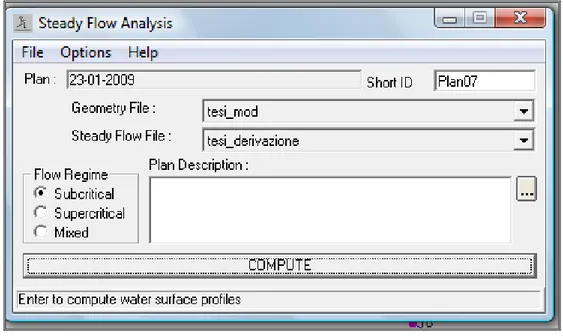
• elaborazione dei dati attraverso il comando ‘Run Steady Analysis’ (Figura 33), che permette la verifica a moto permanente.

88

Figura 33: Steady Flow Analysis

• il programma restituisce come risultato l’andamento dei profili liquidi degli alvei ( vedi Figura 34 e Figura 35).

I simboli presenti hanno il seguente significato: EG= linea dell’energia;

WS= altezza del pelo libero; Crit= altezza critica;

Ground= fondo del canale; Left Levee= sponda sinistra; Right Levee= sponda destra.

89

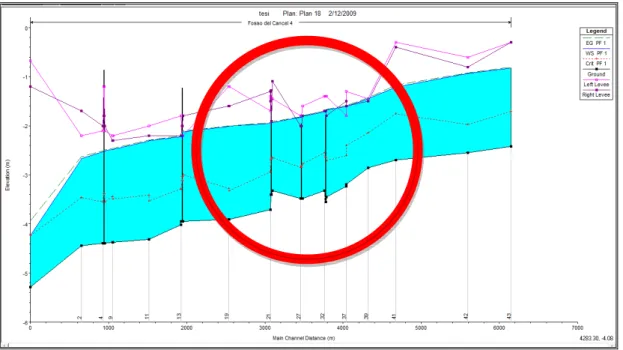
Figura 34: Profilo liquido del ramo denominato Fosso del Cancellino

Figura 35: Profilo liquido del ramo denominato Traversagna

Il coefficiente di Manning è stato considerato uguale per tutte le sezioni e pari a 0.029 dato che la maggior parte dei canali e dei fossi, allo stato attuale, sono in buono stato e sottoposti a manutenzione ordinaria.

Si vede chiaramente dai profili l’effetto di chiamata dovuto alla presenza dell’impianto idrovoro di Vecchiano.

90

Dai profili risultanti è possibile vedere come si hanno problemi di esondazione per Tr 25 anni nel tratto schematizzato che va dal Fosso del Cancellino fino al Collettore di Vecchiano, in particolar modo nei canali II Traversa Baldacci e Immaginetta ( dalla sezione 39 alla sezione 27 come si vede nella Figura 34 all’interno del cerchio rosso). Tale fenomeno risulta dalla derivazione che è stata fatta attraverso la paratoia nel canale Traversagna, perciò attraverso tale manufatto viene spostato il problema di esondazione da tale canale a quelli sopra citati, tale decisione risulta dalla volontà di andare a salvaguardare la parte industriale a scapito di quella agricola, andando così a diminuire i danni di un eventuale esondazione.

Nel canale Immaginetta le sezioni risultano insufficienti anche a causa della presenza di tre ponticelli che creano rigurgito nelle sezioni di monte.

Si riportano di seguito le tabelle di output del programma HEC-RAS nelle quali vengono riassunti i dati più importanti risultanti dalla elaborazione dei dati input immessi nel programma, come la portata defluente, l’area di deflusso, la velocità della corrente, il numero di Froude, l’altezza critica, la linea dell’energia, etc.

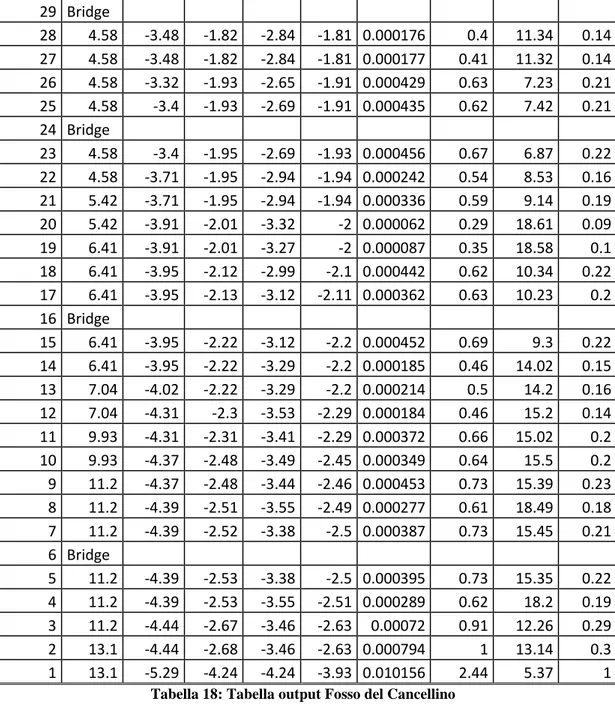
La Tabella 18 è quella associata al tratto di rete schematizzata come Fosso del Cancellino, che và a raccogliere le acque nella parte ovest e nord del bacino in esame, passando dalle aree più depresse e andando a confluire nel Collettore di Vecchiano. River station Q (m3/s) Min Ch El (m) WS Elev (m) Crit WS (m) EG Elev (m) EG slope Vel Chnl (m/s) Flow Area (m2) Froude 43 1.95 -2.42 -0.82 -1.71 -0.81 0.000606 0.58 3.36 0.22 42 1.95 -2.55 -0.93 -1.98 -0.93 0.000107 0.32 6.11 0.1 41 1.95 -2.7 -1.21 -1.75 -1.17 0.001373 0.81 2.4 0.32 39 4.36 -2.86 -1.45 -2.14 -1.43 0.000572 0.6 7.23 0.24 38 4.36 -3.19 -1.61 -2.4 -1.59 0.000531 0.61 7.13 0.23 37 4.58 -3.23 -1.6 -2.61 -1.59 0.000329 0.51 8.96 0.18 36 4.58 -3.45 -1.68 -2.71 -1.66 0.000274 0.51 9.03 0.17 35 4.58 -3.55 -1.68 -2.65 -1.67 0.000337 0.54 8.49 0.19 34 Bridge 33 4.58 -3.49 -1.71 -2.62 -1.69 0.000376 0.56 8.16 0.2 32 4.58 -3.32 -1.71 -2.55 -1.69 0.00042 0.58 7.86 0.21 31 4.58 -3.48 -1.81 -2.78 -1.79 0.000292 0.52 8.83 0.18 30 4.58 -3.48 -1.81 -2.84 -1.8 0.000168 0.4 11.52 0.13

91 29 Bridge 28 4.58 -3.48 -1.82 -2.84 -1.81 0.000176 0.4 11.34 0.14 27 4.58 -3.48 -1.82 -2.84 -1.81 0.000177 0.41 11.32 0.14 26 4.58 -3.32 -1.93 -2.65 -1.91 0.000429 0.63 7.23 0.21 25 4.58 -3.4 -1.93 -2.69 -1.91 0.000435 0.62 7.42 0.21 24 Bridge 23 4.58 -3.4 -1.95 -2.69 -1.93 0.000456 0.67 6.87 0.22 22 4.58 -3.71 -1.95 -2.94 -1.94 0.000242 0.54 8.53 0.16 21 5.42 -3.71 -1.95 -2.94 -1.94 0.000336 0.59 9.14 0.19 20 5.42 -3.91 -2.01 -3.32 -2 0.000062 0.29 18.61 0.09 19 6.41 -3.91 -2.01 -3.27 -2 0.000087 0.35 18.58 0.1 18 6.41 -3.95 -2.12 -2.99 -2.1 0.000442 0.62 10.34 0.22 17 6.41 -3.95 -2.13 -3.12 -2.11 0.000362 0.63 10.23 0.2 16 Bridge 15 6.41 -3.95 -2.22 -3.12 -2.2 0.000452 0.69 9.3 0.22 14 6.41 -3.95 -2.22 -3.29 -2.2 0.000185 0.46 14.02 0.15 13 7.04 -4.02 -2.22 -3.29 -2.2 0.000214 0.5 14.2 0.16 12 7.04 -4.31 -2.3 -3.53 -2.29 0.000184 0.46 15.2 0.14 11 9.93 -4.31 -2.31 -3.41 -2.29 0.000372 0.66 15.02 0.2 10 9.93 -4.37 -2.48 -3.49 -2.45 0.000349 0.64 15.5 0.2 9 11.2 -4.37 -2.48 -3.44 -2.46 0.000453 0.73 15.39 0.23 8 11.2 -4.39 -2.51 -3.55 -2.49 0.000277 0.61 18.49 0.18 7 11.2 -4.39 -2.52 -3.38 -2.5 0.000387 0.73 15.45 0.21 6 Bridge 5 11.2 -4.39 -2.53 -3.38 -2.5 0.000395 0.73 15.35 0.22 4 11.2 -4.39 -2.53 -3.55 -2.51 0.000289 0.62 18.2 0.19 3 11.2 -4.44 -2.67 -3.46 -2.63 0.00072 0.91 12.26 0.29 2 13.1 -4.44 -2.68 -3.46 -2.63 0.000794 1 13.14 0.3 1 13.1 -5.29 -4.24 -4.24 -3.93 0.010156 2.44 5.37 1

Tabella 18: Tabella output Fosso del Cancellino

Come si vede i valori delle velocità in tali canali rispettano praticamente tutti i valori limiti fissati pari a 0,5 – 0,6 m/s per tali tipi di canali. Solo nelle ultime sezioni le velocità si innalzano considerevolmente, ma tale aspetto risulta giustificato dal profilo di chiamata dovuto alla presenza dell’impianto idrovoro.

La Tabella 19 riporta i dati delle sezioni ( river station) appartenenti al secondo tratto della rete schematizzata che parte dal canale Traversagna, raccoglie le acque di pioggia che vanno a cadere nella parte sud ed est del bacino, per poi immettersi nel tratto finale del collettore di Vecchiano a circa 300 m dall’impianto di sollevamento.

92

In tale tratto sono numerosi gli attraversamenti, infatti nella zona del canale Traversagna, essendo presente una zona industriale abbastanza ampia (50 ha) e in espansione, sono presenti 7 ponticelli, per permettere il collegamento della via Traversagna con tali aree.

River station Q (m3/s) Min Ch El (m) WS Elev (m) Crit WS (m) EG Elev (m) EG slope Vel Chnl (m/s) Flow Area (m2) Froude 121 2.5 -1.82 0.35 -1.13 0.36 0.000056 0.25 10.15 0.08 120 2.5 -1.82 0.33 -1.27 0.33 0.000026 0.2 12.38 0.05 119 2.5 -1.82 0.33 -1.27 0.33 0.000026 0.2 12.38 0.05 118 Bridge 117 2.5 -1.82 0.33 -1.27 0.33 0.000027 0.2 12.33 0.05 116 2.5 -1.82 0.33 -1.27 0.33 0.000027 0.2 12.33 0.05 115 2.5 -1.82 0.32 -1.24 0.33 0.000041 0.21 11.86 0.07 114 2.5 -1.84 0.32 -1.36 0.32 0.000022 0.19 13.43 0.05 113 Bridge 112 2.5 -1.84 0.32 -1.36 0.32 0.000022 0.19 13.4 0.05 111 2.5 -1.84 0.32 -1.36 0.32 0.000022 0.19 13.4 0.05 110 2.5 -1.86 0.32 -1.24 0.32 0.000027 0.2 12.38 0.06 109 2.5 -1.86 0.32 -1.24 0.32 0.000028 0.2 12.38 0.06 108 Bridge 107 2.5 -1.86 0.3 -1.24 0.3 0.000028 0.2 12.22 0.06 106 2.5 -1.86 0.3 -1.24 0.3 0.000028 0.2 12.22 0.06 105 1.2 -1.87 0.3 -1.41 0.3 0.000005 0.09 14.06 0.02 104 1.2 -1.87 0.3 -1.41 0.3 0.000005 0.09 14.06 0.02 103 Bridge 102 1.2 -1.87 0.3 -1.41 0.3 0.000005 0.09 14.03 0.02 101 1.2 -1.87 0.3 -1.41 0.3 0.000005 0.09 14.03 0.02 100 1.2 -1.87 0.3 -1.36 0.3 0.000007 0.09 12.81 0.03 99 1.2 -1.89 0.3 -1.47 0.3 0.000004 0.08 15.72 0.02 98 Bridge 97 1.2 -1.89 0.3 -1.47 0.3 0.000004 0.08 15.69 0.02 96 1.2 -1.89 0.29 -1.43 0.3 0.000006 0.09 13.48 0.03 95 1.2 -2 0.29 -1.59 0.29 0.000005 0.08 14.32 0.02 94 1.2 -2 0.29 -1.72 0.29 0.000004 0.08 15.41 0.02 93 Bridge 92 1.2 -2 0.29 -1.72 0.29 0.000004 0.08 15.4 0.02 91 1.2 -2 0.29 -1.72 0.29 0.000004 0.08 15.4 0.02 90 1.2 -2 0.29 -1.52 0.29 0.000011 0.12 10.42 0.03

93 89 1.2 -2 0.29 -1.5 0.29 0.000006 0.1 12.51 0.03 88 Bridge 87 1.2 -2 0.29 -1.5 0.29 0.000006 0.1 12.47 0.03 86 1.2 -2 0.29 -1.5 0.29 0.000006 0.1 12.47 0.03 85 2.5 -1.63 0.28 -0.68 0.29 0.000315 0.42 5.99 0.16 84 2.5 -1.63 0.22 -1.02 0.23 0.000094 0.31 8.12 0.1 83 2.5 -1.64 0.22 -1.07 0.23 0.000072 0.26 9.57 0.09 82 Bridge 81 2.5 -1.64 0.22 -1.07 0.22 0.000073 0.26 9.53 0.09 80 2.5 -1.64 0.22 -1.07 0.22 0.000073 0.26 9.52 0.09 79 2.5 -1.64 0.21 -1 0.21 0.000113 0.33 7.63 0.11 78 2.5 -1.64 0.14 -0.77 0.16 0.000622 0.63 4 0.23 77 2.5 -1.64 0.14 -0.76 0.16 0.000739 0.65 3.86 0.24 76 Bridge 75 2.5 -1.64 0.1 -0.76 0.12 0.000833 0.68 3.68 0.25 74 2.5 -1.7 0.09 -0.79 0.12 0.000834 0.68 3.69 0.25 73 2.5 -1.7 0.05 -0.93 0.05 0.000259 0.44 5.68 0.16 72 2.5 -1.7 0.04 -0.98 0.05 0.000376 0.5 5 0.18 71 Bridge 70 2.5 -1.7 0.02 -0.98 0.04 0.000393 0.51 4.9 0.18 69 2.5 -1.7 0.02 -0.98 0.03 0.000397 0.51 4.87 0.19 68 2.5 -1.8 0.01 -1.15 0.02 0.000115 0.31 8 0.11 67 2.5 -1.8 -0.07 -1.08 -0.06 0.000272 0.43 5.77 0.16 66 2.5 -1.8 -0.25 -0.96 -0.23 0.000499 0.57 4.36 0.21 65 2.5 -1.8 -0.34 -1.03 -0.32 0.000518 0.6 4.17 0.22 64 2.5 -1.8 -0.33 -1.15 -0.32 0.000217 0.43 5.82 0.15 63 Bridge 62 2.5 -1.8 -0.34 -1.15 -0.33 0.000221 0.43 5.78 0.15 61 2.5 -1.87 -0.34 -1.21 -0.33 0.000273 0.47 5.37 0.16 60 2.5 -1.9 -0.4 -1.35 -0.39 0.000182 0.4 6.33 0.14 59 2.5 -2 -0.43 -1.56 -0.42 0.000092 0.31 8.03 0.1 58 2.5 -2 -0.43 -1.47 -0.43 0.000091 0.32 7.83 0.1 57 Bridge 56 2.5 -2 -0.45 -1.47 -0.44 0.000096 0.32 7.71 0.1 55 2.5 -2 -0.45 -1.34 -0.44 0.000159 0.38 6.54 0.13 54 2.5 -2 -0.49 -1.38 -0.48 0.000216 0.42 5.89 0.15 53 4.9 -2.8 -0.57 -1.43 -0.49 0.002309 1.23 4 0.39 52 4.9 -3.1 -0.77 -2.05 -0.75 0.000494 0.72 6.78 0.2 51 4.9 -3.15 -0.81 -1.92 -0.76 0.001212 1.02 4.78 0.27 50 Bridge

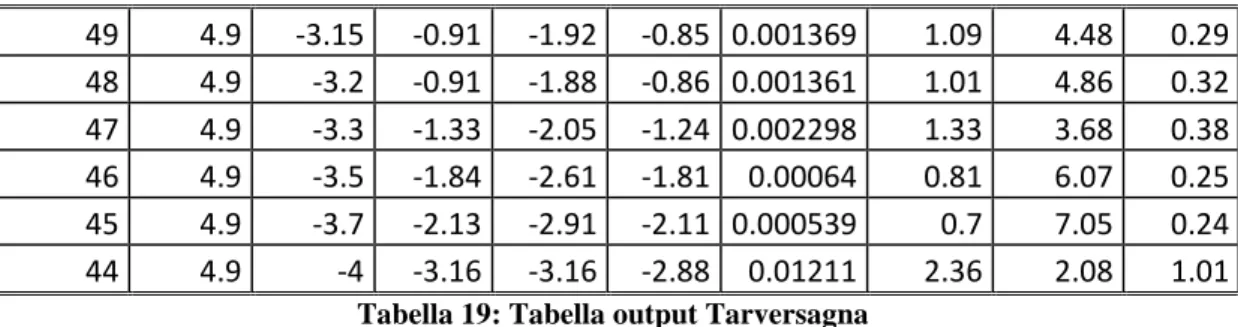
94 49 4.9 -3.15 -0.91 -1.92 -0.85 0.001369 1.09 4.48 0.29 48 4.9 -3.2 -0.91 -1.88 -0.86 0.001361 1.01 4.86 0.32 47 4.9 -3.3 -1.33 -2.05 -1.24 0.002298 1.33 3.68 0.38 46 4.9 -3.5 -1.84 -2.61 -1.81 0.00064 0.81 6.07 0.25 45 4.9 -3.7 -2.13 -2.91 -2.11 0.000539 0.7 7.05 0.24 44 4.9 -4 -3.16 -3.16 -2.88 0.01211 2.36 2.08 1.01

Tabella 19: Tabella output Tarversagna

Anche in questo caso le velocità dell’ultimo tratto risultano troppo elevate, e ciò è dovuto sia presenza dell’impianto idrovoro, ma anche ad un’eccessiva pendenza dell’alveo; di tale fatto si terrà di conto nella fase successiva.

Per meglio capire la schematizzazione della rete si riportano gli intervalli delle numerazioni assegnate alle sezioni di ciascun collettore:

• Traversagna 121-86; • Gorello 85-54; • Fossa Nuova 53-44;

• Fosso del Cancellino 43-40; • II Traversa Baldacci 39-38; • Immaginetta 37-22;

• Fossa Magna I 21-20; • Fossa Magna II 19-14; • Collettore di Vecchiano 13-1.

4.2.2 ANALISI A MOTO VARIO

L’analisi a moto permanente non riesce però a descrivere il comportamento reale delle acque all’interno della rete. Nel momento in cui inizia a cadere la pioggia sul bacino, la rete di bonifica si trova parzialmente piena, in quanto l’impianto in condizioni normali mantiene una quota nella vasca di aspirazione pari a -3,2 m, e quindi una quota fissa anche in tutti i canali della rete. Quando inizia l’afflusso alla rete tutta la rete funge da invaso.

Al momento si concentra l’attenzione sui due collettori secondari, Guscionetto e Gambini-Rosselli, prossimi all’impianto che, ubicati in una delle zone maggiormente depresse del bacino, vengono allagate da eventi di piena con tali tempi di ritorno,

95

come già visto nei layout del capitolo 3. Tali collettori, che non sono stati schematizzati nella rete a moto permanente, vengono adesso presi in considerazione ma non con la loro sezione d’alveo bensì con la sezione che va da un capofosso e l’altro, distanza di circa 400 m. Questo con lo scopo di andare a simulare l’esondazione extra-alveo.

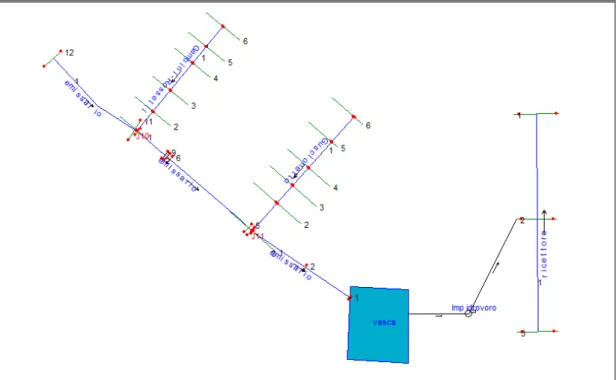
La rete principale a monte del Collettore di Vecchiano è stata tagliata così come il ramo del Traversagna, e sono stati schematizzati nei nodi con gli idrogrammi rispettivi; la rete è visibile in Figura 36.

Figura 36: Schematizzazione moto vario

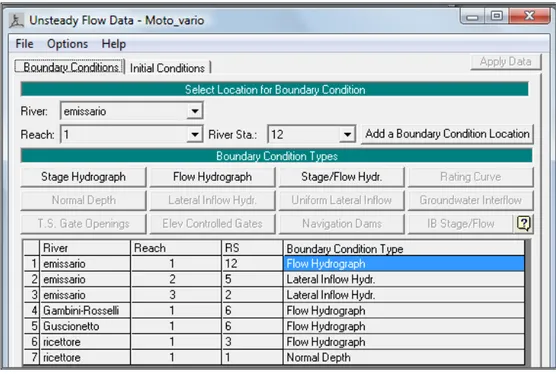
Nella rete è stata schematizzata la vasca di aspirazione e l’impianto idrovoro attraverso l’immissione delle 4 pompe esistenti con le relative portate sollevate. In Figura 37 si riporta la finestra dell’unsteady flow data, nei quali sono stati introdotti gli idrogrammi aventi Tr 25 anni.

96

Figura 37: Unstedy flow data

Le sezioni riportate per i due canali secondari sono state ricavate direttamente dal GIS andando ad effettuare delle sezioni sul rilievo LIDAR, tali sezioni sono state esportate su HEC-RAS e sono del tipo riportato in Figura 38.

97

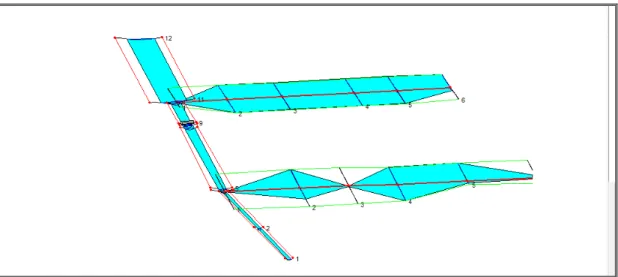
In Figura 39 si riporta uno schema tridimensionale dell’output dell’analisi a moto vario, immagine scattata in un certo istante; si vede come le aree limitrofe agli alvei dei canali Guscionetto e Gambini-Rosselli effettivamente si allaghino al transitare degli idrogrammi di piena calcolati.

Figura 39: Veduta tridimensionale del Collettore Vecchiano e dei canali secondari Guscionetto e Gambini-Rosselli