Capitolo 2 LogLog Counting

Capitolo 2

LogLog Counting

Il LogLog counting è un algoritmo probabilistico proposto in [1] e serve in generale a stimare la cardinalità di un insieme di dati, ovvero il numero di elementi distinti che lo compongono. Un esempio di applicazione può essere andare a stimare, con un errore relativo lieve e occupando poca memoria, il numero di parole diverse che compaiono in tutto il complesso delle opere di Shakespeare.

L’algoritmo LOGLOG riesce a svolgere la sua funzione sfruttando solo una piccola quantità di memoria aggiuntiva, all’incirca loglogN_max bit, con Nmax pari al limite superiore

delle cardinalità che questa tecnica riesce a stimare; il nome stesso dell’algoritmo deriva da questa caratteristica. Le proprietà di questo metodo sono che la stima della cardinalità è asintoticamente non polarizzata, e che, poiché l’algoritmo opera in modo incrementale, esso può essere applicato a flussi che richiedono una stima da realizzare on-line, timebin dopo timebin.

Per rendere casuali i dati, cioè fare in modo che abbiano caratteristiche di uniformità e indipendenza, si utilizza una funzione hash, ed è sul dataset ottenuto in uscita dalla funzione hash che si valuta la cardinalità; inoltre la stima finale è totalmente indipendente dalla natura e dall'ordine dei dati, sui quali non è necessaria nessuna informazione. In particolare, poiché non richiede assunzioni sulle caratteristiche statistiche dei dati, l’algoritmo rivela una natura general purpose.

2.1 L’algoritmo LogLog di base

Dato un multiset M di dati, appartenenti a un universo discreto U, supponiamo di volerne stimare la cardinalità.

Si assuma di avere a disposizione una funzione hash h che traduca gli elementi di U in stringhe x binarie sufficientemente lunghe, in modo che i bit che compongono i valori ottenuti dalle funzioni hash somiglino molto a bit casuali distribuiti uniformemente: in questo senso, M sarà il multiset ideale (random) ottenibile tramite tale trasformazione.

Per semplicità assumiamo inizialmente che le stringhe siano infinitamente lunghe, cioè U={0,1}∞_{, l'idea di base è}

iniziale delle stringhe, ottenute in uscita dalla funzione hash h. Si definisce quindi la funzione ρ(x), come la posizione del primo bit settato a 1 nel valore x restituito dal calcolo della funzione hash, ad esempio ρ(1...)=1, ρ(001...)=3, ecc. Sulla base delle ipotesi fatte ci si aspetta che circa n 2/ k _elementi

distinti di M avranno un valore della funzione ρ pari a k. Quindi, la quantità

 

M

 

x R M x   max ₍₁₎

può essere considerata una stima approssimata del valore di n

2

log _{; inoltre, a causa della presenza dell’operazione di}

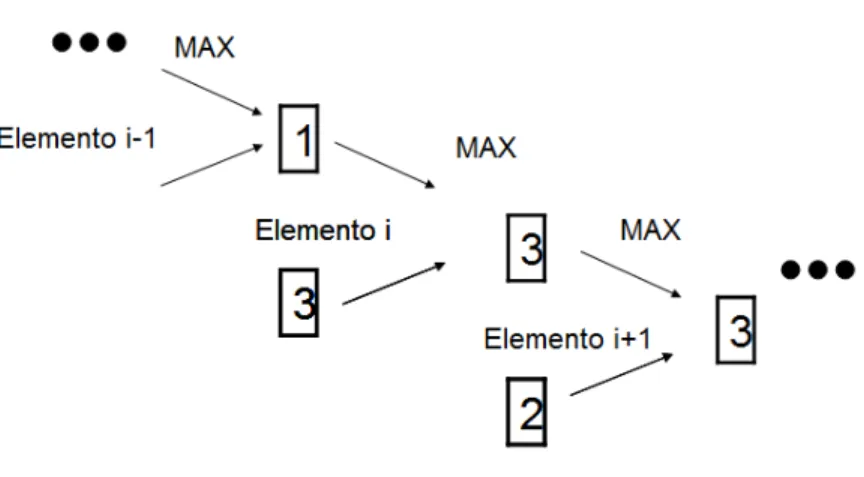
massimizzazione, R sarà completamente indipendente da eventuali duplicati all'interno del multiset M e dall'ordine di presentazione delle stringhe. È possibile osservare un esempio di applicazione della formula (1) in figura 4: all’ingresso dell’elemento i, il LogLog Counter è aggiornato prendendo il massimo tra i valori relativi all'uscita dell’elemento i-1 e l’elemento i, producendo in questo modo un valore che dovrà essere confrontato con quello legato all’elemento i+1.

Figura 4. Esempio di aggiornamento di un LogLog Counter, secondo la formula (1).

In particolare, in [1] gli autori hanno valutato che la formula di R stima “logaritmicamente” n all’interno di ±1.87 ordini di grandezza binari, poiché la deviazione standard associata allo stimatore è di 1.87; inoltre la polarizzazione, di tipo additivo, vale 1.33.

Per migliorare la stima di R, piuttosto che usare un LogLog Counter unico, lo si divide in m=2 gruppi e si k considerano i k bit più significativi del valore in uscita dalla funzione hash come indice del sottoblocco in binario (ciò significa raggruppare gli elementi in modo che quelli che iniziano ad esempio con 001 cadranno nel sottogruppo 1, se m=8). ρ(x), invece, si calcolerà adesso come la posizione del

primo bit diverso da 0 a partire dal bit k+1; pertanto si indicherà questa nuova funzione con la notazione ρk(x).

Di conseguenza, la stima R(j) per ogni sottogruppo j(con j=0,2,...,m-1) vale  

_{ }

x ρ = R _k j x j  max (2)

Se si effettua la media aritmetica sugli m sottogruppi

 



m = j j R m 1 1 (3)

ci si aspetta che questo valore corrisponde a log2n /m più una polarizzazione additiva, dove n è la cardinalità dell’insieme. Allora, la stima di n secondo l’algoritmo LogLog è

 



j m R m 1 m2 α = F (4)

dove αm è il fattore di correzione della polarizzazione nel limite

asintotico, e può essere valutato in questo modo:





m m m= Γ m α           log2 1 2 / 1 / 1 (5)

 

_

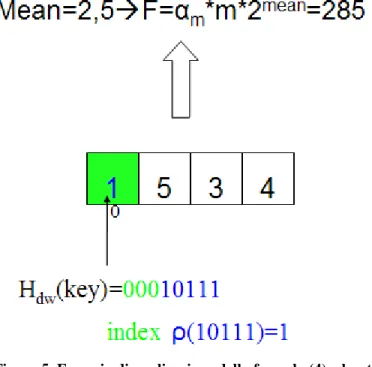
  0 1 dt t e s = s Γ t s . (6)

In figura 5 è mostrato l'uso pratico dei LogLog Counter: viene usata la prima parte della funzione Hdw per selezionare il

sottogruppo e la seconda per incrementarlo; alla fine si applica la formula (4).

Figura 5. Esempio di applicazione della formula (4), che stima la cardinalità.

In conclusione, i passi da effettuare per implementare l’algoritmo LOGLOG,nell’ipotesi che M sia il set dei valori in uscita dalle funzioni hash e m=2k, sono:

o per x=b₁b₂...m

o assegnare a j il valore dei primi k bit di x in base 2

o indicare con ρk(x) la posizione del primo bit

settato a 1 in x a partire da sinistra, dopo aver scartato i k bit più significativi;

o impostare R(j)= max(R(j), ρk(x)); o ritornare  



j m R m 1 m2 α = F

Le caratteristiche principali dell'algoritmo possono essere riassunte attraverso il seguente teorema, dove E indica l’aspettazione e V la varianza.

Teorema 1. Consideriamo l'algoritmo di base LogLog,

applicato a un multiset ideale di cardinalità n (non nota) e sia F il valore stimato della cardinalità restituito dall'algoritmo.

o La stima F è asintoticamente non polarizzata, cioè per   n , 1Ε

 

F =1+θ +o

 

1 n n 1,n , con

 

6 1, 10  < θ _n .

o L’errore standard, definito come V

 

F n n 1 , per n  tende al valore +θ +o( ) m β n 2, m 1 , con

 

6 2, 10  < θ _n . Nota: β₁₂₈ =1.30540, β₁₀₂₄ =1.29897, 1.29806 6 1 2 log 12 1 2 2 = π + = β_ .

Dimostrazione. Consideriamo la variabile

 



j m M 2 1 m2 = α F =

Z / , che è la versione non normalizzata dello stimatore F. Per le relazioni di convoluzione multinomiale relative alle potenze m-esime delle funzioni generatrici, il valore atteso e la varianza di Z sono rispettivamente

 

 

m m n n , m z G z mn! = Z Ε       1/ 2 e

 

 

 

2 / 1 / 2 2 2                            n n m m m m n 2 n , m z G z ! m , m z G z n! m = Z V ,

dove con l’espressione

 

zn f

 

z si rappresenta il coefficiente zn nella serie di potenze f(z) e con G(z,u) si indica la funzione generatrice della famiglia delle distribuzioni di probabilità di

una variabile aleatoria che corrisponde al massimo di t variabili aleatorie indipendenti e distribuite geometricamente .

La dimostrazione del teorema 1 consiste nello stimare asintoticamente le quantità Εn

 

Z e Vn

 

Z .

Per semplificare, supponiamo di poissonizzare il problema del calcolo del valore atteso ε e della varianza _n ν , _n in modo da utilizzare le proprietà della trasformata di Mellin, utilizzando per queste approssimazioni la notazione ε e n ν . n

Sfruttando infatti le caratteristiche del modello

poissoniano, si ha che n m m n , e m n mG = ε        1/ 2 e 2 / 1 / 2 2 2                             n m m n n m m 2 n , e m n G m e , m n G m = ν quando

la cardinalità dell’insieme rispetta una legge di Poisson con rate λ=n. Per n, ε Γ



m



+δn n m m n                    log2 1 2 / 1 / 1 e









2 2m / 1 / 2 log2 1 2 / 1 log2 1 2 / 2 m Γ m +η n Γ ν _n m m m n                           

La trasformata di Mellin per una funzione reale f(x) è definita come la funzione complessa f

 

s =

_

f

 

t ts 1dt, ed è tale che

(i) c’è una corrispondenza tra le proprietà asintotiche della funzione originaria f e le singolarità della trasformata f*_;

(ii) le somme armoniche definite come



λf

 

μx si possono fattorizzare come



_

λμs



 f

 

s .

È possibile quindi riscrivere il valor medio e la varianza come ε_n =mA

 

n m e 2

 

m

2 n

n+ε =m B n

ν , dove A(x) e B(x)

sono le somme armoniche

 

i m





i+

 

i





x x = x A 2 / /2 1 /2 



,

 

m





i+

 

i





x x = x B

_

22i/ /2 1  /2 con

 

x =ex/m, che ha come trasformata

 

s =msΓ

 

s ; di conseguenza

 

 



s



_{m s} s = s A 2 2 1 1 1 2 _1/     e

 

 



s



_{m s} s = s B 2 2 1 1 1 2 _21/     .

Allora, il contributo asintotico principale di A è dovuto alla singolarità posta sull’asse reale, per cui, vicino a s=1/m

si ha

 

m + s a s A / 1    con





log2 1 2 / 1 / 1 /     m m 1 m Γ m = a ,

mentre le altre singolarità producono un contributo asintotico molto piccolo. Quindi, il valore ε_n =mA

 

n m coincide asintoticamente con mamn+δ_nn dove δ è una fluttuazione di _n ampiezza minore di 10-6.

Per quanto riguarda la varianza, il polo principale è m

=

s 2/ , cosa che determina

 

2 + s b s B   con





log2 1 2 / 2 / 2 /     m m 2 m Γ m = b . Il contributo di questa

singolarità a B(x) è quindi bx2/m: trascurando le fluttuazioni piccole, per le proprietà della trasformata di Mellin si ha

m 2 bx = B(x) / .

I primi due momenti dello stimatore LOGLOG, grazie al Lemma di Depoissonizazione illustrato in [7], sotto l’ipotesi di modello di Poisson e quello reale risultano asintoticamente equivalenti, cioè Ε_n

 

Z ε_n e V_n

 

Z ν_n .

Lo stimatore non normalizzato Z cresce come n /α_m per quanto detto finora; quindi lo stimatore normalizzato F è

sotto ipotesi di fluttuazioni trascurabili, tende asintoticamente a 1 2m   a

bm . La quantità mostrata è esattamente β_m/ m nella notazione del teorema 1.□

In conclusione, il teorema 1 dichiara che, trascurando le piccole fluttuazioni, di ampiezza minore di 10-6, l’algoritmo fornisce una stima asintoticamente valida del valore della cardinalità. L’errore standard, che misura in senso quadratico medio la deviazione che ci si aspetta, è ben approssimato dalla formula

Standard error m

=1.30. (7)

Scegliendo m=1024 e m=2048 si otterrà un errore standard rispettivamente del 4% e del 3%.

Inoltre, m + α α_m 48 2 log 2π2 2   _ , dove 0.39701 2 2 = e = α_ γ e γ è la costante di Eulero.

Notare che, per giungere a una stima sufficientemente accurata, sarà necessario scegliere un valore di m>> 1.

Finora, si è ipotizzato di impiegare per ogni gruppo j un registro R(j) che memorizza numeri interi di valore potenzialmente illimitato, tuttavia questa era soltanto una semplificazione. Definiamo allora un algoritmo l-limitato, tale che i registri R(j) siano memorizzati su l bit, ovvero ogni registro possa rappresentare un numero intero compreso tra 0 e

1

2 l invece che qualsiasi .

Teorema 2. Sia ω

 

n una funzione che tende a infinito molto lentamente, e si consideri la funzione

 

+ω

 

n m n = n l       2 2log

log . Allora, l’algoritmo l(n)-limitato e l’algoritmo LOGLOG forniscono lo stesso risultato con

probabilità che tende a 1 per n che tende a infinito.

Dimostrazione. A causa delle proprietà standard delle distribuzioni multinomiali, la probabilità che un qualsiasi bucket contenga più di 2n/m elementi è esponenzialmente piccola; tali casi possono quindi essere scartati. Allora, la probabilità che un qualsiasi bucket abbia un valore M del registro che superi k è



1



12k



2n/m



. Di conseguenza, la probabilità globale di fallimento è limitata superiormente dalla

approssimata dal valore  1 2 2 4m 2 4n + n ω l m n =          . Quindi, la

probabilità di fallimento diminuisce più velocemente rispetto alla potenza di n. □

Ogni registro è formato da m interi su l(n) bit, e la quantità di memoria necessaria all’algoritmo per stimare le cardinalità fino a n è log 2log2



1+o

 

1



m n m       ; la funzione hash h deve convertire i valori dall’universo di dati originario a esattamente l n + m

2

log

2 bit. Come ci si può aspettare, inoltre, questa seconda versione dell'algoritmo funziona correttamente per ogni n'  . n

Ad esempio, se lo scopo è contare le cardinalità al massimo fino a n=227, si può usare m=1024, per ottenere un errore del 4% circa, in base alla formula (7) del teorema 1. Allora, si accede a ogni gruppo circa n/m=217 volte, e quindi log2log2 217=4.09. Se ogni registro ha dimensione l=5 bit,

ovvero w=0.91, si ottiene che la limitazione a l ha una incidenza così piccola che la probabilità di discrepanza tra le due versioni dell’algoritmo è minore del 12%.

standard del 4% occupando soltanto 1024 registri di 5 bit, cioè in totale una tabella di 640 byte.