STATO DELL’ARTE

Capitolo 2

STATO DELL’ARTE

In questo capitolo sono passati in rassegna i principali lavori di ricerca sulle caratteristiche di trasmissioni a cinghia trapezoidale. Tali lavori riguardano lo sviluppo di modelli analitici [3], di modelli agli elementi finiti (FEM) [4] [5] e di modelli a parametri concentrati [6] [7] utilizzati per studiare il comportamento dinamico della trasmissione.

La maggior parte dei lavori esaminati sono incentrati essenzialmente sulla valutazione delle sollecitazioni nella cinghia, con particolare attenzione alla tensione e alla pressione sui fianchi, mentre in [3] il livello di dettaglio permesso da un modello analitico consente di fare delle previsioni sugli andamenti di numerosi parametri della trasmissione, a prezzo però di una notevole complicazione matematica del modello.

Nell’esporre i lavori presenti in letteratura, particolare attenzione è stata posta nell’analisi delle ipotesi sostenute, nelle equazioni analitiche del modello e nei risultati ottenuti, per fornire dei riferimenti utili per una valutazione oggettiva del modello di trasmissione che sarà sviluppato in questa sede.

Non sono invece stati presi in considerazione i numerosi lavori attinenti il funzionamento delle trasmissioni a cinghie metalliche o ibride, in quanto le modalità con cui esse esplicano la loro azione si discostano sensibilmente da quelle delle cinghie trapezoidali in gomma.

2.1 Modello analitico di trasmissione a cinghia

In questo paragrafo si riassumono i risultati principali dello studio condotto da G. Gerbert [3] sulle trasmissioni a cinghia trapezoidale, esponendo sinteticamente le equazioni ottenute. Per chiarimenti e approfondimenti in merito al modello si rimanda a [3].

G. Gerbert propose una nuova teoria in cui si considera il moto radiale e circonferenziale della cinghia nella gola della puleggia, e basata sulle deformazioni longitudinali e trasversali della cinghia. Il modello ottenuto necessita la conoscenza delle proprietà elastiche della cinghia per descriverne la caratteristica forza – deformazione.

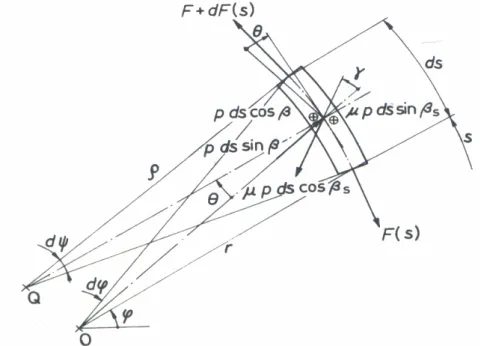
La differenza fondamentale tra una cinghia piatta e una trapezoidale è la possibilità di quest’ultima di muoversi nella direzione radiale. La cinghia, sottoposta a deformazioni trasversali dovute alla pressione esplicata dal contatto sui fianchi, si restringe diminuendo il suo spessore e per riempire la gola della puleggia deve possedere un movimento radiale. In più la variazione di tensione della cinghia lungo l’arco di contatto causa deformazioni longitudinali. Il movimento longitudinale e radiale della cinghia fa sì che la direzione della forza d’attrito formi un angolo di scorrimento γ rispetto alla direzione radiale (figura 2.1), mentre per la teoria delle cinghie piatte la forza d’attrito è sempre circonferenziale.

2.1.1 Ipotesi

G. Gerbert assume le seguenti ipotesi:

o si considera la cinghia come un nastro dotato di un certo spessore, priva d’altezza, e coincidente con il rinforzo in fibre; si trascurano quindi le deformazioni interne dell’intera sezione trapezoidale;

o il coefficiente d’attrito è costante;

o la cinghia è priva di rigidezza flessionale, quindi si trascurano tutti i momenti flettenti; o la cinghia è priva di massa, o la velocità di rotazione è molto piccola, quindi si

trascurano tutte le forze d’inerzia, e la dinamica del sistema.

2.1.2 Equazioni del modello

Con riferimento alla figura 2.1 rappresentante le forze agenti su un elemento infinitesimo ds di cinghia, i seguenti simboli sono utilizzati:

F tensione della cinghia;

p forza di compressione laterale tra cinghia e puleggia per unità di lunghezza; r,φ coordinate polari;

s coordinata lungo la cinghia;

γ angolo tra il raggio e la velocità di slittamento nel piano di rotazione; θ angolo tra la direzione della cinghia e la tangente alla puleggia; µ coefficiente d’attrito;

ρ raggio di curvatura della cinghia;

O centro della puleggia su cui l’elemento è avvolto; Q centro di curvatura dell’elemento di cinghia;

Altri simboli utilizzati nella trattazione sono:

ω velocità angolare pulegge motrice e condotta (considerando stesso raggio d’avvolgimento); c rigidezza longitudinale della cinghia (N);

ε deformazione longitudinale;

vs velocità di slittamento;

vb velocità della cinghia in condizioni di esercizio; V velocità della cinghia scarica;

Pf potenza persa per slittamento su una puleggia.

Fig. 2.1 Elemento infinitesimo di cinghia

Si scrivono le equazioni d’equilibrio nella direzione longitudinale e perpendicolare all’elemento di cinghia (quest’ultima inclinata di θ rispetto alla direzione radiale).

.1.3 Deformazione longitudinale

una molla lineare, per cui si ha:

del rinforzo è molto maggiore rispetto alla rigidezza della

2.1.4 Deformazione trasversale

(

)

[

]

⋅ ⋅

=2 p sin sin cos _s sin

ds

dF _(2.1)

2

Si assume che la cinghia si comporti come

(

)

[

]

ρ =2⋅p⋅ sin ⋅cos − ⋅cos s ⋅cos +

F (2.2) (2.3) ε ⋅ = c F

Nella (2.3), poiché la rigidezza

gomma, non è inclusa la deformazione longitudinale indotta dalla deformazione trasversale della cinghia. Tale deformazione longitudinale è, infatti, “bloccata” dalla resistenza opposta dal rinforzo.

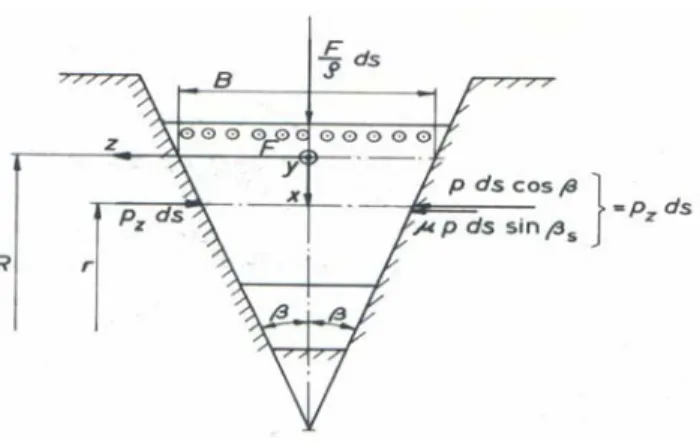
Fig. 2.2 Sezione trasversale della cinghia

figura 2.2 è riportata un azione θ è trascurata). Le

In a sezione trasversale della cinghia (l’inclin

forze che agiscono sulla cinghia e che inducono uno spostamento radiale sono la tensione F, la forza perpendicolare all’elemento di cinghia F/ρ (2.2), e la forza trasversale per unità di lunghezza pz. La forza trasversale pz induce una riduzione dello spessore della cinghia, la

quale subisce uno spostamento radiale per riempire la gola della puleggia; la tensione F provoca una deformazione longitudinale, che contribuisce al restringimento ulteriore dello

compressione in direzione X (figura 2.2), inducendo una deformazione trasversale (diventa più spessa), che causa uno spostamento radiale opposto a quello dovuto alle altre due forze. Lo spostamento radiale (in direzione X definita in figura 2.2) è dunque dato dalla seguente equazione:

ove s’indicano con k1, k2, k3, le rigidezze lineari che sono il carico rispettivamente

2.1.5 Condizione di slittamento D

trasversale, longitudinale, perpendicolare che danno uno spostamento radiale unitario (ovviamente k2<0); tali rigidezze vengono misurate per mezzo di prove sperimentali.

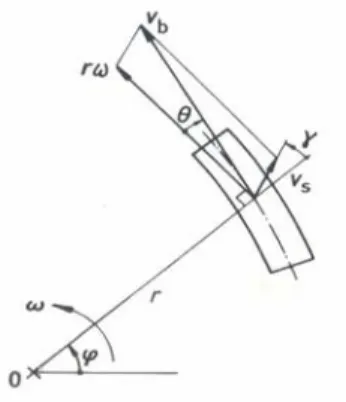
Fig. 2.3 Componenti della velocità di un elemento di cinghia

on riferimento alla figura 2.3, la velocità vb è diretta tangenzialmente all’elemento di

C

cinghia, in quanto, in condizioni di stazionarietà del moto, un qualsiasi elemento infinitesimo di cinghia non può avere una componente ad essa perpendicolare di velocità, essendosi stabilizzato ad una certa quota radiale nella gola della puleggia. La velocità di slittamento vs è

la differenza vettoriale tra la velocità della puleggia di modulo e la velocità vb della cinghia;

tale differenza eseguita nelle direzioni circonferenziale e radiale, fornisce due relazioni che unite mediante l’eliminazione di vs, danno la seguente:

(

)

La cinghia è soggetta a deformazioni longitudinali variabili lungo l’arco di contatto, che

onsiderando la (2.6) si ottiene la seguente condizione di slittamento:

i osserva che l’angolo di slittamento γ giace nel piano di rotazione, per cui vs non è la

2.1.6 Condizioni geometriche

Il modello si completa aggiungendo due equazioni esprimenti legami geometrici tra alcune

ove R è il raggio d’avvolgimento delle pulegge quando la cinghia è scarica;

e equazioni del modello sono poi modificate aggiungendo altre relazioni geometriche, in implicano una velocità variabile secondo la seguente relazione di continuità (cfr. [2] pag. 327):

(

)

velocità di slittamento assoluta, ossia quella che si ha nel fianco a V della cinghia; quest’ultima sarà data da vs/cosβs.

(2.6) (2.7) (2.8) (2.9)

(

)

modo tale da sostituire ds e il raggio di curvatura ρ in funzione delle coordinate polari (r, φ), ed ottenere un sistema di 7 equazioni (derivanti da (2.1), (2.2), (2.3), (2.4), (2.7), (2.8), (2.9)) in sette incognite che sono F, θ, p, x, βs, e, γ nella sola variabile φ. Il sistema contiene quindi

tre equazioni differenziali ordinarie del primo ordine con le derivate prime F’, θ’, x’ rispetto a

φ. Per ulteriori chiarimenti sui passaggi da effettuare per ottenere il sistema finale si rimanda a

2.1.7 Risultati

Il sistema di equazioni descrivente il modello analitico può essere integrato sia per una puleggia motrice che per una condotta, secondo le condizioni iniziali imposte (se il rapporto di trasmissione è diverso da uno si devono considerare due diversi raggi di avvolgimento, Rm, Rc, rispettivamente per la motrice e la condotta).

Il sistema in questione necessita in generale l’assunzione di quattro condizioni iniziali (cfr. [3] pag.22); nella trattazione G. Gerbert prende in considerazione vari tipi di condizioni iniziali, che rappresentano i valori d’alcune grandezze incognite in un arbitrario punto dell’arco di contatto della puleggia motrice o condotta, diversi, a seconda che si voglia ottenere la soluzione del problema per l’una o per l’altra (cfr. [3] pag.29-32).

Il sistema è risolto numericamente con il metodo di Runge – Kutta, perché è impossibile ottenere una soluzione in forma chiusa per le varie grandezze.

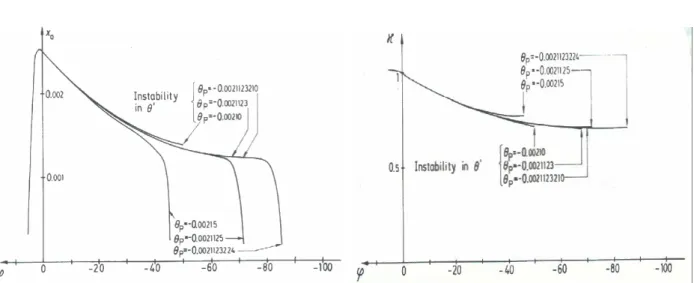
Si illustrano nelle figure 2.4 e 2.5 le soluzioni ottenute per la puleggia condotta adottando le condizioni iniziali (φ = 0) x0P = 0.0025, γP = 130°, θ’P = 0, e riportanti rispettivamente

l’andamento di x0, F0, funzioni adimensionali, per vari valori della quarta condizione iniziale θP, in modo da mostrare la dipendenza di tali soluzioni da quest’ultima condizione.

L’utilizzo di tali condizioni iniziali, e la discussione sulle varie tipologie di condizioni da imporre deriva da considerazioni per cui si rimanda a [3] pag.23.

Le grandezze adimensionalizzate in questione sono:

1 2 0 0 k R F F R x x ⋅ = =

Quando la cinghia entra od esce dalla puleggia, dalle soluzioni del sistema si deve trovare p = 0, quindi dalla (2.2) ρ = 0, e dalla (2.11) θ’ = 1: raggiunti tali valori la simulazione numerica può essere interrotta.

Dai grafici riportati si nota che solo per un range molto ristretto di valori di θP si ottengono

delle soluzioni stabili. Si nota altresì che fornendo dei valori di θP in modo da ottenere degli

angoli d’avvolgimento sempre più grandi la soluzione s’avvicina alla condizione (in prossimità dell’ingresso della condotta) γ = 180° e θ = 0° (quest’ultima si evince dalle soluzioni numeriche non riportate; cfr. [3] pag.29), per cui per un breve tratto iniziale in cui la cinghia non offre spinta d’attrito tangenziale alla puleggia condotta (non avviene trasferimento di coppia), si ha moto esclusivamente radiale della cinghia.

L’andamento della pressione di contatto sui fianchi non è esplicitamente calcolata, ma essa presumibilmente ricalcherà l’andamento dello spostamento radiale in figura 2.4. Durante l’attraversamento della puleggia condotta, la tensione nella cinghia s’incrementa passando dal valore F1 nel ramo lento, a F2 nel ramo teso, perciò lo spostamento radiale cresce

nell’attraversamento dell’arco di contatto (per φ < 0 si ha l’ingresso della cinghia nella puleggia), come dimostra la figura 2.5.

2.2 Modello di trasmissione a cinghia agli elementi finiti

Un modello di trasmissione a cinghia sviluppato con il metodo degli elementi finiti è stato proposto da Leamy e Wasfy [4] [5]; tale modello è stato utilizzato per il calcolo, tra le altre grandezze, della distribuzione di pressioni nel contatto cinghia – puleggia e della tensione nei rami rettilinei.

Una delle ipotesi base del modello riguarda l’utilizzo delle sole coordinate cartesiane dei nodi degli elementi finiti quali gradi di libertà del sistema nel piano; ai nodi degli elementi sono dunque consentiti solo spostamenti, mentre non sono previsti gradi di libertà di rotazione. Tutti i gradi di libertà sono riferiti ad uno stesso sistema di riferimento inerziale globale; a tale sistema di riferimento sono anche riportate tutte le forze di inerzia e le forze interne agenti sui singoli elementi.

Le equazioni del moto scritte elemento per elemento rispetto al sistema di riferimento globale indicato assumono la forma matriciale seguente:

E I F

F X

dove X è il vettore delle posizioni nodali rispetto al riferimento globale, FI il vettore delle

forze interne, FE quello delle forze esterne e M la matrice di massa del sistema. L’equazione

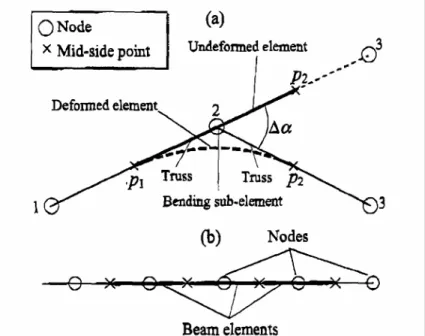
(2.10) è stata risolta utilizzando un algoritmo di integrazione di Newmark a passo variabile. Per poter modellare la rigidezza flessionale della cinghia senza utilizzare gradi di libertà di rotazione, è stato sviluppato un elemento finito trave a 3 nodi avente esclusivamente gradi di libertà di spostamento. L’elemento completo è costituito da due sottoelementi asta (p12 e 2p2)

e da un elemento elastico flessionale a molla di torsione (p12p2) come mostrato in figura 2.6;

la forza interna assiale nel sottoelemento asta è data da

l l CA l l l EA F & 0 0 0 ) ( − + = _(2.11)

dove E è il modulo di Young, C il modulo di smorzamento, A l’area effettiva della sezione trasversale, l e l0 le lunghezze effettive e a riposo dell’elemento.

Il momento flessionale nel sottoelemento è invece dato da α α & 0 0 L CJ L EJ M = ∆ + _(2.12)

in cui J è il momento di inerzia effettivo della sezione trasversale della cinghia, L0 è la

lunghezza indeformata dell’elemento flessionale data da p12 più 2p2 e ∆α è la variazione di

angolo tra p12 e 2p2.

Fig. 2.6 (a) Elemento trave a 3 nodi

(b) suddivisione di una trave usando elementi trave a 3 nodi

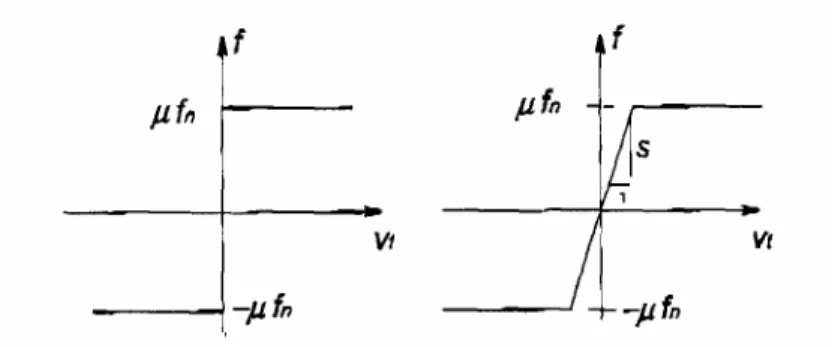
Il contatto tra cinghia è puleggia è modellato utilizzando una formulazione Penalty ed una legge di attrito trilineare dipendente dallo scorrimento tra le superfici in contatto (figura 2.7). Quando un nodo di un elemento finito impatta la superficie della puleggia (assimilata ad un corpo rigido) si sviluppa una forza di contatto proporzionale alla penetrazione fittizia che il nodo ha subito all’interno della superficie di contatto. La ricerca della condizione di impatto viene eseguita calcolando la distanza del nodo dall’asse di rotazione della puleggia e confrontandola con il raggio della puleggia stessa; quando la distanza risulta minore del raggio, la loro differenza indica la penetrazione del nodo all’interno della superficie e fornisce quindi il corrispondente valore della forza di contatto sul nodo.

Fig. 2.7 Leggi di attrito (a) coulombiano (b) trilineare dipendente dallo scorrimento

Per quanto concerne le condizioni al contorno, è imposta la velocità angolare della puleggia motrice così come la coppia resistente sull’albero della puleggia condotta.

L’accelerazione angolare della puleggia condotta viene calcolata considerando la coppia resistente applicata e la somma delle azioni tangenziali di attrito esplicate nel contatto con la cinghia:

belt accessory T

T

Iω& = + (2.13)

Taccessory è la coppia resistente applicata agli elementi condotti, Tbelt è la coppia esercitata dagli

elementi di cinghia e vale

∑

dove Fbelt è la forza di attrito esercitata sul nodo i-esimo e N il numero di nodi in contatto.

I risultati forniti dal modello riguardano l’andamento delle forze tangenziali nella cinghia e delle pressioni normali; di particolare interesse risultano i grafici della pressione laterale calcolati al variare del parametro rigidezza flessionale della cinghia.

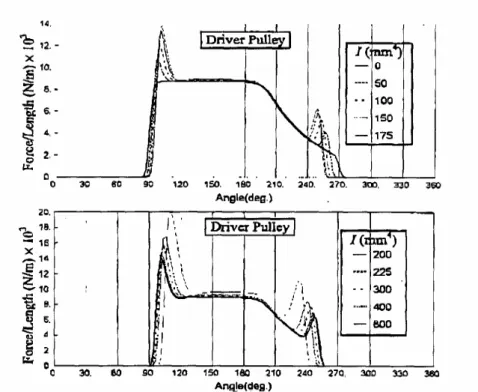
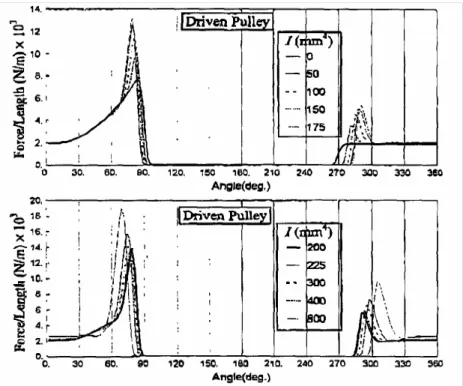
In figure 2.8 e 2.9 sono riportati tali andamenti per la puleggia motrice e condotta; in entrambi i casi le curve ottenute presentano degli importanti picchi di pressione nelle fasi di ingresso e uscita dalle pulegge. Questi picchi si amplificano notevolmente all’aumentare del momento di inerzia della sezione trasversale, mentre nella zona centrale dell’arco di contatto l’influenza di questo parametro è trascurabile.

Questo fenomeno può essere giustificato con il fatto che nelle zone di ingaggio e disingaggio la cinghia è soggetta a sollecitazioni maggiori a causa del cambio repentino del raggio di curvatura; all’aumentare del momento di inerzia la cinghia si adegua con sempre maggiori difficoltà a questa rapida rotazione, risente di una inerzia più elevata e tende maggiormente ad “appoggiarsi” alla puleggia per frenare la sua inerzia. Nel lavoro non sono state tuttavia condotte prove comparative su pulegge di raggio diverso per verificare che effettivamente il fenomeno dipenda essenzialmente dal raggio di curvatura della puleggia.

Inoltre è stato osservato che il raggio di avvolgimento della cinghia sulle pulegge decresce all’aumentare della rigidezza a flessione; indicativamente si passa da un angolo di avvolgimento di 180° con rigidezza nulla a un angolo prossimo ai 140° con una rigidezza flessionale pari a 800 mm4.

Fig. 2.8 Effetto del momento di inerzia flessionale sulla pressione laterale nella puleggia motrice

Fig. 2.8 Effetto del momento di inerzia flessionale sulla pressione laterale nella puleggia condotta

2.3 Modello a parametri concentrati per l’analisi di trasmissioni a

serpentina

Un modello di trasmissione a parametri concentrati piuttosto semplificato è quello illustrato nel lavoro di Barker e Breig [6]; il modello proposto ha lo scopo di analizzare l’andamento delle tensioni in un sistema di trasmissione a serpentina utilizzato nelle automobili per l’azionamento dei servizi ausiliari (pompa dell’acqua, ventola di raffreddamento, ecc.).

Sulla base di osservazioni e misurazioni sperimentali su un sistema funzionante, gli autori propongono nel lavoro le seguenti ipotesi semplificative:

o si trascurano tutti gli slittamenti macroscopici tra cinghia e pulegge;

o si considera la deformazione della cinghia esclusivamente in direzione longitudinale, trascurando le deformazioni trasversali;

o si trascura la massa della cinghia, eccetto che per l’influenza sulla tensione dovuta alla forza centrifuga;

o si trascura l’andamento della tensione all’interno degli archi di contatto con le pulegge, considerando i soli valori all’ingresso e all’uscita.

Il dato di ingresso da fornire al modello è il profilo di accelerazione imposto al volano dell’albero motore, mentre vengono calcolate le velocità angolari delle altre pulegge rispetto a quella del volano e le tensioni nei rami rettilinei.

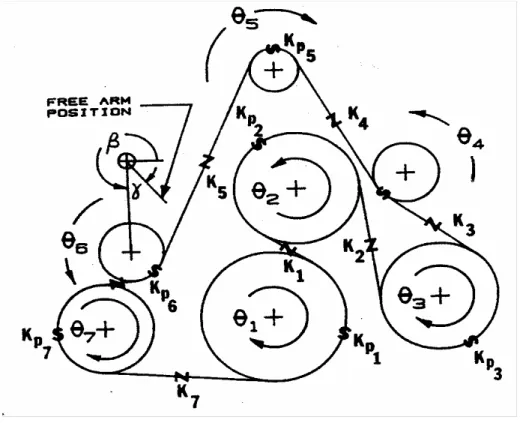
Per fare ciò la cinghia è stata suddivisa in più parti: i rami rettilinei e gli archi di contatto sono sostituiti da molle lineari prive di massa (si veda la figura 2.9), la cui costante elastica è calcolata dividendo la rigidezza estensionale della cinghia per la lunghezza a riposo delle molle.

La tensione nel ramo di trasmissione i-esimo può essere rappresentata dalla relazione i i i i T v T K F = + = 0 + ∆ 2 ρ (2.15) in cui

Fi = tensione totale nel ramo i-esimo

Ti = componente della tensione senza il termine centrifugo T0 = tensione statica

Ki = rigidezza della molla i-esima ∆i = deformazione della molla i-esima ρv2 = componente centrifuga della tensione

La deformazione delle molle nei tratti a contatto con le pulegge viene valutata considerando una media pesata tra le tensioni nei rami di ingresso e uscita secondo la relazione

2 1

, T T (1 ) v

T_iaver = _i ⋅ε_i + _i+ ⋅ −ε_i +ρ (2.16)

dove il valore di εi varia con il carico; per semplicità si è assunto nel lavoro εi = 0.5.

Il valore della deformazione della molla lineare che sostituisce il ramo rettilineo può essere calcolato secondo il seguente approccio: si consideri il primo tratto tra le pulegge 1 e 2 in

figura 2.9; quando le pulegge subiscono uno spostamento rigido sotto forma di rotazioni θ1 e θ2 la cinghia lascia la puleggia 2 e si avvolge sulla puleggia 1 (seguendo il verso indicato dalle

rotazioni delle pulegge). In più c’è una parte aggiuntiva di cinghia che lascia la puleggia 2 dovuta all’allungamento della molla Kp2; l’allungamento totale della molla K1 può essere

allora scritto come

2 2 2 1 1 1 = θ − θ −δ ∆ R R (2.17) dove

R1θ1 = cinghia che si avvolge sulla puleggia 1 R2θ2 = cinghia che lascia la puleggia 2

2 0 2 , 2 p aver K T T − =

δ contributo dovuto all’allungamento di Kp2

Tenendo presente la relazione generale

i i i R

R₁(θ₁ − )φ = θ (2.18)

che lega cinematicamente la rotazione del volano con la rotazione delle pulegge condotte nel caso di allungamenti elastici dei rami, si ottiene la relazione per l’allungamento del ramo K1:

2 2 1

1 = φ −δ

∆ R (2.19)

Scrivendo relazioni analoghe alla (2.15) per tutti i rami rettilinei e aggiungendo le relazioni per il ramo a contatto con il tensionatore si ottiene un sistema di N equazioni (N è il numero dei rami rettilinei) da cui è possibile ricavare il valore delle tensioni nei rami per diversi valori dell’angolo di fase Φi tra il volano e la puleggia i-esima.

Per ottenere infine le equazioni del moto delle pulegge basta scrivere l’equazione di equilibrio a rotazione attorno al proprio asse considerando quali forze attive le tensioni esercitate dai

Più che per i risultati ottenuti, che riguardano il caso specifico delle trasmissioni a serpentina, il modello proposto risulta di interesse per la metodologia di analisi di una trasmissione a cinghia che esso propone. Risulta evidente che, a causa delle ipotesi semplificative fatte all’inizio del paragrafo, un modello siffatto non è utilizzabile nel caso di una trasmissione CVT, in cui interessa invece conoscere il valore della tensione e della pressione laterale in ogni punto dell’arco di contatto e in cui non ci si può accontentare della semplice relazione (2.16) proposta in [6]. Tuttavia il modello esposto si propone come un primo passo verso la definizione di un modello a parametri concentrati completo che evidenzi con buona accuratezza gli aspetti essenziali di una trasmissione CVT; il modello proposto nel paragrafo successivo rappresenta un ulteriore passo in avanti nello sviluppo di uno strumento che possa essere effettivamente di aiuto nelle fasi di definizione di massima delle caratteristiche di una trasmissione.

2.4 Modello per l’analisi dell’andamento delle tensioni nell’arco di

contatto tra cinghia e puleggia

Un modello di trasmissione più accurato rispetto al precedente è stato sviluppato da Harrison [7]; lo scopo principale del lavoro di Harrison è quello di determinare l’effettivo andamento delle tensioni all’interno dell’arco di avvolgimento tra cinghia e puleggia, in modo da ricavare per via numerica il classico andamento esponenziale delle tensioni previsto nei modelli presenti in letteratura. Inoltre il modello serve anche per una stima più precisa del coefficiente di attrito effettivo tra cinghia e puleggia servendosi delle tensioni calcolate nei rami teso e lento.

Il lavoro di Harrison prevede la suddivisione della parte di cinghia a contatto con la puleggia in elementi discreti dotati di massa e collegati tra loro tramite elementi elastici e smorzanti di rigidezza opportuna come illustrato in figura 2.10.

I rami rettilinei sono assimilati a molle lineari il cui valore di rigidezza è legato a quello delle molle che schematizzano l’arco di contatto e alla lunghezza dei tratti rettilinei.

La puleggia è libera di spostarsi in direzione orizzontale in modo da settare prima della simulazione il livello di pretensione voluto nella cinghia.

Le ipotesi principali che l’autore propone sono le seguenti:

o ciascuna molla è collegata alla massa in una posizione tale da non generare momenti a rotazione della stessa attorno al proprio asse (in sostanza la massa è assimilata ad un punto materiale in moto esclusivamente attorno alla puleggia);

o si trascurano gli spostamenti radiali delle masse verso il centro della puleggia; o si trascurano gli eventuali urti tra massa e puleggia;

o si assume che il coefficiente di attrito tra cinghia e puleggia sia quello statico in condizioni di aderenza e passi istantaneamente al valore dinamico nelle fasi di slittamento.

La condizione al contorno imposta al modello è una coppia motrice applicata alla puleggia in maniera crescente fino al punto in cui tutte le masse passano dalla condizione di aderenza alla condizione di strisciamento; quando questa condizione si verifica la simulazione viene interrotta.

Durante la simulazione viene registrata la posizione di tutte le masse e la tensione delle molle, legata allo spostamento relativo tra le masse.

Le prove condotte hanno interessato cinghie ad elevata rigidezza a trazione (k = 1000 kN/m), in pratica le cinghie in gomma rinforzate già descritte nel capitolo 1 e utilizzate nelle trasmissioni CVT; la cinghia è stata modellata con 4 elementi massa e 5 molle sull’arco di contatto ed è stata pretensionata fino ad un valore di 100 kN.

Nelle figura 2.11 sono riportati gli andamenti temporali delle tensioni nelle molle all’interno dell’arco di contatto, mentre nella figura 2.12 sono indicati gli andamenti delle tensioni nei rami rettilinei. Le tensioni raggiunte prima dello scorrimento valgono T1 = 202 kN e T2 = 8

kN, per un rapporto T1/T2 = 25.25; utilizzando la relazione classica µβ

e TT =₂

1

e assumendo un valore dell’arco di contatto β = 220° si trova un valore del coefficiente di attrito effettivo µ = 0.84.

Se la pretensione iniziale cala a 85 kN, le tensioni nei rami valgono rispettivamente T1 = 172

kN e T2 = 14.1 kN, per un rapporto T1/T2 = 12.226; il coefficiente di attrito in questo caso vale

µ = 0.654.

Fig. 2.12 Tensioni nei rami rettilinei in funzione del tempo

Nel lavoro si evidenzia chiaramente il legame tra la pretensione iniziale applicata alla cinghia e i valori di tensione nei rami teso e lento; in particolare un aumento della pretensione garantisce un rapporto T1/T2 più elevato, e quindi una tensione utile più elevata (oppure, come

indicato nel lavoro, un coefficiente di attrito “apparente” più elevato).

Tuttavia nel modello esposto in questo paragrafo manca del tutto qualsivoglia indicazione sulla dinamica radiale della cinghia, ossia sulle pressioni di contatto che nascono al contatto con la puleggia e sull’incuneamento nella gola della stessa.

Per questo il modello di Harrison [7], pur costituendo uno strumento decisamente più accurato di quelli di Barker [6] illustrato nel paragrafo precedente, non rappresenta ancora un valido aiuto nell’analisi della dinamica di un sistema complesso quale una trasmissione a cinghia CVT.

2.5 Limiti dei modelli trattati

A conclusione di questo capitolo, si esaminano i vari modelli proposti riassumendone i limiti e pregi nella trattazione del problema.

Lo studio teorico condotto da G. Gerbert [3], si colloca nell’ambito di un’estesa ricerca delle caratteristiche di funzionamento di trasmissioni a cinghia trapezoidale, mettendo in risalto il meccanismo di moto radiale e circonferenziale della cinghia nella gola della puleggia, e determinando quindi l’andamento dell’angolo di scorrimento e dello spostamento radiale nell’arco di contatto. La trattazione seguita per determinare la soluzione del problema nell’arco di contatto richiede l’integrazione numerica di un sistema d’equazioni differenziali piuttosto complicato. Si mette in luce l’esistenza di una zona attiva nell’arco di contatto, in cui si ha spostamento circonferenziale (relativo alla puleggia) della cinghia e conseguente forza d’attrito che trasmette coppia, ed una zona inattiva in cui lo spostamento della cinghia è sostanzialmente radiale.

Il modello, pur essendo in grado di fornire l’andamento della pressione laterale esercitata sulla cinghia nell’arco di contatto e l’influenza su di essa di alcuni parametri, richiede, per l’integrazione, delle condizioni iniziali di difficile attribuzione, e come visto, le soluzioni vengono a dipendere fortemente da quest’ultime, dando origine in certi casi ad instabilità e quindi inaccettabilità della soluzione; il modello risulta quindi difficilmente utilizzabile in fase di progettazione, anche per le numerose prove sperimentali da eseguire per determinare

alcune costanti utilizzate nel modello stesso (es. le rigidezze k1, k2, k3 descritte nel paragrafo 2.1.4).

Il modello in questione, inoltre, non tiene conto delle forze d’inerzia subite dalla cinghia e tratta casi in cui la velocità di rotazione è molto piccola o la massa della cinghia trascurabile, ipotesi che nel caso di moderni CVT per motorscooter appaiono entrambe inaccettabili.

Ulteriore limite è rappresentato dal fatto che il modello tiene in considerazione la soluzione del problema nell’arco di contatto, non trattando la trasmissione nel suo insieme, e trascurando la sua dinamica, come le proprietà inerziali delle pulegge e della cinghia; ad esempio la coppia trasmessa non è un dato iniziale del problema, ma è funzione del valore della tensione dato come condizione iniziale nell’arco di contatto. La teoria inoltre può non essere adeguata per cinghie dentellate come quelle normalmente utilizzate in un CVT.

Il lavoro proposto da Leamy e Wasfy [5] si inserisce invece in un filone di ricerca che si propone di rappresentare la dinamica delle trasmissioni a cinghia utilizzando modelli di analisi agli elementi finiti o di tipo multibody, risolti per via numerica grazie alle potenzialità oggi offerte dai moderni sistemi di calcolo.

In particolare il modello di Leamy si basa sulla tecnica di discretizzazione di un corpo in elementi finiti delimitati da nodi in comune tra più elementi; la scrittura delle equazioni di equilibrio e delle equazioni di congruenza per ogni nodo e per ogni elemento finito garantisce la continuità della soluzione trovata e il rispetto delle condizioni al contorno imposti su alcuni nodi specifici. Il modello proposto utilizza in particolare elementi trave a 3 nodi appositamente messi a punto per la specifica analisi ed è in grado di rappresentare il comportamento dell’intera trasmissione, adattandosi anche all’analisi di trasmissioni con più pulegge disposte secondo un layout qualsiasi.

Nel lavoro emerge chiaramente l’influenza di alcuni parametri sui risultati forniti dal modello, con particolare attenzione per l’effetto della velocità di rotazione e della rigidezza flessionale della cinghia. In questo senso il lavoro di Leamy risulta utilizzabile in maniera più rapida rispetto al complesso sistema di equazioni del modello analitico di Gerbert in quella fase della progettazione di una trasmissione in cui si richiedono scelte di massima, di cui occorre prevedere l’influenza sul funzionamento reale senza che si debba ricorrere a complicati ed onerosi schemi di calcolo.

Tuttavia anche un modello agli elementi finiti come quello appena descritto si presta poco a tale utilizzo, essendo più indicato per uno studio approfondito di verifica del comportamento di una trasmissione già esistente.

I modelli di calcolo che sembrano più adatti ad essere utilizzati nelle fasi di scelta e confronto tra soluzioni costruttive differenti sono quelli a parametri concentrati, schema a cui possono essere ricondotti quelli illustrati nei lavori di Barker [6] ed Harrison [7].

Il modello proposto da Barker tuttavia risulta forse giustificato per il campo specifico per cui è stato sviluppato, ossia l’analisi delle tensioni nei rami di una trasmissione a serpentina; in questa sede è stato riportato unicamente per evidenziare il procedimento logico che consente di passare dal sistema reale ad un modello avente un certo numero finito di parametri attraverso step successivi di approssimazioni, considerando prima uno schema semplificato ed aggiungendo poi quei dettagli che sembrino indispensabili per una corretta rappresentazione del sistema reale.

Seguendo la logica appena esposta, il modello proposto da Harrison [7] costituisce lo step successivo nello sviluppo del modello di Barker; esso infatti consente di conoscere punto per punto l’andamento della tensione nella cinghia avvolta sulla puleggia e di prevedere la quantità di coppia motrice disponibile per l’azionamento della seconda puleggia, fornendo in qualche modo una stima, sebbene piuttosto grossolana, delle perdite di coppia nella trasmissione.

Il modello di Harrison presenta comunque delle ipotesi semplificative che risultano inaccettabili in un modello che descriva il funzionamento di una trasmissione CVT. In particolare la mancanza di azioni inerziali sulle masse discrete del modello non consente uno studio del sistema ad elevata velocità, così come la mancanza di uno schema per il computo della penetrazione radiale della cinghia non consente di fare previsioni circa l’andamento delle pressioni laterali.

Per quanto detto nel paragrafo 1.5, proprio la pressione laterale sui fianchi della cinghia rappresenta invece un parametro fondamentale per una stima della durata della stessa e, quindi, per una valutazione oggettiva sulla bontà della progettazione della trasmissione. Risulta evidente quindi che un modello di calcolo accurato dell’intera trasmissione debba prevedere degli schemi per descrivere il contatto tra cinghia e puleggia, per descrivere le azioni di attrito scambiate e per tenere conto degli scorrimenti locali, che determinano delle dissipazioni di lavoro e, in ultima analisi, un calo di rendimento della trasmissione.

Inoltre è necessario che il modello tenga conto del contributo dell’inerzia delle pulegge sulla dinamica dell’intero sistema.

Lo sviluppo di un modello con queste caratteristiche sarà tentato nel presente lavoro di tesi; nel capitolo 3 saranno introdotti gli elementi costitutivi fondamentali del modello, mentre nel

capitolo 4 e nel capitolo 5 saranno indicate le problematiche relative al suo funzionamento e