Capitolo 3 Disuguaglianza nella distribuzione della ricchezza

Capitolo 3

Disuguaglianza nella distribuzione della ricchezza

Una volta esaminato, nell’ambito di un’economia stazionaria, l’impatto di variabili demografiche sul livello di ricchezza aggregata e sul rapporto ricchezza-reddito, resta da chiedersi come queste variabili possano influenzare la distribuzione della ricchezza stessa. Sebbene, infatti, il modello del ciclo di vita sia in grado di dare origine ad un sistema perfettamente ugualitario, ipotizzando che tutti gli individui effettuano lo stesso consumo programmato e ricevono lo stesso ammontare di reddito annuo, la ricchezza, essendo funzione dell’età degli individui, non è affatto distribuita in maniera ugualitaria. Questo aspetto fu messo in evidenza per la prima volta da Atkinson, nel 19711.

L’obiettivo di questo capitolo è, quindi, quello di riprendere l’analisi di Atkinson e di ampliarla al modello del ciclo di vita con consumo costante per adulto equivalente, per valutare l’influenza delle variabili demografiche sulla distribuzione della ricchezza in una società perfettamente ugualitaria.

Per far questo è innanzitutto indispensabile dedicare un primo paragrafo alla trattazione delle principali misure di variabilità, in modo da poterle successivamente utilizzare per misurare il grado di disuguaglianza sia nel modello di base di Modigliani – Brumberg, sia nella sua versione estesa. L’analisi sarà rivolta soprattutto a tre indici: il rapporto di concentrazione di Gini, il coefficiente di variazione e l’indice T di Theil. E’ importante precisare che oltre agli indici appena citati, esistono molti altri modi per misurare la variabilità di una distribuzione, alcuni dei quali verranno brevemente illustrati nella prima parte di questo paragrafo. A conclusione di questo paragrafo, infine, saranno enunciate le principali proprietà desiderabili per le misure di variabilità, al fine di individuare la misura più idonea.

Esaurita questa prima parte statistico – matematica, passeremo all’analisi della disuguaglianza nella distribuzione della ricchezza. Nel secondo paragrafo, riprendendo il lavoro di Atkinson, esamineremo il grado di disuguaglianza nel modello di base di Modigliani – Brumberg. Nel terzo paragrafo, invece, analizzeremo l’andamento della disuguaglianza nel modello del ciclo di vita che considera come unità economica

1

Atkinson A.B., The distribution of wealth and the individual life cycle. In: Oxford Economic Papers, New Series, Vol. 23, No. 2, July 1971, pp. 239-254.

rilevante la famiglia. Utilizzando i tre indici di concentrazione precedentemente descritti, si guarderà all’andamento della disuguaglianza a seguito di variazioni del tempo in cui vengono generati i figli, T, e del loro periodo di mantenimento, M.

3.1

Misure di variabilità: dispersione e disuguaglianza

2

Per variabilità si intende la capacità di una variabile di assumere differenti modalità, in quanto un fenomeno può variare in ragione del tempo, del territorio e dei soggetti. La variabilità è, quindi, tanto maggiore quanto più grandi sono le differenze tra i soli termini della distribuzione, oppure tra di essi ed un valore caratteristico del fenomeno in questione. Per questo, nel misurare la variabilità di una distribuzione, si distingue tra dispersione e disuguaglianza. La dispersione, infatti, misura di quanto, in media, le quantità rilevate sono distanti da un valore centrale, identificato con un indice di posizione (generalmente media o mediana). La disuguaglianza, invece, misura di quanto, in media, le varie grandezze rilevate differiscono tra loro. Un indice di variabilità per essere tale deve possedere almeno due proprietà:

- essere nullo quando tutti i termini della distribuzione sono uguali tra loro; - crescere all’aumentare della disuguaglianza tra i termini.

Se la variabile osservata è trasferibile tra le unità del collettivo, cioè se è possibile ammettere che gran parte dell’ammontare totale della variabile sia posseduto da una piccola frazione dell’insieme delle unità statistiche, allora è possibile parlare di concentrazione. Più esiste disparità tra le unità statistiche in relazione alla quantità di carattere posseduto, maggiore è il grado di disuguaglianza e più elevata è la variabilità del carattere. Si ha la massima concentrazione quando tutto l’ammontare complessivo della variabile è posseduto da una sola unità statistica. Per contro, la variabile non è affatto concentrata se il suo ammontare è distribuito uniformemente tra tutte le unità statistiche; in tal caso si parla di equidistribuzione.

2

Questo paragrafo è stato scritto facendo riferimento ai seguenti libri:

- Cowell F.A., Measuring Inequality,, Harvester Wheatsheaf, Hemel Hempstead, 1995. - Girone G., Salvemini T., Lezioni di statistica, ed. Bari: Cacucci Editore, 2001, pp. 157-191. - Leti G, Statistica descrittiva, ed. Bologna: il Mulino, 1983, pp. 367-466.

Qualsiasi misura di concentrazione deve essere in grado di misurare i trasferimenti della variabile tra le unità statistiche, ciò significa che se una frazione dell’ammontare totale passa da un’unità all’altra, senza però modificare né l’ammontare complessivo né la media della variabile in esame, la misura di concentrazione deve comunque variare. Inoltre, ogni misura di concentrazione deve essere nulla nel caso di equidistribuzione e massima nel caso di massima concentrazione.

Nel corso di questo paragrafo presenteremo le principali misure di variabilità presenti in letteratura. Vedremo però, che non tutte possono essere considerate misure di concentrazione, proprio a causa della loro incapacità di misurare i trasferimenti della variabile tra le unità. Ovviamente, avendo come obiettivo ultimo quello di misurare la disuguaglianza nella distribuzione della ricchezza da ciclo di vita, un’attenzione maggiore sarà posta a quelle misure che, invece, sono in grado di farlo.

3.1.1 Alcune misure di variabilità

Gli indici più semplici che possono essere utilizzati per misure la variabilità di una distribuzione sono quelli che si basano sulla graduatoria dei termini. Un esempio di questi indici è il campo di variazione, che è dato dalla differenza tra il termine più grande e il termine più piccolo della distribuzione in esame:

(1) V =xN −x1,

dove è l’ultimo termine nel caso in cui le siano ordinate in modo non decrescente.

N

x xi

E’ evidente che quanto maggiore è V tanto maggiore è la differenza tra le grandezze rilevate. Il campo di variazione presenta però un grosso inconveniente, in quanto tenendo conto solamente dei due valori estremi e prescindendo da tutti gli altri termini della distribuzione, risulta essere una misura molto sensibile a situazioni eccezionali, che facilmente possono influenzare i valori estremi. Inoltre, aumentando la numerosità del campione aumenta la probabilità di includere termini che possono far aumentare sensibilmente V. Per questo motivo il confronto tra distribuzioni diverse, attraverso la misura del campo di variazione, può avvenire solo quando le distribuzioni in esame possiedono all’incirca lo stesso numero di osservazioni.

Proprio a causa di questa sua eccessiva sensibilità, spesso è preferibile utilizzare la differenza interquartilica che, appunto, è data dalla differenza tra il terzo e il primo quartile:

(2) d_q =Q₃ −Q₁.

Si ricordi che per primo quartile, Q1, di una variabile X si intende quel valore al di

sotto e al di sopra del quale stanno, rispettivamente, ¼ e i ¾ dei valori della variabile. Simmetricamente, il terzo quartile, Q3, rappresenta quel valore al di sotto e al di sopra

del quale stanno, rispettivamente, i ¾ e ¼ dei valori della variabile X. Dalle seguenti

definizioni risulta chiaro che tra Q1 e Q3 si trova il 50% delle osservazioni della

variabile in esame.

Questo indice è meno sensibile del campo di variazione. Inoltre, tanto minore è la differenza interquartilica, tanto minore è la differenza tra le grandezze osservate, poiché significa che il 50% di esse si trova in un intervallo più piccolo. L’inconveniente più grande della differenza interquartilica è dato dal fatto che, anche in questo caso, si tiene solamente conto di due valori della distribuzione; di conseguenza, i termini interni ed esterni a

(

Q₁,Q₃

)

non influenzano il suo valore.

Facendo sempre riferimento ai quartili è anche possibile calcolare il rapporto interquartilico:

(3) r_q =Q₃ Q₁.

Questo rapporto può assumere qualsiasi valore tra uno ed infinito e bassi valori di riflettono una più bassa disuguaglianza. Anche il rapporto interquartilico, però, guarda solamente a due distinti punti della distribuzione, senza considerare la maggior parte dei dati.

q

r

Appare, quindi, evidente che le misure appena citate, oltre a presentare dei grossi inconvenienti, non sono in grado di misurare i trasferimenti della variabile tra le unità statistiche, per questo spesso vengono impiegate misure di variabilità maggiormente sofisticate3.

3

Per non rendere questo paragrafo eccessivamente pesante, l’analisi sarà rivolta esclusivamente alle tre misure di variabilità che verranno successivamente utilizzate in questo lavoro. E’ opportuno, però, precisare che esistono altre misure di disuguaglianza ampiamente utilizzate in letteratura, come l’indice di Atkinson e l’indice di Dalton; per un’analisi più approfondita si faccia riferimento al seguente testo: - Cowell F.A., Measuring Inequality (second edition), Harvester Wheatsheaf, Hemel Hempstead, 1995.

3.1.2 Il rapporto di concentrazione di Gini

Nel 1914 lo statistico Corrado Gini propose una nuova misura di disuguaglianza, che nel tempo ha avuto un vasto successo.

Per facilitare l’esposizione supponiamo che la variabile X rappresenti la distribuzione

della ricchezza in un’economia; tenendo presente, però, che quanto diremo è valido per qualsiasi variabile trasferibile.

Siano le modalità della variabile statistica, corrispondenti, nel nostro caso, a diverse quantità di ricchezza, disposte in ordine non decrescente. Essendo N il

numero di unità osservate (individui), si ponga: N x x x1, 2,..., (4) 1 = 1 , 2 = 2 ,..., = ,..., = =1 N N p N i p N p N p i N ;

con che rappresenta del numero totale delle unità osservate, che ne rappresenta i e così via; con che rappresenta, quindi, la frazione cumulata dei primi i individui. Si definisca inoltre:

1

p 1/N p₂

N

/

2 p_i

(5) S₁ = x₁, l’ammontare di ricchezza detenuto dalla prima unità; S₂ = x₁+x₂, l’ammontare di ricchezza detenuto dalle prime due unità; ...

Si =x1+x2 +...+xi, l’ammontare di ricchezza detenuto dalle prime i unità; ...

S_N =x₁ +x₂ +...+x_N, l’ammontare complessivo di ricchezza. A questo punto è possibile determinare i seguenti rapporti:

(6) , 2 2 ,..., ,..., 1 1 1 = = = = = N N N N i i N N S S q S S q S S q S S q ;

con che rappresenta la frazione di ammontare totale di ricchezza detenuto dalla prima unità, la frazione di ammontare totale detenuto dalle prime due unità e così via.

1

q

2

q

Se la ricchezza è ugualmente distribuita tra le N unità si ha che , in quanto una data frazione di individui possiede la medesima frazione dell’ammontare totale di ricchezza; altrimenti si ha che in quanto, avendo ordinato in senso non decrescente le modalità , una data frazione di individui deve possedere necessariamente una frazione minore dell’ammontare totale di ricchezza. Un fenomeno sarà tanto più concentrato quanto più piccola sarà la frazione dell’ammontare

i i q p = i i q p > i x

complessivo di ricchezza che spetta a quella data frazione di individui; in altre parole, un fenomeno sarà tanto più concentrato quanto maggiori saranno le differenze . Infatti, quanto maggiore è la differenza

i

i q

p −

i

i q

p − , tanto maggiore è l’ammontare di

ricchezza concentrato nelle mani dei rimanenti N−i individui. In altre parole, la differenza misura l’ammontare di ricchezza che manca ai primi i individui per

trovarsi in una situazione di equidistribuzione. Da quanto detto si deduce che le differenze costituiscono già di per sé una misura di concentrazione.

i i q p − i i q p −

In effetti, il rapporto di concentrazione di Gini altro non è che una normalizzazione di tali differenze: (7)

(

)

∑

∑

− = − = − = ₁ 1 1 1 N i i N i i i p q p R .

E’ facile verificare che il rapporto di concentrazione di Gini oscilla tra zero, nel caso di equidistribuzione, cioè quando pi = per ogni i, e uno nel caso di massima qi concentrazione, cioè quando q_i =0 per i che va da 1 a N−1 e q_N = p_N =1.

Tutti i possibili casi di concentrazione posso essere rappresentati graficamente ponendo in ascissa i valori ed in ordinata i corrispondenti valori , ottenendo in questo modo la

i

p q_i

curva di Lorenz, detta anche curva di concentrazione. La curva di Lorenz è contenuta in un quadrato di lato unitario ed è sempre convessa verso l’asse delle ascisse, in quanto, avendo orinato le in ordine non decrescente, ad incrementi unitari delle corrispondono incrementi crescenti delle .

i x i p q_i 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Pi Qi O A B

Il punto individuato dalla coppia di valori

(

p ,_i q_i

)

rappresenta i primi i individui più

poveri, che sono i N del totale degli individui e possiedono una frazione della

ricchezza totale pari a

(

)

∑

= + + + N j j i x x x x 1 2 1 ... .

La situazione di equidistribuzione è rappresentata dalla bisettrice del quadrato di lato unitario, nota come segmento di equidistribuzione, i cui punti hanno ascissa e ordinata uguali; mentre la situazione di massima concentrazione è rappresentata dai lati OA e BA del triangolo OAB in figura 3.1. La concentrazione è, quindi, tanto maggiore quanto più la curva di Lorenz è lontana dal segmento di equidistribuzione.

E’ facile dimostrare che il rapporto di concentrazione di Gini è uguale a due volte l’area compresa tra la curva di Lorenz e il segmento di equidistribuzione, detta area di concentrazione. Difatti, il numeratore di R, che può essere scritto come

∑

(

)

− = − 1 1 1 N i i i q p N ,

non è altro che la somma delle aree dei rettangoli di base 1 N e altezza pi − e qi rappresenta, quindi, un valore approssimato dell’area di concentrazione. Analogamente il denominatore di R, che può essere scritto come

∑

− = 1 1 1 N i i p N , rappresenta il valore

approssimato dell’area del triangolo di massima concentrazione, pari ad ½. Quindi:

= = ione concentraz massima di ta approssima area ione concentraz di ta approssima area R ione concentraz di ta approssima area ione concentraz di ta approssima area * 2 2 = = .

Tanto più elevato è il numero delle unità statistiche, N, tanto più fitti sono i rettangoli e tanto migliore è l’approssimazione.

Un’altra procedura utilizzata per calcolare il rapporto di concentrazione di Gini è il cosiddetto metodo dei trapezi, che consiste nel determinare l’area residua (la differenza tra l’area di massima concentrazione e l’area di concentrazione), tenendo presente che essa è uguale alla somma delle aree dei trapezi sottostanti alla curva di Lorenz:

(8)

(

)(

i i N i i i p q q p R = − − ₊ + − = +

∑

1 1 0 1 * 1

)

.

I risultati che si ottengono da R e da R non coincidono, in quanto R è *

un’approssimazione per eccesso dell’area di concentrazione, mentre R lo è per difetto. *

(9) R N N

R* = −1 .

In altre parole, la misura ottenuta con il metodo dei trapezi è inferiore rispetto a quella ottenuta con il metodo dei rettangoli e la divergenza tra le due misure si riduce al crescere del numero di N; quando, infatti, N è molto grande,

(

N −1

)

N diviene approssimabile all’unità e quindi si ha R* =R.

Il principale svantaggio del rapporto di concentrazione di Gini risiede nel fatto che può assumere uno stesso valore per due situazioni distributive sensibilmente differenti (due diverse curve di Lorenz), come mostrato in figura 3.2.

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Pi Qi

Figura 3.2 – Curve di Lorenz diverse per uno stesso valore di R.

3.1.3 La varianza e il coefficiente di variazione

La varianza è una misura di dispersione, in quanto misura la variabilità di una distribuzione calcolando la media degli scarti, tra le singole quantità rilevate e la media aritmetica μ, al quadrato4: (10)

(

)

N x N i i 2 1 2

∑

= − = μ σ .

Data una distribuzione di N termini, che abbia media aritmetica μ e che sia ottenuta in base ad una variabile trasferibile le cui modalità sono non negative e per la quale

4

Nel caso di una distribuzione in cui le xi sono associate alle frequenze ni si ha: ( )

N n xi i

∑

− = 2 2 μ σ .

hanno significato le modalità 0 e N , la varianza di tale distribuzione è una misura non μ

negativa che varia tra 0 (nel caso in cui tutte le modalità sono tra loro uguali) ed un massimo (nel caso in cui una sola modalità racchiude l’intero fenomeno) pari a:

.

(

1

)

2 2 max =μ N− σ

Essendo però espressa nell’unità di misura della variabile al quadrato, spesso è preferibile usare lo scarto quadratico medio, che è definito come la radice quadrata della varianza: (11)

(

)

N x N i i

∑

= − = 1 2 μ σ .

Sia lo scarto quadratico medio sia la varianza sono considerati indici di variabilità assoluta, in quanto sono espressi nella stessa unità di misura della variabile in esame. Il fatto che la varianza non sia indipendente dall’unità di misura fa sì che se una data variabile X, che supponiamo rappresenti la distribuzione della ricchezza in un’economia, viene moltiplicata per una qualsiasi costante b, la sua varianza non resta costante ma viene moltiplicata per b2. Questo risultato, però, non è auspicabile, in quanto non permette di eseguire correttamente il confronto tra le variabilità di distribuzioni differenti. Se, infatti, tutte le modalità della variabile X cambiano nella stessa proporzione, è necessario poter argomentare che non c’è stata nessuna alterazione nella distribuzione della ricchezza; di conseguenza, la misura di variabilità deve rimanere invariata. Per questo motivo è sempre preferibile utilizzare indici di variabilità relativa (indipendenti dalla unità di misura in cui è espressa la variabile), che consistono nel dividere l’indice di variabilità assoluta o per la media aritmetica o per il massimo valore di variabilità.

Prendendo come indice di variabilità assoluta lo scarto quadratico medio e dividendolo per la media μ si ottiene il coefficiente di variazione:

(12)

μ σ

=

CV ,

che misura la variazione media del fenomeno in rapporto alla sua media aritmetica5. Nel caso in cui si faccia riferimento ad una variabile trasferibile, sotto la condizione che 0 e Nμ siano modalità della variabile in esame, si ha che più basso è il coefficiente

5

Dividendo σ per il suo massimo valore si ottiene, invece, il cosiddetto scarto quadratico medio relativo, 1

−

N

μ

di variazione più ugualitaria è la distribuzione. Nel caso, infatti, di equidistribuzione tutte le modalità saranno uguali alla media e sia lo scarto quadratico medio sia il coefficiente di variazione saranno pari a zero. All’aumentare della concentrazione del fenomeno in esame, gli scostamenti dalla media in valore assoluto aumenteranno ed il coefficiente di variazione sarà via via sempre più grande, fino a raggiungere un valore massimo pari a N−1.

3.1.4 L’indice T di Theil

Nel 1967 Henri Theil propose una nuova misura di disuguaglianza a partire da un’analogia con la teoria dell’informazione e più in particolare con il concetto di entropia.

La teoria dell’informazione è parte della teoria della probabilità e riguarda la possibilità che un certo evento si verifichi. Senza entrare specificatamente nei suoi contenuti, l’analisi che segue si limita ad esporre i passaggi principali che hanno condotto alla costruzione dell’indice T di Theil.

Vi siano gli eventi , ai quali siano associate le probabilità .

Ciascun valore è compreso tra 0, nel caso in cui l’evento sia impossibile, e 1, nel caso in cui l’evento sia certo. Si supponga, ad esempio, che si verifichi l’evento e si voglia assegnare un numero, , al valore di questa informazione. Se l’evento è considerato essere molto probabile, allora l’informazione non ha molto valore, in quanto è plausibile attendersi il verificarsi dell’evento; di conseguenza,

3 2 1,e ,e e p1,p2,p3 i p 1 e

( )

p1 h e₁

( )

p1 h sarà piuttosto piccolo. Per contro, se l’evento è quasi impossibile, allora l’informazione è decisamente più importante e sarà piuttosto elevato. Da quanto detto deriva che il valore assegnato all’informazione ricevuta,

1 e

( )

p1 h

( )

p1 h , diminuisce all’aumentare di . Inoltre, se ipotizziamo che gli eventi e siano tra loro indipendenti (poiché la probabilità che si verifichi non dipende dal verificarsi o meno di ), allora la probabilità che entrambi gli eventi si verifichino insieme è data da . Ne discende che se vogliamo assegnare un valore a questa informazione,

1 p 1 e e2 1 e e₂ 2 1p p

(

p1p2

)

h , è corretto

(13) h

(

p₁p₂

) ( ) (

=h p₁ +h p₂

)

.

È immediato riconoscere che l’unica funzione in grado di soddisfare l’equazione (13), per tutti i possibili valori di p, è la funzione logaritmica. Quindi, è possibile scrivere: h=−ln

( )

p .

Se supponiamo, però, che gli eventi da prendere in considerazione siano N, allora diviene piuttosto difficile lavorare con un set di N numeri (che rappresentano le probabilità legate ai possibili eventi); per questo la teoria dell’informazione propone di aggregare tutte le probabilità in un singolo numero, capace di descrivere il “grado di disordine” del sistema. Questo numero, conosciuto tecnicamente come entropia, si ottiene calcolando l’informazione media contenuta nel sistema, che altro non è che la somma pesata di tutti i valori delle informazioni per i vari eventi, dove il peso per l’evento j è dato dalla probabilità p_j; ovvero:

(14)

( )

(

_i . N i i N i i ih p p p p entropia log 1 1

∑

∑

= = − = =

)

L’entropia è minima ed uguale a zero quando la probabilità per un particolare evento

j è pari a uno e tutti gli altri eventi hanno probabilità pari a zero. In questo caso si dice che il sistema è perfettamente ordinato e l’informazione che l’evento j si sia verificato è senza valore.

A partire da questi risultati, Theil interpreta gli N possibili eventi come gli N individui di una popolazione, ed interpreta la probabilità come l’ammontare di reddito posseduto dall’individuo j, , in rapporto al reddito totale:

j p j y (15)

∑

= = N i i j j y y s 1 , con 1. 1 =

∑

= N i i s

Infine, sottraendo il valore attuale dell’entropia legata alla distribuzione del reddito, pari a , dal massimo valore possibile, che si ottiene quando ciascun individuo possiede la stessa quota di reddito (

( )

i N i ih s s

∑

=1 N

s_i =1 ), Theil ottiene la seguente misura di disuguaglianza, che successivamente è divenuta nota come indice T di Theil:

(16)

( )

= ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

∑

∑

= = = N i y i i i N i i N i N y s N N s h s N h N T 1 1 1 ln 1 ln 1 1 1 μ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ =

∑

= N i y i y i N N N y N y 1 1 ln 1 ln μ μ

⎟= ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ =

∑

∑

= = N N y N y y N N i y i y i N i y i 1 ln 1 ln 1 ln 1 1 1 μ μ μ _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ =

∑

= y i N i y i y y N μ ln μ 1 1 ;

dove μ_y rappresenta la media aritmetica della variabile y. Il rapporto

( )

(

) (

)

{

1 N ⋅ yi μy ⋅ln yi μy

}

rappresenta il contributo di ciascun individuo alla variabilità totale.

L’indice T di Theil è a tutti gli effetti una misura di disuguaglianza. Si guardi, infatti, cosa accade a seguito di un trasferimento Δs, da un individuo A che possiede una quota

di reddito ad un individuo B che possiede una quota , con e .

La quota di reddito dell’individuo B aumenta di A

s s_B s_A >s_B Δs<<s_A,s_B

s

Δ , mentre quella dell’individuo A si riduce di Δs. Ricordando che h

( )

s =−ln

( )

s , attraverso un operazione differenziale si trova che il cambiamento nell’indice T di Theil è pari a:

(17)

[

( ) ( )

]

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ Δ − = − Δ = Δ B A B A s s s s h s h s T ln .

Com’è ragionevole attendersi da una qualsiasi misura di disuguaglianza, il trasferimento , da un individuo più ricco ad un più povero, ha provocato una variazione negativa, e quindi una riduzione, dell’indice T di Theil. Si noti, inoltre, che la grandezza della riduzione di T dipende solo dal rapporto di su ; di conseguenza, per ogni coppia di individui per cui si ha lo stesso rapporto di quote, un qualsiasi trasferimento conduce alla stessa riduzione dell’indice T, indipendentemente dai valori assoluti delle quote.

s

Δ

A

s s_B

E’ facilmente intuibile che l’indice T di Theil varia tra zero, nel caso di equidistribuzione, e , nel caso di massima concentrazione e che può essere calcolato solo se tutte le modalità della variabile in esame sono non negative. Il fatto che il limite superiore dipenda dalla numerosità della popolazione, rende difficile il confronto tre le variabilità di due distribuzioni caratterizzate da differenti popolazioni.

N

3.1.5 Scelta della misura di variabilità più idonea

A questo punto appare evidente che in letteratura esistono diversi modi per misurare la variabilità di una distribuzione; può, quindi, risultare difficile scegliere la misura di variabilità più idonea. Il modo più semplice di compiere tale scelta consiste nel determinare le proprietà desiderabili per le misure di variabilità e nell’eliminare quelle misure che non possiedono le caratteristiche elencate.

Abbiamo già visto, parlando della varianza e del coefficiente di variazione, l’importanza dell’indipendenza dall’unità di misura della variabile in esame. In quanto, ad esempio, a seguito di un cambiamento della stessa proporzione nella ricchezza di ogni individuo, la distribuzione della ricchezza resta invariata, e di conseguenza deve restare tale anche la misura di variabilità.

Un altro principio simile a quello sopra elencato è il principio di popolazione, secondo il quale il grado di disuguaglianza non deve dipendere dal numero di individui che compongono la popolazione in esame. Questo significa che replicando una certa economia, nonostante la popolazione raddoppi, la misura di disuguaglianza deve restare invariata. Tuttavia, la desiderabilità di questa proprietà può essere contestata. Si consideri, ad esempio, un sistema formato da due persone, in cui un unico individuo possiede l’intero ammontare di ricchezza. Replicando l’economia, si ottiene un sistema formato da quattro persone, due delle quali sono nullatenenti, mentre le altre due possiedono in parti uguali la ricchezza totale. In questo caso sembrerebbe del tutto plausibile affermare che le due economie non sono affatto uguali.

Qualora la popolazione sia divisibile in sottogruppi, una proprietà che può risultare fondamentale è la proprietà della scomponibilità, che consiste nella possibilità di scomporre la disuguaglianza totale come una funzione della disuguaglianza tra i gruppi e all’interno di ciascun gruppo.

Infine, esiste un principio che è indispensabile per poter considerare un indice una misura di disuguaglianza a tutti gli effetti: il debole principio di trasferimento. Si considerino due individui, il primo con una ricchezza y e l’altro, più ricco, con una ricchezza pari a y+ρ, con ρ positivo. Il debole principio di trasferimento afferma che, se si trasferisce un ammontare di ricchezza yΔ dall’individuo più ricco a quello più povero, la disuguaglianza deve ridursi, indipendentemente dai valori di y e ρ. Questo principio è indispensabile, in quanto altrimenti si potrebbe verificare una situazione

paradossale in cui, a seguito di una redistribuzione tra ricchi e poveri, non si osserva nessun cambiamento nella distribuzione della ricchezza. Si parla di debole principio di trasferimento in quanto viene richiesto solamente che, a seguito di un trasferimento, la disuguaglianza si riduca, senza porre condizioni su quanto o come debba ridursi.

Al fine di inserire condizioni più restrittive, viene introdotto il forte principio di trasferimento. Si consideri un trasferimento tra l’individuo A che possiede una quota di ricchezza s_A e l’individuo B che ne possiede una quota , con . Una misura di disuguaglianza soddisfa il forte principio di trasferimento se e solo se l’ammontare di

riduzione della disuguaglianza dipende solo dal rapporto di su ,

indipendentemente dai valori assoluti delle quote di ricchezza. B

s s_A >s_B

A

s s_B

A questo punto è utile capire quali indici soddisfano le caratteristiche elencate. Nel paragrafo 3.1.4 si è mostrato come l’indice T di Theil verifichi il debole principio di trasferimento. E’ facile constatare che anche il rapporto di concentrazione di Gini ed il coefficiente di variazione soddisfano tale principio. Inoltre, tutte e tre, essendo misure relative, verificano anche il principio di indipendenza dall’unità di misura della variabile in esame. Il principio di popolazione, invece, non viene soddisfatto dal rapporto di concentrazione di Gini. Riprendendo, infatti, l’esempio delle due economie composte rispettivamente da due e quattro individui e calcolando il loro grado di disuguaglianza, si osservano i seguenti valori:

economia con 2 individui economia con 4 individui

Gini 1 0,667

CV 1 1

T di Theil 0,693 0,693

Ricordando che i limiti superiori dell’indice T di Theil e del coefficiente di variazione dipendono da N, essendo rispettivamente pari a lnN e a N −1, si potrebbe obiettare che anche questi due indici non soddisfano appieno il principio di popolazione. Sebbene, infatti, al replicarsi dell’economia, il loro valore resti invariato ( , ) i loro limiti superiori si modificano, passando rispettivamente da 0,693 a 1,386 e da 1 a 1,732. Ricordando che il limite superiore rappresenta il caso di massima concentrazione, la sua variazione sta a significare che nel primo caso la concentrazione della ricchezza è effettivamente massima, mentre nel secondo non lo è. In realtà, però, è facilmente verificabile che per valori di N molto grandi, dell’ordine di 10

693 , 0 = T 1 = CV 6 , quanto detto non è più valido, almeno per l’indice T di Theil. Supponendo, infatti, di moltiplicare la

popolazione per un fattore r, il limite superiore dell’indice di Theil sarà dato da ; di conseguenza, la variazione relativa del limite superiore sarà uguale a

N r rN) ln ln

ln( = +

(

lnr lnN

)

. E’ evidente che per valori di N molto grandi, a seguito di un cambiamento della popolazione, la variazione del limite superiore dell’indice T di Theil tenderà a zero. Quanto detto non è vero per il coefficiente di variazione, in quanto la variazione del suo limite superiore, essendo pari a r −1, non dipende da N e, quindi, sarà sempre piuttosto significativa.

Il fatto, però, che il rapporto di concentrazione di Gini e, in parte, il coefficiente di variazione non soddisfino il principio di popolazione non può portare alla loro esclusione, in quanto, come già precedentemente detto, la desiderabilità di tale principio non è affatto ovvia. Inoltre, entrando nel merito del seguente lavoro, poiché la nostra analisi è svolta nell’ambito di un’economia stazionaria, non ha importanza capire se sia auspicabile o meno che il grado di disuguaglianza non dipenda dal numero di individui che compongono la popolazione, poiché la popolazione in esame sarà sempre costante.

Il rapporto di concentrazione di Gini non soddisfa nemmeno il principio di scomponibilità, in quanto è possibile registrare un aumento della disuguaglianza in ogni sottogruppo della popolazione e, allo stesso tempo, registrare una riduzione della disuguaglianza totale. Anche in questo caso, però, l’utilizzo del principio di scomponibilità esula da questo lavoro. Nei paragrafi successivi, infatti, verranno effettuate delle simulazioni, per misurare il grado di disuguaglianza in un’economia perfettamente ugualitaria, facendo esclusivamente riferimento a dati individuali. Infine, né il rapporto di concentrazione di Gini, né il coefficiente di variazione verificano il forte principio di trasferimento. Tuttavia, per gli obiettivi di questo lavoro è unicamente richiesto che gli indici soddisfino il debole principio di trasferimento.

Appare evidente che la misura che meglio soddisfa i principi precedentemente elencati è l’indice T di Theil che fa parte di un ampio insieme di misure di disuguaglianza (indici di entropia generalizzata), le quali sono tutte esprimibili nella forma dell’equazione (18), o in una sua trasformazione.

(18) ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − =

∑

= 1 1 1 1 2 θ θ _{θ θ} N i i y y N E ,

dove θ è un parametro reale che può assumere qualsiasi valore, al quale è associata una diversa misura di disuguaglianza; per θ =1 si ottiene una misura equivalente all’indice T di Theil.

In conclusione, nello scegliere un’idonea misura di variabilità è ragionevole richiedere che siano soddisfatte le proprietà sopra descritte; in base a ciò è possibile affermare che l’indice T di Theil è una valida misura di disuguaglianza. Tuttavia, per gli obiettivi di questo lavoro, è possibile affermare che anche il coefficiente di variazione e il rapporto di concentrazione di Gini possono essere considerate misure sufficientemente valide, nonostante non presentino tutte le caratteristiche richieste. Si è visto, infatti, che ai fini del nostro lavoro è di poco interesse sapere se una misura soddisfa o meno il principio di popolazione, il principio di scomponibilità e il forte principio di trasferimento.

Nei paragrafi che seguiranno analizzeremo il grado di disuguaglianza in società perfettamente ugualitarie utilizzando le tre misure sopra descritte. Inizialmente, faremo uso del rapporto di concentrazione di Gini e, successivamente, le stesse misure verranno effettuate con gli altri due indici, al fine di confutare o convalidare i risultati precedentemente trovati.

3.2

Distribuzione della ricchezza nel modello del ciclo di vita

Nel suo articolo del 1971, Atkinson cerca di capire in che misura la disuguaglianza nella distribuzione della ricchezza osservata nel Regno Unito sia attribuibile all’accumulazione da ciclo di vita. Per far questo calcola il grado di disuguaglianza esistente in un’ipotetica società che ha origine dal modello del ciclo di vita, per poi confrontare i risultati trovati con il grado di disuguaglianza osservato nella realtà. L’idea di base è che se questo confronto risulta essere quantitativamente significativo, allora è possibile ritenere che una parte sostanziale della disuguaglianza osservata sia dovuta all’accumulazione da ciclo di vita. Poiché i contenuti ed i principali risultati di questo lavoro sono già stati affrontati nel primo capitolo, in questo paragrafo saranno solamente illustrati i risultati relativi alla misura del grado di disuguaglianza in una società perfettamente ugualitaria, che ha origine dal modello del ciclo di vita.

Atkinson adotta il modello di Modigliani - Brumberg in un’economia stazionaria,

assumendo e , e mostra che anche in una società perfettamente

ugualitaria la ricchezza è distribuita in maniera disuguale, a causa della sola differenza di età tra gli individui. In effetti, basta dare un rapido sguardo al “triangolo di

40 =

Modigliani” dal punto di vista sezionale (figura 2.1) per verificare che, all’interno della popolazione, esiste una sostanziale disuguaglianza tra l’ammontare di ricchezza posseduto dai più giovani (o dai più vecchi) e quello detenuto dagli individui che sono prossimi all’età di pensionamento. Ipotizzando che popolazione e produttività del lavoro siano costanti e che il tasso di interesse reale sia uguale a zero, Atkinson calcola la quota di ricchezza detenuta dal 10% più ricco della popolazione, pari al 19% della ricchezza totale. Successivamente calcola la stessa quota di ricchezza introducendo assunzioni più realistiche, come un tasso di interesse reale positivo, profili più realistici del reddito nel tempo e la presenza di eredità di uguale ammontare per tutti gli individui, ottenendo risultati che si discostano tra di loro solamente di alcuni punti percentuali.

Per avere un’idea del grado di disuguaglianza, oltre a calcolare la quota di ricchezza posseduta dal 10% più ricco della popolazione, può essere anche opportuno calcolare, sempre ipotizzando N =40 e L=50, il rapporto di concentrazione di Gini, il coefficiente di variazione e l’indice T di Theil. Tali indici risultano rispettivamente pari a: 0,334, 0,579, 0,195. Il grado di disuguaglianza nella distribuzione della ricchezza può essere anche mostrato graficamente attraverso l’utilizzo della curva di Lorenz che, nel caso specifico, appare piuttosto distante dalla retta di equidistribuzione (figura 3.3) .

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Pi Qi

Figura 3.3 – Curva di Lorenz nel modello di Modigliani.

Nonostante, quindi, la natura ugualitaria del sistema, la disuguaglianza nella distribuzione della ricchezza risulta essere piuttosto significativa.

3.3

Distribuzione della ricchezza nel modello del ciclo di vita

con consumo costante per adulto equivalente

L’analisi che segue è volta ad estendere i risultati ottenuti nel precedente paragrafo ad un sistema che considera come unità economica rilevante, non più l’individuo, ma la famiglia. L’obiettivo di questo paragrafo è, quindi, quello di analizzare la disuguaglianza nella distribuzione della ricchezza nel modello esteso del ciclo di vita.

L’indagine condotta nel secondo capitolo ha mostrato come la ricchezza aggregata sia fortemente influenzata da variazioni di T, M, q e (L-N); di conseguenza, è ragionevole attendersi che anche la sua distribuzione, all’interno di una popolazione stazionaria, sia altrettanto influenzata da variazioni delle variabili sopra elencate. In questo paragrafo concentreremo la nostra attenzione esclusivamente sull’influenza che variazioni di T e M hanno sull’andamento della disuguaglianza nella distribuzione della ricchezza. Nel far questo le altre variabili del modello saranno supposte costanti e ad esse saranno attribuiti dei valori arbitrari, pari a: Y =100, L=50, N =40 e . La scelta di limitare la nostra analisi alle sole variabili T e M, mantenendo costanti i parametri q e (L-N), è legata all’obiettivo di questo lavoro che è quello di esplorare l’influenza della dinamica familiare sulla distribuzione della ricchezza.

4 , 0 =

q

La disuguaglianza nella distribuzione della ricchezza sarà misurata, inizialmente, utilizzando il rapporto di concentrazione di Gini e, successivamente, utilizzando il coefficiente di variazione e l’indice T di Theil, al fine di determinare la robustezza dei risultati trovati. Inoltre, per valutare come sia cambiata la distribuzione della ricchezza, all’interno della popolazione, faremo riferimento alla distribuzione stessa normalizzata alla ricchezza totale. La distribuzione normalizzata permette, infatti, di determinare, in un modo più immediato, i cambiamenti nelle quote di ricchezza possedute dai singoli individui. Si ricordi che per quota di ricchezza si intende il rapporto tra l’ammontare di ricchezza posseduto dall’individuo considerato e la ricchezza totale.

3.3.1 Effetto di una variazione di T

Abbiamo più volte ribadito che anche in un sistema perfettamente ugualitario, generato dal modello del ciclo di vita, la ricchezza risulta essere distribuita in maniera

disuguale a causa della differenza di età tra gli individui, che fa sì che i lavoratori più anziani o coloro che sono in pensione da pochi anni possiedano un ammontare di ricchezza molto maggiore rispetto a quello detenuto dai più giovani o dai più vecchi.

Dall’analisi svolta nel secondo capitolo abbiamo visto come il rapporto ricchezza-reddito sia funzione crescente di T. Difatti, a seguito di un suo aumento, le generazioni più vecchie (attive o in pensione) continuano a detenere lo stesso ammontare di ricchezza, mentre le famiglie più giovani arrivano a possederne un ammontare maggiore (ad eccezione di quelle che si trovano nei primi anni di vita lavorativa, che continuano a detenere lo stesso ammontare di ricchezza). Da quanto detto è ragionevole aspettarsi che, a seguito di un aumento di T, la ricchezza risulti distribuita tra gli individui in maniera più uniforme, dal momento che si registra un aumento dell’ammontare di ricchezza detenuto dalle generazioni più giovani, che sono tra le classi di età più povere della popolazione. Difatti, sia un aumento delle quote di ricchezza per le classi di età più povere sia una riduzione delle quote per le classi di età più ricche hanno l’effetto di ridurre il grado di disuguaglianza, dove per poveri e ricchi è legittimo intendere coloro che detengono una quota di ricchezza, rispettivamente, minore o maggiore della quota media di ricchezza (0,02)6.

In effetti, guardando la figura 3.4, che rappresenta le distribuzioni delle quote di ricchezza di due economie che differiscono unicamente per il diverso tempo in cui vengono generati i figli (assumiamo M =20, 2T'= e ), osserviamo una distribuzione più uniforme per l’economia caratterizzata da un T maggiore.

10 ''₌

T

La figura mostra che un aumento di T produce, sul grado di disuguaglianza nella distribuzione della ricchezza, due effetti di segno opposto. Da una parte, si ha l’effetto positivo, che riduce il grado di disuguaglianza, determinato da un aumento delle quote di ricchezza per la maggior parte delle famiglie più giovani e, parallelamente, da una riduzione delle quote detenute dalle classi di età più ricche. Dall’altra, si ha l’effetto negativo, che aumenta il grado di disuguaglianza, determinato da una riduzione delle quote possedute dai più anziani e dalle classi di età che si trovano nei primi anni di vita lavorativa. Nel caso in esame è evidente che il primo effetto prevale sul secondo e la disuguaglianza si riduce. Difatti, calcolando il rapporto di concentrazione di Gini, al fine di valutare il grado di concentrazione della ricchezza nei due sistemi in esame, si

6

Poiché stiamo lavorando con distribuzioni normalizzate, la ricchezza totale è pari a uno, di conseguenza, essendo la popolazione composta da cinquanta individui, avremo che la quota media di ricchezza della popolazione è pari a: 1/50=0,02.

ottengono due valori decisamente differenti, pari a 0,427 per T =2 e a 0,258 per . 10 = T 0 0,01 0,02 0,03 0,04 0,05 0,06 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 classi di età W normaliz z a ta

ricchezza normalizzata per T=2 ricchezza normalizzata per T=10

Figura 3.4 – Effetto di una variazione di T sulle quote di ricchezza possedute dagli individui.

In realtà, però, calcolando il rapporto di concentrazione di Gini, relativo alla distribuzione della ricchezza, per tutti i possibili valori di T (0≤ T ≤20), con , non si osserva un andamento monotono decrescente, come invece era plausibile attendersi in conseguenza di quanto precedentemente osservato (figura 3.5).

20 = M 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 0,6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 T Gini

Quindi, l’affermazione, che all’aumentare di T il grado di disuguaglianza nella distribuzione della ricchezza diminuisce, non è più incondizionatamente vera. La figura 3.5 mostra, infatti, un andamento del rapporto di concentrazione solo inizialmente decrescente, per poi divenire crescente per valori di T piuttosto elevati. Naturalmente, il valore di T per il quale viene raggiunto il punto di minimo (nel nostro caso T =14) dipende dai valori assegnati alle altre variabili.

Questo risultato sta a significare che, quando i figli vengono generati in età molto avanzate, un aumento di T, nonostante provochi un aumento della ricchezza aggregata, è in grado di peggiorare il grado di disuguaglianza nella distribuzione della ricchezza. Per capire come mai questo avvenga, guardiamo nuovamente alle distribuzioni delle quote di ricchezza, di due economie, A e B, che differiscono unicamente per il diverso tempo in cui vengono generati i figli; assumiamo in questo caso M =20, 14TA = e TB =20.

0 0,005 0,01 0,015 0,02 0,025 0,03 0,035 0,04 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 classi di età W normaliz z a ta

ricchezza normalizzata per T=14 ricchezza normalizzata per T=20

Figura 3.6 – Effetto di una variazione di T sulle quote di ricchezza possedute dagli individui.

La figura 3.6 mostra che, in questo caso, un aumento di T provoca sul grado di disuguaglianza nella distribuzione della ricchezza soprattutto effetti negativi. Difatti, si ha una perdita di ricchezza da parte dei pensionati più vecchi e delle generazioni più giovani che ancora devono generare i figli. Quest’ultima perdita è decisamente più grande rispetto al caso precedente, in quanto, se i figli vengono generati in età molto avanzate, aumenta considerevolmente il numero di classi che, a seguito di un aumento di T, perdono quote di ricchezza. Inoltre, sebbene alcune classi di età più ricche

continuano a subire una riduzione delle loro quote, la maggior parte registrano un aumento. In questo secondo caso, si ha quindi la prevalenza degli effetti negativi su quelli positivi e si registra un aumento del grado di disuguaglianza.

Se calcoliamo il rapporto di concentrazione di Gini, relativo alla distribuzione della ricchezza, per tutti i possibili valori di T, assumendo però un periodo di mantenimento più lungo (M =24), otteniamo lo stesso andamento osservato in figura 3.5, con l’unica differenza che il punto di minimo viene osservato in T =12, anziché in T =14.

L’andamento prima decrescente e poi crescente del rapporto di concentrazione di Gini, al variare di T, viene anche osservato calcolando il coefficiente di variazione e l’indice T di Theil. Calcolando, infatti, i due indici, per tutti i possibili valori di T (0≤ T≤20), con M =20, si ottiene lo stesso andamento osservato in figura 3.5, con l’unica differenza che l’indice T di Theil raggiunge il punto di minimo in , anziché in , come avviene per il rapporto di concentrazione di Gini e il coefficiente di variazione (figura 3.7).

12 = T 14 = T

Tuttavia, a prescindere dal diverso punto di minimo e dai valori assoluti dei tre indici7, ciò che più conta di quanto osservato in figura 3.7 è l’identico andamento, prima decrescente e poi crescente, delle tre misure di variabilità, che permette di considerare i risultati trovati, relativi agli effetti di una variazione di T sul grado di disuguaglianza nella distribuzione della ricchezza, piuttosto robusti.

0,4 0,5 0,6 0,7 0,8 0,9 1 0 2 4 6 8 10 12 14 16 18 20 T CV 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 T di Theil CV indice T di Theil Figura 3.7 – Andamenti del coefficiente di variazione e dell’indice di Theil al variare di T, con M=20.

7

I tre indici hanno dinamica di variazione diversa: il rapporto di concentrazione di Gini varia tra [0;1]; il coefficiente di variazione tra [0; 7] e l’indice T di Theil tra [0; 3,912].

Esaminiamo, infine, il grado di disuguaglianza nella distribuzione della ricchezza di due economie caratterizzate da uno stesso T medio e da una diversa dispersione nelle nascite. È facilmente verificabile che la disuguaglianza nella distribuzione della ricchezza diminuisce con la riduzione della dispersione. Calcolando, infatti, il rapporto di concentrazione di Gini, relativo alla distribuzione della ricchezza, per due economie,

A e B, caratterizzate da uno stesso T medio e da una diversa dispersione ( e , ), con , otteniamo un valore pari a 0,313, per l’economia A, ed un valore pari a 0,326, per l’economia B. Questo risultato può essere facilmente spiegato osservando la figura 2.4: poiché la ricchezza aggregata delle due economie è la stessa, si vede immediatamente che nell’economia A, caratterizzata da una minore dispersione, si hanno alcune generazioni più giovani che stanno meglio delle corrispondenti generazioni dell’economia B ed alcune generazioni più vecchie, e più ricche, che stanno peggio; entrambi gli effetti incidono positivamente sul grado di disuguaglianza che, quindi, si riduce. Si osservi, infine, che questo risultato resta valido anche per valori di M più grandi, dal momento che l’unico effetto di M è quello di determinare le classi di età, dell’economia A, che subiranno una riduzione delle loro quote di ricchezza, rispetto alle corrispondenti classi dell’economia B. Questi risultati

trovano conferma anche calcolando il coefficiente di variazione ( ,

per ; , per ) e l’indice T di

Theil ( , per 6 2 1 = = A A T T 2 1 = B T T₂B =10 M =20 571 , 0 = A CV 583 , 0 = B CV M =20 CVA =0,461 CVB =0,487 M =28 167 , 0 = A T TB =0,177 M =20; TA =0,124, TB =0,137 per M =28). In conclusione, è possibile affermare che la distribuzione della ricchezza tra le famiglie dipende fortemente dal tempo in cui vengono generati i figli. La disuguaglianza nella distribuzione della ricchezza è, infatti, elevata quando T è molto piccolo, si riduce progressivamente al crescere di T fino a raggiungere un minimo, dopo il quale comincia ad aumentare. Inoltre, la disuguaglianza nella distribuzione della ricchezza diminuisce con la riduzione della dispersione nelle nascite.

3.3.2 Effetto di una variazione di M

Dall’analisi svolta nel secondo capitolo abbiamo visto come l’andamento del rapporto ricchezza-reddito, al variare di M, dipenda anche dal valore di T. Difatti, se T è grande (T ≥6, per i valori di L, N e q assunti), il rapporto ricchezza-reddito è sempre

funzione crescente di M, mentre se T è piccolo ha un andamento prima decrescente e poi crescente. Si ricordi, infatti, che un aumento di M provoca, sulla ricchezza aggregata, i seguenti effetti:

(i) un aumento dell’ammontare di ricchezza detenuto dalle classi di età più giovani, che ancora devono generare i figli;

(ii) una riduzione dell’ammontare di ricchezza detenuto dalle classi più vecchie, attive e in pensione;

(iii) un aumento dell’ammontare di ricchezza per le famiglie più giovani con figli a carico;

(iv) una riduzione dell’ammontare di ricchezza per le famiglie più vecchie che continuano ad avere figli a carico, in conseguenza di un M più grande.

Abbiamo visto come l’incidenza sulla ricchezza aggregata di tutti e quattro gli effetti dipenda dal valore di M e dall’ampiezza della sua variazione, oltre ad osservare che l’effetto (i) è più o meno significativo a seconda del valore di T.

Ovviamente, questi effetti incidono fortemente anche sulla distribuzione della ricchezza, sebbene il loro impatto dipenda, oltre che dai valori di M e T, anche dalla variazione di ricchezza aggregata; per questo è nuovamente opportuno lavorare con le distribuzioni delle quote di ricchezza e non ragionare più in termini di ammontari.

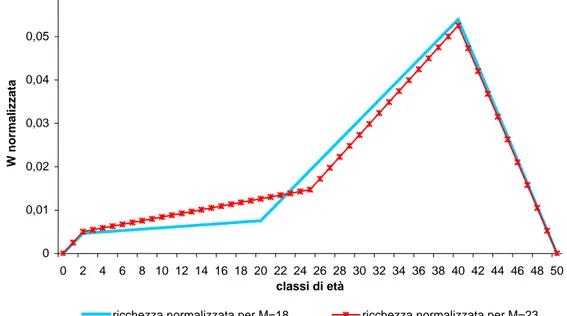
Consideriamo, ad esempio, due economie, A e B, che differiscono per un diverso valore di M ( , ) e assumiamo che tutte le famiglie generino figli gemelli al tempo 20 = A M MB =25 2 = T (figura 3.8). 0 0,01 0,02 0,03 0,04 0,05 0,06 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 classi di età W normaliz z a ta

ricchezza normalizzata per M=18 ricchezza normalizzata per M=23

La figura 3.8 mostra come in questo caso un maggior valore di M conduca ad un minor grado di disuguaglianza nella distribuzione della ricchezza. Difatti, un aumento di

M provoca sul grado di disuguaglianza soprattutto effetti positivi: quasi tutte le classi di età più povere (coloro che detengono quote di ricchezza inferiori a 0,02) registrano un aumento di ricchezza e tutte le classi di età più ricche subiscono una riduzione. Fanno eccezione i più anziani e le famiglie più vecchie che continuano ad avere figli a carico, le quali, subendo una riduzione delle quote di ricchezza, incidono negativamente sul grado di disuguaglianza. Tuttavia, poiché quest’ultime riduzioni sono piuttosto piccole, gli effetti positivi prevalgono e il grado di disuguaglianza si riduce.

In effetti, calcolando il rapporto di concentrazione di Gini, relativo alla distribuzione della ricchezza, per tutti i possibili valori di M (18≤ M ≤33), sotto l’ipotesi che tutte le famiglie generino due figli gemelli al tempo T =2, si osserva un andamento monotono decrescente (figura 3.9a).

0,2 0,25 0,3 0,35 0,4 0,45 0,5 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 M Gini

Figura 3.9a - Andamento del rapporto di concentrazione di Gini al variare di M, con T=2.

Purtroppo, però, l’analisi non è cosi semplice e, per valori di T più grandi (ad esempio, T =7 e T =12), si osserva un andamento diverso del rapporto di concentrazione di Gini (figura 3.9b), che per elevati valori di M raggiunge un punto di minimo e, successivamente, incomincia a crescere. Inoltre, il punto di minimo viene raggiunto per M via via sempre più piccoli al crescere di T.

0,23 0,245 0,26 0,275 0,29 0,305 0,32 18 20 22 24 26 28 30 32 M Gini

Gini per T=7 Gini per T=12

Figura 3.9b - Andamento del rapporto di concentrazione di Gini al variare di M, con T=7 e con T=12.

Questo risultato sta a significare che, quando i figli vengono generati in età molto avanzate, un aumento di M, se M è piuttosto elevato, è in grado di peggiorare il grado di disuguaglianza nella distribuzione della ricchezza. Per capire come mai questo avvenga, guardiamo a titolo indicativo la figura 3.10 che mostra le distribuzioni delle quote di ricchezza, di due economie, A e B, che differiscono unicamente per il diverso periodo di mantenimento dei figli; ipotizziamo: T =12, 24MA = e MB =28.

0 0,005 0,01 0,015 0,02 0,025 0,03 0,035 0,04 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 classi di età W normaliz z a ta

ricchezza normalizzata per M=24 ricchezza normalizzata per M=28

Figura 3.10 - Effetto di una variazione di M sulle quote di ricchezza possedute dagli individui, con T=12.

La figura 3.10 mostra che, in questo caso, un aumento di M provoca un aumento del grado di disuguaglianza. Difatti, in questo caso, non si ha più l’effetto positivo legato ad un aumento delle quote di ricchezza per le famiglie che ancora devono generare i figli e, sebbene alcune classi di età più ricche subiscano una riduzione delle loro quote, la maggior parte di esse registrano un aumento. A quest’ultimo effetto negativo vi si deve aggiungere anche la perdita di quote di ricchezza da parte dei pensionati più vecchi. Gli effetti negativi prevalgono così su quelli positivi e la disuguaglianza aumenta.

Per valori di T e M relativamente grandi, è, quindi, possibile affermare che un aumento del periodo di mantenimento è in grado di peggiorare la disuguaglianza all’interno del sistema.

A questo punto è opportuno constatare se è possibile pervenire agli stessi risultati utilizzando il coefficiente di variazione e l’indice di Theil. Calcolando, al variare di M, per i valori di T assunti in precedenza, il coefficiente di variazione e l’indice T di Theil, otteniamo gli stessi andamenti osservati nelle figure 3.9a e 3.9b.

0,4 0,5 0,6 0,7 0,8 0,9 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 M CV 0,1 0,15 0,2 0,25 0,3 0,35 0,4 T di Theil CV indice T di Theil

Figura 3.11a - Andamenti del coefficiente di variazione e dell’indice T di Theil al variare di M, con T=2.

0,4 0,42 0,44 0,46 0,48 0,5 18 19 20 21 22 23 24 25 26 27 28 M CV 0,11 0,115 0,12 0,125 0,13 0,135 T di Theil CV indice T di Theil

Figura 3.11b - Andamenti del coefficiente di variazione e dell’indice T di Theil al variare di M, con T=12.

Guardiamo, infine, alla disuguaglianza nella distribuzione della ricchezza di due economie caratterizzate da uno stesso M medio e da una diversa dispersione. Riproponiamo di seguito l’esempio già presentato nel secondo capitolo, di due economie, A e B, che differiscono unicamente per il diverso periodo di mantenimento

dei figli ( , e , ), assumendo che tutti i figli

vengono generati al tempo 20 1 = A M ₂A =30 M ₁B =25 M ₂B =25 M 2 =

T . Calcolando il rapporto di concentrazione di Gini, relativo alla distribuzione della ricchezza, per le due economie, otteniamo un valore pari a 0,379 per l’economia A ed un valore pari a 0,383 per l’economia B. Questo risultato mostra, quindi, un minor grado di disuguaglianza per l’economia caratterizzata da una maggiore dispersione. In realtà, però, se calcoliamo nuovamente il rapporto di concentrazione di Gini assegnando a T un valore più grande (T =10) si ottiene esattamente il risultato opposto: un valore di 0,254 per l’economia A ed un valore di 0,245 per l’economia B. Questi risultati apparentemente contrastanti possono essere spiegati osservando le figure 3.12a e 3.12b, che rappresentano rispettivamente le distribuzioni delle quote di ricchezza nei casi di T =2 e T =10.

0 0,01 0,02 0,03 0,04 0,05 0,06 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 classi di età W normalizzata

ricchezza normalizzata con M=25 ricchezza normalizzata con M=20,30

Figura 3.12a - Effetto di una variazione di M (diversa dispersione e stesso M medio)

sulle quote di ricchezza possedute dagli individui, con T=2.

0 0,005 0,01 0,015 0,02 0,025 0,03 0,035 0,04 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 classi di età W normaliz z a ta

ricchezza normalizzata con M=25 ricchezza normalizzata con M=20,30

Figura 3.12b - Effetto di una variazione di M (diversa dispersione e stesso M medio)

sulle quote di ricchezza possedute dagli individui, con T=10.

Nel secondo capitolo abbiamo visto come l’economia caratterizzata da una maggiore dispersione (A) detenga sempre una quantità maggiore di ricchezza aggregata. Questo fa

sì che in entrambi i casi la maggior parte delle generazioni del paese A si trovano a detenere delle quote di ricchezza minori rispetto a quelle detenute dalle corrispondenti generazioni del paese B, tranne quelle classi di età che differiscono per il numero di figli che hanno a carico, le quali, invece, arrivano a detenere delle quote maggiori. Ora, mentre con un T più basso le generazioni del paese A che detengono quote di ricchezza maggiori rispetto a quelle del paese B sono relativamente povere, con un T più alto queste generazioni sono, invece, le più ricche. In conseguenza di quanto detto, nel primo caso, con T =2, si registrerà una disuguaglianza maggiore per il paese con minore dispersione, mentre nel secondo caso, con T =10, si avrà esattamente la situazione opposta. Questi risultati trovano conferma anche dai calcoli effettuati con il coefficiente di variazione (CVA =0,667, CVB =0,682 per T =2; ,

per ) e l’indice T di Theil ( , per

443 , 0 = A CV 431 , 0 = B CV T =10 TA =0,224 TB =0,228 T =2; , per ). 122 , 0 = A T TB =0,117 T =10

In conclusione, è, quindi, possibile affermare che l’influenza di una variazione di M sulla distribuzione della ricchezza dipende da T. Se T è piccolo, un aumento di M, provoca una riduzione della disuguaglianza, mentre se T è piuttosto grande, una variazione di M, può causare sia una riduzione sia un aumento della disuguaglianza, a seconda del valore di M. Inoltre, la disuguaglianza nella distribuzione della ricchezza diminuisce con la riduzione della dispersione di M se T è grande, mentre aumenta se T è piccolo.