Capitolo5: Modello Proposto

Capitolo5:

Modello Proposto

In questo capitolo s’illustra una modo per valutare lo scorrimento fra una barra d’acciaio ed il calcestruzzo. Il metodo si sviluppa dagli aspetti teorici del legame d’aderenza, già affrontato nella letteratura tecnica ed illustrato nel capitolo 1; proponendo un algoritmo di risoluzione dell’equazione differenziale che regge il problema, fornendo l’andamento, lungo l’ascissa della barra, delle tensione tangenziali, delle tensioni normali e dello scorrimento.

5.1 Aspetti teorici dell’aderenza

Nel capitolo 1 si è illustrato in modo qualitativo il meccanismo di aderenza. Andare a studiare l’interazione meccanica fra le nervature della barra ed il getto richiede uno studio approfondito a livello microstrutturale, che esula dal nostro scopo. La presenza delle nervature fa sì che la distribuzione delle forze fra acciaio e calcestruzzo lungo l’ascissa della barra , risulta essere discontinua presentando dei picchi di massimo in corrispondenza delle nervature. Per facilitare gli sviluppi analitici, e per tenere di conto anche dell’attrito fra la barra ed il getto, la barra nervata è schematizzata liscia: la distribuzione delle forze tangenziali sarà continua. In pratica la forza tangenziale esercitata fra nervatura e biella in calcestruzzo è spalmata sul tratto di lunghezza p, dove p è il passo delle nervature.

5.1.1 - Impostazione analitica

Consideriamo un tirante in cemento armato costituito da una barra di area As, avvolta da un getto di calcestruzzo di area Ac. Ad un estremità del tirante è applicata la forza F0, mentre l’altra estremità è fissa.

L F0 Fs Fc Fc F0 x

Andiamo ascrivere l’equazione di equilibrio di un concio di lunghezza x

Differenziando:

La variazione di tensione nell’acciaio è opposta alla variazione di tensione nel calcestruzzo, ciò vuol dire che se l’andamento della tensione nell’acciaio è crescente, nel calcestruzzo l’andamento delle tensioni è decrescente.

Adesso andiamo a scrivere l’equilibrio di un tratti di barra dx

σc+dσc σc+dσc σs+dσs σc σs σc dx εc dx εs dx s dx As _Ac c c

Azioni tangenziali del CLS sulla barra

fig.5- 2: Concio di tirante

F0 Fs Fc+

dσ_s π φ⋅ 4

⋅ π φ⋅ τ s⋅ ( )⋅dx Eq. 5- 2: Equazione di Equilibrio del _{tratto di barra lungo dx} dF0 dFs dFc+ dσs π φ⋅ 4 ⋅ +_{Ac dσc}⋅ 0 ρ As Ac dσ_c − dσρ⋅ _s ε_s−ε_c

(

)

⋅dx ds ⇒ x s x( ) d d ε_s−ε_c 2 x s d d 2 x ε_s d d x ε_c d d − σ_sεs x σ_s d d ⋅ d d σ_c ε_c x σ_c d d ⋅ d d − σ_sεs d d ρ σ_cεc d d ⋅ +

⎛

⎜

⎝

⎞

⎟

⎠

xσs d d ⋅ σ_sεs d d ρ σ_cεc d d ⋅ +

⎛

⎜

⎝

⎞

⎟

⎠

4⋅τ s( ) φ ⋅ 2s d2 σ εs d d ρ σ εc d d ⋅ +

⎛

⎜

⎝

⎞

⎟

⎠

4⋅τ s( ) φ ⋅

Eq. 5- 3: Equazione di equilibrio globale

Eq. 5- 1: Equazione di congruenza

Eq. 5- 5:Equazione differenziale risolutrice Eq. 5- 4: Equazione di equilibrio globale intermini differenziali

Questa è un’equazione differenziale del secondo ordine non lineare e non omogenea. Per risolvere questa equazione differenziale occorre esplicitare il legame costituivo del calcestruzzo teso, dell’acciaio e la legge τ(s) che lega le tensioni tangenziali d’aderenza con lo scorrimento.

5.1.2 - Calcestruzzo teso collaborante con la barra

Definire l’area di calcestruzzo teso che collabora con la barra è oggetto di studi approfonditi. In questa trattazione si ipotizza che il tirante in Cemento Armato ha un’area di calcestruzzo quadrata, i cui lati hanno una lunghezza pari a 2c+φ, dove

c è la distanza della barra tesa dalla faccia esterna della trave. L’area collaborante

varia lungo la barra con una legge di tipo esponenziale come illustrato nel prospetto: sulla faccia in cui si è aperta la lesione l’area di conglomerato è pari all’area d’acciaio, mentre a distanza pari a c dalla fessura l’area collaborante è pari al 99% dell’area totale.

Prospetto 1:Definizione dell’area di calcestruzzo teso

Ac0 π φ 2 ⋅ 4 = c = 42 mm _AcF =

(

φ +2 c⋅

)

2 a −1 c ln 1 0.99 AcF⋅ −Ac0 AcF Ac0− −

⎛

⎜

⎝

⎞

⎟

⎠

⋅

= Ac x( ) = _Ac0+

(

_{AcF Ac0}−

)

⋅

(

1−e− xa⋅

)

Legenda:

Ac0 area di calcestruzzo collaborante con la

•

barra in prossimità della fessura

Acf area di calcestruzzo collaborante con la

•

barra asufficiente distanza dalla fessura Ac(x) andamento dell'area di calcestruzzo

•

collaborante

ρ rapporto fra l'area di calcestruzzo e l'area •

di acciaio

c distanza netta della barra dal bordo •

φ diametro della barra • ρ x( ) Ac0 Ac x( ) = Ac0 = 201.1 mm2 AcF = 10000 mm2 ρ 200( ) = 0.0201 mm 0 50 100 150 0 5000 1 .104 Ac x( ) x 0 50 100 150 0 0.01 0.02 0.03 ρ x( ) x

5.1.3 - Definizione del legame costitutivo dell’acciaio

Per risolvere l’equazione differenziale, occorre esplicitare il legame costitutive dell’acciaio. Fra i vari modelli si sceglie la legge di Ramberg-Osgood, perché è una funziona continua che presenta caratteristiche analitiche simili al diagramma sperimentale dell’acciaio. Nel prospetto che segue è illustrata tale legge.

La bilatera in colore nero rappresenta il legame elasto-plasto-incrudente dell'acciaio per evidenziare la bontà della legge di Ramberg-Osgood

Legenda : E_a Modulo Elastico • E_P Modulo Plastico • f_y tensione di snervamento • f_u tensione a rottura •

εsy deformazione allo snervamento

• εsu deformazione a rottura • 0 200 400 600 0 0.005 Tensioni Normali Deformazioni ds σs

( )

1 Ea a n⋅( −1) Ea σ_sn 1− fyn 1− ⋅ + = Derivata di ε_{s rispetto a σs} ε_{s σs}

( )

σs Ea a Ea σ_sn fyn 1− ⋅ + =

Legame costitutivo dell'acciaio

Parametri della legge di Ramberg-Osgood n = 80 a = 0.3 Ep 1624= N/mm2 Ep = α 1_{β 1−}− ⋅Ea β εsu ε_sy = α fu fy = ε_su = 0.055 ε_sy = 2.646×10−3 ε_sy fy Ea = fu = 630 N/mm2 fy = 545 N/mm2 Ea = 206000 N/mm2

Prospetto 2: Legame costitutivo dell’acciaio

Eq. 5- 6:Legame costitutivo dell’acciaio

5.1.4 - Definizione del legame costitutivo del calcestruzzo teso

Anche per il Calcestruzzo teso si utilizza una legge simile alla legge dell’acciaio. Per quanto riguarda i parametri εc0, Et, fcm, fct, sono stati ricavati secondo quanto esposto dall’Eurocodice2 ε_ct = 1.12264×10−4 Deformazione a rottura 0 2 4 6 0 5 .10 5 1 .10 4 1.5 .10 4 Tensioni Normali Deformazioni dc σc

( )

1 Et a n⋅( −1) Et σ_cn 1− fctn 1− ⋅ + =

Derivata diε_{c rispetto a σc} ε_{c σc}

( )

σc fct a σ_cn fctn ⋅ +

⎛

⎜

⎜

⎝

⎞

⎟

⎟

⎠

ε1 ⋅ =

Legame costitutivo del Calcestruzzo teso n = 40 a = 0.01 fct 0.3 fc 2 3 ⋅ if _fc < 50 2.12 ln 1 fcm 10 +

⎛

⎜

⎝

⎞

⎟

⎠

⋅ otherwise = Legenda :

E_t Modulo Elastico tangente

•

f_c resistenza cilindrica

•

f_cm resistenza cilindrica media

•

f_ct resistenza a trazione

•

εct deformazione a rottura per

• trazione fcm = fc + 8 Et 2.15 10⋅ 4 3 fc 10 ⋅

⎛⎜

⎜⎝

⎞⎟

⎟⎠

= ε_c0 = 0.0022 fc = 56.191 N/mm2

Prospetto 3: Legame costitutivo del Calcestruzzo teso

Eq. 5- 8: Legame costitutivo del Calcestruzzo

5.1.5 - Legame costitutivo Tensioni tangenziali scorrimento

Prospetto 4: Legge tensioni tangenziali scorrimento secondo il CEB

Eq. 5- 10: Legame tensione tangenziale-scorrimento

Rck = 67.7 N/mm2 _fc = −0.83⋅_Rck N/mm2 _fc = −56.191 N/mm2 τ_max = 2.5⋅ _fc τ_F = 0.4 _fc α = 0.4 s 1 3 10

⎛⎜

⎜

⎜⎝

⎞⎟

⎟

⎟⎠

= τ_max= 18.74 N/mm2 τ_F = 2.998 N/mm2 τ u( ) u s₁

⎛

⎜

⎝

⎞

⎟

⎠

α τ_max ⋅ ⋅sign u( ) if −s₁ ≤ u ≤ s₁ τ_{max sign u}⋅ ( ) if s₁< u ≤ s₂ τ_{max sign u}⋅ ( ) τ_F−τ_max s₃−s₂ ⋅

(

u −s2

)

⋅sign u( ) + if s₂< u < s₃ τ_{F sign u}⋅ ( ) otherwise = 0 2.5 5 7.5 10 12.5 15 5 10 15 20 Scorrimento Tensioni Tangenziali Legenda

R_ck resistenza cubica del calcestruzzo •

fc resistenza cilindrica del calcestruzzo

•

τmax tensione tangenziale massima

•

τF tensione tangenziale finale

5.2 Risoluzione dell’equazione differenziale

La soluzione dell’equazione differenziale, da un punto di vista analitico, consiste nel fissare le condizioni al contorno e determinare l’integrale generale.

5.2.1 - Integrale generale

Risolvere l’equazione differenziale in forma chiusa, cioè esplicitando la funzione

s(x) è piuttosto complicato, perché al secondo membro dell’equazione differenziale

ci sono delle funzioni in x e s di cui è laborioso trovare le primitive. Perciò l’integrazione si effettua mediante il metodo numerico alle differenze finite, che consiste nel suddividere l’insieme di definizione i n punti e di trovare la soluzione in questi punti. Per risolvere l’equazione 5-4 si esplicita alle differenze finite l’operatore derivata seconda come illustrato nell’equazione 5-11.

È un metodo approssimato, la cui precisione dipende dalla distanza Δ fra i punti in cui andiamo a trovare la soluzione.

2 x_k s x

( )

_k d d 2 _s k 1+ −2 s⋅ k+ sk 1− Δ2

Prospetto 5: algoritmo di risoluzione dell’equazione differenziale

Eq. 5- 11: operatore derivata seconda

Δ←0.1 x₁←0 s₁←_s0 εc1←εc₀ εs₁←εs₀ s₂←s₁+ Δ εs⋅

(

₁−εc₁

)

xk←xk 1− + Δ τk←τ s

( )

k σs_k σs_{k 1−} 4 φ τ s

( )

_k −τ s

(

_{k 1−}

)

2 ⋅ ⋅Δ + ← σc_k←σc_{k 1−} −ρ x

( )

_k ⋅

(

σs_k−σs_{k 1−}

)

s_{k 1}+ 2 s⋅ _k−s_{k 1}− Δ2 4 φ⋅τ x

( )

k σs_kεsk d d ρ x

( )

_k σc_kεck d d

⎛

⎜

⎝

⎞

⎟

⎠

⋅ +

⎡

⎢

⎣

⎤

⎥

⎦

⋅

⎡

⎢

⎣

⎤

⎥

⎦

⋅ + ← k∈2 n.. for output←s Eq. 5- 13 Eq. 5- 14 Eq. 5- 12’ Eq. 5- 15’

Le equazioni 5-2’ e 5-3’ sono rispettivamente le equazioni 5-2 e 5-3 espresse in incrementi finiti, invece che in termini differenziali. L’equazione 5-12 si ricava sostituendo la 5-11 nella 5-5 ed isolando al primo membro il termine sk+1.

Al k-esimo passo, supponiamo di conoscere la funzione s(x) nei primi k punti e di sapere la distribuzione delle funzioni τ, σs, σc nei primi k-1 punti. Sia sk il valore di

s(x) in xk, dall’equazione 5-10’ si ricava il valore di τk, dall’equazione 5-3’ si ricava il valore di tensione σsk nell’acciaio, dalla 5-2’ si ricava la tensione σck nel calcestruzzo. Note le tensioni nel punto xk, si possono ricavare i valori delle

equazioni 5-6 e 5-7 in xk e quindi mediante la 5-12 si trova il valore di sk+1 in xk+1. Si

ripete questa procedura fino al punto n.

Per poter innescare il procedimento di risoluzione è necessario conoscere i valori

s1 e s2 della funzione s(x) nei primi due punti: s1 si ricava imponendo che lo scorrimento sia pari al valore s0, mentre s2 si ricava imponendo lo stato di deformazione (o tensione) nel punto iniziale.

5.2.2 - Condizioni al Contorno

Nel risolvere il problema dell'aderenza occorre specificare il dominio di esistenza della soluzione e le condizioni al contorno sullo scorrimento e sulla sua derivata prima. Le condizioni al contorno possono essere:

• il valore dello scorrimento e della sua derivata ad un’estremità • il valore dello scorrimento ad entrambe le estremità

• il valore della derivata ad entrambe le estremità

• il valore dello scorrimento ad una estremità e della derivata all'altra Quando le condizioni al contorno sono entrambe su un estremo deve essere nota la distanza fra questi due estremi. Se questa distanza non è nota occorre conoscere un'altra condizione su s(x) o s'(x) su di un estremo, cioè se la distanza fra gli estremi è incognita occorre conoscere tre condizioni al contorno.

Per come è impostato l’algoritmo di risoluzione le condizioni al contorno devono essere fissate nel punto iniziale: nel punto x1 deve essere noto lo scorrimento s(x1) ed il valore della sua derivata. Da un punto di vista meccanico la conoscenza della derivata prima dello scorrimento implica la conoscenza della deformazione dei due materiali nel punto x1.

5.2.3 - Esempio di risoluzione dell’equazione differenziale

Di seguito riportiamo degli esempi di risoluzione per vari valori di s0, imponendo nel punto iniziale una deformazione del calcestruzzo nulla e una deformazione dell’acciaio pari al 40% della deformazione allo snervamento

Con questi esempi si vuole mettere in evidenza che su un dato dominio di esistenza (L=500 mm), a parità dello stato tensionale nel punto iniziale, all’aumentare di s0 il punto in cui s(x) si annulla si sposta verso destra, verso le ascisse maggiori. Inoltre la deformazione a trazione nel calcestruzzo, in alcuni punti supera di molto quella massima εct. Si osserva che c’è un valore particolare

s0* per cui lo scorrimento si annulla con tangente orizzontale. Questa situazione analitica di flesso orizzontale della funzione s(x) ha un significato meccanico importante: se s(x )=0, allora anche τ( x )=0 ed allora in x le variazioni di tensione e deformazione nei due materiali è nulla. Poiché anche s’(x)=0, vuol dire che le deformazioni in x sono uguali, quindi in x si è raggiunta la perfetta aderenza fra i due materiali. Per x> x lo scorrimento e le tensioni tangenziali, da un punto di vista

meccanico, devono essere nulle, mentre le deformazioni nei materiali devono essere uguali.

Oltre questo valore di s0* lo scorrimento non ha un punto di nullo e raggiungono valori talmente grandi che non hanno significato fisico.

-0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0 50 100 150 200 250 300 350 400 450 500 ascissa S c or ri m e nto (m m ) s0=0.02 s0=0.05 s0=0.07 s0=0.083 s0=0.09 s0=0.095 -10 -5 0 5 10 15 0 50 100 150 200 250 300 350 400 450 500 Ten s io ni tan g e nzi a li ( N /m m ^ 2) s0=0.02 s0=0.05 s0=0.07 s0=0.083 s0=0.09 s0=0.095

-0.00015 -0.0001 -0.00005 0 0.00005 0.0001 0.00015 0.0002 0 50 100 150 200 250 300 350 400 450 500 ascissa D e for m az io ne nel cal cest ru z z o s0=0.02 s0=0.05 s0=0.07 s0=0.083 s0=0.09 s0=0.095

fig.5- 5: andamento delle deformazioni nel calcestruzzo per diversi valori di s0

-5.00E-04 0.00E+00 5.00E-04 1.00E-03 1.50E-03 2.00E-03 2.50E-03 3.00E-03 0 50 100 150 200 250 300 350 400 450 500 ascissa D e fo rm az io ne nel l' acci ai o s0=0.02 s0=0.05 s0=0.07 s0=0.083 s0=0.09 s0=0.095

5.3 Modello Proposto

Allo scopo di calcolare la rotazione della sezione fessurata della sezione d’interfaccia fra trave e pilastro, c’interessa correlare lo scorrimento che si manifesta fra l’acciaio ed il Calcestruzzo adiacente la fessura, con lo stato deformativo (o tensionale) della barra tesa.

Analizzando il quadro fessurativo di fig. 4-6, si è pensato di valutare lo scorrimento che si manifesta nella zona tesa come lo scorrimento che si manifesta nel tirante di fig. 5-1.

Con quest’ipotesi si trascurano le tensioni tangenziali fra il calcestruzzo della zona tesa adiacente la barra e quello del resto della trave

L’estremità libera del tirante di fig. 5-1 coincide con la fessura fra trave e pilastro, mentre dove si colloca l’estremità fissa non c’interessa, perché si vuole valutare lo scorrimento e quante fessure si formano sulla base di misura degli induttivi.

5.3.1 - Comportamento del tirante in Cemento Armato

Consideriamo il nostro tirante in cemento Armato, vogliamo trovare una correlazione fra la deformazione della barra all’estremità libera e lo scorrimento rispetto al calcestruzzo che qui si manifesta.

Supponiamo di eseguire un processo di carico che parte da livelli bassi di tensione

Deformazione dell'acciaio Deformazione del Cls Scorrimento Lf s 0

ε

s0 ε= ε ct Deformazione dell'acciaio Deformazione del Cls s 0

ε

s0 Deformazione dell'acciaio Deformazione del Cls Scorrimento La s 0

ε

s0 ε< ε ct

a) Prima della fessurazione

b) Incipiente fessurazione

(deformazione) nell’acciaio fino ed oltre lo snervamento. Attraverso le tensioni tangenziali si trasferisce una quota di sollecitazione dall’acciaio al conglomerato che avvolge la barra. Per livelli bassi di carico è presumibile che la tensione massima nel calcestruzzo non superi fct , perciò nel tirante non si formerà alcuna fessura e la distribuzione dello scorrimento e delle deformazioni si presenterà come in fig. 5-7a. Sul tratto iniziale di lunghezza La, c’è uno spostamento relativo fra barra e calcestruzzo, ma oltre la distanza La dalla faccia iniziale c’è perfetta aderenza fra acciaio e calcestruzzo. Aumentando la sollecitazione nella barra, aumenta la distanza La per trasferire la parte di sollecitazione dall’acciaio al conglomerato, ed aumenta anche la tensione di trazione nel calcestruzzo. Per un certo valore del carico sulla barra, alla distanza Lf si raggiunge nel calcestruzzo la resistenza a trazione con la formazione della fessura. In questo istante nel concio che si è appena formato e nella parte rimanente del tirante si ha una ridistribuzione dello stato tensionale e deformativo: nel punto in cui si è formata la lesione, la tensione dell’acciaio è pari a quella dell’estremità libera, quindi dopo la formazione della fessura la tensione media nell’acciaio nel tratto Lf è aumentata. Per contro, nel punto in cui si è creata la lesione la tensione ( e deformazione) del calcestruzzo si annulla.

A questo punto nel concio la distribuzione delle tensioni nell’acciaio decrescerà dai bordi del concio verso il suo interno, viceversa nel calcestruzzo lo stato tensionale e deformativo crescerà dal valore nullo ai bordi verso l’interno del concio. Rispetto alla mezzeria del concio la distribuzione delle tensioni e deformazioni dei materiali è simmetrica, mentre la distribuzione delle tensioni tangenziali e dello scorrimento saranno antisimmetriche.

Nella parte restante del tirante, dopo la formazione della fessura si ricrea la stessa situazione che si aveva in tutto il tirante prima della fessurazione.

Incrementando ancora il carico, nel concio aumentano i valori tensionali nell’acciaio e nel calcestruzzo, e se la distanza Lf è sufficientemente grande da permettere al calcestruzzo di raggiungere ancora la resistenza a trazione fct , a metà del concio si forma un’altra fessura. Si continua ad incrementare il carico finche non si raggiunge un livello deformativo tale per cui non ha significato continuare.

5.3.2 - Algoritmo di risoluzione.

Dobbiamo adattare opportunamente l’algoritmo di risoluzione dell’equazione differenziale per ricreare il comportamento del tirante durante il processo di carico e per costruire la tabella deformazione acciaio-scorrimento.

C’interessa la soluzione nel tratto iniziale in cui la funzione s(x) decresce dal valore

s0 al valore nullo, perciò l’algoritmo di risoluzione si deve arrestare, quando s(xk) diventa negativo. Però abbiamo visto che al variare di s0 può non esserci il punto in cui s(x) si annulla, allora per evitare che l’algoritmo fornisca risultati privi di significato, esso deve arrestarsi anche quando εck>εct .

Nel processo di carico illustrato precedentemente si individuano due fasi:

Fase1: calcestruzzo non fessurato

Fase2: calcestruzzo fessurato

Nel primo caso la soluzione è illustrata nella figura 5.3-a). si fissa lo stato deformativo nel punto iniziale εc0=0 ed εs0= 0.1 εsy ,so che la soluzione deve essere tale che a distanza La (incognita) deve risultare s(La)=0 ed εc(La)-εs(La)=s’(La)=0. Per risolvere l’equazione differenziale fisso un valore di tentativo per s0 ed in genere al primo tentativo non verrà soddisfatta la condizione s’(La)=0. Il valore

assunto da s’(x) in x=La è funzione del valore di s0, allora mediante il metodo numerico delle secanti per la ricerca della radice di una funzione si trova il valore di s0 che annulla s’(La). Questo è il metodo di “shooting” per trovare la soluzione per via numerica di un’equazione differenziale con valori al contorno. A questo punto ho una coppia (εs0 ,s0) cercata, quindi incremento εs0 , ad esempio porto εs0=

0.2 εsy , e ripeto la procedura ora esposta trovando un nuovo valore di s0, continuo in questo modo fintantoché trovo una coppia (ε_s0 ,s_o) tale che in x=La ottengo εc(La)= εs(La)=εct. Questa coppia (ε_s0,s_o) è quella che produce la lesione e segna il termine della fase1.

Nella seconda fase il dominio di esistenza in cui andiamo a cercare la soluzione è fissa è pari a Lf, anzi stante la simmetria andiamo a ricercare la soluzione su Lf/2. perché così diminuisce il numero di punti in cui trovare la soluzione e quindi diminuisce il tempo di elaborazione dell’algoritmo.

Si fissa εs0= εs0 e si va cercare, sempre con la tecnica di “shooting” il valore di s0 tale che in s(Lf/2)=0. Sia s il valore cercato, risulta 0 s0 >s0. Per spiegare questo risultato occorre ricordare che lo scorrimento che si manifesta al bordo è l’integrale della differenza della deformazione fra i due materiali: il secondo integrale risulta più piccolo perché l’intervallo d’integrazione è la metà.

Si incrementa ancora εs0, si trova il relativo s0 e controlliamo se εc≥εct, se questa ultima condizione è vera vuol dire che si forma una lesione in x=Lf'/2, ed allora bisogna cambiare il dominio di esistenza e porlo a Lf/4. si continua ad incrementare εs0 fintantoché εs0@10 εsy . s0⎯ 0 Lf x ε_{s x}( )−ε_{c x}( )

(

)

⌠ ⎮ ⌡ d s0⎯ ⎯ 0 Lf 2 x ε_{s x}( )−ε_{c x}( )

(

)

⌠ ⎮ ⎮ ⌡ d

Si fissa εs0 Valore di tentativo per s0 Risoluzione equazione differenziale Coppia di valori εs0, s0 Stop: output tabella εs0, s0 No No Si Si εc(La)=εs(La) εc(La)=εct

fig.5- 8: Diagramma di flusso dell’algoritmo nella prima fase

5.3.2.1 - Applicazione dell’algoritmo utilizzando il legame d’aderenza del CEB Applichiamo l’algoritmo sopra esposto utilizzando il modello del CEB per legge tensioni tangenziali-scorrimento. Nella tabella 5-1 si riporta la deformazione iniziale εs0, lo scorrimento s0, la distanza L è il dominio di esistenza della soluzione che coincide con La nella prima fase, mentre quando si formano le lesioni coincide con

L/2. Si sono riportate anche le deformazioni dei materiali alla distanza L per

Si fissa εs0 Valore di tentativo per s0 Risoluzione equazione differenziale Coppia di valori εs0, s0 Stop: output tabella εs0, s0 No No Si Si εc(Lf/2)= εct εs0= εs0.max s(L.f/2)=0 Si No Dimezza la lunghezza Lf

In questo esempio di risoluzione si formano due fessure una a L@250 mm e la seconda a 125 mm. Lo scorrimento s0 è il valore massimo della funzione s(x) e si osserva che i valori riportati in tabella sono sempre minori di 1 mm, quindi nel modello del CEB ci spostiamo sul primo ramo senza attingere alla τmax e nemmeno al ramo post-critico del legame d’aderenza. Questa osservazione ci ha spinto a modificare la legge proposta dal CEB alterando i punti caratteristici di tale legge.

Tabella 5- 1

εs0/εsy εs0 s0 εc εa L (mm) Δc (mm)

0.1000 2.654E-04 0.011485 2.75E-05 2.8257E-05 132.9 1.38E-03 0.2000 5.308E-04 0.030962 5.44E-05 5.5342E-05 181.7 2.21E-03 0.3000 7.962E-04 0.055295 8.13E-05 8.1369E-05 221.8 2.89E-03 0.4000 1.062E-03 0.083435 1.08E-04 1.0802E-04 253.7 3.47E-03 0.4095 1.087E-03 0.086282 1.11E-04 1.1181E-04 251.7 3.53E-03 0.4095 1.087E-03 0.08009 7.57E-05 4.1790E-04 125.8 3.29E-03 0.5000 1.327E-03 0.10344 8.52E-05 5.7385E-04 125.8 3.68E-03 0.6000 1.592E-03 0.130068 9.46E-05 7.5567E-04 125.8 4.06E-03 0.7000 1.858E-03 0.157352 1.03E-04 9.4613E-04 125.8 4.40E-03 0.8000 2.123E-03 0.185142 1.12E-04 1.1430E-03 125.8 4.71E-03 0.8000 2.123E-03 0.115714 4.91E-05 1.6946E-03 62.9 1.88E-03 0.9000 2.389E-03 0.131415 5.18E-05 1.94E-03 62.9 1.98E-03 1.0000 2.654E-03 0.143001 5.36E-05 2.11E-03 62.9 2.04E-03 1.2500 3.318E-03 0.150039 5.44E-05 2.17E-03 62.9 2.08E-03 1.5000 3.981E-03 0.154421 5.48E-05 2.19E-03 62.9 2.09E-03 2.0000 5.308E-03 0.161988 5.54E-05 2.21E-03 62.9 2.12E-03 3.0000 7.962E-03 0.175766 5.64E-05 2.23E-03 62.9 2.16E-03 4.0000 1.062E-02 0.188893 5.73E-05 2.23E-03 62.9 2.19E-03 5.0000 1.327E-02 0.20163 5.81E-05 2.23E-03 62.9 2.23E-03 6.0000 1.592E-02 0.214177 5.89E-05 2.24E-03 62.9 2.26E-03 7.0000 1.858E-02 0.226525 5.98E-05 2.23E-03 62.9 2.29E-03 8.0000 2.123E-02 0.238722 6.06E-05 2.23E-03 62.9 2.32E-03 9.0000 2.389E-02 0.250746 6.13E-05 2.23E-03 62.9 2.36E-03 10.0000 2.654E-02 0.262741 6.21E-05 2.23E-03 62.9 2.39E-03

0 0.05 0.1 0.15 0.2 0.25 0.3

0.00E+00 5.00E-03 1.00E-02 1.50E-02 2.00E-02 2.50E-02 3.00E-02 εs0 sco rr im en to ( m m )

fig.5- 10: diagrammo εs0,s0 con la legge d’aderenza del CEB

Di seguito riportiamo dei grafici che mostrano l’andamento dello scorrimento, delle tensioni tangenziali, delle deformazioni per vari rapporti di εs0/εsy

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0 50 100 150 200 250 300 Ascissa S c o rri me n to es0/esy=0.1 es0/esy=0.2 es0/esy=0.3 es0/esy=0.4095 0 1 2 3 4 5 6 7 8 0 50 100 150 200 250 300 Ascissa Te n s ioni Tange nz ia li ( N /m m 2 ) es0/esy=0.1 es0/esy=0.2 es0/esy=0.3 es0/esy=0.4095 0.00E+00 2.00E-04 4.00E-04 6.00E-04 8.00E-04 1.00E-03 1.20E-03 0 50 100 150 200 250 300 D e fo rm a z io n e m a te ri a li es0/esy=0.1 es0/esy=0.2 es0/esy=0.3 es0/esy=0.4095 Deformazione del CLS Deformazione dell’acciaio

-0.25 -0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25 0 50 100 150 200 250 300 Ascissa S c or ri m e nt o es 0/esy=0.5 es 0/esy=0.7 es 0/esy=0.8 -15 -10 -5 0 5 10 15 0 50 100 150 200 250 300 Ascissa Te ns io n i Ta nge nz ia li ( N /m m 2) es0/esy=0.5 es0/esy=0.7 es0/esy=0.8 0.00E+00 5.00E-04 1.00E-03 1.50E-03 2.00E-03 2.50E-03 0 50 100 150 200 250 300 Ascissa D e fo rm az io n e n e ll 'acci ai o es0/esy=0.5 es0/esy=0.7 es0/esy=0.8 0.00E+00 2.00E-05 4.00E-05 6.00E-05 8.00E-05 1.00E-04 1.20E-04 0 50 100 150 200 250 300 Ascissa D e fo rm az io n e d e l C a lcestr u z z o _es0/esy=0.5 es0/esy=0.7 es0/esy=0.8

-0.3 -0.2 -0.1 0 0.1 0.2 0.3 0 20 40 60 80 100 120 140 Ascissa Sc o rri me n to es0/esy=1.5 es0/esy=4 es0/esy=7 es0/esy=10 -15 -10 -5 0 5 10 15 0 20 40 60 80 100 120 140 Ascissa Te n s ioni Ta ng e n z ia li ( N /m m 2 ) es0/esy=1.5 es0/esy=4 es0/esy=7 eso/esy=10 0.00E+00 1.00E-05 2.00E-05 3.00E-05 4.00E-05 5.00E-05 6.00E-05 7.00E-05 0 20 40 60 80 100 120 140 Ascissa D e fo rm az io n e ca lces tr u z z o es0/esy=1.5 es0/esy=4 es0/esy=7 es0/esy=10 0.00E+00 5.00E-03 1.00E-02 1.50E-02 2.00E-02 2.50E-02 0 20 40 60 80 100 120 140 Ascissa D e fo rm a z ione a c c ia io es0/esy=1.5 es0/esy=4 es0/esy=7 eso/esy=10

5.3.3 - Calcolo del diagramma M-

θ

.

Adesso vediamo come si sfrutta la tabella ottenuta col metodo proposto per calcolare il diagramma momento-rotazione. Imponendo l’equilibrio della sezione fessurata si ricava il valore del momento flettente e la posizione dell’asse neutro, che ci servirà per il. calcolo della rotazione.

5.3.3.1 - Calcolo della rotazione

Prima di andare a calcolare la rotazione media del concio di trave di Lunghezza D=90 mm, bisogna indagare sugli spostamenti che gli induttivi di fig. 4-2 leggono. Per quanto riguarda lo spostamento nella zona tesa della trave, riprendiamo in considerazione il tirante in calcestruzzo, supponiamo di posizionare uno strumento di misura degli spostamenti tra l’estremità libera della barra ed una sezione S del tirante distante B dall’estremità.

Nel caso di tirante non fessurato (fig. 5-10b), l’ipotetico strumento misura lo

scorrimento s fra barra e calcestruzzo più lo spostamento Δc risultante dall’integrazione delle deformazioni del calcestruzzo teso sulla base di misura B. Quando il tirante si fessura in modo tale che la lesione è esterna alla base di misura (fig. 5-10c), lo strumento legge lo scorrimento s’ e lo scorrimento Δc’

Deformazione dell'acciaio Deformazione del Cls Lf Lf Deformazione dell'acciaio Deformazione del Cls La

b) Tirante non fessurato

c) Tirante fessurato con lesione esterna alla base di misura

δc δs s δs' s' δc' δs' s' δc' δs'' s'' δc'' δs'' s'' δc''

d) Tirante non fessurato con lesione interna alla base di misura

B

a) Tirante indeformato

s'' δs''

δc''

integrale delle deformazioni del calcestruzzo sul tratto di misura B. Osservando la

fig. 5- 10d, la lesione si forma nel tratto B, allora lo strumento misura 3 volte lo

scorrimento s’’ e lo spostamento Δc pari all’integrazione delle deformazioni del calcestruzzo sul tratto B-Lf.

Invece, per quanto riguarda lo scorrimento delle barre tese nel nodo, in prima approssimazione lo poniamo uguale allo scorrimento calcolato con il metodo proposto. Ad esempio se si forma la lesione all’esterno della base di misura lo spostamento letto dagli induttivi, secondo quanto detto precedentemente, è 2s’+Δc Riportiamo le formule del calcolo di queste rotazioni evidenziando il contributo di Δc e quello dovuto allo scorrimento (slip).

θ_slip 2 s0⋅

h−_yn contributo dovuto allo scorrimento

θ_CLS Δc

h−_yn

(

)

contributo dovuto al calcestruzzo teso θ_modello θ_slip+ θ_CLS

5.3.3.2 - Calcolo del momento e della posizione dell’asse neutro.

Il calcolo del momento e la posizione dell’asse neutro si esegue modificando l’algoritmo di calcolo visto al punto 2.1.1 per la determinazione del diagramma momento curvatura. Le ipotesi sono:

a) Deformazione piana della sezione

b) Legame costitutivo del calcestruzzo parabola rettangolo, non reagente a trazione con deformazione massima a compressione del 3.5‰. La resistenza cilindrica varia col campione.

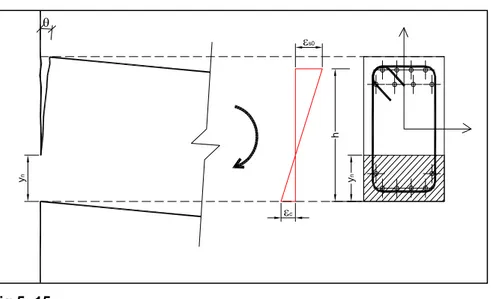
c) Legame costitutivo dell’acciaio di Ramberg-Osgood visto nel Prospetto2. Si fissa una distribuzione lineare ε(y), questa distribuzione dipende da due parametri: la curvatura χ e la deformazione dell’acciaio teso εs0. Dai legami

θ y n εs0 εc y n h fig.5- 15:

delle tensioni interne non è nulla. Trovato il valore della curvatura che soddisfa l’equilibrio, sappiamo trovare il valore della deformazione al lembo più compresso della sezione d’interfaccia e quindi ricavare la posizione dell’asse neutro.

In cui

• εc è la deformazione al lembo compresso • εs0 è la deformazione dell’acciaio teso

• h è la distanza delle barre tese dal lembo compresso.

Dall’equazione di equilibrio alla rotazione possiamo ricavare il valore del momento flettente che corrisponde al valore di εs0 fissato. A questo punto per ogni coppia

yn

ε_c ε_s0−ε_c⋅h

fig.5- 16: diagramma di flusso per il calcolo del diagramma M-θ Si assegna la distribuzione di ε(y) ε y( ) ε_s0 + χ y⋅ Si ricavano le distribuzioni di tensione σ_{c y}( ) σ_{s y}( ) Si ricava il valore di M dall’equazione di equilibrio alla traslazione M, θ Assegnare un nuovo valore di χ Si No Assegnare un altro valore di εs0 Stop:output diagramma M,θ Si ricava il valore di εc, yn,θ εc<εcu L’equilibrio alla traslazione è soddisfatto? No Si

(εs0,s0), determinata con l’algoritmo, corrisponde una coppia (M,θ) e quindi siamo in grado di costruire un diagramma M-θ da confrontare con quello trovato sperimentalmente per ogni campione.

Nell’allegato C è riportato il foglio di calcolo del diagramma momento curvatura. 5.3.3.3 - Diagramma M-θ con il legame d’aderenza proposto dal CEB.

tabella 5- 2: Valori delle rotazioni e momenti

Come si può osservare dalla fig. 5-17, la legge proposta dal CEB conduce ad un diagramma M-θ che discosta parecchio dal diagramma sperimentale. Da questo confronto, s’intuisce la necessità di una calibrazione del modello d’aderenza che effettueremo nel prossimo capitolo

Nella tabella 5-2 sono riportati i valori delle rotazioni e dei momenti calcolati secondo quanto esposto in questi due ultimi paragrafi. Dai valori riportati nella tabella 5-2 si osserva che il contributo del calcestruzzo teso è modesto.

θslip θCLS θ M (kN m)

6.49E-05 3.90E-06 6.88E-05 25.195 1.75E-04 6.25E-06 1.81E-04 50.412 3.13E-04 8.19E-06 3.21E-04 75.6 4.73E-04 9.84E-06 4.83E-04 100.755 4.90E-04 1.00E-05 5.00E-04 103.124 4.54E-04 9.33E-06 4.64E-04 103.13 5.88E-04 1.05E-05 5.98E-04 125.785 7.40E-04 1.16E-05 7.51E-04 150.774 8.96E-04 1.25E-05 9.09E-04 175.795 1.06E-03 1.34E-05 1.07E-03 200.673 6.60E-04 5.36E-06 6.65E-04 200.673 7.51E-04 5.66E-06 7.56E-04 225.584 8.16E-04 5.82E-06 8.22E-04 245.027 8.43E-04 5.85E-06 8.49E-04 261.23 8.55E-04 5.78E-06 8.60E-04 265.728 8.78E-04 5.74E-06 8.83E-04 271.41 9.31E-04 5.72E-06 9.36E-04 279.116 9.89E-04 5.73E-06 9.95E-04 284.826 1.05E-03 5.80E-06 1.06E-03 289.237

Braccio Sinistro -500 -400 -300 -200 -100 0 100 200 300 400 -0.006 -0.004 -0.002 0 0.002 0.004 0.006 Rotazione Mome n ti ( k N m ) Campione B3.1 rotazionesenza scorrimento modello CEB

fig.5- 17:confronto fra il diagramma sperimentale M-θ del Campione B3.1 con quello ottenuto utilizzando la legge d’aderenza del CEB.