PARTE SECONDA: Moti di Whirl e Meccanica Celeste PARTE SECONDA: Moti di Whirl e Meccanica Celeste PARTE SECONDA: Moti di Whirl e Meccanica Celeste PARTE SECONDA: Moti di Whirl e Meccanica Celeste

(1)

PARTE SECONDA: Moti di Whirl e Meccanica Celeste

In questa seconda parte della Tesi, prenderemo in considerazione un caso particolare di rotore formato da due cilindri coassiali accoppiati fra loro da quattro molle di costante elastica k. Questo modello di rotore permette di comprendere alcuni aspetti caratteristici dell’evoluzione dinamica di GGG. Lo sviluppo di tale modello permette di formalizzare una legge per il trasferimento di energia che va ad alimentare il moto di whirl del rotore. Tale legge di trasferimento di energia ha un’analogo con la legge di trasferimento di energia che regola l’evoluzione del sistema pianeta-satellite nella Meccanica Celeste. Questa analogia è stata esplicitamente espressa dalla nota “GG: Energy Gained by Whirling Motion as Fraction of Energy Lost by Spinning Rotor” di A.M. Nobili, D. Bramanti e G. Catastini di cui questo capitolo è un sostanziale sviluppo ed approfondimento. Dall’analisi più approfondita dell’analogia risulta che tale legge di trasferimento di energia ha in realtà un carattere molto più generale (vedi II.2), che accomuna tutti i sistemi fisici che possono essere considerati come rotori istantaneamente conservativi con origine della variazione energetica nella variazione di energia rotazionale. Con il termine istantaneamente conservativo, si intende identificare un sistema fisico per il quale, istantaneamente (cioè fissando il tempo), le leggi di evoluzione del sistema sono quelle di un sistema conservativo. Sostanzialmente un sistema istantaneamente conservativo è un sistema conservativo a cui viene fatta variare l’energia in funzione del tempo. Per cui un sistema istantaneamente conservativo può essere considerato come una famiglia di sistemi conservativi parametrizzata in funzione dell’energia del sistema la quale generalmente può essere espressa come funzione del tempo (se abbiamo una legge temporale che regola la variazione di energia). In questi casi dunque avere una legge regola l’evoluzione temporale dell’energia risulta fondamentale per studiare l’evoluzione del sistema.

In questo capitolo vedremo che se siamo in presenza di un rotore e la variazione di energia del sistema dipende dalla velocità di rotazione degli elementi del rotore attorno al proprio asse, allora la legge del trasferimento di energia è sempre la stessa, ciò che invece può cambiare da un sistema all’altro è la legge che regola l’evoluzione dinamica dell’energia del sistema (la legge che esprime l’energia in funzione del tempo). Le condizioni richieste al sistema per poter applicare questa legge di trasferimento sono soddisfatte in un gran numero di sistemi fisici e meccanici: infatti nella maggior parte dei rotori, l’attrito, e la conseguente variazione di energia rotazionale, dipende dalla velocità di rotazione degli elementi del rotore e non dalla ampiezza delle loro vibrazioni meccaniche, similmente nei sistemi pianeta-satellite la variazione di energia orbitale del sistema dipende dalla variazione di energia rotazionale dei corpi celesti dovuta all’attrito mareale.

Questa legge di trasferimento dell’energia è dunque propria di un grande numero di sistemi fisici e può essere uno strumento utile per ottenere delle stime qualitative. Per quanto riguarda l’analogia fra rotori accoppiati tramite un potenziale elastico e pianeti accoppiati tramite potenziale gravitazionale, l’analogia si estende oltre essendo il potenziale elastico strettamente legato al potenziale gravitazionale (o un potenziale coulombiano in genere), per cui entro certe approssimazioni realistiche le equazioni del

(2)

differenze fisiche sostanziali dei due sistemi tuttavia impediscono di estendere l’analogia oltre un certo limite che analizzeremo.

Infine nell’ultimo capitolo della sezione (II.7) prenderemo in considerazione due esempi realistici di accelerometri differenziali (GG e il Sistema Terra-Luna) per la verifica del Principio di Equivalenza al fine di illustrare le sostanziali differenze dinamiche che incorrono in rotori supercritici accoppiati con potenziale elastico e rotori supercritici accoppiati con potenziale gravitazionale. Vedremo che il richiedere come potenziale di accoppiamento il potenziale gravitazionale comporta alcune differenze sostanziali nella definizione di rotore e nel suo comportamento dinamico come la scomparsa dell’eccentricità del rotore (nei limiti della validità del Principio di Equivalenza) e di tutti i fenomeni ad essa correlati. In caso di violazione del Principio di Equivalenza invece vedremo come sia possibile costruire rotori gravitazionali con eccentricità non nulla e dunque avere fenomeni di risonanza e di autocentratura simili al caso di rotori accoppiati con potenziale elastico.

I. I moti di

I. I moti di whirl

whirl

whirl in rotori supercritici debolmente accoppiati

in rotori supercritici debolmente accoppiati

1. Rotori su 1. Rotori su 1. Rotori su

1. Rotori supercritici debolmente accoppiatipercritici debolmente accoppiatipercritici debolmente accoppiatipercritici debolmente accoppiati

In questo paragrafo vedremo un esempio classico di rotore supercritico formato da due cilindri accoppiati fra di loro grazie a quattro molle di costante elastica k per studiare gli effetti della dissipazione di energia dovuta alla deformazione delle molle.

(3)

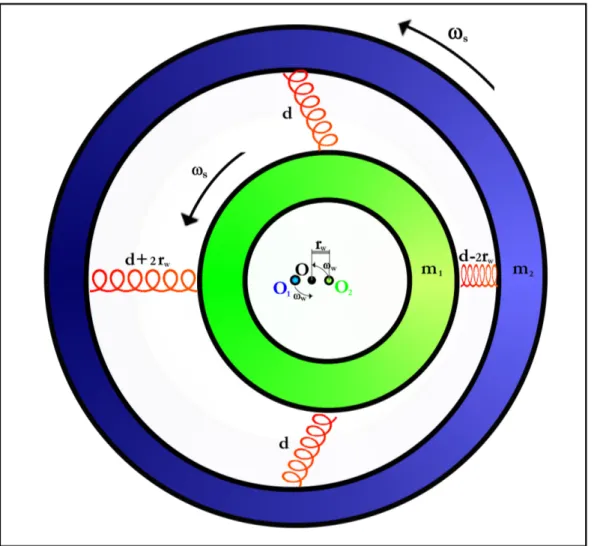
fig II.1:Rotori debolmente accoppiati (due cilindri concentrici accoppiati da 4 molle di bassa costante elastica)

Il rotore rappresentato in figura è formato da due cilindri concentrici di massa m che ruotano attorno all’asse di simmetria con una velocità angolare di ωs che è maggiore

della frequenza naturale. La non perfetta centratura fra i centri di massa (distanza relativa 2rw) provoca una forza di richiamo operata dalle molle le quali nel corso di

un ciclo variano in lunghezza per un totale di 4rw. In rotazione supercritica le molle si

deformano e dissipano energia secondo una legge che può essere ricondotta a quella dell’attrito viscoso con coefficiente di attrito dipendente dal fattore qualita Q delle molle e dalla velocità di rotazione. Per cui possiamo considerare la dissipazione interna delle molle come una sorgente di attrito viscoso rotante.

La dissipazione di energia dovuta alle molle rallenta la velocità di rotazione per cui diminuisce il momento angolare della rotazione attorno al proprio asse. Poichè il momento angolare totale deve essere conservato, i corpi aumentano l’energia del moto di whirl relativo fra i due cilindri. Tale moto, non potendo crescere in velocità di rotazione, cresce dunque in ampiezza. L’effetto destabilizzante della dissipazione interna di energia rientra nella tipica casistica che abbiamo analizzato riguardo ai moti di whirl dovuti ad attrito viscoso. I due casi infatti – quello della dissipazione

(4)

strutturale interna e quella dell’attrito viscoso- si sono esattamente equivalenti se poniamo come coefficiente di attrito

d rot Q k c

ω

= , dove ω_d rappresenta la velocità angolare relativa alla frequenza di dissipazione e Q il fattore qualità, ovvero il rapporto fra energia del sistema e energia dissipata durante una rotazione [14].

Per calcolare ωd basta la frequenza con cui una molla compie una totale

deformazione per ritornare alla situazione originale. Riprendendo l’immagine precedente, calcoliamo il periodo impiegato da una molla per ottenere due contrazioni massime.

La molla al punto uno è in uno stato di massima contrazione, nel corso di un periodo di rotazione essa si allunga per poi tornare a contrarsi secondo un periodo di spin Ts=2π/ ωs,

nel mentre compie questo percorso però i centri di massa dei due cilindri si

sono mossi a causa dei moti di whirl di un angolo 2πωw/ωs, dove ωw sta a

rappresentare la velocità del moto di whirl che può essere ωcr o -ωcr a seconda che si

consideri il moto di whirl diretto o inverso. Questo significa che la velocità della frequenza di dissipazione dell’energia altro non è che

ω

d =

ω

s ±

ω

cra seconda di

(5)

fig II.2: modello matematico per rotori accoppiati

Per scrivere le equazioni del moto consideriamo la seguente modellizzazione (fig.II.2). In questo caso le equazioni del moto possono essere scritte come:

(1)     − × − − − + − − = − × − − − + − − = )) ( ( ) ( )) ( ( ) ( 2 1 2 1 2 1 2 2 1 2 1 2 1 1 r r r r c r r k r m r r r r c r r k r m s rot s rot

ω

ε

ω

ε

& & & & & & & & Chiamando

ξ

=r₁−r₂ , m_r =m₁m₂/(m₁+m₂) e n k/mr 2 = ω possiamo scrivere

l’equazione del moto relativo dei due cilindri che altro non è che

(2)

ξ

=−

ω

2(

ξ

−

ε

)− (

ξ

−

ω

s×

ξ

) r rot n m c & & &

Considerando il caso in cui la velocità di rotazione è molto superiore alla velocità critica, possiamo considerare la velocità di dissipazione uguale a quella di rotazione e, sostituendo k, otteniamo che

s n r rot Q m c

ω

2 = ,

che, inserita nell’equazione del moto relativo fornisce

(3) ( ) 2 ( ) 2 2 2 t Q Q _s s n n n s n

_ω

_ξ

_ω

_ε

ω

ξ

ω

ξ

ω

ξ

_=      × − + + & & & _,

(6)

dove è stato scritto in funzione del tempo nel riferimento inerziale come )) sin( ), (cos( ) (t

ε

ω

st

ω

st

ε

= .

Introduciamo ora la coordinata complessa z=ξ1+iξ2 e riscriviamo l’equazione come

del moto come

(4) n i t s n n s n _z _e s Q i z Q z

ω

ε

ω

2 2 2 2 =       − + + & & &

L’equazione del moto è concettualmente uguale a quella del rotore che avevamo sviluppato per il rotore in Parte Prima II.2 in presenza di attrito e le soluzioni dell’equazione omogenea possono essere ottenute a partire da quelle soluzioni considerando che il coefficiente di attrito non rotante è nullo. In definitiva nel caso di velocità di rotazione molto maggiore alla velocità critica abbiamo come autovalori dell’equazione differenziale

[

i Q

]

n 1 /2 2 , 1 ≅

ω

−

λ

m

Questi autovalori sono il risultato di ordinarie manipolazioni algebriche e di una approssimazione canonica cioè:

(5) ₂ ₂ 2 1 1 1 1 1 x x x n s + ≈       + ⇒ >> =

ω

Quindi il risultato in questione può essere considerato valido nei limiti di questa approssimazione.

Dati questi autovalori complessi possiamo tornare nei reali e scrivere la soluzione omogenea per il moto relativo dei due corpi che risulta essere

(6)         + + +         + − + − = − ) sin( ) cos( ) sin( ) cos( ) ( 2 2 A n A n Q t A n A n Q t om t t Be t t Ae t n n ϕ ω ϕ ω ϕ ω ϕ ω ξ ω ω

Come nel caso precedente, la soluzione dell’omogenea descrive due moti di whirl indipendenti: uno inverso al senso di rotazione che decresce rapidamente in ampiezza, l’altro (quello diretto) che cresce in funzione del tempo secondo una legge esponenziale il cui esponente è inversamente proporzionale al fattore qualità.delle molle. Una soluzione particolare dell’equazione del moto è data da

(7) ( ) ) ( ) ( ₂ ₂ 2 t t s n n p

ε

ω

ξ

− =

(7)

(8)         + + +         + − + − + − = = + = − ) sin( ) cos( ) sin( ) cos( ) ( ) ( ) ( ) ( ) ( 2 2 2 2 2 A n A n Q t A n A n Q t s n n om p t t Be t t Ae t t t t n n

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

ω

ε

ω

ξ

ω ω

Per dare un’idea della crescita dei moti di whirl, riportiamo un’integrazione numerica dell’equazione del moto fatta con un Q molto alto (Q=10).

fig II.3: simulazione moti di whirl (Q=10)

Come si vede dalla figura, il raggio di whirl rw cresce esponenzialmente con il tempo.

In effetti dalle equazioni ricavate, possiamo estrarre una legge che determini l’incremento del raggio di whirl in funzione del tempo e che risulta essere semplicemente (9) Q t w w n e r t r ( ) (0) 2 ω =

Per cui, nel limite realistico Q >> 1, abbiamo che in un periodo naturale Tn il raggio

di whirl subisce un incremento pari a

n n w w T Q r r 2 ) 0 (

ω

≅ ∆

(8)

Dunque, riassumendo brevemente gli elementi risultanti da questo paragrafo, notiamo che nel caso di rotori supercritici accoppiati debolmente:

1. La dispersione di energia a causa delle molle può tradursi formalmente in un attrito viscoso rotante non nullo

2. L’Energia dissipata ha frequenza

ω

d =

ω

s ±

ω

n che, in caso di

velocità altamente supercritica è essenzialmente la velocità di rotazione.del rotore.

3. Tale attrito rallentando la rotazione dei rotori porta ad un’incremento dei moti di whirl

4. Il moto di whirl inverso cade esponenzialmente con il tempo, mentre il moto di whirl diretto (in assenza di attrito non rotante) cresce secondo una legge esponenziale che dipende dal fattore qualità del sistema ovvero

Q t w w n e r t r 2 ) 0 ( ) ( ω =

2. Trasferimento di Energia nei moti di Whirl 2. Trasferimento di Energia nei moti di Whirl 2. Trasferimento di Energia nei moti di Whirl 2. Trasferimento di Energia nei moti di Whirl

In questo paragrafo vogliamo scrivere il guadagno energetico del moto di whirl in rapporto con la quantità di energia dissipata, per vedere quanto di questa energia viene dispersa sottoforma di calore e quanta di essa invece si trasferisce direttamente al moto di whirl. Come vedremo questa legge sul trasferimento di Energia ha un carattere molto più generale che non si applica esclusivamente alla classica dinamica dei rotori. L’energia del rotore può essere ricavata facilmente con la formula

(1) 2 2 1 s rot I E = ω

Dove I rappresenta il momento di inerzia del rotore nel suo insieme attorno all’asse di rotazione.

L’Energia totale del moto di whirl può essere considerata come somma di due componenti, cioè dell’energia cinetica più l’energia elastica ovvero:

(2) 2 2 2 2 2 2 1 2 1 w n w w n elas cin whirl mr m r m k r m E E E = + = ω + = ω

Derivando le due energie rispetto al tempo otteniamo

s s rot I E& ₌ ω ω& _e w w n whirl m r r E& ₌₂ _ω2 &

(9)

Poichè il momento angolare totale deve essere conservato abbiamo che (3) Ltot =Lwhirl +Lrot =0

& &

&

e, dato che i rispettivi momenti angolari risultano essere

s rot I

L =

ω

e Lwhirl =mωnrw2

Abbiamo che la conservazione del momento angolare totale ci fornisce (4) I

ω

&s +2m

ω

nrwr&w =0

Questa equazione ci permette di ricavare la variazione nella velocità di rotazione

(5) I r r m n w w s & & ω ω =−2

Che sostituita nella derivata dell’Energia del rotore ci fornisce la legge di trasferimento dell’energia che stavamo cercando cioè

(6) s n rot whirl E E

ω

− = & &

Notiamo che se la velocità di rotazione è prossima alla frequenza naturale del sistema l’energia dissipata si trasferisce quasi totalmente in un’incremento dell’energia del moto di whirl, viceversa se la velocità di rotazione è altamente supercritica (ωs>>ωn)

abbiamo che l’energia effettiva trasferita dalla dissipazione delle molle direttamente al moto di whirl è molto bassa. Il rimanente quantitativo di energia –che risulta dunque essere la maggior parte dell’energia dissipata- si disperde nelle molle sotto forma di calore.

II. Analogia fra moti di w

II. Analogia fra moti di whirl e moti derivanti da Attrito Mareale

hirl e moti derivanti da Attrito Mareale

1. Legge sul trasferimento di Energia nel caso celeste 1. Legge sul trasferimento di Energia nel caso celeste 1. Legge sul trasferimento di Energia nel caso celeste 1. Legge sul trasferimento di Energia nel caso celeste

Una formula del tutto equivalente a quella ottenuta per i rotori di GG e GGG vale nel caso dell’evoluzione dinamica di sistemi pianeta satellite in presenza di attrito mareale. In questo paragrafo riportiamo per completezza il metodo canonico con cui questa legge viene ritrovata nel pre-print “GG: Energy Gained by Whirling Motion as Fraction of Energy Lost by Spinning Rotor” con il tipico linguaggio della meccanica celeste, tenendo di conto che comunque nel paragrafo successivo questa legge verrà generalizzata ad un vasto numero di sistemi fisici.

Supponiamo di avere due pianeti di massa m, momento di inerzia I e velocità angolare attorno al proprio asse ωs che orbitano su orbite circolari con distanza

(10)

relativa fra i due pari a 2r e velocità angolare orbitale n. Il momento angolare del sistema dato dalla rotazione dei corpi attorno al loro asse di rotazione risulta così essere:

(1) Lspin =2Iωs

Mentre la componente orbitale del momento angolare è data da (2) L_orb=2mr2n

Le derivate temporali dei due risultano dunque essere

s spin I

L& ₌₂

ω

& _,_L _mr_r_n _mr _n

orb & &

& 2

2

4 +

=

Dalla III legge di Keplero abbiamo che ) 2 ( ) 2 ( 3 2 m G r n =

da cui se ne deriva la relazione

(3) 2 +3 =0

r r n n& &

La derivata del momento angolare orbitale può essere dunque riscritta come (4) L&_orb₌mrr&n

A questo punto, considerando che il momento angolare totale deve essere conservato, otteniamo la relazione

(5) Lspin+Lorb =0 & &

Esplicitando la velocità angolare di spin otteniamo

(6) r I mnr s & & ₌₋ _⋅ 2 ω

Calcoliamo ora l’energia del sistema, la componente dell’energia dettata dalla rotazione dei corpi attorno al proprio asse è

(7) Espin=I

ω

s2

(11)

(8) ) 2 ( 2 2 r Gm E_orb =−

Derivando le due equazioni e sostituendo in esse la formula per la derivata della velocità angolare di spin e la terza legge di Keplero si ottiene che

r r mn Eorb & & ₌ 2 _e r nr m Espin s & & ₌₋

_ω

ovvero (9) s spin orb n E E ω − = & &

che è la legge del trasferimento di energia che avevamo ottenuto nel caso dei rotori di GGG. In questa argomentazione (ripresa da [15]) è stata usata una notazione ed un approccio tipico della Meccanica Celeste e per ottenere tale legge di trasferimento dell’energia è stata usata la terza legge di Keplero, nonchè l’ipotesi sulla circolarità delle orbite dei pianeti. Nel prossimo paragrafo generalizzeremo questi risultati disgiungendoli così dalla III legge di Keplero e dalle approssimazioni fatte.

2. Legge sul Trasferimento di Energia nel caso generale 2. Legge sul Trasferimento di Energia nel caso generale 2. Legge sul Trasferimento di Energia nel caso generale 2. Legge sul Trasferimento di Energia nel caso generale

Una legge del tutto simile alla legge trovata per il trasferimento di energia nel caso dei due rotori accoppiati di GG e nel caso del sistema pianeta satellite, sussiste nel caso generale di un sistema fisico che possa essere considerato come un rotore istantaneamente conservativo con origine della variazione energetica nella variazione di energia rotazionale. In particolare supponiamo per il nostro sistema due corpi rotanti su assi paralleli e con uguale velocità di spin, accoppiati tramite un campo centrale di potenziale V(r) e supponiamo che l’energia totale del sistema vari in funzione del tempo. Ciò che richiediamo al fine di poter ritenere valida la legge di trasferimento è che, istantaneamente, le equazioni dinamiche che descrivono il moto orbitale delle due componenti del rotore siano le equazioni del moto relative al sistema conservativo equivalente, dunque non vogliamo che in tali equazioni del moto compaiano forze di attrito. Una situazione del genere può essere ottenuta nel caso in cui la sorgente della variazione di energia sia data dalla rotazione dei corpi attorno al proprio asse (come avviene nei casi che abbiamo precedentemente considerato).

L’altra richiesta è semplicemente la conservazione del momento angolare totale del sistema. Questa ipotesi automaticamente si traduce nella validità della formula cercata. Abbiamo dunque la conservazione del momento angolare totale che (decomponendo nel solito modo in momento angolare dettato dalla rotazione dei corpi attorno al proprio asse e momento angolare orbitale) può essere scritta come:

0 = + ⇒ =

+ orb rot orb

rot L c L L

(12)

Invece abbiamo supposto che l’energia totale del sistema non si conservi in quanto supponiamo che associata alla rotazione dei corpi attorno al proprio asse vi sia una variazione di energia rotazionale, una parte della quale si dissipa sotto forma di calore, mentre un’altra parte si trasferisce nell’energia orbitale, abbiamo cioè

(1) Erot Eorb Ediss

& & & ₋ ₌

Nei due casi precedenti avevamo trovato che

(2) + =0 orb orb rot rot E E

ω

& &

Ora vogliamo vedere la legge di trasferimento equivalente in un caso del tutto generale, per questo svolgeremo i calcoli senza porre in anticipo alcuna limitazione sulle orbite (a priori cioè non chiediamo nè che siano circolari, nè chiuse, nè limitate).

Se chiamiamo

ϕ

&rot la velocità angolare attorno all’asse di rotazione dei corpi abbiamo

(3) Lrot =I

ϕ

&rot

(4) Erot =I

ϕ

&rot2

(5) Lrot Iϕrot Iϕ&rot

& & & & ₌ ₊

(6) Erot I

ϕ

rot

ϕ

rot I

ϕ

rot Lrot

ϕ

&rot

& & & & & & & ₌ ₊ 2 ₌ ovvero (7) rot rot rot E L

ϕ

& & & ₌

Per quanto riguarda invece la parte relativa al moto orbitale abbiamo mettendoci nel sistema di riferimento del centro di massa e chiamando m la massa ridotta e M la massa totale

(8) Lorb mr ϕ&orb

2 = (9) ( ) 2 1 2 1 2 2 2 r V mr r m

Eorb = & + ϕ&orb+

(13)

(10) ( ) 2 1 2 1 2 2 2 r V mr L r m E orb orb = & + +

Abbiamo dunque ottenuto le espressioni per le due componenti dell’energia del sistema (energia rotazionale e l’energia orbitale). Derivando rispetto al tempo otteniamo

(11) r r r V r mr L mr L L r r m

E orb orb orb

orb & &

& & & & & ∂ ∂ + − + = ₃ ( ) 2 2 ovvero (12) orb orb orb orb r E r r V mr L r m

L& & && _&₊ &      ∂ ∂ − + − = ₃ ( ) 2

ϕ

Notiamo che nel caso di moto in assenza di dissipazione abbiamo che le equazioni del moto orbitale delle due componenti del rotore sono date dall’equazione

(13) ₃ ( ) 0 2 =       ∂ ∂ − + − r r V mr L r m_&_& orb

Ora è da notare che nel nostro modello la diminuzione di energia rotazionale avviene solo a causa di fenomeni che incorrono a causa della rotazione dei corpi attorno al proprio asse e che il sistema è istantaneamente conservativo. Intuitivamente potremmo dire che se la diminuzione di energia rotazionale dovesse cessare –come ad esempio avviene nel caso di sistemi pianeta satelliti che diventano sincroni- il momento angolare orbitale diventerebbe nuovamente una costante del moto ed il sistema sarebbe nuovamente governato dall’equazione

(14) ₃ ( ) 0 2 =       ∂ ∂ − + − r r V mr L r m_&_& orb

Il sistema diventerebbe un ordinario problema dei due corpi in campo centrale [16]. Si può dunque dire che il sistema è istantaneamente un problema dei due corpi che vuol dire che fissato il momento angolare orbitale, le traiettorie descritte dal moto sono quelle derivanti dalle equazioni che regolano un moto nel problema dei due corpi ordinario. Ai fini pratici conviene parametrizzare il momento angolare orbitale in funzione della velocità angolare dei due corpi.

Il momento angolare orbitale dunque può essere scritto come funzione di

ϕ

&

rot

(14)

e abbiamo che l’equazione del moto che descrive il comportamento del raggio nel tempo e che è dipendente dalla velocità di rotazione diventa:

(16)

(

( ₃ )

)

( ) 0 2 =         ∂ ∂ − + − r r V mr L r

m_&_& orb

ϕ

&rot

In particolare, dunque, abbiamo che il raggio orbitale deve soddisfare l’equazione

(17) orb orb L r r V mr L r m _≡ ∀      ∂ ∂ − + − ₃ ( ) 0 2 & &

In pratica l’equazioni del moto possono essere descritte tramite una famiglia di equazioni differenziali che può essere parametrizzata in funzione del momento angolare orbitale oppure della velocità rotazionale dei corpi. Questo implica che indipendentemente dal momento che stiamo prendendo in considerazione

(18) Lorb orb Eorb

& & & _ϕ ₌ Ovvero (19) orb orb orb E L

ϕ

& & & ₌

Che assieme alla legge della conservazione del momento angolare diventa

(20) orb orb rot rot rot orb E E L L

ϕ

& & & & & & ₊ ₌₀₌ ₊

La legge in questione è dunque una legge di carattere generale indipendente dal potenziale centrale cui sono soggetti i corpi, indipendente dalla forma geometrica, dall’orbita da essi percorsa ed indipendente dalla legge che origina la dissipazione di energia. Le uniche condizioni vincolanti richieste sono che la dissipazione sia originata esclusivamente dal moto rotatorio attorno al proprio asse e che il momento angolare totale si conservi.

3. L’Analogia nelle equazioni del moto 3. L’Analogia nelle equazioni del moto 3. L’Analogia nelle equazioni del moto 3. L’Analogia nelle equazioni del moto

La legge sul trasferimento di Energia dunque è una legge di carattere generale che accomuna sistemi fisici radicalmente diversi fra di loro, essa dunque non esprime una corrispondenza stretta fra moti di whirl e moti mareali, bensì evidenzia una caratteristica comune ad una categoria molto più ampia di sistemi fisici. Approfondendo le equazioni del moto dei due sistemi tuttavia si nota che la corrispondenza fra i due sistemi è più stretta. In particolare potremmo dire che le equazioni del moto che regolano

(15)

l’evoluzione dei moti di whirl sono con un certo grado di approssimazione le stesse che regolano l’evoluzione secolare di un sistema pianeta satellite.

Dalla discussione precedente abbiamo visto che

(1)

(

)

r r V m r m L t r orb rot rot ∂ ∂ − = ( ) 1 ( ) ) , ( ₂ ₃ 2

ϕ

& & & &

E’ l’equazione del moto che regola l’evoluzione del raggio del sistema in funzione della velocità angolareϕ&rot e del tempo in presenza di un campo centrale generato dal

potenziale V(r). Ovvero (scrivendo in modo esplicito la dipendenza dalla velocità angolare) abbiamo (2)

(

)

r r V m r m I c t r rot rot ∂ ∂ − − = 1 ( ) ) , ( ₂ ₃ 2 ϕ ϕ& & & &

A questo punto introduciamo i due potenziali che ci interessano per i moti di whirl ed i moti mareali ed otteniamo le rispettive equazioni del moto:

per i moti di whirl

(3)

(

)

r m k r m I c t r rot rot − − = ₂ ₃ 2 ) , (

ϕ

&

ϕ

& & &

per i moti mareali

(4)

(

₂ ₃

)

₂ 2 ) , ( r GM r m I c t r rot rot − − = ϕ ϕ& & & &

Ora nella prima equazione relativa ai moti di whirl possiamo chiamare

m k

n =

2

ω

rappresentante la frequenza naturale del sistema. In generale tale frequenza naturale del sistema si può considerare costante in quanto la costante elastica delle molle non subisce alterazioni a meno di forti deformazioni. Per cui, chiamando

(5)

(

₂

)

2 ) ( m I c _rot rot ϕ ϕ γ & ₌ − &

Possiamo scrivere l’equazione relativa al moto di whirl come

(6)

(

)

r r t r n rot rot 2 3 ) , (ϕ& = γ ϕ& −ω & &

(16)

Viceversa studiamo invece l’equazione relativa ai moti mareali. Abbiamo che per il sistema mareale istantaneamente vale la terza legge di Keplero

(7) n a =GM ∀ϕ&rot

3 2

Dove sia l’asse maggiore che il moto medio sono dipenti da

ϕ

&rot. Ora, considerando

che (8) a −e2 =b≤r≤a 1 Abbiamo che (9) GM −e ≤n r ≤GM ∀ϕ&rot 3 2 2 1 ovvero poichè 2 0 > r (10) rot r GM r n e r GM ϕ& ∀ ≤ ≤ − 2 2 ₂ 2 1

Che vuole dire

(11) rot e r n r GM r n _∀

ϕ

& − ≤ ≤ 2 2 2 2 1

Chiamando dunque

ω

n =nil moto medio abbiamo che l’equazione relativa al sistema

mareale può essere maggiorata e minorata nel seguente modo

(12)

(

)

(

)

r e r t r r r n rot rot n rot 2 2 3 2 3 1 ) , ( − − ≤ ≤ −

ω

ϕ

γ

ϕ

ω

ϕ

γ

& & & & & Le due equazioni (13)

(

)

1 2 3 1 1( , ) r r t r n rot rot ω ϕ γ ϕ& = & − & & (14)

(

)

₂ 2 2 3 2 2 1 ) , ( r e r t r rot n rot − − =

γ

ϕ

ω

ϕ

& & & &

Descrivono il comportamento entro il quale deve svolgersi il moto del nostro sistema mareale, abbiamo cioè

(17)

Ovvero le due equazioni differenziali trovate descrivono la frontiera della regione di confidenza in cui può trovarsi il raggio del sistema mareale preso in considerazione. E’ importante notare che le due equazioni tendono a convergere fra di loro man mano che l’eccentricità diminuisce. Questo è importante perchè nella maggior parte dei sistemi fisici reali l’azione mareale tende a circolarizzare l’orbita. Se l’effetto mareale tende a circolarizzare l’orbita, esso tende anche a ridurre i limiti della nostra maggiorazione e facendo tendere l’equazione del moto mareale a

(16)

(

)

r r t r rot _n rot 2 3 ) , (ϕ& =γ ϕ& −ω & &

Ora bisogna tuttavia notare una differenza concettuale fra l’equazione soprariportata relativa ai moti mareali e l’equazione equivalente relativa ai moti di whirl. Mentre i moti di whirl hanno una frequenza naturale che può essere considerata costante, qui il moto mareale ha una velocità orbitale media variabile in quanto dipendente dall’asse maggiore dell’orbita dunque non è costante. Dunque la nostra analogia l’evoluzione dei moti di whirl e dei moti mareali va considerata valida fintanto che

ω

&_n ≅0_{. In realtà questa} condizione non è troppo limitante perchè, in effetti, prima di avere un cambiamento sensibile nella velocità orbitale bisogna avere un grande cambiamento nell’asse maggiore dell’orbita del pianeta. Dalla terza legge di Keplero, infatti, abbiamo che

GM a

n2 3= derivando rispetto al tempo abbiamo (17) 2n&a+3na&=0 ovvero (18) a a n n& & 2 3 − =

se consideriamo la variazione in un intervallo di tempo finito

(19) a a n n ∆ − = ∆ 2 3

Quindi in prima approssimazione potremmo dire che la variazione relativa dell’asse maggiore corrisponde alla variazione relativa della velocità orbitale. Per avere un’idea di cosa questo significhi basta presentare un caso pratico: quello del sistema Terra-Luna. In questo caso

m a;R ≅3.84⋅108

(18)

s rad n 2.5 10−6 / ⋅ ≅ R

Per ottenere una modificazione sensibile della velocità orbitale media della Luna (i.e.

s rad

n'R≅2.49⋅10−6 / ) l’asse maggiore si deve essere modificato di almeno 10

6 _metri

ovvero più di 1000 km e una modificazione del genere avviene nell’ordine del milione di anni.

Detto questo, nei limiti fisici ω&_n≅0 e _e_≅₀che sono spesso soddisfatti nei sistemi

mareali ordinari, abbiamo che l’equazione del moto relativa al sistema mareale può essere scritta nella forma di un’equazione del moto relativa ad un moto di whirl cioè

(20)

(

)

r r t r rot _n rot 2 3 ) , (ϕ& =γ ϕ& −ω & &

Questo significa che se la legge che regola l’evoluzione della velocità rotazionale fosse la stessa, ovvero

(21)

ϕ

&_rot(whirl)(t)=

ϕ

&_rot(maree)(t)= f(t)

i due sistemi si comporterebbero allo stesso modo nel tempo. Questa analogia non è casuale, il motivo di tale analogia infatti risiede nella speciale relazione che incorre fra problema di Keplero e problema dell’oscillatore armonico e nella possibilità di trasformare l’uno nell’altro.

Dualismo fra il Potenziale dell’Oscillatore Armonico e il Potenziale di Coulomb

La possibilità di ricondurre le equazioni del moto descriventi l’evoluzione del sistema mareale nelle equazioni del moto descriventi l’evoluzione del sistema nel caso dei moti di whirl è data formalmente dall’esistenza della terza legge di Keplero per il problema dei due corpi in campo gravitazionale. Questa possibilità è data dall’esistenza di un dualismo fra il potenziale dell’oscillatore armonico e il potenziale gravitazionale che ha un carattere molto più generale e che ancora non è stato completamente chiarito. Si può dimostrare, infatti, che il potenziale gravitazionale e il potenziale elastico sono del tutto equivalenti operando un cambio appropriato dello spazio geometrico di definizione. Questa trasformazione che permette di convertire un potenziale nell’altro fu ideata da Levi-Civita nel caso bidimensionale e poi estesa da Kustaanheimo e Steifel al caso tridimensionale [18]. Tale dualismo fra potenziali si esplica poi nel noto teorema di Bertrand per cui gli unici due potenziali per cui ogni orbita limitata è chiusa sono il potenziale dell’oscillatore armonico e quello gravitazionale [17]. Questa equivalenza teorica fra i due potenziali, però, non è il genere di equivalenza che ci interessa. Nella trasformazione di Levi-Civita come nelle trasformazioni di Kustaanheimo e Steifel, un potenziale (tipicamente il potenziale Coloumbiano che è singolare nell’origine) viene trasformato nell’altro potenziale operando un cambiamento dello spazio di definizione [19]. Lo spazio risultante su cui viene definito il potenziale non ha un significato fisico immediato, bensì ha il solo significato matematico di permettere l’integrazione del

(19)

problema. Il procedimento da noi svolto invece mira a studiare un’equivalenza fra i due sistemi –seppur parziale – sullo stesso spazio geometrico spazio-temporale. Dal punto di vista teorico e matematico, questo non è rigorosamente possibile. Da un punto di vista funzionale al procedimento svolto da noi le condizioni richieste sono alquanto più lasche. Questo sostanzialmente è dato dal fatto che non stiamo richiedendo una piena equivalenza teorica fra i due sistemi, ma una equivalenza pratica fra di essi sotto certe approssimazioni realistiche. Quello che richiediamo insomma è che esista un’equivalenza fisica fra i due sistemi al di fuori di una pura un’equivalenza matematica fra le equazioni che li governano.

4. Differenza sostanz 4. Differenza sostanz 4. Differenza sostanz

4. Differenza sostanziali nell’evoluzione dei due sistemiiali nell’evoluzione dei due sistemiiali nell’evoluzione dei due sistemiiali nell’evoluzione dei due sistemi

Le considerazioni precedenti ci hanno portato ad evidenziare la necessità di uno studio più approfondito sul comportamento temporale locale della velocità di rotazione dei due corpi. Qui il comportamento dei due sistemi cambia radicalmente e ciò è dovuto ad una sostanziale differenza fisica del fenomeno. Nei moti di whirl infatti la variazione di energia rotazionale è data dalla dissipazione di energia dovuta alle molle, quindi - indipendentemente dagli altri parametri fisici - abbiamo

(1) Erot ≤0 & e poichè

(2) Erot Iϕrotϕrot Lrotϕ&rot

& & & &

& ₌ ₌

e

ϕ

&rotè sempre positiva, questo significa che

(3)

ϕ

&&rot ≤0 e Lrot ≤0

&

Cioè, proprio per il sistema fisico preso in considerazione, l’Energia rotazionale diminuisce, la velocità angolare diminuisce assieme al momento angolare rotazionale, per cui il momento angolare orbitale aumenta. Questo vuol dire che nei moti di whirl, a causa del fatto che l’Energia rotazionale è sempre decrescente, avremo sempre una crescita del raggio di whirl, questo non accade nei sistemi mareali pianeta satellite dove la velocità di rotazione diminuisce o aumenta a seconda che il corpo sia nel caso di rotazione veloce o rotazione lenta.

Sintesi qualitativa dell’evoluzione di sistemi pianeta-satellite

Per capire la distinzione sostanziale fra i moti di whirl ed i moti derivanti dall’attrito mareale nei sistemi pianeta-satellite è necessario riassumere brevemente i risultati notevoli riguardanti quest’ultimi.

Chiamiamo ωpian la velocità angolare del pianeta attorno al proprio asse,

ω

sat la

(20)

eccentricità zero e chiamiamo

ω

orb la velocità angolare orbitale del satellite.

L’evoluzione mareale di un sistema pianeta-satellite può essere studiata dividendo il sistema in due fasi distinte: una prima fase che studia l’evoluzione del sistema pianeta-satellite dalla sua formazione fino alla corotazione del pianeta-satellite attorno al pianeta (

ω

sat =

ω

orb), una seconda fase che invece studia l’evoluzione del sistema dopo la

corotazione del satellite [20]. La suddivisione dell’evoluzione del sistema in queste due fasi trova ragione di esistere dal fatto che nella prima fase dell’evoluzione del sistema è possibile disinteressarsi del comportamento del pianeta e considerarlo come puntiforme, mentre nella seconda parte dell’evoluzione del sistema è possibile considerare il satellite come puntiforme e concentrarsi sul comportamento del pianeta (cfr. Secular Effets of Tidal Friction on the Planet-Satellite System A. Nobili). Durante ciascuna di queste fasi è dunque possibile considerare uno dei due corpi celesti come puntiformi e concentrarsi sul comportamento dell’altro.

Analizziamo dunque la prima fase dell’evoluzione del sistema pianeta satellite supponendo il pianeta come puntiforme ed analizzando il comportamento del satellite sotto l’influenza del campo gravitazionale creato dal pianeta. Se la sorgente del potenziale del campo gravitazionale può essere considerata come puntiforme, il satellite –in questa fase dello studio- deve essere considerato come un corpo esteso. Per semplicità espositiva supponiamo il satellite coperto da uno strato di fluido ideale. La differenza di potenziale gravitazionale tra i vari punti del satellite dà origine al potenziale mareale e alla formazione dei bulges mareali ( fig. II.4 ) dovuti all’adeguarsi del fluido alle nuove linee equipotenziali.

fig II.4: forze mareali e formazione di bulges mareali (nel riquadro)

Nella situazione ora descritta (con un fluido ideale) il fluido si adatterebbe istantaneamente ai cambiamenti di posizione della sorgente del campo gravitazionale e la conformazione dei rigonfiamenti mareali sarebbe indipendente dalla velocità angolare del satellite

ω

sat ed essi sarebbero sempre posizionati lungo la congiungente

pianeta-satellite. Nel caso reale invece i rigonfiamenti mareali possono trovarsi disallineati rispetto alla congiungente pianta satellite dando così origine ad un momento non nullo

(21)

manifestarsi due configurazioni possibili discriminate dal rapporto

ω

sat/

ω

orb(cfr.

Goldreich & Soter 1966) :

1. Rotazione veloce (

ω

sat/

ω

orb > 1.5 ): in questo caso la rotazione del satellite spinge i

rigonfiamenti a procedere oltre la congiungente creando così un momento risultante che tende a frenare la rotazione del satellite.

2. Rotazione lenta (

ω

sat/

ω

orb < 1.5 ): i rigonfiamenti a precedono la congiungente creando

così un momento risultante che tende a accelerare la rotazione del satellite.

fig II.5: l’attrito mareale proveniente da una coppia non nulla di forze generata dai bulges mareali, caso rotazione veloce (1) caso rotazione lenta (2)

La decelerazione del satellite porta –per la conservazione del momento angolare totale del sistema- ad aumentare la distanza relativa fra pianeta e satellite mentre l’accelerazione porta a diminuire tale distanza.

Gli stessi due casi (rotazione lenta e rotazione veloce) incorrono nella seconda fase dell’evoluzione del sistema, dove, stavolta, ad essere considerata come una sorgente di potenziale gravitazionale puntiforme è il satellite, mentre il pianeta viene considerato come corpo esteso. E’ da notare come in ciascuna di queste due fasi uno dei due corpi celesti può essere considerato come puntiforme e dunque la rotazione attorno al proprio asse di inerzia può essere considerata nulla. Questo permette di ricondurre la forma dell’energia rotazionale del sistema alla forma

(22)

Dove I rappresenta il momento di inerzia del satellite o del pianeta (a seconda se siamo nella prima o nella seconda fase dell’evoluzione del sistema) e ϕ&rot la sua velocità. La

possibilità di scrivire l’energia rotazionale in questa forma ci permette di utilizzare la modellizzazione e le argomentazioni svolte nei paragrafi precedenti per ricavare la legge sul trasferimento di energia.

A differenza del caso dei moti di whirl, però, in questo caso l’Energia Rotazionale può essere crescente o decrescente a seconda del caso in cui ci troviamo (rotazione lenta o rotazione veloce). Nei moti di whirl, invece, l’Energia rotazionale è sempre decrescente e dunque avremo che, in generale, i moti di whirl generati dalla conservazione del momento angolare nei rotori accoppiati avranno un comportamento simile solo ai sistemi mareali in cui l’Energia rotazionale è decrescente (rotazione veloce) ed il raggio orbitale è crescente .

5. Leggi di variazione della velocità 5. Leggi di variazione della velocità 5. Leggi di variazione della velocità 5. Leggi di variazione della velocità

Come abbiamo visto data l’analogia esistente fra le equazioni del moto ciò che determina l’evoluzione dinamica dei due sistemi è la legge che regola la variazione del momento angolare orbitale, ovvero la legge che regola la variazione dell’energia rotazionale, ovvero –supponendo i momenti d’Inerzia dei corpi costanti- la legge che regola il rallentamento della rotazione dei corpi attorno al proprio asse. Facendo queste premesse è necessario studiare più approfonditamente la legge che regola l’evoluzione della velocità di rotazione nei due sistemi indicati.

Caso mareale

E’ possibile fare una stima qualitativa del fenomeno di rallentamento nella rotazione planetaria dovuto alle maree prendendo assumendo il pianeta in rotazione attorno al proprio asse come rivestito di un fluido incomprimibile ma viscoso. Il pianeta, ruotando sul proprio asse trascina il bulge mareale dando così origine ad una coppia non nulla di momenti di forza che ostacola o avvantaggia la rotazione del pianeta attorno al proprio asse a seconda che la rotazione del pianeta sia lenta o veloce. D’ora in avanti

(23)

studieremo il sistema pianeta satellite come nel caso del sistema Terra-Luna dunque nella fase 2 (in cui il satellite è già in corotazione attorno al pianeta), ma questa distinzione è una semplice distinzione notazionale perchè lo stesso fenomeno può essere studiato relativamente alla fase 1 dell’evoluzione del sistema. Indicando con i segni _{; ,}R_{le quantità relative al pianeta e al satellite, abbiamo che l’altezza locale di}

un’onda mareale per un punto di latitudine Λ e longitudine λ è

(1)

(

)

cos( ) 2 1 cos 3 1 ) , ( 2 2 Λ − ≅ Φ = Λ λ λ 2 R ; ; R ; R r R r GM g g h mareale considerando che (2) ₂ ; ; R GM g=

possiamo scrivere l’altezza mareale come

(3)

(

)

cos( ) 2 1 cos 3 ) , ( 2 3 Λ −       ≅ Λ λ λ ; R ; ; ; R R r R M M h

Per cui la massa di liquido origine del torque mareale è

(4)

∫

Σ

Λ

=

;

d

h

m

ρ

(

λ

,

)

λ

considerando che (5) ₂ ; ; R GM g=

possiamo scrivere l’altezza mareale come

(6)

(

)

cos( ) 2 1 cos 3 ) , ( 2 3 Λ −       ≅ Λ λ λ ; R ; ; ; R R r R M M h ovvero (7)

∫

(

)

Σ Λ Λ −       ≅ ; ; R ; ; ; R d d R r R M M m ρ λ cos( ) λ 2 1 cos 3 2 3

(24)

Il termine

∫

(

)

Σ Λ Λ − ; ; d d R λ λ ) cos( 2 1 cos 3 2

rappresenta un volume e possiamo identificarlo con la lettera V ottenendo così per la massa spostata dal potenziale di marea la formula (8)

V

r

R

M

m

ρ

3













≅

R ; ; ; R

Supponiamo ora che i due rigonfiamenti siano simmetrici e calcoliamo la forza risultante dalla loro azione differenziale. La forza risultante può essere scritta come

(9)

(

)

2

1 2 2 1

a

m

F

ris

=

−

=

−

Essendo (10) 3 R ; ; R r R GM a a₁− ₂ ≅2

Abbiamo che la Forza risultante è

(11) V r R M M GM F 6 ρ R ; 4 ; ; R R =

Abbiamo indicato con la lettera V il Volume e non abbiamo esplicitato la sua dipendenza dal raggio del pianeta perchè generalmente la Forza in questione viene calcolata per unità di Volume dV della massa spostata. Quello che ci interessa vedere infatti è che per unità di Volume la forza è (unendo le costanti fra di loro)

(12) 6 R ; ;

r

R

F

4

α

=

Questo porta a un momento risultante pari a

(13) 6 R ; ; r R F R M 5 ' α = ∧ =

Questo è un calcolo qualitativo, la formula esplicita per α’ è (cfr. “Q in the solar system” Soter & Goldreich, 1966 [21])

(25)

(14)         + = 2 ; ; ; 2 GM R Q GM 3 38 1 4 9 ' 4

_µ

π

α

Dove Q;è la funzione di dissipazione del pianeta e

µ

;la rigidità del pianeta.

Dalla formula canonica

(15) rot

rot _I _I

dt dL

M ₌ ₌

ω

& ₌

ϕ

&&

; abbiamo che (16)

(

)

(

)

'

(

0

)

...

5 0

+

−

+

≅

t

r

R

I

t

o t rot rot 6 R ; ;

α

ϕ

&

Che esprime il modo in cui varia la velocità rotazionale del pianeta al primo ordine di approssimazione. In particolare il coefficiente α’ può essere sia positivo che negativo in funzione della velocità orbitale al tempo t0.

E’ importante notare che in questa modellizzazione, che riguarda esplicitamente l’attrito mareale, non vi è dispersione di energia rotazionale sotto forma di calore. Questo non è dovuto al fatto che in realtà non vi sia un riscaldamento mareale (termine indicato per la dispersione di energia rotazionale in energia termica dovuto al bulge mareale), ma è dovuto al fatto che al momento stiamo semplicemente considerando la sorgente principale del rallentamento del pianeta. Il rallentamento del pianeta non è dato principalmente dall’attrito della massa che si sposta, bensì dall’attrito mareale e dal momento risultante causato dalla massa spostata del pianeta. Questo è importante perchè è l’origine della principale differenza dinamica fra attrito mareale e moti di whirl. La principale variazione dell’energia rotazionale nei moti di whirl è data da una dissipazione di energia a causa della deformazione delle molle, questo implica che l’energia rotazionale può solo diminuire ed il raggio orbitale può solo crescere. Un fenomeno equivalente nel caso dell’attrito mareale –in cui l’energia rotazionale è decrescente indipendentemente dalla velocità angolare del pianeta, cioè il pianeta viene sempre rallentato- potrebbe avvenire nel caso in cui la maggiore sorgente della variazione di energia rotazionale fosse l’attrito derivante dalla rotazione del pianeta in un’atmosfera composta da un fluido viscoso che rallenta la rotazione della sfera come sembra sia il caso del satellite Io.

Il bulge mareale assume la stessa configurazione che abbiamo descritto sopra ciò che varia nella situazione è che il pianeta deve la componente maggiore del suo rallentamento alla dispersione termica dovuta alla rotazione nel fluido più che al momento risultante dal bulge mareale. In questo caso la variazione di energia cinetica

(26)

può essere calcolata a partire dal coefficiente di attrito viscoso del fluido η secondo la legge [22] (17)

∫

_      ∂ ∂ + ∂ ∂ = dV x v x v E i k k i rot 2 2 1 η &

Che permette di ricavare la variazione di energia rotazionale del pianeta e dunque ottenere la variazione di energia orbitale secondo il procedimento di II.2.

Caso meccanico

Nel caso dei moti di whirl la sorgente della diminuzione dell’energia rotazionale è diversa di quella presente nell’attrito mareale. In questo caso infatti abbiamo una dispersione di energia dovuta alla deformazione delle molle.

Dalle considerazioni fatte in precedenza (vedi paragrafo sul trasferimento di energia e usando le stesse notazioni) si può dedurre la frequenza di dissipazione di energia che è

n

s

ω

− e definire così un parametro chiamato fattore qualità Q che tenga in conto di ogni perdita di energia indipendentemente da quale sia la sorgente di questa dispersione di energia. Tale parametro deve essere poi misurato sperimentalmente. Si definisce così il fattore qualità Q in base all’energia persa dalle molle di richiamo

(18) Q t elast elast w s e E t E ) ( ) 0 ( ) ( ω ω − − =

Questo parametro, essendo misurato sperimentalmente tiene in conto di tutte le perdite di energia, indipendentemente dalla sorgente che le causa [23].

A questo punto, assieme ad i risultati dei paragrafi precedenti, possiamo ricavare la variazione nella velocità di spin. Definiamo infatti il fattore qualità del moto di whirl Qw

come (19) w w Q t wh wh t r e r ( ) (0) 2 ω − =

I due momenti angolari in questione sono (20) Lwh mr whωw 2 2 = , (21) Lrot mR ωs 2 2 =

per cui dalla conservazione del momento angolare abbiamo (22) Lrot +Lwh =0

& &

(27)

(23) wh w wh s r R r _& & ₌₋ _⋅ 2 2 ω ω

derivando l’equazione relativa al raggio di whirl abbiamo

(24) wh w w wh r Q r 2 ω − = & ovvero (25) ₂ 2 2 R r Q w w w s

ω

& =

Qui è da notare che la velocità angolare diminuisce in quanto il fattore Qw, per la

definizione che ne abbiamo dato, è negativo. Quello che manca è una stima del fattore di qualità di whirl rispetto al fattore di qualità delle molle. Questa relazione si ottiene dalla conservazione dell’energia.

(26) s w2 _w2 elast kr Q E& =−

ω

−

ω

Ovvero (27) 2 2 2 _n _w w s elast r Q E& =−

ω

−

ω

Poichè per la conservazione totale dell’energia abbiamo (28) E&_rot −E&_wh =E&_elast

e dato che (29) + =0 wh wh rot rot E E

ω

& &

Mettendo tutto insieme otteniamo la relazione

(30) s w w w s w s n w w w w Q R r Q R r R r Q

ω

2 2 2 2 2 2 2 2 2 + − − = Ovvero (31) ₂ 2 n w w Q Q

ω

− =

(28)

Ovvero (32) ₂ 2 2 R r Q w n s

ω

& =−

Ritornando dunque alla notazione relativa alla trattazione comune di entrambi i casi abbiamo che la legge con cui si modifica la velocità di rotazione per i moti di whirl approssimata al primo ordine è

(33) ( ) ( ) 2 ( 0) ... 2 2 0 − − + ≅ t t R r Q t t o t w n rot rot ω ϕ ϕ& &

Che può anche essere vista come la decelerazione angolare prodotta dal momento di una forza Fattr

(34) ₍ ₎≅ ₍₀₎+ ₍t−t₀₎+_... I M t t o t attr rot rot ϕ ϕ& & con

(35) _attr _attr _wh _wh Felastr_wh

Q kr Q r F Q M 1 1 2 1 − = − = ∧ − =

che fornisce anche indicazioni su come ostacolare la decelerazione dovuta dalla dispersione. Come si può notare, in questo caso il segno del coefficiente lineare è sempre negativo per cui la velocità angolare è sempre una funzione decrescente.

6 66

6. I vincoli dell’analogia. I vincoli dell’analogia. I vincoli dell’analogia . I vincoli dell’analogia

Dalle considerazioni precedenti abbiamo notato che l’analogia fra i moti di whirl e l’attrito mareale sarebbe perfetta se la legge che regola il rallentamento dei corpi fosse identica. Per fare una stima del comportamento qualitativo abbiamo trovato un’approssimazione del prim’ordine che ha portato ai seguenti risultati

(1) () ( ) ' ( 0) ... 5 0 ) ( ) ( + − + ≅ t t r R I t t o t maree rot maree rot 6 R ; ; α ϕ ϕ& & (2) ( ) ( ) 2 ( 0) ... 2 2 0 ) ( ) ( + − − ≅ t t R r Q t t o t w n whirl rot whirl rot ω ϕ ϕ& &

(29)

(3) o o t w n t R r Q r R I 2 2 2 5 ' ω α − ≈ 6 R ; ;

Con lo scorrere del tempo, tuttavia, essendo la principale variazione del coefficiente dovuta al raggio orbitale o al raggio di whirl, la velocità rotazionale dei due sistemi diminuirebbe in modo diverso –stiamo parlando di una variazione della velocità al secondo ordine di approssimazione- ed il comportamento dei due sistemi diventerebbe diverso. Per mantenere l’analogia, sarebbe necessario ricalibrare la massa del rotore di modo da modificarne la frequenza naturale di modo da compensare la diversa legge che regola l’evoluzione della velocità rotazionale.

Il reale motivo fisico per cui le leggi di decelerazione rotazionali sono distinte fra di loro è la diversa dipendenza dell’attrito dall’azione del potenziale centrale. Nel caso dei moti di whirl infatti abbiamo che l’attrito può essere visto come dipendente dall’azione di un potenziale centrale, abbiamo infatti che

(4) w r r elast whirl attr r V M = ∂ ∂ ∝ ) (

Nel caso delle maree invece l’attrito dipende dalla differenza del potenziale cioè

(5) R r r grav R r r grav maree attr r V r V M + = − = ∂ ∂ − ∂ ∂ ∝ ) (

Questo è dato dal fatto che il potenziale mareale genera due rigonfiamenti mareali e quindi il momento risultante è la differenza dei due. Se infatti, per pura ipotesi supponessimo di avere solo un bulge mareale (richiesta questa che non ha alcun significato fisico, ma è utilizzata solo per spiegare il concetto) avremmo che

(6) R r GM m M_attrmaree R ; ' ) ( α =

Ovvero, usando la terza legge di Keplero ed esplicitando dal momento di inerzia la dipendenza quadratica dal raggio del pianeta avremmo che

(7) ( ) ... ' '' ) ( ) ( 0 0 ) ( ) ( _≅ ₊ ₋ ₊ t t R r I t t o t maree rot maree rot 2 ; 2 R ; α ϕ ϕ& &

Che è l’equivalente della legge di decelerazione angolare nei moti di whirl.

Pur essendoci dunque una stretta analogia concettuale fra evoluzione dei sistemi pianeta satellite e moti di whirl, l’analogia reale è sostanzialmente limitata a causa del fatto che il termine dominante nell’evoluzione dei sistemi pianeta satellite è il termine mareale che è un termine differenziale, mentre l’attrito nei moti di whirl può essere semplicemente visto come l’azione diretta di un potenziale centrale.

(30)

7 77

7. Il Caso reale. Il Caso reale. Il Caso reale . Il Caso reale

In questo paragrafo prenderemo in considerazione due accelerometri differenziali usati la verifica diretta del Principio di Equivalenza e ne analizzeremo le analogie e le differenze sostanziali in virtù degli elementi raccolti nei paragrafi precedenti. Nella parte successiva della Tesi ci concentreremo poi nello studio dei moti di whirl per uno di essi esaminandoli nel dettaglio nel suo adattamento terrestre (GGG).

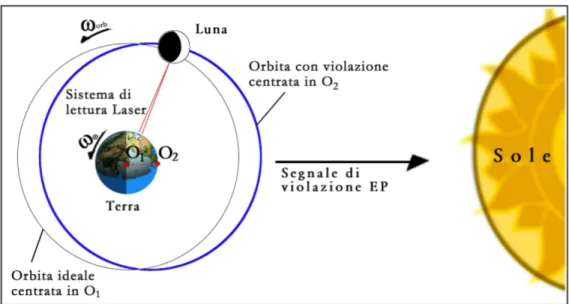
I due accelerometri differenziali che prenderemo in considerazione sono GG nel campo della Terra (fig.II.6) e l’accelerometro naturale formato dal sistema Terra-Luna nel campo del Sole (fig.II.7). Come è possibile notare dalle due immagini, i due accelerometri, pur essendo nella loro realizzazione pratica radicalmente distinti, hanno vari tratti in comune.

Ad prima analisi intuitiva –manifesta dalle figure- i due sistemi fisici sembrano estremamente simili e tali somiglianze lasciano presupporre la possibilità di poter trattare formalmente entrambi i sistemi nello stesso ambiente dei rotori supercritici debolmente accoppiati. Se questa affermazione ha un senso manifesto per quanto riguarda l’accelerometro GG, è necessario tuttavia specificare meglio questa affermazione per quanto riguarda il sistema Terra-Luna, analizzando i vincoli e i limiti di questo approccio.

Per questa discussione considereremo l’orbita della Luna come un orbita circolare e priva di inclinazione, e l’asse di rotazione terrestre (Polo Nord Terrestre) coincidente con la normale al Piano dell’Eclittica (Polo Nord Celeste). Per quanto riguarda la velocità di rotazione della Luna attorno al proprio asse, tale satellite è corotante con la Terra, per cui ai fini dell’analisi dell’evoluzione del sistema [20] è possibile assumere tale corpo come puntiforme e dunque disinteressarsi a posteriori della velocità di rotazione in questione.

(31)

fig. II.6: l’accelerometro differenziale GG nel campo della Terra

fig. II.7: l’accelerometro differenziale Terra-Luna nel campo del Sole

In questa modellizzazione le analogie fra i due sistemi sono evidenti. In entrambi i sistemi abbiamo due corpi rotanti attorno ad un asse principale di inerzia con direzione fissa nello spazio inerziale, i due corpi rotanti sono accoppiati fra di loro da un potenziale di accoppiamento che è il potenziale elastico per GG e il potenziale gravitazionale per il sistema Terra-Luna. In entrambi i casi i centri di massa dei due corpi (O1 e O2 per GG e CMT e CML per il sistema Terra-Luna) orbitano fra di loro con una velocità angolare che è la velocità critica del sistema. In particolare i corpi ruotano attorno al proprio asse con una velocità angolare maggiore della velocità critica quindi sono in regime supercritico (per il sistema Terra-Luna, come spiegato la Luna può essere considerata come puntiforme e l’unica velocità di rotazione da considerare è quella diurna della Terra). In entrambi i casi presi in considerazione, un eventuale

(32)

segnale di violazione del principio di equivalenza viene misurato a partire da una polarizzazione dell’orbita dei centri di massa dei corpi. Riassumendo in uno schema le analogie fra i due accelerometri differenziali abbiamo:

GG GGGG

GG TerraTerraTerraTerra----LunaLunaLunaLuna

Sorgente del Segnale ∇Φ_⊕ ∇ΦQQQQ

Corpi Test M1, M2 Terra, Luna

Velocità di rotazione dei corpi Hz s ≅2

ω

h s 24 1 ≅ ω Centri di massa O1, O2 CMT, CML Potenziale di accoppiamento 2 ) (r k r V = e 1 ) (r =k r− V g (conk_g =GMm)

Velocità critica del sistema 2 2 s e cr m k ω ω = << 2 2 2 s orb cr ω ω ω = <<

Sistema di Lettura Capacitivo Laser

Quantità da rilevare ∆x= O₁−O₂ ∆rp = O1−O2

Questo schema identifica rapidamente le analogie intuitive che intercorrono fra i due accelerometri e che lascerebbero presagire la possibilità di trattare i due strumenti in modo unitario considerandoli entrambi come rotori supercritici debolmente accoppiati. Tuttavia i sistemi fisici, a parte queste analogie hanno anche delle nette differenze che vincolano un’analisi di questo tipo.

La definizione di rotore è quella di un corpo sospeso tramite un insieme di supporti cilindrici ruotante attorno ad un asse la cui direzione è fissa nello spazio inerziale. Chiaramente per quanto riguarda un corpo celeste come la Terra o la Luna non è possibile parlare di sospensione grazie ad un insieme di supporti cilindrici, ma solo di corpo ruotante attorno ad un asse la cui direzione è fissa nello spazio inerziale (in virtù delle ipotesi fatte).

Il non poter parlare di sospensione tramite un insieme di supporti cilindrici impedisce nel caso planetario il poter distinguere fra il punto di sospensione del rotore e il centro di massa del rotore. Nella definizione ordinaria di rotore, infatti, tali punti sono