Capitolo 3
Strutture dati per la ricerca in insiemi di
espressioni regolari
Come già accennato nell’introduzione, per effettuare in modo efficiente la ricerca di un determinato insieme di espressioni regolari, che soddisfano una certa stringa in ingresso, abbiamo bisogno di meccanismi che ci consentano di recuperare, in modo abbastanza veloce, le informazioni richieste. Sebbene siano stati proposti diversi metodi di indicizzazione (si pensi ai suffix tree [9]) per velocizzare la ricerca di dati in testi e documenti sfruttando le potenzialità delle espressioni regolari, per il problema inverso di indicizzazione, cioè data una stringa recuperare tutte le espressioni regolari che la soddisfano, non si conoscono ancora molte soluzioni, anche se recentemente, sono stati presentati diversi metodi [4, 6, 7, 8] di indicizzazione per le espressioni particolari utilizzate per effettuare il filtering di documenti XML [4, 6 , 7, 8].
In questo capitolo mostriamo le strutture dati fondamentali, introdotte finora, per la memorizzazione di insiemi di espressioni regolari. In particolare, trattiamo due tipi di strutture (il numero è limitato poiché il problema del RE-retrieval è
stato sollevato negli ultimi anni): il RE-tree e l’Interval Tree. La prima struttura è di recente realizzazione; la seconda, in realtà, è un tipo di indice che memorizza insiemi di intervalli numerici e non di espressioni, ma verrà adattato in seguito secondo le nostre esigenze, sfruttandone le caratteristiche fondamentali. Quindi, nel corso del capitolo, faremo una carrellata sia sulla struttura di questi due indici, sia sulle operazioni previste: creazione, inserzione, cancellazione, ricerca di un’informazione all’interno della struttura dati.
3.1 Indice RE-tree
In questa sezione presentiamo le caratteristiche e il funzionamento della struttura dati indice RE-tree.
Il RE-tree indicizza una grande collezione di espressioni regolari in modo tale che, data in ingresso un’arbitraria query string qx, le espressioni presenti nella
collezione che soddisfano qx, vengono velocemente recuperate. Sebbene la
struttura complessiva del RE-tree assomigli nello spirito all’R-tree [3], la esigenza di memorizzare grosse quantità di espressioni fa si che vengano proposti non solo nuovi ed interessanti algoritmi, ma anche nuove tecniche utili per effettuare più efficientemente le operazioni sulla struttura.
3.1.1 Struttura dell’indice
Un RE-tree è una struttura dati indice dinamica, bilanciata in altezza, gerarchica, in cui le foglie contengono i dati corrispondenti alle espressioni regolari indicizzate e i nodi interni contengono “directory” che puntano ai nodi del livello successivo. In particolare, ogni elemento di un nodo foglia è della forma (id, M), dove id rappresenta l’identificatore unico di una espressione regolare r ed M è un automa finito che rappresenta r. Ogni nodo interno memorizza una collezione di automi finiti; ciascun elemento del nodo è della forma (M, ptr), dove M rappresenta un automa finito e ptr è un puntatore a qualche nodo N (del livello successivo nell’albero) tale che la seguente proprietà
di contenimento è soddisfatta: se per un insieme di automi H, L(H) = ∪Mi∈H L(Mi)
e H(N) denota la collezione degli automi contenuti nel nodo N, allora si ha che L(H(N)) ⊆ L(M). Quindi, individuiamo l’automa M come l’automa limite per
H(N). La proprietà di contenimento è la chiave per migliorare l’esecuzione della ricerca di insiemi di espressioni regolari in strutture indice gerarchiche come il RE-tree: se una query string qx non è contenuta in L(M), allora segue che qx ∉
L(Mi) per tutti gli Mi ∈ H(N). Questa osservazione consente di escludere dal
raggio di ricerca l’intero sottoalbero avente radice in N. Ovviamente, più L(M) sarà vicino a L(H(N)) e minore sarà lo spazio di ricerca su cui ci restringiamo per individuare le espressioni che soddisfano la query in ingresso.
In generale, ci sono un infinito numero di automa limite per H(N) con differenti gradi di precisione, dal meno preciso automa limite con L(M) = * al più preciso automa limite chiamato automa limite minimale, con L(M) = H(N).
Poiché lo spazio per la memorizzazione di un automa dipende dalla sua complessità (vista in termini del numero di stati e transizioni), c’è un trade-off spazio- precisione coinvolto nella scelta dell’automa limite di ciascuna entrata di un nodo interno1. Per tale motivo, sebbene l’automa limite minimale sia la scelta migliore per restringere lo spazio di ricerca, non sempre è possibile memorizzarlo nel RE-tree, poiché potrebbe richiedere troppo spazio ed eccedere così la dimensione del nodo, con un conseguente basso fan-out della struttura. Quindi, per garantire un ragionevole fan-out della struttura RE-tree, si impone una restrizione sul massimo numero di stati (denotato con ) che un automa limite può avere.
Gli automi memorizzati nei nodi del RE-tree sono, in generale, automi a stati finiti non deterministici con il minor numero di stati [1]. Inoltre, per motivi di efficienza, in termini di spazio, è stabilito che ciascun nodo del RE-tree contenga almeno m elementi.
1 Questo è in contrasto con la filosofia dell’R-tree, in cui lo spazio di un bounding rectangle è
indipendente dalla sua precisione e perciò i bounding rectangle negli alberi R sono tutti minimal
Un esempio di RE-tree è illustrato in fig. 3.1, in cui vengono mostrati solo i primi tre livelli dell’albero. Ciascun nodo interno possiede dai due ai tre elementi, con ogni Mi rappresentante un automa limite; i dettagli di alcuni di
questi automi sono mostrati sotto forma di espressioni regolari (per motivi di spazio) nella tabella 3.1. E’ da notare che ogni coppia padre - figlio di entrate di un generico nodo soddisfa la proprietà di contenimento. Per esempio, se consideriamo la collezione H(N) = {M6, M7}, abbiamo che L(H(N)) ⊆ L(M2).
M1 M2
M3 M4 M5 M6 M7
M8 M9 M10 M11 M12 M13 M14 M15 M16 M17 M18 M19
Fig. 3.1 Esempio di RE-tree
M2 a(a | b | c | e)*(b | d | e)* M6 a(a | b | c)* M7 ab(b | ac | eb)*(b | d | e) M16 a(a | b)c* M17 aa(a | b | c)*c M18 abb*(d | e) M19 ab(ac | eb)*b
3.1.2 Algoritmi di ricerca e mantenimento
Ricerca. La query in ingresso all’algoritmo di ricerca è una stringa qx ∈ * e il
risultato è l’insieme di tutte le espressioni regolari il cui linguaggio contiene la stringa qx. La ricerca procede secondo una metodologia top-down; infatti, si parte
dal nodo radice e si procede visitando la struttura seguendo cammini multipli. Al generico passo in un nodo interno N, la stringa qx è confrontata con ciascun
elemento (M, ptr) del nodo N tale che se qx è accettata da M, allora la ricerca
prosegue nel nodo puntato dal puntatore ptr, altrimenti, la ricerca lungo quel cammino può considerarsi terminata. Nel momento in cui si giunge in un nodo foglia N, ciascun automa M contenuto in N è confrontato con qx e se M accetta qx,
allora M viene restituito come parte del risultato. In figura 3.2 mostriamo l’algoritmo di ricerca appena enunciato.
Algoritmo Ricerca(N, qx)
Input: N nodo dell’indice da cui comincia la ricerca.
qx è una query string.
Output: R è l’insieme di espressioni regolari contenute
nei nodi foglia del sottoalbero radicato nel nodo N.
(r ∈ R se e solo se qx ∈ L(r))
1. R = ∅ ;
2. if (N è un nodo interno) then
3. for each coppia (M, ptr) in N do
4. if (qx ∈ L(M)) then
5. R = R ∪ Ricerca(N′, qx), dove N′ è il nodo
puntato da ptr; 6. else
7. for each entrata del nodo (id, M) do
8. if (qx ∈ L(M)) then
9. R = R ∪ {M};
10. return R;
Inserzione. L’algoritmo per inserire un nuovo automa M nel RE-tree consiste di due fasi principali. Nella prima fase viene determinato un cammino ottimale in cui inserire M. Ovviamente, tale cammino parte dalla radice e termina in un nodo foglia N. L’obiettivo di eseguire l’inserzione lungo un cammino ottimale dovrebbe assicurare la minore espansione possibile del nodo N in cui l’automa M verrà inserito. Un cammino ottimale di nodi è determinato scegliendo il miglior nodo per l’inserzione ad ogni livello (a partire dal livello del nodo radice) usando l’algoritmo ChooseBestFa di cui parleremo dopo.
Nella seconda fase, il nuovo automa M viene inserito nel nodo foglia N selezionato. Le operazioni eseguite in questa fase sono mostrate in fig. 3.3 della pagina seguente (il parametro ptr è inizializzato al valore id dell’espressione r). Se il nodo N non ha spazio a sufficienza per memorizzare M, allora, come mostrato nel passo 6 dell’algoritmo, N viene suddiviso in un altro nodo foglia N′, distribuendo la collezione di automi H(N)∪{M} tra i nodi N ed N′ usando l’algoritmo SplitFa (discusso in un secondo momento).
Nella chiamata ricorsiva Insert al passo 15, due tipi di aggiornamenti per
l’inserzione devono essere effettuati. Tali aggiornamenti si propagano dal nodo foglia N alla radice, lungo il cammino selezionato nella prima fase. E’ da notare che &N′ indica l’indirizzo di N′ nel passo. Il primo tipo di aggiornamento consiste nel garantire la proprietà di contenimento tra le varie entrate dei nodi interni appartenenti al cammino selezionato. In particolare, poiché l’inserzione di M modifica la collezione di automi in N, occorre aggiornare anche le entrate del nodo padre di N, ovvero Np, con un nuovo bounding automaton per H(N), il
quale è tipicamente un automa più generale di ∪Mi∈H(N) Mi, calcolato con
l’algoritmo GeneralizeFa discusso nella sezione 3.1.4; il tipo di aggiornamento appena enunciato modifica H(Np) e viene propagato lungo tutto il cammino
selezionato, fino al nodo radice.
Il secondo tipo di aggiornamento riguarda i nodi che vengono suddivisi in seguito all’inserzione. Se la suddivisione si verifica al nodo N, allora deve essere
inserita una nuova entrata nel nodo padre Np, in modo da puntare al nuovo nodo
ottenuto dalla suddivisione del nodo N. L’inserzione di una nuova entrata in un nodo interno Np modifica H(Np), il quale necessita a sua volta di un
aggiornamento per garantire la proprietà di contenimento. Nel caso particolare in cui si verifichi una suddivisione del nodo radice verrà creato un nuovo nodo radice.
Algoritmo Insert(N, (M, ptr))
Input: N nodo che deve essere aggiornato.
(M, ptr) è una entrata da inserire nel nodo N. 1. M′ := N′ := ∅;
2. if (M ≠ ∅) then
3. if ( N ha posto per (M, ptr) ) then
4. Insert (M, ptr) in N;
5. else
6. (N, N ′ ) := SplitFa ( H(N)∪{M} );
7. M′ := GeneralizeFa ( H(N′ ) ); 8. Sia M := GeneralizeFa ( H(N) ); 9. if ( N è il nodo radice) then
10. if (N′≠ ∅) then
11. Creazione nuova radice Nr con due entrate
(M, &N) e (M′, &N′ ); 12. else
13. Sia Np il padre del nodo N;
14. Rimpiazziamo le vecchie entrate di N nel nodo Np con
(M, &N)
15. Insert (Np, (M′, &N′ ) );
Fig. 3.3 Algoritmo che propaga gli aggiornamenti durante una inserzione nel RE-tree
Cancellazione. La cancellazione di una espressione regolare dal RE-tree è eseguita in modo simile all’R-tree [3], solo che, per computare il nuovo automa limite per i nodi, viene utilizzato, come abbiamo visto anche per l’operazione di inserzione, l’algoritmo GeneralizeFa.
Mentre l’inserzione di un nuovo automa può provocare la suddivisione di un generico nodo N in due o più nodi, l’operazione di cancellazione può provocare una fusione tra due o più nodi. Ovviamente, come nel caso dell’inserzione, dovrà sempre essere garantita la proprietà di contenimento tra i vari nodi dell’albero.
3.1.3 Nuovi problemi affrontati nel RE-tree
Come abbiamo avuto modo di capire finora, i RE-tree sono concettualmente simili ad altre strutture dati indice gerarchiche (ad esempio gli R-tree). Infatti, questo lo si può facilmente constatare studiando gli algoritmi utilizzati per la ricerca e il mantenimento. Però, la differenza fondamentale, che c’è fra il RE-tree e altre strutture gerarchiche, sta nel tipo di dati indicizzati: i linguaggi regolari memorizzati nei nodi del RE-tree sono oggetti molto più complessi dei rettangoli multidimensionali trattati negli alberi R. Questa differenza comporta la nascita di nuovi problemi e spinge di conseguenza allo sviluppo di nuovi algoritmi per ottimizzare al meglio la performance di tale struttura.
Di seguito riassumiamo i tre problemi fondamentali che si presentano nello studio del RE-tree.
(P1) Selezione di un nodo ottimale per l’inserzione di un nuovo automa nell’albero: l’obiettivo è quello di selezionare un cammino in modo tale che l’espansione del nodo in cui inserire il nuovo bounding automata sia minima. Quindi, data la collezione di automi H(N) di un nodo interno N e un nuovo automa M, abbiamo bisogno di trovare l’Mi ottimale appartenente a H(N) tale che
(P2) Computazione di una suddivisione ottimale dei nodi: considerata la collezione di automi H = { M1, M2, …, Mk} in un nodo eccedente, vogliamo
trovare la partizione ottimale di H in due sottoinsiemi disgiunti H1 ed H2 tale che
la quantità | H1 | ≥ m, | H2 | ≥ m e la quantità |L(M1)| + |L(M2)| è minima.
(P3) Computazione di un automa generalizzato ottimo: durante l’operazione di inserzione, suddivisione dei nodi e fusione, abbiamo bisogno di identificare un bounding automata, per un insieme di espressioni regolari, tale che data una collezione di automi H, l’automa generalizzato M (bounding automata), che cerchiamo, soddisfi le seguenti caratteristiche: |M| ≤ α, L(H) ⊆ L(M) e la quantità
|L(M)| è minima.
Ciascuno di questi tre problemi viene risolto utilizzando gli algoritmi presentati nella sezione successiva, con i quali si cerca di massimizzare lo spazio da “potare” durante la ricerca e minimizzare l’espansione dei bounding automata dei nodi interni dell’albero.
3.1.4 Algoritmi di supporto alle operazioni del RE-tree
Gli algoritmi che presentiamo sono rispettivamente abbinati ai problemi P1, P2 e P3 enunciati nella sezione precedente ed eseguono, in generale, le seguenti operazioni sugli automi: unione, intersezione, conversione di un NFA in un DFA [1].
E’ da notare che mentre è possibile computare l’unione o l’intersezione di una coppia di automi Mi e Mj, in tempo proporzionale a |Mi||Mj|, nel caso pessimo la
complessità temporale, di conversione di un NFA in un DFA, potrebbe risultare esponenziale in |M|.
Algoritmo ChooseBestFa. Questo algoritmo restituisce l’automa Mi, a partire
massima. Per ciascun Mi ∈ H(N), l’algoritmo costruisce il DFA Mi ∩ M e
computa |L(Mi∩ M)| usando le misure Max-Count o MDL enunciate nel capitolo
precedente. L’automa M rappresenta l’automa da inserire nel RE-tree.
Algoritmo SplitFa. Questo algoritmo, dato un insieme di automi H = { M1, M2,
…, Mk}, partiziona la collezione H di automi in due sottoinsiemi disgiunti H1 ed
H2,tale che la quantità |H1| ≥ m, |H2| ≥ m e la quantità |L(M1)| + |L(M2)| è minima.
Sfortunatamente, se L(Mi) per ciascun Mi ∈ H è finito, il problema della
suddivisione ottimale di H è NP-hard. Quindi, ci si può aspettare che per linguaggi infiniti il problema sia molto più difficile.
Il teorema che segue (di cui rimandiamo la dimostrazione in [5]) conferma l’affermazione appena fatta.
Teorema 3.1. Data una collezione di insiemi finiti di elementi S1,…, Sn, il
problema di partizionarli in due insiemi G1 e G2 (ciascuno contenente almeno m
elementi) tale che |∪Si∈G1 Si | + |∪Si∈G2 Si | è minima, è NP-hard.
Poiché il problema della computazione della partizione ottimale dell’insieme H è NP-hard, viene utilizzata un’euristica (simile a quella in [3]) per generare i due insiemi H1 e H2. In fig. 3.4 della pagina seguente viene mostrato l’algoritmo
per esteso.
Algoritmo GeneralizeFa. Questo algoritmo viene utilizzato per la risoluzione del problema esposto in P3. Anche questo problema, come il precedente, risulta essere NP-hard. Il teorema che segue (di cui rimandiamo la dimostrazione in [5] ) ne è la conferma.
Teorema 3.2. Dato un insieme di automi H, il problema di computare un DFA M con non più di α stati, e per il quale L(H) ⊆ L(M) e la quantità |L(M)| è
minima, è NP-hard.
Algoritmo SplitFa(H)
Input: H insieme di automi da suddividere.
Output: due insiemi H1 ed H2 risultanti dalla suddivisione.
1. Mi e Mj ∈ H tale che |L(Mi∪ Mj)|-|L(Mi∩ Mj)| è massima;
2. H1 := { Mi }, H2 := { Mj }; 3. H := H - { Mi, Mj }; 4. while (H ≠ ∅) do 5. if (|H| = m - | H1|) then 6. H1 := H1 ∪ H; 7. break; 8. if (|H| = m - | H2|) then 9. H2 := H2 ∪ H; 10. break;
11. Sia Mi∈ H l’automa t.c. min{|L(H1 ∪ {Mi})|-|L(H1)|,
|L(H2 ∪{Mi})|-|L(H2)|} è minima; 12. if ( |L(H1∪ {Mi})|-|L(H1)|≤ |L(H2∪ {Mi})|-|L(H2)| ) then 13. H1 := H1 ∪ {Mi}; 14. else 15. H2 := H2 ∪ {Mi}; 16. H := H- {Mi}; 17. return (H1 , H2)
L’algoritmo utilizzato per la generalizzazione di un insieme di automi H è mostrato in fig. 3.5. L’algoritmo fonde coppie di stati, risultanti dagli automi che rappresentano i linguaggi più piccoli dell’insieme H, in un unico stato del corrispondente automa generalizzato M, fino a quando |M| ≤ α.
Algoritmo GeneralizeFa(H, α)
Input: H insieme di automi da generalizzare.
Output: l’automa generalizzato per H.
1. Calcola DFA M per ∪ Mi ∈H Mi ;
2. while (|M| > α) do
/* M(si , sj) è l’automa risultante quando gli stati si e sj
in M sono fusi */
3. Siano si e sj una coppia di stati in M t.c. |L(M(si , sj ))|
è la più piccola fra tutte le coppie di stati in M;
4. Assegniamo ad M il “valore” del DFA per M(si , sj) ;
5. return M;
L’euristica utilizzata per determinare le coppie di stati si e sj, da fondere, è la
seguente: vengono scelte le coppie (si , sj) tale che lo stato si ha transizioni simili,
sia in entrata che in uscita, a quelle dello stato sj. Questo perché è più probabile
che, l’automa risultante dalla fusione, rappresenti un linguaggio che è il più compatto possibile.
Fig. 3.5 Algoritmo per generalizzare un insieme di automi
3.2 Indice Interval Tree
In questa sezione mostriamo le caratteristiche e le operazioni di un’altra struttura dati che utilizzeremo, in maniera leggermente diversa da come viene proposta, per memorizzare insiemi di espressioni regolari. L’adattamento delle caratteristiche di tale struttura alle nostre esigenze verrà ampiamente discusso nel capitolo 4.
In generale, l’Interval Tree è un indice che memorizza insiemi di intervalli numerici che sostanzialmente rappresentano insiemi di segmenti collocati nel piano individuato dagli assi x e y. Per soddisfare un certo query point in ingresso, abbiamo bisogno di una struttura dati che memorizzi questi insiemi in modo tale che tutti i segmenti che soddisfano il query point possano essere restituiti efficientemente. Vediamo come l’Interval Tree si presta alla risoluzione del problema appena esposto. Inoltre, si noti come tale problema somigli molto al problema del RE-retrieval.
3.2.1 Struttura dell’indice
Consideriamo I := {[x1:x′1], [x2:x′2], …, [xn: x′n]} un insieme di intervalli finiti
definiti sulla linea dei reali e qx un query point da cercare. Indichiamo con xmid il
punto mediano dei 2n estremi che delimitano gli intervalli contenuti nell’insieme I. In questo modo, al più la metà degli estremi, appartenenti agli intervalli in I, potrà giacere alla sinistra di xmid e al più l’altra metà potrà giacere alla destra di
xmid. Se qx giace alla sinistra di xmid allora gli intervalli collocati completamente
alla destra di xmid , ovviamente, non contengono qx.
Costruiamo un binary tree basato su questa idea. Memorizziamo nel sottoalbero destro dell’intero albero l’insieme Iright degli intervalli collocati
completamente alla destra di xmid e nel sottoalbero sinistro l’insieme Ileft di
intervalli che sono collocati completamente alla sinistra di xmid. Tali sottoalberi
un problema: come memorizzare gli intervalli che contengono proprio la stringa xmid ? Una possibile soluzione sarebbe quella di memorizzare tali intervalli in
entrambi i sottoalberi, ma si potrebbe presentare ricorsivamente la stessa situazione anche per i figli di un generico nodo. Infatti, un intervallo potrebbe essere memorizzato più volte, con conseguente continuo ingrandimento della struttura.
Per evitare la proliferazione degli intervalli possiamo risolvere il problema accennato nel seguente modo: memorizziamo l’insieme Imid, di intervalli
contenenti xmid , in una struttura separata e associamo tale struttura alla radice del
nostro albero, proprio come mostrato in fig. 3.6.
Sappiamo che tutti gli intervalli appartenenti all’insieme Imid contengono il
punto xmid. Supponiamo, per esempio, di considerare qx collocata alla sinistra di
xmid , come mostrato nella fig. 3.7 della pagina seguente. Ovviamente, il valore
di qx può anche essere collocato alla destra di xmid.
Imid Ileft Iright xmid Iright Ileft Imid
In questo caso sappiamo già che l’estremo destro di tutti gli intervalli in Imid
giace alla destra di qx. Di conseguenza, sono importanti solo gli estremi sinistri
degli intervalli, per cui si può dire che: qx è contenuta in un intervallo [xj : x′j] se
e solamente se xj [ qx. Se memorizziamo gli intervalli in una lista ordinata per
estremi sinistri crescenti, allora qx può essere contenuta in un intervallo se e solo
se è contenuta in tutti i suoi predecessori presenti nella lista. In poche parole, possiamo semplicemente muoverci lungo la lista ordinata riportando tutti gli intervalli che contengono qx, fino a quando non incontriamo un intervallo che
non contiene qx. Nel momento in cui incontriamo un intervallo che non contiene
qx ci fermiamo, poiché nessuno degli intervalli rimanenti può contenere qx.
Ovviamente, si verifica una situazione simile a quella appena descritta anche nel caso in cui qx si trova a destra di xmid. L’unica differenza è che in questo caso
ci muoviamo lungo la lista ordinata per estremi destri decrescenti. Nel caso in cui si verifica che qx = xmid , allora possiamo riportare tutti gli intervalli contenuti in
Imid .
Diamo ora una descrizione succinta della struttura dati che memorizza l’insieme I:
• se I = ∅ allora l’Interval Tree è una foglia;
• altrimenti, indicando con xmid la stringa mediana degli estremi degli intervalli,
si ha che:
qx xmid
Ileft := { [ xj : x′j] ∈ IR : x′j <L xmid },
Imid := { [ xj : x′j] ∈ IR : xj≤L xmid≤ L x′j },
Iright := { [ xj : x′j] ∈ IR : xmid <L xj }.
L’Interval Tree consiste di un nodo radice V che memorizza xmid. Inoltre si ha
che:
• l’insieme Imid è memorizzato due volte; una prima volta in una lista Lleft(V),
ordinata per estremi sinistri degli intervalli, una seconda volta in una lista Lright(V), ordinata per estremi destri degli intervalli,
• il sottoalbero sinistro di V è un interval tree per l’insieme Ileft,
• il sottoalbero destro di V è un interval tree per l’insieme Iright.
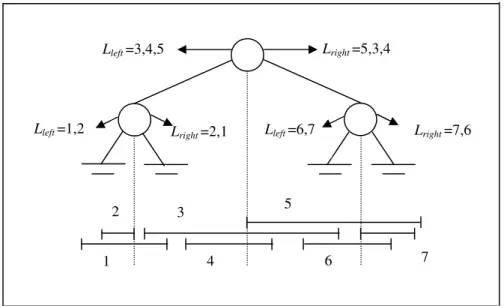
In fig. 3.8 mostriamo un esempio della struttura Interval Tree.
I segmenti verticali tratteggiati, della fig. 3.8, indicano il valore di xmid per il
rispettivo nodo.
Nella sezione che segue presentiamo gli algoritmi che supportano le operazioni dell’Interval Tree.
Lleft =6,7 Lright =7,6 Lright =5,3,4 Lleft =3,4,5 Lright =2,1 Lleft =1,2 2 1 3 4 5 6 7
3.2.2 Operazioni nell’Interval Tree
In questo paragrafo mostriamo le operazioni di creazione di un Interval Tree e di ricerca di un insieme di intervalli che soddisfano un query point qx in ingresso.
Per quanto riguarda l’algoritmo ricorsivo di costruzione di un Interval Tree, possiamo dire che esso segue fedelmente la definizione data nella sezione precedente. Di seguito, in figura 3.9, mostriamo la versione dell’algoritmo in dettaglio.
Algoritmo CONSTRUCTINTERVALTREE(I)
Input. Un insieme I di intervalli sulla linea reale. Output. La radice di un interval tree per I.
1. if (I = ∅)
2. then return una foglia vuota
3. else Crea un nodo V. Calcola, il punto mediano xmid
di un insieme di estremi di intervalli e memorizza xmid con V.
4. Calcola Imid e costruisce due liste ordinate
per Imid: una lista Lleft(V) ordinata in base agli
estremi sinistri, una lista Lright(V) ordinata
in base agli estremi destri. Memorizza le due liste in V.
5. lc(V) := CONSTRUCTINTERVALTREE(Ileft);
6. rc(V) := CONSTRUCTINTERVALTREE(Iright);
7. return V.
Le variabili lc(V) e rc(V) rappresentano, rispettivamente, il figlio sinistro e destro del nodo V.
Trovare il punto mediano di un insieme di punti comporta tempo lineare. In questo caso, sarebbe conveniente calcolare il punto mediano ordinando a priori l’insieme dei punti. Sia nmid := card(Imid). La creazione delle liste Lleft(V) e
Lright(V) comporta tempo O(nmid log nmid). Per cui, il tempo speso è O(n + nmid log
nmid), ma usando le argomentazioni del lemma 10.2 in [10] si può concludere che
la complessità totale temporale dell’algoritmo sopra esposto è O(n log n).
Fatte le dovute osservazioni sulla struttura dell’interval tree, rimane da mostrare l’uso di tale indice per recuperare gli intervalli contenenti il query point qx. L’algoritmo adottato è il seguente:
Algoritmo QUERYINTERVALTREE(V, qx )
Input. La radice V di un interval tree e un query point qx.
Output. Tutti gli intervalli che contengono qx.
1. if V non è una foglia
2. then if qx < xmid(V)
3. then Ci muoviamo lungo la lista Lleft(V),
e iniziamo dall’intervallo con estremo più a sinistra, riportando tutti gli intervalli contenenti qx. Ci si ferma
quando si trova un intervallo che non contiene qx.
4. QUERYINTERVALTREE(lc(V), qx )
5. else Ci muoviamo lungo la lista Lright(V),
e iniziamo dall’intervallo con estremo più a destra, riportando tutti gli intervalli contenenti qx. Ci si ferma
quando si trova un intervallo che non contiene qx.
6. QUERYINTERVALTREE(rc(V), qx )
Analizzare la complessità temporale dell’algoritmo non è complicato. Qualunque nodo v visitiamo, il tempo speso è pari a O(1+kv), dove kv rappresenta
il numero di intervalli restituiti al nodo v. La somma dei termini kv, sui nodi
visitati, è pari a k. Inoltre, visitiamo al più un nodo a qualsiasi profondità dell’albero. La profondità dell’interval tree è O(log n), per cui la complessità risultante è O(log n+ k).
Vediamo un esempio di applicazione dell’algoritmo di ricerca di un insieme di intervalli che contengono un query point qx specificato in ingresso.
Esempio 3.1 Supponiamo di riprodurre la stessa situazione presentata in fig. 3.8 considerando il seguente insieme di intervalli: I := {[1:7], [2:4], [6:13], [8:11], [9:16], [12:15], [14:16]}. Le linee tratteggiate in fig. 3.8 rappresentano i valori xmid di ogni nodo e in questo caso, partendo dal nodo più a sinistra, si ottengono i
seguenti valori di xmid: 4, 9,14.
Consideriamo come query point in ingresso qx = 3. Seguendo i passi
dell’algoritmo mostrato in fig. 3.10 si ha che, partendo dalla radice, qx< xmid(v),
cioè 3 < 9, per cui ci si muove lungo la Lleft(v), che contiene gli elementi 6, 8, 9,
del nodo in esame. Il primo estremo memorizzato nella Lleft(v) è 6. L’intervallo
[6:13] non contiene qx = 3 quindi lo scorrimento della lista viene sospeso e si
prosegue con la ricerca nel nodo figlio sinistro. Si controlla se qx< xmid(v). In
questo caso 3 < 4 per cui si visita la Lleft(v), che contiene gli elementi 1,2, del
nodo in esame. Il primo estremo memorizzato nella Lleft(v) è 1. L’intervallo [1:7]
contiene qx = 3, per cui si prosegue, a differenza del passo precedente, con lo
scorrimento di Lleft(v). L’elemento che si incontra è 2, quindi l’intervallo [2:4]
contiene qx = 3 e la terminazione della lista fa concludere la ricerca in questo
nodo. Essendo la funzione ricorsiva si prosegue controllando se il nodo che viene preso in esame è una foglia. In questo caso la visita dell’albero termina poiché si è giunti in fondo e gli intervalli contenenti qx = 3 restituiti dall’algoritmo sono
Nel capitolo 4, mostreremo l’estensione dell’interval tree al caso in cui gli intervalli da memorizzare sono intervalli di stringhe e non numerici, ovvero gli estremi di un generico intervallo [xj : x′j] sono stringhe e non numeri reali e la
query qx in ingresso è una stringa. In questo caso, usando la tecnica generale
presentata in [11,12], è possibile ottenere, come complessità dell’algoritmo di ricerca, un tempo pari a O(log n + k +| qx |) con qx composta da | qx | caratteri