28
CAPITOLO 2
TEORIA DELLE SCELTE DI PORTAFOGLIO
2.1 Sintesi degli sviluppi teorici
La Teoria di Portafoglio costituisce attualmente uno dei campi di maggior rilievo presso gli studiosi di discipline finanziarie.
Nella scelta di un investimento le variabili determinanti sono il rischio ed il
rendimento. Il merito di aver introdotto il concetto di trade-off tra le due
variabili spetta a Markowitz, che negli anni cinquanta elaborò una prima formulazione della ”moderna teoria di portafoglio”, successivamente ripresa e sviluppata da altri studiosi, tra cui Tobin ed Hicks.
Markowitz nel suo articolo “Portfolio selection” del 1952, che gli varrà il Nobel 38 anni dopo “per i contributi pioneristici nell’ambito dell’economia finanziaria”, basa la sua analisi sul processo che genera la domanda e l’offerta di attività finanziarie in funzione del rapporto rischio – rendimento in esse espresso. Egli per primo comprese che al fine di costruire un Portafoglio efficiente bisognava combinare più titoli, in modo da poter massimizzare il rendimento complessivo a parità di rischio; tale “diversificazione del portafoglio” avrebbe compensato la rischiosità associata a fluttuazioni nel valore di una data attività finanziaria con quella derivante da movimenti di segno opposto nel valore di attività finanziarie alternative, poiché i flussi delle attività non hanno un andamento esattamente concorde, ovvero non sono perfettamente correlati; la diversificazione infatti riduce il rischio quando la correlazione è minore di 1 e produce il miglior risultato quando due attività sono perfettamente correlate negativamente.
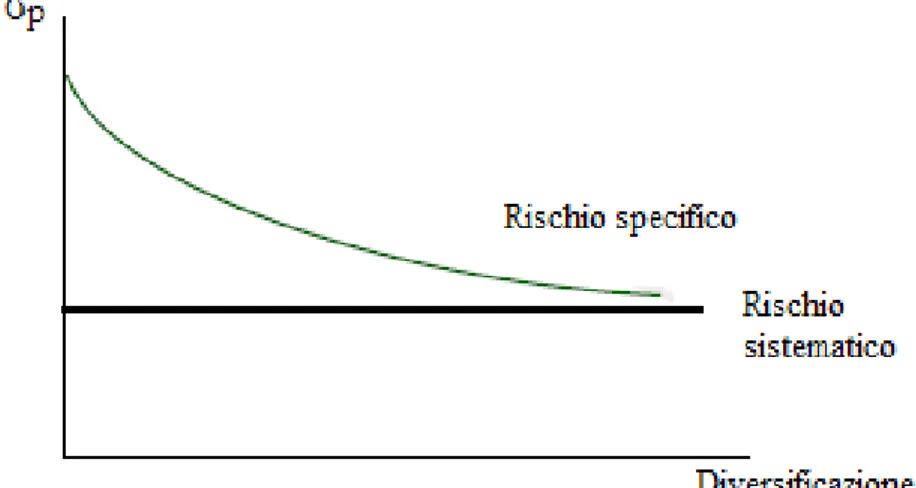
In particolare, la diversificazione del portafoglio consente di eliminare quello che è definito “rischio specifico”, ovvero il rischio associato alle caratteristiche delle singole attività finanziarie. Da questa tipologia di rischio si distingue il rischio “sistematico”, comune a tutte le attività finanziarie scambiate sul mercato, (il
29
cosiddetto rischio di mercato), per il quale dunque la diversificazione non ha
effetto; entrambi sono raffigurati in Figura 1
Figura 1: rischio specifico e sistematico
Ad un notevole perfezionamento della teoria elaborata da Markowitz contribuì James Tobin il quale si chiese cosa succedesse in termini di rischio e rendimento combinando ad attività rischiose, attività prive di rischio (risk-free).
Egli elaborò tali considerazioni nel suo articolo “Liquidity Preference as Behavior Towards Risk” del 1958, in cui è presente il concetto noto come “il teorema di separazione” con il quale si distingue nettamente dall’approccio di Markowitz il quale si limitava alla scelta tra attività rischiose o attività risk-free.
2.2 Scelte in condizioni di incertezza
2.2.1 Variabili determinanti nella scelta di investimento
Se tutti gli investitori fossero dotati di tutte le informazioni necessarie a conoscere con certezza i loro fabbisogni finanziari correnti e futuri, non si porrebbe il problema delle scelte di portafoglio poiché in questo caso, non ci sarebbe la necessità di strumenti di riserva di valore dato che ogni attività rappresenterebbe un mezzo di pagamento.
30
Questa ovviamente risulta essere un’ipotesi ideale, in quanto il mondo reale è caratterizzato da incertezza, data dal fatto che gli individui non conoscono l’esito degli eventi.
La selezione del portafoglio è un classico problema di scelta in condizione di incertezza: un investitore deve decidere come investire un importo monetario in un portafoglio di titoli rischiosi con valore futuro incognito al momento della scelta; entra così in campo il fattore rischio.
Si suppone tuttavia, per semplicità, che gli individui conoscano l’insieme dei possibili risultati associati ad ogni evento e a ciascun evento siano in grado di associare l’insieme degli m possibili risultati, indicati con il vettore (a1……..am),
derivanti dall’azione appartenente all’insieme di scelta del soggetto, e le specifiche probabilità, indicate con (p1… ..pm) con cui ciascun risultato si può
realizzare9.
Data una determinata azione del soggetto, si definisce lotteria, il vettore ad essa associato, dato dall’insieme dei risultati possibili e dalle probabilità ad essi associati:
L = (a1,a2,….am;p1,p2,…..pm). (2.1)
La lotteria è uno strumento utilizzato per rappresentare situazioni rischiose. Si può definire un criterio che consenta di ordinarle in base alle preferenze, in modo che se una determinata lotteria è preferita dal soggetto, è possibile stabilire qual è la sua scelta migliore. Un criterio utilizzato è quello del “valore atteso
VA” inteso come la sommatoria dei possibili risultati ai moltiplicati ognuno per
la rispettiva probabilità pi:
VA = ∑i= 1,m aipi (2.2)
9
ad esempio, nel caso dei titoli azionari si possono attribuire le probabilità del verificarsi di determinati rendimenti facendo riferimento alle serie storiche passate.
31
Considerando inoltre che per partecipare ad una lotteria è richiesto un pagamento
PL, le lotterie si distinguono a seconda che tale pagamento sia uguale, maggiore o
minore del valore atteso della vincita V: in tali casi si parla di lotteria attuarialmente equa, vantaggiosa e svantaggiosa.
Tuttavia questo criterio che orienta la scelta verso la lotteria con VA più alto non tiene conto del grado di avversione al rischio dei partecipanti alla lotteria, pertanto si ritiene più valido il criterio dell’ “utilità attesa UA”, che invece ne tiene conto; la teoria dell’utilità attesa è stata formulata dai due economisti Von Neumann e Morgestern nel 1944, per cui viene indicata con VNM. Tramite questo criterio è infatti possibile stabilire una relazione d’ordine tra tutte le varie combinazioni di titoli e che rappresenta le preferenze del consumatore; l’ipotesi di base è che il soggetto agisca in maniera razionale e dunque:
- conosce le alternative a sua disposizione
- è in grado di dare un ordine alle varie alternative - individua l’alternativa migliore e la sceglie - spende tutto il suo reddito.
Secondo la teoria dell’utilità attesa la scelta tra alternative rischiose è fatta confrontando i valori attesi della funzione di utilità, per cui tra le alternative rischiose y, z, diremo che y è preferita a z se e solo se
E[u(y)] > E[u(z)]. (2.3) Considerando una generica lotteria L = (a1, a2; p1, p2) e ipotizzando che ogni
soggetto sia in grado di assegnare ad ogni ai un determinato livello di utilità u(ai);
l’utilità attesa di questa generica lotteria U(L) può essere rappresentata dalla seguente funzione:
32
Pertanto sia U(L) che E[u(a)] indicano entrambi l’utilità attesa della suddetta lotteria, la quale altro non è che il valore atteso delle utilità derivate dalle somme di denaro a1, a2 ottenute con certezza.
La teoria dell’utilità attesa di VNM si conforma a certi assiomi:
- assioma di completezza secondo il quale date due alternative il consumatore sa dire quale preferisce;
- assioma di transitività per il quale date le alternative a,b,c, se a è preferita a b e b è preferita a c allora a sarà preferita a c;
- assioma di non sazietà per il quale un consumatore non si sazia mai, poiché una quantità maggiore di bene è sempre preferibile ad una minore; - assioma di indipendenza per il quale date due alternative rischiose y e z,
se y è preferito a z, qualsiasi combinazione con una terza alternativa q, non modifica l’ordine di preferenza; se y > z => ( y + q) > (z + q);
se il comportamento del soggetto si conforma a questi assiomi, dire che una
lotteria L1 è preferita rispetto a L2, significa che L1 ha un utilità attesa maggiore.
In base a questo criterio, dunque, il soggetto che dovrà scegliere tra diverse lotterie, li paragonerà in base ai livelli di utilità attesa e preferirà quella alla quale è associata l’utilità attesa più elevata, poi via via le altre in ordine decrescente.
Riepilogando, il soggetto che vorrà adottare questo criterio, dovrà calcolare
l’utilità associata ad ogni premio monetario ai di ciascuna lotteria u(ai)
utilizzando la propria funzione di utilità; poi dovrà calcolare l’utilità attesa di ogni lotteria, come illustrato dall’equazione 2.3, scegliendo infine la lotteria con maggiore livello di utilità attesa.
Naturalmente in tale contesto bisogna tener conto della forma della funzione di utilità u che differisce da soggetto a soggetto e che tiene conto del grado di avversione al rischio nel processo di ordinamento delle lotterie; come vedremo più avanti, più tale funzione è concava e più il soggetto è avverso al rischio.
33
2.2.2 Comportamento nei confronti del rischio
Il grado di avversione al rischio, ovvero il comportamento più o meno incline del soggetto nei confronti del rischio, è cruciale nella scelta della quota da detenere nel proprio portafoglio di un certo titolo, ma per quanto riguarda la scelta tra detenere o meno un determinato titolo, la presenza di costi d’informazione e monitoraggio, comporta la necessità di assumersi un rischio connesso al fatto che su certi titoli si hanno poche informazioni; pertanto si fa dipendere la scelta delle quote dall’avversione al rischio, e quella dei titoli da detenere in portafoglio dall’avversione all’incertezza. In riferimento alla capacità dei soggetti di attribuire una probabilità agli eventi, nel 1921 Knight definì il “rischio” in riferimento ad una situazione in cui è possibile assegnare una specifica probabilità e “incertezza” come riferita invece alle situazioni in cui tale probabilità non può essere specificata. Tuttavia è ragionevole pensare che la seconda sia una conseguenza della prima poiché la medesima scelta risulterà più o meno rischiosa in base al livello di conoscenza delle probabilità associate alle conseguenze che il rischio comporta.
Le variabili determinanti nella scelta del portafoglio risultano dunque dipendere dalle preferenze del soggetto rispetto al rischio pertanto la scelta è effettuata perseguendo uno dei due obiettivi:
- la massimizzazione del rendimento atteso (e quindi del profitto) dato un certo livello di rischio,
- oppure la minimizzazione del rischio dato un certo rendimento atteso. Dati un numero n di portafogli, ognuno con un determinato tasso di rendimento r, un soggetto che classifica i portafogli solo in relazione al rendimento atteso sarà
neutrale al rischio: tra due portafogli egli preferirà quello con rendimento atteso
più elevato indipendentemente dal fatto che sia o meno il più rischioso; tuttavia molti soggetti non sono neutrali al rischio: a parità di rendimento atteso, gli
34
guadagno ma allo stesso tempo anche di perdita, viceversa gli avversi al rischio preferiranno il portafoglio con minore rischiosità di guadagno e di perdita.
Come spiegato in precedenza, in condizioni di incertezza, le preferenze degli individui sono generalmente rappresentate da una funzione di utilità attesa, pertanto è fondamentale studiarne forma e proprietà. Dal momento che si assume che i risultati delle lotterie siano premi monetari, si assume che tale funzione sia sempre crescente nei risultati, tale che:
u’(a) =
> 0 ; (2.5)
vale a dire saranno sempre preferiti i pagamenti più elevati rispetto a quelli minori.
Ma passiamo alla curvatura della suddetta funzione, che come detto in precedenza esprime il comportamento nei confronti del rischio dell’investitore; una curva di indifferenza nello spazio dei punti a1, a2 è data dalla seguente
equazione:
U(a1,a2) = costante (2.6)
Sostituendo nella 2.4 si ha:
p1a1 + p2a2 = costante (2.7)
dal differenziale totale si ottiene:
p1 ∂u(a1) ∂a1 + p2
∂
u(a2) ∂a2 = 0 (2.8)∂a1 ∂a2
(dove
è la derivata prima di u(a) rispetto ad a)
da cui
∂ a2 = - p1 ∂ u(a1) p2
∂
u(a2) (2.9)∂ a1 ∂a1 ∂a2
dove
35
- p1 ∂ u(a1) p2
∂
u(a2) ci dà l’inclinazione della curva di indifferenza, (data∂a1 ∂a2
dal rapporto delle utilità marginali in quel punto).
Le curve di indifferenza hanno dunque inclinazione negativa, pertanto in base alle caratteristiche della funzione u, esse assumeranno una diversa forma:
- Se u è concava spostandoci verso il basso lungo la curva di indifferenza, a1 che si trova sull’asse delle ascisse aumenta e a2 che si trova sull’asse
delle ordinate diminuisce, pertanto du(a1)/da1 diminuisce e invece
aumenta du(a2)/da2 tale che l’inclinazione data da da2/da1 diminuisce; è
dunque chiaro che se u è concava, le curve di indifferenza saranno convesse;
- Viceversa se u è convessa, varrà il discorso opposto tale che le curve di indifferenza saranno concave, ed infine
- Se u è lineare, l’inclinazione delle curve di indifferenza sarà costante e le curve saranno lineari.
Graficamente è possibile indicare il comportamento dei soggetti nei confronti del rischio come indicato in Figura 2
36
1) Caso di avversione al rischio
Come già detto, un soggetto avverso al rischio avrà una funzione di utilità concava e curve di indifferenza convesse come in Figura 3.
Figura 3: avversione al rischio
Dove u(a1) e u(a2) indicano l’utilità del soggetto nel caso disponesse con certezza
delle somme a1 e a2.
Un avverso al rischio preferirà ricevere un reddito certo R piuttosto che partecipare ad una lotteria che da un reddito atteso dello stesso importo; il valore
atteso della lotteria è dato da µL mentre l’utilità attesa sull’asse delle ordinate è
data da E[u(a)] in corrispondenza del punto d, punto medio della retta ac ( se si
assume che p1 = p2 = 0.5) ; dal grafico è chiaro che:
E[u(a)] < U(µL). (2.10)
Vale a dire che un soggetto avverso al rischio attribuisce una maggiore utilità alla somme che ottiene con certezza piuttosto che ad una lotteria con uguale valore atteso.
37
Per poter meglio misurare l’atteggiamento nei confronti del rischio è utile far
riferimento al concetto di “equivalente certo”, indicato in figura 2 da CEL dato
dalla somma ottenuta con certezza,che da un’utilità pari a quella ottenuta affrontando il rischio che comporta giocare alla lotteria e che rende le due alternative a lui indifferenti; esso è dato dall’equazione
u(CEL) = p1 u(a1) + p2 u(a2) (2.11)
Nel caso di avversione al rischio quindi l’equivalente certo sarà inferiore al valore atteso della lotteria come indicato dall’equazione 2.9.
Utile è anche la definizione del concetto di “premio per il rischio” che il soggetto è disposto a pagare per assicurarsi un risultato certo della lotteria ed eliminare l’eventualità di ricevere come risultato della stessa una somma inferiore al suo valore medio eliminando così il rischio della scelta; questo è dato dalla differenza tra l’equivalente certo della lotteria e il valore atteso della stessa come indicato di seguito:
PR = p1u(a1) + p2u(a2) – CEL (2.12)
Chiaramento essendo in questo caso CEL < p1u(a1) + p2u(a2) il premio per il
rischio sarà positivo. Naturalmente anche l’entità del premio per il rischio dipende dal grado di concavità della funzione u: ad una concavità maggiore, corrisponde un maggiore premio per il rischio e a sua volta un maggior grado di avversione al rischio da parte del soggetto.
Riepilogando il caso di atteggiamento avverso al rischio è caratterizzato da: -funzione di utilità concava con curve di indifferenza convesse
-equivalente certo minore del valore atteso della lotteria considerata -premio per il rischio positivo.
In questo caso, egli sarà dunque disposto a pagare pur di “assicurarsi dal rischio”, la somma positiva data dal PR.
38
Approfondiamo il concetto di domanda di assicurazione: si ipotizza che il soggetto possegga un bene e che esista la probabilità p che questo bene possa essere rubato (ex: una macchina, un gioiello); tutto può essere rincondotto ad una lotteria i cui esiti siano:
a1: non viene derubato, con probabilità p1e in questo caso il valore della lotteria
sarà dato da v;
a2: viene derubato, con probabilità p2 (o 1-p1) e con valore pari a zero;
pertanto il valore atteso della lotteria sarà:
E(L) = p1 v + p2 0 (2.13)
E(L) = p1 v. (2.14)
che si può scrivere anche [(1-p2) v];
l’utilità associata è:
U(L)= p1 u(v) + p2 u(0), (2.15)
E il premio per il rischio è pari a:
PR= (p1 v) – CEL (2.16)
In altre parole PR misura l’extra guadagno necessario a compensare il rischio di perdita insito nella lotteria.
Si dimostra inoltre che un soggetto avverso al rischio preferirà sempre assicurarsi completamente: si suppone che la compagnia assicurativa rimborsi il valore intero del bene, v, nel caso venisse rubato e chiedesse un premio costante pari a
D; in entrambi gli stati del mondo a1, a2, il soggetto avrà v e pagherà un premio D
con un ammontare finale pari a (v-D); vediamo inoltre qual è il premio più elevato che il soggetto è disposto a pagare: si ipotizza che il premio sia proporzionale e pari a D= d*v; dove d indica il tasso per euro di copertura; allora PR sarà dato da:
39
PR= [( p1v )+ (p2 0)] PR= (p1 v); (2.17)
Mentre il ricavo della compagnia assicurativa sarà:
[(d v) – ( p2 v)] (d-p2) v (2.18)
Dalla precedente definizione di lotteria equa, diremo allora che è equa una assicurazione il cui premio è pari al ricavo atteso dalla compagnia assicurativa, ovvero
(d-p2) v = 0 d = p2 (caso assicurazione equa) (2.19)
Riepilogando, nel caso di copertura completa il consumatore avrà in entrambi i casi a1, a2, un valore pari a (v – dv) ovvero il valore del bene meno il premio
pagato, scritto anche (1-d) v e, se d= p2 si avrà che il valore certo è:
[(1-p2) v] ovvero uguale al valore atteso della lotteria E(L) (2.14)
Tale per cui e come detto precedentemente, per un soggetto avverso al rischio l’equivalente certo della lotteria sarà sempre inferiore a al suo valore atteso E(L) per tale motivo egli preferirà assicurarsi una copertura completa nel caso di assicurazione equa poiché significherà assumere una posizione “certa”.
2) Caso di propernsione al rischio
40
Figura 4: propensione al rischio
La funzione di utilità di un soggetto propenso al rischio ha una forma convessa verso il basso e di conseguenza, le curve di indifferenza saranno concave; inoltre dal grafico è facile osservare che u(µL) stavolta è minore di E[u(a)] e quindi
anche di u(CEL) pertanto il soggetto preferisce azzardare per avere la possibilità
di una vincita più elevata, anche se questo vorrà dire correre il rischio di una vincita minore al valore medio della lotteria, piuttosto che accontentarsi del valore certo µL. Pertanto l’equivalente certo è maggiore del valore atteso della
lotteria e di conseguenza il premio per il rischio negativo.
3) Caso neutralità al rischio
Infine l’ultimo dei tre tipi di comportamenti nei confronti del rischio è
41
Figura 5: neutralità al rischio
Come si evince dal grafico questo è il caso in cui il valore dell’equivalente certo della lotteria è uguale al suo valore atteso, questo rende il soggetto indifferente tra ricevere il valore certo e giocare la lotteria; il premio per il rischio sarà nullo.
2.2.3 Scelte di portafoglio
2.2.3.1 modello media- varianza
Come affermato nel paragrafo precedente, la teoria dell’utilità attesa ci dice che l’investitore conoscendo le alternative che ha a disposizione, sceglierà il portafoglio con la combinazione di titoli che gli assicura l’utilità attesa maggiore, che si traduce nella massimizzazione del rendimento atteso (e quindi del profitto) o la minimizzazione del rischio.
Si ipotizza che la funzione di utilità VNM utilizzata sia quadratica pertanto si avrà:
U(W) = W – k W2 (2.20) dove w è il risultato in termini di ricchezza finale che l’investitore ottiene
42
preferenze dell’investitore; da questa funzione di utilità è possibile ottenere il valore dell’utilità attesa mediante la preventiva scomposizione della varianza:
Var(W) = E[W – E(W)]2, da cui E(W2) = Var (W) + [E(W)]2;
considerando il valore atteso della (2.20) si ottiene: E[U(W)] = E(W) – k E(W2);
e sostituendo a quest’ultima il valore di [E(W2
)] trovato, risulta:
E[U(W)] = E(W) – k{ [E(W)]2 +Var(W)};
E[U(W)] = E(W) – k [E(W)]2 – kVar(W);
pertanto si ha: E[U(W)] = F [(E(W), Var(W)];
si osserva dunque che l’utilità attesa è funzione solo del valore atteso della ricchezza e della sua varianza, in particolare essa è direttamente proporzionale alla prima e inversamente proporzionale alla seconda.
Si è dimostrato come dalla funzione di utilità VNM è possibile ricavare la funzione di utilità media-varianza, che rappresenta le preferenze degli investitori (avversi al rischio) nelle loro scelte di portafoglio e che è funzione solo del tasso
di rendimento atteso del portafoglio (µp), anziché della ricchezza finale del caso
precedente (W), e della varianza di tale rendimento (σP2); esiste infatti una
relazione tra la ricchezza finale prodotta dal portafoglio e il suo rendimento (rp) :
W= W0(1+rp); pertanto dal valore atteso di a segue che:
E(W)= [W0 (1+µp)] e var(W)= [W02 σ2(W)] che conduce alla funzione
media-varianza indicata con MV(µp, σP2).
Riepilogando se si utilizza una funzione di utilità quadratica l’utilità attesa è funzione solo di media e varianza.
Il trade – off tra rendimento e rischio può essere misurato attraverso l’utilizzo del
“modello media-varianza” introdotto da Harry Markowitz nel 1952 il quale, come suggerisce il nome stesso, utilizza solo i primi due momenti della distribuzione di probabilità, vale a dire media e varianza, proprio come nel caso della funzione di utilità vista prima.
43
Il problema della selezione di portafoglio qui consiste nella scelta di un portafoglio P tra tutti i portafogli che possono essere costruiti con i titoli presenti sul mercato alla data di selezione; si tratta dunque di attuare una “portfolio selection” ovvero scegliere al tempo t un portafoglio in modo che il suo rendimento soddisfi determinati criteri di ottimalità.
Secondo l’approccio rischio-rendimento, i criteri di ottimalità sono generalmente costituiti o da un certo livello di profitto da massimizzare a parità di rischio o da un livello di rischio da minimizzare a parità di rendimento atteso. Nello schema media – varianza il profitto è misurato dal valore atteso del rendimento del portafoglio e il rischio dalla sua varianza.
Non sapendo infatti con certezza cosa accadrà nel futuro, è necessario fare delle previsioni circa l’andamento dei titoli e, tenedo presente che le nostre previsioni non saranno esatte, valutare quanto il valore del titolo da noi previsto si discosta dal suo vero valore, oltre alla possibilità che tale titolo è soggetto a subire delle perdite. L’elevata variabilità del titolo può essere fonte di grossi guadagni o di elevate perdite, pertanto un investitore avverso al rischio sceglierà un tale titolo solo se adeguatamente compensato da un elevato rendimento atteso.
La “misura del rischio”, la varianza indicata con σ2, è utilizzata in statistica per
misurare l’ampiezza della dispersione di un campione di dati adottata, poi quale misura della variabilità della performance di uno strumento finanziario in un dato periodo di tempo in quanto misura il grado di dispersione dei rendimenti intorno alla loro media; essa è data dal quadrato della deviazione standard che ci dice quanto le singole osservazioni tendono a scostarsi dal loro valore medio: date un
insieme di osservazioni ai con i=1…n
σ2 = E[(ai – E(a)) 2]. (2.22)
Indicando con re il rendimento effettivo del portafoglio e con µp quello medio,
con µP= E(re), la funzione di utilità che rappresenta le preferenze dell’investitore
44
Ipotizzando che si tratti di un soggetto avverso al rischio, U è crescente e in µP,
quindi la derivata parziale di U rispetto µP sarà positiva: ∂u/∂ µP > 0, tale che al
crescere del rendimento atteso l’utilità di quel portafoglio aumenta, viceversa è
decrescente in σ2
P ovvero: ∂u/∂ σ2P < 0 con un utilità che aumenta al decrescere
del rischio associato al portafoglio;
Le varie alternative, cioè i portafogli P1, P2, P3, possono essere rappresentate
come punti su un piano cartesiano, dove sull’asse delle ascisse viene indicata la
varianza e sulle ordinate la media, come in Figura 6:
Figura 6: curve di indifferenza nel modello media varianza
In figura 6 è inoltre possibile osservare la forma delle curve di indifferenza, le quali rappresentano l’insieme di tutte le combinazioni di media e varianza dei vari portafogli, che danno all’investitore lo stesso livello di utilità e che li rendono dunque indifferenti;
analizzandone la forma, vediamo che:
- tali curve sono inclinate positivamente, visto che per restare sulla stessa curva ed avere così lo stesso livello di utilità, man mano che aumenta il
45
rischio, deve aumentare anche il rendimento; ciò è dovuto al fatto che il saggio marginale di sostituzione tra rendimento e rischio è positivo:
SMSµP,σ2P = (∂ µP / ∂ σ2P)>0 (2.24)
che esprime l’inclinazione positiva delle suddette curve in ogni punto; - passando da una curva di indifferenza ad una più in alto l’utilità cresce,
poiché a parità di rendimento si ha un rischio inferiore e a parità di rischio un rendimento maggiore;
- infine sono convesse verso l’origine degli assi, in questo modo, dati due titoli posti sulla stessa curva di indifferenza, un uguale incremento del rischio di entrambi i titoli, comporta che per restare indifferenti, il rendimento del titolo che sta alla destra subisca un incremento maggiore rispetto al titolo che sta sulla sinistra (più in basso);
2.2.3.2 La diversificazione del portafoglio
Alla base di una corretta asset allocation10 c’è il concetto della diversificazione del portafoglio, usato per la prima volta da Harry Markowitz, secondo il quale un classico errore compiuto dagli investitori è quello di concentrare i propri investimenti su un ristretto numero di titoli, spesso quotati sulla borsa locale, e magari anche appartenenti a pochi settori (ad esempio il finanziario o gli energetici).
Egli stesso ha infatti coniato l’aforisma “non mettere tutte le uova nello stesso paniere” perché se cade la cesta si rompono tutte, che ben rende l’idea del rischio
insito nella concentrazione del portafoglio; distribuendo dunque le uova tra due panieri, si riduce la probabilità di una perdita totale; un'altra assunzione è che i destini dei due panieri sono indipendenti.
10
asset allocation, un termine inglese per definire la ripartizione degli investimenti tra diverse classi di titoli con l’obiettivo di massimizzare il profitto, diminuendo al contempo il rischio.
46
In particolare il modello di Markowitz si basa sulle seguenti ipotesi:
gli investitori massimizzano la ricchezza finale e sono avversi al rischio;
la scelta si basa unicamente su due parametri dati dal valore atteso e la deviazione standard;
il periodo d’investimento è unico
costi di transazione e imposte pari a zero
attività perfettamente divisibili
mercato perfettamente concorrenziale
Vediamo di seguito come la diversificazione è tanto più efficace quanto più le attività (azioni, obbligazioni, valute, materie prime, ecc.) sono poco correlate tra loro e quanto più si diversifica all’interno delle stesse classi, ad esempio scegliendo azioni di diversi settori e aree geografiche o ricorrendo a strumenti (come i fondi comuni d’investimento) che permettono con un unico investimento di prendere posizione su una pluralità di titoli a costi ridotti.
Si inizia dunque dal caso particolare di un investitore con massima avversione al rischio, il quale sceglierà indipendentemente dal rendimento atteso, l’investimento che dà il rischio minore, in questo caso avremo dunque delle curve di indifferenza perfettamente verticali in quanto
SMSµP,σ2P = ∞; (2.25)
Frontiera dei portafogli efficienti 1)portafoglio con due titoli rischiosi
Indicando con ai con i=1...n la quota di ricchezza investita nel titolo i-esimo del
portafoglio considerato, ipotizziamo il caso semplice di un P costituito da soli due titoli rischiosi (n=2) e ne indichiamo il rendimento atteso e la volatilità:
47
= a1 µ1 + a2 µ2
=> µP = a1 µ1 +(1- a1) µ2 (2.26)
per cui il rendimento µP dipende linearmente dalla quota a1 investita nel titolo 1;
si ipotizza inoltre che μ1<μ2 e σ1<σ2, pertanto la retta del piano a, µ, individuata
dall’equazione del rendimento, ha coefficiente angolare positivo.
Figura 7:portafoglio con due titoli
Nel quadrante negativo della Figura 7 sono indicati, con la parte tratteggiata della retta a sinistra di a1, i portafogli nel caso di vendita allo scoperto del titolo 2
al fine di poter investire il ricavato nel titolo 1, viceversa la parte tratteggiata alla destra di a2 corrisponde al caso di vendita allo scoperto (short sales) del titolo 1
per poter acquistare una quantità maggiore dell’altro che in questo caso avrà un rendimento più elevato ma andando incontro anche ad un rischio più elevato;
la volatilità è data da:
48 σP2 = E{[ a1r1 + a2r2 - (a1 μ1 + a2 μ2)]2}; σP2 =E {[ a1(r1 -μ1) + a2(r2 - μ2)]2}; σP2=E [ a12(r1 -μ1) 2 + a22 (r2 - μ2)2+2a1a2 (r1 -μ1)(r2 - μ2)]; σP2=a12 E[ (r1 -μ1) 2] + a22 E[(r2 - μ2)2]+2a1a2 (r1 -μ1)(r2 - μ2); σP2= a12σ21+ a22 σ22 + 2 a1a2σ12 σP2= a12σ21+ a22 σ22 + 2 a1a2 ρij σi σj (2.28) dove:
- a2 = (1- a1) e rappresenta la quota di ricchezza investita nel secondo titolo;
- σ la deviazione standard dei titoli;
- σij = E[(σ1- μ1)(σ2- μ2)] scritto anche ρijσiσj esprime la loro covarianza che
misura quanto i rendimenti dei due titoli siano legati da una relazione lineare,essa può assumere valore positivo, negativo o nullo a seconda che i rendimenti dei due titoli si muovono insieme, in senso opposto o sono del tutto indipendenti l’uno dall’altro;
- ρ= σ12/σ1σ2 indica il coefficiente di correlazione tra i tassi di rendimento
(quindi la covarianza tra i due titoli σ12 = E[(r1-µ1) (r2-µ2)] non è altro che
la loro correlazione moltiplicata per lo scarto quadratico medio di ciascuna attività);
Il coefficiente di correlazione è un buon indice poiché -1≤ ρ ≤1 (tale per cui la covarianza raggiunge il suo valore massimo per ρ=1); in seguito si analizzano pertanto i tre casi particolari ρ= 0, 1, -1
Dati i due titoli considerati è possibile costruire l’insieme dei portafogli che possono essere formati dalla loro combinazione; all’interno di tale insieme i portafogli che a parità di rendimento hanno la varianza minima costituiscono i portafogli detti “a varianza minima”, quelli che a parità di varianza massimizzano il rendimento atteso sono i cosiddetti “portafogli efficienti”, per cui un portafoglio efficiente è un portafoglio a varianza minima ma non è detto il
49
contrario in quanto un portafoglio a varianza minima non è necessariamente efficiente; tale distinzione risulta più chiara guardando alla Figura 8 di seguito:
Figura 8: Frontiera dei portafogli di minima varianza ed efficienti Troviamo i portafogli a varianza minima.
L’intera curva AA’ rappresenta la frontiera dei portafogli di minima varianza, dove sono indicati quei portafogli che in corrispondenza di ogni rendimento atteso µ hanno la varianza minima; la parte superore di tale frontiera evidenziata dal colore rosso e dalle lettere AB rappresenta invece la frontiera dei portafogli efficienti: come risulta chiaro a questo punto, nel tratto AB ad ogni valore di σ2 corrisponde il portafoglio con µ maggiore; presi ad esempio i portafogli P1 e P2 è
facile osservare che a parità di varianza, σ*, il portafoglio P2 posizionato lungo la
frontiera dei portafogli efficienti ha un rendimento atteso maggiore rispetto a P1.
Riprendendo l’esempio con due soli titoli rischiosi, si ipotizza che il titolo 1 abbia rendimento atteso e varianza minori del secondo; il problema di minimizzazione del rischio implica:
min σ2p= a12σ21+ a22 σ22 + 2 ρij σi σj (2.29) = ∑i=i,n∑j=1,n aiajσij
50
s.v µP = a1 µ1 + a2 µ2 (2.30)
= ∑i=i,nai µi
e a1+ a2 =1 (2.31)
=∑i=i,nai =1.
a questo punto si ricavano i valori ottimi di a1 e a2 che risolvono il problema di
ottimo dell’equazione 2.29 con il vincolo 2.30 che si può riscrivere:
µp= a1 µ1 + (1- a1)µ2 (2.32) = a1(µ1- µ2) + µ2. Da cui a1 =
(2.33)
e da a1+ a2 =1 si ha: a2= 1- a1 => a2 = 1-=> a
2 da cui a2=
. (2.34)
Sostituendo i valori di a1 e a2 trovati, nell’equazione della varianza si ha:σ2 p = 2
[
2 σ 12 + 2 σ22 + 2ρ σ1 σ2 ( ] = 2{
(σ12 + σ22- 2ρ σ1 σ2) - 2[σ12 σ22 ρ σ1 σ2 ]µP+ + (σ12µ22+ σ22 µ12-2ρ σ1 σ2µ1 µ2} (2.35)che è l’equazione di una parabola ed è la funzione da minimizzare. Dopo aver determinato il rendimento atteso e la varianza del portafoglio considerato, di seguito si analizza come una diversa correlazione tra i rendimenti dei titoli
51
influenza la capacità della diversificazione del portafoglio di ridurre il rischio ad esso connesso;
Caso ρ =1 perfetta correlazione positiva
Nel caso in cui i rendimenti dei titoli sono correlati perfettamente in senso positivo, tra essi esiste, in qualsiasi stato del mondo, una relazione lineare positiva;
sostituendo nella varianza del portafoglio
ρ =
σ σ
= 1
si ottiene:
σ2 p= a12σ21+ (1- a1)2 σ22 + 2 a1(1- a1) σ1 σ2 (2.36) = [a1σ1+ (1- a1) σ2]2 e σP = [a1σ1+ (1- a1) σ2] (2.37)che è dunque una combinazione lineare degli scarti quadratici medi dei rendimenti dei due titoli.
Con ρ=1 sia il rendimento che il rischio sono rispettivamente le medie ponderate dei rendimenti e del rischio dei titoli in portafoglio; dal concetto di media investendo in due titoli non è possibile ridurre il rischio del portafoglio al di sotto di quello del titolo meno rischioso; pertanto l’unico modo per minimizzarlo è investire tutto nel titolo a più basso rischio e quindi in questo caso la diversificazione non può essere sfruttata.
Infine sostituendo il valore di a1 nell’equazione dello scarto quadratico mediosi
ottiene che la frontiera dei portafogli efficienti è una retta anziché un’ iperbole: σP={(
)
σ1+ )] σ2} σp = ((
σ1 - σ2) + σ2 (2.38)52
da cui si ottiene µP funzione lineare di σP: µP = (µ2- σ2)+
σP
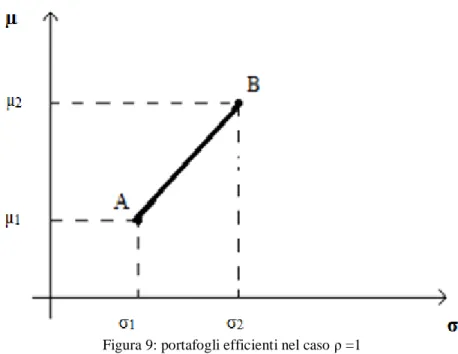
In Figura 9 si osserva che tutti i portafogli possibili appartengono alla frontiera dei
P efficienti rappresentata dalla retta AB
Figura 9: portafogli efficienti nel caso ρ =1
Caso ρ = -1 perfetta correlazione negativa
In questo caso il coefficiente di correlazione sarà dato da:
ρ =
= -1 (2.39)
sostituendolo alla varianza del portafoglio si ottiene:
σ2
p= a12σ21+ (1- a1)2 σ22 + 2 a1(1- a1)
ρ
σ1 σ2 σ2p = [a1σ1- (1- a1) σ2]2 (2.40)
e σp= a1σ1- (1- a1) σ2 (2.41)
In questo caso l’investitore pur operando su due titoli a rendimento variabile, ha la possibilità di annullare il rischio di portafoglio e ottenere così un rendimento certo, che chiameremo µc ; questo è possibile solo investendo nei titoli a1 e a2 le
53 a1σ1- (1- a1) σ2 = 0 a1σ1- σ2+ a1 σ2 = 0 a1(σ1+ σ2) - σ2 = 0 => a1(σ1+ σ2) = σ2 da cui: a1 = σ σ σ
(2.42)
e
a2= (1-a1) =>a2= σ σ σ
(2.43)
sostituendo la (2.33) nell’equazione dello scarto quadratico medio (2.41) si ottiene: σp = σ – ( 1-)
σ2 = σ – σ = σ σp = - per µ1 ≤ µp ≤ c (2.44) - + per µc ≤ µp ≤ 2 (2.45)dove µc è il rendimento “certo” del portafoglio senza rischio così ottenuto, punto
C della figura 10, composto da 2 titoli rischiosi e con ρ= -1; tale rendimento certo è ricavato sostituendo, infine, il valore della (2.42) nella (2.32) :
µc = σ σ σ µ1 + (1- σ σ σ
)
µ2; µc = σ σ σ σ σ σ σ σ ; µc = σ σ σ σ(2.46)
54
Graficamente si avranno dunque due segmenti: il primo decrescente e il secondo crescente, entrambi caratterizzati da uguale coefficiente angolare 11
(primo fattore della parte destra dell’equazione) e uguale intercetta (secondo fattore della parte destra dell’equazione) ma di segno opposto.
A questo punto si ricava µp in funzione di σp dalle (2.44) e (2.45):
dalla (2.44) µp = dalla (2.45) µp =
Graficamente: come illustrato in Figura 10 la frontiera dei portafogli passerà per un punto sull’asse delle ordinate indicato con il punto C in cui σp si annulla e
tenendo conto che dato ρ = -1, per cui la frontiera è lineare, e che σ non può assumere valore negativo la frontiera dei portafogli avrà la forma della spezzata che in figura unisce i punti ABC
Figura 10: frontiera dei portafogli nel caso ρ = -1
In cui i due segmenti rappresentano media- varianza di tutti i portafogli possibili con i due titoli, ma solo il tratto crescente rappresenta i portafogli efficienti. 11
essendo µ1 < µ2 la prima equazione indica una pendenza negativa, che diventa invece positiva nella seconda equazione con davanti il segno meno; caso opposto vale invece per il segno dell’intercetta, ovvero l’ordinata del punto di intersezione con l’asse y della retta.
55
Caso -1 <ρ< 1 correlazione non perfetta
Infine si considera il caso di correlazione non perfetta con -1< ρ < 1, che in genere corrisponde alla realtà; in questo caso la frontiera efficiente non è una funzione lineare, come nei casi precedenti, ma avrà la forma di iperbole con concavità verso destra, che aumenta al diminuire del coefficiente di correlazione ρ. Essa risulta dalla funzione radice quadrata di un polinomio di secondo grado: per l’analisi di ciò è sufficiente esaminare il rischio di tale portafoglio che sarà dato da: σp = [a12σ12+ (1- a1)2 σ22 + 2 a1(1- a1)
ρ
σ1 σ2]½
(2.47) a cui sostituendo la (2.33) si ottiene:
σp =[ 2 σ1
+ 1-
2
σ
2+
2
ρ
σ1 σ2] ½ (2.48)da cui è evidente che il rischio del portafoglio σp dipende positivamente da ρ e si
riduce al diminuire dello stesso.
Procedendo allo sviluppo della (2.48)si ottiene: σp = [ 2
σ
+
2+2
ρ σ1 σ2 ]1/2 = µP2 – ρ
-2 µP – + σ ρ σ σ
Questa funzione è una parabola in µ nel piano (σ2, µ) mentre è un’iperbole nel piano (σ, µ) ; esso inoltre presenta un minimo che può essere uguale o minore del
minimo tra σ1 e σ2 che, come si è ipotizzato inizialmente, è dato da σ1; il caso σp
< σ1 rispecchia l’effetto della diversificazione.
Il valore di a1 che consente di minimizzare il rischio si determina ponendo a zero
56 ∂ σp = 1 2 a1 σ12 +2 a1 σ22 -2 σ22 +2ρ σ1 σ2 = 0 (2.49) ∂ a1 2 [a12 σ12 + (1-a1)2 +2 a1 (1-a1) ρ σ1 σ2]1/2 e risolvendo per a1 : a1 = σ22 - ρ σ1 σ2 (2.50) σ12+σ22- 2ρ σ1 σ2
da cui facilmente si ottiene il valore di a2 considerando che esso è dato dalla
differenza (1- a1):
a2= σ12 - ρ σ1 σ2 (2.51) σ12+σ22- 2ρ σ1 σ2
è possibile a questo punto analizzare anche il caso intermedio ρ = 0 12 in cui a1 = σ22 a2 = σ22
σ12+σ22- 2ρ σ1 σ2 σ12+σ22- 2ρ σ1 σ2 .
Supponendo di non investire tutto nell’attività a1, vale:
a1 = σ22 - ρ σ1 σ2 < 1 (2.52) σ12+σ22- 2ρ σ1 σ2
e ponendo il denominatore >0 vale che: σ22 - ρ σ1 σ2 < σ12 + σ22- 2ρ σ1 σ2 ,
pertanto si avrà ρ< σσ che comporta un rischio di portafoglio inferiore a σ1
altrimenti continuerà a valere che il minor rischio si ottiene investendo tutto nell’alternativa meno rischiosa a1.
Graficamente, dunque, per valori di ρ compresi tra (-1,1) la frontiera efficiente dei portafogli si collocherà all’interno del triangolo costituito dai punti ABC in
Figura 11, dalla quale si osserva che al diminuire di ρ è possibile ridurre la
variabilità dei due titoli a parità di rendimento atteso.
12
sostituendo a σ2p il valore di a12 troviamo: σ2p= (σ22/ σ21+ σ22)2 σ21 +(σ21/ σ21+ σ22)2 σ22; =>(σ2 4 σ1 2+ σ 1 4 σ2 2)/( σ2 1+ σ 2 2) 2 => σ1 2 σ2 2(σ2 1+ σ 2 2)/ (σ 2 1+ σ 2 2) 2 => σ2p= σ1 2(σ 2 2/ σ2 1+ σ 2 2) Si osserva facilmente che essendo il termine dentro parentesi <1 si ha che σ2
p< σ1 2
; ciò dimostra che anche quando i titoli non sono correlati è comunque possibile ridurre il rischio associato al portafoglio a parità di rendimento atteso mediante una buona diversificazione.
57
Figura 11: Frontiera dei portafogli con 2 titoli
Riassumendo quanto appena esposto, mediante un’adeguata diversificazione del portafoglio è possibile ridurre il rischio ad esso associato, tenendo conto che quanto più il coefficiente (
ρ
) di correlazione tende al valore minimo (-1) tanto più è possibile ridurreσ2p.2.2.3.3 Il modello di Tobin
Portafoglio con n titoli tra cui un titolo risk-free
Dalle precedenti considerazioni sulla diversificazione, ne segue che un portafoglio con n titoli consente una maggiore differenziazione del portafoglio e pertanto la possibilità di raggiungere un determinato rendimento al minor rischio; formalmente si avrà che un portafoglio sulla frontiera sarà dato dalla combinazione degli n titoli sulla base delle quote in essi investiti (a1, a2…an) che
soddisfano il problema di ottimo; graficamente la frontiera illustrata in Figura 11 man mano che n aumenta si sposta verso sinistra.
Mentre Markowitz considera solo titoli e portafogli rischiosi, Tobin cerca di perfezionare la teoria di Markowitz ipotizzando anche l’esistenza di un titolo caratterizzato da rischio nullo (Risk Free Rate), che garantisce quindi un
58
rendimento sicuro e dà la possibilità di costruire ulteriori portafogli combinando quelli sulla frontiera efficiente con il titolo privo di rischio; esso può essere dato ad esempio da un titolo obbligazionario o più semplicemente un deposito bancario; egli enunciò il risultato del suo lavoro nel suo celebre articolo
“Liquidity Preference as Behavior Towards Risk” presentato nel 1958 e che gli valse nel 1981 il premio nobel per l’Economia; in questo articolo egli esprime il suo punto di distacco da Markowitz mediante il cosiddetto “Teorema di
separazione”.
Ipotizziamo quindi che tra i titoli che costituiscono il portafoglio ce ne sia uno privo di rischio (con media e varianza rispettivamente r0, 0), nel quale viene
investita la quantità a0 di ricchezza, che dunque presenterà un rendimento
minore della parte del portafoglio composta dai titoli rischiosi (che supponiamo abbia µB, σB) in cui viene investita la rimanente quota di ricchezza (1- a0), e allo
stesso tempo una minore varianza; il portafoglio così composto presenterà media e varianza rispettivamente: µP= a0 r0 +(1- a0) µB (2.53) σ2 p= 0+(1- a0)2 σB2 da cui σp= (1- a0) σB, (2.54) e segue che (1- a0)= σp/ σB da cui a0 = (σB - σp)/ σB.
Sostituendo il valore di a0 e (1- a0) nel rendimento atteso del portafoglio si ha
che:
µP= [(σB - σp)/ σB] r0 + (σp/ σB) µB
59
frontiera dei portafogli ( lineare) µP= r0 + (µB- r0) σp (2.55)
σB
Quando nel portafoglio, oltre ai titoli rischiosi c’è un titolo risk-free, la relazione tra µP e σp è lineare e questo vale per tutti i portafogli così combinati; come
illustrato in Figura 12, dunque, si avrà che i portafogli si trovano su una semiretta, con intercetta sull’asse delle ordinate in corrispondenza di r0 con
inclinazione (µB- r0)/σB positiva poiché in genere vale, come supposto
inizialmente, che r0< µB. ;
Figura 12: frontiera dei portafogli con titoli rischiosi più un titolo risk-free
Si avranno così tante semirette ottenute dalla combinazione del PB costituito dai
soli titoli rischiosi con il titolo senza rischio, ma solo una di essa costituisce la frontiera efficiente che sarà data dalla semiretta uscente dal punto A tangente alla frontiera dei portafogli con soli titoli rischiosi passante per il punto B, in cui risiede il cosiddetto portafoglio di tangenza, indicata nel grafico dalla linea ABC; essa rappresenta dunque l’insieme dei portafogli più efficienti costruiti investendo in combinazioni di titolo risk-free e titoli rischiosi.
Il portafoglio di tangenza B è dunque il portafoglio che tra tutti i portafogli ottenuti combinando il titoli risk-free con il portafoglio di titoli rischiosi,
60
consente di ottenere un maggior rendimento atteso a parità di rischio o il minor rischio a parità di rendimento atteso; questo è dovuto al fatto che B risiede sull’unica semiretta tangente alla frontiera con soli titoli rischiosi, che pertanto è
posizionata più in alto e a sinistra di tutte le altre semirette che originano da µ0 e
passano per un qualsiasi punto della suddetta frontiera.
In particolare nel grafico rischio-rendimento avremo diverse scelte di investimento, per cui l’investitore potrà:
- investire tutta la sua ricchezza nel titolo privo di rischio PA per cui (a0=1),
concedendo di fatto denaro a prestito dato che parte della sua ricchezza viene investita in un titolo a rischio nullo;
- investire tutta la sua ricchezza nel titolo rischioso PB per cui a0 =0 e (1- a0)=1;
- man mano che ci sposta da A a B investe sempre meno nel titolo senza rischio
e quote sempre maggiori nei titoli rischiosi;
- prendendo in considerazione il portafoglio indicato con C, si osserva che la sua posizione è oltre il portafoglio B pertanto non può essere acquistato spendendo solo la ricchezza a disposizione, per tale motivo egli potrà permettersi questo investimento solo prendendo a prestito al tasso risk- free e investendo la somma così ottenuta nel portafoglio rischioso.
La differenza tra il rendimento del titolo privo di rischio e il rendimento espresso dai portafogli efficienti di attività rischiose, è denominata “premio per il rischio”. Per ciò che attiene la derivazione analitica della frontiera nel caso di n=3 titoli tra cui uno senza rischio, vedere Appendice 1.
61
Teorema di separazione (o Teorema dei due fondi)
Nel modello di Tobin il portafoglio di tangenza indicato (punto B nella Figura 12)
è lo stesso per tutte le categorie di investitori avversi al rischio e viene denominato “portafoglio di tangenza”13.
Tobin enuncia un teorema di separazione secondo il quale, il processo di scelta del portafoglio si articola in due fasi distinte:
1) nella prima fase si individua il portafoglio di tangenza costituito dai soli titoli rischiosi, che sarà uguale per tutti gli investitori
2) ogni investitore sula base delle proprie preferenze e dunque della propria funzione di utilità decide in quali proporzioni ripartire la ricchezza tra il titolo risk-free e il portafoglio tangente.
Naturalmente questa scelta sarà differente da soggetto a soggetto, pertanto ognuno allocherà una diversa frazione di ricchezza in tioli rischiosi, ma acquisterà gli stessi n titoli in proporzione uguale.
Questa conclusione deriva dal fatto che in base al modo in cui è stata costruita la frontiera efficiente, ottenuta dalla combinazione di titolo risk-free con il portafoglio tangente, si avrà che in ogni portafoglio la quota di titoli rischiosi sarà ripartita nelle stesse proporzioni tra gli n titoli rischiosi. A questo contribuisce l’ipotesi di base del modello, di perfetta informazione di tutti gli investitori e di assenza di costi o tasse di transazione; ciò infatti fa si che tutti gli operatori utilizzeranno l’informazione disponibile nello stesso modo e avranno la stessa valutazione delle proprie prospettive di investimento, anche nel caso in cui tali investitori hanno atteggiamenti diversi rispetto al livello di rischio. In definitiva si ha che:
13
Ovvero per ogni investitore che guarda solo alla media e varianza dei rendimenti il portafoglio tangente sarà lo stesso per tutte le categorie di investitori con le stesse credenze su medie, varianze e covarianze dei rendimenti dei titoli; (Fiaschi, Meccheri pag75).
62
- le proporzioni con cui i titoli rischiosi entrano nel fondo comune non dipendono dal livello della ricchezza ,né dalle loro preferenze individuali;
- la scelta dell’investitore concerne soltanto l’allocazione della stessa tra il titolo privo di rischio e il fondo comune.
Scelta del portafoglio ottimo
Dalla Figura 13 si evince che ogni investitore sceglierà, tra tutti i portafogli efficienti sulla frontiera, il portafoglio ottimo P*, dato dalla combinazione del portafoglio tangente e del titolo privo di rischio, che pertanto presenterà
rendimento atteso µp* dato dalla media ponderata del tasso privo di rischio µ0 e
del rendimento atteso del portafoglio tangente µB, e varianza σp* data dalla sola
deviazione standard del portafoglio rischioso poiché quella del titolo risk-free è nulla; rispettivamente si avrà:
µp*= a1 µ0 + (1- a1) µB e σp*= (1- a1) σB
dove a1 è la quota del titolo risk-free nel portafoglio ottimo.
Il portafoglio ottimo P*, è dunque ottenuto massimizzando la funzione di utilità
in corrispondenza del punto di tangenza tra la frontiera efficiente e la curva di indifferenza più alta che presenteranno la stessa pendenza data da:
(µp- µ0)/ σP = (∂ µp/ ∂ σP) . (2.56)
Per ciò che attiene la massimizzazione della funzione di utilità, se si assume che
le curve di indifferenza hanno una forma del tipo: U = µ- rσ2 , dove µ indica il
rendimento atteso del portafoglio, σ2 la sua varianza e r il grado di avversione al rischio dell’investitore, sostituendo i valori di µp* e σp* trovati, si ottiene U*,
ossiail livello di utilità che l’investitore ottiene investendo nel portafoglio P* :
63
Figura 13: scelta del portafoglio ottimo nel modello di Tobin
2.4 Misura delle performance delle attività finanziarie
La valutazione della qualità degli strumenti finanziari, molto usati specie nel caso di fondi comuni d’investimento, avviene mediante indicatori di performance denominati risk-adjusted performance (RAP), che mettono in relazione il rendimento con il rischio che è stato necessario assumere per raggiungere tale rendimento; il prodotto con maggior valore dell’indice RAP sarà il migliore tra quelli messia confronto poiché si aggiudica una posizione migliore nella relazione rischio-rendimento.
Indice di Sharpe
Il più famoso tra questi è l’indice di Sharpe che prende nome dal suo ideatore che lo propone nel 1966 con il termine “reward to variability ratio”, cui faranno seguito molte varianti, di cui l’ultima pubblicata nel 1994 sul Journal of Portfolio Management.
Tale indice misura quanto affidabile possa risultare un investimento nel rapporto fra maggior rendimento e minor rischio; si basa infatti sul confronto tra l’extra-rendimento di uno strumento finanziario (che può ad esempio essere costituito da
64
un fondo comune d’investimento) rispetto al rendimento di un’attività risk-free,
rapportato alla rischiosità del portafoglio. L'indice è tanto più elevato quanto un
maggior rendimento in un dato periodo considerato è ottenuto con minor rischiosità.
Analiticamente esso è definito come:
RAPs= (µi- µ0) / σi (2.58)
dove i identifica l’attività i-esima.
Secondo tale impostazione, un maggior valore dell’indice di Sharpe indica una migliore valutazione della qualità del rendimento dell’attività poiché si è avuto un extra-rendimento rispetto al risk-free.
Esso misura il coefficiente angolare della semiretta che dal punto µ0, ovvero il
rendimento dell’attività risk-free sull’asse delle ordinate, passa per il portafoglio considerato; ad una maggiore inclinazione della stessa corrisponde una maggiore
differenza tra i rendimenti µi e µ0 per unità di rischio, naturalmente l’inclinazione
è massima per i portafogli efficienti.
65
In particolare in Figura 14 appare chiaro che il portafoglio A si siede su una
semiretta ad inclinazione maggiore rispetto al portafoglio B, pertanto: - La performance di A sarà migliore di B
- sicuramente B non apparterrà alla frontiera efficiente
Se alla formula dell’indice di Sharpe vengono sostituite le informazioni del fondo (o portafoglio) con quelle inerenti al portafoglio benchmark14 si determina l’indice di Sharpe del benchmark; se l’indice di Sharpe risulta migliore dell’indice benchmark vuol dire che il gestore del fondo ha ottenuto un miglior risultato rispetto al benchmark e quindi un maggior rendimento per unità di rischio.
Indice di Modigliani
Una misura di performance RAP alternativa è data dell’indice proposto dall’economista Franco Modigliani nel 1997; tale indice ha lo scopo di confrontare portafogli aventi lo stesso benchmark, portando la loro rischiosità allo stesso livello di quella del benchmark per poi, misurarne il rendimento; in questo modo l’investitore può avere una visione più chiara del confronto tra i due portafogli poiché a parità di rischio vede con semplicità la differenza di rendimento, per tale motivo questo indice risulta di più facile comprensione rispetto all’indice di Sharpe; un’altra differenza sostanziale è che quest’ultimo è rappresentato da un coefficiente angolare, l’indice di Modigliani da una percentuale.
In termini analitici tale indice si presenta come:
14
il benchmark è un parametro usato in materia di investimento come parametro oggettivo di riferimento per poter fare dei confronti tra la performance del portafoglio rispetto all’andamento del mercato; ogni benchmark dovrebbe essere caratterizzato da alcuni elementi fondamentali, tra i quali: trasparenza, in quanto devono essere calcolati con regole che ogni investitore può replicare; rappresentatività, in quanto deve esprimere le politiche di gestione del portafoglio; replicabilità, poiché dovranno essere replicabili con attività acquistabili sul mercato direttamente (fonte www.borsaitaliana.it).
66
RAPM= σB + (σB/ σP)( µi- µ0) (2.59)
= µ0+ σB(RAPS) (2.60)
da cui è facile notare che l’indice di Modigliani RAPM, è dato dalla somma del
rendimento del titolo risk-free µ0, e l’indice di Sharpe (RAPS) moltiplicato per la
deviazione standard del benchmark σB; pertanto utilizzando lo stesso benchmark
entrambi forniranno lo stesso risultato.
In Figura 15 sono indicati sia i rendimenti originari (µ) dei titoli, sia quelli
modificati (RAP); i rombi indicano il punto in cui questi assumono il valore di rischio del benchmark in corrispondenza dei quali sull’asse delle ordinate è espresso il valore del rendimento modificato; in questo caso il portafoglio A presenta un indice di Modigliani più elevato rispetto B poiché ha ottenuto un rendimento aggiustato per il rischio maggiore; inoltre come nel caso precedente, l’indice di Modigliani maggiore si avrà in corrispondenza del portafoglio sulla frontiera efficiente.