Sommario
Sommario
Lo sviluppo di questa tesi di laurea ha avuto come obiettivo iniziale quello di effettuare il porting di una libreria di algoritmi di cifratura a curva ellittica, la libreria EccM 2.0, sui nodi sensore Tmote Sky della Moteiv, che utilizzano Contiki come sistema operativo, al fine di valutarne le prestazioni sia dal punto di vista temporale sia per quanto riguarda l’ occupazione di memoria.
I risultati sono stati confrontati con quelli ottenuti in passato utilizzando lo stesso hw e la stessa libreria ma con un sistema operativo differente, TinyOs.
Si è quindi cercato di migliorare le prestazioni andando a lavorare:
• sugli algoritmi della libreria sostituendo alcune operazioni fondamentali con altre più efficienti;
• sulla implementazione della libreria cercando di renderla più idonea alle capacità del microcontrollore dei nodi sensore.
Per il primo punto abbiamo distinto due possibili livelli di intervento:
• operazioni sul campo;
Sommario
Per operazioni sul campo si intendono le operazioni, che non coinvolgono punti della curva, effettuate dalla libreria. Si è cercato di migliorare le prestazioni andando a sostituire l’ algoritmo di moltiplicazione modulare “shift and add” della libreria con quello di Karatsuba.
Le operazioni sulla curva sono invece le operazioni, che coinvolgono punti della curva, effettuate dalla libreria. Si è sostituito l’ algoritmo della libreria che esegue la moltiplicazione scalare di un punto della curva per un intero, l’ algoritmo “double and add”, con quello di Montgomery.
Fra una sostituzione e l’ altra si è lavorato sul secondo livello sopra introdotto, ovvero su una differente implementazione della libreria per provare ad adattarla alle caratteristiche del microcontrollore a disposizione. Infatti il microcontrollore ci permette di lavorare a 16 bit, mentre la libreria EccM 2.0 utilizza word a 8 bit. Si sono allora convertite alcune funzioni fondamentali per capire l’ impatto che tali cambiamenti potevano avere sulle prestazioni.
I test effettuati ci hanno permesso di valutare le nuove implementazioni sia per quanto riguarda i tempi necessari alle esecuzioni degli algoritmi sia per quanto riguarda l’ occupazione di memoria, confrontando i risultati con quelli inizialmente ottenuti in fase di porting.
Di seguito viene spiegato, in maniera sintetica ma un po’ più dettagliata di quanto fatto fino ad ora, il lavoro svolto.
Le reti di sensori costituiscono un esempio di rete wireless formata da nodi sensore con caratteristiche peculiari: ridotte dimensioni dei nodi, potenza di elaborazione limitata, memoria (RAM e ROM) ridotta e necessità di un ridotto consumo di energia. Tali nodi sono utilizzati con tre scopi principali:
Sommario
• raccogliere dati dall’ ambiente circostante, grazie ai sensori di cui sono dotati (tipicamente luce,umidità e temperatura);
• effettuare elaborazioni locali (operazioni sui dati raccolti);
• trasmettere e ricevere tali dati con altri nodi sensore nelle vicinanze o con la stazione base.
Gli ambiti applicativi dove possono essere utilizzate sono numerosi: monitoraggio ambientale, controllo medico, ambito militare oppure controllo di apparati domestici.
In alcune di queste situazioni può nascere l’ esigenza di dotare i sensori di un’ infrastruttura software di sicurezza che riesca a garantire:
• la generazione di segreti condivisi, da utilizzare in schemi a chiave simmetrica;
• la segretezza delle informazioni scambiate tra i nodi sensore;
• l’ autenticazione dei messaggi ricevuti da un nodo.
I tradizionali algoritmi a chiave pubblica, come RSA, sono ritenuti troppo costosi dal punto di vista computazionale per le reti di sensori, come è stato dimostrato da alcune implementazioni. Il tempo computazionale richiesto per l’ operazione di esponenziazione modulare, che è alla base delle operazioni di cifratura/decifratura e di firma digitale, può richiedere tempi compresi tra 5 e 10 minuti, rendendo estremamente improbabile la loro utilizzazione pratica. Recentemente la crittografia a
Sommario
curva ellittica è stata proposta come soluzione alternativa per cercare di ridurre i tempi di esecuzione a parità di livello di sicurezza garantito. Questo tipo di crittografia è particolarmente adatta ai dispositivi con risorse limitate, come i nodi sensore, in quanto consente operazioni più veloci di RSA e una minore occupazione di memoria, grazie all’ utilizzo di chiavi più piccole delle chiavi RSA.
Questa tesi si è occupata del porting di una libreria crittografica a curva ellittica (EccM 2.0 [6]) per reti di sensori su nodo sensore Tmote Sky della Moteiv [1] (8 Mhz, 48KB ROM, 10 KB RAM) che utilizza come sistema operativo Contiki [13] e come linguaggio di programmazione il C. Tale libreria era già stata implementata e testata su sensori Tmote Sky della Moteiv [1] che utilizzavano però un differente sistema operativo e un differente linguaggio di programmazione, rispettivamente TinyOS (1.1.11) e nesC.
Gli obiettivi che ci siamo prefissati sono stati:
• garantire il funzionamento della libreria e verificare la correttezza dei risultati;
• cercare di ridurre i tempi di esecuzione.
La libreria EccM 2.0 implementa:
• l’ algoritmo Diffie-Hellmann, per la generazione e lo scambio di chiavi;
• gli algoritmi di firma digitale ECDSA e Nyberg-Rueppel.
Sommario
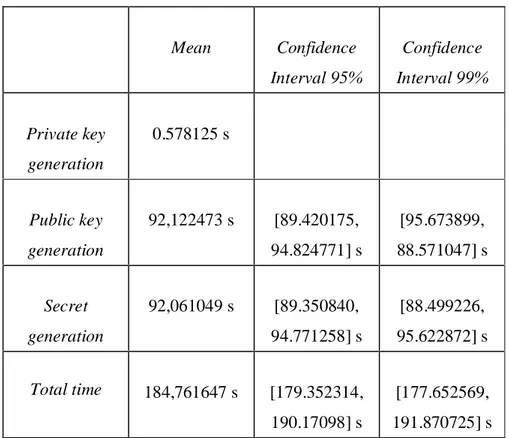
• per Diffie-Hellmann, 51 secondi per l’ operazione di generazione della chiave pubblica (una moltiplicazione di un punto della curva per un intero) e 1 minuto e 40 secondi per l’ esecuzione del protocollo completo;
• per Ecdsa e Nyberg-Rueppel, i tempi sono tra loro simili. Per la firma circa 51 secondi (una moltiplicazione di un punto della curva per un intero) e per la verifica 1 minuto e 50 secondi (due moltiplicazioni di un punto della curva per un intero).
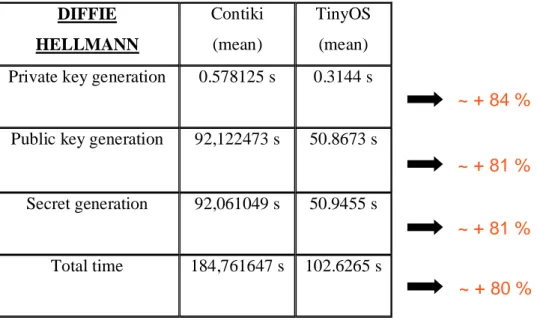
I risultati che sono stati ottenuti sul sensore Tmote Sky (TelosB) con sistema operativo Contiki sono più elevati di circa l’ 80%, 40 secondi, per ogni operazione di moltiplicazione fra un punto e un intero:
• per Diffie-Hellmann, 92 secondi per l’ operazione di generazione della chiave pubblica e 3 minuti e 4 secondi per l’ esecuzione del protocollo completo;
• per Ecdsa, 90 secondi per la firma e 3 minuti e 6 secondi per la verifica;
• per Nyberg-Rueppel, 92 secondi per la firma e 3 minuti e 5 secondi per la verifica.
La causa di tale peggioramento va probabilmente ricercata nell’ utilizzo di un sistema operativo e di un linguaggio di programmazione differente.
Sommario
Si è potuto ridurre il tempo necessario per la moltiplicazione di un punto per un intero ricorrendo all’ utilizzo dell’ algoritmo di Karatsuba per rendere più efficienti le moltiplicazioni modulari sul campo.
Il tempo necessario per la generazione della chiave pubblica e per la firma digitale (entrambe richiedono una moltiplicazione di un punto per un intero) è sceso di circa il 6,7%, 6 secondi. Il tempo per la verifica della firma (che richiede due moltiplicazioni di un punto per un intero) è sceso di circa il 6,45% , 12 secondi.
In seguito si è lavorato per convertire alcune delle funzioni della libreria utilizzata, che lavora a 8 bit, a 16 bit. In questo modo possiamo sfruttare pienamente le caratteristiche del microcontrollore che abbiamo a disposizione. La conversione di alcune funzioni fondamentali ci ha permesso di abbassare i tempi di circa il 2,86%, 2,4 secondi, rispetto all’ utilizzo di funzioni solo a 8 bit, in fase di firma digitale. I tempi sono scesi di circa il 2,3%, 4 secondi, nelle operazioni di verifica.
Infine si è deciso di provare ad utilizzare un differente algoritmo per eseguire la moltiplicazione fra un intero e un punto della curva. Il nuovo algoritmo utilizzato è quello di Montgomery. Per le moltiplicazioni modulari sul campo abbiamo continuato ad usare l’ algoritmo di Karatsuba sopra citato.
Si è avuto un netto miglioramento delle prestazioni. I tempi per l’ esecuzione di una moltiplicazione intero-punto sono scesi del 64,3%, 54 secondi, rispetto all’ utilizzo del solo Karatsuba. Per una operazione di firma digitale siamo intorno ai 30 secondi. Per la verifica si è avuto un miglioramento del 62,1%, 108 secondi. E questo senza utilizzare nessuna delle funzioni a 16 bit già presentate.
Il loro utilizzo permette di far scendere ulteriormente i tempi di circa il 13,3%, 4 secondi, in fase di firma e di circa l’ 10,61%, 7 s, in fase di verifica.
Sono però emersi problemi di spazio, dovuti alla poca memoria disponibile sui nodi sensori. A causa di questa limitazione non è possibile caricare insieme su un nodo
Sommario
sensore il software con Montgomery e Karatsuba per l’ esecuzione della firma digitale e quello necessario alla verifica della firma.
Indice
Indice
1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8Introduzione alla curva ellittica
Introduzione Aspetti di sicurezza
Crittografia nelle reti wireless di sensori Crittosistemi a curva ellittica
Interpretazione geometrica delle curve ellittiche Curve ellittiche utilizzate in crittografia
Curve ellittiche sui campi finiti GF(p) Curve ellittiche sui campi finiti GF(2m)
15 15 17 18 21 23 27 28 30 2 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.7.1 2.8
Crittografia a curva ellittica
Introduzione
RSA nelle reti di sensori
Problema del logaritmo discreto ECC vs RSA
Inizializzazione
Generazione della coppia di chiavi
Protocollo di distribuzione delle chiavi Diffie-Hellman Esempio numerico
Protocolli di firma digitale
33 33 33 35 36 37 39 40 42 44
Indice 2.9 2.10 ECDSA Nyberg-Rueppel 45 48 3 3.1 3.2 Contiki Introduzione
Runes middleware e contiki
50 50 52 4 4.1 4.2 4.3 4.4 4.5 4.5.1 4.5.2 4.5.3 EccM 2.0 Introduzione Components
Parametri della curva Rappresentazione dei dati Risultati ottenuti Diffie-Hellmann ECDSA Nyberg-Rueppel 55 55 56 59 59 60 61 65 68 5 5.1 5.2 5.2.1 5.2.2 5.2.3 5.3 5.3.1 Ottimizzazioni Introduzione Algoritmo di Karatsuba x*x mod f x*y mod f Prestazioni
Conversione della libreria EccM 2.0 da 8 a 16 bit Prestazioni 71 71 72 76 80 82 84 89
Indice 5.4 5.4.1 5.5 Algoritmo di Montgomery Prestazioni Conclusioni 91 94 96
Elenco figure
Elenco figure
1.1 1.2 1.3 1.4Curva ellittica y = x3 − 7x + 5, definita sui numeri reali −P = (x,−y) è l’ inverso del punto P = (x, y)
Somma tra due punti della curva ellittica, T = P + Q Somma tra due punti coincidenti, ovvero raddoppio di un punto, R = 2P 24 25 26 26 3.1 3.2
Component, interface, receptacle Interazione fra components
54 54 4.1 4.2 4.3 4.4 4.5 4.6 4.7
Struttura della libreria EccM 2.0
Schema di funzionamento generale del protocollo Diffie-Hellmann
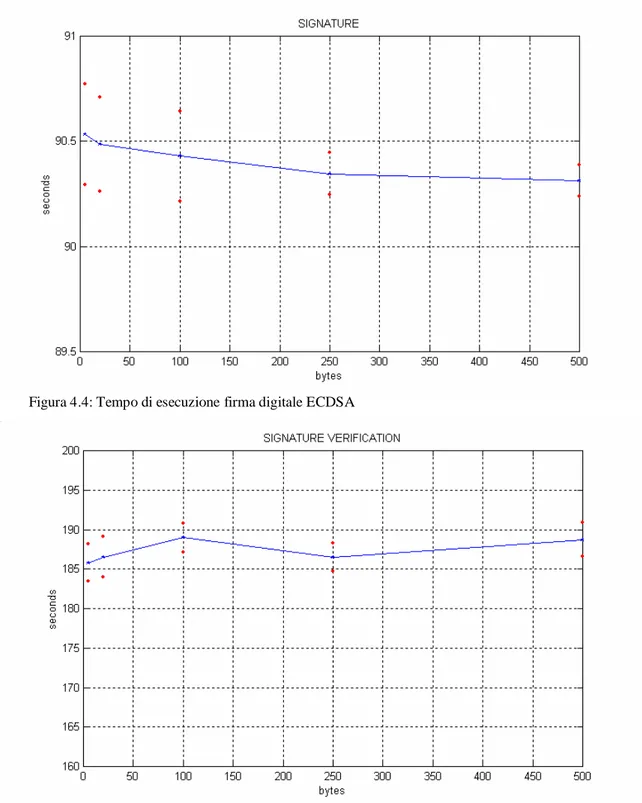
Tempo di esecuzione per il calcolo della hash Tempo di esecuzione per la firma digitale ECDSA
Tempo di esecuzione per la verifica della firma digitale ECDSA
Tempo di esecuzione per la firma digitale Nyberg-Rueppel
Tempo di esecuzione per la verifica della firma digitale Nyberg-Rueppel 56 61 66 67 67 69 70
Elenco Figure
5.1 5.2 5.3
Tabella precomputata 16x16 per la square
Tempo di esecuzione per la firma digitale ECDSA Tempo di esecuzione per la verifica della firma digitale ECDSA
79 83
Elenco tabelle
Elenco tabelle
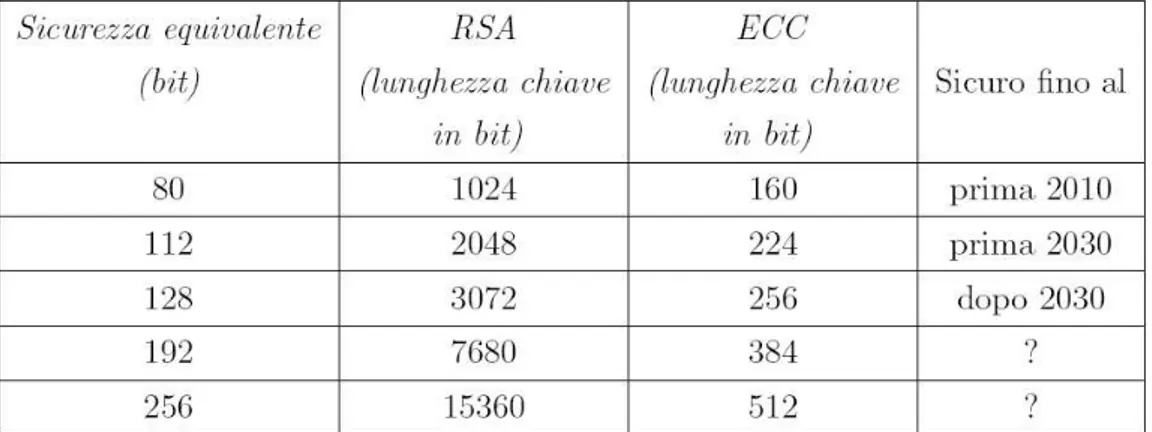
2.1 Lunghezze di chiave raccomandate dal NIST per il futuro
(ECC e RSA) 37 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8
Funzioni implementate dal modulo generator Funzioni implementate dal modulo sha1
Funzioni implementate dal modulo ecdsa e dal modulo nr riguardanti la firma digitale sui nodi sensore
Funzioni implementate dal modulo networking Tempi medi su 140 esecuzioni per l’ esecuzione del protocollo Diffie-Hellmann
Confronto Diffie-Hellmann usando Contiki e TinyOs Confronto ECDSA con contiki e tinyOs
Confronto Nyberg- Rueppel con Contiki e TinyOs
57 57 58 58 62 64 68 70 5.1 Riepilogo risultati 96
Elenco strutture
Elenco strutture
4.1 4.2
Struttura dati utilizzata per rappresentare un intero Struttura dati utilizzata per rappresentare un punto della curva
59
Capitolo 1
Introduzione alla curva ellittica
1.1 Introduzione
La crittografia a chiave pubblica (PKC, Public Key Encryption) si basa sull’ esistenza di due chiavi per ogni entità, una pubblica e l’ altra segreta, e consente
di instaurare un canale sicuro di comunicazione, senza la conoscenza di un segreto condiviso a priori tra i partecipanti, ammesso che l’ autenticità delle chiavi pubbliche venga certificata1. Mentre negli algoritmi a chiave simmetrica la sicurezza si basa sul fatto che la chiave segreta è nota soltanto ai due attori della comunicazione2, negli algoritmi a chiave pubblica (o asimmetrica) la chiave pubblica può essere distribuita a chiunque e solo la chiave privata rimane un segreto del possessore. Questi ultimi algoritmi sono stati progettati in modo tale che sia computazionalmente impossibile ricavare la chiave pubblica dalla chiave privata.
In linea di massima, le famiglie di algoritmi a chiave pubblica più importanti sono:
da una terza entità fidata mediante il meccanismo dei certificati.
ciò fa nascere il problema di come distribuire in modo sicuro la chiave alle due entità.
1 2
1.1 Introduzione
• algoritmi basati sul problema della fattorizzazione, ovvero dato un numero n = pq, dove p e q sono numeri primi grandi, trovare p e q (p e q sono detti i fattori primi di n). Un esempio è lo schema RSA [10], utilizzabile per garantire sia la segretezza sia l’ autenticazione;
• algoritmi basati sul problema del logaritmo discreto, ovvero dati y, q e p tali che y = qx mod p (dove p è un numero primo grande, y, q, x sono interi positivi e mod indica l’ operazione di modulo, ovvero il resto della divisione intera tra i suoi argomenti), trovare il valore di x che soddisfa la precedente equazione;
• algoritmi basati sulla curva ellittica, che basano la propria sicurezza sul problema del logaritmo discreto a curva ellittica, che sarà trattato successivamente.
I crittosistemi a curva ellittica sono la famiglia più recente di algoritmi a chiave pubblica ma stanno ricevendo una certa attenzione, soprattutto negli ambiti in cui sono disponibili poche risorse computazionali, come nei sistemi embedded. A causa dei minori requisiti necessari per realizzare le operazioni crittografiche tipiche della curva ellittica, questa trova un ideale campo di applicazione nell’ ambito dei dispositivi con risorse limitate (CPU e memoria).
I crittosistemi a chiave pubblica risolvono in modo elegante il problema della distribuzione delle chiavi, che invece è presente negli schemi a chiave simmetrica, tuttavia hanno lo svantaggio di essere computazionalmente più costosi; inoltre, mentre con una sola chiave gli algoritmi simmetrici offrono un canale bidirezionale o di gruppo (una sola chiave simmetrica utilizzata da due o più nodi sia per inviare che
1.2 Aspetti di sicurezza
per ricevere messaggi), gli schemi asimmetrici offrono un canale unidirezionale con una coppia di chiavi (chiunque può inviare messaggi al possessore della coppia di chiavi ma solo lui, che conosce la chiave privata, può decifrarli correttamente). In generale, quindi, la crittografia a chiave pubblica è utilizzata per stabilire una chiave segreta tra due entità (chiave di sessione) e per l’ autenticazione attraverso la firma digitale, mentre la crittografia a chiave simmetrica è utilizzata per cifrare il trasferimento dei dati della comunicazione, ottenendo throughput maggiori.
1.2 Aspetti di sicurezza
Le attuali tecniche di crittografia sono utilizzate per garantire diversi aspetti della sicurezza di una rete di nodi:
• generazione di un segreto condiviso: meccanismo per stabilire un valore segreto noto solo a due entità attraverso un canale insicuro, in assenza di altri segreti condivisi a priori. E’ realizzato con tecniche a chiave pubblica (tipicamente con il supporto di una terza entità fidata e il meccanismo dei certificati);
• segretezza (o confidenzialità): i dati scambiati tra due entità sono cifrati in modo da poter essere comprensibili solo a loro (dopo un’ opportuna decifratura) e non ad altri. Ciò si realizza con algoritmi di cifratura/decifratura;
1.3 Crittografia nelle reti wireless di sensori
• integrità: la possibilità di verificare se i dati inviati sono stati alterati rispetto a quando sono stati originati. Si realizza con le funzioni hash crittografiche;
• autenticazione: modo per verificare se un certo messaggio è stato originato da una certa entità. Essa lega in modo indissolubile un messaggio con una certa chiave privata. E’ realizzata comunemente con il meccanismo della firma digitale.
Come sarà discusso in seguito, la crittografia a curva ellittica, che è intrinsecamente un meccanismo a chiave pubblica, consente di gestire tutti questi aspetti, anche se normalmente nella pratica per la segretezza si utilizzano cifrari simmetrici a blocchi in quanto le prestazioni di questi ultimi sono notevolmente superiori.
1.3 Crittografia nelle reti wireless di sensori
Il problema della confidenzialità e dell’ autenticazione si pone anche nell’ ambito delle reti wireless di sensori. Una rete wireless di sensori è una rete i cui nodi sono dispositivi di piccole dimensioni (detti nodi sensori o motes), dotati di un microcontrollore (tipicamente con frequenza operativa di 8Mhz), una memoria flash per la programmazione e un chip di comunicazione wireless per ricevere e trasmettere dati da e verso gli altri sensori o verso una stazione base. Tipicamente sono dotati anche di sensori di temperatura, luce e umidità. Tali nodi possono essere utilizzati in diversi ambiti applicativi quali il monitoraggio di ambienti, di persone e il
1.3 Crittografia nelle reti wireless di sensori
coordinamento di mezzi mobili. Ciò che caratterizza in modo significativo una rete di sensori è la scarsità di risorse di ogni nodo:
• spazio di memoria limitato: solo pochi kilobytes sono disponibili per il codice applicativo. Ciò comporta che il codice che implementa l’ infrastruttura di sicurezza deve occupare a sua volta uno spazio limitato.
Analogamente, oltre al codice, anche i dati degli algoritmi utilizzati (vettori di inizializzazione, chiavi, altri parametri) dovrebbero occupare il minor spazio possibile;
• limitazione di potenza: soprattutto nel caso in cui le batterie di un nodo non possano essere sostituite o ricaricate il consumo di potenza deve essere limitato quanto più possibile poiché incide direttamente sul tempo di vita del
sensore. Il consumo di potenza attribuibile alla sicurezza è dovuto all’ esecuzione delle funzioni vere e proprie (cifratura, decifratura, firma
digitale, verifica...) e alla trasmissione di dati correlati alla sicurezza (ad esempio lo scambio delle chiavi pubbliche nel protocollo Diffie-Hellmann);
• banda limitata e buffer di ricezione dei pacchetti limitati possono condurre a congestione di rete;
• canale wireless inaffidabile e possibili collisioni tra trasmissioni di nodi diversi in reti ad alta densità.
Data la varietà di applicazioni che possono essere realizzate e gli ambienti (anche ostili) in cui le reti di sensori possono essere utilizzate è necessario porsi il problema
1.3 Crittografia nelle reti wireless di sensori
della sicurezza della rete sia in termini di segretezza (i dati che vengono scambiati tra i nodi potrebbero essere sensibili e devono essere protetti) sia in termini di autenticazione (potrebbe essere necessario dover identificare quali nodi appartengono ad un certo insieme e quali no). La crittografia a chiave simmetrica da sola non può essere considerata una soluzione ottimale in quanto porta con se il problema della distribuzione delle chiavi. In una rete con N nodi in cui ogni nodo può comunicare con i restanti N−1 nodi sarebbe necessario stabilire e memorizzare circa N2 chiavi (una chiave segreta per ogni coppia di nodi della rete). Inoltre i nodi stessi possono essere mobili e spostarsi, nuovi nodi possono unirsi ad un gruppo di nodi oppure nodi esistenti possono sparire dal gruppo; questa dinamicità mal si adatta alle caratteristiche della cifratura simmetrica che in generale richiede una pre-distribuzione delle chiavi. La crittografia a chiave pubblica può essere pensata come una possibile soluzione a queste limitazioni: ogni nodo possiede una coppia di chiavi, una segreta e l’ altra pubblica, ed è possibile creare un canale sicuro tra due sensori senza la necessità di pre-distribuire segreti condivisi.
In una rete con N nodi, essa necessita soltanto di 2N chiavi (2 chiavi per ogni nodo), con una crescita lineare delle chiavi all’ aumentare del numero di utenti. Nonostante
la convinzione diffusa che essa sia troppo costosa dal punto di vista dell’ elaborazione e del consumo di energia per dispositivi quali i nodi sensore, lo
sviluppo di schemi a curva ellittica e l’ utilizzo di alcune ottimizzazioni, eventualmente di basso livello, hanno dimostrato una quasi accettabile realizzabilità pratica di queste soluzioni.
1.4 Crittosistemi a curva ellittica
1.4 Crittosistemi a curva ellittica
Una curva ellittica è una funzione matematica della forma generica y = f(x) che può essere rappresentata come una curva su un piano cartesiano ortogonale. Formalmente è definita come l’ insieme dei punti (x, y) che soddisfano la seguente equazione:
y2 + a1xy + a3y = x 3
+ a2x 2
+ a4x + a6 (1.1)
dove a1, a2, a3, a4, a6 sono dei coefficienti. Nell’ ambito della crittografia sia i
punti (x, y) sia i coefficienti appartengono ad un campo finito. Un campo finito (spesso indicato con F) è un sistema algebrico formato da un insieme finito di elementi su cui sono definite due operazioni, addizione e moltiplicazione, e che soddisfa i seguenti assiomi:
• F è un gruppo abeliano (si veda sotto) rispetto all’ addizione;
• F (tranne lo 0) è un gruppo abeliano rispetto alla moltiplicazione;
• F gode della proprietà distributiva, cioè ∀ a, b, c ∈ F
a × (b + c) = (a × b) + (a × c) (a + b) × c = (a × c) + (b × c)
Un gruppo abeliano (spesso indicato con G) è un insieme di elementi su cui è definita un’ operazione binaria (indicata con •) tale che valgano le seguenti proprietà:
1.4 Crittosistemi a curva ellittica
• Chiusura:
∀a, b ∈ G a • b ∈ G
• Associatività:
∀a, b, c ∈ G (a • b) • c = a • (b • c)
• Esistenza dell’ elemento identità:
∀a ∈ G ∃e ∈ G tale che a • e = e • a
• Esistenza dell’ elemento inverso:
∀a ∈ G ∃a’ ∈ G tale che a • a’ = a’ • a = e dove e è l’ elemento identità, come definito sopra
• Commutatività:
∀a, b ∈ G a • b = b • a
Il numero degli elementi di un tale insieme è detto ordine del campo. Esiste un campo finito di ordine q (quindi con q elementi) se e solo se q è la potenza di un numero primo, cioè q = pm dove m è un intero positivo (che può valere anche 1) e p un
1.5 Interpretazione geometrica delle curve ellittiche
numero primo. Un campo finito di questo tipo si indica come GF(pm)3 e p è detta la caratteristica del campo finito.
1.5 Interpretazione geometrica delle curve ellittiche
Se si considerano le curve ellittiche definite sui numeri reali si può trovare un’ interpretazione geometrica alle operazioni di addizione e moltiplicazione.
Considerando il caso semplice dell’ equazione 1.1 in cui a1= a2= a3= 0 i punti che
soddisfano l’ equazione sono della forma:
y = 4 6 3 a x a x + +
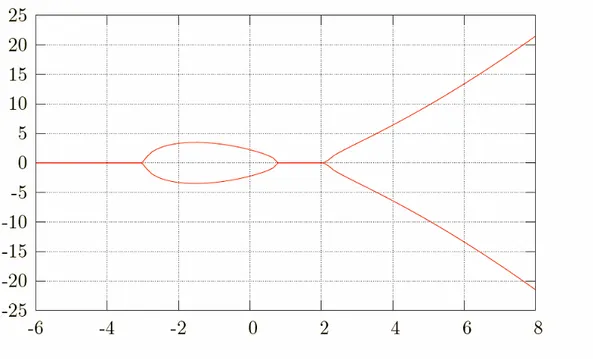
Le curve di questo tipo sono pertanto funzioni simmetriche rispetto all’ asse x. Un esempio di curva ellittica tracciata sul piano cartesiano è illustrata in figura 1.1; è stata ottenuta con i valori a4 = −7, a6 = 5.
GF sta per Gailois Field, dal nome del matematico francese che per primo studiò tali insiemi.
1.5 Interpretazione geometrica delle curve ellittiche
Figura 1.1: Curva ellittica y = x3 − 7x + 5, definita sui numeri reali
Per ogni curva è definito anche un punto infinito (indicato con O) che rappresenta l’ elemento neutro rispetto alla somma, come verrà illustrato sotto.
Dati due punti (P, Q) appartenenti alla curva, tali che P O e Q O la loro somma è un altro punto R, anch’ esso appartenente alla curva. L’ addizione è definita in accordo alle seguenti regole:
1. è l’ elemento neutro della somma, tale che O=-O e P+O=P;
2. il negativo di un punto P=(x,y) si ottiene negando l’ ordinata, cioè -P=(x,-y) (figura 1.2);
1.5 Interpretazione geometrica delle curve ellittiche
3. se P e Q hanno una coordinata x differente, la retta passante per P e Q interseca la curva in un altro punto, R. Il punto simmetrico di R rispetto all’ asse x è il punto T, somma di P e Q. Nel caso in cui la retta sia tangente alla curva in uno dei due punti, T coinciderà con P o Q.(figura 1.3);
4. se P=-Q allora per definizione P+Q=O (nella costruzione geometrica la retta passante per i due punti non interseca altri punti della curva, ma va all’ infinito parallelamente all’ asse y);
5. se P=Q si traccia la tangente alla curva nel punto P, si trova l’ intersezione della tangente con un altro punto della curva, T; anche in questo caso il punto simmetrico di T rispetto all’ asse x è il punto R somma di P e Q (figura 1.4).
1.5 Interpretazione geometrica delle curve ellittiche
Figura 1.3: Somma tra due punti della curva ellittica, T = P + Q
1.6 Curve ellittiche utilizzate in crittografia
1.6 Curve ellittiche utilizzate in crittografia
In ambito crittografico, per evitare i problemi derivanti dalla rappresentazione dei numeri reali, i coefficienti e le variabili della curva assumono valori interi compresi tra 0 e pm-1, dove p è un numero primo e m un intero positivo.
In questo modo la curva ellittica risulta costituita da un insieme finito di punti (sebbene molto grande poiché p viene scelto molto grande); il numero di punti che formano una curva ellittica è detto ordine o cardinalità della curva stessa. In una curva ellittica viene definito anche un punto base, indicato spesso con G, che abbia un ordine molto grande; tale punto è un parametro pubblico ed è quello che viene usato come punto iniziale di tutte le operazioni sulla curva. L’ ordine di un punto P è
invece il minimo valore dell’ intero k tale per cui kG = O dove O è il punto all’ infinito. Intuitivamente si può affermare che il punto base è il punto di partenza
su cui inizialmente si posizionano tutte le entità che utilizzano quella curva; sommando il punto base a se stesso si ottiene una sequenza di punti tutti appartenenti alla curva (come evidenziato dall’ interpretazione geometrica). Il percorso effettuato è uguale per tutti ed essendo l’ ordine del punto molto elevato si può sommare molte volte il punto base prima di arrivare al punto all’ infinito4, che è l’ elemento neutro dell’ addizione (ulteriori somme produrrebbero sempre il punto all’ infinito, cioè non ci si sposterebbe più da O). Come sarà evidenziato successivamente, la sola conoscenza del punto di partenza e di un altro punto del percorso (ovvero un multiplo del punto base) non consente facilmente di calcolare quanti passi sono necessari per andare dall’ uno all’ altro (in altre parole, noti i punti G e Q tali che Q = kG, è computazionalmente impossibile5 determinare l’ intero k). Questa è l’ origine della
sicurezza dei crittosistemi a curva ellittica; esiste un certo parallelismo con l’ aritmetica tradizionale del logaritmo discreto: usando una notazione simile il
1.7 Curve ellittiche sui campi finiti GF(p)
problema precedente di trovare k è analogo al problema di trovare k in questa espressione q = gk mod p, noti tutti gli altri termini (la moltiplicazione sulla curva è l’ analogo dell’ elevamento a potenza nell’ aritmetica modulare).
Questa analogia ha consentito di sviluppare algoritmi a curva ellittica che sono la ”traduzione” dei tradizionali algoritmi crittografici (es. algoritmo Diffie-Hellman). Sono stati definiti diversi campi finiti su cui considerare le curve ellittiche, ma due in particolare sono stati considerati in ambito crittografico: il campo GF(p) e il campo GF(2m), che vengono brevemente accennati nei paragrafi successivi.
1.7 Curve ellittiche sui campi finiti GF(p)
Il campo finito GF(p), indicato anche come Zp, è formato da tutti gli interi compresi tra 0 e p−1 (con p numero primo). Le operazioni aritmetiche realizzate su questo insieme sono tutte definite modulo p (indicato con mod p), ovvero considerando il resto dell’ operazione di divisione per il numero primo p. In questo caso l’ equazione di definizione della curva diventa:
y2 ≡ (x3 + a4x + a6) mod p
in ogni caso quando si calcola kG viene calcolato in realtà k0G, dove k0 = k mod n,
con n ordine del punto base. allo stato attuale delle conoscenze.
4 5
1.7 Curve ellittiche sui campi finiti GF(p)
dove deve valere la condizione (4a3 4+27a
2
6) ≠ 0 mod p. Le operazioni definite su
questo insieme sono l’ addizione tra due interi o tra due punti della curva e la moltiplicazione tra due interi o tra un intero e un punto della curva. Non ha senso moltiplicare tra di loro due punti della curva ellittica. Tra coppie di interi queste due operazioni sono le consuete operazioni di addizione e moltiplicazione realizzate modulo p (a+b mod p e ab mod p). L’ addizione tra due punti della curva si realizza secondo le seguenti formule, che costituiscono l’ equivalente algebrico delle costruzioni geometriche precedenti nell’ insieme dei numeri interi: dati due punti
distinti P = (xp, yp) e Q = (xq, yq), tali che P ≠ Q la loro somma è il punto R = (xr, yr) tale che
Si noti che altro non è che il coefficiente angolare della retta passante per i punti P e Q nella figura 1.3. Come illustrato più estesamente nel seguito, la moltiplicazione di un punto per un intero viene scomposta in una serie di addizioni e raddoppi. Di conseguenza, oltre alle formule per l’ addizione sopra illustrate, è sufficiente conoscere le formule per calcolare R=2P:
1.8 Curve ellittiche sui campi finiti GF(2m)
1.8 Curve ellittiche sui campi finiti GF(2m)
Un altro possibile insieme di definizione per le curve ellittiche è il campo finito GF(2m
), dove m è un intero positivo maggiore o uguale a 1. L’ equazione della curva generica 1.1 su questo campo si semplifica nel seguente modo:
dove x, y, a e b sono interi appartenenti all’ insieme [0,2m −1] con b 0. Gli elementi di questo insieme vengono di solito rappresentati come polinomi di grado m-1 o minore i cui coefficienti binari sono la rappresentazione binaria dell’ elemento del campo. In altre parole, se a ∈ [0, 2m
− 1] allora a viene rappresentato nella forma
dove gli ai ∈ [0, 1] sono le cifre binarie dell’ intero a. L’ addizione tra interi del campo è quindi definita nel modo seguente: se a = am−1x
1 − m + am−2x 2 − m +. . . + a1x + a0 e b = bm−1x 1 − m + bm−2x 2 − m
+ . . . + b1x + b0 allora r=a+b è il polinomio r =
rm−1xm−1+rm−2xm−2+. . .+r1x+r0 tale che ri = ai XOR bi; s=ab è il polinomio s = sm−1x 1 − m +sm−2x 2 − m
+. . .+s1x+s0 tale che s è il resto della divisione di ab per f(x),
dove f(x) è un polinomio irriducibile che costituisce uno dei parametri pubblici e fissati della curva ellittica6.
Dati due punti distinti P = (xp, yp) e Q = (xq, yq), tali che P Q la loro somma è il punto R = (xr, yr) tale che
1.8 Curve ellittiche sui campi finiti GF(2m)
Le formule per calcolare il punto R = 2P sono le seguenti:
lo standard SEC2 riporta per ogni curva ellittica standard definita su GF(2m) il polinomio irriducibile da utilizzare [8].
1.8 Curve ellittiche sui campi finiti GF(2m)
Quindi la somma tra punti richiede 2 moltiplicazioni, una divisione e 9 operazioni di somma; il raddoppio richiede 2 moltiplicazioni, 1 divisione e 6 operazioni di somma (la somma e la sottrazione sono equivalenti in questo campo finito). Questo campo e le operazioni associate sono utilizzate dalla libreria EccM 2.0, che sarà illustrata in 4.1.
Capitolo 2
Crittografia a curva ellittica
2.1 Introduzione
I crittosistemi a curva ellittica sono stati proposti per la prima volta verso la metà degli anni ’80 indipendentemente da Victor Miller [7] e Neal Koblitz [4] come un’ alternativa agli schemi a chiave pubblica esistenti, quali RSA.
Sebbene l’ uso della crittografia a curva ellittica sia relativamente nuovo, si è sviluppata un’ ampia ricerca in questo campo in quanto, alla luce delle conoscenze attuali, offre complessivamente un sistema più sicuro dei crittosistemi precedenti poiché, come sarà illustrato sotto, basa la sue operazioni sul problema del logaritmo discreto che è considerato più difficile da risolvere dell’ analogo problema definito sull’ aritmetica intera.
2.2 RSA nelle reti di sensori
L’ algoritmo a chiave pubblica RSA [10] non è una soluzione ritenuta conveniente nell’ ambito delle reti di sensori a causa principalmente del costo computazionale
2.2 RSA nelle reti di sensori
necessario per eseguire l’ operazione di esponenziazione. Le operazioni di cifratura e decifratura in RSA prevedono entrambe una esponenziazione:
cifratura : c = me mod n decifratura : m = cd mod n
dove m è il testo in chiaro (m < n), n è il modulo, c il testo cifrato, e la chiave pubblica e d la chiave privata. Il costo per eseguire tali operazioni dipende dal numero di bit a ’1’ dell’ esponente. Spesso l’ esponente e viene scelto uguale ad un numero di Fermat (3 o 216+1) in quanto in questi numeri ci sono pochi bit a ’1’, facilitando l’ operazione di cifratura. Tuttavia la grandezza dell’ esponente d fa si che l’ operazione di decifratura non possa essere realizzata sui nodi sensore in tempi accettabili, come dimostrano i risultati ottenuti da alcune implementazioni di RSA. In [6] si evidenzia che su un nodo sensore MICA2 il tempo richiesto per l’ operazione di esponenziazione con esponente su 768 bit e modulo su 1024 bit è di circa 5 minuti. La libreria TinyPK [12], anch’ essa per piattaforma MICA2, nonostante riesca ad effettuare l’ elevamento a potenza per l’ esponente e in 14.5 secondi, richiede più di 3 minuti per eseguire il protocollo di scambio delle chiavi Diffie-Hellmann.
Inoltre gli autori indicano che l’ operazione di decifratura (che coinvolge l’ esponente d) richiede un tempo dell’ ordine della decina di minuti, rendendola non plausibile dal punto di vista pratico.
2.3 Problema del logaritmo discreto
2.3 Problema del logaritmo discreto
Mentre la sicurezza di RSA dipende dalla intrattabilità del problema della fattorizzazione di un numero nel prodotto dei suoi fattori primi (fattorizzazione), i crittosistemi a curva ellittica si basano sul problema del logaritmo discreto (ECDLP, Elliptic Curve Discrete Logarithm Problem). Il problema del logaritmo discreto tradizionale può essere definito come segue: dato il numero primo p e gli interi y e x tali che x sia un generatore di p1 e che y = xa (mod p) trovare l’ intero a. Tale problema viene considerato di difficile soluzione se il numero primo p è grande; l’ algoritmo noto più veloce per risolverlo è il metodo Pollard rho che necessita di circa O( p ) passi. Nell’ ambito della curva ellittica il problema assume la seguente forma: data una curva ellittica E definita su un campo finito GF(q), il punto base della curva G e un punto tale che P = kG, trovare l’ intero k, ammesso che esista. La ricerca esaustiva di tale valore consisterebbe nel sommare G a se stesso in modo cumulativo per calcolare 2G, 3G = 2G+G, 4G = 3G+G e così via, confrontando il punto ottenuto ad ogni passo con P; l’ uguaglianza tra i due punti rivelerebbe il valore di k. Nella pratica k assume valori talmente grandi (ad esempio espressi su 160 bit) che questo attacco risulta computazionalmente impossibile. Non sono noti al momento algoritmi per risolvere l’ ECDLP sulle curve ellittiche in tempo subesponenziale. Il problema ECDLP è inoltre più complesso del problema della fattorizzazione. Di conseguenza in questi sistemi si possono usare parametri di dimensione minore (chiavi…) ed ottenere una sicurezza equivalente a quella offerta da altri crittosistemi.
Un generatore di p è un numero che elevato alla potenza i (modulo p) genera tutti i numeri compresi tra 0 e p-1 (al variare di i). Si può dimostrare che esiste sicuramente un generatore di p se p è primo.
2.4 ECC vs RSA
E’ stato stimato che una curva ellittica definita su un campo finito di 160 bit offre una sicurezza equivalente a RSA con il modulo espresso su 1024 bit [2].
2.4 ECC vs RSA
Ricapitolando i vantaggi offerti dalla crittografia a curva ellittica sulla crittografia basata su RSA nell’ ambito delle reti di sensori sono i seguenti:
• maggiore sicurezza: il problema del logaritmo discreto sulle curve ellittiche (ECC) è al momento considerato più difficile da risolvere del problema della fattorizzazione (RSA);
• dimensione minore delle chiavi: a parità di sicurezza offerta la coppia di chiavi pubblica-privata in ECC occupa meno memoria della coppia RSA. Inoltre, come indicato nella tabella 2.1 che riporta le lunghezze di chiave raccomandate per il futuro dal NIST, le chiavi RSA sono destinate a crescere fino a 15 volte, mentre le chiavi ECC dovrebbero crescere nello stesso intervallo temporale di 3.2 volte. Questa ridotta dimensione ben si adatta ai limiti di memoria dei nodi sensore;
• maggiore velocità di esecuzione: le operazioni matematiche in ECC sono normalmente più veloci dell’ esponenziazione RSA e in generale richiedono meno risorse computazionali, un aspetto che le rende particolarmente adatte ai sistemi embedded;
2.5 Inizializzazione
• risparmio complessivo di memoria, energia e banda.
Tabella 2.1: Lunghezze di chiave raccomandate dal NIST per il futuro (ECCe RSA)
Esistono diversi protocolli crittografici che utilizzano le operazioni basate sulle curve ellittiche. Nella maggior parte dei casi essi sono l’ equivalente dei protocolli tradizionali tenendo conto che il problema del logaritmo discreto viene sostituito con l’ ECDLP e l’ esponenziazione di un numero viene sostituita con la moltiplicazione. Qui verranno presi in considerazione soltanto i protocolli che sono stati effettivamente implementati o di cui è stato fatto il porting nella libreria EccM 2.0 [6], sviluppata appositamente per nodi sensore.
2.5 Inizializzazione
Prima che qualsiasi protocollo venga eseguito dai nodi della rete, è necessario che vengano inizializzati i valori che definiscono la curva ellittica che si intende
2.5 Inizializzazione
utilizzare. Se la curva è definita su un campo finito Fp allora è caratterizzata da sei valori:
parametri
p
F = {p, a4, a6, G, n, h}
ovvero:
• il numero primo p che definisce il campo finito;
• i coefficienti a4 e a6 che definiscono l’ equazione della curva 1.7;
• il punto base G = (xG, yG);
• l’ ordine n del punto G;
• il cofattore h, ovvero il rapporto tra il numero dei punti della curva e n.
Lo standard SEC2 [8] definisce i parametri precedenti per alcune curve con lo scopo di promuovere l’ interoperabilità e facilitare implementazioni efficienti.
In particolare a seconda del livello di sicurezza desiderato si possono scegliere curve con la dimensione desiderata di p (i valori ammessi sono 112, 128, 160, 192, 224, 256, 384, 521 bit). Si ritiene che una curva ellittica con p espresso su k bit fornisca una sicurezza equivalente di bit, ovvero sono necessarie operazioni per risolvere il problema del logaritmo discreto. Per quanto riguarda le curve ellittiche
k
2 2
2.6 Generazione della coppia di chiavi
definite sul campo finito GF(2m) i parametri di dominio che le definiscono sono sette:
parametriF2m = {m, f(x), a4, a6, G, n, h}
ovvero sono presenti al posto del numero primo p:
• m, l’ intero positivo che definisce il campo finito;
• f(x) che rappresenta il polinomio irriducibile necessario nelle operazioni tra interi del campo.
Lo standard SEC2 definisce i parametri da utilizzare a seconda del livello di sicurezza desiderato.
2.6 Generazione della coppia di chiavi
Come tutti i crittosistemi a chiave pubblica ogni nodo deve innanzitutto generare la chiave privata e la chiave pubblica che utilizzerà nei protocolli crittografici. Nell’ ambito della crittografia a curva ellittica ciò si realizza in due passi:
1. generazione di un intero casuale su t bit, dove t è il numero di bit su cui vengono rappresentati i numeri interi del campo finito. Questo intero, indicato con k, è la chiave privata;
2.7 Protocollo di distribuzione delle chiavi Diffie-Hellman
2. moltiplicazione della chiave privata per il punto base della curva ellittica (G) per ottenere un punto Q che rappresenta la chiave pubblica (Q = kG).
La chiave privata k è l’ unica quantità che deve essere mantenuta segreta, mentre Q, G e in generale tutti i parametri della curva ellittica definiti precedentemente sono quantità pubbliche. In virtù della difficoltà del problema del logaritmo discreto, un avversario che conosce Q e G non può risalire a k, assicurando quindi una delle proprietà fondamentali della coppia di chiavi (data la chiave pubblica è computazionalmente difficile risalire alla chiave privata). Si noti che k è un intero (compreso tra 0 e p − 1) mentre Q è una coppia di interi (coordinate cartesiane), anch’ essi compresi tra 0 e p − 1.
Scegliendo p espresso su 160 bit la coppia di chiavi occupa in totale 480 bit (=160 * 3); per confronto RSA ha una dimensione raccomandata del modulo di 1024 bit.
2.7 Protocollo di distribuzione delle chiavi Diffie-Hellman
Il protocollo di distribuzione delle chiavi di Diffie-Hellman, ideato nel 1976, è stato il primo protocollo a chiave pubblica inventato per l’ individuazione di un segreto condiviso tra due nodi comunicanti a partire da quantità pubbliche (le due entità non hanno segreti condivisi a priori [3]). Esso consente ai due nodi di accordarsi su una quantità segreta nota solo a loro, ammesso che ciascuno dei due abbia la certezza che la chiave pubblica dell’ altro sia valida e corrisponda effettivamente all’ identità dichiarata2.
Se questo non accadesse il protocollo sarebbe esposto ad attacchi man-in-the-middle, in cui un avversario potrebbe riuscire a stabilire un segreto condiviso con entrambi i nodi.
2.7 Protocollo di distribuzione delle chiavi Diffie-Hellman
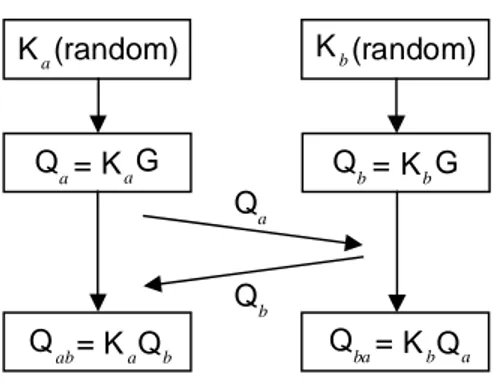
Generalmente il segreto condiviso prodotto da questo protocollo viene utilizzato come chiave segreta dai cifrari simmetrici per la cifratura/decifratura dei messaggi. Indicando con A e B i due nodi partecipanti, il protocollo può essere definito in accordo ai seguenti passi:
1. A e B si accordano sulla curva ellittica che utilizzeranno e su tutti i parametri pubblici che la definiscono;
2. A genera la propria chiave privata (un intero ka ∈ [0, p − 1] scelto in modo random);
3. B genera la propria chiave privata (un intero kb ∈ [0, p − 1] scelto in modo random);
4. A genera la propria chiave pubblica Qa = kaG con G punto base della curva e la invia a B;
5. B genera la propria chiave pubblica Qb = kbG con G punto base della curva e la invia ad A;
6. A calcola il segreto condiviso come Qab = kaQb = kakbG;
2.7.1 Esempio numerico
Come descritto nel capitolo precedente, le curve ellittiche sono un gruppo abeliano rispetto alla moltiplicazione quindi per esse vale anche la proprietà associativa della moltiplicazione; questo assicura che le moltiplicazioni che producono Qab e Qba siano equivalenti (nonostante cambi l’ ordine dei fattori il prodotto non cambia). Un avversario che non conosce né ka né kb non può calcolare il segreto condiviso per la difficoltà del problema del logaritmo discreto; viceversa, la conoscenza di anche una sola delle due chiavi private coinvolte consentirebbe all’ avversario di violare il segreto con una semplice moltiplicazione. Si noti che il segreto condiviso è un punto della curva Qab = Qba = (xQ, yQ); generalmente è necessario ottenere un valore unico come chiave segreta per cui normalmente si utilizza la sola componente xQ del punto trovato o la sua hash. Le chiavi pubbliche delle due entità che partecipano al protocollo devono essere certificate per evitare l’ attacco detto man-in-the-middle. Un avversario che riesce a spacciare la propria chiave pubblica per la chiave pubblica di uno dei due nodi può arrivare a generare un segreto condiviso con uno dei due (ad esempio, il nodo A calcola kaQc e l’ avversario calcola kcQa, dove (kc, Qa) è la coppia di chiavi dell’ avversario).
Sarebbe desiderabile infine che ogni nodo riceva qualche assicurazione che i parametri della curva ellittica utilizzati siano validi per evitare che un avversario possa indurre un nodo ad utilizzare parametri non sicuri.
2.7.1 Esempio numerico
I valori numerici sono volutamente interi piccoli per rendere rendere più chiara la trattazione. Si consideri la curva ellittica definita da y2=x3−2x+5 e si scelga come
2.7.1 Esempio numerico
punto base della curva il punto G = (2, 3). Sia p = 41 l’ ordine della curva. Il protocollo si evolve nel modo seguente:
• A sceglie ka = 3 in modo random;
• B sceglie kb = 5 in modo random;
• A calcola Qa = kaG = 3G = 2G + G = (27, 35);
• B calcola Qb = kbG = 5G = 2G + 2G + G = (33, 1);
• A calcola Qab = ka Qb = 3 Qb = (23, 21);
• A calcola Qba = kb Qa = 5 Qa = (23, 21).
Questi valori sono stati ottenuti applicando le formule introdotte in 1.7 ricordando di eseguire le varie operazioni algebriche modulo l’ ordine della curva (41 in questo caso). Per somma, sottrazione e moltiplicazione ciò significa eseguire la normale operazione aritmetica e poi calcolare il resto della divisione tra il valore ottenuto e l’ ordine della curva3. La divisione modulare, necessaria per calcolare il valore sia per la somma che per il raddoppio ha il seguente significato:
2.8 Protocolli di firma digitale
dove b−1 mod p è quel valore di b per cui è soddisfatta questa equivalenza
ab = 1 mod p.
2.8 Protocolli di firma digitale
Per la curva ellittica sono stati definiti anche dei protocolli di firma digitale ed in particolare sono stati qui implementati i protocolli ECDSA (Elliptic Curve Digital Signature Algorithm) e il protocollo di Nyberg-Rueppel. Lo scopo di questi protocolli è quello di assicurare (in modo verificabile) che un messaggio è stato firmato con una certa chiave privata. Così come avviene nella crittografia a chiave pubblica tradizionale, anche nella crittografia a curva ellittica la firma digitale deve soddisfare certe proprietà generali:
• la firma digitale è una quantità che dipende dalla chiave privata del firmatario e dal contenuto del messaggio;
• in caso di disputa (ad esempio, il firmatario che cerca di ripudiare la firma che ha generato un avversario che cerca di falsificare la firma originale) la firma digitale deve essere verificabile da una terza entità esterna senza accedere alla chiave privata del firmatario ma solo con le quantità disponibili;
questo assicura che tutti i valori ottenuti siano ancora interi compresi tra 0 e p-1, dove p è l’ ordine.
2.9 ECDSA
• la firma digitale deve essere computazionalmente impossibile da falsificare eventualmente anche contro attacchi di tipo chosen-message: un avversario che dispone di coppie messaggio-firma digitale non deve essere in grado di falsificare la firma dell’ entità su qualsiasi altro messaggio.
2.9 ECDSA
L’ algoritmo di firma digitale ECDSA è l’ analogo sulla curva ellittica dell’ algoritmo di firma DSA. Venne proposto nel 1992 da Vanstone [11] e basa la propria validità sulla difficoltà del problema del logaritmo discreto. Si supponga che una certa entità, Alice, voglia inviare un messaggio m firmato ad un’ altra entità, Bob. Innanzitutto Alice e Bob si accordano sulla curva ellittica che utilizzeranno nel protocollo scegliendo tutti i parametri che la definiscono come indicato in 2.5; tali parametri possono anche essere stati convenuti precedentemente4. Alice firma il messaggio m in accordo ai seguenti passi:
1. genera la propria coppia di chiavi privata-pubblica (dA,QA), come indicato in 2.6;
2. genera un valore random, k, tale che 1 k n − 1, dove n è l’ ordine del punto base G;
3. calcola R = kG e r = x1 mod n dove x1 è l’ ascissa del punto R. Se r = 0 torna al passo 2;
2.9 ECDSA
4. calcola l’ inverso modulare k−1 mod n, cioè l’ intero a tale che ak = 1 mod n;
5. calcola la hash SHA-1 di m, e = SHA1(m);
6. calcola s = k−1 (e + dr) mod n. Se s = 0 torna al passo 2;
7. la firma di Alice sul messaggio è la coppia (r,s).
Bob riceve il messaggio m, la firma (r,s) e la chiave pubblica di Alice QA.
ad esempio se le due entità sono nodi sensore i parametri vengono generalmente stabiliti e fissati uguali per tutti i nodi direttamente nel codice.
2.9 ECDSA
Per verificare la firma sul messaggio Bob esegue i seguenti passi:
1. verifica che r e s appartengano all’ intervallo [1, n − 1];
2. calcola la hash SHA-1 del messaggio, e = SHA1(m);
3. calcola w = s−1mod n;
4. calcola u1 = ew mod n e u2 = rw mod n;
5. calcola il punto X = u1G + u2 QA. Se X = O rifiuta la firma (O è il punto all’ infinito);
6. calcola v = x1 mod n dove x1 è l’ ascissa del punto X;
7. accetta la firma come valida se v = r.
Si nota che se la firma è stata effettivamente generata da Alice, che è l’ unica che conosce il valore random k e la propria chiave segreta d, allora s = k−1 (e + dr) mod n quindi :
k = s−1 (e + dr) = (s−1e) + (s−1dr) = we + wdr = u1 + u2d
Di conseguenza quando si calcola u1G + u2Q poichè Q = dG si ottiene (u1 + u2d) G cioè kG = R e quindi l’ uguaglianza con il punto calcolato da Alice. Come si nota la firma digitale dipende da quantità note solo ad Alice (k e d) e dal messaggio m; per la
2.10 Nyberg-Rueppel
verifica della firma sono necessari la chiave pubblica del firmatario (QA) e i parametri della curva ellittica.
2.10 Nyberg-Rueppel
L’ altro schema di firma digitale che è stato implementato solo nella libreria EccM 2.0 è lo schema Nyberg-Rueppel. Per firmare il messaggio Alice esegue i seguenti passi:
1. genera la propria coppia di chiavi privata-pubblica (dA, QA), come indicato in 2.6;
2. genera un valore random, k, tale che 1 k n − 1, dove n è l’ ordine del punto base G;
3. calcola R = kG e r = x1 mod n dove x1 è l’ ascissa del punto R. Se r = 0 torna al passo 2;
4. calcola c = x1 + e mod n dove e è la hash SHA-1 del messaggio m, e = SHA1(m);
5. calcola d = k − dAc mod n;
2.10 Nyberg-Rueppel
Bob riceve il messaggio m, la firma (c, d) e la chiave pubblica di Alice QA. Per verificare la firma sul messaggio Bob esegue i seguenti passi:
1. verifica che c e d appartengano all’ intervallo [1, n − 1];
2. calcola la hash SHA-1 del messaggio, e = SHA1(m);
3. calcola R’ = dG + cQA;
4. calcola e’ = c − x’modn dove x’ è l’ ascissa di R’;
5. verifica se e = e’ e accetta la firma in caso positivo.
Nel processo di firma il passo 4 nasconde la hash del messaggio sommandovi una quantità casuale; nel passo 5, la firma è legata al sottoscrittore dall’ uso della chiave privata dA che è necessaria per ottenere la componente d. Nel processo di verifica la
moltiplicazione dG, tenendo conto del passo 5 della firma, è equivalente a kG − dAcG = R − cQA. Sommando cQA a questa quantità si riottiene R, ovvero il
punto generato originariamente da Alice; il fatto che venga utilizzata la chiave privata dA (insieme con qualche assicurazione che QA sia la chiave pubblica effettiva di Alice) assicura che la firma sia stata realizzata con la chiave privata di Alice altrimenti non si potrebbe riottenere il punto originario R.
Capitolo 3
Contiki
3.1 Introduzione
Contiki [13] è un piccolo sistema operativo open source distribuito sotto licenza BSD. E’ altamente portabile e appositamente concepito per essere utilizzato in
dispositivi con risorse computazionali limitate, come i nodi sensore. Infatti l’ hardware utilizzato nello sviluppo di questa tesi di laurea, il nodo sensore Tmote
Sky della Moteiv [1], mette a disposizione 10 kilobytes di RAM e 48 kilobytes di ROM.
Questo sistema operativo è stato scritto da Adam Dunkels del gruppo di Networked Embedded Systems allo Swedish Institute of Computer Science. Il suo nome deriva da Kon-Tiki, un’ imbarcazione di tipo preistorico, con cui Thor Heyerdahl fece una spedizione per dimostrare che i polinesiani erano in grado di ritornare dal Sud America verso il loro arcipelago.
E’ scritto in linguaggio C, il che spiega la sua portabilità a livello di codice sorgente. Contiki dispone di un kernel di tipo event-driven: eventuali elaborazioni e trasmissioni sono eseguite solo quando si verificano certi eventi. Il kernel deve essere
3.1 Introduzione
il più leggero possibile, perciò anche se è supportato il preemptive multi-threading, questi è implementato tramite una libreria che viene caricata solo se una applicazione la richiede.
E’ possibile caricare applicazioni sia in modo statico che in modo dinamico (a runtime), e dinamicamente è possibile anche scaricarle.
Contiki, oltre ai già citati eventi, permette anche l’ utilizzo dei processi. In particolare fra i processi spiccano i protothreads: particolari thread estremamente leggeri, privi di stack, che garantiscono un alto livello di funzionalità. “Purtroppo i processi, per la mancanza della MMU nei sistemi target, girano su un unico spazio di indirizzamento e senza protezione”.
Il punto di forza di Contiki è soprattutto il networking, con la presenza di uno stack TCP/IP, studiato appositamente per sistemi ad 8 e 16 bit, open source e conforme a RFC, chiamato uIP. Questo permette a livello pratico di usare un Web Server, un browser testuale che è il più piccolo finora creato: è richiesta solo una memoria di 4 KB per farlo girare.
E' disponibile anche un client telnet. Ed è a disposizione anche una versione di VNC, il noto programma di remote desktop, grazie al quale è possibile accedere da quasi ogni altro sistema operativo.
Contiki dispone inoltre di un altro stack, Rime, concepito per sistemi a bassa potenza, che fornisce un elevato numero di primitive di comunicazione: dal best-effort local area broadcast, fino al multi-hop bulk data flooding.
E’ prevista anche un’ interfaccia grafica. Questa è gestita dal Contiki Tool-Kit ed è composta di 3 moduli: quello di base testuale, il ctk-conio per i sistemi più poveri di ram, seguito da ctk-eyecandy, fino ad arrivare al più sofisticato ctk-blueround.
Contiki gira su una vasta gamma di microcontrollori embedded, fra i quali ovviamente quello utilizzato in questa sede, il microcontrollore MSP430.
3.2 Runes middleware e Contiki
3.2 Runes middleware e Contiki
RUNES, Reconfigurable Ubiquitous Networked Embedded Systems, è un progetto europeo fortemente incentrato sullo sviluppo di una piattaforma hardware e software in supporto a sistemi embedded in generale e reti di sensori in particolare.
Per poter programmare su sistemi di questo tipo è importante conoscerne le caratteristiche e gli elementi di cui si compongono.
RUNES middleware è caratterizzato da:
• Components; • Interfaces; • Receptacles; • Using components; • Dynamic rebinding; • Registry;
• Compiling and installing; • Known limitations.
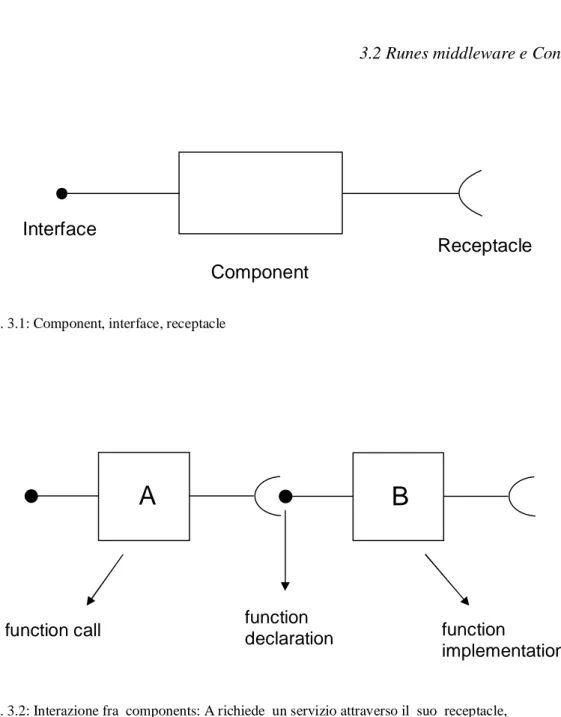
Component: è un’ entità che implementa alcune funzionalità specifiche.
Implementa delle funzioni che possono essere usate all’ interno del component stesso Funzioni (o servizi) usate da altri component. Queste sono fornite ad altri tramite un’ interface. Per usare servizi offerti da altri components tramite le loro interfaces necessita di almeno un receptacle.
3.2 Runes middleware e Contiki
Interface: è una lista di funzioni implementate da un component e messe a disposizione di altri components. L’ interface contiene sola la dichiarazione delle funzioni.
Receptacle: è un link fra un componente e l’ interfaccia del componente che offre delle funzionalità.
Alcuni limiti noti:
• un componente, prima di essere caricato, è automaticamente instanziato;
• un componente può essere instanziato una e una sola volta;
• componenti caricati dinamicamente vengono posti nella RAM, solitamente molto piccola;
• non è possibile scaricare componenti che si trovano nella ROM;
• non è ancora possibile usare la memoria flash esterna da 1MB per caricare e scaricare componenti.
3.2 Runes middleware e Contiki
Fig. 3.1: Component, interface, receptacle
Fig. 3.2: Interazione fra components: A richiede un servizio attraverso il suo receptacle, B offre quel servizio attraverso la sua interface.
A
B
function declaration
function call function
implementation Interface
Component
Capitolo 4
EccM 2.0
4.1 Introduzione
L’ obiettivo iniziale che ci siamo proposti è stato quello di installare ed eseguire, sui nodi sensori Tmote Sky della Moteiv [1] dotati di Contiki [13] come sistema operativo, la libreria EccM 2.0 [6], apportando le modifiche necessarie al codice. Di questa era già stato fatto il porting sui sensori Tmote Sky dotati però di TinyOs come sistema operativo.
La libreria ci fornisce un’ implementazione delle operazioni di base per l’ aritmetica della curva ellittica per reti di sensori (essenzialmente addizione tra punti e moltiplicazione tra un punto e un intero) insieme ad un’ implementazione del protocollo ECDH (Elliptic Curve Diffie Hellman) per la generazione di un segreto condiviso tra due sensori e alle implementazioni degli algoritmi di firma digitale (e relativa verifica) ECDSA (Elliptic Curve Digital Signature Algorithm) e Nyberg-Rueppel.
4.2 Components
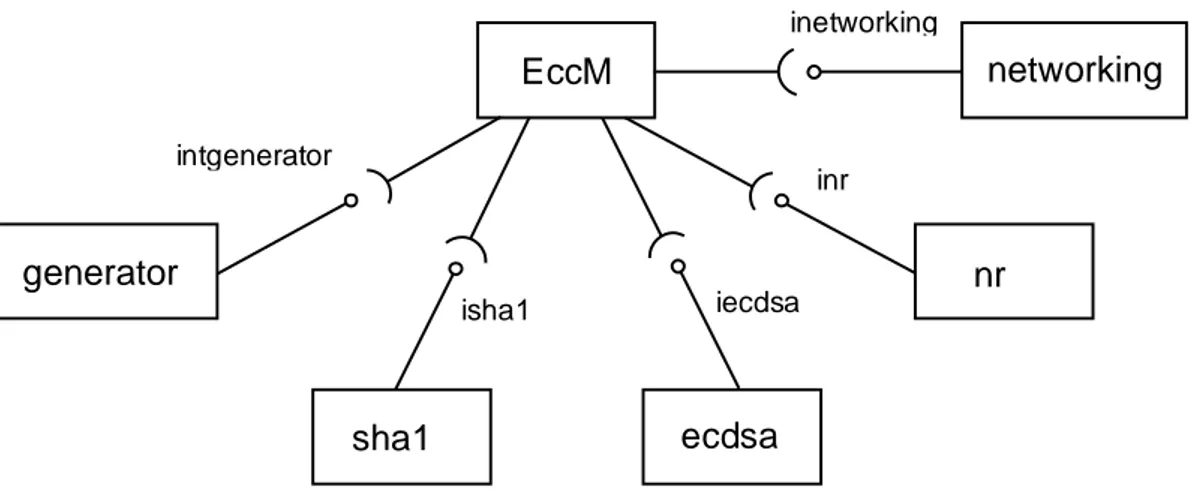
Figura 4.1 Struttura della libreria EccM 2.0
La figura 4.1 illustra la struttura della libreria EccM 2.0 realizzata ad hoc in questa tesi per poter essere utilizzata con Contiki. Per ciascun component, rappresentati dai rettangoli, sono illustrati i rapporti di “dipendenza”, ovvero chi offre i servizi e chi ne usufruisce. Le interfacce sono indicate dai cerchietti, i receptacles sono rappresentati dagli archi.
EccM, generator, sha1, ecdsa, nr e networking sono i components. Intgenerator, isha1, iecdsa, inr e inetworking rappresentano le interfaces.
4.2 Components
EccM è il component principale che utilizza tutti gli altri component della libreria, compreso quello che si occupa della comunicazione con l’ altro nodo sensore (invio e ricezione di messaggi). E’ il component che va in esecuzione all’ avvio del mote e
isha1 inr iecdsa intgenerator inetworking EccM generator networking sha1 nr ecdsa
4.2 Components
che si occupa dell’ inizializzazione delle strutture dati (tra cui i parametri della curva ellittica cablati direttamente nel codice).
Generator è il componente che si occupa della generazione della chiave privata e della chiave pubblica di un nodo sensore.
Le funzioni implementate da questo componente sono:
generate_privKeyA calcola la chiave privata generate_pubKey calcola la chiave pubblica
Tabella 4.1: Funzioni implementate dal modulo generator
sha1 è il componente che permette il calcolo della hash. La funzione implementata da questo componente è:
Tabella 4.2: Funzioni implementate dal modulo sha1
sha_1 inizializza le strutture dati per il calcolo della hash, fa partire le operazioni per il calcolo della hash e infine recupera il valore della hash;
4.2 Components
ecdsa e nr sono componenti molto simili. Gestiscono le operazioni di firma digitale e di verifica dei protocolli per ECDSA e Nyberg-Rueppel.
Le funzioni implementate da questi componenti sono:
sign firma un messaggio con la chiave privata del firmatario verify verifica la firma digitale di un messaggio
Tabella 4.3: Funzioni implementate dal modulo ecdsa e dal modulo nr riguardanti la firma digitale sui nodi sensore
networking è il componente che permette la comunicazione, lo scambio di informazioni fra le motes.
Le funzioni implementate da questo componente sono:
send invio di un messaggio receive e ricezione di un messaggio
Tabella 4.4: Funzioni implementate dal modulo networking
I componenti generator, ecdsa e nr implementano le funzioni aritmetiche sugli interi su 163 bit, le operazioni di addizione tra due punti della curva e moltiplicazione tra un punto e un intero e le operazioni modulari del campo finito che devono essere eseguite nel momento in cui vengono invocate le funzioni di generazione della chiave pubblica, firma e verifica.
4.3 Parametri della curca / 4.4 Rappresentazione dei dati
4.3 Parametri della curva
La libreria utilizza la curva ellittica denominata sect163k1, i cui parametri sono riportati nello standard SEC2 ([8]) e definita sul campo finito GF(2163) (gli interi che costituiscono la curva e i coefficienti stessi della curva sono interi espressi su 163 bit). In particolare, a differenza delle curve definite sui campi finiti GF(p), le operazioni di addizione e moltiplicazione sono realizzate modulo il polinomio irriducibile seguente:
x163 + x7 + x6 + x3 + 1
4.4 Rappresentazione dei dati
Nella libreria necessitano di essere rappresentate 2 entità:
1) gli interi su 163bit ;
2) i punti della curva ellittica.
Gli interi sono rappresentati con un array, come mostrato nella struttura 4.1. Essendo le word della libreria su 8 bit, NUMWORDS potrebbe essere scelto pari a 21, creando
struct El t {
u8_ t val [NUMWORDS] ; };