Extraction, integration and probabilistic characterization of web data

(1)

UNIVERSITÀ DEGLI STUDI

TRE

Roma Tre University

Ph.D. in Computer Science and Engineering

Extraction, integration and

probabilistic characterization of

web data

(2)

(3)

A thesis presented by Lorenzo Blanco

in partial fulfillment of the requirements for the degree of Doctor of Philosophy

in Computer Science and Engineering Roma Tre University Dept. of Informatics and Automation

(4)

Prof. Paolo Merialdo REVIEWERS:

Prof. Alberto Laender Prof. Divesh Srivastava

(5)

(6)

(7)

Abstract

Extraction, integration and probabilistic

characterization of web data

Lorenzo Blanco

Advisor:

Professor Paolo Merialdo

Computer Science and Engineering

The web contains a huge amount of structured information provided by a large number of web sites. Since the current search engines are not able to fully recognize this kind of data, this abundance of information is an enormous oppor-tunity to create new applications and services.

To exploit the structured web data, several challenging issues must be ad-dressed, spanning from the web pages gathering, the data extraction and integra-tion, and the characterization of conflicting data. Three design criteria are critical for techniques that aim at working at the web scale: Scalability (in terms of com-putational complexity), unsupervised approach (as human intervention can not be involved at the web scale), and domain–independence (to avoid custom solu-tions).

The thesis of this dissertation is that the redundancy of information provided by the web sources can be leveraged to create a system that locates the pages of in-terest, extracts and integrates the information, and handles the data inconsistency that the redundancy naturally implies.

(8)

List of Figures

1.1 Three web pages containing data about stock quotes from Yahoo! finance,

Reuters, and Google finance web sites. . . 1

1.2 Google results for the queries “YHOO”, and “michael jordan” (structured data results are highlighted). . . 3

1.3 The generative process applied to the publication of stock quote pages by GoogleFinance, YahooFinance, and Reuters. . . 5

1.4 The goal of the extraction/integration module. . . 6

1.5 The uncertain data about one attribute of one instance, and the associated probability distribution over the possible values. . . 7

2.1 Precision-Recall of Mdl-U by varying α . . . 28

2.2 Running Time of Mdl-U versus CP-SL . . . 29

2.3 Running Time of Mdl-U . . . 29

3.1 Web pages representing instances of the BASKETBALLPLAYERentity. . . 31

3.2 The OUTDESITalgorithm. . . 38

3.3 Pages as sequences of tokens. . . 41

3.4 The TEMPLATETOKENSalgorithm to detect tokens belonging to the tem-plate of a set of pages. . . 42

3.5 Generated descriptions for four entities. . . 43

3.6 Extracted keywords. . . 45

3.7 Performance of the isInstance() function varying the threshold t. . . 46

3.8 Pages and players found by OUTDESIT. . . 47

4.1 Three web pages containing data about stock quotes from Yahoo! finance, Reuters, and Google finance web sites. . . 50

4.2 The publishing process: the web sources are views over the hidden rela-tion generated by four operators. . . 53

4.3 DOM trees of four stock quote pages. . . 65 4.4 Extraction rules as XPath absolute expressions for the pages of Figure 4.3. 67

(11)

4.5 The relation extracted by the extraction rules in Figure 4.4 from the pages in Figure 4.3. . . 67 4.6 SplitAndMerge over a mapping m. Labels on edges indicate matching

scores. e1and e2belong to the same source; d(e1, e2) = 0.29. . . 70

4.7 The values of attribute a3partially match with the values of the attributes

in m. . . 71 4.8 Comparison of the NaiveMatch and the SplitAndMerge algorithms with

different thresholds. . . 76 4.9 Synthetic setting: running time of the system over the number of analyzed

sources. . . 77 4.10 Growing of the number of real-world objects over the number of sources. 77 4.11 Precision, Recall, and F-measure of the mappings of four different

exe-cutions: naive matching, naive matching with wrapper refinement (WR), SplitAndMerge (SM), SplitAndMerge with wrapper refinement (SM+WR). 78 4.12 Precision, recall, and F-measure for mappings composed by attributes that

appeared in at least 8 sources. . . 80 5.1 Three sources reporting stock quotes values. . . 88 5.2 Configurations for the synthetic scenarios. . . 97 5.3 Synthetic experiments: MultiAtt(5) outperforms alterative configurations

in all scenarios. . . 98 5.4 Settings for the real-world experiments. . . 99 5.5 Real-world summary experiments. . . 100

(12)

List of Tables

2.1 Comparison of the different clustering techniques . . . 27 3.1 INDESITexperimental results. . . 37

4.1 Effect of the dynamic matching threshold on the mapping Precision. . . . 79 4.2 Top-8 results for 100 web sources: for each mapping m the most likely

(13)

(14)

Introduction

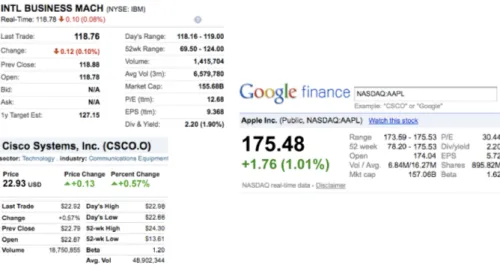
The web is a surprisingly extensive source of information. It is made up of a large number of sources that publish information about a disparate range of topics. Unfor-tunately it is an environment specifically built for human fruition, not for automatic processing of the data. Nevertheless, this abundance of information is an enormous opportunity to create new applications and services capable of exploiting the data in ways that were not possible in the past. In this context, an increasing number of web sites deliver pages containing structured information about recognizable concepts, rel-evant to specific application domains, such as movies, finance, sport, products, etc. Consider for example the web page fragments shown in Figure 1.1. At first glance a human can easily understand that they contain information about stock quotes, that specific values are in evidence, that the data pertain to three distinct stock quotes, and so on. Traditional search engines are extremely good at finding and ranking

docu-Figure 1.1: Three web pages containing data about stock quotes from Yahoo! finance, Reuters, and Google finance web sites.

(15)

ments, but they are not capable of distinguish instances, attributes, data formats. They can not process queries such as the current value of the “Apple Inc.” stock quote, or the biggest change of price in the NASDAQ stock market in the last three (working) days. Before answering to such queries you have to address several very challenging issues. The list can contain (and is not limited to) the following:

• Which pages contain the information you are looking for on the web? Or, going on with the stock quote running example, which pages are about the finance domain?

• Suppose you want to store the information you need in a relational database, how do you extract all and only the useful values from the pages? These pages contain not only the data, but also noise values such as advertisements, page formatting elements, etc. How do you extract only the useful values?

• What is the semantics of data in web pages? Consider again the fragments shown in Figure 1.1. You want to group together the values with the same semantics. For a human it is trivial to associate the “last trade” semantics to the values “118.76”, “22.93”, and“175.48”, but for an automatic system this can be very challenging.

• How do you deal with data inconsistencies? Imagine that for the same stock quote some web sources state that the minimum price in the last year is “10.00” and other sources state it is “11.00”. Which ones will you trust?

To address the above issues, a system that aims at exploiting data on the web needs to be:

• Scalable: scaling of the web implies the processing of a very large number of sites that, in turn, can potentially publish millions of pages. To cope with this amount of data all the tasks (even the most complex, such as the integration of the data coming from multiple sources) have to be computationally-efficient. • Unsupervised: a lot of intermediate steps would be much easier if they were

executed completely or partially by a human. Unfortunately, this is not possible: we would loose the scalability of the approach.

• Domain–independent: as we want to be able to apply our solutions to general entities we avoide the use domain–dependent knowledge, or custom solutions. For example, in the case of the finance domain we could easily extract only the values containing the symbol “$” (or, at least, give them more importance), but this would be useless for the vast majority of the web.

(16)

This dissertation examines how to automatically locate, extract, integrate and rec-oncile structured web data about an entity of interest (the “StockQuote” entity in the running example). We concentrate on a specific type of pages, that is the pages that publish information about a single instance of the entity of interest. Even if this is only one of the existing publication pattern, the the web scale involves an impressive amount of data.

For example, the pages depicted in Figure 1.1 are examples of this kind of pages: each page publishes structured data about a single instance of the “stock quote” entity. The results obtained with our approach promise a number of compelling applica-tions. For example:

• Dataset creation: on the web you can find massive data about nearly every-thing. Manually locating useful sources, extracting data, and integrating all the information can be a tedious or impossible task. Instead, with our techniques

(17)

you can create big datasets from a large number of sources, you can know from which website every single data comes from and how trustable it is.

• Enhanced search engine results: with our results a search engine could improve the results showing more precise and updated information, rather than simply the web pages urls. This already happens for a limited set of results. Consider, for example, the results returned by Google if we search for a stock quote or a famous basketball player. As you can see in Figure 1.2 for the former we get structured data just before the other results, but for the latter we get only urls. We can accumulate data to provide such information, providing updated and trustworthy data.

In the rest of this chapter we introduce the main challenges that will be tackled in the next chapters and the contributions of this dissertation. Finally, we provide an overview of the dissertation’s general organization.

1.1 Challenges

In this section we introduce the main challenges tackled in the dissertation.

The publishing process of structured data

In large data–intensive web sites, we observe two important characteristics that sug-gest new opportunities for the automatic extraction and integration of web data. On the one hand, we observe local regularities: in these sites, large amounts of data are usually offered by hundreds of pages, each encoding one tuple in a local HTML tem-plate. For example, each page shown in Figure 1.1 (which are from three different sources) publishes information about one company stock. If we abstract this repre-sentation, we may say that each web page displays a tuple, and that a collection of pages provided by the same site corresponds to a relation. According to this abstrac-tion, each web site in Figure 1.1 exposes its own “StockQuote” relation. On the other hand, we notice global information redundancy: as the web scales, many sources pro-vide similar information. The redundancy occurs both a the schema level (the same attributes are published by more than one source) and at the extensional level (some instances are published by more than one source). In our example, many attributes are present in all the sources (e.g., the company name, last trade price, volume); while others are published by a subset of the sources (e.g., the “Beta” indicator). At the extensional level, there is a set of stock quotes that are published by more sources. This redundancy is a fundamental opportunity for us. In fact, as we will describe in the following chapters, we leverage it to accomplish several tasks that span from the

(18)

Figure 1.3: The generative process applied to the publication of stock quote pages by GoogleFinance, YahooFinance, and Reuters.

web source collection to the data extraction and integration. Nevertheless, as web information is inherently imprecise, redundancy also implies inconsistencies; that is, sources can provide conflicting information for the same object (e.g., a different value for the volume of a given stock).

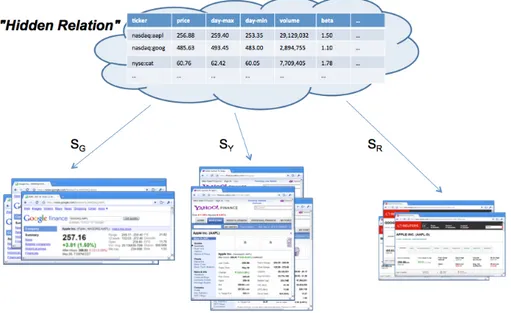
These observations lead us to hypothesize that underlying sources of the same do-main there is a hidden conceptual relation from which pages of different sources are generated. According to this model, each of the sources can be seen as the result of a generative process applied over the hidden relation. Each source publishes infor-mation about a subset of the tuples in the hidden relation, and different sources may publish different subsets of its attributes. Moreover, the sources may introduce errors, imprecise or null values, or they may publish values by adopting different formats (e.g., miles vs. kilometers). Figure 1.3 depicts this process applied to three finance web sources that publish their own views of the hidden relation.

Inverting the publishing process

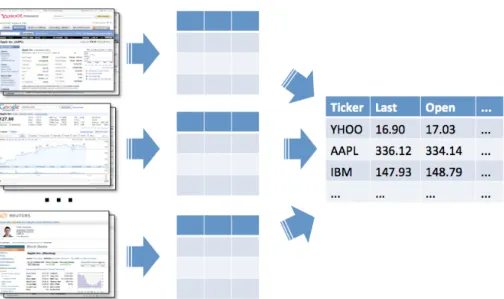
From this perspective, the data extraction and integration problem can be seen as the problem of inverting this publishing process to reconstruct the hidden relation, as visually represented in Figure 1.4. We want to extract the data from the pages and obtain partial views over the hidden relation. Then, we integrate the data by leveraging the redundancy of the information.

(19)

Figure 1.4: The goal of the extraction/integration module.

A state-of-the-art natural solution to the above problem is a two steps waterfall approach, where a schema matching algorithm is applied over the relations returned by automatically generated wrappers. However, important issues arise when a large number of sources is involved, and a high level of automation is required:

• Wrapper Inference Issues: since wrappers are automatically generated by an unsupervised process, they can produce imprecise extraction rules (e.g., rules that extract irrelevant information mixed with data of the domain). To obtain correct rules, the wrappers should be evaluated and refined manually.

• Integration Issues: the relations extracted by automatically generated wrappers are “opaque”, i.e., their attributes are not associated with any (reliable) seman-tic label. Therefore the matching algorithm must rely on an instance-based approach, which considers attribute values to match schemas. However, due to errors introduced by the publishing process, instance-based matching is chal-lenging because the sources may provide conflicting values. Also, imprecise extraction rules return wrong, and thus inconsistent, data.

Our techniques to invert the publishing process look for the correct extraction rules and mappings contextually, and leverage the redundancy among the sources to guide the choice of the rules and their grouping into cohesive mappings.

(20)

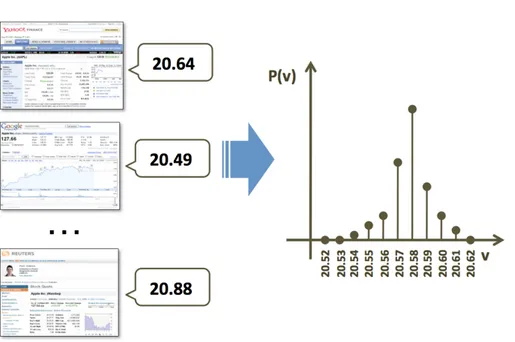
Figure 1.5: The uncertain data about one attribute of one instance, and the associated probability distribution over the possible values.

Characterizing the uncertainty of web data

The web data is inherently imprecise. Multiple web sites can publish conflicting val-ues for the same attribute of the same instance, at the same time. To deal with this uncertainty we analyze the data published by the web sources as a whole, and we look for the agreement among the sources to detect which are the most trustworthy web sites. Building on previous results from the literature, our model can also deal with sources that copy from other sources. If this happens the copied values are not taken in account (otherwise they would interfere with the agreements detection) and the most probable values will be determined. Figure 1.5 shows an hypothetical ex-ample of conflicting web data resolution. By analyzing a dataset of conflicting data, our model produces, for each instance and for each attribute, a probability distribution that represents the probability of correctness of each possible value.

Page gathering

So far we assumed that we know in advance the web sources that publish the informa-tion about the entity of interest, but collecting these sources is a challenging issue. In the finance domain this could be quite easy: if you cover the most important sites you can probably cover the majority of the stock quotes. However, in other domains this is challenging. For example, for the “BasketBallPlayer” entity you can go on collecting

(21)

web sources for a very long time, and you will always discover new titles. Our ap-proach is the following: given a web site and a sample page, we develop a technique to collect all the pages similar to the sample page. Then, we iterate by discovering new sources and by applying again the technique to collect similar pages on them. The process goes on until no new sources are found.

Page clustering

We start by tackling the problem of how to divide the whole set of pages of a website in clusters, where each cluster contains pages that publish similar data. This is a central task of the page gathering process: given a website and some example pages about the entity of interest we want to discover as many pages as possible that expose the same kind of information. To do this we assume we have the snapshot of the site and we cluster the pages mainly relying only on the urls of the pages. The key idea is to not use standard clustering algorithms, that rely on pairwise comparison of the elements (the string comparison of the urls is not effective); instead, we adopt an information-theoretic formulation of the problem. We consider the whole set of urls and we detect the recurring patterns. As detailed in the chapter this process is highly scalable and produces good results.

Web sources discovery

To discover the sources of interest the clustering algorithm is used as a sub–routine in an algorithm named OUTDESIT.1

OUTDESITtakes as input a small set of sample pages publishing data about the

tar-get entity, automatically infers a description of the underlying entity and then searches the web for other pages containing data representing the same entity. OUTDESIT

queries a search engine with the available data about the known instances to discover new candidate sites. Then, the description is used to filter out the non–relevant sources and the clustering algorithm is used to discover all the useful pages on the relevant sources. This process is iterated until new useful sources are found.

1.2 Contributions

As described above, three design criteria are critical for techniques that aim at work-ing at the web scale. The techniques must be: scalable, completely unsupervised, and domain–independent. In this dissertation we applied these criteria to design so-lutions that, applied together, constitute a whole system that is able to complete all

1_{If the snapshot of the analyzed web sites is not available we can adopt an alternative algorithm (called} INDESIT) that, for the purpose of OUTDESIT, is equivalent to the clustering solution.

(22)

the tasks required to create a dataset of structured web data about a conceptual entity of interest. These tasks span from the web pages gathering to the probabilistic model used characterize the uncertainty of web data. Moreover, the contributions are the following:

• The clustering algorithm explores the novel idea of using URLs for structural clustering of web sites. We develop a principled framework, grounded in infor-mation theory, that allows us to leverage URLs effectively, as well as combine them with content and structural properties. We propose an algorithm, with a linear time complexity in the number of webpages, that scales easily to web sites with millions of pages. We perform an extensive evaluation of our tech-niques over several entire web sites, and demonstrate the effectiveness of our techniques.

• The OUTDESITalgorithm discovers pages publishing data about a certain

con-ceptual entity, given as input only a small set of sample pages. It is a completely unsupervised technique that creates a description of the target entity and inter-acts with a search engine filtering out the web sites that do not fit the description. We conducted experiments that produced interesting results. This work appears in the 2008 WIDM workshop [BCMP08b] and, as a demo, at the 2008 EDBT conference [BCMP08a].

• With the extraction/integration algorithm we introduce an instance based schema matching algorithm with linear complexity over the number of sources, which is adaptive to the actual data. It presents significant advantages in general settings where no a priori knowledge about the domain is given, and multiple sources have to be matched. Our approach takes advantage of the coupling be-tween the wrapper inference and the data integration tasks to improve the qual-ity of the wrappers; to the best of our knowledge, this is the first attempt to face both issues contextually. We conducted a large set of experiments using real-world data from three different domains, including 300 web sites. The experi-ments demonstrate that our techniques are effective and highlight the impact of their components. This work appears in the 2010 WebDB workshop [BPC+_10]

and, as a demo, at the 2010 WWW conference [BBC+_10].

• We developed a probabilistic model that manages the uncertainty of the web data. This model assigns correct trustworthiness scores to the sources, even if some of them are copying data from other sources. We conducted experiments to verify the correctness of the approach in challenging synthetic scenarios and

(23)

real cases. The main contribution is that our model processes together all the attributes of the entity; this holistic approach produces better results in terms of copiers detection and, therefore, trustworthiness scores. The model was pub-lished at the 2010 CAiSE conference [BCMP10].

1.3 Structure of the Dissertation

Each of the following chapters tackles one of the problems introduced above. Each one contains a formalization of the problem, the study of the related scientific litera-ture, our solution to the problem, and the experimental results.

Chapter 2 covers the clustering problem. Chapter 3 describes the details of the OUTDESITalgorithm and its relation with the clustering technique. Chapter 4 intro-duces the extraction/integration process. Finally, Chapter 5 describes the probabilistic model we use to characterize the uncertainty of web data. A final chapter with con-clusive remarks will be added in the final version of the thesis.

(24)

Clustering Web Pages

To extract and integrate information about an entity of interest you need to locate the pages containing the data you are looking for. As we observed in [BCM08] in data–intensive web sites the structure of the page is related with the semantics of the contained information: if two pages share the same structure it is very likely that they publish information about the same subject. In this chapter we describe an highly scal-able technique to divide structured web pages in groups, called “clusters”, that share the same structure. To do this we rely mainly on the urls of the pages, but, as detailed later, the same algorithms can take in account also the page content. Moreover, this technique works on the whole set of urls of a web site, so you need a dump of the considered web sites or, at least, the complete listing of the urls1_.

In Chapter 3 we describe how the solution of the clustering problem can be used to collect pages about an entity of interest from web sources we do not already know.

2.1 Introduction

Several web sites use scripts to generate highly structured HTML: this includes shop-ping sites, entertainment sites, academic repositories, library catalogs, and virtually any web site that serves content from a database. Structural similarity of pages gener-ated from the same script allows information extraction systems to use simple rules, called wrappers, to effectively extract information from these webpages. While there has been an extensive work in the research community on learning wrappers [LRNDSJ02, CKGS06], the complementary problem of clustering webpages generated from differ-ent scripts to feed the wrappers has been relatively unexplored. The focus here is to develop highly scalable and completely unsupervised algorithms for clustering web-pages based on structural similarity.

1_{This kind of information was available when we experimented the algorithms, in fact this chapter is} the result of a summer internship at the Yahoo! Research Labs in Santa Clara (California), and is a joint work with Nilesh Dalvi and Ashwin Machanavajjhala

(25)

In this chapter, we develop highly scalable techniques for clustering web sites. We primarily rely on URLs, in conjunction with very simple content features, which makes the techniques extremely fast. Our use of URLs for structural clustering is novel. URLs, in most cases, are highly informative, and give lots of information about the contents and types of webpages. Still, in previous work [CMM02b], it was observed that using URLs similarity does not lead to an effective clustering. We use URLs in a fundamentally different way. We share the intuition in XProj [ATW+_07]

that pairwise similarity of URLs/documents is not meaningful. Instead, we need to look at them holistically, and look at the patterns that emerge. In this chapter, we develop a principled framework, based on the principles of information theory, to come up with a set of scripts that provide the simplest explanation for the observed set of URLs/content.

2.2 Related Work

There has been previous work on structural clustering. We outline here all the works that we are aware of and state their limitations. There is a line of work [ATW+_07,

CMOT04, DCWS06, LYHY02, LCMY04] that looks at structural clustering of XML documents. While these techniques are also applicable for clustering HTML pages (for example in [dCRGdSL04] standard clustering algorithms are used to group pages in order to extract the relevant information), HTML pages are harder to cluster than XML documents because they contain more noise, they do not confirm to sim-ple/clean DTDs, and they are very homogeneous because of the fixed set of tags used in HTML. At the same time, there are properties specific to HTML setting that can be exploited, e.g., the URLs of the pages. There is some work that specifically tar-get structural clustering of HTML pages [CMM02b, CMM05]. Several measures of structural similarity for webpages have been proposed in the literature (for example: [FMM+_{02, FMM}+_{05]). A recent survey [Got08] looks at many of these measures,}

and compares their performance for clustering webpages.

We propose the clustering problem in order to locate collections of pages that will be analyzed later to extract structured data. From this perspective this work is related to the problem of fetching structurally similar pages of the “hidden” web [LdSGL02, Kru97, RGM01, GLdSRN00, DEW97].

However, all the techniques that we list here have a fundamental issue: they do not scale to large web sites. Real web sites routinely have millions of pages, and we want the ability to cluster a large number of such web sites in a reasonable amount of time. The techniques covered in the survey [Got08] do not scale beyond few hundred webpages. In fact, most of the techniques based on similarity functions along with

(26)

agglomerative hierarchical clustering have a quadratic complexity, and cannot handle large sites. The XProj [ATW+_{07] system, which is the state of the art in XML}

cluster-ing, even though have a linear complexity, still requires an estimated time of around 20 hours for a site with a million pages2_.

2.3 Overview

In this section, we introduce the clustering problem and give an overview of our information-theoretic formulation. The discussion in this section is informal, which will be made formal in subsequent sections.

Website Clustering Problem

Websites use scripts to publish data from a database. A script is a function that takes a relation R of a given schema, and for each tuple in R, it generates a webpage, consisting of a (url,html) pair. A web site consists of a collection of scripts, each rendering tuples of a given relation. E.g., the web site imdb.com has, among others, scripts for rendering movie, actor, user, etc.

In structured information extraction, we are interested in reconstructing the hidden database from published webpages. The inverse function of a script, i.e., a function that maps a webpage into a tuple of a given schema, is often referred to as a wrapper in the literature [LRNDSJ02, Ant05, HD98a, HBP01, KWD97, MJ02, SA99]. The target of a wrapper is the set of all webpages generated by a common script. This motivates the following problem:

Website Clustering Problem : Given a web site, cluster the pages so that the pages generated by the same script are in the same cluster.

The clustering problem as stated above is not yet fully-specified, because we haven’t described how scripts generate the urls and contents of webpages. We start from a very simple model focussing on urls.

Using URLs For Clustering

An url tells a lot about the content of the webpage. Analogous to the webpages gen-erated from the same script having similar structure, the urls gengen-erated from the same script also have a similar pattern, which can be used very effectively and efficiently

2_{It takes close to 1200 seconds for 16,000 documents from DB1000DTD10MR6 dataset, and the} doc-uments themselves are much smaller than a typical webpage.

(27)

cluster webpages. Unfortunately, simple pairwise similarity measures between urls do not lead to a good clustering. E.g., consider the following three urls:

u1 : site.com/CA/SanFrancisco/eats/id1.html

u2 : site.com/WA/Seattle/eats/id2.html

u3 : site.com/WA/Seattle/todo/id3.html

u4 : site.com/WA/Portland/eats/id4.html

Suppose the site has two kinds of pages : eats pages containing restaurants in each city, and todo pages containing activities in each city. There are two “scripts” that generate the two kind of pages. In terms of string similarity, u2 is much closer to

u3, an url from a different script, than the url u1from the same cluster. Thus, we

need to look at the set of urls in a a more principle manner, and cannot rely on string similarities for clustering.

Going back to the above example, we can use the fact that there are only 2 distinct values in the entire collection in the third position, todo and eats. They are most like script terms. On the other hand, there are a large number of values for states and cities, so they are most likely data values. We call this expected behavior the small cardinality effect.

Data terms and script terms often occur at the same position in the url. E.g., the same site may also have a third kind of pages of the form:

site.com/users/reviews/id.html

Thus, in the first position we have the script term users along with list of states, and in second position we have reviews along with cities. However, if one of the terms, e.g reviews, occurs with much higher frequency than the other terms in the same position, it is an indication that its a script term. We call this expected behavior the large component effect.

In order to come up with a principled theory for clustering urls, we take an infor-mation theoretic view of the problem. We consider a simple and intuitive encoding of urls using scripts, and try to find an hypothesis (set of scripts) that offer the simplest explanation of the observed data (set of urls). We give an overview of this formu-lation in the next section. Using an information-theoretic measure also allows us to incorporate addition features of urls, as well as combine them with the structural cues from the content.

An Information-Theoretic Formulation

We assume, in the simplest form, that a url is a sequence of tokens, delimited by the “/”character. A url pattern is a sequence of tokens, along with a special token called

(28)

“_{∗ ”. The number of “ ∗ ” is called the arity of the url pattern. An example is the} following pattern:

www.2spaghi.it/ristoranti/*/*/*/*

It is a sequence of 6 tokens: www.2spaghi.it, ristoranti, ∗, ∗, ∗ and ∗. The arity of the pattern is 4.

Encoding URLs using scripts

We assume the following generative model for urls: a script takes an url pattern p, a database of tuples of arity equal to arity(p), and for each tuple, generates an url by substituting each ∗ by corresponding tuple attribute. E.g., a tuple (lazio, rm, roma, baires) will generate the url:

www.2spaghi.it/ristoranti/lazio/rm/roma/baires Let S = {S1, S2,· · · Sk} be a set of scripts, where Si consists of the pair (pi, Di),

with pi a url pattern, and Di a database with same arity as pi. Let ni denote the

number of tuples in Di. Let U denote the union of the set of all urls produced by the

scripts. We want to define an encoding of U using S.

We assume for simplicity that each script Si has a constant cost c and each data

value in each Dihas a constant cost α. Each url in U is given by a pair (pi, tij), where

tijis a tuple in database Di. We write all the scripts once, and given a url (pi, tij), we

encode it by specifying just the data tijand an index to the pattern pi. The length of

all the scripts is c·k. Total length of specifying all the data equals�iα·arity(pi)·ni.

To encode the pattern indexes, the number of bits we need equals the entropy of the distribution of cluster sizes. Denoting the sum�iniby N, the entropy is given by

�

inilog_nN_i.

Thus, the description length of U using S is given by ck +� i nilogN ni + α� i arity(pi)· ni (2.1) The MDL Principle

Given a set of urls U, we want to find the set of scripts S that best explain U. Using the priciple of minimum description length [Gru07], we try to find the shortest hypothesis, i.e., S that minimize the description length of U.

The model presented in this section for urls is simplistic, and serves only to illus-trate the mdl principle and the cost function given by Eq .(2.1). In the next section, we define our clustering problem formally and in a more general way.

(29)

2.4 Problem Definition

We now formally define theMdl-based clustering problem. Let W be a set of web-pages. Each w ∈ W has a set of terms, denoted by T (w). Note that a url se-quence “site.com/a1/a2/ . . .” can be represented as a set of terms {(pos1 =

site.com), (pos2 = a1), (pos3 = a2),· · · }. In section 2.4, we will describe in more

detail how a url and the webpage content is encoded as terms. Given a term t, let W (t)denote the set of webpages that contain t. For a set of pages, we use script(W ) to denote ∩w∈WT (w), i.e., the set of terms present in all the pages in W .

A clustering is a partition of W . Let C = {W1,· · · , Wk} be a clustering of W ,

where Wihas size ni. Let N be the size of W . Given a w ∈ Wi, let arity(w) =

|T (w) − script(Wi)|, i.e., arity(w) is the number of terms in w that are not present

all the webpages in Wi. Let c and α be two fixed parameters. Define

mdl(C) = ck +� i nilogN ni + α � w∈W arity(w) (2.2) We define the clustering problem as follows:

Problem 1. (Mdl-Clustering) Given a set of webpages W , find the clustering C that minimizes mdl(C).

Eq. (2.2) can be slightly simplified. Given a clustering C as above, let si denote

the number of terms in script(Wi). Then,�w∈Warity(w) =

�

w∈W|w|−

�

inisi.

Also, the entropy �_inilognNi equals N log N −

�

inilog ni. By removing the

clustering independent terms from the resulting expression, the Mdl-Clustering can alternatively be formulated using the following objective function:

mdl∗(C) = ck₋� i nilog ni− α � i nisi (2.3)

Instantiating Webpages

The abstract problem formulation treats each webpage as a set of terms, which we can use to represent its url and content. We describe here the representation that we use in this work:

URL Terms

As we described above, we tokenize urls based on “/” character, and for the token tin position i, we add a term (posi = t)to the webpage. The sequence information

(30)

For script paramters, for each (param, val) pair, we construct two terms: (param, val) and (param). E.g., the url site.com/fetch.php?type=1&bid=12 will have the following set of terms: { pos1=site.com, pos2=fetch.php, type, bid,

type=1, bid=12}. Adding two terms for each paramter allows us to model the two cases when the existence of a parameter itself varies between pages from the same script and the case when parameter always exists and its value varies between script pages.

Many sites use urls whose logical structure is not well seperated using “/”. E.g., the site tripadvisor.com has urls of the form

www.tripadvisor.com/Restaurants-g60878-Seattle Washington.html for restaurants and has urls like

www.tripadvisor.com/Attractions-g60878-Activities-Seattle Washington.html

for activities. The only way to separate them is to look for the keyword “Restau-rants” vs. “Attractions”. In order to model this, for each token t in position i, we further tokenize it based on non-alphanumeric characters, and for each subterm tj, we

add (posi = tj)to the webpage. Thus, the restaurant webpage above will be

rep-resented as { pos1=tripadvisor.com, pos2=Restaurants, pos2=g60878, pos2=Seattle,

pos2=Washington}. The idea is that the term pos2=Restaurants will be inferred as

part of the script, since its frequency is much larger than other terms in co-occurs with in that position. Also note that we treat the individual subterms in a token as a set rather than sequence, since we don’t have a way to perfectly align these sequences. Content Terms

We can also incorporate content naturally in our framework. We can simply put the set of all text elements that occur in a webpage. Note that, analogous to urls, every webpage has some content terms that come from the script, e.g., Address: and Open-ing hours:, and some terms that come from the data. By puttOpen-ing all the text elements as webpage terms, we can identify clusters that share script terms, similar to urls. In addition, we want to disambiguate text elements that occur at structurally different positions in the document. For this, we also look at the html tag sequence of text elements starting from the root. Thus, the content terms consist of all (xpath, text) pairs present in the webpage.

2.5 Properties of MDL Clustering

We analyze some properties of Mdl-Clustering here, which helps us gain some in-sights into its working.

(31)

Local substructure

Let opt(W ) denote the optimal clustering of a set of webpages W . Given a clus-tering problem, we say that the problem exhibits a local substructure property, if the following holds : for any subset S ⊆ opt(W ), we have opt(WS) = S, where WS

denotes the union of web pages in all clusters in S, Lemma 2.5.1. Mdl-Clustering has local substructure.

Proof. Let W be any set of pages, S0⊂ opt(W ) and S1= opt(W )\ S0. Let N0and

N1be the total number of urls in all clusters in S0and S1respectively. Using a direct

application of Eq. (2.2), it is easy to show the following: mdl(opt(W )) = N1log N N1 + N2log N N2 + mdl(S0) + mdl(S1)

Thus, if opt(W0) �= S0, we can replace S0with opt(W0)in the above equation to

obtain a clustering of W with a lower cost than opt(W ), which is a contradiciton. Local substructure is a very useful property to have. If we know that two sets of pages are not in the same cluster, e.g., different domains, different filetypes etc., we can find the optimal clustering of the two sets independently. We will use this property in our algorithm as well as several of the following results.

Small Cardinality Effect

Recall from Section 2.3 the small cardinality effect. We formally quantify the effect here, and show that Mdl-Clustering exhibits this effect.

Theorem 1. Let F be a set of terms s.t. C = {W (f) | f ∈ F } is a partition of W and |F | ≤ 2α−c_{. Then, mdl(C) ≤ mdl({W }).}

A corollary of the above result is that if a set of urls have less than 2α−c_distinct

values in a given position, it is always better to split them by those values than not split at all. For |W | � c, the minimum cardinality bound in Theorem 1 can be strength-ened to 2α_.

Large Component Effect

In Section 2.3, we also discussed the large component effect. Here, we formally quan-tify this effect for Mdl-Clustering.

(32)

Given a term t, let C(t) denote the clustering {W (t), W −W (t)}, and let frac(t) denote the fraction of webpages that have term t.

Theorem 2. There exists a threshold τ, s.t., if W has a term t with frac(t) > τ, then mdl(C(t)≤ mdl({W }).

For |W | � c, τ is the positive root of the equation αx + x log x + (1 − x) log(1 − x) = 0. There is no explicit form for x as a function of α. For α = 2, τ = 0.5.

For clustering, α plays an important role, since it controls both the small cardi-nality effect and the large component effect. On the other hand, since the number of clusters in a typical web site is much smaller than the number of urls, the parameter cplays a relatively unimportant role, and only serves to prevent very small clusters to be split.

2.6 Finding Optimal Clustering

In this section, we consider the problem of finding the optimal MDL clustering of a set of webpages. We start by considering a very restricted version of the problem: when each webpage has only 1 term. For this restricted version, we describe a polynomial time algorithm in Section 2.6. In Appendix 5.5, we show that the unrestricted version of Mdl-Clustering is NP-hard, and remain hard even when we restrict each webpage to have at most 2 terms. Finally, in Section 2.6, based on the properties of Mdl-Clustering (from Section 2.5) and the polynomial time algorithm from Section 2.6, we give an efficient and effective greedy heuristic to tackle the general Mdl-Clustering problem.

A Special Case : Single Term Webpages

We consider instances W of Mdl-Clustering where each w ∈ W has only a single term. We will show that we can find the optimal clustering of W efficiently.

Lemma 2.6.1. In Opt(W ), at most one cluster can have more than one distinct values.

Proof. Suppose there are two clusters C1and C2in Opt(W ) with more than 1 distinct

values. Let there sizes be n1 and n2 with n1 ≤ n2 and let N = n1+ n2. By

Lemma 2.5.1, {C1, C2} is the optimal clustering of C1 ∪ C2. Let ent(p1, p2) =

−p1log p1− p2log p2denote the entropy function. We have

mdl(_{C1, C2}) = 2c + N · ent(

n1

N, n2

(33)

Let C0be any subset of C1consisting of unique tokens, and consider the clustering

{C0, C1∪ C2\ C0}. Denoting the size of C0by n0, the cost of the new clustering is

2c + N_{· ent(}n0 N,

n1

N) + α(N− n0)

This is because, in cluster C0, every term is constant, so it can be put into the script,

hence there is no data cost for cluster C0. Also, since n0 < n1≤ n2< n2, the latter

is a more uniform distribution, and hence ent(n0

N, n1 N) < ent( n1 N, n2

N). Thus, the new

clustering leads to a lower cost, which is a contradiction. Thus, we can assume that Opt(W ) has the form

{W (t1), W (t2),· · · , W (tk), Wrest}

where W (ti)is a cluster containing pages having term ti, and Wrestis a cluster with

all the remaining values.

Lemma 2.6.2. For any term r in some webpage in Wrestand any i ∈ [1, k], |W (ti)| ≥

|W (r)|.

Proof. Suppose, w.l.o.g, that |W (t1)| ≤ |W (r)| for some term r ∈ Wrest. Lemma 2.5.1

tells us that C0={W (t1), Wrest} is the optimal clustering of W0= W (t1)∪ Wrest.

Let C1 ={W (v), W0\ W (v)} and let C2 ={W0}. From first principles, it is easy

to show that

max(mdl(C1), mdl(C2)) < mdl(C0)

This contradicts the optimality of C1.

Lemma 2.6.1 and 2.6.2 give us an obvious PTIME algorithm for Mdl-Clustering. We sort the terms based on their frequencies. For each i, we consider the clustering where the top i frequent terms are all in separate cluster, and everything else is in one cluster. Among all such clusterings, we pick the best one.

The General Case : Hardness

In this section, we will show that Mdl-Clustering is NP-hard. We will show that the hardness holds even for a very restricted version of the problem: when each webpage w_{∈ W has at most 2 terms.}

We use a reduction from the Set-Packing problem. In 2-Bounded-3-Set-Packing, we are given a 3-uniform hypergraph H = (V, E) with maximum degree 2, i.e., each edge contains 3 vertices and no vertex occurs in more than 2 edges. We want to determine if H has a perfect matching, i.e., a set of vertex-disjoint edges that cover all the vertices of H. The problem is known to be NP-complete [CC03].

(34)

We refer an interested reader to Appendix 5.5 for further details about the reduc-tion.

The General Case : Greedy Algorithm

Algorithm 1 RecursiveMdlClustering Input: W , a set of urls

Output: A partitioning C

1: Cgreedy← FindGreedyCandidate(W )

2: if Cgreedyis not nullthen

3: return ∪W�_∈C_greedyRecursiveMdlClustering(W�)

4: else

5: return {W } 6: end if

In this section, we present our scalable recursive greedy algorithm for clustering webpages. At a high level our algorithm can be describe as follows: at every step, we refine the intermediate clustering by greedily partitioning one of the clusters if the mdl score of the new partitioning improves. We stop when none of the intermediate clusters can be further partitioned without decreasing the mdl score. We implement efficiently the above outlined procedure as follows:

• Using the local substructure property (Lemma 2.5.1), we can show that a recur-sive implementation is sound (Section 2.6).

• We greedily explore a set of partitions, each of which is a set cover with small cardinality k, where urls in k − 1 sets have at least one term in common (i.e., at least one new script term). The small set covers include (a) {W (t), W −W (t)}, and (b) {U1, U2, . . . , Uk−1, W − ∪k�=1−1U�}, where Ui’s are first k − 1 sets in

the greedy set covering using the sets {W (t)}t. The intuition behind using set

covers of small size is motivated by the optimal solution for the special case for single term web pages (Lemma 2.6.1). In fact we show that our greedy partitioning is optimal for single term web pages (Section 2.6).

• Rather than actually computing the mdl score of the current clustering, we show that one can equivalently reason in terms of δmdl, the decrease in mdl∗

(Equa-tion 2.3) of the child clusters with respect to the parent cluster. We show that δmdlcan be efficiently computed using the set of functional dependencies in the

parent cluster (Section 2.6).

• Finally, we show how to incorporate additional information to improve the web site clustering solution (Section 2.6).

(35)

Algorithm 2 FindGreedyCandidate Input: W , a set of urls

Output: A greedy partitioning C if mdl cost improves, null other-wise

1: T =_∪w∈WT (w)− script(W )

2: _{Set C ← ∅ // set of candidate partitions} 3:

4: // Two-way Greedy Partitions

5: for t ∈ T do

6: Ct={W (t), W − W (t)}, where W (t) = {w|t ∈ T (w)}

7: _{C ← C ∪ {C}t}

8: end for 9:

10: // k-way Greedy Partitions (k > 2)

11: Let Ts = {a1, a2, . . .} be an ordering of terms in T such that ai appears in the

most number of urls in W − ∪i−1 �=1W (a�). 12: for 2 < k ≤ kmaxdo 13: Ui= Wai− ∪ i−1 �=1Wa�, Wrest= W − ∪ k �=1Wa� 14: Ck ={U1, U2, . . . , Uk, Wrest} 15: _{C ← C ∪ C}k 16: end for 17:

18: // return best partition if mdl improves

19: Cbest← arg minC∈Cδmdl(C)

20: if δmdl(Cbest) > 0then 21: return Cbest 22: else 23: return null 24: end if Recursive Partitioning

Our recursive implementation and greedy partitioning are outlined in Algorithms 1 and 2 respectively. We start with W , the set of all web pages and greedily find a par-titioning with the lowest mdl cost (highest δmdl). If the mdl of the solution improves

(i.e., δmdl> 0), we proceed to recursively partition the clusters. Else, we return W .

Candidates Greedy Partitions

As mentioned above, we use explore set covers with small cardinality to compute the greedy partition. First, we find the best two-way partitioning of W . In order to reduce the mdl cost, at least one of the two clusters must have more schema terms than W . That is, one of the clusters must have at least one more term that appears in all web pages than in W . We accomplish this by exploring all splits of the form {W (t), W − W (t)}, for all t that is not a script term in W .

(36)

A greedy strategy that only looks at 2-way splits as described above may not suffi-ciently explore the search space, especially if none of the two-way splits {W (t), W − W (t)} reduce the mdl cost. For instance, consider a scenario with 3N webpages W , N of which have exactly one term names a1, N others have a2and the final N have

a single term a3. Then, mdl∗({W }) = c − 3N log(3N) − α · 0 (a single cluster

has no script terms). Any two-way split has cost mdl∗₍_{{W (a}

i), W − W (ai)}) =

2· c − N log N − 2N log(2N) − α · N. It is easy to check that mdl∗_{of any two-way}

split is larger than mdl∗₍_{{W }) for a sufficiently large N and α = 1. Hence, our}

recursive algorithm would stop here. However, from Lemma 2.6.1, we know that the optimal clustering for the above example is {W (a1), W (a2), W (a3)}.

Motivated by the small cardinality effect, (Theorem 1), we also explore k-way splits that partition W into k clusters, where k −1 clusters have at least one new script term. However, since we can not efficiently enumerate all the k-way splits (O(nk_),

where n is the number of distinct non-script terms in W ), we limit our search to the following. We first order the non-script terms in W as a1, a2, . . . , an, and then for

every 2 < k ≤ kmaxwe partition W into {U1, U2, . . . , Uk−1, W − ∪iUi}. Uiis the

set of web pages that contain aibut none of preceding a�, � < i. Since, we would like

to cluster W into k sets whose sizes are as large as possible, we order the non-schema terms as follows: aiis the non-schema term that appears in the most number of urls

that do not contain any a�, � < i. Note that this is precisely the ordering returned by

the greedy algorithm for set cover, when the sets are {Wt}. We show that if kmaxis

sufficiently large, then the above algorithm discovers opt(W ) for a set of single term web pages.

Lemma 2.6.3. If kmaxis sufficiently large, Algorithm 2.6 discovers the optimal

solu-tion when W is a set of single term web pages. Efficiently computing the best greedy partition

In order to find the best greedy partition, when generating each partition we also com-pute δmdl, the decrease in description length when replacing {W } with the partition

{W1, W2, . . . , Wk}. That is, δmdl = mdl∗({W }) − mdl∗({W1, W2, . . . , Wk}) = −c +� i |Wi| log |Wi| + ∆ (2.4) ∆ = � i |Wi| · si− |W | · s (2.5)

where, siis the size of script(Wi)and s is the size of script(W ). Since every script

(37)

terms in Wi. We now show how to efficiently compute (si− s) for all clusters in

every candidate partition in a single pass over W . Thus if the depth of our recursive algorithm is �, then we make at most � passes over the entire dataset. Our algorithm will use the following notion of functional dependencies to efficiently estimate (si−

s).

Definition 1 (Functional Dependency). A term x is said to functionally determine a term y with respect to a set of web pages W , if y appears whenever x appears. More formally,

x_→W y ≡ W (x) ⊆ W (y) (2.6)

We denote by F DW(x)the set of terms that are functionally determined by x with

respect to W .

Two-way splits First let us consider the two-way split {W (t), W − W (t)}. Since t appears in every web page in W (t), by definition a term t�_{is a script term in W (t) if}

and only if t�_{∈ F D}

W(t). Similarly, t does not appear in any web page in W − W (t).

Hence, t�_{is a script term in W −W (t) if and only if t}� _{∈ F D}

W(¬t); we abuse the FD

notation and denote by F DW(¬t) the set of terms appear whenever t does not appear.

Therefore, script(W (t)) = F DW(t), and script(W − W (t)) = F DW(¬t).

The set F DW(t)can be efficiently computed in one pass. We compute the number

of web pages in which a single term (n(t)) and a pair of terms (n(t, t�₎₎_appears.

F DW(t) ={t�|n(t�) = n(t, t�)} (2.7)

To compute F DW(¬t), we find some web page w that does not contain t. By

defini-tion, any term that does not appear in T (w) can not be in F DW(�= t). F DW(¬t) can

be computed as

{t�|t�∈ T (w) ∧ n − n(t) = n(t�)− n(t, t�)} (2.8) where, n = |W |.

k-way splits Given an ordering of terms {a1, a2, . . . , akmax}, our k-way splits are

of the form {U1, U2, . . . , Uk−1, W − ∪iUi}, where Ui denotes the set of web pages

that contain ai but none of the terms a�, � < i. Therefore (again abusing the FD

notation), script(Ui) = F DW(¬a1∧ ¬a2¬ . . . ¬ai−1∧ ai). The final set does not

contain any of the terms a�, � < k. Hence, script(W − ∪iUi) = F DW(∧ki=1−1ai).

The F D sets are computed in one pass over W as follows. We maintain array C such that C(i) is the number of times aiappears and none of a�appear 1 ≤ � < i. For

(38)

times t appears when aiappears and none of a�appear 1 ≤ � < i. Similarly, array R

is such that R(i) = |W |−�i

�=1C(�). For each non script term t in W , Rtis an array

such that Rt(i) =|W (t)| −�i_�=1Ct(�). The required F D sets can be computed as:

F DW((∧�−1i=1¬ai)∧ a�) = {t|C(�) = Ct(�)} (2.9)

F DW(∧�i=1¬ai) = {t|R(�) = Rt(�)} (2.10)

Incorporating additional knowledge

Our problem formulation does not take into account any semantics associated with the terms appearing in the urls or the content. Thus, it can sometimes choose to split on a term which is “clearly” a data term. E.g., consider the urls u1, u2, u3, u4

from Section 2.3). Intuitively, picking a split Ceats ={W (eats), W − W (eats)}

correctly identifies the scripts eats and todo.

However, sometimes the split CSeattle = {W (Seattle), W − W (Seattle)}

has a lower description length than the correct split. This is because of a functional dependency from Seattle to WA. Thus, a split on Seattle makes two terms contants, and the resulting description length can be smaller than the correct split. If we have regions and countries in the urls in addition to states, the Seattle split is even more profitable.

If we have the domain knowledge that Seattle is a city name, we will know that its a data term, and thus, we won’t allow splits on this value. We can potentially use a database of cities, states, or other dictionaries from the domain to identify data terms. Rather than taking the domain centric route of using dictionaries, here we present a domain agnostic technique to overcome this problem. Recall that our goal is to identify clusters such that the web pages in each cluster can be generated using a single script and a set of tuples. We impose the following semantic script language constraint on our problem formulation – if t is a script term for some cluster W , then it is very unlikely that t is a data term in another cluster W�_{. This constraint}

immediately solves the problem we illustrated in the above example. CSeattlehas one

cluster (W (Seattle)) where WA is a script term and another cluster where WA is a data term. If we disallow such a solution, we indeed get the right clustering Ceats.

Hence, to this effect, we modify our greedy algorithm to use a term t to create a partition W (t) if and only if there does not exist a term t� _{that is a script term}

in W (t) and a data term is some other cluster. This implies the following. First, if t� _{∈ script(W (t)), then t}� _{∈ F D}

W(t). Moreover, both in the two-way and k-way

greedy partitions generate by our greedy algorithm, t�_{can be a data term in some other}

(39)

script language constraint in our greedy algorithm as:

split on t if and only if F DW(t)⊆ script(W ) (2.11)

In Algorithm 2.6, the above condition affects line number 5 to restrict the set of terms used to create two-way partitions, as well as line number 11 where the ordering is only on terms that satisfy Equation 2.11.

2.7 Experiments

We first describe the setup of our experiments, our test data, and the algorithms that we use for evaluation.

Datasets As we described in Section 2.1, our motivation for structural clustering stems from web-scale extraction. We set up our experiments to target this. We con-sider a seed database of italian restaurants, which we created by searching the web. Table 2.1 shows a subset of web sites that we found using this process. Most of these are web sites specializing in Italian restaurants, although we have a couple which are generic restaurant web sites, namely chefmoz.com and tripadvisor.com. For each web site, we crawl and fetch all the webpages from those sites. The second col-umn in the table lists the number of webpages that we obtained from each site. Every resulting site has, along with a set of restaurant pages, a bunch of other pages that include users, reviews, landing pages for cities, attractions, and so on. Our objective is to identify, from each web site, all the pages that contain restaurant information, which we can use to train wrappers and extraction.

For each web site, we manually identified all the webpages of interest to us. We use this golden data to measure the precision/recall of our clustering algorithms. For each clustering technique, we study its accuracy by running it over each web site, pick-ing the cluster that overlaps the best with the golden data, and measurpick-ing its precision and recall.

Algorithms We will consider several variants of our technique: Mdl-U is our clustering algorithm that only looks at the urls of the webpages. Mdl-C is the variant that only looks at the content of the webpages, while Mdl-UC uses both the urls and the content.

In addition to our techniques, we also look at the techniques that are described in a recent survey [Got08], where various techniques for structural clustering are com-pared. We pick a technique that has the best accuracy, namely, the one that uses a Jaccard similarity over path sequences between webpages, and uses a single-linkage hierarchical clustering algorithm to cluster webpages. We call this method CP-SL.

(40)

Website Pages Mdl-U Mdl-C Mdl-UC CP-SL p r t(s) p r t(s) p r t(s) p r 2spaghi.it 20291 1.00 1.00 2.67 1.00 1.00 182.03 0.99 0.34 128.79 1.00 0.35 cerca-ristoranti.com 2195 1.00 1.00 1.17 1.00 0.91 8.01 1.00 0.91 7.39 0.99 0.74 chefmoz.org 37156 1.00 0.72 16.18 1.00 0.98 116.73 1.00 0.98 75.54 1.00 0.93 eristorante.com 5715 1.00 1.00 2.07 1.00 1.00 13.63 1.00 1.00 12.62 0.43 1.00 eventiesagre.it 48806 1.00 1.00 15.96 1.00 1.00 799.79 1.00 1.00 484.28 1.00 1.00 gustoinrete.com 5174 1.00 1.00 1.04 1.00 1.00 16.84 1.00 1.00 15.03 - -ilmangione.it 18823 1.00 1.00 2.08 1.00 1.00 262.44 1.00 0.29 214.24 1.00 0.63 ilterzogirone.it 6892 1.00 0.26 1.32 1.00 1.00 108.93 1.00 1.00 103.22 1.00 0.44 iristorante.it 614 1.00 0.54 0.49 1.00 0.96 26.45 1.00 0.96 25.12 1.00 0.95 misvago.it 14304 0.36 1.00 3.66 0.99 0.93 387.13 0.99 0.93 297.72 1.00 1.00 mondochef.com 1922 1.00 0.79 1.04 1.00 0.79 11.90 1.00 0.79 10.79 0.23 0.89 mylunch.it 1500 0.98 0.94 1.41 0.98 1.00 4.26 0.98 1.00 3.82 0.98 0.97 originalitaly.it 649 1.00 0.96 0.48 0.97 0.85 37.67 0.97 0.85 31.95 0.49 0.93 parks.it 9997 1.00 1.00 1.67 1.00 1.00 15.28 1.00 0.50 14.91 - -prenotaristorante.com 4803 1.00 0.50 1.33 1.00 0.63 16.62 1.00 0.63 14.05 1.00 0.66 prodottitipici.com 31904 1.00 1.00 4.58 0.72 0.68 522.79 0.72 0.68 465.39 0.49 0.51 ricettedi.it 1381 1.00 1.00 0.88 0.60 0.94 5.63 0.60 0.94 5.29 1.00 0.74 ristorantiitaliani.it 4002 0.99 0.82 1.28 0.99 0.92 15.63 0.62 0.64 12.31 0.77 0.50 ristosito.com 3844 1.00 1.00 1.37 1.00 1.00 19.91 1.00 1.00 17.36 1.00 0.97 tripadvisor.com 10000 0.96 1.00 15.01 1.00 0.82 1974.58 0.12 0.98 1527.70 1.00 0.64 zerodelta.net 191 1.00 1.00 0.21 1.00 1.00 96.21 0.85 1.00 102.16 0.03 1.00 borders.com 176430 0.95 1.00 8.50 0.95 1.00 8.50 1.00 0.93 1055.29 0.97 0.94 chegg.com 8174 0.95 0.99 2.04 0.95 0.99 2.04 0.99 0.95 30.70 1.00 0.53 citylights.com 3882 1.00 0.63 1.65 1.00 0.63 1.65 1.00 0.99 21.30 1.00 0.95 ebooks.com 51389 1.00 1.00 4.96 1.00 1.00 4.96 0.95 0.99 1406.89 1.00 0.87 houghtonmifflinbooks.com 23651 0.76 1.00 3.41 0.76 1.00 3.41 0.92 0.86 240.97 0.41 1.00 litlovers.com 1676 1.00 1.00 1.09 1.00 1.00 1.09 0.92 0.92 5.25 1.00 0.93 readinggroupguides.com 8587 0.88 1.00 2.19 0.88 1.00 2.19 0.92 0.85 79.80 0.50 1.00 sawnet.org 1180 1.00 1.00 0.61 1.00 1.00 0.61 1.00 0.85 2.97 1.00 0.61 aol.com 56073 1.00 1.00 11.97 0.98 0.80 508.76 1.00 1.00 605.67 0.71 1.00 bobandtom.com 1856 1.00 0.89 1.07 0.82 0.96 7.87 0.96 0.82 9.04 1.00 0.82 dead-frog.com 2309 1.00 1.00 1.45 0.72 0.88 31.91 1.00 0.95 37.98 1.00 0.93 moviefone.com 250482 1.00 1.00 8.19 0.91 0.59 3353.17 0.97 1.00 3854.21 1.00 0.94 tmz.com 211117 1.00 0.88 10.74 0.87 0.88 1712.31 0.93 0.82 2038.46 - -yahoo.com 630873 0.26 1.00 9.39 0.99 0.79 11250.44 0.98 0.94 12931.55 0.38 0.36 dentistquest.com 2414 1.00 1.00 0.97 1.00 1.00 7.08 1.00 1.00 12.15 1.00 0.33 dentists.com 8722 0.99 1.00 1.69 0.69 0.99 12.89 1.00 1.00 43.27 0.23 1.00 dentistsdirectory.us 625 0.97 0.99 0.37 0.95 0.99 2.53 0.95 0.99 2.78 0.96 0.75 drscore.com 14604 1.00 1.00 3.53 1.00 0.72 124.92 1.00 1.00 199.57 1.00 0.67 healthline.com 98533 1.00 1.00 23.33 1.00 0.85 2755.18 1.00 1.00 1624.53 1.00 0.54 hospital-data.com 29757 1.00 1.00 4.91 1.00 1.00 344.82 1.00 1.00 143.60 1.00 0.79 nursinghomegrades.com 2625 1.00 1.00 1.32 0.90 1.00 15.08 0.98 1.00 17.68 1.00 0.45 vitals.com 34721 1.00 1.00 7.46 0.99 0.92 422.26 0.99 0.92 793.10 1.00 0.50 Average 0.95 0.93 0.91 0.87 0.97 0.93 0.84 0.77 Total 1849843 186.74 24143.35 29799.22

Table 2.1: Comparison of the different clustering techniques

Accuracy

Table 2.1 lists the precision/recall of various techniques on all the sites, as well as the average precision and recall. We see that Mdl-U has an average precision of 0.95 and an average recall of 0.93, supporing our claim that urls alone have enough information to achieve high quality clustering. On some sites, Mdl-U does not find the perfect cluster. E.g., in chefmoz, a large fraction of restaurants (72% to be exact), are from United States, and therefore Mdl-U thinks its a different cluster, separating it from the other restaurants. Mdl-UC, on the other hand, corrects this error, as it finds that the content structure in this cluster is not that different from the other restaurants. Mdl-UC, in fact, achieves an average precision and recall close to 1. On the other hand, Mdl-C performs slightly worse that Mdl-U, again confirming our belief that urls are often more informative and useful than the content.

(41)

0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 precision recall

Figure 2.1: Precision-Recall of Mdl-U by varying α

is really slow, so to keep the running times reasonable, we sampled only 500 webpages from each web site uniformly at random, and ran the algorithm on the sample. For a couple of sites, the fraction of positives pages was so small that the sample did not have a representation of positives pages. For these sites, we have not included the precision and recall. We see that the average precision/recall, although high, is much lower that what we obtain using our techniques.

Dependency on α

Recall that the α parameter controls both the small cardinality and large compenent effect, and thus affects the degree of clustering. A value of α = 0 leads to all pages being in the same cluster and α = ∞ results in each page being in its own cluster. Thus, to study the dependency on α, we vary α and compute the precision and recall of the resulting clustering. Fig. 2.1 shows the resulting curve for the Mdl-U algorithm; we report precision and recall numbers averaged over all Italian restaurant websites. We see that the algorithm has a very desirable p-r characteristic curve, which starts from a very high precision, and remains high as recall approaches 1.

Running Times

Figure 2.2 compares the running time of Mdl-U and CP-SL. We picked one site (tripadvisor.com) and for 1 ≤ � ≤ 60, we randomly sampled (10 · �) pages from the site and performed clustering both using Mdl-U and CP-SL. We see that as the number of pages increased from 1 to 600, the running time for Mdl-U increases

(42)

0.001 0.01 0.1 1 10 100 0 100 200 300 400 500 600 time (sec) # of webpages MDL-U CP-SL

Figure 2.2: Running Time of Mdl-U versus CP-SL

0 200 400 600 800 1000 1200 1400 1600 1800 0 100 200 300 400 500 600 700 time (sec) # of webpages (thousands)

Figure 2.3: Running Time of Mdl-U

from about 10 ms to about 100 ms. On the other hand, we see a quadratic increase in running time for CP-SL (note the log scale on the y axis); it takes CP-SL about 3.5 seconds to cluster 300 pages and 14 (= 3.5 ∗ 22_{) seconds to cluster 600 pages.}

Extrapolating, it would take about 5000 hours (≈ 200 days) to cluster 600,000 pages from the same site.

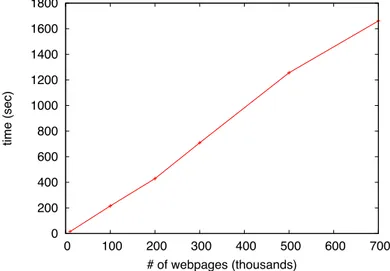
In Figure 2.3 we plotted the running times for clustering large samples of 100k, 200k, 300k, 500k and 700k pages from the same site. The graph clearly illustrates

(43)

that our algorithm is linear in the size of the site. Compared to the expected running time of 200 days for CP-SL, Mdl-U is able to cluster 700,000 pages in just 26 minutes!

2.8 Conclusions

In this chapter, we present highly efficient and accurate algorithms for structurally clustering webpages. We explored the idea of using URLs for structural clustering of web sites by proposing a principled framework, grounded in information theory, that allows us to leverage URLs effectively, as well as combine them with content and structural properties. We proposed an algorithm, with a linear time complexity in the number of webpages, that scales easily to web sites with millions of pages. The proposed approach has been tested with several experiments that proved the quality and the scalability of the technique. We found that, for example, we were able to cluster a web site with 700,000 pages in 26 seconds, an estimated 11,000 times faster than competitive techniques.

(44)

Web Source Discovering And Analysis

In Chapter 2 we have proposed a solution to the problem of how to automatically cluster structured web pages. The technique resulted to be very scalable, but it relies on the dump of the analyzed web sources or, at least, the knowledge of all the urls. Keeping in mind that the final goal is to collect large amount of structured information from the web, in this chapter we propose techniques to discover new the web sites that contain the information we are looking for and to identify which pages are of interest. To do this we build a description of the target entity and we query a search engine to discover new web sites and select the ones containing the correct information. The clustering of the web pages is used to determine which pages, among all the pages in the web sites, contain the data of interest.

3.1 Introduction

For the sake of scalability of the publishing process, data–intensive web sites publish pages where the structure and the navigation paths are fairly regular. Within each