Capitolo 1 Il problema dei cammini bilanciati in reti acicliche

Capitolo 1

Il problema dei cammini bilanciati in reti acicliche

1.1 Formulazione

Sia G = (V, E) una rete orientata e aciclica con #V = n e #E = m. Sotto queste ipotesi G ha una struttura a livelli che è possibile mettere in evidenza rinumerando i suoi nodi in accordo ad un ordinamento topologico. Sia h il numero di livelli di G e sia

V =V₁UV₂U U... V_h una partizione dell’insieme dei nodi tale che

( )

,i j E

∀ ∈ ∃ p q, ∈

{

1, 2,...,h

}

tali che i V∈ , _p j V∈ e p < q. _q

Ad ogni arco

( )

,i j ∈E è associato un costo intero e non negativo che indichiamo con

il simbolo . Siano dati inoltre k nodi sorgente c_ij

{

s s₁, ,...,₂ s_k

}

e k nodi destinazione

{

t t1, ,...,2 tk

}

con . Il problema dei cammini bilanciati su G è il problema di

indivi-duare k cammini che connettano le k sorgenti e le k destinazioni date minimizzando la differenza in costo tra il cammino più costoso e quello meno costoso. Ogni sorgente può essere connessa a una qualsiasi destinazione e nessun nodo sorgente o destinazione può rimanere escluso.

2 k ≥

Senza perdere di generalità si può assumere che i nodi sorgente appartengano a e che i nodi destinazione appartengano a . Inoltre, ci si può ricondurre ad una formulazione del problema che fa uso di un unico nodo sorgente e di un unico nodo destinazione nel seguente modo: inseriamo in V due nuovi nodi s e t e in E i 2k archi di costo zero

1

V

h

V

( )

s s, _i

e per i = 1, 2, …, k. In tal modo s e t appartengono a due livelli fittizi di G che indichiamo con e , rispettivamente. Il problema dei cammini bilanciati può ora essere formulato in maniera equivalente come il problema di individuare k cammini da s a t, che coinvolgano tutti gli archi del tipo

(

t t_i,

)

0

V V_h+1

bilanciati, tali cioè che sia minimizzata la differenza in costo tra il cammino più costoso e quello meno costoso.

Nelle varianti arc-disjoint e node-disjoint del problema si richiede anche che i k cammi-ni non abbiano, rispettivamente, alcun arco e alcun nodo in comune.

Un’ulteriore variante del problema è quella in cui vengono date k coppie di nodi origi-ne-destinazione,

(

s t1 1,

)

,

(

s t2, 2

)

, … ,

(

s tk, k

)

, e i k cammini bilanciati da individuare

devono connettere ogni origine con la rispettiva destinazione.

1.2 Complessità computazionale in tempo

In questa sezione si fa ricorso al Subset Sum problem [9] per mostrare che il problema dei cammini bilanciati in reti acicliche è NP-arduo. In un’istanza del Subset Sum pro-blem, dato un intero positivo C e q coefficienti interi positivi , i = 1, …, q, si deve stabilire se esiste un sottoinsieme di tali coefficienti la cui somma è esattamente C. In [9] è dimostrato che il Subset Sum problem è NP-completo.

i

a

Teorema 1.1 ( [6] ) Il problema dei cammini bilanciati in reti acicliche è NP-arduo. Dim. Per semplicità nella dimostrazione si considera il caso k = 2. La dimostrazione viene effettuata mostrando come il Subset Sum problem si riduce polinomialmente alla versione decisionale del problema dei cammini bilanciati. Il problema dei cammini bi-lanciati, nella sua versione decisionale, generalizza il seguente problema: data una rete pesata aciclica G, esistono due cammini il cui costo è esattamente C, per un dato intero positivo C? Data un’istanza del Subset Sum problem, si costruisce una rete con h = q+2 livelli: il livello contiene due nodi sorgente e , il livello contiene due nodi destinazione e . In ogni livello intermedio , 1 < i < h, viene inserito un unico no-do 1 V s₁ s₂ V_h 1 t t₂ V_i i

x , corrispondente al coefficiente (i-1)-esimo ai−1. L’insieme degli archi è definito come segue:

{

(

x xi, j

)

|i< j i, =2,...,q

}

U

{

(

x t_i, ₁

)

|i=2,...,q+ U1

}

{

(

s t₂, ₂

)

}

e i costi degli archi sono: _{1 1} i s x i c =a₋ per i=2,...,q+ 1 cx x_{i j} =aj−1 per i< j i, =2,...,q 1 0 i x t c = per i=2,...,q+ 1 c_{s t2 2} = C

Ci si riporta infine al caso di un’unica sorgente e un’unica destinazione, aggiungendo i due nodi s e t e i quattro archi di costo zero

(

s s, 1

)

,

(

s s, 2

)

,

( )

t t1, e . La rete a li-velli ottenuta è mostrata nella figura sottostante (Figura 1).

(

t t2,

)

2 i x 2 x x_q+1 1 t 2 t 2 s 1 s s t 0 0 0 0 0 0 0 C 1 a q a q a 1 i a₋ 1 i a₋ 1 V V₂ i V ₁ h V₋ h V Figura 1

Bisogna ora mostrare che il Subset Sum problem ha soluzione se e solo se nella rete a livelli costruita esistono due cammini da s a t che connettono s1 e a e s2 t1 t ,

rispetti-vamente, e il cui costo sia esattamente C. Supponiamo che esista un sottoinsieme dei coefficienti a_i la cui somma è esattamente C e sia

{

}

1, 2,..., p | per

i i i j l

a a a i <i j< tale l sottoinsieme. Vale quindi

1 j p i j a C = =

∑

. Allora i cammini 1 2 1 ( , ,1 i 1, i 1,..., ip 1 1, , ) P = s s x ₊ x ₊ x ₊ t t

e P₂ =( , , , )s s t t_{2 2} hanno entrambi costo C.

Viceversa, se esistono due cammini di costo C che connettono

rispettivamente, uno dei due, sia esso , deve necessariamente contenere gli archi

. è dunque un cammino del tipo con

1 e P P_{2 2}

)

1 e a e 2 1 s s t t 1 P

(

s s, 1

) (

e t t1, P1 ( , ,s s x1 i1+1,xi2+1,...,xip+1 1, , )t t

{

1,...,

}

per 1,..., j

i ∈ q j= p, e quindi la somma dei coefficienti

1, 2,..., p

i i i

a a a è

esattamen-te C. □ Il Subset Sum problem dunque ha soluzione se e solo se il problema dei cammini bilan-ciati da s a t ad esso associato restituisce zero come valore ottimo della funzione obiet-tivo.

1.3 Un algoritmo pseudopolinomiale

Nella descrizione dell’algoritmo si fa riferimento alla formulazione del problema con un’unica sorgente s, connessa alle k sorgenti del livello , e con un’unica destina-zione t, connessa ai nodi destinadestina-zione del livello .

i

s V₁

i

t V_h

1.3.1 Descrizione

Sia U il costo (oppure una stima per eccesso del costo) del cammino più costoso di G. Si costruisca una nuova rete G_U =

(

V_U,E_U

)

, detta rete espansa, nel seguente modo:

{

, ,...,1

}

U k V = s s s U

{

ip,p=0,1,..., |U i V∈ \ , ,...,

{

s s₁ sk

}

}

{

(

p, p cij

)

| ( , ) ,

}

U ij E = i j + i j ∈E p≤ −U c .

In sono state inserite U copie di ogni nodo i di G: la p-esima copia di i rappre-senta il nodo i in quanto raggiungibile dalla sorgente s in G attraverso un cammino di

U

costo esattamente p. Ad ogni cammino da s a t di costo p in G corrisponde quindi un cammino orientato da s a in p .

t G_U

La rete è una rete a livelli la cui dimensione è pseudopolinomiale nella dimensione della rete di input G; infatti ha

U

G

U

G Ο(nU ) nodi e (mU )Ο archi.

Una volta costruita la rete G_U, si effettua una ricerca binaria nell’intervallo

[

0,U

]

e, per ogni valore intero δ∈

[

0,U

]

, si eseguono le seguenti operazioni:

• si costruisce la famiglia di sottografi di contenente tutti i cammini di che vanno da s ai nodi in

U

G G_U

{

p,..., p

}

t t +δ per ogni intero p U≤ − ; δ

• si verifica se almeno uno dei sottografi costruiti contiene k cammini distinti. Più precisamente, si verifica se almeno uno dei sottografi contiene k cammini distin-ti da s a desdistin-tinazioni appartenendistin-ti all’insieme

{

p,..., p

}

t t +δ , in cui sono coinvolti gli archi

(

s s, _i

)

∀ ∈i

{

1, 2,...,k

}

.

L’ultimo insieme di cammini restituito è un insieme ottimo di cammini e il corrispon-dente δ è il valore ottimo della funzione obiettivo, cioè la minima differenza in costo tra i cammini.

Dato δ∈

[

0,U

]

e un sottografo di G_U contenente i cammini di G_U da s ai nodi in

{

p,..., p

}

t t +δ , per verificare se il sottografo in esame contiene k cammini distinti si pro-cede con i seguenti cinque passi:

1. i nodi

{

p,..., p

}

t t +δ vengono fusi in un unico nodo, sia esso t%;

2. ∀ =i 1, 2,...,k si fondono in un unico nodo t% tutte le copie del nodo destinazione _i originale appartenenti al sottografo; t_i

3. si connettono i nuovi nodi tramite gli archi

( )

t t%%_i, per 1,2,...,i= k;

4. si assegna capacità unitaria agli archi uscenti da s e agli archi ; ai restanti archi invece si assegna una capacità arbitrariamente alta;

(

t t%%_i,

)

Se il valore del flusso massimo è uguale a k, allora in G esistono k cammini distinti la cui differenza in costo tra il più costoso e quello meno costoso è al più δ . Se invece il valore del flusso massimo è minore di k per ogni sottografo contenente cammini la cui distanza in costo è al più δ , allora la differenza in costo di ogni insieme di k cammini distinti è maggiore di δ . In entrambi i casi l’algoritmo procede con il successivo valore di δ come stabilito dalla ricerca binaria.

1.3.2 Complessità computazionale in tempo dell’algoritmo

Effettuando una ricerca binaria nell’intervallo

[

0,U

]

, l’algoritmo controlla (log )Ο U valori di δ . Per ogni valore δ considerato, si calcola il valore del flusso massimo in

reti che hanno archi. Poiché il valore del flusso massimo è al più k, que-sto può essere calcolato in tempo

( )U

Ο Ο(mU)

) (kmU

Ο tempo in ogni sottografo. La complessità in tempo dell’intero algoritmo è quindi ₍ 2_log .

kmU U

Ο )

)

1.4 Le varianti arc-disjoint e node-disjoint

Consideriamo ora le varianti arc-disjoint e node-disjoint del problema dei cammini bi-lanciati. Tali versioni sono NP-ardue in senso forte. Nel seguito mostreremo come la richiesta che i cammini siano node-disjoint può essere trasformata, in tempo polinomia-le, in una equivalente richiesta di cammini arc-disjoint e viceversa. Nel seguito verrà quindi analizzato esplicitamente solo il caso node-disjoint; i risultati ottenuti potranno essere poi applicati al caso arc-disjoint tramite la riduzione polinomiale sotto riportata.

1.4.1 Equivalenza delle varianti node-disjoint e arc-disjoint

Sia G = (V, E) il grafo di input su cui è formulato il problema dei cammini bilanciati node-disjoint. Per formulare un problema equivalente, in cui però si richiede che i cam-mini bilanciati siano arc-disjoint anziché node-disjoint, si costruisce un grafo

nel seguente modo:

(

' ', '

{ }

1 2 ' , i V V i ∈ =

_U

i

( )

{

1 2

}

{

(

2 1

)

( )

}

' , | , | , E = i i i V∈ U i j i j ∈E = 2 dove ∀ ∈i V c_{i i}1 2 =0 e ∀

( )

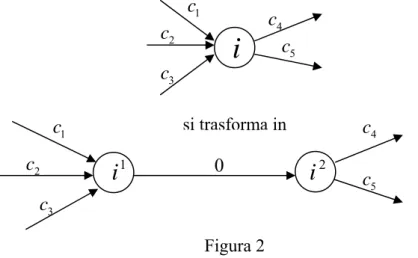
i j, ∈E c_{i j}2 1 c_ij.

In Figura 2 è mostrata la trasformazione effettuata localmente ad un nodo.

Figura 2 1

i

i

si trasforma in 1 c 1 c 2 c 2 c 3 c 3 c 4 c 4 c 5 c 5 c 0 2

i

Se è un cammino orientato in G, il corrispondente cammino in è . E’ immediato verificare che due cammini in G sono node-disjoint se e solo se i corrispondenti cammini in G sono arc-disjoint.

1 2 ( , ,..., )_l P= i i i G' 1 2 1 2 1 2 1 1 2 2 ' ( , , , ,..., , )_{l l} P = i i i i i i P₁ e P 1' e '2 P P '

La riduzione in tempo polinomiale dal caso arc-disjoint a quello node-disjoint si ottiene come descritto in [12] costruendo il line graph (definito in [10]) associato al grafo di in-put G. Più precisamente, il line graph orientato L G

( ) (

= V E', '

)

di un grafo orientato G

è così definito:

( )

{

}

' u| , v V = x u v ∈E

(

)

( )

( )

{

}

' u, v | , e , v l E = x x u v ∈E v l ∈E . In Figura 3 è mostrato un esempio di costruzione di line graph.

1 4 3 2 1 2 x x42 3 2 x 1 3 x x34 Figura 3 G L(G)

Sia G = (V, E) il grafo di input su cui è formulato il problema dei cammini bilanciati arc-disjoint. Come primo passo della trasformazione si aggiungono a G due archi

( ) (

s s, e ,t t

)

di costo 0 . Si costruisce ora il line graph associato a G denotando con

i nodi corrispondenti agli archi

' e '

s t

( ) ( )

s s, e ,t t , rispettivamente, e assegnando

co-sto 0 a tutti gli archi. A queco-sto punto, si sdoppia ogni vertice del line graph in due copie e e si crea un arco

u v

w=x

1

w w₂

(

w w₁, ₂

)

assegnandogli un costo pari a , in

mo-do che tutti gli archi entranti in (uscenti da) sono ora entranti in (uscenti da ). Il grafo costruito è aciclico e in esso ci sono k cammini node-disjoint da se e solo se in G ci sono k corrispondenti cammini arc-disjoint da . L’intera

trasforma-zione può essere effettuata in tempo

uv c w w₁ w₂ ' G s' a 't a s t

( )

m

Ο . Algoritmi e risultati computazionali ottenu-ti per il caso node-disjoint possono quindi essere applicaottenu-ti anche al caso arc-disjoint so-stituendo Ο

( )

n con Ο

( )

m nelle valutazioni della complessità in tempo.

1.4.2 Complessità computazionale in tempo

Teorema 1.2 Il problema dei cammini bilanciati node-disjoint è NP-arduo in senso for-te.

Dim. La dimostrazione si effettua per riduzione dal problema 3-Dimensional Matching (3DM). In 3DM sono date q triple <i,j,p> di interi compresi compresi tra 1 e k, e si cer-cano k di queste triple in modo tale che, per ogni intero r∈

[ ]

1,k , tra esse ci sia

esatta-mente una tripla <i,j,p> con i r= , esattamente una con j r= ed esattamente una con p= . r

Data dunque un’istanza di 3DM, si costruisce una rete con un nodo sorgente s, un nodo destinazione t e tre livelli intermedi in cui i nodi rappresentano gli interi tra 1 e k, siano essi V₁=

{

u₁,...,u_k

}

, V₂ =

{

v₁,...,v_k

}

e V₃ =

{

w₁,...,w_k

}

. L’insieme degli archi è invece il

seguente:

E=

{

( )

s t,

}

U

{

( )

s u, j | j=1,...,k

}

U

{

( )

w tj, | j=1,...,k

}

U

(

,

) (

, ,

)

|

, , è l' esima tripla tra quelle date in input

i j j p u v v w i j p r ⎧ ⎫ ⎪ ⎪ ⎨ ⎬ < > − ⎪ ⎪ ⎩ ⎭

I costi degli archi sono:

cst = + q 1 0 j su c = per j=1,...,k 0 j w t c = per j=1,...,k i j u v c =r e 1 j p v w

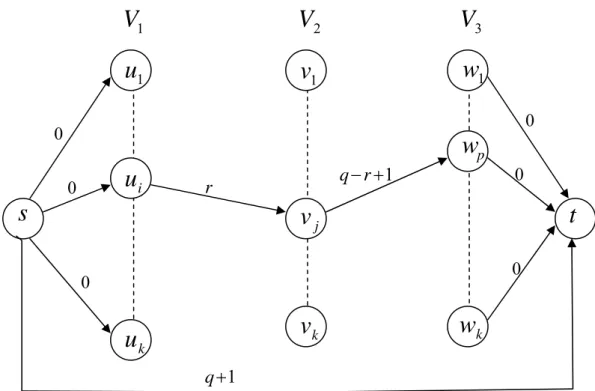
c = − +q r con <i j p, , > r-esima tripla di input In Figura 4 è mostrata la rete così ottenuta.

E’ semplice vedere che, oltre al cammino composto dal singolo arco

(

, c’è una cor-rispondenza biunivoca tra i cammini da s a t di costo q+1 e le triple di 3DM. Si può concludere quindi che ci sono k+1 cammini node-disjoint da s a t, ognuno di costo q+1,

)

,

se e solo se c’è una soluzione ammissibile per l’istanza di 3DM in esame. Si noti che, se tali cammini esistono, ad essi è associato un valore ottimo della funzione obiettivo pari a zero. □

Corollario 1.1 Il problema dei cammini bilanciati node-disjoint in una rete a livelli con un numero costante di livelli è anch’esso NP-arduo in senso forte.

Teorema 1.3 Il problema dei cammini bilanciati arc-disjoint è NP-arduo in senso for-te.

Corollario 1.2 Il problema dei cammini bilanciati arc-disjoint in una rete a livelli con un numero costante di livelli è NP-arduo in senso forte.

Figura 4 1

u

i

u

k

u

1

v

j

v

k

v

1

w

p

w

k

w

s

t

1 q r− + r 1 q+ 1

V

V

₂

V

₃ 0 0 0 0 0 0

1.4.3 Il caso node-disjoint: numero di livelli costante

Si consideri ora il caso in cui il numero di livelli h della rete aciclica di input sia costan-te. Una situazione del genere si presenta nel campo del trasporto, in cui bisogna asse-gnare ai membri di un equipaggio i turni di lavoro in un orizzonte temporale di h gior-ni. In questi casi valori tipici di h sono 5 o 6 per i turni settimanali e 30 per i turni men-sili.

Come visto nel paragrafo precedente, il problema dei cammini bilanciati node-disjoint con un numero di livelli costante è NP-arduo in senso forte. Tuttavia, quando k è

, l’algoritmo pseudopolinomiale descritto in 1.3 può essere adattato per risol-vere anche la variante node-disjoint del problema. Nell’algoritmo che verrà ora descritto si fa uso del metodo color-coding per il calcolo di cammini semplici, ovvero senza ri-petizioni di nodi, descritto in [1]. Come definito in [1], dato un grafo G e una colorazio-ne random dei suoi vertici, un cammino in G si dice colorful se tutti i nodi del cammino sono colorati con colori distinti. Chiaramente un cammino colorful in G è semplice. In [1] viene poi descritto un algoritmo che, dato un grafo

(

log n Ο

)

(

,

)

G= V E e una colorazione

{

}

: 1,...,

r V → l dei vertici di G con colori, determina un cammino colorful di

lun-ghezza al più (se ne esiste uno) con una complessità in tempo pari a

l

1

l− 2Ο( )l ⋅|E| nel

caso pessimo.

Prima di procedere con la descrizione dell’algoritmo, si osservi che ogni soluzione am-missibile del problema contiene al più hk nodi, cioè Ο

(

hlogn

)

nodi, e che quindi il

problema può essere formulato come il problema di individuare nodi che formino cammini da s a t che siano bilanciati e node-disjoint.

(

hlogn Ο

)

)

n

(

log k = Ο

1.4.3.1 Descrizione dell’ algoritmo

Data una colorazione random r dei vertici di G effettuata con esattamente hk colori,

{

}

: 1,...,

r V → hk , si estende la definizione di cammino colorful ad un insieme di k

cammini da s a t in G dicendo che tale insieme è colorful se i nodi toccati dai k cammini sono colorati con colori distinti rispetto ad r.

Come primo passo, si effettua un’estensione della colorazione r ai nodi di : tutte le copie (

U

G

p

i p=1,...,U ) di uno stesso nodo i vengono colorate con lo stesso colore di i , cioè r i

( )

.

Si applica ora una variante dell’algoritmo descritto in 1.3.1 in cui, per ogni sottografo di generato durante la ricerca binaria in

U

G

[

0,U

]

, si cercano k cammini node-disjoint da

s a t e si usa la colorazione r per assicurarsi che i cammini calcolati non abbiano nodi in comune. Prima di dare una descrizione più accurata di questo passo dell’algoritmo, si osservi che un insieme colorful di k cammini può essere trasformato in un unico cam-mino semplice da s a t colorful effettuando una semplice modifica del sottografo su cui i k cammini vengono cercati: si aggiungono gli archi

( )

t s%_i, _j ,∀i j =1,...,k, e si cerca un cammino semplice da s a t%contenente k-1 di questi nuovi archi. La ricerca dell’insieme colorful di k cammini quindi si effettua assegnando costo 0 agli archi originali e costo 1 ai nuovi archi, e cercando un cammino colorful da s a t%di costo massimo. Un insieme colorful di k cammini esiste se e solo se il costo massimo restituito è uguale a k-1. La ricerca di tale cammino può essere effettuata adattando il metodo proposto in [1] per il calcolo di un cammino semplice di cardinalità fissata in un grafo orientato. Più precisa-mente, si procede come segue: si supponga che per ogni vertice j del sottografo siano già stati trovati i possibili insiemi di colori di cammini colorful di lunghezza l che con-nettono s a j, siano essi 1_, 2_,..., fjl

jl jl jl

C C C . Per ogni j e per ogni l vale

(

!

)

! ! jl hk f hk hk l ≤ −

e ad ognuno di questi sottoinsiemi di colori è associato il costo massimo dei cammini associati a quel sottoinsieme di colori. Per ogni nodo j, si analizza la sua collezione di insiemi di colori controllando, per ogni insieme b e per ogni arco

jl C

( )

j i, , se . Se

( )

appartiene o meno a b jl r i C r i

( )

∉Cjlb, allora si aggiunge

{ }

( )

b jl C U r i alla

col-lezione di i corrispondente ai cammini colorful di lunghezza l+1, cioè

( )

{ }

( 1)

b

jl i l

C U r i =Cβ₊ per qualcheβ. Il sottografo in esame contiene un insieme colorful

almeno una (tra quelle relative ad una opportuna lunghezza l, con ) non vuota e contenente almeno un insieme con costo associato uguale a k-1.

2k+ ≤ ≤1 l hk+1

1.4.3.2 Complessità computazionale in tempo dell’algoritmo

La ricerca di un cammino semplice colorful richiede

(

2kh

)

mU

Ο . Poiché h è costante e k è Ο

(

log n

)

, Ο

(

2khmU

) (

è Ο n mUp

)

dove p è Ο

( )

h . Data una colorazione r dei

ver-tici di G, come nel caso generale, l’algoritmo effettua una ricerca binaria nell’intervallo

[

0,U

]

e controlla quindi Ο(log )U valori di δ . Per ogni valore di δ considerato, si controlla in ( )ΟU reti se esiste un cammino colorful di costo k-1, operazione che ri-chiede . Fissata quindi una colorazione r, l’algoritmo determina un insieme colorful di cammini bilanciati in tempo

(

p n mU Ο

)

(

p 2_log

)

n mU U Ο .

Come indicato da Alon et al. in [1], esiste una lista di colorazioni di V tale che, per

o-gni sottoinsieme V' di V con #V'≤hk, esiste una colorazione nella lista che assegna

colori distinti ad ogni vertice in . La cardinalità di tale lista è . Quindi, se si applica l’approccio descritto precedentemente per ogni colorazione r di tale lista, si ottiene un algoritmo deterministico che risolve il problema in tempo

. ' V Ο

(

nplogn

)

(

p 2_{log log}

)

n mU n U Ο

1.5 Il caso di coppie origine-destinazioni date

Consideriamo ora la versione del problema in cui sono fornite in input k coppie di nodi origine-destinazione,

(

s t_{1 1},

) (

,..., s t_k, _k

)

, e in cui i k cammini bilanciati che si cercano

devono connettere rispettivamente . Tale versione può essere risolta con l’algoritmo descritto in 1.4.3.1 semplicemente modificando il grafo nel seguente modo:

1 a ,..., 1 k a

s è connesso solo ad s₁, è connesso a t_i s_i+1 per ogni i=1,...,k− , e solo la destinazio-1 ne viene connessa alla super-destinazione t. Ad ogni iterazione si cerca un cammino colorful da s a t che includa, in tale ordine, gli archi

k

t