Capitolo 4

(1)

Capitolo 4

Analisi delle prestazioni

In questo capitolo sono riportati i risultati delle simulazioni per un diverso numero di sottoportanti, per un diverso valore di e un diverso formato di modulazione.

τ

Specificatamente vengono riportate le curve di BER (Bit Error Rate) in funzione di

E N

_b

/

₀, dove

E

_b è l’energia media per bit d’informazione.

Per il calcolo della BER si utilizza il metodo “Montecarlo”: la simulazione ha termine quando il numero di bit trasmessi raggiunge un numero prestabilito oppure quando il numero di bit errati raggiunge un numero di errori prestabilito. Inoltre si è operato in condizioni di canale noto.

Le curve di BER sono state ottenute per tre tipi di canale: • Canale Gaussiano (AWGN).

• Canale TU50@800MHz (Typical Urban 50 Km/h e frequenza portante =800 MHz) con una banda Doppler normalizzata rispetto all’intervallo

di segnalazione . 0 f 0 0154 d B T ≅ .

(2)

• Canale HT200@800MHz (Hilly Terrain 200 Km/h e frequenza portante =800 MHz) con una banda Doppler normalizzata rispetto all’intervallo di segnalazione 0 f 0 062 d B T ≅ .

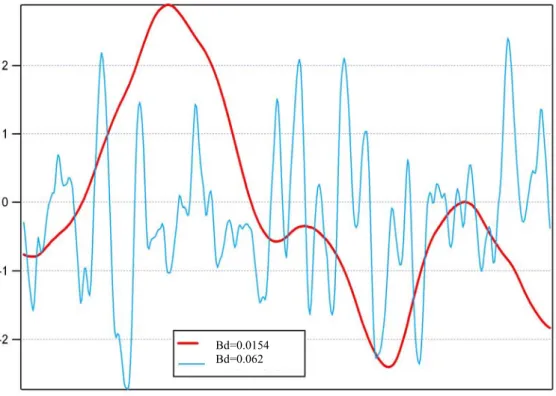
In fig. 4.1 è mostrato l’andamento temporale delle realizzazioni dei canali utilizzati nelle simulazioni.

Bd=0.0154 Bd=0.062

(3)

4.1 Durata dei filtri

Per poter fissare la durata, in termini di intervalli di segnalazione (L), dei filtri di trasmissione e ricezione si è reso necessario effettuare simulazioni al variare del numero di sottoportanti.

Dopo aver scelto come formato di modulazione la costellazione 16QAM, si è calcolato l’MSL in

dB

{

}

{ }

2 2

(

) 10log

k k k

E x

a

MSL dB

E a

−

=

(4.1)

dove

x

_k sono i simboli ricevuti e

a

_k quelli trasmessi.

In Fig 4.2 è riportato il grafico dell’andamento dell’MSL per • N=16,32,64,128,256,512

• L=8T,16T

su canale gaussiano in assenza di rumore termico

-21 -20 -19 -18 -17 -16 -15 -14 -13 -12 MSL (dB) 512 480 448 416 384 352 320 288 256 224 192 160 128 96 64 32 N (num sottoportanti) L=8 L=16 16QAM Fig. 4.2:MSL (dB) vs N

(4)

In Fig 4.3 è riportato il confronto in termini di BER per diversi valori di

in tra la curva teorica e quelle ottenute dalle simulazioni per durata dei filtri di trasmissione pari a 8 e 16 intervalli di segnalazione.

0

/

b

E N

dB

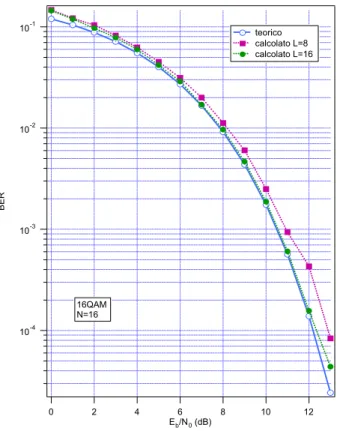
10-4 10-3 10-2 10-1 BER 12 10 8 6 4 2 0 Eb/N0 (dB) teorico calcolato L=8 calcolato L=16 16QAM N=16

Fig. 4.3:BER per L=8 e L=16 vs E N_b/ ₀

Analizzando il grafico in Fig. 4.3 si nota che non vi sono differenze in termini di BER particolarmente significative tra L=8 e L=16, mentre in termini di MSL, come si vede in Fig. 4.2, la differenza tra L=8 e L=16 è circa 6-7

dB

.

E’ quindi stato scelto di utilizzare una durata dei filtri di trasmissione pari a 16 intervalli di segnalazione

(5)

4.2 Canale AWGN

Di seguito sono riportati i risultati delle simulazioni su canale gaussiano.

7 8 9 0.001 2 3 4 5 6 7 8 9 0.01 2 3 4 5 6 7 8 9 0.1 BER 10 8 6 4 2 0 Eb/N0 (dB) N=16 N=32 N=64 AWGN L=8 16QAM Fig. 4.4:BER vs E N_b/ ₀

In Fig. 4.4 è riportato il grafico della BER in funzione di con lunghezza dei filtri di trasmissione pari a 8 intervalli di segnalazione e modulazione 16QAM. Come si può notare al variare del numero di sottoportanti N le prestazioni

risultano sostanzialmente invariate.

0

/

b

(6)

10-4 10-3 10-2 10-1 BER 10 8 6 4 2 0 E_b/N₀ (dB) 4QAM 16QAM 64QAM AWGN L=8 N=16 Fig. 4.5:BER vs E N_b/ ₀

In Fig. 4.5 è invece riportato l’andamento della BER una volta fissato il numero di sottoportanti (N=16) al variare della modulazione. Si nota che le prestazioni degradano all’aumentare del numero di punti della costellazione.

Analogamente in Fig. 4.6 è riportato il grafico della BER con lunghezza dei filtri di trasmissione pari a 16 intervalli di segnalazione e modulazione 16QAM al variare del numero di sottoportanti. Anche qui si nota che le prestazioni non variano apprezzabilmente.

In Fig. 4.7 è riportato l’andamento della BER per un numero di sottoportanti pari a 16. come prima le prestazioni peggiorano all’aumentare del numero di punti della costellazione.

(7)

5 6 7 8 9 0.001 2 3 4 5 6 7 8 9 0.01 2 3 4 5 6 7 8 9 0.1 BER 10 8 6 4 2 0 E_b/N_o (dB) N=16 N=32 N=64 AWGN L=16 16QAM Fig. 4.6:BER vs E N_b/ ₀ 5 6 7 8 0.001 2 3 4 5 6 7 8 0.01 2 3 4 5 6 7 8 0.1 BER 10 8 6 4 2 0 Eb/N0 (dB) 4QAM 16QAM 64QAM AWGN L=16 N=16 Fig. 4.7:BER vs E N_b/ ₀

(8)

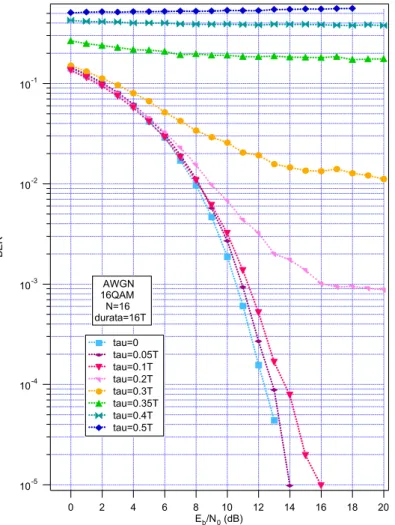
Quando nel sistema simulato si introduce un errore di sincronizzazione di timing le prestazioni degradano. In Fig 4.8 è mostrato l’andamento della BER per N=16 con modulazione 16QAM per diversi valori dell’errore di sincronizzazione di

timing (frazioni dell’intervallo di segnalazione T).

τ

10-5 10-4 10-3 10-2 10-1 BER 20 18 16 14 12 10 8 6 4 2 0 E_b/N₀ (dB) tau=0 tau=0.05T tau=0.1T tau=0.2T tau=0.3T tau=0.35T tau=0.4T tau=0.5T AWGN 16QAM N=16 durata=16T

Fig. 4.8:BER vs E N_b/ ₀ al variare di tau

Per la BER risulta circa costante e pari a 0.5 per qualsiasi .

Analogamente per (BER ) e (BER ). Per

le prestazioni cominciano a peggiorare rispetto al caso ideale ( )

per e si discostano notevolmente già a (si

perdono 2 ). Per le prestazioni cominciano a degradare a partire da

0.5T

τ

=

0.3T

0

/

b

E N

=

dB

0

/

b

E N

0.1 −

0 τ

=

8dB

0.4T

τ

=

2dB

0.2T

τ

=

0.3 ≅

τ

=

0.35T

≅

0.2

0

/

b

E N

=

τ

=

(9)

0

/

8

b

E N

=

dB

dove si perdono . In tutti questi casi è evidente la presenza di un floor che invece non si presenta nei casi e

per rapporti segnale-rumore fino a 16 .

0.5 ≅

dB

0.1T

τ

=

τ

=

0.05T

10 10 10 10 BER 20 18 16 10 8 E_b / b E

0.35T

τ

≤

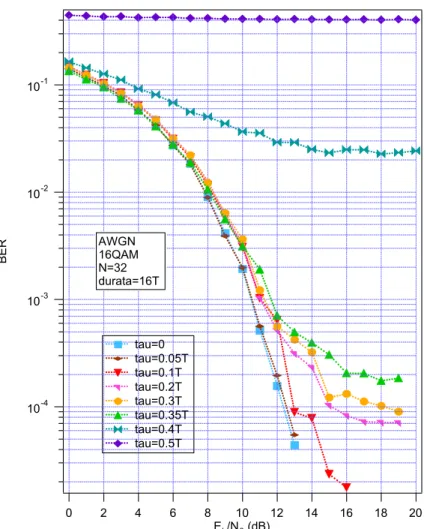
In Fig 4.9 sono riportate le curve di BER per gli stessi valori di della figura precedente ma per un numero di sottoportanti pari a 32.

τ

-4 -3 -2 -1 6 4 2 0 /N₀ (dB)12 14 tau=0 tau=0.05T tau=0.1T tau=0.2T tau=0.3T tau=0.35T tau=0.4T tau=0.5T AWGN 16QAM N=32 durata=16T

Fig. 4.9:BER vs N₀ al variare di tau

Come prima le prestazioni peggiorano all’aumentare di ma le curve cominciano

a discostarsi dal caso ideale a partire da almeno per .

All’aumentare del numero di sottoportanti N la presenza di un errore di sincronizzazione degrada le prestazioni in modo meno significativo.

τ

2dB

0

/

1

b

E N

(10)

4.2 Canale statico

In questo paragrafo vengono riportati i risultati ottenuti su canale multipath statico.

In Fig 4.10 e Fig 4.11 vengono mostrate le curve di BER con modulazione 16QAM al variare del numero di sottoportanti per il canale TU50@800MHz e HT200@800MHz rispettivamente. Come si può notare le prestazioni sono sostanzialmente identiche nei due casi, questo perchè nelle simulazioni si è supposto il canale perfettamente noto.

10-4 10-3 10-2 10-1 BER 24 22 20 18 16 14 12 10 8 6 4 2 0 Eb/N0 (dB) N=16 N=32 N=64 TU50@800MHz statico 16QAM L=16 Fig. 4.10:BER vs E N_b/ ₀

(11)

10-4 10-3 10-2 10-1 BER 24 22 20 18 16 14 12 10 8 6 4 2 0 Eb/N0 (dB) N=16 N=32 N=64 HT200@800MHz statico 16QAM L=16 Fig. 4.11:BER vs E N_b/ ₀

All’aumentare del numero di sottoportanti le prestazioni peggiorano, in particolare, fissata BER , passando da N=16 a N=32 si perdono , passando da N=16 a N=64 si perdono . 2

10

−

=

∼

3dB

6dB

∼

Quando nel sistema simulato si introduce un errore di sincronizzazione di timing le prestazioni degradano.

In Fig 4.12 è riportato l’andamento della BER per diversi valori di con modulazione 16QAM e N=16. A titolo di confronto viene riportata anche la curva relativa al canale AWGN senza errore di sincronizzazione.

(12)

10-4 10-3 10-2 10-1 BER 28 24 20 16 12 8 4 0 Eb/N0 (dB) AWGN tau=0 STATICO tau=0 tau=0.05T tau=0.1T tau=0.2T tau=0.3T tau=0.35T tau=0.4T tau=0.5T STATICO 16QAM N=16 durata=16T Fig. 4.12:BER vs E N_b/ ₀

Fissata una BER , il canale multipath statico perde rispetto al canale AWGN. Sempre per un valore della probabilità di errore pari a

10

si può

notare che per e le curve non si discostano in maniera

significativa dalla curva per , per si perdono

∼

, per

si perdono , per si perdono .

2

10

−

=

0.05 =

6 ∼

7dB

∼

12dB

2 −

4dB

T

τ

dB

0.1T

τ

=

0 τ

=

τ

=

0.2T

τ

=

T

0.3T

τ

=

0.35 ∼

(13)

10-4 10-3 10-2 10-1 28 24 20 16 12 8 4 0 AWGN tau=0 tau=0.05T tau=0.1T tau=0.2T tau=0.3T tau=0.35T tau=0.4T tau=0.5T STATICO 16QAM N=32 durata=16T Fig. 4.13:BER vs E N_b/ ₀

In Fig 4.13 vengono riportate le curve di BER al variare di con modulazione 16QAM e N=32. Rispetto al caso con N=16 le prestazioni peggiorano anche in assenza dell’offset di timing. In compenso, fissata una BER , la presenza di un errore di sincronizzazione di timing fino a

0.35

non degrada le prestazioni.

τ

10

−2

=

T

(14)

4.3 Canale tempo-variante

4.3.2 Scenario collinare

In questo paragrafo vengono riportati i risultati delle simulazioni su canale

multipath tempo-variante con scenario HT200@800MHz.

10-4 10-3 10-2 10-1 BER 35 30 25 20 15 10 5 Eb/N0 (dB) AWGN tau=0 tau=0.05T tau=0.1T tau=0.2T tau=0.3T tau=0.4T tau=0.5T HT200@800MHz Bd=0.062 16QAM N=16 durata=16T Fig. 4.14:BER vs E N_b/ ₀

La Fig 4.14 riporta l’andamento della BER per N=16 e modulazione 16QAM.

Fissata una BER , per , il canale HT200 perde rispetto al

canale AWGN. Una volta introdotto l’errore di sincronizzazione di timing, le

2

2 10

−

(15)

prestazioni peggiorano all’aumentare dello stesso. In particolare, sempre per una BER

= ⋅

2 10

−2, l’effetto dell’offset di timing comincia a sentirsi per

τ

≥

0.2T

.

10 10 10 10

BER

In Fig 4.17 sono riportate le curve di BER con modulazione 16QAM per N=32.

-4 -3 -2 -1 30 28 26 24 22 20 18 16 14 12 10 8 6 Eb/N0 (dB) AWGN tau=0 tau=0.05T tau=0.1T tau=0.2T tau=0.3T tau=0.4T tau=0.5T HT200@800MHz Bd=0.062 16QAM N=32 durata=16T Fig. 4.15:BER vs E N_b/ ₀

La presenza di un offset di timing inferiore a non degrada le prestazioni per rapporti segnale-rumore fino a , per le prestazioni degradano

a partire da mentre per le curve si discostano

notevolmente già a .

0.3T

τ

=

τ

=

25dB

∼

B

10dB

0.4T

0.5T

0

/

16

b

E N

d

0

/

b

E N

(16)

4.3.1 Scenario urbano

In questo paragrafo vengono riportati i risultati ottenuti su canale multipath tempo-variante con scenario TU50@800MHz.

In Fig 4.16 è riportato l’andamento della BER con modulazione 16QAM per N=16. 10-4 10-3 10-2 10-1 BER 35 30 25 20 15 10 5 Eb/N0 (dB) AWGN tau=0 tau=0.05T tau=0.1T tau=0.2T tau=0.3T tau=0.4T tau=0.5T TU50@800MHz Bd=0.0154 16QAM N=16 durata=16T Fig. 4.16:BER vs E N_b/ ₀

Fissata una BER

=

10

−2 si perdono

∼

25dB

rispetto al canale AWGN.

Introducendo un errore di sincronizzazione di timing, fissata una BER

=

, si

nota che per si perdono , per si perdono

2

10

−

0.05T

(17)

2.5dB

∼

0.3T

τ

=

, per si perdono

∼

. Per quanto riguarda il caso

la perdita risulta essere .

0.2T

τ

=

3dB

5dB

∼

20 18 /N0 (dB) TU50@800MHz Bd=0.0154 16QAM N=32 durata=16T / b E N

T

In Fig 4.17 sono riportate le curve di BER con modulazione 16QAM per N=32.

10-1 10-2 10-3 10-4 BER 30 28 26 24 22 16 14 12 10 8 6 Eb AWGN tau=0 tau=0.05T tau=0.1T tau=0.2T tau=0.3T tau=0.4T tau=0.5T Fig. 4.17:BER vs ₀

Rispetto al caso con numero di sottoportanti pari a 16 le prestazioni peggiorano. La presenza di un offset di timing inferiore a