CCaappiittoolloo 33

C

C

a

a

p

p

i

i

t

t

o

o

l

l

o

o

3

3

C

C

a

a

l

l

c

c

o

o

l

l

o

o

d

d

e

e

i

i

f

f

l

l

u

u

s

s

s

s

i

i

a

a

t

t

t

t

r

r

a

a

v

v

e

e

r

r

s

s

o

o

l

l

e

e

p

p

r

r

o

o

b

b

a

a

b

b

i

i

l

l

i

i

t

t

à

à

Nel Capitolo precedente è riportato il modello di domanda con il quale studiare il comportamento di scelta degli utenti del sistema di trasporto.

Questo modello genererà dei flussi sugli archi, in particolare su quelli appartenenti all’arteria in esame, i quali identificheranno l’andamento di scelta degli utenti: essendo valutati attraverso la conoscenza delle probabilità di utilizzare l’arco, questo ultimo elemento è fondamentale.

La verifica del LOS dell’arteria prevede la conoscenza del T.G.M.A., mentre le verifiche di capacità, nella fase progettuale, delle rotatorie si innescano attraverso la conoscenza delle portate in entrata e in uscita in rotatoria; siccome sono tutti elementi funzione dei flussi, è necessario arrivare alla loro determinazione.

3

3

.

.

1

1

.

.

P

P

r

r

o

o

b

b

a

a

b

b

i

i

l

l

i

i

t

t

à

à

c

c

o

o

n

n

d

d

i

i

z

z

i

i

o

o

n

n

a

a

t

t

a

a

d

d

i

i

u

u

n

n

a

a

r

r

c

c

o

o

a

a

p

p

p

p

a

a

r

r

t

t

e

e

n

n

e

e

n

n

t

t

e

e

a

a

g

g

l

l

i

i

i

i

t

t

i

i

n

n

e

e

r

r

a

a

r

r

i

i

n

n

u

u

o

o

v

v

i

i

,

,

p

p

e

e

r

r

t

t

u

u

t

t

t

t

e

e

l

l

e

e

c

c

o

o

p

p

p

p

i

i

e

e

O

O

-

-

D

D

La probabilità Pp di scegliere l’itinerario p tra l’insieme Pw degli itinerari relativi

alla coppia O-D, applicando il Modello Logit, è data da:

∑ ⋅ ⋅ = ∈P_w q q p p ) C exp(-α ) C exp(-α P ∀ coppia O-D ( w )

La probabilità di utilizzare l’arco l da parte di un utente che si sposta da O a D, è data dalla somma delle probabilità associate a tutti gli itinerari Xl che collegano la

coppia O-D e che contengono l’arco l.

∑ ⋅ ⋅ = ∈ ∈

∑

La probabilità condizionata Pl/k che un utente spostandosi dal nodo O al nodo D

usi l’arco l convergente nel nodo k, è data dal rapporto tra la probabilità associata all’arco l e la somma di quelle associate a tutti gli archi convergenti in k. Indicando con Lk l’insieme degli archi che convergono in k, si ha:

∑

∑

∑

Considerando un nodo k, i flussi che lo attraversano Fk sono dati dalla somma dei flussi sugli archi che in esso convergono e, per l’equilibrio del nodo, anche dalla somma dei flussi sugli archi che da esso si dipartono. Dunque, il flusso fl sull’arco l che

converge in k, è dato dal prodotto tra la probabilità condizionata Pl/k dell’arco l e la

somma dei flussi Fk che attraversano il nodo k.

fl = Fk · Pl/k ∀ coppia O-D ( w )

Nell’Allegato 3 si osserva quali sono le alternative a disposizione dagli utenti per ogni coppia O-D, una fra queste è il nuovo percorso pn in cui, per ogni nodo k ( che in

questo caso sono tutti nodi O/D ), converge un solo arco il quale appartiene all’itinerario pn stesso. La probabilità di utilizzare l’itinerario pn è funzione delle altre alternative

fornite agli utenti che si spostano da O a D ( coppia w ).

Per spiegare meglio, si prende in considerazione la coppia A-F (vedi Allegato 3). L’insieme Pw degli itinerari che collegano A ad F, sono rappresentati da due vecchi ( pv1

e pv2 ) e uno solo nuovo ( pn ). La probabilità di utilizzare l’itinerario pn è:

) C exp(-α ) C exp(-α ) C exp(-α ) C exp(-α P v2 p v1 p n p n p n p ⋅ + ⋅ + ⋅ ⋅ =

Per ogni nodo dell’itinerario nuovo vi è un solo arco che converge e uno solo che vi si diparte ( infatti, i vecchi e il nuovo itinerario non hanno archi in comune ), perciò la probabilità di utilizzare gli archi di pn ( relativi alla coppia A-F ), è pari alla probabilità di utilizzare pn. Inoltre, la probabilità condizionata Pl/k di ogni arco l (

appartenente a pn ) convergente in un qualsiasi nodo k dell’itinerario nuovo è la probabilità di utilizzare l’arco l. Si conclude che, la probabilità condizionata Pl/k di

qualsiasi arco l convergente nel nodo k per una considerata coppia O-D, è pari alla probabilità di utilizzare l’itinerario nuovo pn.

Queste probabilità sono riportate nell’Allegato 3 per ogni coppia O-D. Lo studio delle probabilità mostra la relazione esistente tra il nodo A origine ( relazioni A-i ), destinazione ( relazione i-A ) e gli altri nodi i, tra il nodo B origine ( relazione B-i ), destinazione ( relazione i-B ) e gli altri nodi i-A, ed infine il nodo C origine ( relazione C-i ), destinazione ( relazione i-C ) e gli altri nodi i – (A,B).

Ma cosa succede se si vogliono considerare tutte le coppie O-D? Prendendo un’altra coppia O^-D^ diversa da O-D, le alterative degli utenti sono diverse da quelle precedenti, con un percorso nuovo pn^ diverso da pn. L’arco l che appartiene

all’itinerario pn può però appartenere anche all’itinerario pn^ che collega la coppia

O^-D^ ma la probabilità condizionata Pl/k^ dell’arco l è diversa perché diversi sono gli

attributi dal quale dipende l’itinerario pn^.

Questo è valido per tutte le coppie O-D. Considerando che la scelta del nuovo itinerario pn che collega una coppia w, è un evento indipendente dalla scelta effettuata

per il nuovo itinerario p^

n che collega la coppia w^, si può affermare che la probabilità

condizionata P^

l/k di utilizzare l’arco l convergente nel nodo k, tenendo in

considerazione tutte le coppie O-D, è data dal prodotto delle rispettive probabilità condizionate Pl/k dell’arco l:

∏

∏

dove Xl è l’insieme degli itinerari che collegano varie O-D e passano per l. Quindi tutto

ciò vale per l’universo degli itinerari pn che contengono l.

3

3

.

.

2

2

.

.

C

C

a

a

l

l

c

c

o

o

l

l

o

o

d

d

e

e

l

l

l

l

e

e

p

p

r

r

o

o

b

b

a

a

b

b

i

i

l

l

i

i

t

t

à

à

c

c

o

o

n

n

d

d

i

i

z

z

i

i

o

o

n

n

a

a

t

t

e

e

d

d

e

e

g

g

l

l

i

i

a

a

r

r

c

c

h

h

i

i

i

i

n

n

r

r

e

e

l

l

a

a

z

z

i

i

o

o

n

n

e

e

a

a

l

l

l

l

e

e

v

v

a

a

r

r

i

i

e

e

c

c

o

o

p

p

p

p

i

i

e

e

O

O

-

-

D

D

d

d

’

’

i

i

n

n

t

t

e

e

r

r

e

e

s

s

s

s

e

e

Un arco può appartenere ad uno o più itinerari che collegano varie coppie O-D; perciò, la probabilità condizionata dell’arco al passaggio da un nodo k dipende dalle probabilità di utilizzare gli itinerari nuovi considerando tutte le coppie O-D. Ad esempio, l’arco BC, appartiene sia agli itinerari che hanno come origine B e destinazione tutti gli altri nodi successivi a B, ma anche a tutti gli itinerari che, avendo come origine A ( nodo antecedente a B ), passano per il nodo B.

Si indica con Pl/kN la probabilità condizionata dell’arco l convergente in k

essere origine o destinazione a seconda della direzione dell’arco l), mentre Pl/k

rappresenta la probabilità condizionata dell’arco l convergente in k appartenente agli itinerari considerando tutte le coppie O-D.

Il calcolo di queste probabilità è necessario per determinare i flussi sugli archi; nelle tabelle seguenti si riportano i risultati per ogni arco dell’arteria, con riferimento ai valori dell’Allegato 3.

1. Probabilità condizionata dell’arco l appartenente agli itinerari A-i Pl/kA:

A Arrccoo ll PPrroobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee AA--ii )) PPll//kkAA A ABB P(196-A 195)/B =PN_A−I ⋅PN_A−H⋅PN_A−G⋅PN_A−F ⋅PN_A−E⋅PN_A−D⋅PN_A−C⋅PN_A−B 0.676360 B BCC P(195A -194)/C =PN_A−I⋅PN_A−H⋅PN_A−G⋅PN_A−F⋅PN_A−E⋅PN_A−D⋅PN_A−C 0.677347 C CDD P(194A -192)/D =PN_A−I⋅PN_A−H⋅PN_A−G⋅PN_A−F⋅PN_A−E⋅PN_A−D 0.677669

2. Probabilità condizionata dell’arco l appartenente agli itinerari i-A Pl/kA:

A Arrccoo ll PPrroobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee ii--AA )) PPll//kkAA B BAA P(195A -196)/A =PN_I−A⋅PN_H−A⋅PN_G−A⋅PN_F−A⋅PN_E−A⋅PN_D−A⋅PN_C−A⋅PN_B−A 0.643771 C CBB = N_I−A⋅ N_H−A⋅ N_G−A⋅ N_F−A⋅ N_E−A⋅ N_D−A⋅ N_C−A A 195)/B -(194 P P P P P P P P 0.644711 D DCC P(192A -194)/C =PN_I−A⋅PN_H−A⋅PN_G−A⋅PN_F−A⋅PN_E−A⋅PN_D−A 0.644864

La PAl/k degli archi BA e AB sono anche le probabilità Pl/k.

3. Probabilità condizionata dell’arco l appartenente agli itinerari i-B e B-i Pl/kB: A Arrccoo ll PrProobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee ii--BB )) PPll//kkBB D DCC P(192B -194)/C =PN_I−B⋅PN_H−B⋅PN_G−B⋅PN_F−B⋅PN_E−B⋅PN_D−B 0.990309 A Arrccoo ll PrProobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee BB--ii )) PPll//kkBB C CDD P(194B -192)/D=PN_B−I⋅PN_B−H⋅PN_B−G⋅PN_B−F⋅PN_B−E⋅PN_B−D 0.954708

4. Probabilità condizionata dell’arco l appartenente agli itinerari( i-B / i-A ) e ( B-i /i-A ) Pl/k: A Arrccoo ll PrProobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee ii--BB // ii--AA )) PPll//kk C CBB P_{(194−195)/B} =PN_I−B⋅PN_H−B⋅PN_G−B⋅PN_F−B⋅PN_E−B⋅PN_D−B⋅PN_C−B⋅P₍₁₉₄A _−195)/B 0.638155 A Arrccoo ll PPrroobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee BB--ii //AA-- ii )) PPll//kk B BCC P(195-194)/C=PN_B−I⋅PN_B−H⋅PN_B−G⋅PN_B−F⋅PN_B−E⋅PN_B−D⋅PN_B−C⋅P(195A −196)/C 0.64636

5. Probabilità condizionata dell’arco l appartenente agli itinerari i-C e C-i PCl/k: A Arrccoo ll PrProobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee ii--CC )) P PCCll//kk D DCC P(192C -194)/C=PN_I−C⋅PN_H−C⋅PN_G−C⋅PN_F−C⋅PN_E−C⋅PN_D−C 0.997608 A Arrccoo ll PrProobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee CC--ii )) P PCCll//kk C CDD P(194C -192)/D=PN_C−I⋅PN_C−H⋅PN_C−G⋅PN_C−F⋅PN_C−E⋅PN_C−D 0.982583

6. Probabilità condizionata dell’arco l appartenente agli itinerari ( i-C/i-B/i-A) e ( C-i/ B-i / A-i ) Pl/k:

A Arrccoo ll PrProobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll ((rreellaazziioonnee ii--CC // ii--BB // ii--AA )) P Pll//kk D DCC P(192−194)/C=P(192C -194)/C⋅P(192B -194)/C⋅P(192A -194)/C 0.637088 A Arrccoo ll PrProobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll (( rreellaazziioonnee CC--ii // BB--ii //AA-- ii )) P Pll//kk C CDD P(194−192)/D=P(194C -192)/D⋅P(194B -192)/D⋅P(194A -192)/D 0.635705

3

3

.

.

3

3

.

.

F

F

l

l

u

u

s

s

s

s

i

i

s

s

u

u

g

g

l

l

i

i

a

a

r

r

c

c

h

h

i

i

r

r

i

i

c

c

a

a

v

v

a

a

t

t

i

i

c

c

o

o

n

n

i

i

l

l

m

m

o

o

d

d

e

e

l

l

l

l

o

o

d

d

i

i

d

d

o

o

m

m

a

a

n

n

d

d

a

a

La conoscenza dei flussi, per ogni coppia O-D, sugli archi che appartengono all’insieme degli itinerari che collegano la coppia O-D, porta alla determinazione del

flusso totale su ogni arco degli itinerari, che è pari alla somma dei vari flussi sull’arco stesso calcolati per tutte le coppia O-D. Sarebbe veramente facile in questo modo determinarne il valore, ma purtroppo è una via che non può essere adottata in questo caso.

Il paragrafo precedente riporta il calcolo della probabilità condizionata di ogni arco l dell’arteria oggetto di studio convergente nel nodo k per tutte le coppie O-D.

Da questo risultato è ora possibile determinare i flussi sugli archi dell’arteria convergenti nel nodo k, attraverso la somma dei flussi sugli altri archi che si dipartono dal nodo k ( fu ); invece, i flussi sugli archi che si dipartono dal nodo k sempre appartenenti all’arteria, sono funzione dei flussi convergenti nel nodo k degli altri archi ( fe ). Nel calcolo dei flussi non si tiene conto delle eventuali inversioni di marcia.

Per le strade della rete di trasporto si è ipotizzato un livello di servizio D o C, in funzione dell’importanza della strada; i flussi, dunque, sugli archi che convergono nei nodi dell’arteria e che non fanno parte degli itinerari nuovi, si ricavano dalla matrice dei costi. Tra gli archi che convergono nel nodo o che da esso si dipartono, si devono considerare anche i rami che, pur non presenti nella rete di trasporto, partecipano alla distribuzione dei flussi nel nodo.

Il sistema di trasporto, in qualsiasi situazione, deve trovarsi in equilibrio; come si osserverà in seguito, però, la determinazione dei flussi sugli archi interessati, porterà ad una differenza di flusso tra quelli entranti e quelli uscenti, diversa da zero ( il metodo di calcolo non è correlato tra loro ).

A questo proposito, per portare l’equilibrio nel nodo, si deve pensare che, se esso è un nodo destinazione, i flussi che vi transitano sono dati dalla somma dei flussi sugli archi che da esso si dipartono e dalla domanda generata dal nodo. A ritrosi, quindi si può assumere che, nei nodi k in cui non c’è equilibrio ( in questo caso A,B,C ) e che sono destinazione, la differenza tra i flussi entranti e quelli uscenti dal nodo è proprio la domanda generata dal nodo k:

∑

∑

La domanda dk, poi, sarà distribuita proporzionalmente tra i flussi degli archi

entranti n nel nodo k, portando così il nodo in equilibrio:

∑

Tutti i risultati sono riportati di seguito, per ogni nodo:

N

NOODDOOAA::

I flussi che partecipano alla distribuzione, sono riportati in tabella insieme: 196 Semianello ( 3 ) Cassia Sud ( 1 ) Via Diaz ( 2 ) 195 y x 64 A B

Figura 3-1 : Schema del nodo A.

I flussi sull’arco AB ( f3u ) ( 196-195 ) e sull’arco BA ( f3e ) ( 195-196 ) sono ricavati dalla probabilità di utilizzare l’arco stesso:

195) (196 195)/B (196 ' e P f f ⋅ ₋ = ₋

∑

(

)

∑

(

)

58 f f

∆f

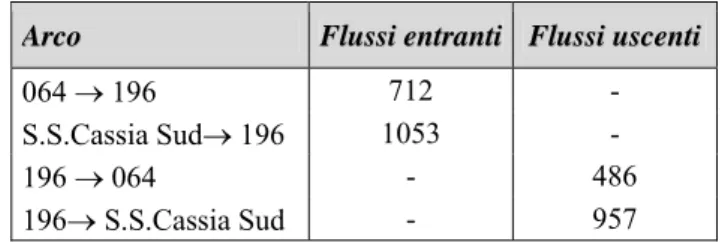
d_A = =

∑

∑

A Arrccoo FFlluussssii eennttrraannttii FlFluussssii uusscceennttii 064 → 196 712 - S.S.Cassia Sud→ 196 1053 - 196 → 064 - 486 196→ S.S.Cassia Sud - 957

- Distribuzione della domanda proporzionalmente ai flussi entranti nel nodo A: D Doommaannddaa xx aarrccoo FlFluussssii eennttrraannttii ccoorrrreettttii d1 = 23 ⇒ f(S.S.CassiaSud-196) = f1e = 1031 d2 = 16 ⇒ f(064-196) = f2e = 697 d3 = 20 ⇒ f(195-196) = f3e = 910 F Flluussssii uusscceennttii ddaall nnooddoo AA f(196-S.S.CassiaSud) = f1u = 957 f(196-064) = f2u = 486 f(195-196) = f3u = 1194

Tabella 3-2: Ripartizione domanda sul nodo A.

N

NOODDOOBB::

Nella schematizzazione del nodo B, si riportano gli archi che partecipano alla distribuzione:

Tabella 3-3: Flussi sugli archi del nodo B.

I flussi sull’arco BC ( f3u ) ( 195-194 ) e sull’arco CB ( f3e ) ( 194-195 ) sono calcolati considerando le probabilità di utilizzare il percorso relativo:

194) (195 194)/C (195 ' e P f f ⋅ ₋ = ₋

∑

(

)

Semianello dir. Sud

( 1 ) A 196 B S. Martino ( 2 )

Semianello dir. Nord

( 3 ) 194

195

x _y

C

195) (194 195)/B (194 ' u P f f ⋅ ₋ = ₋

∑

(

)

archi stessi. Per quanto concerne invece la verifica di capacità della rotatoria, che nel nodo B è ( come si vedrà in seguito ) a livelli sfalsati, i flussi sopra trovati porterebbero ad un sovradimensionamento dell’infrastruttura; l’ideale sarebbe invece, considerare le varie manovre che gli utenti eseguono nel nodo ( attraverso una sua rappresentazione dettagliato ) con le rispettive probabilità di utilizzare l’arco, e trovare così dei flussi più attendibili.

A questo proposito si deve riprendere il tema delle probabilità. Per portare in equilibrio il nodo si tiene conto delle probabilità associate alle varie rampe: rampa 1 in ingresso e in uscita, rampa 3 in ingresso e in uscita ).

Nello schema riportato in figura 3-3, nel nodo B sono riportate tutte le manovre possibili; si indica con 1 il nodo in cui i flussi, che hanno come origine A, possono proseguire lungo il tracciato avendo come destinazione il nodo C e gli altri più avanti, ma possono anche lasciare il percorso ed entrare in rampa 1e fino al nodo 5, situato sulla rotatoria.

Figura 3-3: Schema dettagliato del nodo B.

f1u Rampa 1u f1e Rampa 1e 196 ( A ) f1A-B

1

2

6

5

3

4

Semianello dir. Sud _{Semianello dir. Nord}

Lo stesso nodo 1 rappresenta, per i flussi con destinazione A, il punto d’unione tra quelli provenienti dalla rampa 1u e quelli che hanno l’origine in tutti gli altri nodi che precedono B.

Anche il nodo 3 ha un’utilità simile al nodo 1; rappresenta il punto in cui i flussi, provenienti dal centroide attraversabile C, possono scegliere di proseguire con destinazione A oppure imboccare la rampa 3e. Per i flussi invece che si dirigono verso C, il nodo 3 rappresenta il punto in cui i flussi provenienti dal nodo origine A e quelli uscenti dalla rampa 3u si uniscono.

Per tutte queste manovre possibili, si deve trovare la probabilità di utilizzare l’arco corrispondente.

Se per esempio si analizza il nodo 1 in direzione C, si osserva che la probabilità di utilizzare l’arco 1-5 è la stessa del percorso A-5, che nella schematizzazione del nodo B non dettagliata è proprio il percorso A-B ( essendo in questo caso il nodo B rappresentato dal nodo 5 ). Lo stesso dicasi per l’arco 1-3 la cui probabilità di essere utilizzato è data dalla probabilità di andare dal nodo A verso tutti gli altri nodi eccetto B.

La probabilità di utilizzare l’arco A-1 per gli utenti che hanno scelto, per arrivare alla destinazione, l’itinerario nuovo è evidentemente uno, perciò la somma delle probabilità dell’arco 1-5 e dell’arco 1-3 deve essere uno.

Le probabilità trovate per gli archi, riportate nel § 3.2., non hanno nessuna correlazione tra loro ( cioè sono indipendenti ), per cui è impossibile ottenere un risultato del genere; ma se si riprendono quelle relative agli archi nel nodo in esame e ognuna di esse si divide per la somma delle probabilità degli archi stessi, si ottiene una nuova probabilità che tiene conto delle scelte che l’utente può effettuare raggiungendo il nodo. Si riportano le probabilità:

A

Arrccoo ll PPrroobbaabbiilliittàà ccoonnddiizziioonnaattaa ddeellll’’aarrccoo ll PPll//kk

1

1--33 P1-3=PN_A-I⋅PN_A-H⋅PN_A-G⋅PN_A-F⋅PN_A-E⋅PN_A-D⋅PN_A-C 0.68542

1 1--55 P1-5=PN_A-B 0.99843 3 3--11 P3-1=PN_I-A⋅PN_H-A⋅PN_G-A⋅PN_F-A⋅PN_E-A⋅PN_D-A⋅PN_C-A 0.64471 6 6--11 P6-1=PN_B-A 0.99854 3 3--66 P3-6=PN_I-B⋅PN_H-B⋅PN_G-B⋅PN_F-B⋅PN_E-B⋅PN_D-B⋅PN_C-B 0.98983 5 5--33 P3-1=PN_B-I⋅PN_B-H⋅PN_B-G⋅PN_B-F⋅PN_B-E⋅PN_B-D⋅PN_B-C 0.99988

A Arrccoo ll NuNuoovvaa PPrroobbaabbiilliittàà ccoonnddiizziioonnaattaa d deellll’’aarrccoo ll PP ^ ^ l l//kk 1 1--55 P₁^₋₅=P_1-5/

(

)

(

)

(

)

(

)

Tabella 3-5 : Nuova probabilità condizionata dell'arco l.

Con le nuove probabilità, con i dati della tabella 3.3. e con i flussi degli archi (195-194)/(194-195) è possibile determinare i flussi sulle rampe della rotatoria.

F Flluussssii ssuullllee rraammppee f^ 1e ⇒ f(196-195) · P^1-5 708 f^ 1u ⇒ f(195-196) · P^6-1 587 f^ 3e ⇒ f(194-195) · P^3-6 724 f^ 3u ⇒ f(195-194) · P^5-3 1656

Tabella 3-6 : Flussi sulle rampe.

La differenza tra i flussi entranti e quelli uscenti in rotatoria, da luogo alla domanda generata dal nodo B; questa, come nel caso del nodo A, viene ripartita proporzionalmente tra i flussi entranti portando il nodo in equilibrio.

- Domanda generata dal nodo B:

61 f f ∆f d 4 1 i iu 4 1 i ie B = =

∑

∑

Str. Cimina dir. Ovest

( 4 )

Semianello dir. Sud

( 1 ) 195

B

66

Str. Cimina dir. Est

( 2 )

Semianello dir. Nord

( 3 )

D

C 194

x y

192

- Distribuzione della domanda proporzionalmente ai flussi entranti nel nodo B: D Doommaannddaa xx aarrccoo FFlluussssii eennttrraannttii ccoorrrreettttii d1 = 10 ⇒ fr1 = f1e = 699 d2 = 23 ⇒ f(S.Martino-195) = f2e = 1682 d3 = 10 ⇒ fr3 = f3e = 715 d3 = 19 ⇒ f(197-195) = f4e = 1397 F Flluussssii uusscceennttii ddaallllaa rroottaattoorriiaa f(195-196) = f1u = 587 f(195-S.Martino) = f2u = 1492 f(195-194) = f3u = 1656 f(195-197) = f4u = 758

Tabella 3-7 : Flussi corretti sulle rampe.

N

NOODDOOCC::

Per ogni arco, i flussi sono riportati in tabella.

I flussi sull’arco CD ( f3u ) ( 194-192 ) e sull’arco DC ( f3e ) ( 192-194 ) sono riportati di seguito e calcolati attraverso la relazione che lega i flussi entranti ed uscenti:

192) (194 192)/D (194 ' e P f f ⋅ ₋ = ₋

∑

(

)

Tabella 3-8 : Flussi sugli archi del nodo C. Figura 3-4: Schema del nodo C.

194) (192 194)/C (192 ' u P f f ⋅ ₋ = ₋

∑

(

)

- Domanda generata dal nodo C:

128 f f ∆f d 4 1 i iu 4 1 i ie C = =

∑

∑

( differenza di flusso nel nodo C )

- Distribuzione della domanda proporzionalmente ai flussi entranti nel nodo C: D Doommaannddaa xx aarrccoo FFlluussssii eennttrraannttii ccoorrrreettttii d1 = 42 ⇒ f(195-194) = f1e = 2747 d2 = 21 ⇒ f(Str.Cimina-194) = f2e = 1363 d3 = 48 ⇒ f(192-194) = f3e = 3129 d3 = 17 ⇒ f(066-194) = f4e = 1131 F Flluussssii uusscceennttii f(194-195) = f1u = 2016 f(194-Str.Cimina) = f2u = 1581 f(194-192) = f3u = 3383 f(194-066) = f4u = 1390

Tabella 3-9 : Flussi corretti sugli archi del nodo C.

La conoscenza dei flussi sugli archi dell’arteria, permette un avanzamento di livello nello studio proposto.

In una rete di trasporto, infatti, quando sono noti i flussi, è possibile portare a termine le verifiche, dimensionare gli elementi del tracciato funzione di tali grandezze e, in questo studio, permette anche di stabilire se l’ipotesi iniziale sul livello di servizio (ipotizzato C per il ‘Semianello’ ) è verificata; i risultati che si otterranno, affinché siano accettabili, devono essere non inferiore a quello stabilito.