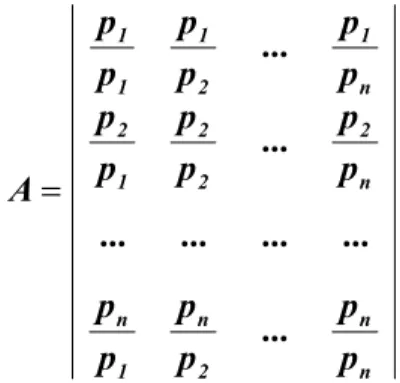Capitolo IV Metodologie multi-attributo: AHP.

Capitolo IV

Metodologie multi-attributo: AHP.

Introduzione.

L’obiettivo del progetto IN.DI.CA. di sviluppare un software specifico ha richiesto: • L’analisi dello stato dell’arte della manutenzione nelle aziende cartarie del comparto

di Capannori;

• Una fase di co-design per la definizione delle specifiche del CMMS.

Per quanto riguarda il primo punto, le motivazioni che hanno richiesto una simile analisi sono state ampiamente discusse nel presente lavoro e lo strumento utilizzato per tale scopo è stato l’AUDIT aziendale.

Dal passo successivo, la fase di co-design, è scaturita, come implicazione diretta, l’analisi dei CMMS presenti sul mercato tecnologico mondiale. L’obiettivo era quello di individuare, nella vasta gamma di CMMS commerciali, quello le cui caratteristiche meglio rispondono alle specifiche richieste del settore cartario, per poter disporre di una valida base di partenza nella realizzazione dell’architettura del software richiesto.

Per poter procedere, in modo sistematico, alla valutazione dei CMMS si è scelto di utilizzare una metodologia multi-criterio: l’Analythic Hierarchy Process ( AHP) [16].

I modelli matematici che vengono in genere utilizzati per lo studio dei problemi prevedono l’ottimizzazione di una “funzione obiettivo” attraverso la sua massimizzazione o minimizzazione. Essa è funzione di un certo numero di variabili decisionali e di criteri di valutazione, combinati a formare un’espressione algebrica. Purtroppo questi modelli sono applicabili soltanto in casi molto semplici, sotto ipotesi semplificatrici abbastanza restrittive.

L’ AHP è in grado di trattare un elevato numero di fattori differenti e, quindi, di rappresentare le situazioni complesse proprio come appaiono, piuttosto che modificare il modello di studio facendo delle ipotesi semplificatrici [3]. Inoltre, la metodologia AHP permette di ottenere particolari benefici quando si devono tenere in considerazione, per la risoluzione del problema, elementi dalle caratteristiche intangibili.

L’uso della metodologia AHP richiede l’applicazione del principio di “decomposizione” e di “sintesi”.

E’ necessario scomporre una situazione complessa e non strutturata in una serie di elementi, definiti come criteri e alternative, per poterli poi arrangiare in un albero delle gerarchie strutturato su più livelli, dal più elevato (obiettivo) al più basso (alternative), passando attraverso i livelli intermedi (criteri e sub-criteri). E’ evidente che la costruzione della struttura gerarchica richiede una conoscenza profonda del problema che si è chiamati ad affrontare.

Completata questa fase, il metodo effettua una comparazione a coppie ( pairwise comparisons) degli elementi appartenenti ad uno stesso livello della gerarchia in relazione al grado di importanza o di probabilità di successo, rispetto all’elemento presente al livello superiore della gerarchia, ottenendo una scala relativa di valori, che pesano gli elementi e ne determinano il ranking locale, cioè relativo all’elemento da cui discendono.

Il punto di partenza dell’albero gerarchico è costituito dall’obiettivo dell’analisi, detto anche Goal, procedendo a ritroso, dai livelli più bassi fino alla radice dell’albero, si determina il ranking globale di tutte le alternative, ordinate e pesate in relazione all’obiettivo dello studio.

4.1 Le basi dell’AHP.

Concettualmente la metodologia AHP è applicabile alla modellizzazione di ogni situazione che si presti ad una rappresentazione gerarchica di almeno due livelli:

• CRITERI DI VALUTAZIONE - Elementi che permettono di assumere la decisione. • ALTERNATIVE - Elementi che influiscono sui criteri di valutazione.

Essa si basa sui principi di decomposizione dei problemi, di assegnazione di punteggi comparativi e di sintesi delle priorità.

L’applicazione della tecnica AHP inizia con la definizione del problema e l’individuazione dell’obiettivo da perseguire insieme ai criteri che regoleranno la scelta. In questa fase è importante dare una definizione precisa di ogni elemento introdotto per evitare controversie nella successiva fase di valutazione [3].

La metodologia viene attuata secondo le seguenti fasi:

1. Definire l’obiettivo dell’analisi e identificare i criteri e le alternative che lo influenzano;

2. Costruire la struttura gerarchica dall’alto (obiettivo generale) verso il basso (lista delle alternative) passando attraverso i livelli intermedi (criteri di valutazione);

3. Costruire una serie di matrici in cui riportare le valutazioni riguardanti i confronti tra criteri in riferimento all’obiettivo globale;

4. Calcolare il vettore delle priorità per i criteri di valutazione; 5. Ripetere le fasi 3 e 4 per le alternative al livello più basso; 6. Determinare la formula finale del vettore delle priorità.

Sulla base della struttura gerarchica del problema, si deve sviluppare un metodo per determinare “l’intensità” con cui i vari elementi di un livello influenzano quelli del livello superiore, così che sia possibile calcolare l’influenza di ogni alternativa al più basso livello sull’obiettivo globale.

Ciò viene ottenuto chiedendo ad un campione di persone qualificate in materia di valutare il set di elementi in una serie di confronti a coppie, sempre in riferimento all’elemento presente al livello immediatamente superiore.

Per fornire un giudizio numerico in una valutazione così qualitativa, è richiesta una scala di valori appropriata. Assumendo che gli elementi coinvolti nel confronto siano di importanza comparabile e che i loro “pesi” relativi non differiscano di più di un fattore 9, è possibile adottare una scala di punteggi strutturata su 9 punti come quella presentata nella Tabella 4.1,

Valutazione linguistica del confronto in termini di importanza

1 Le due alternative hanno uguale peso nei confronti di un dato criterio, o due criteri contribuiscono ugualmente all’obiettivo. 2

3 L’esperienza indica una moderata prevalenza di un elemento rispetto ad un altro in riferimento ad un certo criterio o obiettivo.

4

5 A è sensibilmente più importante

6

7 A è molto più importante di B

8

9 A è estremamente più importante di B

Tabella 4.1– Scala dei punteggi nella metodologia AHP

La scala di nove punti è stata spesso utilizzata in studi ad approccio gerarchico - analitico e si è dimostrata molto affidabile. I nove punti derivano dalla capacità umana di fare distinzioni qualitative secondo cinque attributi: uguale, moderato, forte, molto forte, estremo. Per quei casi in cui è richiesta una maggiore precisione, il sistema di calcolo accetta sia valori interi intermedi, tra attributi adiacenti, sia valori decimali.

Il risultato finale del calcolo è un vettore, normalizzato a uno, che permette l’individuazione della migliore alternativa nei confronti dell’obiettivo generale e viene definito “vettore delle priorità”. Determinato il vettore delle priorità, la tecnica AHP consente inoltre all’analista di valutare la correttezza e la consistenza delle valutazioni a coppia fornite dagli esperti attraverso l’indice di inconsistenza IR, di cui parleremo in maniera più dettagliata nei prossimi paragrafi.

Il modello matematico che sta alla base dell’AHP si basa su quattro assiomi principali [16], che dovrebbero essere sempre osservati rigorosamente durante l’analisi, essendone il fondamento teorico e la giustificazione analitica.

• Comparazione: i paragoni fra le alternative considerate devono sempre essere

condotti a coppie. Si prende a modello una scala di riferimento da 1 a 9, possibilmente utilizzando espressioni linguistiche preventivamente concordate per facilitare il confronto, attribuendo valori maggiori all’alternativa più importante, o comunque preferibile, nei confronti del criterio in esame. Ovviamente il confronto produce un rapporto tra due valori e quindi la procedura di assessment, cioè di attribuzione dei valori numerici ai giudizi, determina la costruzione di una matrice A di dimensioni n , se n è il numero delle alternative considerate. Se un’alternativa A vale p volte una seconda alternativa B, è ovvio che B debba valere

n

×

p 1

volte A. In teoria dovrebbe anche essere sempre rispettata la proprietà transitiva: se A vale p volte B e B vale m volte C, allora A dovrebbe valere p× volte C. m

• Omogeneità: rappresenta, forse, l’assioma più importante fra i quattro. Le preferenze

devono essere attribuite sempre in relazione ad una stessa scala di giudizio e, soprattutto, le alternative da giudicare devono essere commensurabili. In altre parole, non deve sussistere più di un ordine di grandezza nella differenza fra due alternative, poiché non avrebbe alcun senso logico paragonare oggetti troppo diversi tra loro. Per fare un esempio piuttosto eloquente, basti pensare al confronto tra alcuni numeri per determinare quale sia il più grande: potremmo dire con certezza che 1000 è molto più grande di 10 e che, precisamente, 1000 è 100 volte più grande di 10. D’altra parte, in matematica, si è soliti utilizzare il termine infinito (∞ ) per rappresentare un numero non meglio identificato ma estremamente grande. E’ ovvio che esso sia estremamente più grande tanto di 10 che 1000, ma in realtà questo confronto non ha un’interpretazione così semplice ed immediata come invece può averne il rapporto 1000 10 . Infatti, sia ∞ 10 , sia ∞ 1000

danno come risultato 0: se dovessimo utilizzare questi pesi per ordinare i numeri otterremo certamente un risultato erroneo e insignificante. Allo stesso modo, utilizzando alternative troppo diverse tra loro come, ad esempio, una piccola macchina manuale ed una linea produttiva completamente automatizzata, otterremmo un ranking privo di significato rispetto all’analisi che si sta conducendo.

• Indipendenza: ogni giudizio deve essere assolutamente indipendente dalle proprietà

delle varie alternative: infatti, ogni paragone deve riguardare solo due alternative ed il giudizio deve essere dato solo in relazione al criterio attualmente in esame, senza

considerare in alcun modo gli altri criteri e le altre alternative. Solo in questo modo si sfrutta appieno la potenza del metodo, rendendo significativa la scomposizione del problema nell’albero gerarchico: infatti, se ogni volta che si procede ad effettuare un confronto si dovesse tener conto di tutti gli altri nodi, non si sfrutterebbero per niente gli enormi vantaggi ottenuti con la suddivisone in tante parti più semplici.

• Completezza: è l’assioma della completezza. Per essere certi che il ranking finale sia

corretto ed omogeneo, la struttura ad albero gerarchico, preventivamente costruita, deve essere completa e dettagliata. In ogni altro caso non potremmo considerare tutti i criteri realmente implicati nella decisione, che risulterebbe, infine, lacunosa e priva di significato.

4.2 La teoria.

La base matematica posta a fondamento dell’AHP è costituita dall’algebra delle matrici [16]. Secondo Saaty il ranking delle varie alternative è ben rappresentato dall’autovettore corrispondente all’autovalore principale della matrice dei confronti

reciproci, opportunamente normalizzato.

Consideriamo un insieme S di n elementi, A1, A2, …, An, ciascuno caratterizzato da una grandezza che diremo peso pi (con i = 1..n). Possiamo formare la matrice A, le cui righe sono costituite dai rapporti tra i pesi di ciascun elemento rispetto ai pesi di tutti gli altri: in breve, ogni riga è costituita dalle misure relative dei pesi degli elementi (Fig. 4.2.1).

n n 2 n 1 n n 2 2 2 1 2 n 1 2 1 1 1 p p ... p p p p ... ... ... ... p p ... p p p p p p ... p p p p A=

Tutti gli elementi sono positivi e per ciascuno di essi vale la relazione ji ij a 1 a = , a

conferma della reciprocità di ogni matrice derivante da una pairwise comparison. Tale proprietà è condizione necessaria per garantirne anche la consistenza, che riveste

un’importanza fondamentale per l’applicabilità della metodologia, mentre la condizione sufficiente affinché ciò sia verificato è che l’autovettore principale sia uguale alla dimensione

n della matrice: d’altra parte, è facile dimostrare come entrambe siano soddisfatte nel caso in

considerazione. Sappiamo che, se λ è un autovalore di A= a_ij , gli autovettori si ottengono risolvendo il problema rappresentato dal sistema

λ(v) (v)

a_ij = (4.1)

Osservando la matrice, è ben visibile che le sue righe sono linearmente dipendenti e che potrebbero, per esempio, essere riscritte con facilità come multiple della prima. Questo fa sì che tutti gli autovalori, eccetto uno, siano nulli; poiché la somma degli autovalori di una matrice deve essere uguale alla sua traccia, cioè alla somma degli elementi della sua diagonale principale, risulterà anche che l’autovalore principale ed unico sarà proprio uguale all’ordine

n della matrice.

L’autovettore v, associato all’autovalore appena trovato, risulta essere l’unico

autovettore non nullo della matrice e dunque, a parte un’eventuale costante moltiplicativa, sarà sufficiente normalizzarlo, generalmente ad 1, per ottenere il ranking degli elementi dell’insieme S.

Quanto appena esposto fa riferimento al caso ideale di una matrice perfettamente reciproca, mentre, nei casi più generici potrebbe accadere di avere a che fare con matrici che si discostano anche sensibilmente da questa situazione. Uno dei compiti più importanti da assolvere durante l’analisi, è proprio quello di procedere alla costruzione di un array di giudizio che sia il più consistente possibile. Il controllo può essere effettuato facendo ricorso alla proprietà transitiva durante l’assegnamento dei valori numerici ai confronti: se l’alternativa A viene giudicata n volte più importante di B e B è m volte più importante di C,

allora A dovrebbe risultare n volte più importante di quest’ultima. Talvolta, per fare in modo che questa proprietà sia automaticamente verificata si procede all’assegnamento considerando solamente gli elementi della matrice a sinistra o a destra della diagonale

m

principale. L’assioma di omogeneità ci assicura, allora, che piccoli errori durante la fase di immissione dei dati si ripercuoteranno in modo limitato sulla soluzione.

In definitiva, la consistenza della matrice dei confronti reciproci è l’indicatore migliore per verificare la bontà dei giudizi forniti sulle alternative, poiché, altrimenti, significherebbe che è stato effettuato un erroneo assegnamento degli stessi. L’argomento in questione è talmente importante da richiedere un approfondimento e la definizione di due indici ampiamente utilizzati durante il processo di analisi.

Supponiamo di aver costruito una matrice di cui sia necessario determinare la consistenza. Conoscendo il suo autovalore principale, che diremo λ_max, potremo scrivere allora l’Indice di Consistenza (Consistency Index, CI):

1 max − − = n n CI λ (4.2)

Mediante questo valore potremo definire quello che viene comunemente indicato come Rapporto di Inconsistenza (Inconsistency Ratio, IR):

RI CI

I_R = (4.3)

In quest’ultima espressione RI rappresenta il valore medio casuale di CI per una

generica matrice n . I valori di questo indice sono stati calcolati da Saaty (1980) ed alcuni di essi sono riportati in tab. 4.3.1.

n

×

N 1 2 3 4 5 6 7

RI 0 0 0,52 0,89 1,11 1,25 1,35

Tab. 4.3.1 Valori di RI per matrici di ordine n

Se IR è minore di 0,1 la soluzione può essere considerata vicina a quella ideale, in

quanto l’autovalore calcolato e quello della matrice perfettamente reciproca e consistente tendono ad assumere lo stesso valore. Quando l’indice diventa maggiore di 0,1, invece,

significa che sono state commesse incongruenze durante l’attribuzione dei giudizi: l’analisi dovrebbe essere fermata, per aver modo di rivedere i confronti.

Vediamo adesso, brevemente e con l’ausilio di un esempio molto semplice, come la metodologia procede al calcolo dell’autovalore principale, dell’autovalore associato e dell’indice di inconsistenza. A questo proposito considereremo un insieme di tre elementi, A, B e C, da giudicare rispetto ad un generico criterio mediante valutazioni di preferenza o di importanza: se A è 2 volte preferibile rispetto B, il corrispondente elemento nella matrice di giudizio varrà:

1 2

a₁₂ = (4.4)

Allo stesso modo, imponendo che A è 4 volte migliore di C, otterremo l’elemento e di conseguenza tutti gli altri elementi della matrice, che potrà quindi essere scritta nella forma: 13 a 1 2 1 4 1 2 1 2 1 4 2 1 A= (4.5)

Osservando la matrice si nota che, durante l’assegnamento dei giudizi, si è osservata puntualmente la proprietà transitiva e, perciò, essa è perfettamente reciproca. E’ ovvio attendersi che l’autovalore principale sia anche l’unico non nullo e che la consistenza sia perfettamente garantita. Effettivamente, svolgendo i calcoli, otteniamo che λ_max =3 e che

.

0

=

R

I

Saaty [16] ha proposto un metodo iterativo che conduce, in un numero non troppo elevato di passi, ad una valutazione molto precisa dell’autovalore principale della matrice. Sinteticamente, è possibile rappresentare l’algoritmo nel modo seguente:

1. Si riscrivono gli elementi dell’array in termini reali stabilendo a priori la precisione, cioè il decimale cui fermare il calcolo dei rapporti (questo è particolarmente importante qualora si debba tradurre l’algoritmo in un programma per calcolatore); 2. Si quadra la matrice e si sommano gli elementi di ogni riga, ottenendo in questo

modo un autovettore di primo tentativo che deve essere normalizzato ad 1 (non è determinante, ma è la convenzione più comunemente adottata);

3. Se si è alla prima iterazione si torna a quadrare la matrice ottenuta al passo precedente e si calcola il nuovo autovettore, nello stesso modo;

4. Si calcola lo scostamento tra le componenti dei due autovettori: se questo è minore di un livello precedentemente fissato come tolleranza per ottenere una soluzione ottimale, allora il processo si ferma, altrimenti si procede reiterando dal passo 2;

Nel caso preso in esame, l’applicazione del metodo produce i seguenti risultati: la matrice viene riscritta nella forma

1 0,5 0,25 2 1 0,5 4 2 1 (4.6)

e la sua quadratura conduce al risultato

3 1,5 0,75 6 3 1,5 12 6 3 (4.7)

Sommando gli elementi di ogni riga si ottiene l’autovettore di primo tentativo:

5,25 10,5 21

(4.8)

che, normalizzato ad 1 ed arrotondato a tre cifre decimali, fornisce il ranking delle 3 alternative:

0,142 0,285 0,571

(4.9)

A questo punto si itera una seconda volta, quadrando la matrice (4.7) per ottenere un vettore più preciso. Questo procedimento conduce alla nuova matrice

27 13,5 6,75 54 27 13,5 108 54 27 (4.10)

dalla quale ricaveremo, infine, il nuovo autovettore (già normalizzato ad 1):

0,142 0,285 0,571

(4.11)

che appare identico al vettore ottenuto alla prima iterazione. A questo punto il procedimento si chiude, poiché si è ottenuta certamente una soluzione ottima (e si potrebbe facilmente verificare che, in questo caso, si tratta anche di quella esatta). Ricordando la relazione (4.1) si può valutare l’autovalore e confermare che λ_max =3.

Consideriamo adesso lo stesso problema di ordinamento dei tre elementi, ma, adesso, introduciamo volutamente un errore piuttosto evidente nell’attribuzione dei giudizi: assumiamo che l’alternativa A sia ancora 2 volte più importante di B, e che B sia 2 volte più importante di C. Questa volta, tuttavia, scriveremo che A è ugualmente importante all’elemento C, in modo da non rispettare la proprietà transitiva. La matrice che deriva da queste ipotesi è perciò:

1 0,5 1 2 1 0,5 1 2 1 (4.12)

Procedendo ancora come indicato in precedenza, otterremo come risultato l’autovettore normalizzato:

0,255 0,325 0,420

(4.13)

che consente di valutare l’autovalore principale λ_max ≈3,16. Utilizzando la formula data in (4.2) possiamo valutare l’indice di consistenza e verificare che esso è CI , mentre il rapporto di inconsistenza, tenendo conto del valore tabulato di RI, varrà:

08 , 0 = 15 , 0 = R I (4.14)

Il valore, maggiore di 0,1, assunto da quest’ultimo indica chiaramente che esiste una leggera inconsistenza nel giudizio. Se avessimo giudicato A non uguale, ma 3 volte più importante di C, l’inconsistenza sarebbe stata più piccola (I_R =0,01) e il giudizio più corretto, con un errore dell’ordine di circa il 10%. In definitiva, la misura di questi indici, alla fine del procedimento di calcolo, dovrebbe indicare al team di esperti che stanno conducendo l’analisi se sia o no il caso di ripetere l’attribuzione dei giudizi, per essere certi di avere un risultato non solo matematicamente corretto, ma anche valido dal punto di vista logico.

E’ necessario porre l’accento, a questo punto, su un particolare decisamente interessante riguardante la metodologia. Uno degli aspetti più influenti sulla consistenza di un giudizio, è certamente il numero di alternative che un singolo individuo si trova a dover confrontare e valutare. Appare immediatamente evidente che in una valutazione diretta, il numero massimo di elementi che possono essere presi in considerazione senza invalidare il procedimento è piuttosto esiguo. D’altra parte, grazie al processo di confronto a coppie, l’AHP permette di aumentare sensibilmente le capacità di valutazione rispetto ad un determinato criterio: tuttavia, alcuni studi molto importanti, presi in considerazione da Saaty nella definizione stessa del metodo [16], precisano che la mente umana non può confrontare più di un certo numero di elementi, senza che la valutazione fornita diventi a mano a mano più inconsistente, vaga ed incerta. In particolare, uno studio molto approfondito da parte di Shim e Shin [17] avevano già ampiamente dimostrato, qualche decennio prima, che generalmente un individuo di medie capacità riesce a confrontare in modo coerente fino a sette elementi, con una tolleranza di due alternative in più o in meno.

Tenendo conto sia dei vantaggi sia dei limiti che questo procedimento presenta, sono stati compiuti numerosi esperimenti in molteplici campi di applicazione: in effetti, il pregio maggiore dell’AHP risiede nella possibilità di poter essere sfruttato ampiamente in analisi multi-scenario e multi-attributo, indipendentemente dal numero di criteri scelto e dalla complessità dell’albero decisionale costruito.

4.3 I CMMS analizzati.

Prima di procedere all’anali multi-attributo e alla costruzione dell’albero gerarchico, è opportuno analizzare brevemente quelli che sono i cmms scelti per effettuare la valutazione:

• Txbase plantware Maintenance System; • MP2 Professional;

• ProTeus Enterprise • Ivara EXP;

• Cwork.

Txbase plantware Maintenance System: prodotto dalla Txbase System Incorporation,

rappresenta un sistema pienamente integrato in grado di rispondere alle esigenze manutentive in maniera completa. Ha una logica di applicazione molto flessibile che gli permette di essere implementato sia come interfaccia per l’utente, sia come base di dati. Per la sua adattabilità è usato indistintamente in aziende di grandi dimensioni così come in organizzazioni che contano pochi utenti.

I sistemi operativi che lo supportano sono: Windows 95/NT, Unix, HP, Solaris. Il prezzo di acquisto si aggira intorno ai $ 50.000.

MP2 Professional: prodotto dalla Datastream System Incorporation, è un pacchetto per la

gestione della manutenzione che ben risponde alle aspettative della piccola e media impresa. Rappresenta un valido supporto per ridurre i downtime, e le problematiche che si verificano nell’area manutentiva.

I sistemi operativi con cui è in grado di lavorare sono: Windows 95/NT. Il prezzo di acquisto è pari a $ 35.000.

ProTeus Enterprise: prodotto dalla Eagle Technology Incorporation, è in grado di supportare

in maniera completa le richieste manutentive. Fra le sue caratteristiche: la facilità d’uso, la possibilità di gestire le comunicazioni via Internet, l’integrazione con Microsoft-Office. I sistemi operativi con cui è in grado di interagire sono: Windows 95/98/NT, Oracle, Novell. Il prezzo di acquisto è di circa $21.000.

Ivara EXP: prodotto dalla Ivara Corporation, permette di definire ed implemantare una serie

di programmi per la gestione della manutenzione. Può essre utilizzato per gestire tutti gli aspetti della manutenzione predittiva e sotto condizione.

I sistemi operativi con cui è in grado di lavorare sono: Windows 95/NT. Il prezzo di acquisto è pari a $ 10.000.

CWorks: prodotto dalla Clueword DotCom, è di semplice utilizzo; permette una gestione dei

work-orer, dei costi e dei tempi. Inoltre è dotato di moduli per il controllo della manutenzione preventiva e predittiva. E’ supportato da Microsoft Access I sistemi operativi con cui è in grado di lavorare sono: Windows 95/NT.

Il prezzo di acquisto è pari a $ 2.400.

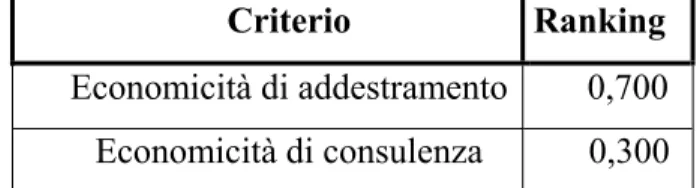
I cmms scelti per effettuare la valutazione presentano cratteristiche comuni, come ad esempio la modularità, pur differenziandosi nella loro architettura di base, dove è possibile rilevare come si siano prediletti, alternativamente, alcuni aspetti rispetto ad altri.

E’ per questo motivo che, a nostro avviso, i cinque Cmms analizzati, ben rappresentano la vasta gamma di software di manutenzione attualmente in commercio.

moduli Txbase Plantware Maintenance System ProTeus

Enterprise Professional MP2 Ivara.EXP CWorks

Equipment _{∗ ∗ ∗ ∗ ∗}

Work order/work request _{∗ ∗ ∗ ∗ ∗}

Planned/preventive maintenance ∗ ∗ ∗ ∗ ∗ Corrective maintenance _{∗ ∗ ∗ ∗ ∗} Outage/overhaul _{∗ ∗ ∗} Calibration _{∗ ∗ ∗} Inventory _{∗ ∗ ∗} Requisitioning/purchasing _{∗ ∗ ∗} Planning/scheduling _{∗ ∗ ∗} Personnel/labor _∗ Engineering _∗ Reports _{∗ ∗ ∗ ∗ ∗} Other _∗ Maintenance procedures _{∗ ∗ ∗ ∗ ∗}

Project management and accounting _{∗ ∗ ∗}

Work history _{∗ ∗ ∗ ∗ ∗}

Asset hierarchy _{∗ ∗ ∗ ∗ ∗}

Key/badge inventory _{∗ ∗ ∗}

Multiple inventory part locations _{∗ ∗ ∗}

Predictive interfaces _{∗ ∗ ∗ ∗ ∗}

CMMS system diagnostics _{∗ ∗ ∗}

Work prioritization system _{∗ ∗ ∗ ∗} Bar-code reading and printing _{∗ ∗ ∗}

Asset drawings/graphics ∗ ∗ ∗

User-definable standard reports _{∗ ∗ ∗}

Text import/export capability _{∗ ∗ ∗ ∗} Data import/export capability _{∗ ∗ ∗ ∗ ∗}

Data entry validation _{∗ ∗ ∗ ∗}

User-customizable screens and menus _{∗ ∗ ∗ ∗} Built-in report writer and e-mail _{∗ ∗ ∗} Scratch pads/bulletin board _{∗ ∗}

Root cause ∗ ∗ ∗ ∗ ∗

Cost _{∗ ∗ ∗ ∗}

Time/labor ∗

Equipment/vehicle _{∗ ∗ ∗}

Work request/work order _{∗ ∗ ∗ ∗}

Downtime _{∗ ∗ ∗}

Vendor performance _{∗ ∗ ∗}

Employee training _{∗ ∗ ∗}

Resource productivity _{∗ ∗ ∗}

Tabella 4.3.1 Funzionalità e caratteristiche dei CMMS.

4.4 L’analisi AHP per la scelta del cmms.

La costruzione del modello per l’analisi multi-attributo si è basata su quelli che sono i risultati dell’audit di manutenzione e sull’apporto fondamentale dei manager di manutenzione, chiamati a partecipare alla fase di co-design del cmms del progetto IN.DI.CA.

In base ai dati raccolti è stato possibile identificare, tramite un approfondito livello di analisi (brainstorming del problema), tutti i criteri rilevanti per la scelta e la loro collocazione all’interno della struttura gerarchica.

La struttura decisionale per la scelta del cmms è rappresentata in figura 4.5.1.

Figura 4.4.1 struttura decisionale scelta cmms.

Come appare evidente, la struttura si sviluppa su cinque livelli complessivi, essendo il quinto livello della rappresentativo delle alternative, cioè dei cmmms coinvolti nella scelta.

I criteri introdotti sono sufficienti per descrivere ed affrontare la scelta, ma soprattutto rispettano le specifiche richieste delle aziende partners del progetto.

Al primo livello dell’albero decisionale si identificano quattro criteri di valutazione:

• Economicità: è un elemento che in ogni azienda deve esere valutato con estrema

oculatezza; se è vero, infatti, che il basso costo di acquisto e di gestione del software può rappresentare una caratteristica allettante, di contro è opportuno tener presente che ciò può voler dire rinunciare a funzionalità e caratteristiche che, nel tempo, possono rivelarsi fondamentali per la gestione del processo manutentivo.

• Performance: prestazioni di cui può fruire l’utilizzatore. E’ ovvio, che la possibilità di sfruttare un elevato numero di performance, permette all’azienda di organizzare in maniera organica la manutenzione preventiva, predittiva e sotto condizione, di gestire

correttamente il magazzino ricambi, i down-time, i work-order, il personale di manutenzione e di attivare moduli per effettuare analisi di criticità ( FMECA).

• Facilità di implementazione: è una caratteristica che molto spesso non viene tenuta in debita considerazione, ma che rappresenta un requisito essenziale per un buon cmms.

Si tratta di un aspetto intimamente connesso con quelle che sono le peculiarità dell’azienda in cui ci troviamo ad operare; infatti non dobbiamo mai dimenticare che l’utilizzo di un software per la gestione della manutenzione, non può prescindere da quelle che sono le politiche manutentive adottate dal management, le procedure di manutenzione preesistenti in azienda, i software già in uso, con cui il cmms si troverà ad interagire.

Così, ad esempio, in una delle aziende intervistate, l’implementazione di un cmms quale MAXIMO, non ha prodotto i risultati sperati, anche perché, la struttura del software presuppone l’adozione della filosofia TPM, a cui, nello specifico, l’azienda non fa riferimento.

• Addestramento: rappresenta un aspetto rilevante nella scelta di un cmms. I provider, in genere, prevedono la necessità di un addestramento che va da un minimo di tre mesi, per i software più semplici, ad un massimo di ventiquattro, per quelli più articolati. E’ ovvio che ciò presuppone un investimento dell’azienda sia in termini economici, sia in termini di risorse umane (il personale chiamato a frequentare i corsi di addestramento, nella migliore delle ipotesi, non potrà essere utilizzato a tempo pieno per svolgere le normali attività produttive).

I criteri esposti rivestono un’importanza generale, non legata, quindi, alle sole aziende cartarie e che caratterizzano in maniera completa un qualsiasi software.

A questi criteri si sono poi aggiunti i criteri di secondo livello, così direttamente legati all’economicità troviamo:

• Ec. di acquisto: rappresenta il prezzo di acquisto del cmms, che in genere è legato alle funzionalità presenti nel software, alla possibilità di utilizzo da parte di uno o più user, alla possibilità di interagire con diversi sistemi operativi.

• Ec. di implementazione: è legata alla necessità di prevedere un budget per implementare il software, per rendere cioè operativi i moduli presenti, effettuare il

trasferimento dati, integrare l’utilizzo del cmms con gli altri software presenti in azienda e sfruttare a pieno le potenzialità; questo sotto-criterio ha richiesto l’inserimento di due criteri di terzo livello;

• Ec. di adeguamento: tiene conto dell’investimento, in termini economici, necessario per rendere il software compatibile con quelle che sono le necessità aziendali: la customizzazione delle maschere di interfaccia, o la modifica di uno o più moduli, rappresentano un costo di adeguamento.

Per le performance i sotto-criteri scelti sono:

• Facilità d’uso: è una caratteristica importante, soprattutto in aziende, come quelle partecipanti al preogetto IN.DI.CA., dove gli operatori hanno scarse conoscenze informatiche. Infatti, come è stato più volte ribadito nel presente lavoro, la diffidenza del personale riguardo i cmms è spesso una conseguenza diretta della poca dimestichezza nell’utilizzo dell’Information Technology;

• Modularità: caratterizza in maniera peculiare i software di manutenzione; la presenza di moduli specifici per gestire i vari aspetti manutentivi (work-order, menutenzione preventiva, predittiva, sotto condizione, consuntivazione, gestione magazzino), consente un approccio immediato e diretto al cmms;

• Flessibilità: rappresenta la possibilita di customizzare le maschere presenti nel software per renderle più consone a quelle che sono le esigenze delle aziende in cui ci troviamo ad operare; tra le varie possibilità offerte da alcuni cmms commerciali segnaliamo:…

• Completezza: rappresenta il numero di moduli presenti nel software rispetto al massimo numero possibile di moduli che un cmms può contenere (come riferimento è stato scelto MAXIMO che attualmente è il cmms commerciale più completo).

La facilità di implementazione è stata suddivisa nei seguenti criteri di secondo livello:

• Integrazione software: come specificato per la facilità di implementazione, all’introduzione del cmms deve far seguito l’integrazione con i software già presenti in azienda e con cui il sistema computerizzato di manutenzione deve interagire.

• Trasferimento dati: è legata alla possibilità di trasferire facilmente i dati da software già operanti nell’area manutentiva al cmms. Questa caratteristica è strettamente connessa con la capacità che presentano alcuni cmms di dialogare con più sistemi operativi.

• Adattamento procedure: questo criterio fa riferimento alla necessità da parte delle aziende di gestire i processi facendo riferimento a procedure più o meno strutturate; l’introduzione di un cmms richiede, perciò, un adattamento delle stesse e la necessità di ridisegnare alcuni processi di gestione della manutenzione per poter sfruttare a pieno le potenzialità del software.

All’addestramento fanno secuito i sotto-criteri:

• Corsi periodici di formazione: tiene conto della necesità di un addestramento specifico per l’utilizzo del cmms; maggiore è la complessità del software, più lungo è il periodo di tempo richiesto per fornire agli operatori le conoscenze necessarie per una corretta gestione.

• Presenza consulenza esterna: è un crirterio che ci permette di valutare la necesità di richiedere un supporto esterno per effettuare la fase di addestramento. Infatti, pur essendo presenti in azienda tecnici con buone conoscenze informatiche, la complessità del cmms può richiedere il supporto di personale altamente qualificato.

Il primo passo, successivo alla costruzione dell’albero gerarchico, è la valutazione mediante parwise comparison dei criteri adottati. L’attribuzione dei giudizi è stata effettuata tenendo presenti quelli che sono i risultati degli audit condotti in azienda e delle specifiche richieste dei manager di manutenzione che hanno preso parte alla fase di co-design.

E’ evidente che il poter far riferimento ad una valutazione linguistica si ha il considerevole vantaggio di utilizzare i metodi propri del ragionamento umano.

Così, per i criteri di primo livello, si è scelto di privilegiare le performance, tenendo conto del fatto che il cmms scelto rappresenta per le aziende un investimento a lungo termine e deve, quindi, essere in grado di rispondere ad esigenze immediate, ma anche mutevoli nel tempo. Un software altamente performante ben risponde a queste necessità.

Il secondo criterio in ordine di importanza è rappresentato dalla facilità di implementazione, caratteristica rilevante soprattutto nel caso delle aziende prese in esame, in

cui la presenza di operatori poco versatili nell’uso delle tecnologie informatiche, impone che la scelta privilegi un cmms di facile utilizzo.

Per quanto riguarda l’addestramento il suo peso è stato giudicato equivalente a quello riguardante la facilità di implementazione, mentre, all’economicità si è dato minor peso, poiché le aziende fuitrici del software sono tutte di grosse dimensione e, quindi, l’economicità del prodotto rappresenta un elemento importante, ma non fondamentale per la scelta.

E’ ovvio che i giudizi forniti presentano un certo grado di soggettività, ma si attengono, comunque, ai limiti stabiliti durante la costruzione del modello.

A questo punto è stato possibile costruire la matrice della parwise comparison, per i criteri di primo livello, in cui il termine rappresenta il peso del criterio i-esimo rispetto al criterio j-esimo: ij a 1 1 1/3 2 1 1 1/3 2 3 3 1 5 1/2 1/2 1/5 1 A≡ (4.15)

L’applicazione dell’algoritmo di calcolo dell’autovettore consente di valutare il

ranking locale dei criteri.

Si può verificare che già al secondo ciclo dell’iterazione il risultato è ottimale, in quanto gli scarti sono più piccoli di 1/1000. L’autovettore normalizzato fornisce il seguente ranking (Tab. 4.5.1) : Criterio Ranking Performance 0,530 Facilità di implementazione 0,200 Addestramento 0,200 Economicità 0,070

Tab. 4.4.1 Ranking locale dei criteri

Il rapporto di inconsistenza è I_R =0,002. Il giudizio fornito è perciò consistente ed il ranking ottenuto è valido.

A questo punto abbiamo analizzato i criteri di secondo livello.

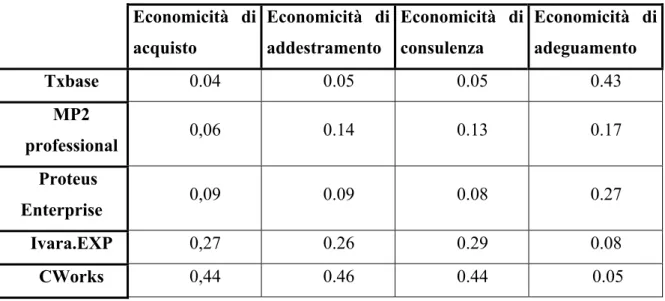
Rispetto all’economicità, il sotto-criterio più rilevante è risultato essere l’economicità

di implementazione; in effetti l’implementazione del pacchetto prevede un rilevante esborso iniziale, ma anche la necessità di un ulteriore investimento per gli anni successivi all’introduzione del software, basti pensare che in una delle aziende intervistate a quattro anni dall’acquisto di MAXIMO la fase di implementazione era ben lungi dall’essere terminata.

I rimanenti due sotto- criteri sono stati giudicati ugualmente importanti.La matrice riguardante i criteri di secondo livello risulta essere così composta:

1 1/6 1 6 1 6 1 1/6 1 B₁ = (4.16)

Il ranking locale dei sotto-criteri è riportato in tabella 4.5.2: Criterio Ranking Economicità di implementazione 0,750 Economicità di addestramento 0,125 Economicità di acquisto 0,125

Tabella 4.4.2 Ranking locale dei sotto-criteri relativi all’economicità

In questo caso il rapporto di inconsistenza è I_R = ed il giudizio fornito è perciò valido. 0

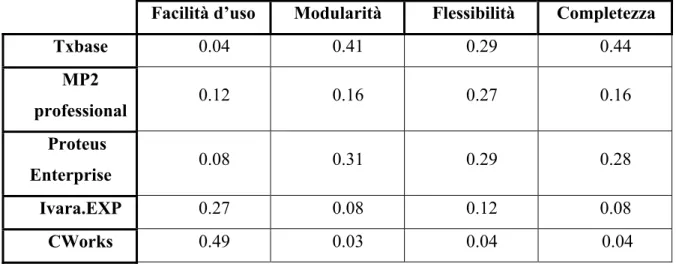
Per i sotto-criteri riguardanti le performance, si è privilegiata lamodularità;in

accordo con i manager di manutenzione che, ritenendo l’acquisto di un cmms un investimento a lungo termine, sentono la necessità di avere a disposizione uno strmento modulare che permetta loro, negli anni, di organizzare i vari aspetti manutentivi. Ad essa fa seguito, in ordine di importanza, la facilità d’uso, data la scarsa dimestichezza con i cmms degli operatori, mentre è stato dato ugual peso alla flessibilità, cioè la possibilità del software di

modificare le maschere presenti per renderle più consone all’utilizzo, e alla completezza. Infatti, secondo i manager di manutenzione è preferibile rinunciare alla presenza di qualche modulo piuttosto che ritrovarsi a gestire un software difficilmente utilizzabile. La matrice del pesi dei sotto criteri citati rispetto al criterio di livello superiore è:

1 1 1/4 1/2 1 1 1/4 1/2 4 4 1 3 2 2 1/3 1 B₂ = (4.17)

Il ranking locale per i sotto-criteri è (Tab. 4.5.3):

Criterio Ranking Modularità 0,548 Facilità d’uso 0,223 Flessibilità 0,115 Completezza 0,115

Tabella 4.4.3 Ranking locale dei sotto-criteri relativi alle performance

Anche in questo caso il giudizio fornito è consistente essendo I_R =0.002.

In riferimento alla facilità di implementazione i sotto-criteri sono stati ordinati a

partire dall’integrazione software fino all’adattamento procedure, passando per il trasferimento dati.

In effetti, come risulta chiaramente dal report, uno dei problemi più sentiti dal personale di manutenzione intervistato è la mancanza di un’integrazione completa dei cmms con i software già in uso in azienda. Questo può spesso comportare dei ritardi nel trasferimento dati che può non risultare immediato, per l’impossibilità di effettuare un collegamento diretto fra il cmms e gli altri programmi utilizzati nell’area manutentiva.

1 1/2 1/3 2 1 1/2 3 2 1 B₃ = (4.18)

Anche in questo caso, seguendo il metodo proposto da Saty, siamo in grado di calcolare il ranking locale della alternative (Tab. 4.5.4)

Criterio Ranking

Integrazione software 0,540 Trasferimento dati 0,297 Adattamento procedure 0,163

Tabella 4.4.4 Ranking locale dei sotto-criteri relativi alla facilità di implementazione

Il giudizio fornito è corretto in quanto I_R =0.008.

Veniamo, dunque, all’ordinamento dei sotto-criteri relativi all’addestramento. In

questo caso si è preferito privilegiare la necessità di corsi periodici di formazione rispetto alla presenza di consulenza esterna. Questo perché, la necessità di prevedere periodi di formazione sull’utilizzo del cmms, può richiedere una riorganizzazione della funzione manutentiva che tenga conto della non disponibilità, in alcuni periodi dell’anno, di tutti gli operatori del settore.

La matrice che deriva dall’analisi è: 1 1/2 2 1 B₄ = (4.19)

Criterio Ranking

Corsi periodici di formazione 0,700 Presenza consulenza esterna 0,300

Tabella 4.4.5 Ranking locale dei sotto-criteri relativi all’addestramento

Anche in questo caso il ciudizio è consistente ed il rapporto di inconsistenza risulta essere I_R =0.

Gli unici criteri di terzo livello presenti, nell’albero gerarchico, riguardano l’economicità di implementazione. Anche in questo caso, in linea con quanto fatto per

l’addestramento, si è dato un peso leggermente maggiore all’economicità di addestramento rispetto all’economicità di consulenza, valutando, in base ai dati forniti dai provider, più oneroso il primo sotto-criterio rispetto al secondo.

La matrice che deriva dall’analisi è:

1 1/2 2 1 C₁ = (4.20)

Il ranking relativo risulta essere:

Criterio Ranking

Economicità di addestramento 0,700 Economicità di consulenza 0,300

Tabella 4.4.6 Ranking locale dei sotto-criteri relativi all’economicità di implementazione

A questo punto, è necessario costruire le classifiche locali di ciascuna alternativa rispetto ai criteri immediatamente precedenti, seguendo una metodologia del tutto analoga a quella utlizzata per i criteri stessi. Si è reso, quindi, necessario stabilire il metro di giudizio secondo cui valutare le alternative rispetto a ciascun sotto-criterio.

Riguardo l’economicità di acquisto, si è attribuito il giudizio migliore al cmms con

il prezzo più basso e si sono valutati i restanti software in base agli scostamenti che presentano rispetto a questo parametro.

L’economicità di addestramento è strettamente connessa al periodo di tempo

necessario per poter fornire agli operatori le conoscenze necessarie alla gestione del software. Quindi, stando ai dati forniti dai provider, è possibile stabilire che il cmms migliore è quello che richiede il tempo di addestramento minore e viceversa (CWorks il migliore, Txbase il peggiore).

Per l’economicità di consulenza si è stabilito di valutare la struttura del software.

Infatti, il costo giornaliero di un consulente esterno si aggira intorno ai $1.000/1.500 e la necessità di far ricorso a tali figure professionali, è direttamente proporzionale alla complessità del prodotto. In genere si stima che i costi di consulenza rappresentano il 15-20% del prezzo di acquisto.

L’economicità di adeguamento è stata valutata in base alla capacità del software di

essere adattabile a quelle che sono le esigenze aziendali: Un cmms in grado di interagire con gli altri software utilizzati in manutenzione, non richiede investimenti elevati in termini di adeguamento; in questo caso il cmms migliore è quello che presenta maggiori funzionalità.

In riferimento alla facilità d’uso si è tenuto conto del fatto che decresce con il

crescere del numero di moduli e delle funzionalità presenti nel software. Questo è tanto più vero, quanto più esiste all’interno del cmms una sostanziale diversificazione tra le maschere di interfaccia dei vari moduli; infatti prima di poter utilizzare in maniera organica il software, è necessaria una lunga fase di addestramento, (Txbase il peggiore, CWorks il migliore).

I giudizi espressi in funzione della modularità, della flessibilità e della completezza

rispecchiano quelli che sono i dati esposti nella tabella 4.4.1. Per la modularità e la completezza si è preso in considerazione il numero di moduli presenti, per la flessibilità, caratteristiche quali la possibilità di customizzare i menù, e di definire la struttura dei report. Il miglior cmms risulta essere Txbase, il peggiore CWorks.

Per quanto riguarda l’integrazione software, il trasferimento dati e l’adattamento procedure i dati forniti dai provider e il ricorso alla tabella 4.4.1 hanno permesso di stilare

integrazione, trasferimento dati e adattamento procedure, è direttamente proporzionale alla complessità del software. Così, ad esempio, l’implementazione di un cmms quale CWorks presenta pochi ostacoli, essendo il prodotto poco strutturato.

In riferimento ai corsi periodici di formazione e alla presenza di consulenza esterna, il giudizio ha tenuto conto del numero di moduli presenti e della necessità, che

spesso si verifica, di modificare questi ultimi in funzione delle necessità aziendali. Ovviamente la presenza di un numero rilevante di moduli può richiedere una maggior necessità di interventi esterni. Per i corsi di formazione, come già accennato in precedenza, i provider prevedono da un minimo di 3 mesi per i cmms meno articolati, ad un massimo di 24, per quelli più complessi: il miglior cmms risulta quindi CWorks, il peggiore Txbase.

L’analisi di cui sopra, è stata condotta con l’ausilio del software CRITERIUM DECISION PLUS che ci ha permesso di elaborare i ranking locali delle cinque alternative

rispetto ai sotto-criteri di livello superiore. Nelle tabelle 4.4.7, 4.4.8, 4.4.9, 4.4.10 sono riportati i risultati ottenuti.

Economicità di acquisto Economicità di addestramento Economicità di consulenza Economicità di adeguamento Txbase 0.04 0.05 0.05 0.43 MP2 professional 0,06 0.14 0.13 0.17 Proteus Enterprise 0,09 0.09 0.08 0.27 Ivara.EXP 0,27 0.26 0.29 0.08 CWorks 0,44 0.46 0.44 0.05

Facilità d’uso Modularità Flessibilità Completezza

Txbase 0.04 0.41 0.29 0.44 MP2 professional 0.12 0.16 0.27 0.16 Proteus Enterprise 0.08 0.31 0.29 0.28 Ivara.EXP 0.27 0.08 0.12 0.08 CWorks 0.49 0.03 0.04 0.04

Tabella 4.4.8 Ranking locali delle alternative rispetto ai sotto-criteri di performance

Integrazione software Trasferimento dati Adattamento procedure Txbase 0.04 0.06 0.05 MP2 professional 0.11 0.09 0.12 Proteus Enterprise 0.07 0.09 0.07 Ivara.EXP 0.28 0.25 0.25 CWorks 0.50 0.51 0.51

Tabella 4.4.9 Ranking locali delle alternative rispetto ai sotto-criteri di facilità di implementazione

Corsi periodici di formazione Presenza consulenza esterna Txbase 0.05 0.05 MP2 professional 0.12 0.11 Proteus Enterprise 0.07 0.07 Ivara.EXP 0.26 0.22 CWorks 0.50 0.56

Tabella 4.4.10 Ranking locali delle alternative rispetto ai sotto-criteri di addestramento

Il passo finale da compiere consiste nel calcolo del ranking globale. Indicando con

il peso locale dell’alternativa i-esima rispetto al criterio j-esimo di primo livello, e con il peso locale del criterio j-esimo di primo livello, potremo scrivere senz’altro il ranking

globale nella forma:

ij a j w 4 3 2 1 44 43 42 41 34 33 32 31 24 23 22 21 14 13 12 11 w w w w a a a a a a a a a a a a a a a a G= × (4.21)

o, molto più concisamente

W A

G= × (4.22)

In pratica il ranking globale è calcolato mediante un prodotto righe per colonne: il peso, rispetto all’obiettivo finale, della generica alternativa assume la forma:

∑

Allora, utilizzando la (4.22), otterremo facilmente la soluzione del problema (Tab.4.5.7): Alternativa Ranking Cworks 0.301 TXbase 0.198 IvaraEXP 0.185 Proteus enterprise 0.174 MP2 Professional 0.143

Tab. 4..4.11 Ranking globale

Il CRITERIUM DECISION PLUS ci da la possibilità di visualizzare questo risultato, come mostrato in figura 4.5.2.

CWorks appare preferibile rispetto agli altri cmms presenti; comunque è opportuno analizzare il risultato ottenuto tramite un’indagine più approfondita, coadiuvata da una efficiente analisi di sensitività, capace di evidenziare l’influenza che variazioni, anche

minime, nel peso dei criteri, potrebbero sortire nei confronti del ranking ottenuto.

Infatti con l’ausilio del software CRITERIUM DECISION PLUS è possibile evidenziare graficamente che, sebbene per la maggior parte dei criteri utilizzati la variazione dei pesi di questi ultimi non comporta una modifica sulla scelta di CWorks quale miglior cmms, per quanto riguarda le performance una variazione del ranking locale determina una

inversione della classifica finale (figura 4.5.3).

4.5 Analisi di sensitività: definizione del problema.

Per determinare il criterio più critico, cioè quello che determina la maggiore sensibilità del sistema di giudizio, considereremo la più piccola variazione dei pesi w che determina

una qualsiasi inversione nella classifica finale.

k

Nel paragrafo precedente, abbiamo definito il renking globale delle alternative definito , la matrice

W A

G = × A dei pesi locali delle alternative rispetto ai criteri di primo livello e il

vettore W dei pesi locali dei criteri di primo livello.

Definiamo δ_k,i,j, con 1≤i< j≤m e 1≤k≤n, la più piccola variazione assoluta del criterio k-esimo che determina l’inversione di posizione nel ranking fra le alternative e

. Questa variazione in termini percentuali, può scriversi:

i A j A k j i k j i k w 100 ' ,, , , × = δ δ (4.24)

doveA₁ indica senz’altro l’alternativa migliore.

A questo punto introduciamo due definizioni: si indica come Percent-Top Criticality Criterion (PTCC) il criterio cui corrisponde il valore più piccolo di δ_{k, j1,} ' (in pratica si considerano le possibili inversioni del primo elemento).Definiamo, invece, Percent-Any Criticality Criterion (PACC) il più piccolo valore della quantità δ_{k, ji,} '.

Accanto a questi concetti basilari possiamo introdurre anche quelli di Grado di Criticità e di Coefficiente di Sensitività per il generico criterio C . _k

Il primo, indicato in genere con , rappresenta la più piccola quantità percentuale di cui deve cambiare il peso del criterio k-esimo affinché ci possa essere un qualsiasi cambiamento nel ranking. Analiticamente scriveremo:

'

k

D

Il secondo, , è il reciproco del precedente. Se il Grado di Criticità non può essere determinato, cioè se non può esserci alcuna inversione del ranking, porremo per definizione: ) (C_k sens 0 ) (C_k = sens (4.26)

Supponiamo ora di voler modificare il risultato finale e quindi il ranking delle alternative A₁ e A₂, modificando esclusivamente il peso w₁ del criterio C₁.

Per fare questo è necessario determinare il valore δ_{k ,,i j} per cui ciò accade. Nel caso preso in esame k=1, i=1, j=2 e dunque dovremo calcolare la quantità δ_1,1,2. Per definizione avremo che: 2 , 1 , 1 1 * 1 = w −δ w (4.27)

Poichè deve sempre essere rispettata la condizione:

∑

dovremo normalizzare nuovamente il vettore W modificato, che indicheremo con W1. I pesi dei criteri saranno allora i seguenti:

          + + + = + + + = + + + = n n n n n w w w w w w w w w w w w w w w .. ' ... .. ' .. ' 2 * 1 2 * 1 2 2 2 * 1 * 1 1 (4.29)

Se indichiamo con G1 _{il nuovo vettore del ranking, per avere l’inversione che ci siamo}

' g '

g₁ < ₂ (4.30)

Ai valori di e possiamo sostituire l’spressione derivante dalla definizione (4.22) ed ottenere quindi: 1 g g₂

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

Sostituendo a w₁* il valore dato dalla (4.26), otterremo molto facilmente:

1,1,2 21 11 2 1 g (a a )δ g − < − (4.34) e quindi, in conclusione:

(

)

(

)

(

)

(

)

a seconda che a₂₁ >a₁₁ o, viceversa, a₂₁ <a₁₁.

0

* 1 ≥

w (4.36)

che si traduce nel vincolo di ammissibilità per la variazione di peso:

1 2 , 1 , 1 ≤w δ (4.37)

Può effettivamente capitare che la variazione di peso assuma valori inammissibili: questo indica chiaramente che il ranking attuale non può essere invertito tramite nessuna variazione del criterio C₁.

Triantaphyllou [19] ha generalizzato la dimostrazione appena esposta, enunciando il seguente teorema:

“La quantità δ_{k ,,i j} di cui è necessario modificare il peso del criterio C , per invertire il ranking delle alternative e , è data da:

k w _k i A A_j

(

)

(

)

(

)

(

)

a seconda che a_jk >a_ik o, viceversa, a_jk <a_ik. Deve inoltre essere sempre rispettata la condizione per cui:

(

)

(

)

affinché il valore ottenuto sia ammissibile.”

Da questo teorema discende immediatamente che, qualora prevalga su per tutti i criteri di giudizio, ovvero

i

jk ik a

a ≥

(

)

allora non sarà possibile in alcun modo invertire la classifica ottenuta. Il verificarsi di questo evento si può intendere come sinonimo di robustezza della soluzione rispetto ad ogni

possibile variazione di peso dei vari criteri.

4.6 L’analisi di sensitività per il caso in esame.

Come risulta dai risultati esposti nel paragrago 4.5 una variazione percentuale del criterio Performance determina l’inversione di posizione nel ranking fra le alternative. In

particolare ci interessa capire quando l’inversione della classifica finale, del miglior cmms, riguarda il primo dei software: CWorks.

Facciamo allora ricorso all’analisi di sensitività, utilizzando le definizioni esposte nel paragrafo precedente.

Abbiamo determinato (tab. 4.6.1) il vettore W dei pesi locali dei criteri di primo livello rispetto al Goal :

k

w

Criterio Ranking

Performance 0,530=w_p

Facilità di implementazione 0,200=w_f,i

Addestramento 0,200=w_a

Economicità 0,070=w_e

Tab. 4.6.1 Ranking locale dei criteri rispetto al goal

Alternativa Ranking Cworks 0.301 TXbase 0.198 IvaraEXP 0.185 Proteus enterprise 0.174 MP2 Professional 0.143

Tab. 4.6.2 Ranking globale

A questo punto dobbiamo determinare, secondo la teoria di Triantaphyllou [19],[20], il vettoreG dei pesi delle alternative rispetto al criterio di primo livello: Performance. _p

Per far questo facciamo ricorso alla teoria di Saaty. Definiamo (tab. 4.6.3), la matrice dei pesi delle alternative rispetto ai sotto-criteri:

p A • Modularità • Facilità d’uso • Flessibilità • Completezza

Modularità Facilità d’uso Flessibilità Completezza

CWorks 0.03 0.49 0.04 0.04 Txbase 0.41 0.04 0.29 0.044 Ivara.EXP 0.08 0.27 0.12 0.08 Proteus Enterprise 0.31 0.08 0.27 0.28 MP2 professional 0.16 0.12 0.29 0.16

Tale matrice può essere così rappresentata: 54 53 52 51 44 43 42 41 34 33 32 31 24 23 22 21 14 13 12 11 p a a a a a a a a a a a a a a a a a a a a A = (4.41)

dove il termini della prima riga rappresentano il peso della prima alternativa (CWorks), rispetto ai sotto-criteri modularità, j=1, facilità d’uso, j=2, flessibilità, j=3, completezza, j=4. 1j a Indicato con 4 3 2 1 b b b b

B = il vettore del ranking locale di questi sotto-criteri rispetto al criterio

Performance: Criterio Ranking Modularità 0,548 Facilità d’uso 0,223 Flessibilità 0,115 Completezza 0,115

Tabella 4.6.4 Vettore Ranking dei sotto criteri rispetto alle B Performance

Il vettore risultante G dei pesi delle alternative rispetto al criterio Performance è dato da: _p

p

p B G

A × = (4.42)

Il risultato di tale operazione è riportato in tabella 4.6.5:

Performance CWorks 0.135 Txbase 0.318 Ivara.EXP 0.128 Proteus Enterprise 0.251 MP2 professional 0.168

Tabella 4.6.5 Vettore G_p Ranking delle alternative rispetto alle Performance.

Andiamo adesso a calcolare le possibili variazioni di peso del criterio performance

che determinano una variazione del ranking globale.

Consideriamo perciò, K=p, i=1, j=2 e scriviamo:

0.530 w 0.563 0.135 0.318 0.301 0.198 δ_p,1,2 =− < _p = − − = (4.43)

Poiché è rispettata la condizione (4.37) tale variazione di peso è ammissibile. Come conseguenza di ciò possiamo affermare che variando il peso del criterio Performance possiamo causare l’inversione fra la prima e la seconda alternativa.