3
3
S
S
T
T
R
R
A
A
T
T
E
E
G
G
I
I
E
E
D
D
I
I
A
A
N
N
A
A
L
L
I
I
S
S
I
I
P
P
E
E
R
R
U
U
N
N
E
E
S
S
P
P
E
E
R
R
I
I
M
M
E
E
N
N
T
T
O
O
D
D
I
I
C
C
L
L
A
A
S
S
S
S
C
C
O
O
M
M
P
P
A
A
R
R
I
I
S
S
O
O
N
N
In un esperimento di “class comparison”, l’obiettivo principale consiste nello stabilire se il livello di espressione dei geni differisce tra le classi o varietà a confronto e, in caso affermativo, nell’identificare quali geni sono differenzialmente espressi tra le classi.
Sebbene semplice in teoria, nella pratica l’identificazione dei geni differenzialmente espressi può rivelarsi alquanto complessa nel caso in cui:
- si vogliano confrontare più classi o condizioni sperimentali;
- i valori di intensità misurati siano affetti da numerose fonti di variabilità e di rumore; - non si disponga di un numero sufficiente di repliche biologiche.
L’enorme quantità di dati generata da un esperimento microarray e la loro intrinseca variabilità ha reso indispensabile lo sviluppo e l’utilizzo di metodi statistici per estrarre l’informazione biologica dai dati e valutare l’incertezza ad essa associata.
Nel seguito del capitolo sono descritti i metodi più largamente usati per individuare i geni differenzialmente espressi tra due o più condizioni.
3.1 METODI DI SELEZIONE DEI GENI
Dopo la fase di elaborazione dell’immagine ed estrazione dei dati di intensità eseguita mediante software dedicati, i dati prodotti per ogni gene su ciascun microarray sono costituiti da una coppia di valori di intensità, uno nel canale rosso e l’altro nel verde.
In generale, i dati utilizzati nella successiva fase di analisi sono ottenuti sottraendo ai dati grezzi il valore medio o mediano del background. Il background o rumore di fondo è dovuto a diversi fattori tra cui l’instaurarsi di legami aspecifici fra il supporto del microarray e il campione ibridizzato, la fluorescenza propria dei reagenti utilizzati nella fase di “spotting”, la contaminazione, durante la fase di “spotting”, di aree esterne allo spot da parte della soluzione contenente le sonde, che consente l’ibridizzazione del campione marcato anche dove non dovrebbe avvenire). Inoltre, per poter utilizzare gran parte dei metodi di analisi che verranno illustrati nei prossimi paragrafi, è necessario operare delle trasformazioni sui dati. La trasformazione più frequentemente utilizzata è quella logaritmica perché dà luogo ad una distribuzione dei dati approssimativamente normale, condizione, questa, necessaria per l’applicabilità di numerosi test statistici. Utilizzando questa scala, yijkg indica il logaritmo (in
base 2) dell’intensità della fluorescenza misurata per l’array i, il fluorocromo j, la varietà o trattamento k e il gene g.
Poiché l‘obiettivo di uno studio di “class comparison” è l’identificazione dei geni differenzialmente espressi tra due o più classi di campioni, il dato di interesse è in realtà rappresentato dalla differenza (yijkg −yijk'g) (dove k e k’ si riferiscono a due varietà), che equivale ad un rapporto (“log-ratio”). Esso rappresenta il valore relativo di espressione genica e coincide con il logaritmo del “fold-change”. Nel caso di disegni sperimentali particolarmente semplici come il “reference design”, l’analisi dei dati può essere eseguita confrontando direttamente i “log-ratio“ per mezzo di opportuni test statistici (per esempio il t-test). Grazie alla sua semplicità, questo tipo di approccio è stato utilizzato per anni da molti ricercatori (Callow et al., 2000; Geiss et al., 2000); esso tuttavia ha dei seri limiti per quanto riguarda la scelta delle tipologie di disegno alle quali può essere applicato. Per tale motivo sono stati sviluppati dei metodi più generali che verranno illustrati in dettaglio nel seguito del capitolo.
3.1.1 Il test delle ipotesi
I metodi statistici utilizzati per operare la verifica di ipotesi scientifiche sono denominati test delle ipotesi o test di significatività. Partendo dalla descrizione delle procedure utilizzate per verificare l’ipotesi che due trattamenti diversi producono in media lo stesso effetto su una qualche variabile (nel caso dei microarray, il livello di espressione di un gene), il test di significatività può essere generalizzato per consentire l’analisi di dati ottenuti da esperimenti che coinvolgono più di due gruppi o trattamenti.
Per eseguire un test delle ipotesi bisogna innanzitutto definire chiaramente il problema di interesse. Si supponga, per esempio, di voler studiare l’effetto sul profilo di espressione genica di un nuovo farmaco antitumorale su animali da esperimento. Poiché è impossibile pensare di testare il farmaco su tutti i soggetti, si estrae casualmente dalla popolazione di animali un certo numero di individui (il campione), assicurandosi che siano il più possibile rappresentativi dell’intera popolazione. Si divide quindi il campione in due gruppi e si procede al trattamento di un gruppo con il nuovo farmaco e dell’altro con un placebo. Attraverso un esperimento microarray si vogliono identificare quali geni risultano differenzialmente espressi nel campione dei trattati rispetto a quello dei controlli.
Dal punto di vista statistico, il livello di espressione di un gene può essere modellato con una variabile aleatoria poiché non è altro che il risultato numerico di un esperimento che non è possibile prevedere con certezza (ossia non è deterministico). Una variabile aleatoria non rappresenta il valore vero di un particolare esperimento, al contrario essa associa una distribuzione di probabilità ai possibili ma non ancora noti risultati di un esperimento. Per esempio, il livello di espressione di un determinato gene g nei soggetti trattati con il farmaco e in quelli ai quali è stato somministrato il placebo può essere rappresentato mediante 2 variabili aleatorie Y1 e Y2. La distribuzione di probabilità di una variabile aleatoria può essere
caratterizzata attraverso alcuni parametri (media, varianza, curtosi, etc…). Nell’esperimento che si sta considerando, le medie delle distribuzioni di probabilità di Y1 e di Y2 verranno
indicate con μ1 e μ2.
Poiché l’analisi non viene condotta sull’intera popolazione, ma su un campione estratto da essa, il valore vero dei parametri rimane sconosciuto allo sperimentatore. Tuttavia è possibile ottenere alcune informazioni utili per quanto riguarda il parametro di interesse applicando al campione una misura numerica descrittiva chiamata “statistica”. Per esempio, si possono calcolare le medie y1 e y2 delle osservazioni disponibili per ciascun gruppo e
utilizzarle come valori rappresentativi del livello medio di espressione del gene g nei due gruppi. L’obiettivo è fornire una stima del valore del parametro a partire dalla conoscenza del valore della statistica corrispondente. Questa procedura di generalizzazione prende il nome di “inferenza statistica”.
Tornando all’esperimento microarray, il problema di stabilire se il gene g è sovra o sottoespresso nel gruppo dei trattati rispetto a quello dei controlli si traduce quindi nel confronto tra le medie dei due campioni.
Tra i campioni ci sono ovviamente delle differenze dovute al campionamento casuale pertanto è molto improbabile che i livelli medi di espressione siano esattamente uguali. Il problema è stabilire se la differenza osservata tra y1 e y2 corrisponde ad una reale differenza
di espressione del gene g tra i due gruppi, attribuibile al trattamento con il farmaco, oppure è semplicemente legata al fatto che il livello di espressione di un gene può variare in modo casuale in soggetti diversi. Questo costituisce di fatto l’obiettivo di un test delle ipotesi.
Il procedimento logico che deve essere seguito per condurre un test delle ipotesi comprende diverse fasi, che possono essere riassunte in 7 passaggi:
2. scegliere il test più appropriato per saggiare l’ipotesi nulla H0, secondo le finalità della
ricerca e le caratteristiche statistiche dei dati; 3. specificare il livello di significatività;
4. trovare la distribuzione di campionamento della statistica test nell’ipotesi nulla H0, di
norma fornita da tabelle; 5. stabilire la regione di rifiuto;
6. calcolare il valore della statistica sulla base dei dati sperimentali, stimando la probabilità P ad esso associata;
7. sulla base del confronto fra le soglie e la probabilità, trarre le conclusioni.
Una volta individuato il problema, il passo successivo consiste nel tradurre il quesito in una coppia di ipotesi che devono essere mutuamente esclusive e “all inclusive”. In altre parole le ipotesi non possono essere entrambe vere o entrambe false e la loro unione deve racchiudere tutte le possibilità. Una delle ipotesi sarà l’ipotesi nulla, tradizionalmente indicata con H0, l’altra ipotesi sarà invece l’ipotesi alternativa o di ricerca, indicata con H1.
L’ipotesi nulla è ciò che è noto o si desume dalla teoria o da ricerche precedenti e rappresenta, in generale, l’ipotesi che si vorrebbe confutare. Essa afferma che gli effetti osservati nei campioni sono dovuti a fluttuazioni casuali, sempre possibili quando esiste variabilità tra gli individui; si tratta di variazioni che sono tanto più marcate quanto più ridotto è il numero di osservazioni. L’ipotesi nulla deve essere rifiutata solamente se esiste l’evidenza che la contraddice. E’ importante comprendere che l’ipotesi nulla non è necessariamente vera, anche quando i dati campionari (eventualmente pochi) non consentono di rifiutarla.
Contrapposta all’ipotesi nulla si ha l’ipotesi alternativa che afferma che le differenze riscontrate nelle statistiche campionarie rispecchiano una reale differenza nei parametri delle popolazioni corrispondenti. Essa, in rapporto al problema e al test utilizzato, può essere di 2 tipi: 1) bilaterale: H0: θ = θ0 contro H1: θ ≠ θ0 2) unilaterale: destra: H0: θ ≤ θ0 contro H1: θ > θ0 sinistra: H0: θ ≥ θ0 contro H1: θ < θ0 dove:
- θ è il valore del parametro (media, varianza, correlazione, etc…) nel campione estratto dalla popolazione studiata;
- θ0 è il valore teorico prescelto come confronto.
Dal punto di vista dell’espressione differenziale dei geni queste ipotesi si possono definire come:
Ipotesi nulla: i due valori di espressione associati al gene che si stanno confrontando indicano che esso non è differenzialmente espresso;
Ipotesi alternativa: i due valori di espressione associati al gene indicano che il gene è differenzialmente espresso.
In simboli:
H0: µ1 ≤ µ2 contro H1: µ1 > µ2 per un’ipotesi unilaterale destra;
H0: µ1 ≥ µ2 contro H1: µ1 < µ2 per un’ipotesi unilaterale sinistra.
Stabilite le ipotesi nulla e alternativa, il passaggio successivo consiste nella scelta del test statistico. Esso può essere definito come quella procedura che, sulla base di dati campionari e con un certo grado di probabilità, consente di decidere se è ragionevole respingere l’ipotesi nulla H0 (ed accettare implicitamente l’ipotesi alternativa H1) oppure se
non esistono elementi sufficienti per respingerla.
La scelta tra le due ipotesi è fondata sulla probabilità di ottenere per caso il risultato osservato nel campione nella condizione che l'ipotesi nulla sia vera. Quanto più tale probabilità (indicata con α) è piccola, tanto più è improbabile che l'ipotesi nulla sia vera. α prende il nome di “livello di significatività” e deve essere stabilito a priori. I livelli di soglia delle probabilità α normalmente utilizzati sono tre: 0.05 (5%); 0.01 (1%); 0.001 (0.1%).
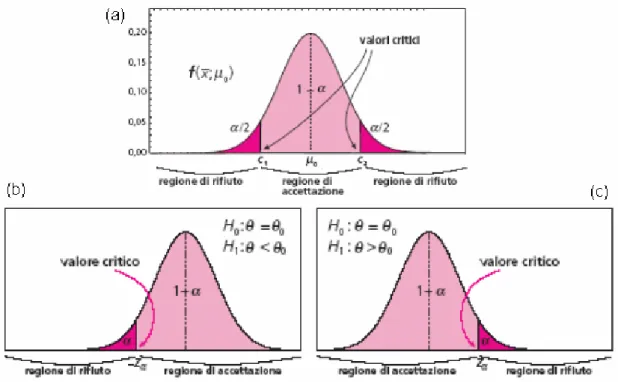
L’insieme di valori ottenibili con il test forma la distribuzione campionaria della statistica test. Essa può essere divisa in due zone (vedi Fig 3.1):
− la regione di rifiuto dell’ipotesi nulla, detta anche regione critica, che corrisponde ai valori collocati agli estremi della distribuzione; sono quei valori che hanno una probabilità piccola di verificarsi per caso, quando l’ipotesi nulla è vera;
− la regione di accettazione dell’ipotesi nulla, che comprende i restanti valori, quelli che si possono trovare abitualmente per effetto della variabilità casuale.
Se il test è unilaterale la regione di rifiuto si trova da una sola parte della curva di distribuzione. Questo tipo di test si usa quando l'effetto atteso è in una direzione precisa. Per un test bilaterale, invece, la regione di rifiuto è formata dall'unione di due intervalli.
Fig. 3.1: Rappresentazione grafica della regione di rifiuto nel caso di test bilaterale (a) e unilaterale (b) e (c).
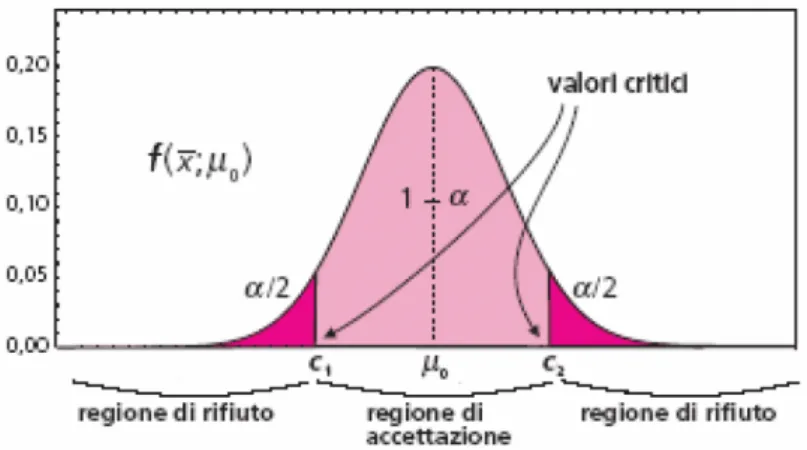
I valori critici che definiscono la regione di rifiuto dipendono dal livello di significatività α: maggiore è il suo valore, più ampia sarà la regione di rifiuto e più potente (meno conservativo) sarà il test cioè sarà più facile rifiutare l’ipotesi nulla. Se il valore della statistica calcolato appartiene alla regione di rifiuto, si respinge l’ipotesi nulla (e si accetta l’ipotesi alternativa); viceversa si conclude che non esistono elementi sufficienti per rifiutare H0.
Fig. 3.2: Distribuzione campionaria della statistica con definizione della regione di rifiuto bilaterale.
In alternativa, una volta calcolato il valore della statistica test sulla base dei dati sperimentali, si stima la probabilità P ad esso associata (definita p-value o probabilità a posteriori o livello di significatività osservato) e la si confronta con α:
- se P < α si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa,
- se, viceversa, risulta P > α si conclude che non è possibile rigettare l’ipotesi nulla.
3.1.2 Parametri di un test delle ipotesi
Nella verifica di un’ipotesi statistica è possibile commettere due tipi di errore: l'errore di primo tipo, se si rifiuta l'ipotesi nulla quando in realtà essa è vera; l'errore di secondo tipo, se si accetta l'ipotesi nulla, quando in realtà essa è falsa.
L’errore di I tipo consiste nell’attribuire al fattore in studio una differenza che è invece dovuta alla semplice fluttuazione statistica (cioè all’errore casuale). L’errore del I tipo incrementa la frazione dei falsi positivi e dipende dalla sensibilità della metodica. Il p-value non è altro che la stima di tale errore; più precisamente, rappresenta la probabilità di ottenere un valore del test statistico uguale o maggiore di quello calcolato dai dati quando, in realtà, non c’è differenza tra i gruppi.
Scegliere un livello di significatività significa quindi stabilire il massimo livello di probabilità di commettere un errore del I tipo che si è disposti ad accettare o, equivalentemente, il massimo livello di incertezza tollerabile.
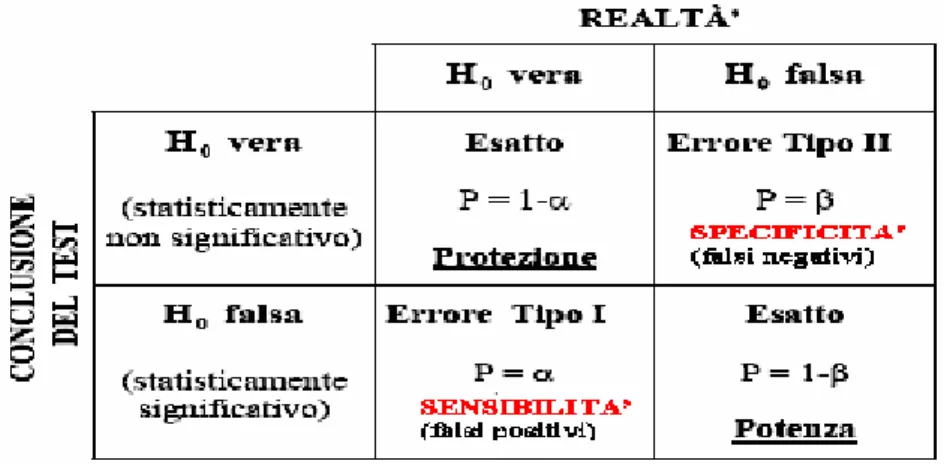
L’errore di II tipo consiste nell’attribuire all’effetto del caso, cioè alla semplice variabilità, una differenza dovuta al fattore in studio. Esso rappresenta quindi la frazione dei falsi negativi e dipende dalla specificità della metodica. La probabilità di commettere un errore di II tipo è indicata con β.
Tab. 3.1: Tabella riassuntiva dei possibili risultati di un test delle ipotesi.
Da questi concetti derivano direttamente anche quelli di livello di protezione e di potenza di un test, che sono i parametri più importanti per scegliere il test più adatto alle caratteristiche dei dati e all’obiettivo dell’esperimento. Sono concetti tra loro legati, secondo lo schema riportato nella tabella precedente, nella quale si confrontano la realtà e la conclusione del test.
Un test statistico conduce ad una conclusione esatta in due casi: − se non rifiuta l’ipotesi nulla, quando in realtà è vera;
− se si rifiuta l’ipotesi nulla, quando in realtà è falsa.
Per aumentare la probabilità (1-α) del primo caso, occorre incrementare la protezione, mentre per aumentare la probabilità (1-β) del secondo caso occorre incrementare la potenza.
La potenza di un test statistico (spesso indicata in letteratura con il simbolo π) è definita come la probabilità di rifiutare l’ipotesi nulla, quando l’ipotesi alternativa è vera; in altri termini, nel confronto tra medie la potenza è la probabilità di trovare una differenza, quando esiste.
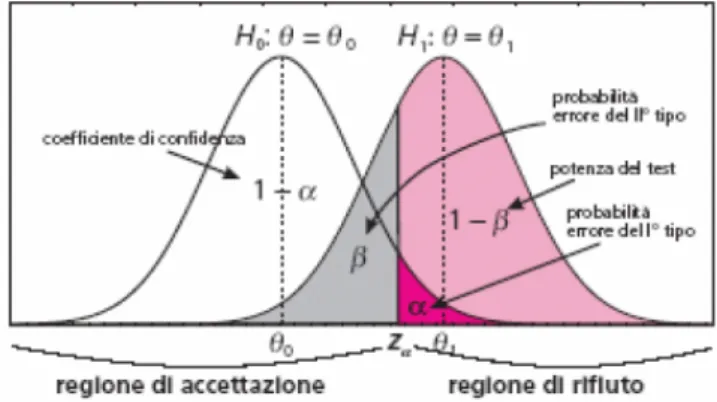
Le probabilità di commettere gli errori corrispondono a delle aree sottese dalle curve di distribuzione. Nel caso dei dati microarray tali curve rappresentano i livelli di espressione genica nei campioni a confronto.
Fig. 3.3: Visualizzazione dei parametri α e β sulle curve di probabilità.
I livelli di α e β sono interdipendenti. Se si vuole essere molto conservativi, bisognerà accettare un rischio maggiore di non riconoscere una differenza che esiste, poiché diminuendo α cresce β; al contrario, per evitare di non osservare una differenza vera, bisognerà accettare un rischio maggiore di trovare una differenza dove in realtà non c’è, poiché diminuendo β cresce α.
Si tratta di vedere quale dei due tipi di errore è più dannoso nella scelta che si deve effettuare.
Poiché in un esperimento microarray il problema più grave è rappresentato dall’elevato numero di falsi positivi, il ricercatore ha interesse a controllare l’errore di I tipo. Di solito, pertanto, si procede fissando il valore di α, e dimensionando il campione in modo da ottenere la potenza desiderata.
3.1.3 Confronto tra due classi: il t-test
A partire dagli stessi dati, non tutti i test hanno la stessa capacità di rifiutare l'ipotesi nulla quando è falsa. E’ quindi molto importante scegliere il test più adatto in rapporto
- alle caratteristiche dei dati (qualitativi o quantitativi), - alla variabilità dei dati,
- alla simmetria della distribuzione,
- alla omoschedasticità ovvero all’uguaglianza delle varianze dei gruppi a confronto.
Test diversi hanno condizioni di validità differenti e sono più o meno robusti cioè forniscono risultati che sono diversamente influenzati dal mancato rispetto delle condizioni di validità.
Il t-test è il test statistico più comunemente usato negli esperimenti microarray che prevedono il confronto tra i valori medi di espressione genica ricavati da due campioni. Il t-test è costruito rapportando la differenza tra le due medie campionarie all’errore standard ad esse associato, in genere stimato a partire dalle varianze dei due campioni.
Nell’ipotesi che i due campioni siano estratti in modo casuale e indipendente dalla stessa distribuzione e che questa sia gaussiana (Normale), il test segue la distribuzione t di
Student (t-Student). Tale distribuzione ha una forma simmetrica a campana come la distribuzione Normale ma con una dispersione tanto maggiore quanto minore è il numero di gradi di libertà ovvero il numero di osservazioni indipendenti necessarie per ottenere la misura della statistica, rispetto al numero di osservazioni totali.
Esistono due versioni del t-test:
t-test per campioni non appaiati o indipendenti,
t-test per campioni appaiati o dipendenti (“paired t-test”).
3.1.3.1 T-test per campioni indipendenti
Il t-test per campioni indipendenti può essere applicato nel caso dell’esperimento microarray descritto in precedenza per determinare se un dato gene risulta differenzialmente espresso tra il campione dei trattati e quello dei controlli, essendo i due gruppi formati da individui biologicamente diversi e quindi indipendenti.
In generale negli esperimenti di “class comparison” realizzati con microarray si ha a che fare con test bilaterali; di conseguenza l’ipotesi nulla H0 e l’ipotesi alternativa H1 possono
essere scritte come: H0: µ1=µ2 oppure µ1-µ2=0
H1: µ1≠µ2 oppure µ1-µ2≠0
Il valore della statistica t è ottenuto mediante la formula: (3.1) ) 1 1 ( ) ( ) ( 2 1 2 2 1 2 1 n n s y y t p + − − − = μ μ dove:
- y1e y2 sono le medie rispettivamente del campione dei trattati e del campione dei controlli;
- μ1 e μ2 sono le rispettive medie attese, espresse nell’ipotesi nulla;
- n1 e n2 sono il numero di osservazioni nei due campioni;
- è la varianza combinata o varianza “pooled” dei due gruppi a confronto. Essa è data dal rapporto tra la somma delle due devianze e la somma dei rispettivi gradi di libertà:
2 p s (3.2) 2 ) 1 ( ) 1 ( 2 1 2 2 2 2 1 1 2 − + − + − = n n s n s n sp , dove (3.3) 2 1 2 ( ) 1 1 i n j ij i i y y n s i
∑
= − − = , per i=1,2rappresenta la migliore stima della variabilità intra-classe dei dati di espressione, nell’ipotesi che le popolazioni da cui sono stati estratti i due campioni abbiano la stessa varianza, cioè sia
. 2 2 2 1 σ σ =
I gradi di libertà sono dati dal numero totale di misure meno il numero di valori intermedi che si sono dovuti calcolare. In questo caso si hanno (n1+n2) misure e due valori
intermedi y1e y2, pertanto la distribuzione t di riferimento sarà caratterizzata da (n1+n2-2)
gradi di libertà.
Se l’ipotesi di uguaglianza delle varianze (omoschedasticità) non è verificata, la formula per il calcolo della statistica t è la seguente:
(3.4) ) ( ) ( ) ( 2 2 2 1 2 1 2 1 2 1 n s n s y y t + − − − = μ μ ,
mentre i gradi di libertà corrispondenti sono dati da:
(3.5) 1 ) ( 1 ) ( ) ( 2 2 2 2 2 1 2 1 2 1 2 2 2 2 1 2 1 − + − + = n n s n n s n s n s υ .
Solitamente la formula restituisce un valore non intero che deve essere pertanto arrotondato per difetto.
Di fatto la statistica t può essere vista come il rapporto tra la variabilità tra i 2 gruppi e la variabilità intra-gruppo del livello di espressione genica. Elevati valori positivi o negativi di t indicano che la variabilità tra i gruppi è maggiore di quella attesa sulla base della variabilità all’interno dei singoli gruppi, pertanto la differenza osservata tra i gruppi non può essere puramente casuale.
Una volta calcolato il valore di t a partire dai dati campionari, per stabilire se la differenza |y1 -. y2| è statisticamente significativa si può procedere in due modi:
1. si ricava dalla distribuzione t-Student, per la quale si sono fissati i gradi di libertà, il valore della variabile t, detto tα, corrispondente al livello di confidenza scelto; dal confronto fra tα
e il valore di t ricavato dalle misure si stabilisce che:
a. se |t| < |tα| Æ la differenza tra y1 e y2 non è statisticamente significativa pertanto non è possibile rifiutare l’ipotesi nulla;
b. se |t| > |tα| Æ la differenza tra y1 e y2 è statisticamente significativa, l’ipotesi nulla
viene pertanto rigettata a favore dell’ipotesi alternativa e il gene viene dichiarato differenzialmente espresso.
2. Si converte il valore della statistica t nel corrispondente p-value P e si confronta P con α: si rifiuta H0 se P < α.
3.1.3.2 T-test per campioni dipendenti
Caratteristica distintiva del confronto tra 2 campioni dipendenti è poter accoppiare ogni osservazione di un campione con una e una sola osservazione dell'altro campione; necessariamente, i due gruppi hanno sempre lo stesso numero di dati. Le tecniche sono 2:
1. dati auto-appaiati,
2. dati naturalmente appaiati.
La situazione più semplice è quella dell'auto-accoppiamento, in cui ogni soggetto serve come controllo di se stesso; si parla anche di dati auto-appaiati e si confrontano i valori presi sugli stessi soggetti in 2 momenti diversi. Un esempio classico è il confronto tra i dati di espressione genica di un insieme di individui prima e dopo un trattamento, per valutarne l’efficacia. Tuttavia questa tecnica non sempre è possibile: se si deve analizzare l’effetto di due sostanze tossiche o l’effetto di due interventi chirurgici su cavie non è possibile applicarli entrambi agli stessi individui, ma è necessario formare due gruppi distinti, facendo in modo che gli individui che li compongono siano tra loro simili a coppie. In questo caso le osservazioni nei due gruppi sono naturalmente appaiate: le misure non si riferiscono agli stessi individui, ma sono effettuate su coppie di individui scelti appositamente. E’ auspicabile che i due individui della coppia siano uguali per età, sesso, dimensioni o rispetto a qualsiasi altro parametro coinvolto nel confronto.
Scopo principale della tecnica di appaiamento dei dati è determinare: - il massimo di omogeneità entro ogni coppia e
- il massimo di eterogeneità tra le coppie.
Il confronto tra trattamento e controllo, fatto sugli stessi individui o tra situazioni simili, tenta di eliminare alcune sorgenti di variabilità che potrebbero essere in grado di nascondere le reali differenze tra le due serie di misure: l'obiettivo è di esaminare le differenze fra due misurazioni, dopo aver ridotto l'effetto della variabilità dovuta agli elementi o individui, poiché sono gli stessi che compongono i due gruppi. Ad esempio, scegliendo due cavie dello stesso sesso/età, si elimina l’eventuale differenza degli effetti di una sostanza tossica nei due sessi o in individui di età diversa.
Tecnicamente il confronto tra le medie di 2 serie di osservazioni appaiate è semplice: l'analisi è applicata ad una nuova serie di dati, quelli risultanti dalle differenze tra gli elementi di ciascuna coppia. Nel caso di un test bilaterale, l’ipotesi nulla è che la media delle differenze sia uguale a zero:
H0: δ = 0
mentre l'ipotesi alternativa H1 è rappresentata da:
H1: δ ≠ 0.
Poiché queste differenze sono indipendenti, il t-test può essere ancora applicato ma si riduce di fatto al t-test per un solo campione:
(3.6) n s d t d δ − = dove:
- d è la media delle differenze,
- δ è la differenza media attesa, spesso uguale a 0,
- sd è la deviazione standard delle differenze campionarie,
- n è il numero di coppie di dati, corrispondente anche al numero di soggetti che costituiscono ciascun campione. Chiaramente in questo caso i gradi di libertà sono n-1.
3.1.4 Confronto tra più di due classi: il test basato sulla statistica F
Il test basato sulla statistica F costituisce una generalizzazione del t-test quando i gruppi a confronto sono più di 2. Per esempio si potrebbe voler verificare che un dato gene risulta differenzialmente espresso tra campioni di individui sottoposti a trattamenti diversi.
Nel confronto simultaneo tra le medie di più di due gruppi non è corretto ricorrere al test t per ripetere l'analisi tante volte, quanti sono i possibili confronti a coppie tra i singoli gruppi. Con il metodo del t-test la probabilità α prescelta per l'accettazione dell'ipotesi nulla è valida solamente per ogni singolo confronto. Se i confronti sono numerosi, la probabilità complessiva che almeno uno di essi si dimostri significativo solo per effetto del caso è maggiore. Se è vera l’ipotesi nulla, la probabilità che nessun confronto risulti casualmente significativo è (1-α)k dove k è il numero di confronti effettuati.
Per esempio, se si eseguono 10 confronti tra le medie di gruppi estratti a caso dalla stessa popolazione e per ognuno di essi α è uguale a 0.05, la probabilità che nessun confronto risulti casualmente significativo diminuisce a circa 0.60 (corrispondente a 0,9510). Di conseguenza, la probabilità complessiva che almeno uno risulti significativo solo per effetto di fluttuazioni casuali diventa 0.40.
In termini più formali, effettuando k confronti con il test t, ognuno alla probabilità α, la probabilità complessiva α’ di commettere almeno un errore di I tipo diventa:
α’ = 1 - (1 -α)k > α
Il test F permette il confronto simultaneo tra due o più medie mantenendo invariata la probabilità α complessiva prefissata.
L'ipotesi nulla H0 e l'ipotesi alternativa H1 assumono una formulazione più generale,
rispetto al confronto tra due medie: H0: μ1 = μ2 = … = μk
H1: le μi non sono tutte uguali (oppure almeno una μi è diversa dalle altre).
Il valore della statistica F è fondato, analogamente al t-test, sul rapporto varianza tra gruppi / varianza entro gruppi:
(3.7) 2 2 entro tra s s F = dove: (3.8) 1 ) ( 1 2 2 − − =
∑
= k y y n s k i i i traè la varianza tra i gruppi che fornisce una stima delle differenze esistenti tra un gruppo e l’altro, e (3.9) k n y y s k i n j i ij entro i − − =
∑∑
=1 =1 2 2 ) (è la varianza entro i gruppi che misura la variabilità esistente attorno alla media aritmetica di ogni gruppo. Elevati valori di F suggeriscono che le differenze osservate tra i valori medi di espressione dei singoli gruppi non possono essere attribuite al caso.
Se i valori medi di espressione y calcolati per ciascuna classe hanno una distribuzione i
approssimativamente normale, la statistica F segue una distribuzione nota come distribuzione F di Fisher, caratterizzata da due parametri: i gradi di libertà del numeratore e del denominatore, che risultano rispettivamente pari υ1 = (k - 1) e υ2 = (n - k) dove n è il numero
totale di osservazioni.
Il valore della statistica F calcolato a partire dai dati campionari viene quindi convertito nel corrispondente p-value e confrontato con il valore di α scelto. Se P < α si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa: almeno una delle medie è diversa dalle altre.
Quando con questo test si rifiuta l’ipotesi nulla, si può essere interessati a procedere nell’indagine per individuare tra quali medie la differenza sia significativa. A tal fine basta eseguire dei confronti a posteriori detti anche “post-hoc” che possono essere:
- semplici, cioè condotti su coppie di singoli trattamenti, - complessi, cioè tra gruppi di trattamenti.
3.1.5 Test basati sulle permutazioni
Sia il t-test che il test che utilizza la statistica F sono esempi di test parametrici cioè di test basati su assunzioni abbastanza forti relativamente alla distribuzione dei dati. Per esempio, nel t-test per calcolare il p-value corrispondente al valore di t ricavato dai dati campionari, si è implicitamente assunto che le differenze tra le medie seguono una distribuzione Normale. Tuttavia questa assunzione può non essere del tutto corretta, in particolare quando il numero
di osservazioni è limitato oppure quando è richiesto un livello di significatività estremamente piccolo.
Sebbene la trasformazione logaritmica dei dati di espressione possa aiutare ad ottenere una distribuzione approssimativamente Normale e ad uniformare le varianze, in ultima analisi la migliore stima della distribuzione dei dati è quella che deriva dai dati stessi.
I test non parametrici presentano il vantaggio di non avere bisogno di ipotesi sulla distribuzione del parametro di interesse. In particolare, i test basati su algoritmi di permutazione catturano meglio la struttura sconosciuta dei dati. Un esempio è il “permutation t-test” che ricava il p-value applicando una serie di permutazioni ai dati, senza utilizzare la distribuzione di probabilità t di Student. Dopo aver calcolato il valore della statistica t, i dati vengono ripetutamente rimescolati tra i due gruppi e ogni volta viene ricalcolato il valore di t indicato con t*. Il p-value per un test bilaterale è stimato mediante il rapporto:
(3.10) random ni permutazio t t con random ni permutazio P _ # 1 * _ _ _ # 1 + ≥ + =
Nel caso di esperimenti che coinvolgono pochi campioni è possibile considerare tutte le possibili permutazioni: (3.11) ! ! )! ( 2 1 2 1 1 2 1 n n n n n n n + ≡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +
e utilizzare per il calcolo di P la formula seguente: (3.12) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ≥ = 1 2 1 * _ _ _ # n n n t t con random ni permutazio P
Un approccio alternativo al t-test basato sulle permutazioni è il test della somma dei ranghi di Wilcoxon (Hollander and Wolfe, 1999).
Il “permutation F-test “ e il test di Kruskal-Wallis sono i corrispettivi dei test appena illustrati quando i campioni a confronto sono più di 2.
Questi test rappresentano la soluzione ideale quando il numero di array (e quindi di repliche) è sufficiente per ottenere il livello di confidenza desiderato. Cui e Churchill (2003) raccomandano almeno sei repliche per gruppo nel confronto tra due sole classi; un numero di repliche inferiore è invece sufficiente quando ci sono molteplici classi a confronto.
Un vantaggio dei metodi di permutazione è dato dal fatto che essi consentono una correzione più affidabile in presenza di test multipli.
3.2 IL PROBLEMA DEI TEST MULTIPLI
Uno dei principali problemi nell’analisi dei dati microarray è rappresentato dalla necessità di dover verificare simultaneamente numerose ipotesi. Più precisamente, stabilire se ogni gene su un array è sovra o sotto regolato tra 2 o più classi a confronto richiede l’esecuzione di un test delle ipotesi. Il numero di geni solitamente presenti su un array è dell’ordine delle decine di migliaia. Poiché ogni test delle ipotesi comporta l’accettazione dell’esistenza di un certo numero di falsi positivi, quando si verificano più ipotesi in parallelo si ha un accumulo di falsi positivi. Diventa pertanto necessario introdurre delle correzioni. C’è una quantità di metodi chiamati procedure per confronti multipli adatti a tale scopo. Essi si basano tutti essenzialmente sul test t ma includono correzioni opportune per il fatto che vengono confrontate più coppie di medie.
Si consideri il problema di testare simultaneamente n ipotesi nulle H0i (i=1,…,n). Per
ogni test i viene costruita una statistica dalla quale può essere derivato un p-value Pi. Si
respinge l’ipotesi nulla H0i se Pi ≤ t per ogni i=1,…n e un fissato valore di soglia t compreso
tra 0 e1.
Le diverse uscite per gli n test possono essere riassunte come riportato nella tabella (3.2) che costituisce un’estensione della precedente tabella (3.1) all’intero set di geni sotto esame:
Non Respinte Respinte Numero di geni
Ipotesi nulle vere U(t) V(t) n0
Ipotesi nulle false T(t) S(t) n1
Totale n-R(t) R(t) n
Tab. 3.2: Tabella riassuntiva dei possibili risultati di un test delle ipotesi condotto su un intero set di geni
dove:
− n0 è il numero di ipotesi nulle vere;
− n1 è il numero di ipotesi nulle false;
− V(t) è il numero di falsi positivi, cioè di errori di I tipo; − T(t) è il numero di falsi negativi, cioè di errori di II tipo; − R(t) è il numero di ipotesi nulle rigettate.
Di queste variabili si conoscono soltanto R(t) ed n, mentre sono incogniti i parametri n0, n1 e le variabili random V(t), T(t), S(t) e U(t).
In generale, si desidera minimizzare il numero V di falsi positivi e il numero T di falsi negativi. L’approccio standard consiste nel fissare il tasso di errore o “error rate” di I tipo α ad un livello ragionevole e nel cercare, fra le classi di test con “error rate” di tipo I uguale al
valore di α specificato, quelli che minimizzano il cosiddetto “error rate” di tipo II, cioè massimizzano la potenza.
Quando viene testata una singola ipotesi nulla H0, la probabilità di commettere un
errore di I tipo, cioè di rigettare l’ipotesi nulla quando essa è vera, viene tipicamente controllata ad un livello fissato α. Esiste una varietà di generalizzazioni di questa definizione per test multipli; gli error rate di tipo I proposti di seguito sono i più comuni:
− Per-Comparison Error Rate (PCER): è definito come il valore atteso del numero di errori di tipo I rispetto al numero di ipotesi totale:
PCER = E(V)/n;
− Per-Family Error Rate (PFER): è definito come il valore atteso del numero di errori di tipo I,:
PFER = E(V);
− Family-Wise Error Rate (FWER): è definito come la probabilità che ci sia almeno un errore di tipo I, indipendentemente dal numero di test effettuati:
FWER = Pr (V ≥ 1);
− False Discovery Rate (FDR): proposto da Benjamini e Hochberg (1995), è la proporzione attesa di errori di tipo I fra le ipotesi rigettate:
FDR = E(V / R) per R > 0 e FDR = 0 per R = 0
In generale per una data procedura di test multipli vale la seguente disuguaglianza (Dudoit et al. 2003): PFER ≤ FWER ≤ PCER
Quindi, per un fissato livello α, i procedimenti che controllano PFER sono più conservativi di quelli che controllano FWER o PCER. Per illustrare le proprietà dei differenti “error rate” di tipo I, si può supporre che ogni ipotesi Hj venga testata individualmente a
livello αj e che la decisione di rigettare o meno tale ipotesi sia basata esclusivamente su questo
test. Sotto l’ipotesi nulla completa, ovvero nessuna delle ipotesi nulle può essere rifiutata, il PCER è semplicemente la media degli αj e il PFER è la somma degli αj, mentre FWER non
dipende da αj, ma coinvolge la distribuzione congiunta delle statistiche Tj.
PFER = (α1+…+ αn) / n ≤ max(α1,…αn) ≤ FWER ≤ PCER = α1+…+ αn
Anche FDR dipende dalla distribuzione congiunta dei test statistici e per un procedimento fissato FDR ≤ FWER, con FDR = FWER sotto l’ipotesi nulla completa.
Il problema principale nella valutazione dell’”error rate” di tipo I è che la probabilità di avere almeno un errore di questo tipo incrementa drasticamente con il numero di ipotesi testate. Come conseguenza di questo comportamento di FWER, si rende necessaria la ridefinizione dell’”error rate” di tipo I nel caso di test multipli, in modo da consentire un controllo globale della porzione di errori sugli n test. Le soluzioni a questo problema sono molteplici; in base al tipo di “error rate” di tipo I che si intende controllare è possibile distinguere tra:
approcci che controllano il FWER; approcci che controllano il FDR.
3.2.1 La correzione di Sidak e l’approssimazione di Bonferroni
La procedura più semplice per controllare il FWER è la correzione di Sidak. Essa sfrutta la semplice relazione tra la probabilità di commettere un errore di I tipo nel singolo confronto (αc) e la probabilità di commettere un errore di I tipo su tutti i test (αe):
(3.13) n
c
e 1 (1 α )
α = − −
dove n è il numero di test effettuati, corrispondente al numero di geni presenti sull’array. L’obiettivo è calcolare il valore di α che si deve utilizzare per i singoli geni (αc) al fine
di garantire un errore di I tipo globale αe minore o uguale del livello di significatività
desiderato. Attraverso semplici manipolazioni algebriche, dall’equazione precedente si ottiene:
(3.14) n
e
c α
α =1− 1−
Per piccoli valori di αc, l’equazione (3.13) può essere approssimata considerando
soltanto i primi due termini dell’espansione binomiale di (1- αc)n:
(3.15) c c n c e α nα nα α =1−(1− ) =1−(1− +...)≈ ottenendo così: (3.16) n e c α α =
nota come correzione di Bonferroni per i confronti multipli.
La correzione di Sidak e l’approssimazione proposta da Bonferroni sono esempi di procedimenti “single-step” la cui peculiarità è rappresentata dal fatto che la regione di rifiuto di ogni test è costante e non dipende dal risultato di test su altre ipotesi. Malgrado la loro semplicità, entrambe queste correzioni sono inadatte per l’analisi dei dati di espressione genica poiché, dato l’elevato valore di n, il livello di significatività richiesto a livello del singolo gene diventa rapidamente molto piccolo al crescere di n. Per valori di α così stringenti, l’approccio basato sul test delle ipotesi non sarà in grado, per la maggior parte dei geni, di rifiutare l’ipotesi nulla producendo così un numero elevato di falsi negativi. In altre parole si può dire che entrambi i metodi sono molto conservativi.
E’ possibile ottenere una potenza maggiore, preservando il controllo dell’”error rate” di tipo I, se si utilizzano delle procedure dette “step-wise”, in cui il rifiuto di una particolare ipotesi dipende non solo dal numero totale delle ipotesi da verificare ma anche dai risultati degli altri test delle ipotesi. I metodi wise” si dividono a loro volta in procedure “step-down” e procedure “step-up”.
3.2.2 La correzione “step-down” di Holm
La correzione proposta da Holm ha una semplicità computazionale pari a quella di Bonferroni ma ha una maggiore potenza. Essa è una procedura di “rifiuto ricorsivo” detta “step-down” poichè applica un criterio di accettazione/rifiuto ad un insieme ordinato di ipotesi nulle, partendo dal più piccolo p-value e procedendo fino al non rifiuto di H0. Per
eseguire il test di Holm si saggiano tutte le coppie di confronti di interesse tramite il t test e si determina il value per ciascun test della famiglia. Successivamente si confrontano questi p-value, ordinati dal più significativo al meno significativo, con i valori critici aggiustati per i confronti multipli: appena si verifica la condizione di rifiuto per un’ipotesi, anche le seguenti meno significative vengono rigettate.
Nella correzione di Holm si procede nel modo seguente: 1. si sceglie un livello di significatività αe;
2. si ordinano i geni seguendo l’ordinamento crescente dei p-value;
3. si confrontano i p-value con una soglia che dipende dalla posizione del gene nella lista di valori ordinati. La soglia viene calcolata in base al seguente criterio: αe / G per il primo
gene, αe / (G-1) per il secondo gene e così via, dove G è il numero di geni.
p1 < αe / G, p2 < αe / (G-1), …pk < αe / (G-k+1), …pG < αe / 1.
4. Sia k il più grande valore di i per il quale vale pi < αe / (G-i+1). Verranno respinte tutte le
ipotesi per le quali i > k.
A differenza delle correzioni di Sidak e Bonferroni in cui la soglia corretta è unica (è la stessa per tutti i geni) e viene calcolata in un solo passaggio, nel procedimento di Holm le soglie sono diverse per ogni gene e dipendono dalla posizione occupata nella lista dei p-value non corretti.
3.2.3 La correzione “step-down” di Westfall & Young
Le correzioni di Sidak, Bonferroni e Holm si basano sull’ipotesi di indipendenza delle variabili. Tuttavia è noto che i geni di un organismo sono coinvolti in complessi meccanismi di co-regolazione. La correzione “step-down” di Westfall e Young è un metodo più generale che corregge i p-value tenendo in considerazione tutte le possibili correlazioni tra le variabili. Esso utilizza un algoritmo di permutazione dei dati. Dopo aver calcolato i p-value relativi al data-set originale, ai dati viene applicata una permutazione casuale e vengono calcolati i nuovi p-value. Questi vengono a loro volta corretti utilizzando il metodo di Holm. L’intero processo (permutazione+calcolo dei p-value+correzione di Holm) viene ripetuto migliaia o decine di migliaia di volte. Alla fine, il p-value per il gene i-esimo è dato dal rapporto:
(3.17) totali ni permutazio t u quali le per ni permutazio p i b j i _ _ _ _ _ ( ) # ≥ # =
dove sono i valori corretti secondo la procedura “step-down” di Holm, relativi alla permutazione b e t ) (b j u
i è il p-value relativo al data-set originale (non corretto).
Il vantaggio principale di questo approccio è rappresentato dal fatto che esso tiene pienamente conto di tutte le possibili forme di dipendenza tra i geni. Questo è estremamente importante quando i geni sotto esame sono strettamente correlati come, per esempio, quelli che sono coinvolti negli stessi “pathway”. Di contro, l’algoritmo di permutazione su cui si basa il metodo di Westfall e Young è pesante dal punto di vista computazionale rendendo di conseguenza l’intera procedura molto più lenta.
3.2.4 Il False Discovery Rate e la correzione di Benjamini e Hochberg
Il procedimento “steup” lavora nella direzione opposta allo “stedown” poiché i p-value sono ordinati dal meno significativo al più significativo; un esempio è la procedura di calcolo del False Discovery Rate sviluppata da Benjamini e Hochberg (Benjamini and Hochberg, 1995).
La procedura di calcolo del False Discovery Rate secondo Benjamini e Hochberg è la seguente:
1. si sceglie un livello di significatività αe;
2. si ordinano i geni seguendo l’ordinamento ascendente dei p-value;
3. si confrontano i p-value con una soglia che dipende dalla posizione del gene nella lista di valori ordinati. La soglia viene calcolata secondo la formula αe / p0G per il primo
gene, dove G è il numero di geni e p0 è la proporzione delle ipotesi nulle che sono
(effettivamente) vere, 2αe / G per il secondo gene e così via. Poiché il valore di questa
proporzione non è noto, ci si mette di solito nella condizione più conservativa ponendo p0=1 che equivale ad assumere che tutte le ipotesi nulle sono vere e quindi che non ci
sono geni differenzialmente espressi. L’aspetto conservativo consiste nel fatto che se l’ipotesi nulla può essere rigettata per un dato gene in queste circostanze, allora essa verrà ancora rifiutata se anche solo alcune ipotesi nulle sono in realtà false e p0 < 1.
p1 < αe / G, p2 < 2αe / G, …pk < kαe / G,...pG < αe.
4. Sia k il più grande indice per il quale vale la disuguaglianza pi < αe / G. Verranno
respinte tutte le ipotesi per le quali i< k.
E’ possibile ricavare una relazione tra il False Dicovery Rate e il livello di significatività α per il singolo confronto. Indicando con #FD (False Discovery) il numero di falsi positivi e con #TD (True Discovery) il numero di veri positivi, il FDR è dato da:
(3.18) ⎢⎣⎡ ⎥⎦⎤ + = TD # FD # FD # E FDR con FDR = 0 se #FD+#TD = 0.
Sia p0 la proporzione di geni differenzialmente espressi; per semplificare i calcoli si
assume che ogni gene o non è differenzialmente espresso oppure è differenzialmente espresso e la differenza tra i livelli medi di espressione tra le due classi è esattamente pari a δ. In tal caso risulta: (3.19) E[#FD]=α(1-p0)N N p E[#TD] (1- ) 0 (3.20) = β da cui si ricava: (3.21) 0 0 0 ) 1 ( ) 1 ( ) 1 ( ] [ p p p FDR E β α α − + − − =
Sviluppando in serie di Taylor fino al I ordine l’espressione (5.6) si ottiene: (3.22) 1 0 0 ) 1 )( 1 ( 1 ] [ − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − + ≈ p p FDR E α β
da cui è possibile risalire al valore da assegnare ad α per mantenere il FDR al livello desiderato.