5
5
C
C
A
A
L
L
C
C
O
O
L
L
O
O
D
D
E
E
L
L
L
L
A
A
N
N
U
U
M
M
E
E
R
R
O
O
S
S
I
I
T
T
À
À
C
C
A
A
M
M
P
P
I
I
O
O
N
N
A
A
R
R
I
I
A
A
P
P
E
E
R
R
U
U
N
N
E
E
S
S
P
P
E
E
R
R
I
I
M
M
E
E
N
N
T
T
O
O
D
D
I
I
C
C
L
L
A
A
S
S
S
S
C
C
O
O
M
M
P
P
A
A
R
R
I
I
S
S
O
O
N
N
La determinazione della dimensione, o numerosità, campionaria, cioè del numero necessario di individui, soggetti o campioni da osservare e studiare, è una componente cruciale della fase di disegno di ogni indagine di laboratorio o clinica. Troppo spesso, infatti, si inizia uno studio avendo soltanto un’idea approssimativa di quanto ampio debba essere il campione da analizzare per testare l'ipotesi di interesse. Nel valutare differenze tra due o più gruppi rispetto ad una certa caratteristica oggetto di studio, ad esempio l’espressione dei geni valutata mediante microarray, è di fondamentale importanza avere ben chiaro che:
- uno studio basato su un campione troppo grande può mettere in evidenza delle differenze di espressione genica anche molto piccole che, pur essendo statisticamente significative, sono biologicamente poco rilevanti;
- uno studio basato su un campione troppo piccolo può far concludere che differenze, nella realtà importanti e reali, sono statisticamente non significative (falsi negativi) o, al contrario, che differenze non reali, cioè differenze che non verrebbero confermate da uno studio condotto con un numero di repliche adeguato, sono statisticamente significative (falsi positivi).
Si comprende così come un’adeguata valutazione della dimensione del campione sia il presupposto irrinunciabile per una corretta interpretazione dei dati.
La stima della numerosità campionaria non ha tuttavia soltanto un’importanza statistica. Nella pianificazione di un esperimento, infatti, il problema della dimensione del campione è profondamente legato a questioni economiche (valutazione costi/benefici) ed etiche (nel caso in cui lo studio coinvolga soggetti umani o animali).
Esistono diversi approcci per il calcolo della numerosità campionaria; per esempio si può specificare l’ampiezza desiderata dell’intervallo di confidenza del parametro di interesse (che rappresenta l’intervallo entro il quale si trova il valore del parametro alla probabilità α
prescelta) e determinare la dimensione del campione necessaria per ottenere tale valore. Uno degli approcci più popolari è tuttavia quello basato sull’analisi della potenza di un test delle ipotesi.
Nel capitolo 3, la potenza di un test statistico è stata definita come la probabilità di accettare l’ipotesi alternativa, quando essa è realmente vera; in altri termini, nel confronto tra medie la potenza è la probabilità di trovare una differenza, quando esiste.
I fattori che, con modalità ed intensità differenti, incidono sulla potenza di un test sono sei:
1. la probabilità di errore di I tipo (o livello di significatività) α che indica il livello di rischio che si è disposti a correre nel concludere che esiste una differenza statisticamente significativa quando in realtà tale differenza non esiste;
2. la dimensione della differenza fra le medie delle due popolazioni, di cui si vuole verificare la significatività. In letteratura tale parametro è denominato “effect size” ed è indicato con il simbolo δ.
3. La variabilità dei dati. Essa è una misura della varianza della popolazione (σ2) oppure più frequentemente della varianza campionaria (s2) da cui dipende la scelta della distribuzione. In particolare la potenza di un test è funzione decrescente della varianza.
4. La direzione dell’ipotesi (unilaterale oppure bilaterale). La differenza tra test unilaterale e test bilaterale non è solamente una questione teorica: è una scelta con effetti pratici rilevanti sulla potenza (1- β) del test, poiché è importante per la determinazione della zona di rifiuto dell'ipotesi nulla. In un test condotto:
a. allo stesso livello di significatività (α), b. con una identica deviazione standard (σ), c. la medesima differenza in valore assoluto (δ), d. un uguale numero di dati (n),
l’ipotesi unilaterale determina un risultato che è sempre più potente della corrispondente ipotesi bilaterale, poiché il valore critico al quale si rifiuta l’ipotesi nulla è sistematicamente minore, in valore assoluto. Un test unilaterale è quindi sempre preferibile. Tuttavia un’ipotesi unilaterale richiede una quantità d’informazione superiore, non disponibile in tutte le situazioni sperimentali. Per esempio non è in generale noto a priori se la somministrazione di un nuovo farmaco darà luogo ad un aumento o ad una diminuzione del livello di espressione genica, consentendo di utilizzare un’ipotesi unilaterale piuttosto che bilaterale.
5. La dimensione (n) del campione;
6. le caratteristiche del test (parametrico oppure non-parametrico).
La dipendenza della potenza statistica π = 1- β, dai parametri sopra definiti, può essere espressa in forma compatta mediante la formula:
,...) , , , ( α δ σ π = f n .
dove i puntini di sospensione si riferiscono agli altri parametri (test parametrico o non parametrico, bilaterale o unilaterale) difficili da tradurre in simboli.
La dimensione del campione richiesta è data dal più piccolo intero n che soddisfa la disuguaglianza: π σ δ α, , ,...) ~ , (n ≥ f .
dove π~ rappresenta il valore della potenza desiderata.
Sperimentazioni condotte correttamente e analizzate con metodi appropriati possono non evidenziare differenze reali e quantitativamente importanti a causa di un campione troppo piccolo, non in grado di fornire una potenza sufficiente per rendere l’effetto statisticamente significativo.
L’analisi della potenza permette anche di valutare a posteriori in modo critico i risultati, al fine di ripetere all’occorrenza l’esperimento con un numero di dati adeguato al reale effetto rilevato.
I grafici riportati nelle figure seguenti (5.1, 5.2 e 5.3) mostrano in che modo il livello di significatività, l’”effect size” e la dimensione del campione agiscono sulla potenza statistica. Nei grafici, la curva a sinistra rappresenta la distribuzione dei dati di espressione quando è vera l’ipotesi nulla di assenza di differenze di espressione mentre la curva a destra mostra la distribuzione dei risultati attesi quando è vera l’ipotesi alternativa. La distanza tra i picchi delle due curve è rappresentativa dell’”effect size”.
Come si vede dalla figura 5.1, abbassando il livello di significatività da 0.05 a 0.01, la soglia per il rifiuto dell’ipotesi nulla si sposta verso sinistra provocando una diminuzione della potenza del test da 0.80 a 0.59.
Fig. 5.1: Effetto della diminuzione del livello di significatività α da 0.05 (a) a 0.01 (b) sulla
potenza a parità di “effect size”
La figura 5.2 mostra invece l’effetto prodotto sulla potenza del test da un aumento dell’”effect size”, mantenendo costanti il livello di significatività α e la numerosità campionaria. Scegliendo un δ maggiore, la curva che rappresenta la distribuzione dei dati sotto l’ipotesi alternativa si sposta più a destra facendo sì che un’area maggiore, coincidente proprio con la potenza, venga a trovarsi a destra della soglia fissata per il rifiuto di H0.
Fig. 5.2: Effetto dell’aumento dell’”effect size” δ sulla potenza.
Poiché sia l’entità dell’effetto che si vorrebbe rilevare che il valore di α sono in generale fissati e la variabilità dei dati è solo in minima parte sotto il controllo dello sperimentatore, l’unico modo per accrescere la potenza statistica è quello di aumentare la dimensione del campione.
La figura 5.3 mostra l’effetto che un aumento della numerosità campionaria ha sulla potenza di uno studio. L’utilizzo di un campione più numeroso determina un restringimento delle curve di distribuzione dei dati in seguito al quale la soglia per il rifiuto di H0 risulta
spostata più a sinistra. In questo modo praticamente tutta l’area sottesa dalla curva che rappresenta la distribuzione dei dati sotto H1 viene a trovarsi a destra della soglia portando ad
un sensibile aumento della potenza statistica.
Fig. 5.3: Aumento della potenza statistica dovuto ad un aumento della numerosità
5.1 PROBLEMI
CONNESSI
AL
CALCOLO DELLA NUMEROSITÀ
CAMPIONARIA NEGLI ESPERIMENTI MICROARRAY
Gli studi realizzati con i microarray sono piuttosto costosi sia in termini di reagenti (array, campioni di RNA, enzimi, fluorofori, etc…) che dal punto di vista del tempo necessario alla realizzazione degli esperimenti e della successiva analisi dei dati. Se a questi limiti si aggiunge la difficoltà che spesso si ha nel reperire quantità sufficienti di materiale biologico, si comprende facilmente perché tali esperimenti spesso utilizzino un numero limitato di campioni (tipicamente da 2 a 8) stabilito esclusivamente sulla base di considerazioni empiriche approssimative (Yang and Speed, 2003). In molti casi, l’ampiezza campionaria così stabilita può non essere adeguata per fornire risposte statisticamente attendibili al quesito biologico di interesse.
Poiché l’obiettivo di uno studio di “class comparison” è quello di identificare i geni differenzialmente espressi tra due o più condizioni sperimentali, quanto detto si traduce in un numero elevato di falsi positivi (geni riconosciuti come differenzialmente espressi che in realtà non lo sono) e di falsi negativi (geni dichiarati non differenzialmente espressi ma che in realtà lo sono). Nella maggior parte degli esperimenti microarray, una volta ricavata la lista dei geni sovra o sotto-regolati, l’espressione differenziale di alcuni di essi viene verificata con altre metodiche di biologia molecolare, come ad esempio la Real-time PCR. Se i risultati dell’esperimento microarray contengono un numero elevato di falsi positivi, questo determina un inutile spreco delle risorse. Aumentando la numerosità del campione, aumenta la potenza del test cioè la capacità di rilevare differenze di espressione reali, mentre diminuisce il tasso di errore di I tipo. Tuttavia è importante trovare il giusto compromesso tra la numerosità campionaria richiesta e gli obiettivi dell’esperimento in modo da ottimizzare l’impiego delle risorse. E’, infatti, altrettanto sconsigliabile collezionare un numero di soggetti (campioni) più grande del necessario, perché, come già detto, si potrebbero ottenere risultati statisticamente significativi ma di nessuna rilevanza biologica.
Prima di eseguire uno studio microarray, è importante quindi pianificare accuratamente gli esperimenti e valutare la numerosità campionaria richiesta in relazione agli obiettivi.
Sfortunatamente i metodi tradizionali per il calcolo della numerosità campionaria sviluppati per singoli test delle ipotesi non sono direttamente applicabili agli esperimenti microarray, in cui le ipotesi da verificare sono tipicamente decine di migliaia. Al problema dei test multipli si aggiunge quello della dipendenza tra le variabili misurate (i livelli di espressione). La determinazione della numerosità campionaria per un esperimento microarray solleva, pertanto, questioni nuove rispetto a quelle tradizionalmente legate al calcolo della dimensione del campione come, ad esempio:
- scegliere se utilizzare un unico valore di potenza ed ”effect size” per tutti i geni oppure valori diversi per geni diversi;
- decidere il tipo di correzione da applicare al tasso di errore di I tipo in presenza di confronti multipli;
Nonostante l’importanza della questione, i lavori presenti in letteratura su questo argomento sono relativamente pochi e, fatta eccezione per alcuni test specifici e per disegni sperimentali molto semplici, non esistono formule esatte per il calcolo della numerosità campionaria, ma solo processi approssimati. Spesso, perciò, è preferibile ricorrere ad appositi software statistici che, utilizzando algoritmi computazionali di calcolo iterativo, consentono di ottenere stime più accurate dell’ampiezza campionaria.
Gli approcci per la stima della numerosità campionaria in esperimenti di “class comparison” sono essenzialmente riconducibili a due, con una serie di varianti intermedie:
1) calcolare la numerosità campionaria costruendo un modello per l’intero sistema (vale a dire l’intero set di dati prodotti da un esperimento microarray) che includa una realistica caratterizzazione della struttura dell’errore e delle dipendenze tra le variabili,
2) calcolare la numerosità campionaria applicando i metodi standard a ciascun gene separatamente e utilizzando i singoli risultati per fornire una stima complessiva del valore del parametro.
Posto che il modello previsto dall’approccio numero 1 sia adeguato, questa scelta dovrebbe produrre una risposta molto accurata. Tuttavia la ricerca di un modello generale può richiedere sforzi enormi, senza considerare la difficoltà di interpolare un modello simile ai dati multivariati generati da un esperimento microarray. Questo tipo di approccio è stato adottato per esempio da Zien e colleghi (2003), che hanno proposto un modello gerarchico complesso che include diverse sorgenti di errore. Il modello di Zien può essere applicato solo a set di dati prodotti da microarray Affymetrix e relativi ad esperimenti con due sole classi a confronto; inoltre, molti ricercatori hanno sottolineato la difficoltà di adattare un simile modello ai dati reali (Warnes and Liu, 2006).
I metodi basati sul secondo approccio, invece, sono caratterizzati da una notevole semplicità di calcolo, sono veloci e di immediata applicazione ai dati microarray; tuttavia potrebbero non riuscire a catturare la struttura complessiva del sistema, portando ad una stima non sempre corretta dell’ampiezza campionaria.
In relazione all’obiettivo di un esperimento di “class comparison”, nel quale si è interessati a identificare quali geni sono differenzialmente espressi, strutturare lo studio della numerosità campionaria sull'inferenza gene per gene è più corretto.
Fino a questo punto si è parlato di “numerosità campionaria” in termini molto generali, tuttavia nel capitolo 2 si è visto che in un esperimento microarray esistono diversi livelli di replicazione che differiscono in relazione al grado di indipendenza che si può attribuire ai dati ottenuti dalla ripetizione della misura e in base alla sorgente di variabilità che si vuole controllare. E’ pertanto necessario precisare a quale tipo di repliche si fa riferimento quando si vuole valutare la dimensione campionaria. In generale, nel calcolo di questo parametro si ritiene implicita l’ipotesi che i soggetti che costituiscono il campione siano indipendenti, in modo da consentire la generalizzazione dei risultati ottenuti dall’esperimento dal campione esaminato all’intera popolazione da cui esso è stato estratto. In questo senso, nell’ambito di un esperimento microarray di “class comparison”, la numerosità campionaria va interpretata
come il numero di repliche biologiche necessarie per rilevare una certa differenza di espressione genica tra due o più classi, con la potenza desiderata.
Nel paragrafo successivo viene descritto un metodo semplice per determinare l’ampiezza campionaria nel caso di esperimenti di “class comparison” che prevedono il confronto tra due soli gruppi con un “reference design”. L’estensione di questo metodo al caso di esperimenti multifattoriali o con più classi a confronto o che utilizzano disegni più complessi del “reference design” non è, in generale, immediata e spesso nemmeno possibile.
5.2 CALCOLO DELLA NUMEROSITÀ CAMPIONARIA PER UN
REFERENCE DESIGN CON 2 GRUPPI A CONFRONTO
Si consideri un esperimento microarray in cui si vogliono confrontare un gruppo di trattati e un gruppo di controlli mediante un “reference design” con lo scopo di individuare i geni che risultano sovra o sotto-espressi in una classe rispetto all’altra. Prima di eseguire l’esperimento non si hanno generalmente osservazioni per poter verificare la distribuzione dei dati. Un’ipotesi molto conveniente e ragionevolmente vicina alla realtà, quando si utilizzano i logaritmi delle intensità, consiste nell’assumere che le misure di espressione relative a ciascun gruppo sono mutuamente indipendenti e seguono una distribuzione approssimativamente Normale con varianza σ2 uguale per entrambi i gruppi. Con queste ipotesi è possibile applicare la statistica Z per campioni indipendenti per rilevare i geni differenzialmente espressi. L’ ipotesi da verificare per ogni gene è solitamente un’ipotesi bilaterale espressa da: H0: μT = μC
H1: μT ≠ μC
dove μT e μC sono i valori medi di espressione di un dato gene nella popolazione dei trattati e
in quella dei controlli, rispettivamente.
Per calcolare la numerosità campionaria è necessario specificare il valore dei seguenti parametri:
- il livello di significatività α, - la potenza desiderata 1-β,
- l’”effect size” δ, ossia la differenza minima tra i livelli medi di espressione che si ritiene biologicamente significativa o che si vorrebbe rilevare, espressa in termini del logaritmo (in base 2) del “fold change”,
- una stima della deviazione standard σ dei dati di espressione all’interno di ciascuna popolazione.
Trascurando per il momento le questioni relative al problema dei confronti multipli e considerando i geni individualmente, il numero totale n di campioni necessario per rilevare, con una potenza (1 – β) e un livello di significatività α, una differenza di espressione δ del gene in esame tra il gruppo dei trattati e quello dei controlli, è dato dalla formula:
(5.1) )) 1 ( ( ) ( 2 2 2 1 2 / 1 q q z z n − + = − − δ σ β α dove :
− e indicano i percentili 100(1-α/2) e 100(1-β) della distribuzione Normale standard,
2 / 1−α
z z1−β
− q è la proporzione di campioni biologici nel primo gruppo. In altre parole, se indichiamo con n1 e n2 le ampiezze campionarie del gruppo dei trattati e di quello dei controlli,
n n n n n q 1 2 1 1 = + = ,
− σ2 è la varianza associata o varianza “pooled” dei due gruppi a confronto.
Se i due gruppi sono formati dallo stesso numero di soggetti, cioè n1 = n2 (da cui segue
che q = ½), l’ equazione (5.1) diventa:
(5.2) 2 2 2 1 2 / 1 ) ( 4 δ σ β α − − + = z z n
e il numero di soggetti da collezionare per classe è pari a n/2. E’ questa la situazione più conveniente, in particolare quando il numero di dati a disposizione è piccolo. Si può infatti dimostrare che un test per due campioni indipendenti raggiunge il massimo di potenza e robustezza quando i due gruppi sono bilanciati, cioè quando hanno la stessa numerosità (Soliani L., 2005).
5.2.1 Criteri per la scelta del livello di significatività e della potenza
I valori da assegnare al livello di significatività α e alla potenza π.= 1 - β devono essere scelti tenendo conto del fatto che in un tipico esperimento microarray bisogna eseguire tanti test delle ipotesi quanti sono i geni presenti sull’array, cioè decine di migliaia.
Gli errori di I e di II tipo sono controllati rispettivamente dai parametri α e β che determinano il massimo numero accettabile di falsi positivi e di falsi negativi.
Se N è il numero di geni presenti sull’array, fissato un livello di significatività pari ad α, il numero atteso di falsi positivi sarà minore o uguale a N*α (il valore massimo N*α si riferisce al caso peggiore in cui non ci sono geni differenzialmente espressi tra gli N testati). Per esempio, se sull’array ci sono 10000 geni, nessuno dei quali è in realtà differenzialmente espresso tra le due classi a confronto, scegliendo α = 0.05 si accetta il rischio di trovare 500 falsi positivi, cioè di dichiarare differenzialmente espressi 500 geni che in realtà non lo sono.
Dato l’elevato valore di N, per limitare il numero di falsi positivi il livello di significatività α deve essere molto piccolo. Nella pratica una scelta appropriata è rappresentata da α = 0.001. In questo caso, se i geni da esaminare sono 10000, nessuno dei quali è (in realtà) differenzialmente espresso, il numero medio di falsi positivi sarà minore o
uguale a 10. Se soltanto l’1% dei 10000 geni mostra una reale differenza di espressione tra le due classi, allora il numero atteso di falsi positivi si riduce a 5.
Per quanto riguarda il valore di β, se su N geni, M sono realmente differenzialmente espressi, con una differenza di espressione almeno pari a δ, allora il numero atteso di falsi negativi sarà minore o uguale a M*β. Se si vuole limitare a F il numero di falsi negativi, bisognerà scegliere β = F / M. Quindi β deve essere uguale alla proporzione di geni differenzialmente espressi che si è disposti a non riconoscere come tali. Una scelta molto frequente nell’analisi dei dati microarray per studi di espressione è β = 0.05 che garantisce una buona potenza statistica ovvero una buona capacità di individuare i geni caratterizzati da una reale differenza di espressione tra le classi. Per β = 0.05, il test statistico ha una potenza π = 1- β = 0.95, che significa che si ha una probabilità pari al 95% di identificare correttamente un gene differenzialmente espresso, o, in altre parole, che ripetendo l’esperimento, un gene differenzialmente espresso verrà dichiarato tale il 95% delle volte.
Per quanto detto è chiaro che, in linea teorica, si vorrebbe che entrambi i livelli α e β fossero minimi. Purtroppo però, dato il legame logico e matematico tra α e β, ciò non è tecnicamente possibile, e quindi si procede fissando prima α ad un livello ragionevolmente basso e in base a questo si cerca successivamente di minimizzare β. Tale modo di operare è motivato dal fatto che si ritiene più importante controllare l'errore di I tipo che è il più grave, piuttosto che quello di II tipo, che è invece il meno grave. Nel far questo si deve tuttavia considerare che la diminuzione di β comporta chiaramente un aumento della potenza dello studio (1 – β), a cui corrisponde un sostanziale aumento della dimensione campionaria. In altre parole, quanto più si vuole mantenere bassa la probabilità che lo studio conduca a delle conclusioni errate, in un senso o nell'altro, tanto più sarà necessario aumentare la dimensione campionaria.
5.2.2 Considerazioni sull’”effect size”
L’”effect size” δ rappresenta l’entità della differenza che si vuole rilevare fra le medie delle due popolazioni.
L’entità dell’”effect size” non deve essere scelta sulla base della differenza più piccola che è possibile dimostrare statisticamente significativa. E’ utile scegliere il valore di δ in rapporto ad una differenza ritenuta importante nell’ambito scientifico di ricerca in cui si applica il test.
Un valore δ che sia troppo piccolo: − richiede un numero di dati troppo alto,
− molto raramente permette un test significativo, − fornisce una risposta biologicamente poco rilevante.
La potenza di un test statistico è funzione crescente di questa differenza, presa in valore assoluto; è infatti intuitivo come sia più facile rilevare differenze grandi piuttosto che differenze piccole.
Negli esperimenti microarray, l’”effect size” è espresso in termini del logaritmo in base 2 del “fold-change”. Un “effect size” δ = 1 è spesso considerato un valore più che ragionevole dal momento che corrisponde ad una differenza (“fold-change”) pari a 2 tra i livelli medi di espressione di un dato gene nei due gruppi a confronto. Per poter rilevare differenze più piccole, mantenendo costanti gli altri parametri (che determinano la numerosità campionaria), sono necessari molti più campioni per classe.
5.2.3 Variabilità della misura di interesse
La variabilità della misura di interesse si esprime in termini di varianza o di deviazione standard della misura di interesse nella popolazione. Un problema centrale che si pone ogni volta che si studia una determinata caratteristica di una popolazione sulla base di un campione estratto da essa, è che il risultato che si ottiene è in parte influenzato dall'effetto del caso (variabilità campionaria attribuibile alle differenze biologiche tra individuo e individuo). Quindi, quanto maggiore è la variabilità intrinseca della caratteristica che si sta misurando, tanto maggiore sarà la variabilità tra le misure rilevate nei possibili campioni. A questa variabilità “biologica” deve essere poi aggiunta una variabilità “tecnica” formata da una componente di errore random più una componente legata alle limitazioni tecniche del metodo di misura.
Si comprende perciò come, al fine di ottenere risultati attendibili, in corrispondenza di un’elevata variabilità della misura di interesse, sarà necessario scegliere un campione sufficientemente ampio da essere rappresentativo della popolazione.
Nella formula (5.2) per il calcolo della numerosità campionaria in un esperimento in cui il confronto tra due gruppi è realizzato mediante un “reference design”, σ2 rappresenta la varianza dei dati di espressione nella popolazione da cui sono stati tratti i due gruppi. Nella pratica tale valore non è noto a priori ma è possibile ottenerne una stima o dalla letteratura esistente sull'argomento oggetto di studio, o utilizzando valori ricavati in esperimenti simili da altri laboratori, oppure attraverso uno studio pilota. McShane e collaboratori (2003) consigliano di considerare una combinazione delle 3 opzioni.
Un grosso limite della valutazione della variabilità del livello di espressione mediante uno studio pilota è costituito dal fatto che esso richiederebbe un numero notevole di campioni per ottenere una stima precisa della deviazione standard. Data l’imprecisione attesa delle stime fornite da uno studio pilota condotto su pochi campioni, un ricercatore potrebbe ottenere un risultato più attendibile confrontando i valori stimati dallo studio pilota con quelli resi disponibili da altri laboratori. L’eventuale constatazione che le stime ricavate dallo studio pilota sono molto maggiori rispetto a quelle ottenute da altri laboratori per esperimenti analoghi, deve indurre lo sperimentatore a verificare se nel corso dell’esperimento ci sono stati problemi tecnici, che potrebbero avere determinato un elevato errore di misura, o problemi relativi alla qualità dei campioni.
σ2 può variare in relazione a numerosi fattori tra cui lo specifico gene esaminato, il tipo di campioni studiati (per esempio, la variabilità dei livelli di espressione intra-classe in
campioni di tessuto umano è maggiore rispetto a quella osservata in campioni di tessuto prelevati da animali geneticamente imparentati o costituiti da linee cellulari) e il laboratorio che ha eseguito l’esperimento. La variabilità associata ad ogni gene può pertanto essere espressa come combinazione lineare di due termini:
1. una componente biologica, indicata con ζ2, dovuta alle differenze del livello di
espressione tra individuo e individuo, all’interno dello stesso fenotipo;
2. una componente di errore sperimentale, indicata con ν2, dovuta all’inaccuratezza della
tecnica di misura.
Esplicitando le componenti della varianza, la formula (5.2) diventa: (5.3) 4( ) ( 2 2 2) 2 2 1 2 / 1 ς ν δ β α + + = z− z− n
dove è la varianza dei “log-ratio” valutati rispetto al campione di riferimento per un dato gene in uno dei due gruppi (varianza intra-classe). E’ evidente che se non sono previste repliche tecniche non è possibile valutare separatamente le due componenti della varianza.
) 2 (ς2+ ν2
Poiché più grande è la varianza, maggiore è il numero di campioni richiesti per ottenere lo stesso livello di potenza, il valore più conservativo per n sarà quello calcolato a partire dalle stime della varianza associate ai geni che mostrano la maggiore variabilità. Una tipica regola empirica suggerisce di utilizzare la mediana, il quartile superiore o il 90-esimo percentile della distribuzione delle varianze gene-specifiche calcolate in uno studio precedente di argomento simile (Yang and Speed, 2002). Secondo studi condotti da diversi centri di ricerca, il valore mediano della deviazione standard intra-classe ricavato a partire dai dati prodotti da un “reference design” su soggetti umani è dell’ordine di 0.5 e si riduce a 0.25 quando l’esperimento è eseguito su topi geneticamente imparentati (Dobbin and Simon, 2005). Valori di σ compresi tra 0.1 e 0.5 sono stati osservati da McShane e collaboratori (2003) in parecchi studi condotti su ratti e topi geneticamente imparentati. Per esempio, nello studio pubblicato da Desai e collaboratori (2002) la mediana delle deviazioni standard intra-classe risulta compresa tra 0.2 e 0.25 per array da 8.700 spot e tra 0.3 e 0.5 per array meno densi (2.700 spot).
La tabella 5.1 (McShane et al., 2003) riporta il numero di campioni indipendenti per classe e la potenza richiesta per rilevare una data differenza tra i livelli medi di espressione tra i due gruppi a confronto, in corrispondenza di un livello di significatività prestabilito (α = 0.001).
La tabella mostra chiaramente che una deviazione standard maggiore richiede un maggior numero di campioni per classe per ottenere la stessa potenza che si osserva in presenza di una variabilità minore. Inoltre l’utilizzo di un maggior numero di repliche biologiche consente di rilevare differenze di espressione più piccole. Infine, le ultime 10 righe della tabella mostrano che quando un numero di repliche disponibili è fissato, la potenza statistica diminuisce al crescere della variabilità intra-classe.
σ δ Fold-change (2δ) Numero di campioni per classe Potenza (%) 0.1 1 2 4 95 0.2 1 2 5 95 0.25 1 2 6 95 0.3 1 2 8 95 0.4 1 2 11 95 0.5 1 2 15 95 0.1 1.32 2.5 3 95 0.2 1.32 2.5 4 95 0.25 1.32 2.5 5 95 0.3 1.32 2.5 6 95 0.4 1.32 2.5 8 95 0.5 1.32 2.5 10 95 0.1 1 2 5 >99 0.2 1 2 5 97 0.25 1 2 5 82 0.3 1 2 5 60 0.4 1 2 5 28 0.5 1 2 5 14 0.1 1.32 2.5 5 >99 0.2 1.32 2.5 5 >99 0.25 1.32 2.5 5 98 0.3 1.32 2.5 5 90 0.4 1.32 2.5 5 59 0.5 1.32 2.5 5 34
Tab. 5.1: Valori di potenza e numerosità campionaria utili per la pianificazione di un
esperimento microarray su modelli animali.
Altre informazioni sulla variabilità dei dati di espressione genica derivano da un progetto del 2001 denominato “Project normal” condotto da Pritchard e collaboratori (2001) con l’obiettivo di valutare le naturali differenze di espressione nei topi. Questo studio ha coinvolto 6 esemplari di topo maschio sano, per ciascuno dei quali sono stati indagati 3 organi diversi (fegato, rene, testicolo) utilizzando 4 repliche tecniche per ogni organo. L’analisi dei dati è stata effettuata utilizzando un modello ANOVA ad effetti misti, in cui l’effetto “Array”, l’effetto “Sample” e l’errore rappresentano gli effetti random, mentre l’effetto “Fluorocromo” e il fattore che indica il tipo di organo considerato sono due effetti fissi. I valori stimati per le
componenti della varianza relative agli effetti random sono riportati nella tabella seguente (Cui and Churchill, 2003).
Componenti della deviazione
standard
Rene Fegato Testicolo
Sample 0.1587 0.0959 0.1122 Array 0.5675 0.5438 0.5539 Media Errore 0.1581 0.1755 0.1562 Sample 0.0949 0.0374 0.0678 Array 0.4656 0.4299 0.4555 Mediana Errore 0.1296 0.1334 0.1241
Tab. 5.2: Media e mediana delle componenti della deviazione standard ricavate dallo studio
di Pritchard e collaboratori.
Dalla tabella risulta che, in generale, il maggiore contributo alla variabilità dei dati deriva dalla deviazione standard dell’effetto “Array” che è circa 5 volte più grande delle deviazioni standard relative all’effetto “Sample” e all’errore. La varianza biologica (tra topo e topo), che nella tabella 5.2 è rappresentata dalla componente della deviazione standard del termine “Sample”, assume invece i valori più piccoli sia che si consideri la media che la mediana. In particolare, tra i 3 organi a confronto, il più piccolo valore della varianza biologica è quello associato al fegato.
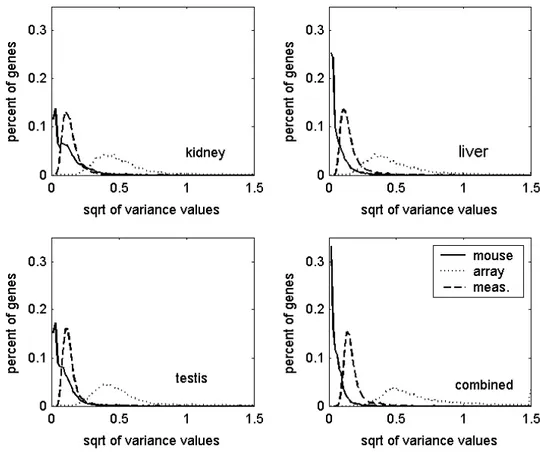
La figura 5.4 mostra le distribuzioni delle componenti della deviazione standard calcolate per tutti i geni, sia organo per organo che complessivamente (Cui and Churchill, 2003).
Fig. 5.4: Distribuzione delle componenti della deviazione standard per (a) il rene, (b) il fegato,
(c) il testicolo, (d) senza distinzioni tra i 3 organi.
Dai grafici si può osservare che la maggior parte dei geni è caratterizzata da una modesta variabilità biologica. Infatti soltanto il 18%, 5% e 6% dei geni, rispettivamente del rene, del fegato e del testicolo, hanno una deviazione standard biologica maggiore di 0.2.
La formula (5.8) si riferisce ad un “reference design” senza repliche tecniche; se con m si indica il numero di repliche tecniche, il numero di campioni totali richiesti è dato da:
(5.4) 4 ( ) ( 2 ) 2 2 2 2 1 2 / 1 m z z m n ς ν δ β α + + = − −
da cui segue che il numero totale di campioni biologicamente distinti è pari a n / m.
A differenza della formula (5.8), in questo caso per calcolare n non è sufficiente una stima della varianza dei “log-ratio” ma occorrono stime separate della varianza biologica e della varianza di errore.
La tabella 5.3 (Dobbin and Simon, 2005) mostra l’effetto prodotto dall’utilizzo di un numero variabile di repliche tecniche sul numero di array richiesti e sul numero totale di campioni, per due diversi valori del rapporto tra la varianza biologica e la varianza di errore. I valori riportati sono stati ricavati scegliendo α = 0.001, β = 0.05, δ = 1 e
=0.5, che corrisponde ad una deviazione standard di 0.707. I risultati dispari vanno arrotondati all’intero superiore così da ottenere due gruppi della stessa dimensione.
2 2 /ν ζ ) 2 (ς2+ ν2
2 2/ν
ζ
Numero di repliche tecniche per ogni
campione Numero di array richiesti Numero totale di campioni richiesti 1 49 49 2 74 37 3 99 33 2 4 124 31 1 49 49 2 82 41 3 114 38 4 4 148 37
Tab. 5.3: Effetto delle repliche sul numero di array e di campioni richiesti
Valori tipici del rapporto sono compresi nell’intervallo tra 2 e 10 (Dobbin and Simon, 2002; Kendziorski et al., 2003).
2 2/ν
ζ
Dalla tabella 5.3 si osserva che c’è una diminuzione del numero di campioni richiesti quando ogni campione viene ibridizzato su più di un array. Questo vantaggio ha, tuttavia, un costo in termini del maggior numero di array che bisogna utilizzare.
Calcoli simili dovrebbero essere applicabili al caso di un “reference design” con “dye-swap”, sebbene, come è stato evidenziato nel capitolo 2, l’inversione della marcatura fornisca risultati migliori dell’utilizzo di semplici repliche tecniche (Liang et al., 2003).
Se con nm si indica il numero di array richiesti quando per ogni campione si
considerano m repliche tecniche, la relazione tra il numero di array necessari per raggiungere la stessa potenza in presenza di una sola replica tecnica o di m repliche tecniche per campione è espressa dalla formula:
(5.5) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + = 2 ) / ( 2 ) / ( 2 2 2 2 1 ς ν ν ς m n nm .
Per esempio, se = 2, allora il numero di array richiesti quando per ogni campione si considerano 2 repliche tecniche (n
2 2 /ν
ζ
2) è pari a : n2 = 1.5n1 mentre quando per ogni
5.3 CALCOLO DELLA NUMEROSITÀ CAMPIONARIA PER UN
DISEGNO A BLOCCHI BILANCIATI
La scelta di un disegno a blocchi bilanciati in luogo del “reference design” consente di ridurre il numero di array necessari per ottenere la potenza desiderata, a parità di valore degli altri parametri. Il numero di array richiesto da un disegno a blocchi bilanciati (che coincide con il numero di repliche biologiche per classe, quando il confronto è tra due soli gruppi), per valori fissati di α, β, δ e τ, è dato dalla formula:
(5.6) 2 2 2 1 2 / 1 ) ( δ τ β α − − + = z z n
dove τ2 è la varianza dei ratio”. Nel disegno a blocchi bilanciati, ciascun
“log-ratio” si riferisce a due campioni indipendenti, uno per ogni classe. Ne deriva, pertanto, che il parametro τ tenderà ad essere maggiore rispetto al parametro σ che figura al numeratore della formula valida per il “reference design”, dal momento che in quest’ultimo il dato di intensità relativo al campione di riferimento è lo stesso in tutti i “log-ratio”.
Quanto detto appare più evidente se si esprime τ2 in funzione della componente
biologica e della componente di errore, in tal caso la formula (5.11) diventa:
(5.7) ( ) ( 2 ) ( ) (2 2 2 2) 2 2 1 2 / 1 2 2 2 2 1 2 2 1 2 / 1 ς ν δ ν ς ς δ β α β α + + ≅ + + + = z− z− z− z− n
dove e sono le varianze delle intensità logaritmiche attribuibili alla variabilità biologica dei livelli di espressione all’interno di ciascuna classe.
2 1
ς 2
2
ς
Dobbin e collaboratori (Dobbin et al, 2003) hanno ricavato una formula semplice che consente di determinare la numerosità campionaria per un disegno a blocchi bilanciati a partire dai dati sulla varianza osservati con un “reference design”. Supponendo di conoscere la varianza dei “log-ratio” σ2 calcolata per un “reference design” e ricordando le seguenti relazioni che esprimono la dipendenza di σ2 e τ2 dalla variabilità biologica e dalla variabilità
attribuibile all’errore sperimentale: (5.8) σ2 =ς2 +2ν2
(5.9) τ2 =2ς2 +2ν2
è possibile ricavare il valore di τ2 noto il valore del rapporto . Per esempio, se in un
esperimento realizzato con un “reference design” si osserva un valore mediano di = 8 (che significa che la varianza biologica è 8 volte la varianza dell’errore) e una deviazione
2 2/ν ζ 2 2/ν ζ
standard σ= 0.5, allora risulta: 0.67 5
9 2 2 = σ ≈
τ . Scegliendo δ = 1, α = 0.001, β = 0.05, il numero di array richiesti nel caso del disegno a blocchi bilanciati risulta pari a 17, contro i 30 necessari per un “reference design”. D’altro canto, mentre per il “reference design” con 30 array sono sufficienti 15 campioni per classe, nel caso del disegno a blocchi bilanciati le repliche biologiche per ciascun gruppo sono 17, per un totale di 34 campioni. Perché il disegno risulti effettivamente bilanciato rispetto all’effetto “fluorocromo” occorre un numero pari di array, quindi sono necessarie 18 repliche biologiche per ciascun gruppo.
5.4 CALCOLO DELLA NUMEROSITÀ CAMPIONARIA PER UN
DISEGNO A BLOCCHI BILANCIATI NEL CASO DI CAMPIONI
APPAIATI
Le formule presentate finora si riferiscono ad esperimenti condotti su campioni indipendenti. Come descritto nel capitolo 3, un esperimento di “class comparison” può coinvolgere anche campioni naturalmente o artificialmente appaiati e quindi dipendenti, come, per esempio, campioni di tessuto dello stesso individuo prima e dopo il trattamento con un farmaco oppure campioni di tessuto tumorale e istologicamente normale tratti dallo stesso organo.
Per confrontare campioni appaiati (per esempio tessuto sano e malato o tessuto trattato e non trattato) utilizzando un disegno a blocchi sono possibili 2 soluzioni. In un caso ogni coppia di campioni viene ibridizzata su un solo array e gli array sono bilanciati in modo tale che i campioni sani (malati) (o i campioni trattati (non trattati)) siano marcati con il fluorocromo verde su metà degli array e con il fluorocromo rosso sull’altra metà (“simple paired design”). In alternativa si può utilizzare un “dye-swap design”, ibridizzando ogni coppia su 2 array con la marcatura invertita (“dye-swap paired design”).
Il numero di array necessari nel primo caso è dato da:
(5.10) ( ) (2 2 2) 2 2 1 2 / 1 ν η δ β α + + = z− z− nbalanced
dove è la varianza dei “log-ratio” per i campioni appaiati e rappresenta la componente biologica della varianza per la quale si è utilizzato un simbolo differente rispetto alle formule precedenti poiché il suo significato è concettualmente diverso. rappresenta infatti la variabilità (biologica) imputabile all’effetto che la patologia/il trattamento produce sul livello di espressione di un dato gene in individui diversi e non la variabilità biologica di base fra soggetti diversi sottoposti allo stesso trattamento o affetti dalla stessa malattia.
) 2
( ν2 +η2 η2
2
η
Il numero di array richiesti nel caso di un “dye-swap paired design” ndye-swap si ricava
può dimostrare che: 1≤ ≤2
balanced dyeswap
n n
. E’ abbastanza intuitivo che il massimo valore del rapporto
balanced dyeswap
n n
non può essere maggiore di 2 perché un “balanced paired design” richiede esattamente lo stesso numero di campioni biologicamente distinti di un “dye-swap paired design” con il doppio degli array.
5.5 EFFETTO DEL POOLING SULLA NUMEROSITÀ CAMPIONARIA
Si supponga di voler confrontare i livelli di espressione di due gruppi mediante un “reference design”, avendo a disposizione p campioni indipendenti per ogni classe. Una strategia che consente di ridurre il numero di array richiesti, aumentando contemporaneamente la precisione della stima della differenza di espressione, consiste nel formare più “pool” indipendenti (costituiti, cioè, da un insieme diverso di repliche biologiche) per ciascuno dei gruppi a confronto. Così facendo il numero totale di array (e quindi di “pool” indipendenti) necessari per rilevare una differenza di espressione δ, ad un livello di significatività α e con una potenza 1 - β è dato dalla formula:
(5.11) 4 ( ) ( 2 ) 2 2 2 2 1 2 / 1 m k z z m n ς ν δ β α + + = − −
dove k è il numero di campioni per “pool” e m rappresenta le eventuali repliche tecniche utilizzate per ogni “pool”.
Nella tabella seguente (Dobbin and Simon, 2005) sono riportati il valore di n e il numero di repliche biologiche richiesti per diversi valori di k. I calcoli si riferiscono ai seguenti valori dei parametri: α = 0.001, β = 0.05, δ = 1, m = 1, = 0.5, che corrisponde ad una deviazione standard pari a 0.707.
2 2 2ν
2 2/ν ζ Numero di campioni per “pool” (k) Numero di array richiesti (n) Numero totale di campioni richiesti 1 49 49 2 37 74 3 33 99 2 4 31 124 1 49 49 2 33 66 3 28 84 4 4 25 100
Tab. 5.4: Numero di array e numero di campioni richiesti per vari livelli di “pooling”
Come si può vedere dalla tabella 5.4 il “pooling” consente di risparmiare sul numero di array a spese, però, di un numero molto maggiore di repliche biologiche.
Introducendo il “pooling”, si è detto che esso consente di ottenere una stima più precisa delle misure di espressione dal momento che riduce la componente biologica della varianza dei “log-ratio” di un fattore k
5.6 ALCUNE
CONSIDERAZIONI SULLA VALIDITÀ DELLE
FORMULE PROPOSTE PER IL CALCOLO DELLA
NUMEROSITÀ CAMPIONARIA
In realtà le formule proposte per il calcolo della numerosità campionaria forniscono dei risultati corretti solo nel caso di campioni molto numerosi (n > 30). Poiché i campioni coinvolti in un esperimento microarray sono solitamente molto pochi, la validità delle formule viene meno essenzialmente per due motivi. Innanzitutto nel ricavare le formule per la determinazione di n si è supposto di conoscere la deviazione standard della popolazione; in realtà il valore di σ stimato a partire da un campione è tanto più lontano dal valore vero quanto più piccolo (e quindi meno rappresentativo) è il campione considerato. In secondo luogo, la distribuzione dei dati può differire significativamente dalla distribuzione Normale per piccoli valori di n. Un’approssimazione migliore si ottiene considerando, al posto della distribuzione Normale, la distribuzione t di Student. Con questa sostituzione, la formula (5.2) diventa: (5.12) 2 2 2 2 , 1 2 , 2 / 1 ) ( 4 δ σ β α − − − − + = t n t n n
dove t1-p,n-2 indica il percentile p della distribuzione t di Student con (n - 2) gradi di libertà,
con p uguale, rispettivamente, ad α/2 e β e in cui gli altri simboli hanno lo stesso significato che avevano nell’espressione (5.2).
Poiché i percentili della distribuzione t dipendono da n, l’equazione (5.17) può essere risolta solo iterativamente. Il metodo iterativo richiede:
a) una prima stima dei gradi di libertà ν = n-2 della distribuzione t; considerando che ogni gruppo abbia almeno n = 3-4 osservazioni; con 2 gruppi, il valore di ν diventa uguale a 5 – 7 e sulla base di questi gradi di libertà si scelgono i due valori di t (quello alla probabilità α / 2 e quello alla probabilità β);
b) se il calcolo determina un valore di n maggiore dei 3-4 preventivati, si stima un nuovo ν e si calcolano due nuovi valori di t;
c) dopo il nuovo calcolo, spesso si può osservare che il terzo valore di n è vicino al secondo: si sceglie quello più conservativo, arrotondato all’unità per eccesso. Se la differenza tra il terzo valore di n ed il secondo fosse ritenuta ancora importante, si effettua un nuovo calcolo dopo aver modificato i valori di t corrispondenti ai nuovi gradi di libertà; quasi sempre la quarta stima è molto simile alla terza e con essa termina il processo iterativo.
5.7 METODI GRAFICI PER IL CALCOLO DELLA NUMEROSITÀ
CAMPIONARIA
Sulla base delle conoscenze e delle valutazioni relative all”effect-size”, alle probabilità α e β, ed alla variabilità della misura di interesse, la numerosità campionaria necessaria ad uno studio può essere calcolata sia attraverso l'utilizzo di equazioni matematiche, sia mediante le cosiddette “curve di potenza”. Tuttavia i metodi grafici rappresentati dall’utilizzo di tali curve sono metodi piuttosto generici che non tengono conto delle differenze fra i vari disegni sperimentali di fondamentale importanza negli esperimenti microarray. Essi pertanto forniscono solo una valutazione indicativa della numerosità campionaria.
Nelle ipotesi di validità della formula (5.2) le curve di potenza per un test bilaterale con
α = 0.05 sono riportate in figura 5.5. Tali curve consentono di stimare: a. il rischio β,
b. il numero minimo n di dati necessari in ogni gruppo, dopo aver calcolato il parametro φ attraverso la relazione: (5.13)
2
σ δ
φ = .
φ prende il nome di “parametro di non centralità” e costituisce una misura della “distanza” fra le distribuzioni dei dati ipotizzate da H0 e H1 e quindi dell’effetto che si
desidera rilevare. La definizione di φ dipende dal test statistico considerato.
Per stimare il rischio β, dopo aver individuato il valore di φ sull’asse delle ascisse, si sale verticalmente fino ad incontrare la curva n in un punto; trasferito orizzontalmente sull’asse delle ordinate, esso indica il rischio β.
Per stimare le dimensioni minime (n) del campione, dopo aver individuato il valore di φ sull’asse delle ascisse, si sale verticalmente e dopo aver prefissato il valore di β ci si sposta in modo orizzontale: il punto di incrocio dei due segmenti ortogonali individua la curva n .
Il procedimento è illustrato in figura 5.5 da cui risulta che, per poter osservare una differenza φ =0.88 con una potenza non inferiore all’80% (a cui corrisponde un valore di β pari a 0.2) ogni gruppo deve essere formato da 10 soggetti.
Fig. 5.5: Curve di potenza per il calcolo della numerosità campionaria
Diagrammi analoghi consentono di determinare la numerosità campionaria quando si utilizza la distribuzione t in luogo della distribuzione Normale (vedi figure 5.6 e 5.7). In questo caso, il parametro di non centralità è dato dal rapporto:
(5.14) σ δ φ 2 n =
Fig. 5.6: Curve di potenza per il test t per campioni indipendenti di taglia uguale α = 0.05
Fig. 5.7: Curve di potenza per il test t per campioni indipendenti di taglia uguale α = 0.01
Il procedimento per il calcolo della numerosità campionaria è più complicato rispetto alla situazione precedente perché n compare sia nell’espressione del parametro di non
centralità sia nei gradi di libertà della distribuzione t. Di conseguenza la ricerca di n avviene per tentativi: prima si fissa n, si calcola 1 - β, poi si itera il calcolo finché la potenza non è vicina al valore desiderato.
5.8 CALCOLO DELLA NUMEROSITÀ CAMPIONARIA PER UN
REFERENCE DESIGN CON PIÙ GRUPPI A CONFRONTO
Le formule ricavate nei paragrafi precedenti consentono di valutare la numerosità campionaria richiesta per alcune tipologie di disegno sperimentale quando l’obiettivo dello studio è il confronto tra i livelli medi di espressione di due soli gruppi.
Nel capitolo 4 è stato illustrato come il metodo dell’analisi della varianza costituisce un valido approccio per l’analisi dei dati microarray e la selezione dei geni differenzialmente espressi quando si vogliono confrontare k ≥ 2 gruppi.
Si supponga di eseguire un esperimento microarray in cui si utilizza un “reference design” per identificare quali geni risultano differenzialmente espressi tra k gruppi a confronto. Si consideri il caso più semplice in cui ogni osservazione è classificata solo sulla base del trattamento o del gruppo al quale appartiene (ANOVA ad una via).
Le ipotesi che stanno alla base del calcolo della potenza e della dimensione campionaria nell’ANOVA non sono diversi da quelli del test t utilizzato nel caso di 2 gruppi. Le uniche differenze sono il modo in cui viene quantificata l’entità dell’effetto minimo rilevabile e il rischio di concludere erroneamente che c’è un effetto del trattamento. La misura dell’effetto del trattamento è più complicata di quella del test t perché deve essere espressa in modo diverso da una semplice differenza fra 2 gruppi. Tuttavia essa può ancora essere descritta per mezzo del parametro di non centralità φ , sebbene questo sia definito in un modo diverso rispetto al test t. Se con k si indica il numero di gruppi o trattamenti a confronto e con n la numerosità campionaria di ciascun gruppo, il parametro di non centralità è dato da:
(5.15) k n 2 σ δ φ = dove:
- δ è la differenza di espressione minima tra ciascuna coppia di trattamenti che si desidera rilevare;
- σ è la deviazione standard dei dati di espressione intra-classe, supposta uguale per tutti i gruppi.
L’analisi della varianza si basa sulla statistica F, la cui distribuzione è individuata da ν1
e ν2, determinati dai gradi di libertà della varianza tra i gruppi e della varianza entro i gruppi.
Come per il test t, anche per l’ANOVA ad una via basata sulla statistica F, è possibile utilizzare il metodo grafico delle curve di potenza per determinare la numerosità campionaria necessaria per rilevare una data differenza di espressione, con una potenza 1 – β e un livello di significatività α specificati. Le curve di potenza per l’ANOVA sono costituite da una famiglia di curve raggruppate in base al numero di gradi di libertà del numeratore della statistica F ossia in base al numero di classi a confronto.
Fissato k, poiché la numerosità campionaria compare sia nell’espressione del parametro di non centralità, sia nei gradi di libertà del denominatore di F, il procedimento per la determinazione di n avviene per tentativi in maniera analoga a quanto visto per le curve di potenza relative al confronto tra due campioni indipendenti basato sul test t.