III.2 Modellazione analitica del comportamento della membrana esterna

III.2

Modellazione analitica del comportamento della membrana

esterna

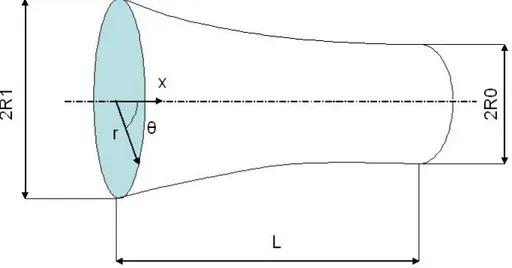
Sia dato un tratto di membrana tubolare di raggio R0 e lunghezza L e si consideri un sistema di riferimento cilindrico con l’origine O in corrispondenza di una delle sezioni trasversali di estremità e l’asse x coincidente con quello del tubo, positivo nel verso entrante nello stesso.

Si applichi quindi uno spostamento assialsimmetrico in direzione radiale in x=0 che deformi la sezione fino ad un valore R1 del raggio. L’estremo opposto si trovi invece a distanza sufficiente da non risentire degli effetti dello spostamento applicato. Si abbia cioè r=R0 in x=L:

Fig. III.2 Tubo deformato assialsimmetricamente in x=0

Si noti che l’assialsimmetria del sistema permette di ricondursi allo studio di un problema piano.

Si tagli quindi il tratto di tubo con un piano contenente l’asse x e si prenda in esame una delle due metà della sezione così ottenuta.

Si esamini quindi un elemento di lunghezza infinitesima tra le ascisse x e x+dx e per questo si impongano le condizioni di equilibrio in direzione assiale e in quella radiale.

Fig. III.3 Modello del tratto di condotto in esame

Equazione di equilibrio in direzione assiale

Nei calcoli a seguire si prendono in considerazione anche le variazioni dell’angolo θ tra le due sezioni di estremità dell’elemento. Per brevità di rappresentazione si decide inoltre di non indicare esplicitamente la dipendenza di tale grandezza da x.

Si conduce per prima cosa una breve analisi trigonometrica.

Per la definizione del significato delle variabili utilizzate si faccia riferimento alla figura 2 che rappresenta un ingrandimento del tratto infinitesimo della membrana preso in esame:

Da qui si possono dunque ricavare le relazioni:

( )

( )

( )

( )

2 2 2 2 2 2 2 1 sin 1 1 cos 1 cos sin 1 1 1       + − =       + =       + = +       + = + − = dx dr(x) dx dr(x) dx dr(x) dx dr(x) dx dr(x) ) ( tg dx dr(x) ) tg( ϑ ϑ ϑ ϑ ϑ ϑ

Dove i segni negativi dipendono dalla scelta fatta per il sistema di riferimento. L’equazione di equilibrio quindi è:

( )

( )

(

) ( )

(

( )

)

[

cos

( )

]

2

(

( )

) ( )

( )

[

cos

( )

]

0

2⋅π ⋅ σ_l x +dσ_l x ⋅ r x +dr x ⋅ ϑ _x+dx − ⋅π⋅ σ_l x ⋅ r x ⋅ ϑ _x =

Il primo termine tra parentesi quadre rappresenta il coseno dell’angolo θ calcolato in x+dx, il secondo invece è il coseno dello stesso angolo valutato in x.

Sviluppando i calcoli:

( )

( )

( )

( )

2 2 2 1 tan       + = − = dx x dr dx x r d d dx x dr a ϑ ϑ Da cui sostituendo:

( )

[

]

( )

( )

( )

( )

( )

dx dx x dr dx x r d dx x dr dx x dr dx x dr dx x ₂ 2 2 2 2 1 1 1 1 cos       + ⋅       + −       + = + ϑ

L’equazione di equilibrio assiale può essere scritta come:

( )

( )

(

) ( )

(

( )

)

( )

( )

( )

( )

( )

( ) ( )

( )

0 1 1 1 1 1 2 2 2 2 2 2 =       + ⋅ +                     + ⋅       + −       + ⋅ + ⋅ + dx x dr x x r dx dx x dr dx x r d dx x dr dx x dr dx x dr x dr x r x d x l l l σ σ σ

( ) ( )

( ) ( )

( )

( ) ( ) ( )

( )

0 1 2 2 2 = ⋅ + ⋅ +                     + ⋅ ⋅ ⋅ − dx dr x σ x r x dσ x dx x dr dx x dr dx x r d x r x σ_{l l l}

E dividendo tutto per dx:

( ) ( )

( ) ( )

( )

( ) ( ) ( ) ( )

0 1 2 2 2 = ⋅ + ⋅ +                     + ⋅ ⋅ ⋅ − dx x dσ x r x σ dx x dr dx x dr dx x dr dx x r d x r x σ l l l

Si può raccogliere ed osservare che quella ottenuta è una equazione differenziale a variabili separabili:

( ) ( ) ( ) ( )

( )

( ) ( )

( )

0 1 1 ₂ 2 2 =                     + ⋅       ⋅       − ⋅ ⋅ + ⋅ dx x dr x r dx x dr dx x r d dx x dr x x r dx x d l l _σ σ

L’ultima equazione scritta ha una forma caratteristica:

( )

x f g f f f f ⋅ = ⋅ − = = ⋅ + ⋅ α β β α ' ' ₀

( )

( )

( )

( )

( )

_{( ) ( )}

( )

                    + ⋅       ⋅       − ⋅ ⋅ − =       2 2 2 1 1 1 dx x dr x r dx x dr dx x r d dx x dr x r x dx x d l l σ σ

Quindi si può procedere all’integrazione:

( )

(

)

[

]

( )

_{( )}

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

[

( )

( )

]

( )

( )

( )

( )

( )

( )

                    ⋅       +       + =       −                       + ⋅ =       −       +       ⋅ =                           +       − ⋅ =

∫

∫

∫

x r r dx dr dx x dr σ x σ x r dx x dr σ x σ dr x r dx dx x dr dx x r d dx x dr σ x σ dx dx x dr dx x r d x r dx x dr x σ l l x x l l x x l l x x l 0 0 1 1 log 0 log 1 log 2 1 0 log 1 1 0 log 1 1 log 2 2 0 0 2 0 2 2 2 0 2 2 2 0 0 Elevando:

( )

( ) ( )

( )

( )

( )

                    + ⋅       + ⋅ = x r dx x dr dx dr r x l l 2 2 1 0 1 0 0 σ σ

Cioè:

( ) ( )

( )

( )

( )

( )

                    + ⋅ =       + ⋅ = x r dx x dr K x σ dx dr σ r K l l 2 2 1 0 1 0 0 Equazione I

Equazione di equilibrio in direzione radiale

Si faccia riferimento ancora alla figura 2. L’equazione di equilibrio in direzione radiale è:

( ) ( )

[

( )

]

(

( )

( )

) ( )

(

( )

)

[

( )

]

( )

( )

      + ⋅ ⋅ = ⋅ + ⋅ + ⋅ − ⋅ ⋅ ⋅ ₊ dx x dr x x dr x r x d x x r x t dx x l l x l 1 2 sin 2 sin 2 σ ϑ σ σ ϑ σ

Il primo termine tra parentesi quadre è il seno dell’angolo θ calcolato in corrispondenza della coordinata assiale x, il secondo è lo stesso termine valutato in x+dx.

In particolare sviluppando quest’ultimo si trova:

( )

( )

[

]

( )

( )

( )

( )

( )

                    + − ⋅       + +       + − = + dx dx x dr dx x r d dx x dr dx x dr dx x dr dx x 2 2 2 2 2 1 1 1 1 sinϑ

Basta quindi inserire tutto nell’equazione di equilibrio:

( ) ( )

( )

( )

(

( )

( )

) ( )

(

( )

)

( )

( )

( )

( )

(

) ( )

(

( )

)

( )

( )

( )

( )

( )

dx dx x dr x σ dx dx x dr dx x r d dx x dr x dr x r x dσ x σ dx x dr dx x dr x dr x r x dσ x σ dx x dr dx x dr x r x σ t l l l l l ⋅       + ⋅                                   + − ⋅       + ⋅ + ⋅ + − +                     + − ⋅ + ⋅ + −                     + − ⋅ ⋅ 2 2 2 2 2 2 2 1 1 1 1 1 1

Si trascurano ancora gli infinitesimi di ordine superiore al primo:

( )

( ) ( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

2 2 2 2 2 2 2 2 1 1 1 +_ _       ⋅       ⋅ +       +       ⋅ +               +       ⋅ ⋅ = dx x dr dx x d dx x dr x r dx x dr dx x r d x dx x dr dx x r d x r x x l l l t σ σ σ σ Equazione II

A questo punto i risultati precedenti possono essere utilizzati per scrivere una equazione di equilibrio complessivo del tubo.

Si sostituisce l’equazione I in II:

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

dx x r dx x dr d dx x dr dx x dr x r K dx x dr dx x r d x r dx x dr K dx x dr dx x r d x r x r dx x dr K x t                     + ⋅       +       ⋅ ⋅ +       +       ⋅                     + ⋅ +               +       ⋅ ⋅                     + ⋅ = 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 σ

La derivata che compare nell’ultimo termine si calcola facilmente:

( )

( )

_{( )}

_{( )}

( )

( )

( )

( )

( )

x r dx x dr dx x dr dx x dr x r dx x r d dx x dr dx x r dx x dr d 2 2 2 2 2 2 1 1 1       + ⋅       +       + ⋅       ⋅       =                     +

( )

( )

( )

( )

( )

( )

( )

2 3 2 2 2 2 2 3 2 2 2 1 1               +       ⋅       ⋅ −               +       ⋅ ⋅ = dx x dr dx x r d dx x dr K dx x dr dx x r d x r K x t σ

Quella appena ottenuta é una equazione differenziale del secondo ordine che può essere scritta sotto forma di sistema di equazioni differenziali del primo ordine:

( )

( )

( )

( )

[

]

( )

( )

[

]

( )

2 2 2 2 3 2 2 2 2 2 2 3 2 2 2 1 2 1 1 1 1 r dx dr K r dx dr r K r dx dr r K x dx x dr r x r r t +       ⋅ = +       ⋅ ⋅ + +       ⋅ ⋅ = = = σ

Da qui è quindi possibile scrivere il sistema costituito dalle due equazioni:

( )

( )

K r x dx dr r dx dr t 2 2 2 2 1 1+ ⋅ = = σ

Calcolo della costante K

Il risultato sopra ottenuto definisce il comportamento della membrana a meno di una costante K che può essere determinata facilmente.

( )

( )

( )

( )

1 1 2 − = =                     + ⋅ = dx dl ε EL_L x σ ε x r dx x dr K x σ l l

Dove ε rappresenta la deformazione assiale dell’elemento infinitesimo preso in esame e EL_Lil modulo di elasticità corrispondente del tessuto. Si noti che la relazione costitutiva non é lineare ma segue un andamento di tipo quadratico.

La terza relazione riporta la definizione di deformazione longitudinale. La lunghezza totale della curva può essere calcolata risolvendo l’integrale:

∫

∫

      + =L L dx dx dr dl 0 2 0 1

Si mettono insieme la seconda e la terza equazione:

( )

( )

dx EL_L x σ dx dl dx dl EL_L x σ l l ⋅ + = − = 1

( )

( )

( )

( )

( )

( )

( )

2 0 2 0 0 2 0 2 0 0 2 0 2 0 2 0 0 2 0 2 0 0 0 2 0 1 1 1 1 1 1 1 1 1 1                             + −       + ⋅ =       + −       + =       + =       + ⋅ +                       + ⋅ + =       + + =       + =

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

L L L L L L l L L l L L L L l L L L dx x r dx dr dx dx dx dr EL_L K dx x r dx dr dx dx dx dr EL_L x σ dx dx dr dx x r dx dr EL_L x σ dx dx EL_L dx dr x r K dx dx dr dx EL_L x σ dx dx dx dr dl

Questo risultato permette infine di scrivere l’andamento completo delle tensioni longitudinali:

( )

( )

( )

( )

                    + ⋅                             + −       + ⋅ =

∫

∫

∫

x r dx x dr dx x r dx dr dx dx dx dr EL_L x L L L l 2 2 0 2 0 0 2 1 1 1 σ