C
C
a
a
p
p
it
i
to
o
l
l
o
o
3
3
C
C
a
a
l
l
i
i
b
b
r
r
a
a
z
z
i
i
o
o
n
n
e
e
d
d
e
e
l
l
m
m
o
o
d
d
e
e
l
l
l
l
o
o
d
d
i
i
r
r
i
i
s
s
c
c
h
h
i
i
o
o
Prima di illustrare le metodologie adottate per l’analisi dei dati raccolti, si ritiene op-portuno dare alcuni cenni di statistica.
La statistica è interessata ad ottenere informazioni su un intero insieme di oggetti de-nominato popolazione. Le popolazioni, quasi sempre, sono troppo grandi per poter essere analizzate nella loro interezza per cui nelle elaborazioni statistiche vengono presi in consi-derazione opportuni sottoinsiemi di esse: tali sottoinsiemi sono chiamati campioni. I criteri di estrazione di un campione dalla popolazione variano a seconda del tipo di analisi che si vuole condurre, ma il requisito a cui esso deve rispondere è la rappresentatività.
Un campione rappresentativo è tale che le considerazioni e le conclusioni a cui si giunge dall’analisi dei dati che esso fornisce possono essere estese all’intera popolazione senza commettere grossi errori. Per l’estrazione di un campione, il più possibile rappresen-tativo, esistono varie tecniche, più o meno complesse, da adottare a seconda del tipo di analisi che si vuole condurre. Ad esempio, se si vuole conoscere il numero medio di fuma-tori di uno stato, non si può considerare rappresentativo il campione estratto dalla
popola-zione dei frequentatori di biblioteche, poiché presumibilmente, essendo lettori, sono più in-formati sui danni causati dal fumo.
La rappresentatività di un campione è, in generale, garantita dalla casualità della scelta degli elementi all’interno della popolazione oggetto di studio.
Una funzione che fa corrispondere ad ogni risultato di un esperimento casuale un nu-mero reale è chiamata variabile aleatoria, il cui valore è determinato dall’esito dell’esperimento. L’insieme di tali funzioni, dipendenti da un certo parametro t, si chiama
processo stocastico; il parametro t, nelle più importanti applicazioni dei processi stocastici
rappresenta il tempo.
3.1. Grandezze statistiche
L’esame dei campioni fornisce dei dati che, per essere interpretabili, devono essere rappresentati in modo chiaro e conciso in maniera da dare un’idea generale delle loro carat-teristiche globali. Una sintesi valida dei dati, che si suddividono in numero relativamente basso di valori, può essere la costruzione di grafici e tabelle delle loro frequenze.
Frequenza
Dato un insieme N di valori (x1, x2,..,xn), si definisce frequenza relativa di un valore la
frazione di volte in cui esso compare nell’insieme di dati; la frequenza assoluta rappresen-ta, invece, il numero di volte che un determinato valore si presenta.
Probabilità semplice (o marginale)
Si definisce probabilità una funzione P che ad ogni evento E di un esperimento asso-cia un numero reale P(E) e che soddisfa gli assiomi:
• La probabilità che si verifichi almeno un evento dello spazio degli eventi è pari a 1 (la certezza):
P(Ω) = 1 Ω = spazio degli eventi
• La probabilità che si verifichi un qualunque evento è comunque un numero reale positivo
P(E) ≥ 0
• La probabilità che si verifichino due eventi disgiunti è pari alla somma delle pro-babilità che i due eventi si verifichino separatamente
P(Ei+ Ej) = P(Ei)+ P(Ej) (Ei ∩ Ej=∅)
Probabilità condizionata
Dati due eventi di uno stesso spazio degli eventi E, F, si definisce probabilità condi-zionata che si verifichi l’evento E dato l’evento F e si indica con P(E⏐F) il rapporto:
) F ( P ) F E ( P ) F | E ( P = ∩
Se (E ∩ F=∅) allora la probabilità condizionata è nulla , mentre se E ed F sono eventi fra loro indipendenti, la probabilità condizionata è pari a:
) F ( P ) E ( P ) F | E ( P = ⋅
Non è raro il caso in cui si dispone di una notevole mole di dati, risulta quindi neces-sario poterli sintetizzare per renderli leggibili. Alcune delle grandezze normalmente adope-rate che sintetizzano i dati, chiamate anche statistiche, sono la media, la mediana la varian-za e la deviazione standard.
Media e mediana
La media (o valore atteso) (E[x]) e la mediana rappresentano i valori attorno ai quali
si distribuisce l’insieme dei dati. La media si ottiene facendo il rapporto tra la somma tra i valori assunti dalle variabili e il numero di elementi del campione.
- Media:
∑
⋅ = M i i x M x 1in cui: x è il valor medio della distribuzione;
xi rappresenta il valore della frequenza relativa per ogni categoria di veicolo e per ogni tipologia di porta in tutte le M stazioni in esame
La mediana è il valore centrale di un insieme di dati ordinati in ordine cresente o de-crescente.
Tali statistiche non sono però sufficienti per rendersi conto di come i dati sono distri-buiti effettivamente perché possono dispersi molto attorno a questi valori, per cui, oltre alla media vengono fornite anche informazioni riguardo all’entità di altre due statistiche molto utilizzate che sono la varianza e la deviazione standard.
Varianza e deviazione standard
La varianza (σ2 o var[x]) e la deviazione standard (σ) danno un’indicazione su
quan-to i valori assunti dai dati siano dispersi atquan-torno al valore medio.
- Varianza: 2 2 1 1 ) x x ( M M i i
∑
− ⋅ − = σ - Deviazione standard: 2 1 1 ) x x ( M M i i∑
− ⋅ − = σPer le elaborazioni statistiche che verranno fatte nel seguito, è di fondamentale impor-tanza la conoscenza di una particolare legge distribuzione delle variabili aleatorie: la di-stribuzione di Poisson.
Processo di Poisson
Il processo di Poisson è un particolare processo stocastico in cui la variabile aleatoria assume solo valori interi non negativi. Il numero di veicoli che attraversano una certa se-zione stradale, l’arrivo di veicoli ad un casello di una stase-zione di pedaggio, si possono ap-prossimare ad un processo di Poisson. La legge di distribuzione di probabilità ha la forma:
! k ) t ( e Pk = −λ⋅t ⋅ λ k
λ si chiama intensità del processo di Poisson e rappresenta il valor medio del numero di eventi che si presentano nell’unità di tempo.
Perché un processo sia di Poisson devono verificarsi una serie di condizioni: • N(0) = 0. Gli eventi al tempo 0 sono nulli.
• Dati due intervalli di tempo qualunque ma disgiunti, t e t+s, il numero degli e-venti che hanno luogo in tali intervalli sono indipendenti.
• La distribuzione del numero di eventi che si verifica in un dato intervallo di tem-po dipende solo dalla lunghezza dell’intervallo e non dalla sua tem-posizione.
• Se si considera un intervallo di tempo molto piccolo (h), vi è una probabilità λ·h che si verifichi un solo evento ed è praticamente nulla la probabilità che se ne ve-rifichino due o più.
3.2. Analisi dei dati
L’analisi dei dati oggetto di studio deve concludersi con la calibrazione di quattro pa-rametri necessari per la valutazione del rischio a cui vanno incontro i conducenti che ogni giorno attraversano i piazzali e le piste riservate al pagamento del pedaggio.
Per una più accurata indagine statistica si è ritenuto opportuno suddividere l’insieme di tutte le stazioni e barriere di pedaggio in tre sottoinsiemi che danno luogo a tre diverse popolazioni: la popolazione delle stazioni piccole, la popolazione delle stazioni medie e in-fine quella delle grandi stazioni che però non fanno parte dell’argomento di questa tesi.
Anche se l’insieme delle stazioni e barriere presenti sulla rete autostradale del nostro paese è stata suddivisa in tre grandi popolazioni, è impensabile estendere lo studio ad ogni singolo elemento appartenente a queste popolazioni. Infatti, fare ciò sarebbe fonte di note-vole dispendio di energie, denaro, tempo e inoltre l’enorme mole di dati a cui si perverreb-be non giustifica un tale gravoso impegno poiché essi comunque devono essere sottoposti ad elaborazioni statistiche con tutte le incertezze ad esse connesse.
Nella popolazione delle stazioni medie è stato estratto un campione costituito da due stazioni, mentre in quelle delle piccole stazioni, il campione estratto contiene al suo interno quattro elementi.
Nel prosieguo dell’esposizione saranno meglio specificate le diverse stazioni insieme alle loro caratteristiche geometriche.
3.3. Raccolta dei dati
I parametri geometrici e i parametri di traffico menzionati nei paragrafi precedenti de-vono avere valenza generale non solo per le stazioni esistenti ma anche per le stazioni in progetto.
Tra i parametri geometrici sono inclusi il numero e la disposizione delle porte delle varie tipologie sul piazzale oltre alla loro reciproca distanza; i parametri di traffico com-prendono i flussi dei veicoli, la loro composizione e la distribuzione tra le corsie in arrivo al piazzale.
Tali parametri, affinché il modello di rischio dia poi dei risultati verosimili, devono essere calibrati su situazioni reali, ovvero i dati di traffico e geometrici raccolti nelle sta-zioni campione, subiranno un processo di analisi alla fine del quale saranno disponibili i ri-sultati che verranno poi confrontati con le osservazioni effettuate. Questo confronto servirà a garantire un buon livello di adattamento tra i valori osservati e quelli calcolati con l’analisi statistica.
I restanti capitoli, incluso il presente, di questa tesi mirano ad illustrare le metodologie adoperate per l’analisi dei dati raccolti in tre stazioni di pedaggio di tratti autostradali in concessione alla S.A.L.T. p.A. (Società Autostrade Ligure Toscana). I risultati dell’analisi sono indispensabili per la determinazione dei parametri necessari alla valutazione del ri-schio, con l’ausilio del modello di assegnazione quadratica.
I dati di traffico sono stati raccolti, previa autorizzazione da parte della S.A.L.T., tramite riprese video da telecamera su postazione fissa in tre punti di esazione della rete autostradale italiana di cui è concessionaria la suddetta società.
1. barriera di Lucca Ovest (S. Donato) dell’autostrada A-12 (Genova-Rosignano); 2. stazione di Lucca Nord dell’autostrada A-11 (Firenze-Pisa);
3. stazione di Livorno ancora sull’autostrada A-12.
Per tutte le stazioni i dati sono stati rilevati sia in ingresso alle autostrade che in uscita in un giorno feriale qualunque in un periodo qualunque dell’anno nella fascia oraria che va dalle ore 10 del mattino fino alle ore 14 del primo pomeriggio, per un totale di 12 ore. La casualità con cui il campione è stato raccolto rispetto all’intera popolazione di veicoli che transitano sulle autostrade, ci “fa stare tranquilli” riguardo alla rappresentatività del cam-pione stesso.
Le stazioni di pedaggio sono qui classificate in base alle loro dimensioni in termini di numero di porte, np, per ognuna delle due direzioni:
• piccole: np ≤ 5; • medie: 6 ≤ np ≤ 10; • grandi: np ≥ 11.
I piazzali delle autostrade A-11 e A-12 presi in esame appartengono alle prime due classi; in particolare, sono piccole:
− barriera di Lucca Ovest sia in ingresso che in uscita (3 porte attive); − stazione Lucca Nord per i flussi provenienti da Viareggio (3 porte attive); − stazione di Livorno in direzione Firenze-Genova (3 porte attive).
Fanno invece parte delle stazioni medie:
− stazione di Lucca Nord verso Viareggio (9 porte attive);
I risultati ottenuti per i parametri TC, LF, VF e GF, hanno validità statistica solo per le stazioni di pedaggio di categorie medie e piccole. Le conclusioni cui si giungerà dall’analisi non si possono estendere anche ai grandi piazzali poichè le dimensioni di essi, com’è stato ricordato più volte, influenzano il comportamento dei conducenti.
Perché sia possibile valutare i quattro parametri, la conformazione geometrica e tipo-logica delle piste, dei piazzali e delle corsie di approccio al piazzale devono avere ben spe-cifiche caratteristiche.
3.3.1. Corsie di arrivo ai piazzali.
Condizione necessaria perché gli intrecci delle traiettorie possano avvenire è che i vei-coli debbano provenire da corsie differenti. Questa condizione non è rispettata solo nella barriera di Lucca Ovest per i veicoli provenienti da Viareggio, in cui è presente una sola corsia della rampa d’uscita dall’autostrada, mentre, sempre nella stessa barriera ma nella direzione opposta, le corsie sono tre: una in arrivo da Lucca centro e due provenienti da Fi-renze. Quest’ultima situazione è stata semplificata considerando la corsie proveniente da Lucca (corsia di destra) come la corsia di marcia e le corsie provenienti da Firenze (corsie di sinistra) come corsie di sorpasso.
3.3.2. Tipologie delle porte di esazione.
Altro requisito che le stazioni di pedaggio devono avere è la contemporanea presenza delle porte stop, nostop e mixed (almeno una per ogni classe) per permettere la valutazione dei fattori di porta misti.
Per quanto riguarda i fattori di porta omogenei nostop-nostop e mixed-mixed, in nes-suna delle realtà osservate è possibile una loro valutazione perché di piste sia nostop che mixed ce n’è una sola. Le stazioni medie presentano un numero di porte stop tali da rende-re possibile la valutazione dell’altro fattorende-re di porta omogeneo, il problema è che sono solo due, su sei totali, le stazioni di questo tipo per cui non sono statisticamente rilevanti.
In conclusione: le caratteristiche di traffico rilevate alle stazioni di pedaggio in esame permettono la determinazione dei soli fattori di porta misti.
3.3.3. Composizione del traffico
Non si pongono problemi circa le condizioni necessarie per la determinazione dei due parametri di traffico (Vehicle Factor, Traffic Composition) perché si può affermare, senza tema di smentite, che il traffico non sarà mai composto solo da autoveicoli nei giorni in cui non c’è divieto di circolazione per i mezzi pesanti, ovvero nei giorni festivi in cui è buona regola non effettuare rilievi di traffico se non specificatamente indicati.
3.4. Dati di traffico
I conteggi del traffico di attraversamento delle stazioni di pedaggio sono stati effettua-ti manualmente in seguito alle riprese video: i risultaeffettua-ti sono esposeffettua-ti nei paragrafi successivi per tutti gli elementi che fanno parte dei campioni estratti dall’intera popolazione di sta-zioni e barriere.
Per una più agevole lettura dei dati riportati nelle tabelle che sono presenti nei para-grafi e nei capitoli successivi, si ritiene opportuno chiarire il significato delle simbologie adottate, riguardanti sia il traffico che la tipologia dei casellli.
np = numero dei veicoli pesanti;
nl = numero dei veicoli leggeri;
M = porte manuali; S = porte Self-Service ; V = porte Viacard, Fastpay;
T = porte elettroniche tipo Telepass.
3.4.1. Stazione di Lucca: direzione Firenze
Questo è un piazzale di piccole dimensioni, ci sono tre porte e il giorno in cui sono stati effettuati i rilievi erano tutte attive.
Le corsie che sboccano sul piazzale sono due e posizionate abbastanza centralmente rispetto ai caselli, che appartengono alle tre tipologie diverse: una è di tipo Mixed, una tipo NoStop e un’altra di tipo Stop.
Le caratteristiche di traffico sono presentate nelle tabelle 3.1 e 3.2
Tabella 3. 1 – Distribuzione del traffico sulle corsie di arrivo nella stazione di Lucca per i veicoli diretti a Firenze
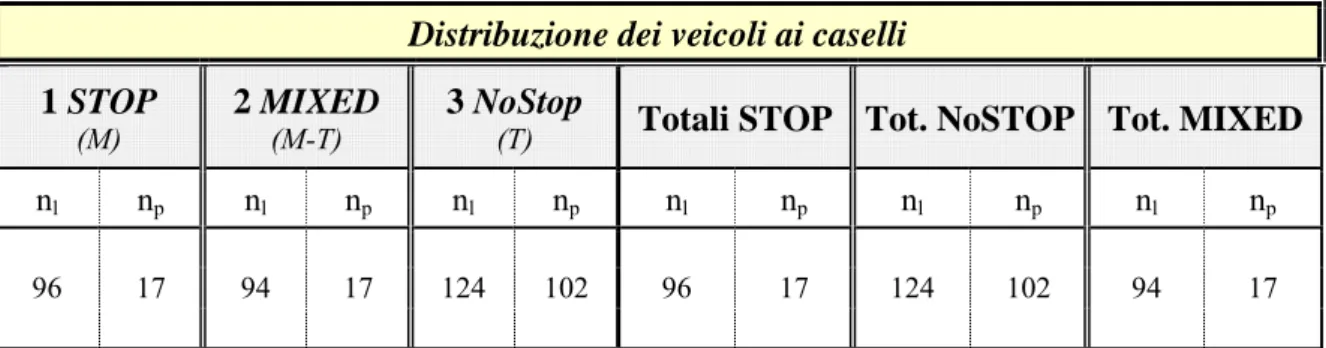
Tabella 3. 2 – Distribuzione del traffico ai caselli di pedaggio della stazione di Lucca per i veicoli diretti a Firenze
Tipo di Veicoli sulle corsie
np nl Tot. veicoli
marcia sorpasso marcia sorpasso n = nl+np
132 4 176 138 450
Distribuzione dei veicoli ai caselli
1 STOP
(M) 2 MIXED (M-T) 3 NoStop (T) Totali STOP Tot. NoSTOP Tot. MIXED
nl np nl np nl np nl np nl np nl np
3.4.2. Stazione di Lucca: provenienza Firenze
Questo è un piazzale di medie dimensioni, ci sono dieci porte ma il giorno in cui sono stati effettuati i rilievi erano attive solo sei, di esse una appartiene al tipo mixed, una alla ti-pologia no-stop e ben 8 sono del tipo stop. I cancelli sono molto decentrati rispetto alle li-nea che divide le due corsie di arrivo al piazzale e precisamente sono spostati molto verso la corsia di destra.
Le caratteristiche di traffico sono riportate nelle tabelle 3.3 e 3.4
Tabella 3. 3 – Distribuzione del traffico sulle corsie di arrivo nella stazione di Lucca per i veicoli provenienti da Firenze
Tipo di Veicoli sulle corsie
np nl Tot. veicoli
marcia sorpasso marcia sorpasso n = nl+np
Tabella 3. 4 – Distribuzione del traffico ai caselli di pedaggio nella stazione di Lucca per i veicoli provenienti da Firenze
Distribuzione dei veicoli ai caselli
1-STOP
(M) 2-STOP(M) 3-STOP(M) 4-STOP(M) 5-(V-S) STOP 6-(V-M) STOP 7-MIXED (V-M-T) 9-NoStop(T) Totali STOP Tot. NoSTOP Tot. MIXED
nl np nl np nl np nl np nl np nl np nl np nl np nl np nl np nl np
Questa stazione è costituita da quattro porte: una mixed, una telepass dedicata e due di tipo stop; il giorno in cui sono stati effettuati i rilievi, una delle porte manuali era inattiva.
Le corsie che sboccano sul piazzale sono tre e posizionate abbastanza centralmente rispetto ai caselli.
Le tabelle 3.5 e 3.6 riportano i rilievi effettuati in termini di numero dei veicoli in arri-vo e loro distribuzione ai caselli.
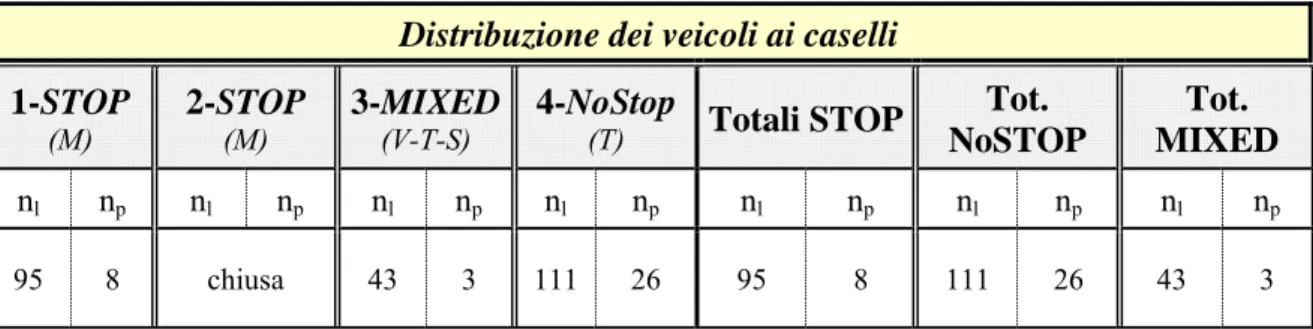
Tabella 3. 6 – Distribuzione del traffico ai caselli di pedaggio alla barriera di Lucca per i veicoli diretti a Viareggio
Tipo di Veicoli sulle corsie
np nl Tot. veicoli
marcia sorpasso marcia sorpasso n = nl+np
30 7 179 70 286
Tabella 3.5 - Distribuzione del traffico sulle corsie di arrivo alla barriera di Lucca per i veicoli diretti a Viareggio
Distribuzione dei veicoli ai caselli
1-STOP (M) 2-STOP (M) 3-MIXED (V-T-S) 4-NoStop (T) Totali STOP Tot. NoSTOP Tot. MIXED nl np nl np nl np nl np nl np nl np nl np 95 8 chiusa 43 3 111 26 95 8 111 26 43 3
Questa stazione, anche nella direzione opposta alla precedente è costituita da quattro porte e delle medesime tipologie: una mixed, una telepass dedicata e due di tipo stop, con tutte le porte attive il giorno in cui sono stati effettuati i rilievi.
La corsia che sbocca sul piazzale è unica e posizionata abbastanza centralmente rispet-to ai caselli. Come si è già avurispet-to modo di ribadire, i dati utili ricavati in questa stazione so-no solo quelli relativi alla composizione del traffico proprio per la presenza di una sola del-le corsie di arrivo.
Le tabelle 3.7 e 3.8 riportano i rilievi effettuati in termini di numero dei veicoli in arri-vo e loro distribuzione ai caselli.
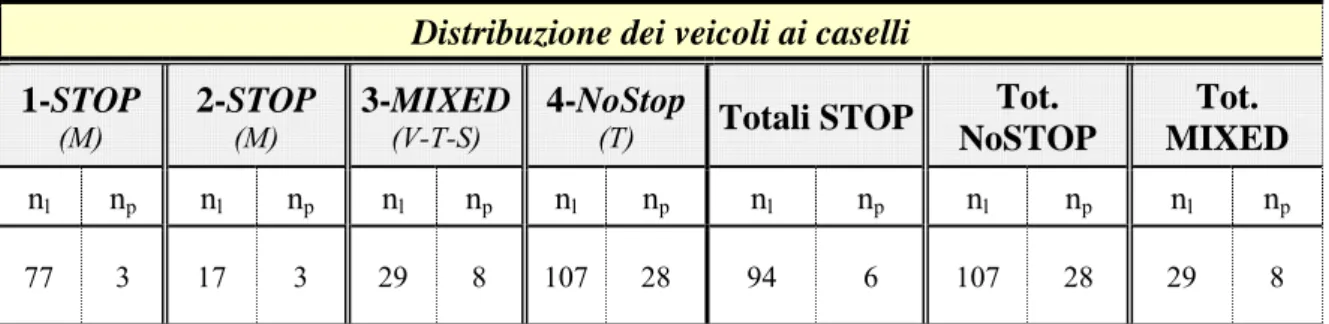
Tabella 3. 8 – Distribuzione del traffico ai caselli di pedaggio alla barriera di Lucca per i veicoli provenienti da Viareggio
Tipo di Veicoli sulle corsie
np nl Tot. veicoli
unica unica n = nl+np
42 230 272
Tabella 3.7 - Distribuzione del traffico sulle corsie di arrivo al-la barriera di Lucca per i veicoli provenienti da Viareggio
Distribuzione dei veicoli ai caselli
1-STOP
(M) 2-STOP (M) 3-MIXED(V-T-S) 4-NoStop (T) Totali STOP
Tot. NoSTOP Tot. MIXED nl np nl np nl np nl np nl np nl np nl np 77 3 17 3 29 8 107 28 94 6 107 28 29 8
3.4.5. Stazione di Livorno: direzione Firenze - Genova
La stazione di Livorno, nella direzione che va verso Firenze e Genova, presenta il numero minimo di porte e di tutte le tipologie che interessano: una mixed, una telepass de-dicata e una di tipo stop, con tutte le porte attive il giorno in cui sono stati effettuati i rilie-vi. Esse sono posizione centralmente rispetto alla mezzeria della carreggiata della rampa che sbocca sul piazzale e che è costituita da due corsie.
Le tabelle 3.9 e 3.10 riportano i rilievi effettuati in termini di numero dei veicoli in ar-rivo e loro distribuzione ai caselli.
Tabella 3. 10 – Distribuzione del traffico ai caselli di pedaggio alla stazione di Livorno per i veicoli diretti a Firenze e Genova
Tipo di Veicoli sulle corsie
np nl Tot. veicoli
marcia sorpasso marcia sorpasso n = nl+np
161 3 212 36 412
Tabella.9 - Distribuzione del traffico sulle corsie di arrivo alla stazione di Livorno per i veicoli diretti a Firenze e Genova
Distribuzione dei veicoli ai caselli
1-STOP
(M)
2-MIXED
(M-T)
3-NoStop
(T) Totali STOP Tot. NoSTOP Tot. MIXED
nl np nl np nl np nl np nl np nl np
I veicoli che da Livorno si dirigono verso Firenze e Genova, si trovano a dover attra-versare una stazione di pedaggio con un discreto numero di porte: ce ne sono ben nove ma solo otto attive. Le otto porte sono così suddivise: una mixed, una telepass dedicata e sei di tipo stop.
Le corsie di approccio al piazzale di stazione sono due e molto decentrate rispetto all’asse mediano dei caselli.
Nelle tabelle 3.11 e 3.12 della pagina successiva, è possibile reperire i dati di traffico che l‘analisi dei dati.
In tutte le stazioni di pedaggio prese in esame, il flusso di veicoli, nell’ora di osserva-zione si è mantenuto sempre, abbondantemente, al di sotto di 500, che è il valore limite massimo al di sopra del quale è lecito nutrire dubbi circa l’ipotesi di indipendenza recipro-ca dei singoli eventi: questa ipotesi è alla base di tutta l’analisi statistirecipro-ca condotta per la ri-cerca dei valori assunti dai parametri del modello di rischio.
La percentuale dei veicoli commerciali che percorrono la corsia di marcia, rispetto a tutti i veicoli commerciali presenti che hanno attraversato il piazzale, è molto maggiore della percentuale dei mezzi pesanti che utilizzano la corsia di sorpasso; mentre nel caso dei veicoli leggeri, la distribuzione di essi sulle due corsie è, approssimativamente, la stessa.
Tipo di Veicoli sulle corsie
np nl Tot. veicoli
marcia sorpasso marcia sorpasso n = nl+np
90 27 128 44 289
Tabella 3.11 - Distribuzione del traffico sulle corsie di arrivo alla stazione di Livorno per i veicoli provenienti da Firenze e Genova
Tabella 3. 12 – Distribuzione dl traffico ai caselli di pedaggio nella stazione di Livorno per i veicoli provenienti da Firenze e Genova
Distribuzione dei veicoli ai caselli
1 -STOP (V) 2-MIXED (M-T) 3-No(T) Stop 4-STOP (V) 5-STOP (V-S) 6-STOP (V-S-M) 7-STOP (M) 8-STOP
(M) Totali STOP Tot. NoSTOP Tot. MIXED
nl np nl np nl np nl np nl np nl np nl np nl np nl np nl np nl np
del piazzale e, perciò, più in linea con la corsia di marcia. Le stazioni medie presentano una disposizione delle porte del tutto casuale.
A questo punto non rimanere altro da fare che calcolare le probabilità con cui avven-gono gli intrecci di traiettorie relativamente alle corsie, ai veicoli e alla tipologia di porta per poi verificare se le configurazioni che hanno attualmente i piazzali studiati, sono quelle di minimo rischio per gli utenti o se le disposizioni dei piazzali necessitano di modifiche per garantire al sicurezza.