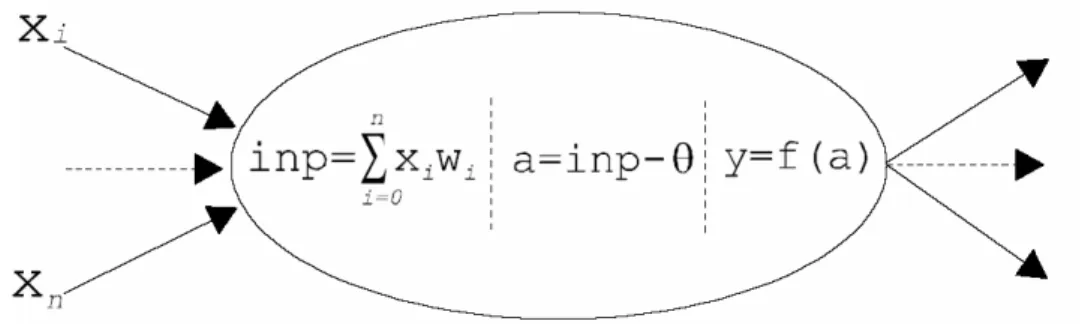Capitolo 2

CAPITOLO 2

Neurone e reti di neuroni. Dall’integrate-and-fire al Leabra

In questo capitolo si vuole cercare di indicare una strada coerente che conduca fino al modello Leabra, che verrà in seguito implementato. Per fare questo è opportuno partire da una breve descrizione dei modelli biofisici del neurone. Poi si passeranno in rassegna le reti neurali e si vedrà cosa significa dire che si ispirano al sistema nervoso per risolvere problemi di modellizzazione. Infine si darà una descrizione dettagliata del Leabra.

2.1 Biofisica della generazione del potenziale d’azione

Nel neurone, per quanto visto nel precedente capitolo, e riducendo in modo brutale la complessità dei processi, i dendriti e il corpo cellulare servono per la ricezione e l’elaborazione dell’informazione, mentre l’assone trasporta il segnale a distanza. L’informazione viaggia sotto forma di potenziale d’azione, variazione non lineare nel tempo del potenziale di transmembrana che si propaga nello spazio. La prima descrizione semi-empirica di questo fenomeno è stata data da Hodgkin e Huxley, che, partendo dalle statistiche di attivazione e inattivazione dei canali del sodio e del potassio, sono arrivati alla descrizione della propagazione del potenziale.

Gli ioni distribuiti sui due lati della membrana, in una condizione in cui tutti sono lontani dal loro stato di equilibrio elettrochimico, tendono a spostare il potenziale di

transmembrana ciascuno verso il proprio potenziale di equilibrio, che può essere calcolato secondo la legge di Nernst:

ln E j I E j j j I j j C RT z F C ⎛ ⎞ ∆Φ = Φ − Φ = ⎜_⎜ ⎟_⎟ ⎝ ⎠ (2.1.1)

dove R è la costante dei gas, T è la temperatura assoluta, F è la costante di Faraday , z è la _j

carica dello ione, CI_je CE_j sono le concentrazioni rispettivamente intra ed extra cellulari

della specie j-esima e ∆Φ è il potenziale di Nernst del j-esimo ione. Se sono presenti più _j specie chimiche, il potenziale di transmembrana è una combinazione lineare dei potenziali di Nernst di ciascuna di esse. Una volta che si sono trovati i valori dei potenziali per ogni ione, si può passare al modello elettrico per la membrana non melinata a riposo.

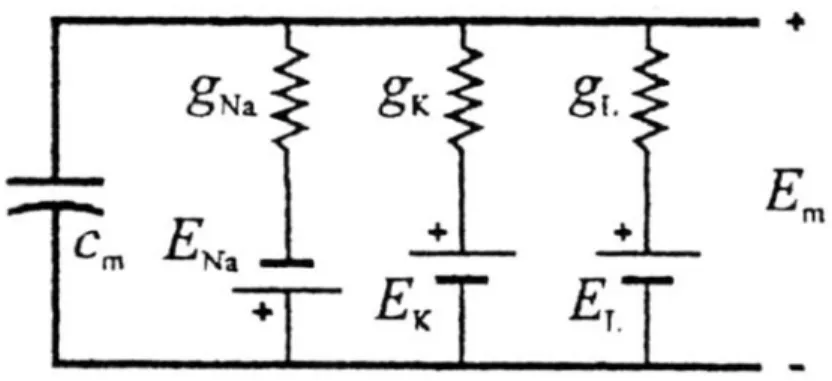
Figura 2.1: schema elettrico della membrana a riposo.

Tale modello è costituito da tre rami contenenti una batteria e una conduttanza: le batterie tengono conto dei potenziali di equilibrio degli ioni sodio (E_Na), potassio (E_K) ed un terzo componente che include globalmente tutti gli altri ioni ed è chiamato leakage (E_L); le conduttanze gNa, gK, gL rappresentano le permeabilità della membrana agli ioni. Inoltre

vi è una capacità c_m che rappresenta l’accumulo di carica sulle facce della membrana. Tutti i parametri elettrici sono espressi per unita di superficie, per renderli indipendenti dalla porzione di membrana considerata. I flussi di corrente ionica possono essere espressi in termini di densità di corrente:

(

)

(

)

(

)

Na Na m Na K K m K L L m L J g E E J g E E J g E E = − ⎧ ⎪ _{= −} ⎨ ⎪ _{= −} ⎩ (2.1.2)

In condizioni di equilibrio, la somma delle correnti nei tre rami deve essere nulla: 0 Na K L J +J +J = (2.1.3) da cui si ricava: Na K L m Na K L m m m g g g E E E E g g g = + + (2.1.4) dove g_m=g_Na +g_K +g_L .

Il potenziale d’azione è la modificazione del potenziale di transmembrana d’equilibrio. Per ogni cellula nervosa si possono riscontrare delle caratteristiche comuni che permettono di generalizzare il modello: l’impulso parte da un valore di riposo di -70 mV fino ad arrivare ad un valore di soglia di -60 mV, superato il quale si scatena il potenziale d’azione propriamente detto, il quale sale rapidamente fino a +40 mV per poi scendere altrettanto velocemente a -90 mV e ritornare al valore di partenza.

Durante il fenomeno della conduzione, la membrana può essere suddivisa in celle elementari da cui scompare il potenziale E in quanto stiamo trattando un circuito _m

dinamico per le variazioni. La genesi dell’impulso dipende dalla variazione delle conduttanze ioniche in funzione del potenziale di transmembrana, quindi esse sono

variabili con la tensione, tranne quella di leakage che è praticamente costante e non influenza in modo apprezzabile il potenziale.

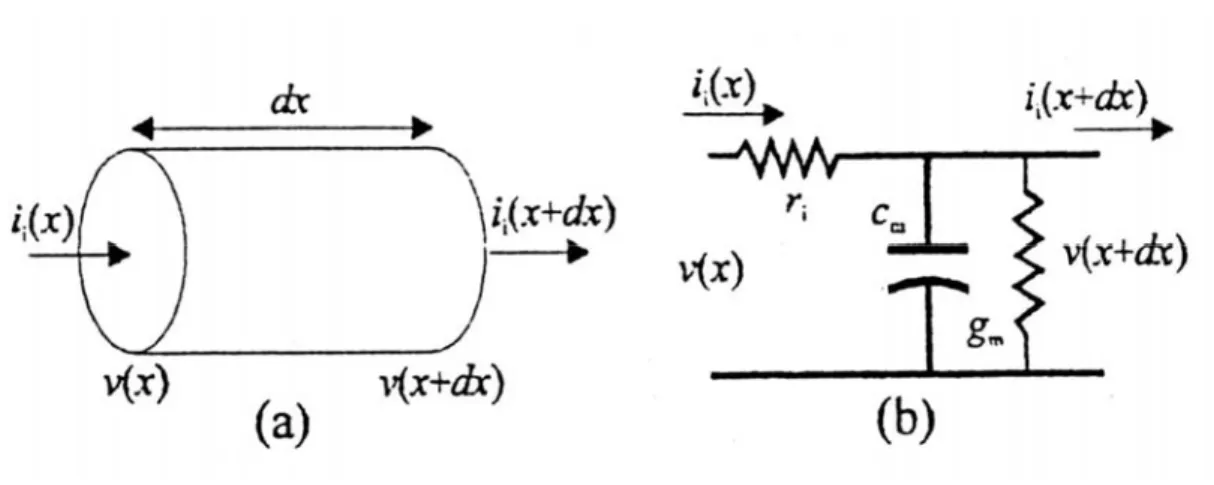
Figura 2.2:(a) tratto elementare di assone durante la conduzione;(b) riduzione alla cella elementare.

Nella propagazione si hanno anche flussi di carica lungo la membrana e ciò è schematizzato considerando una resistenza longitudinale per unità di lunghezza r ( vedi _i

fig. 2.2). La conduzione avviene poiché esiste una differenza di potenziale tra le due estremità della cella elementare e perciò, se consideriamo un tratto lungo dx, le tensioni saranno v x

( )

e v x

(

+dx

)

e le correnti i x_i

( )

e i x_i

(

+dx

)

. Grazie a questa semplificazione si possono scrivere due equazioni, una alla maglia esterna e una al nodo superiore:

( ) (

)

( )

( ) (

)

( )

( )

2 i i i i m m m v x v x dx ri x dx dv x i x i x dx c g v x a dx dt π − + = ⎧ ⎪ ⎛ ⎞ ⎨ − + =_⎜ + _⎟ ⎪ ⎝ ⎠ ⎩ (2.1.5)

dove a è il raggio interno dell’assone e dove 2_m πa dx_m tiene conto del fatto che c e _m g _m

sono grandezze per unità di superficie e r dx che _i r è una resistenza per unità di lunghezza. _i

Dividendo ambo i membri delle equazioni (2.5) per dx e passando al limite per dx→0 si ottiene:

2 i i i m m m v ri x i v c g v a x t π ∂ ⎧− = ⎪ ∂ ⎪ ⎨ ∂ ⎛ ∂ ⎞ ⎪− =_⎜ + _⎟ ⎪ ∂ ⎝ ∂ ⎠ ⎩ (2.1.6)

da cui, derivando la prima equazione rispetto a x e sostituendola nella seconda, si ha:

2 2 1 2 m m m i v v c g v dt πa r x ∂ ₌ ∂ ₋ ∂ (2.1.7)

L’equazione (2.1.7), scritta nella forma consueta delle linee di trasmissione, rappresenta l’onda di potenziale che si propaga lungo l’assone non melinato e se sostituiamo g v con _m

m j si ha: 2 2 1 2 _{m i} m m v v c j a r x t π ∂ ₋ ∂ ₌ ∂ ∂ (2.1.8)

che esplicita la dipendenza delle variazioni temporali e spaziali dal flusso di corrente ionica attraverso la membrana.

I risultati maggiori a proposito del potenziale d’azione si sono ottenuti con la tecnica del

voltage-clamp, che sfrutta un apparato di controllo elettronico in grado di mantenere

costante la differenza di potenziale di transmembrana ( cioè ∂2v ∂ = ) ad un valore 2x 0 impostato dall’esterno. In queste condizioni si può arrivare alla formulazione analitica definitiva di Hodgkin e Huxley, anche se prima bisogna modificare il termine della corrente di transmembrana andando a considerare un opportuno termine forzante che riassuma i contributi delle correnti dendritiche, assoniche e del soma. Alla luce di quanto detto si ha:

m Na K L ext

e se si sostituisce tale espressione nell’equazione di propagazione in regime di voltage-clamp (2.1.8) si ottiene:

(

)

(

)

(

)

ext m Na Na K K L L v j c g v E g v E g v E dt ∂ = + − + − + − (2.1.10)

A questo punto il problema è rappresentato dal calcolo delle conduttanze ioniche del sodio e del potassio che sperimentalmente si è visto dipendere dal potenziale e dal tempo, cioè

( )

,

Na Na

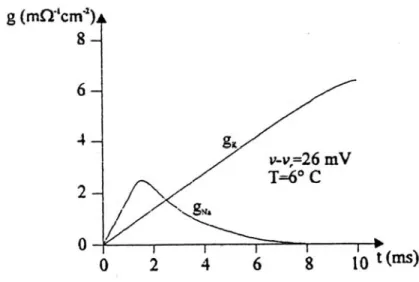
g =g v t e g_k =g_K

( )

v t, .

Figura 2.3: andamento della conduttività del sodio e del potassio nel tempo in regime di voltage-clamp.

In base ai meccanismi di attivazione dei canali del potassio, la conduttanza dei singoli canali può essere considerata costante e identificabile con un valore g_K, per cui si può

ipotizzare che le variazioni nella conduttanza globale siano imputabili al numero n_K

( )

v t,

di canali aperti. Sperimentalmente, l’attivazione dei canali è funzione di v e della

temperatura. Si può interpretare n_K

( )

v t, anche come la probabilità che una canale sia attivo e la sua evoluzione temporale può essere descritta da una statistica del primo ordine come segue:

( )

,

_{( )}

_{( )}

_{( ) ( )}

, 1 , , , K K K n v t f v T n v t w v T n v t t ∂ = ⎡_⎣ − ⎤_⎦− ∂ (2.1.11)

dove f v T

( )

, e w v T

( )

, , rispettivamente le funzioni di attivazione dei canali chiusi e di inattivazione dei canali aperti, sono ricavate sperimentalmente. n4_K

( )

v t, è la funzione che meglio interpola g , quindi si ottiene: _K

( )

4

( )

, ,

K K K

g v t =g n v t (2.1.12)

Con considerazioni leggermente diverse, dovute all’andamento nel tempo non monotono della conduttanza del sodio (vedi fig. 2.3), si arriva a trovare l’espressione di g_Na

( )

v t, :

( )

3

( ) ( )

, , ,

Na Na Na Na

g v t =g m v t h v t (2.1.13)

A questo punto è possibile scrivere la versione finale del modello di Hodgkin e Huxley:

(

)

(

)

(

)

3 4 ext m Na Na Na Na k K K L L dv j c g m h v E g n v E g v E dt = + − + − + − (2.1.14)

L’equazione descrive con buona accuratezza il potenziale d’azione generato, attraverso ingessi rappresentati in forma di correnti ioniche entranti nel soma e nei dendriti dai bottoni sinaptici, da una qualsiasi porzione di membrana eccitabile. Quando il soma e un certo numero di dendriti nel neurone ricevente vengono attivati contemporaneamente, avviene un processo di integrazione che provoca una variazione del potenziale nell’intero neurone. Se la variazione è appropriata, si scatena il potenziale d’azione. L’equazione di Hodgkin e Huxley descrive proprio il processo di generazione, mentre il termine j _ext

rappresenta l’integrazione degli ingressi.

Il modello di Hodgkin e Huxley, fornendo la risposta standard per un solo neurone ad un qualsivoglia ingresso, espresso come corrente ionica, è appropriato per una descrizione che

si voglia soffermare sulla forma d’onda, mentre se si è interessati alla codifica dell’informazione basta cogliere quando e quante volte il potenziale supera la soglia per generare gli spikes. In questa prospettiva il modello precedente, se si considera che la sua implementazione costa 1200 FLOPS per 1 msec, è troppo oneroso da un punto di vista computazionale. Esistono altri modelli che cercano di mantenere un rapporto favorevole tra la capacità di cogliere il maggior numero di aspetti biologici e un’economicità computazionale. Tra questi noi consideriamo brevemente l’integrate-and-fire, che abbandonando la pretesa di incorporare aspetti morfologici, si inserisce nella categoria dei neuroni formali. Il modello dell’integrate-and-fire è descritto dalle equazioni:

(

)

per per m ext th m th dv c g v v I v v dt v v v v ⎧ _{= − + <} ⎪ ⎨ ⎪ = > ⎩ (2.1.15)

dove cè la capacità di membrana, g la sua conduttanza, v il potenziale d’equilibrio e _m v _th

il potenziale di soglia. I neuroni formali descritti dal modello dell’integrate-and-fire sono elementi non lineari che si resettano istantaneamente al valore v ogni volta che superano _m

il valore di soglia v e mimano il comportamento di un solo neurone: lo spike singolo. _th

2.2 Reti neurali

Le reti neurali sono sistemi che, come quelli biologici, imparano dall’esperienza ed ispirandosi ad essi sono analogici e non simbolici. Con le reti neurali cade l’assioma cardine dell’intelligenza artificiale forte “intelligenza = elaborazione simbolica” ed il computer non è più preso come modello di riferimento, ma al più può essere considerato come simulatore numerico di grandezze analogiche. Una rete neurale è costituita da un

insieme di nodi di elaborazione numerica connessi in vario modo tramite le linee in cui si propaga il segnale. Il nodo della rete è costituito da un neurone formale che svolge compiti che discendono dal neurone biologico: somma ed integra gli ingessi afferenti dai nodi collegati pesati dal valore della connessione; somma l’eventuale valore di soglia per determinare l’effettivo valore d’attivazione; determina, attraverso una funzione d’attivazione il valore dell’uscita, che diventa ingesso, nell’epoca successiva, per i nodi in cascata.

Figura 2.4: il neurone formale.

La funzione di trasferimento per i neuroni formali più utilizzata è la funzione sigmoidale o funzione logistica:

( )

1 1 a f a e− = + (2.2.1) dove _{ij i} i

a=

∑

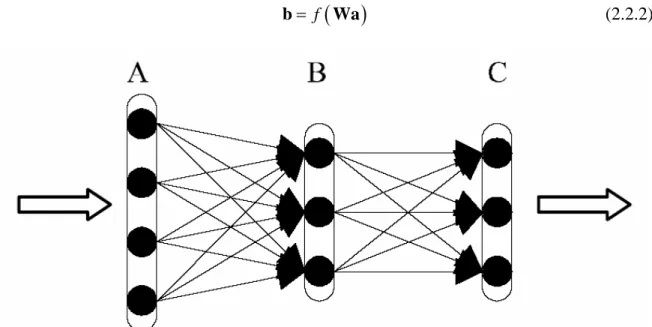
w x −θ è chiamato net input.

La topologia più utilizzata è quella con connessioni unidirezionali in avanti o feed-forward, in cui i neuroni sono organizzati in strati e ogni neurone di uno strato punta tutti o una parte dei neuroni dello strato successivo senza da questo essere ricambiato e senza anelli di richiusura indiretti. Il passaggio da uno strato al successivo può essere visto come una trasformazione non lineare, a causa della funzione di trasferimento f(a) non lineare, del

vettore a delle uscite dei neuroni dello strato A, moltiplicato per la matrice dei pesi W, nel vettore b delle uscite dei nodi dello strato B:

(

)

f

=

b Wa (2.2.2)

Figura 2.5: rete feed-forward multistrato.

L’elaborazione, da un punto di vista geometrico, può essere vista come una trasformazione non lineare dei punti di uno spazio vettoriale di dimensione pari al numero dei nodi dello strato A nei punti di un altro spazio di dimensione pari al numero dei nodi di B. Un aspetto molto importante delle reti feed-forward è l’efficiente metodo di addestramento detto back-

propagation, che consiste in una generalizzazione del metodo di discesa lungo il gradiente.

Scendere lungo il gradiente significa costruirsi una funzione errore E, che ad esempio può essere l’errore quadratico medio, ed applicare una variazione dei pesi tale da opporsi alla derivata dell’errore in funzione di quel peso. Se indichiamo con w t_ij

( )

il peso tra il neurone i-esimo e quello j-esimo, nel primo e nel secondo strato rispettivamente, all’epoca

t, la legge di aggiornamento è data da:

(

1

)

( )

ij ij ij

dove: ij ij E w w ε ∂ ∆ = − ∂ (2.2.4)

con ε <1 chiamato learning rate. Il pregio della back propagation è di permettere il calcolo della derivata dell’errore in un qualunque nodo della rete semplicemente per via ricorsiva. L’addestramento della rete è di tipo supervisionato in quanto vengono forniti gli esempi di comportamento, ossia le associazioni ingresso-uscita corrette, che la rete deve cercare di emulare e generalizzare con un processo di correzioni continue e ripetute. Nell’uso corrente l’equazione (2.2.4) viene modificata aggiungendo un termine che tenga conto dell’ultima modifica in modo da applicare un filtraggio a ∆ e diminuire le discontinuità w_ij

su w t_ij

( )

:

(

1

)

( )

ij ij ij E w t w t w ε ∂ α ∆ + = − + ∆ ∂ (2.2.5)

con α <1 chiamato momentum. Le reti feed-forward forniscono un sistema di simulazione generale, poiché è stato dimostrato che con 3 strati (uno d’ingresso, uno intermedio o

hidden, e uno d’uscita) è possibile realizzare una qualsiasi associazione tra la configurazione d’ingresso e quella d’uscita, superando così l’obiezione di Minsky secondo cui una rete a due strati possa trasformare solo insiemi linearmente separabili.

Riassumendo, possiamo dire che una rete feed-forward può essere allenata a simulare il comportamento di qualunque sistema, mediante addestramento con esempi, e al mappaggio dello spazio d’input con quello d’output. Inoltre, grazie alla natura intrinsecamente parallela e distribuita della rete, porta a fenomeni di generalizzazione e di approssimazione che si prestano a descrivere i sistemi naturali reali. Una difetto delle reti fin qui viste, e che

ci proponiamo di superare con il modello Leabra, è che la tecnica di addestramento della back propagation, seppur efficace e semplice anche nella prospettiva dell’implementazione, è poco plausibile come modello biologico, in quanto nel neurone biologico non è riscontrabile nessun processo che possa essere paragonato al calcolo della derivata per l’ottimizzazione dell’errore nell’apprendimento, ed è applicabile solo nell’addestramento supervisionato.

2.3 Il modello Leabra

Leabra è acronimo di local,error-driven and associative, biologically realistic algorithm e vuole enfatizzare e cogliere il cuore dei principi computazionali che animano la maggior parte dei modelli di reti neurali che sono stati sviluppati fino ad oggi e i loro reciproci legami nel contesto di un’ampia gamma di fenomeni cognitivi. Tale modello spinge le potenzialità dei neuroni formali nella direzione della verosimiglianza rispetto ai sistemi biologici. Il neurone, o il nodo della rete se si vuole mantenere l’analisi ad un livello di astrazione matematica, ha ancora la funzione essenziale di detector: integra l’informazione proveniente da molte sorgenti differenti in un unico numero reale che riflette in che modo esso è in grado di rilevare ciò per cui è specializzato, ed infine invia un’uscita che è il risultato di tale valutazione, diventando l’ingresso di altri neuroni. Nel modello di Hodgkin e Huxley, per descrivere la propagazione dell’attivazione all’interno di un neurone, abbiamo visto avere molta importanza le conduttanze di membrana per gli ioni sodio, potassio e quello che globalmente è definito leakage. Il Leabra mantiene la funzione di detector e, rispetto alle reti tradizionali, introduce le proprietà dei canali ionici, come nei vari modelli matematici, tuttavia in una prospettiva alternativa, che, non implicando la

soluzione di sistemi di equazioni integro-differenziali, mantiene un’elevata velocità computazionale. La caratteristica fondamentale è che nel Leabra le conduttanze non vengono distinte in base alle specie chimiche ma in base all’effetto, così avremo conduttanze eccitatorie (g_e), inibitorie (g_i) e di leakage (g_l). In generale l’ +

Na gioca un ruolo centrale nell’eccitazione del neurone poiché le forze di diffusione tendono a farlo entrare nel neurone provocando così un aumento del potenziale di membrana. La diffusione spinge ad attraversare la membrana verso l’interno del neurone anche gli ioni

-Cl , che in precedenza erano inglobati nel termine di leakage, e, avendo un potenziale di equilibrio proprio pari a quello di riposo dell’intero neurone, hanno un ruolo di inibizione di tipo shunt. La concentrazione diK è funzione sia degli effetti diretti che indiretti della + pompa sodio-potassio, che si manifestano entrambi in un’iniezione consistente all’interno, provocando un innalzamento della concentrazione intracellulare. Come risultato di ciò, la diffusione tende a riequilibrare la concentrazione provocando una perdita continua e costante di K . Questo sarà il contributo di leakage, che precedentemente invece + rappresentava un contributo alla conduttanza a sé stante. In aggiunta a questi meccanismi, il modello dovrebbe tener in considerazione, per una verosimiglianza ancor più fine e per l’importante contributo al comportamento, del fenomeno dell’autoregolazione nella risposta del neurone, riassumibile a sua volta in due effetti: accomodazione ed isteresi. Accomodazione si riferisce tipicamente alla corrente inibitoria che favorisce l’incremento della concentrazione di calcio, che a sua volta aumenta l’inibizione del neurone. Cioè, un neurone che è stato attivato per un certo periodo subirà accomodazione e in futuro sarà sempre meno attivo per la stessa somma di ingressi eccitatori. L’isteresi, di contro, si riferisce alle correnti eccitatorie che sono provocate da un elevato valore del potenziale di

membrana e costringono il neurone a rimanere attivo per un certo lasso di tempo anche dopo che gli ingressi eccitatori si sono esauriti. L’azione combinata di questi due fenomeni in opposizione fa si che i neuroni che sono stati attivati manifestino una tendenza nel breve periodo a rimanere attivi (isteresi), dopo di cui interviene un rilassamento se restano attivi troppo a lungo (accomodazione). Comunque questi due fenomeni non verranno implementati in questa sede. Adesso possiamo passare a riscrivere l’equazione (2.1.12) di aggiornamento del potenziale in funzione delle conduttanze sopra introdotte. In assenza di correnti esterne si ha:

( )

₍

_{( )}

₎

₍

_{( )}

₎

₍

_{( )}

₎

m m e e m i i m l l m V t c g E V t g E V t g E V t t ∂ = − + − + − ∂ (2.3.1)

dove ogni conduttanza è data dal prodotto di una parte variabile nel tempo, che rappresenta la frazione del numero totale di canali aperti ad un certo istante, e di una costante che è la conduttanza massima che si avrebbe se tutti i canali corrispondenti fossero aperti:

( )

c c c

g =g t g (con c=e i l, , ).

Passando dal continuo ad una possibile implementazione numerica dell’espressione di aggiornamento del potenziale si ottiene:

(

1

)

( )

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

m m vm e e e m i i i m l l l m

V t+ =V t +dt ⎡_⎣g t g E −V t +g t g E −V t +g t g E −V t ⎤_⎦

(2.3.2)

in cui per comodità la capacità di membrana è stata inglobata nella parte costante della conduttanza. La costante di tempo dt_vm, compresa tra 0 e 1, rallenta il cambio di potenziale, cogliendo la corrispondente lentezza con cui tale processo avviene anche nel neurone reale, a causa dell’effetto della capacità di membrana. Se poi si va a graficare l’andamento del potenziale in funzione del tempo si vede che, in corrispondenza

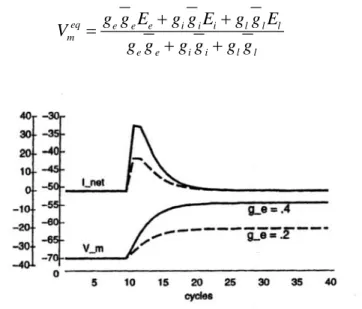
dell’istante in cui si fornisce uno stimolo, che chiamiamo I_net, dato dalla soma delle tre correnti ioniche eccitatorie , inibitorie e di leak, il potenziale inizia a salire fino ad andare al suo valore di regime dato da:

eq e e e i i i l l l m e e i i l l g g E g g E g g E V g g g g g g + + = + + (2.3.3)

Figura 2.6: due andamenti della V_m per valori di g_e =g g t_{e e}

( )

pari a 0.2 e 0.4.

Vediamo ora in che modo il potenziale possa entrare nel meccanismo di attivazione del neurone formale.

2.3.1 Calcolo delle conduttanze d’ingresso

Sappiamo che per una rete neurale artificiale i due parametri fondamentali sono il net input e il valore di attivazione dato da f(a), ed essi forniscono un passaggio diretto tra ingresso e uscita. Nel modello Leabra invece abbiamo introdotto il potenziale V per rispettare il _m

bilanciamento tra ingressi eccitatori ed inibitori, come avviene nella realtà per neuroni eccitatori ed interneuroni inibitori, e solo in seguito c’è un secondo step in cui viene calcolato il valore d’uscita in funzione di V . La conduttanza eccitatoria _m g te

( )

è

essenzialmente una media degli ingressi pesati entranti nel neurone, normalizzata rispetto al numero totale di ingessi:

( )

1 e i ij i ij i g t x w x w n =< >=

∑

(2.3.4)

Esistono però alcuni particolari pratici e biologici che implicano che la media nell’equazione (2.3.4) venga calcolata in un modo più raffinato.

In un tipico neurone corticale, gli ingressi sinaptici eccitatori provengono dai canali situati sui dendriti. Ci possono essere fino a 10000 bottoni sinaptici su un solo neurone e ogni bottone ha più canali per il Na+. Tipicamente, un neurone riceve ingressi da diverse aree del cervello che possono essere riunite in gruppi chiamati proiezioni. Differenti proiezioni spesso sono raggruppate insieme in differenti zone sulla superficie dei dendriti e il calcolo della g t_e

( )

è influenzato dalla struttura delle proiezioni, considerando che ognuna di esse ha un impatto peculiare a seconda dalla regione da cui proviene. Un’altra componente di cui cercheremo di cogliere l’influenza sulla g t_e

( )

è quella rappresentata dall’ingresso di

bias, che riassume le differenze di base nell’eccitabilità tra differenti neuroni. Si pensa che

i neuroni siano differenti l’uno dall’altro nei loro livelli di corrente e che questi potrebbero condurre ad altrettante differenze nel livello di eccitabilità. Alcuni potrebbero aver bisogno di ingressi molto forti per innescare il meccanismo di firing, mentre altri potrebbero averne a sufficienza di più deboli, ed entrambi i tipi potrebbero essere utili in particolari problemi. Perciò si cerca di includere queste differenze di eccitabilità nel modello. Altresì è importante che questi ingressi di bias siano in grado di adattarsi con l’esperienza in modo da adeguarsi a particolari situazioni di impiego. Per mantenere l’implementazione semplice, e per il grado di incertezza ancora elevato sui meccanismi biologici specifici che

fanno sorgere queste differenze nel livello di eccitabilità, indichiamo l’ingresso di bias solo come un termine addizionale, che chiamiamo β, nell’equazione di g t_e

( )

ed è modificato con l’apprendimento. Nel modello è contemplato anche un meccanismo di media nel tempo nel calcolo degli ingressi, per includere la lentezza connaturata alla propagazione e l’aggregazione degli ingressi sinaptici sull’intera membrana dei dendriti. Il processo di media è importante nella somma temporale, cioè quando ingressi che arrivano all’interno di una certa finestra producono un effetto eccitatorio maggiore di quello che produrrebbero gli stessi ingressi se si presentassero scaglionati nel tempo. La media temporale serve dunque a spianare le transizioni brusche e le fluttuazioni che potrebbero far oscillare la rete. Per ogni sinapsi, la frazione di ingressi eccitatori aperti è calcolata come il prodotto dell’attivazione inviata per il peso; gli ingressi provenienti dalla solita proiezione k sono mediati insieme: 1 i ij k i ij i x w x w n < > =

∑

(2.3.5)

dove n è il numero di unità della proiezione. La conduttanza eccitatoria per una data proiezione k è: 1 k e i ij k k g x w α = < > (2.3.6)

dove α_k è un fattore di normalizzazione basato sul livello di attività previsto per quel gruppo di neuroni in modo da stabilire un buon bilanciamento fra tutti gli ingressi per un dato neurone e far si che tutte le proiezioni abbiano la stessa influenza. A questo punto possiamo calcolare g t_e

( )

come una media delle conduttanze eccitatorie risultanti da

ciascuna proiezione in ingresso, sommata al bias input, e integrata nel tempo con una costante tempo dt_net:

( ) (

) (

)

1 1 1 1 e net e net i ij k k p k g t dt g t dt x w n N β α ⎛ ⎞ = − − + ⎜_⎜ < > + ⎟_⎟ ⎝

∑

⎠ (2.3.7)

dove n è il numero di proiezioni ed N è il numero totale di unità e serve per normalizzare p

β, che potrebbe avere un impatto troppo grande rispetto a tutti gli altri ingressi sinaptici. Un ulteriore miglioramento al modello può essere apportato introducendo delle costanti di scaling che vadano a bilanciare l’influenza tra le proiezioni, come avviene nel neurone biologico tra connessioni distali e prossimali, rispettivamente lontane e vicine al corpo cellulare. Queste considerazioni si riflettono in una modifica dell’equazione (2.3.6), e di conseguenza della (2.3.7), come segue:

1 k k e k i ij k p k p r g s x w r α = < >

∑

(2.3.8)

con s è il parametro di scaling assoluto per la k-esima proiezione e _k r è quello relativo. _k

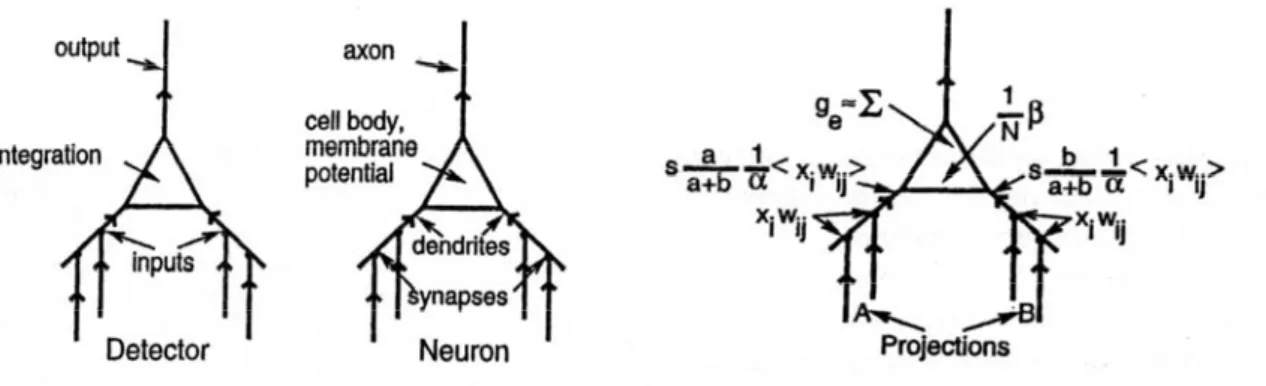
Figura 2.7: passaggio dal neurone biologico al neurone formale classico e al Leabra.

Riassumendo il modo in cui abbiamo calcolato gli ingressi eccitatori, il modello Leabra incorpora la proprietà di integrazione delle sinapsi, il bias input, l’organizzazione degli

ingressi in proiezioni e i loro differenti pesi a seconda che il contatto sia distale o prossimale, la lentezza di propagazione grazie alla media temporale.

2.3.2 Calcolo della funzione d’attivazione

Dopo aver trovato g t_e

( )

per ogni neurone, il passaggio successivo è il calcolo del potenziale di membrana V_m

( )

t secondo l’equazione (2.3.2), avendo prima l’accortezza di effettuare una normalizzazione rispetto ai valori biologici di tutti i parametri che vi compaiono. La normalizzazione è stata fatta sottraendo ad ogni valore il minimo (-90 mV) e dividendo per il range (-90/+55 mV) di variazione del potenziale.

Parametro Valore biologico(mV) Valore normalizzato(0-1) g + (Na ) e E +55 1.00 1.00 (Cl ) i E -70 0.15 1.00 + (K ) l E -70 0.15 0.10 + (K ) a E -90 0.00 0.50 2+ (Ca ) ist E +100 1.00 0.10 Θ -55 0.25 -

Nel modello integrate-and-fire si ha la produzione di uno spike in uscita quando il potenziale di membrana supera un valore di soglia. Ci sono due strade per implementare in modo semplice il firing neurale: o spikes con valori binari ( 1 se V_m>V_th, 0 altrimenti), o un’approssimazione rate-code, in cui l’output è un numero reale continuo che rappresenta una sorta di uscita media di una popolazione di neuroni che sono in uno stato di attivazione simile. La funzione a spikes discreti è quella più reale dal punto di vista biologico, e per ottenerla si può usare un semplice meccanismo di soglia, superata la quale l’uscita va a 1

altrimenti resta a 0. Nel periodo immediatamente successivo alla produzione dello spike, il potenziale di membrana è resettato velocemente ad un valore inferiore di quello di riposo, dovuto agli effetti refrattari che impediscono al neurone di essere immediatamente pronto per un nuovo spike. Inoltre per simulare gli effetti prolungati che un singolo spike può avere su un neurone postsinaptico, l’attivazione può essere mantenuta per un numero di cicli adeguato. Un parametro caratteristico di questo meccanismo, utile anche per rendere più immediato il confronto con la funzione a rate-code, è l’attivazione equivalente, indicata con yeq_j , che in un dato intervallo di tempo è data da:

spikes eq j eq cycles N y N γ = (2.3.9)

dove N_spikes è il numero di spikes che sono stati emessi nell’intervallo, N_cycles è il numero totale di cicli e γeq è un fattore di normalizzazione.

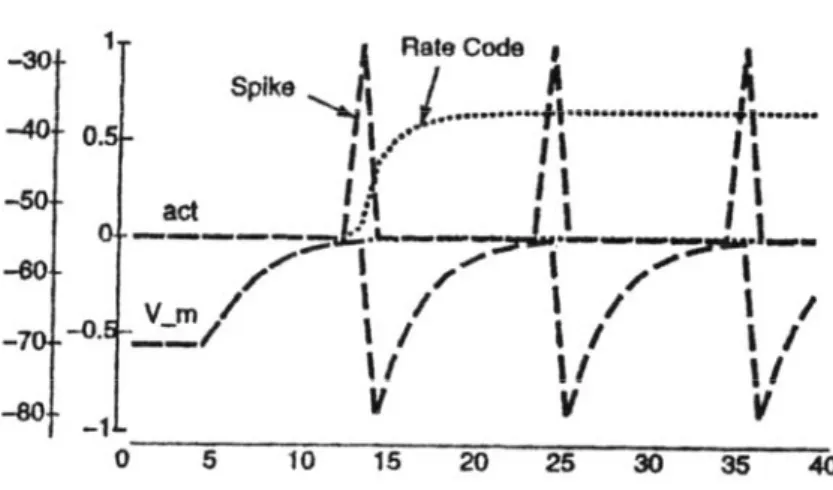
Figura 2.8: Confronto tra le funzioni d’attivazione a spikes discreti e a rate-code.

La funzione d’uscita rate-code fornisce dinamiche d’attivazione più stabili e regolari di quella a firing discreto, in più non è rappresentativa di una sola unità ma può

ragionevolmente simulare il comportamento di una popolazione di neuroni. In questo caso, per il calcolo dell’output, entra direttamente il valore istantaneo del potenziale e, poiché non c’è un vero e proprio firing, questo non viene resettato in modo tale da rappresentare costantemente il bilanciamento tra ingressi eccitatori e inibitori. Nel meccanismo discreto, il parametro che determina il rate di spiking è il tempo impiegato da V_m per ritornare al valore di soglia, una volta che sia andato al minimo valore di iperpolarizzazione dopo il precedente spike. Non andiamo ad esprimere in forma chiusa questo intervallo di tempo, ma cerchiamo di riassumerlo in un’unica funzione che chiamiamo X-over-X-plus-1 (XX1) la cui espressione è data da:

[

]

[

]

1 m j m V y V γ γ ₊+ − Θ = − Θ + (2.3.10)

dove Θ è il valore di soglia normalizzato, γ è un parametro di guadagno e la funzione

[ ]

x ₊ è definita da:

[ ]

se 0 0 se 0 x x x x + > ⎧ = ⎨ _< ⎩ (2.3.11)

L’equazione (2.3.10) da sola non è in grado di fornire un’implementazione corretta dei rates di firing discreti perché non tiene in considerazione la presenza di rumore nel modello. Nonostante il neurone che stiamo esaminando produca spikes cadenzati regolarmente nel tempo in risposta ad un ingresso costante, la temporizzazione è molto sensibile a fluttuazioni anche piccole nel valore del potenziale di membrana. Quindi una volta che un qualche rumore entra nella rete, le fluttuazioni connesse a V_m lo propagheranno a tutti i nodi della rete generando una temporizzazione casuale degli spikes. Ad esempio, queste fluttuazioni potrebbero indurre il neurone ad innescare il potenziale

d’azione anche se il suo potenziale medio di membrana è sotto soglia. L’effetto immediato è equivalente ad una riduzione della discontinuità in corrispondenza del valore di soglia

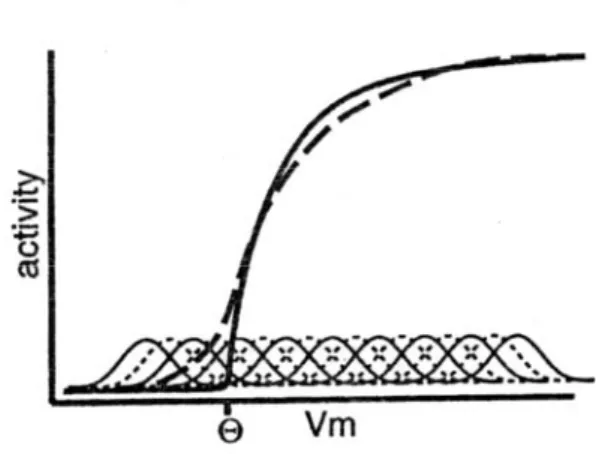
Θ. Se si volesse mantenere inalterata la funzione di trasferimento, la strada più semplice sarebbe quella di sommare a V_m un rumore con la conseguenza di rendere il comportamento dell’intera rete di tipo stocastico. Ma questo rallenterebbe l’elaborazione perché sorgerebbe la necessità di mediare su molti campioni per ottenere valori non affetti da rumore. Un modo più efficiente per simulare la presenza di rumore consiste nel modificare la funzione XX1, in modo che sia essa ad inglobare l’effetto medio delle fluttuazioni rendendo la singole unità deterministiche. Se si ipotizza che il rumore sia gaussiano bianco, la sua conseguenza sulla rete può essere simulata convolvendo la funzione XX1 con una distribuzione gaussiana, per cui si ha:

( )

1 22

(

)

2 z j j y x e σ y z x dz πσ +∞ ₋ ∗ −∞ =

∫

− (2.3.12)

dove x=_⎣⎡V_m

( )

t − Θ⎤_{⎦ . La funzione +} y∗_j

( )

x , che chiamiamo NoisyXX1, ha una soglia molto meno brusca dalla normale XX1, salendo gradualmente invece di partire bruscamente da Θ.

Il fatto di avere una funzione d’attivazione graduale è importante per la rappresentazione, nel neurone reale, di spazi multidimensionali continui, costruiti dal cervello per la codifica dell’ambiente esterno in base a delle features salienti (posizione, angolo, forza, colore, ecc.). Gruppi differenti di neuroni rappresentano valori differenti di queste variabili continue e rispondono con segnali graduali inversamente proporzionali alla distanza tra il valore attuale e quello ottimale. L’andamento della NoisyXX1 implica anche che ci sia una qualche attività associata con potenziali di membrana sotto soglia. Riassumendo, la funzione simula gli effetti medi di una popolazione di neuroni; mantiene la proprietà della saturazione non lineare della sigmoide, che rappresenta la limitazione imposte dal periodo refrattario; risalta piccole differenze nel potenziale di membrana in prossimità della soglia, a discapito di valori sotto o sopra Θ.

2.3.3 Reti di neuroni e inibizione kWTA

Fino ad ora abbiamo visto le proprietà computazionali delle unità base dell’elaborazione, ma per svolgere qualsiasi compito, dal più complicato al più semplice, le unità hanno bisogno di essere organizzate in reti omogenee, come avviene nella corteccia, sia per la funzionalità che per la mappatura delle connessioni. Una prima differenziazione che abbiamo evidenziato nell’implementazione è quella tra neuroni eccitatori e inibitori, che segue la distinzione presente appunto nella corteccia. Noi cercheremo di riassumere gli effetti dell’inibizione corticale in una forma semplificata, che non comporta la modifica della connettività. Nell’equazione (2.3.2) ci sono due termini che possono controbilanciare l’input eccitatorio, di cui il secondo, il leakage, è costante e quindi non può rispondere ai cambiamenti dinamici nell’attivazione dentro la rete. Solo l’inibizione può svolgere il ruolo di contrappeso dinamico, mantenendo, come un termostato, un livello generale di

attivazione e fornendo una quantità variabile, basata proprio su questo livello generale, ai neuroni eccitatori. Questo comportamento, chiamato di tipo set-point, mantiene l’attivazione della rete all’incirca costante variando l’inibizione risultante da tutte le unità, ed è propriamente una reazione negativa. Nella corteccia ci sono due forme di inibizione che coinvolgono gli interneuroni inibitori e la loro topologia di connessioni con quelli eccitatori: inibizione feed-forward e feed-back.

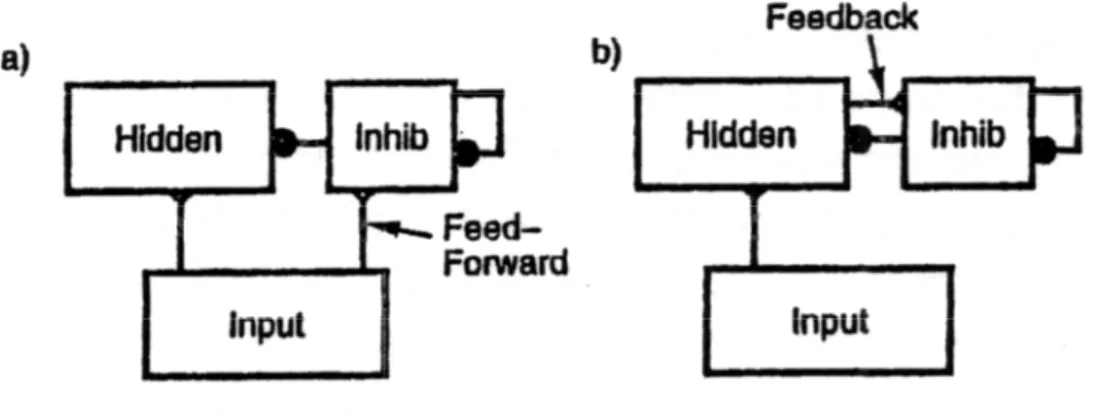
Figura 2.10: i due tipi base di connettività inibitoria.(a) inibizione feed-forward guidata dall’attività dello

strato d’ingresso;(b) inibizione feed-back guidata tramite reazione negativa dallo stesso strato che deve essere inibito.

L’inibizione feed-forward è presente quando gli interneuroni inibitori in uno strato intermedio sono pilotati direttamente dagli ingressi dello strato stesso e quindi portano l’inibizione ai neuroni eccitatori dello strato. Ossia i neuroni eccitatori dello strato intermedio ricevono un livello di inibizione che è funzione dell’attività dello strato da cui ricevono l’ingresso, precedendola e controbilanciandola. Come risultato, lo strato intermedio riceverà un valore di inibizione proporzionale al livello di attività, andando a simulare l’azione di un filtro che renda possibile il meccanismo di firing solo per quelle unità che abbiano dei pesi adeguatamente grandi per determinate configurazioni di I_net.

L’inibizione feed-back avviene quando lo strato che deve essere inibito è lo stesso che eccita gli interneuroni, formando un anello di reazione negativa, che impedisce al livello di attivazione di crescere in modo incontrollato per tutte le unità.

Per rendere veloce la simulazione, includiamo i meccanismi fin’ora visti in una funzione d’inibizione dipendente dall’attività di tutte le unità di un qualsiasi strato, senza però la necessità di dover implementare in modo esplicito la presenza e il ruolo svolto dagli interneuroni. Noi ci soffermiamo su due possibili versioni di una funzione chiamata kWTA (k-Winners-Take-All), il cui tratto essenziale è il comportamento di tipo set-point che garantisce che su uno strato di n unità, se le si ordina per attivazione decrescente, solo le prime k<n sono attive. La conseguenze funzionale più evidente dell’inibizione è la nascita di competizione fra neuroni. I neuroni più fortemente attivati, nel caso di inibizione forward, sono gli unici in grado di superare l’azione inibitoria, mentre nel caso feed-back, essi sono quelli che meglio si oppongono alla retroazione, contribuendo addirittura, con la loro alta componente eccitatoria, all’inibizione delle altre unità. Questo tipo di competizione è positiva per la rete nel suo complesso, visto che fornisce un meccanismo per la selezione delle rappresentazioni più corrette per i patterns d’ingresso attuali. Questo tipo di selezione su base neurale è simile alla selezione naturale, anch’essa basata sulla competizione, ed ha come risultato l’evoluzione. L’inibizione può condurre a rappresentazioni sparse e distribuite, che sono proprie di regioni neurali in cui la percentuale di unità attive è molto piccola, tipicamente intorno al 10-20%. Il cervello usa costantemente rappresentazioni distribuite, così chiamate perchè ogni neurone reagisce ad una varietà di stimoli differenti e più neuroni sono attivi per ogni stimolo. I vantaggi di una rappresentazione distribuita sono notevoli: innanzitutto l’efficienza, visto che basta un

piccolo numero di unità per rappresentare un dato ingresso, come combinazioni diverse di unità attive, le quali forniscono il mezzo naturale per la codifica di rapporti di similitudine tra patterns differenti in base al numero di unità in comune. Oggi si è concordi nel sostenere che l’uso di rappresentazioni sparse e distribuite sia particolarmente appropriato per l’apprendimento in relazione alla struttura generale dell’ambiente naturale. Ad esempio, quando nel cervello avviene l’elaborazione di una scena, un dato oggetto può essere definito e classificato secondo delle proprietà caratteristiche (forma, dimensione, colore, materiale di cui è fatto), con un gran numero di possibili valori lungo ciascuna dimensione. Assumendo che singole unità in una rappresentazione distribuita codifichino questi valori, la rappresentazione di un dato oggetto attiverà solo un piccolo sottoinsieme di neuroni, quello che in un ipotetico iperspazio sui cui assi stanno forma, colore, ecc. individua proprio l’oggetto in considerazione. Sembra che l’ambiente possa essere favorevolmente rappresentato nel nostro cervello in termini di un gran numero di categorie con un gran numero di esemplari per categoria (animali, alberi…). Se si considera il fatto che solo un piccolo numero di tali esemplari può essere processato in un dato momento, la tendenza a favorire rappresentazioni sparse e distribuite appare certamente appropriata. L’inibizione favorisce proprio la propensione a produrre rappresentazioni sparse e distribuite, che abbiamo visto giovare all’apprendimento in un modo che può essere considerato simile a quello che si ha nell’uomo. In questa direzione l’inibizione deve compensare adeguatamente le variazioni dei pesi delle unità che stanno subendo il processo di apprendimento, poiché esse sviluppano livelli molto alti di variazione nella sommatoria degli ingressi eccitatori ricevuti, ossia lo stesso pattern fornisce una forte

eccitazione ad alcuni neuroni e molto bassa ad altri. Questo è tipico della specializzazione dei neuroni per la rappresentazione di alcuni aspetti dell’ambiente e non di altri.

Abbiamo visto che una giusta combinazione di inibizione feed-forward e feed-back fa nascere l’attivazione controllata di neuroni eccitatori. Poiché gli interneuroni inibitori, per il loro comportamento set-point, sono essenzialmente sensibili al livello generale di eccitazione presente in uno strato e forniscono un livello di inibizione ad esso proporzionale, sembra plausibile che gli effetti degli interneuroni siano riassunti direttamente da una corrente inibitoria che porti in sé il resoconto di questo livello di eccitazione. Così facendo sarà possibile evitare di simulare esplicitamente gli interneuroni e le loro connettività, che aumenterebbero considerevolmente la mole di calcoli richiesti. La classe di funzioni inibitorie che implementiamo è la già citata kWTA, che garantisce che non più di k unità siano attive contemporaneamente in uno strato. Da una prospettiva biologica, la funzione kWTA riesce a catturare la proprietà di set-point degli interneuroni inibitori, mantenendo il livello di attività all’incirca costante tramite una reazione negativa; da una prospettiva funzionale, favorisce lo sviluppo di rappresentazioni sparse e distribuite. Nella funzione kWTA è presente un importante compromesso tra la necessità di applicare una limitazione set-point stabile e al contempo flessibile. Da un lato, una restrizione decisa sull’attivazione è necessaria per prevenire una deriva dell’eccitazione nella rete e per rafforzare i meccanismi dell’apprendimento, dall’altro, è ragionevole che uno strato possa beneficiare di un certo margine nel determinare quante unità dovrebbero essere attive per rappresentare un dato ingresso. Una soluzione al trade-off tra stabilità e flessibilità, implementato sia nella versione basic kWTA che in quella average-based kWTA, è di rendere k un limite superiore, permettendo una certa flessibilità nel range tra 0 e k e nei

valori di attivazione classificati per le unità attive. Poter considerare k come un limite superiore è permesso dall’effetto della corrente di leakage, che può essere settata a valori abbastanza alti da lasciar fuori le unità eccitate più debolmente, che avrebbero potuto essere tra le prime k. Interesse principale nel costruire una funzione inibitoria è cogliere, in modo semplice e computazionalmente efficiente, il comportamento di una rete corticale, specialmente nella sua natura di set-point. Fino a quando ciò avviene, non è necessario che i dettagli implementativi siano anch’essi biologicamente plausibili, ed è quello che succede nel nostro caso. Possiamo solo tollerare questa mancanza di plausibilità, sapendo però che la risultato approssima in modo molto buono una rete basata direttamente sugli interneuroni inibitori presenti nella corteccia. Nell’implementazione delle funzioni kWTA, le k unità attive sono quelle che hanno gli ingressi eccitatori (g t_e

( )

) più alti. Quindi il primo passo consiste nel classificare le unità secondo g t_e

( )

, anche se una classificazione completa non è necessaria e quindi il calcolo può essere ottimizzato considerevolmente. Poi viene calcolato un livello di conduttanza inibitoria generale (g t_i

( )

) valido per tutti i neuroni di uno strato in modo tale che i primi k avranno il potenziale di membrana V_m

( )

t sopra il valore di soglia Θ, mentre i restanti rimarranno sotto il valore che innesca lo spike. Per prima cosa, dobbiamo calcolare la somma della corrente inibitoria, che indichiamo con g_iΘ, che porterebbe un’unità al livello di soglia in corrispondenza del suo attuale livello di ingesso eccitatorio. Per fare ciò usiamo l’equazione (2.3.3), calcolata per

eq m V = Θ , e la risolviamo trovando g_iΘ:

(

)

(

)

e e e l l l i i g g E g g E g E ∗ Θ ₌ − Θ + − Θ Θ − (2.3.13)

dove g_e∗ è l’ingresso eccitatorio depurato del contributo di bias (β N ), poiché, sperimentalmente, si è visto che le reti hanno una capacità di apprendimento migliore con tale valore, probabilmente perché ciò permette ai pesi di bias di non tenere di conto delle limitazioni imposte dalla kWTA, introducendo anche un certo grado ci flessibilità.

Nella versione basic, calcoliamo g t_i

( )

semplicemente come un valore intermedio tra i valori di g_iΘ per la k-esima e la (k+1)-esima unità, classificate in base a g t_e

( )

. Questo assicura che la k-esima abbia il potenziale sopra soglia, mentre quello della (k+1)-esima resti ad un livello inferiore. Si ha:

( )

[

1

]

(

[ ]

[

1

]

)

i i i i

g t =gΘ k+ +q gΘ k −gΘ k+ (2.3.14)

dove il parametro q, compreso tra 0 e 1, serve per scegliere dove piazzare esattamente l’inibizione tra la k-esima e la (k+1)-esima unità. Il valore che noi abbiamo scelto nell’implementazione è q=0.25 perché permette alla k-esima unità di essere ragionevolmente sopra il valore di Θ.

Figura 2.11: possibili distribuzioni del livello di eccitazione sulle unità di uno strato.(a) distribuzione

standard in cui le unità più attive sono ragionevolmente sopra soglia.(b) molte unità fortemente attivate sotto soglia danno una piccola differenza tra eccitazione e inibizione per le unità attive.(c) poche unità fortemente attive provocano una differenza consistente con le unità più attivate.

Per avere un esempio pratico di cosa implichi l’algoritmo precedente si può costruire un grafico sulle cui ascisse vengono messi gli indici ordinati delle unità in uno strato e sull’asse delle y i corrispondenti valori di g_iΘ, ottenendo ovviamente una curva monotona decrescente. Il valore di g t_i

( )

calcolato con l’equazione (2.3.14) può essere riportato direttamente in ordinata per mostrare quanto le k unità più eccitate siano sopra questo valore. Quanto più è grande la distanza tra g t_i

( )

e il valore massimo di g_iΘ, tanto più fortemente saranno attive le k unità maggiormente eccitate. L’attività più forte è prodotta quando c’è una netta separazione tra i neuroni che sono più attivi e quelli che lo sono meno.

La versione average-based kWTA fornisce un grado di flessibilità molto ampio a riguardo del livello di attività presente in uno strato e un limite superiore relativamente stabile. Questa volta il trade-off tra precisione e flessibilità è a vantaggio di quest’ultimo. Si calcola prima un valore di g_iΘ medio per le prime k unità e poi per le restanti (n-k) e poi si posiziona g t_i

( )

, rendendo questo parametro funzione di come l’attivazione è distribuita sull’intero strato e non più, come nella versione precedente, delle sole due unità k e k+1. Per i primi k neuroni si ha:

( )

1 1 k i k i j g g j k Θ Θ = < > =

∑

(2.3.15) e per i rimanenti (n-k):

( )

1 1 n i n k i j k g g j n k Θ Θ − = + < > = −

∑

(2.3.16)

( )

(

)

i i n k i k i n k

g t =<gΘ > ₋ + <q gΘ > − <gΘ > ₋ (2.3.17) Nella formula precedente q assume un’importanza notevole, perché tipicamente le

conduttanze inibitorie medie <g_iΘ> e _k <g_iΘ > hanno valori molto diversi e _{n k−} g t_i

( )

non è garantito che sia tra la k-esima e la (k+1)-esima unità.

Figura 2.12: andamento della versione average-based kWTA.

E’ dunque opportuno settare questo parametro in base al livello di attivazione desiderato per lo strato; ad esempio q=0.5 è adatto a livelli di attività del 25%, mentre valori più alti vanno bene per livelli inferiori, q=0.6 corrisponde ad un livello pari a circa al 15%. Poiché l’inibizione dipende dal livello di eccitazione generale di un dato strato, ci possono essere più o meno di k unità attive. Ad esempio, se ci sono alcune unità fortemente attive appena sotto il livello k-esimo, esse tenderanno ad essere sopra soglia per il livello di inibizione calcolato e quindi saranno attive più di k neuroni. Viceversa accade se le unità immediatamente prima della k-esima hanno valori di attivazione abbastanza bassi. Quando l’algoritmo d’apprendimento interviene per formare le rappresentazioni della rete corrispondenti ai patterns d’ingresso,si ha una piccola flessibilità nella scelta dei livelli globali di attività appropriati. La base della flessibilità è che i livelli di attività sono

controllati meno fortemente,e questo può arrecare problemi nei casi di rappresentazioni molto sparse. Per questo si usa la funzione average-based kWTA per strati che abbiano un’attività del 15% o più, mentre per livelli più sparsi si usa la versione basic.

2.3.4 Algoritmo di apprendimento hebbiano

L’apprendimento è il meccanismo forse più importante per una rete neurale perchè fornisce lo strumento principale per il calcolo dei pesi. Al suo sviluppo concorrono sia le proprietà del singolo neurone sia le interazioni presenti in un intero strato, come l’inibizione. I meccanismi che sono alla base dell’apprendimento, come abbiamo introdotto nel primo capitolo, sono il potenziamento a lungo termine (LTP) e la depressione a lungo termine (LTD), che indicano la predisposizione rispettivamente a rafforzare e a indebolire i pesi in modo permanente. La forma in cui ciò si presenta nella corteccia è di tipo associativo o hebbiano, dipende sia dall’attività presinaptica che postsinaptica e può essere visto come il tentativo di costruire un modello il cui obbiettivo sia fornire una rappresentazione interna delle strutture statisticamente rilevanti dell’ambiente esterno. L’apprendimento hebbiano è di tipo self-organizing poiché può essere usato senza alcun esplicito feed-back dall’esterno. La qualifica “a lungo termine” è in contrasto con tutti i fenomeni visti fino ad adesso, che sono transienti e perciò non adatti per l’immagazzinamento permanente di dati in memoria, mentre il potenziamento si riferisce all’incremento nella depolarizzazione provocata dallo stimolo in un neurone. Le forme di LTP e LTD più ricorrenti nella corteccia sono quelle mediate dai recettori di NMDA, ai quali sono connesse dalla caratteristica funzionale associativa, con cui si intende che sia i neuroni presinaptici che quelli postsinaptici hanno un ruolo importante per potenziamento e depressione. Hebb, nel 1949, formula l’idea delle rappresentazioni coattive: se un neurone partecipa in modo considerevole alla formazione

di uno spike da parte di un altro neurone, allora la connessione tra i due si deve rafforzare. Ribadiamo il concetto che l’apprendimento sia un processo tendente a fornire un modello interno della struttura e delle regolarità (leggi naturali, costanti, caratteristiche generali…) del mondo. Basandosi sulla propria esperienza soggettiva, all’uomo può sembrare di avere una conoscenza immediata, senza intermediazione, dell’ambiente a lui circostante, ma in realtà ci sono due problemi fondamentali da affrontare nel modello dell’apprendimento: da un lato la natura intrinsecamente povera dei nostri sensi con cui accediamo al mondo e dall’altro la mole impressionante di dati che arrivano ai nostri sensi. Ossia i nostri sensi hanno a disposizione un gran numero di dati di bassa qualità che devono essere processati ad alto livello per avere un accesso chiaro a ciò che abbiamo esperito. Si può immaginare questo processo come una funzione in grado di proiettare uno spazio ad alta dimensione in uno a bassa, rappresentato dai nostri sensi. Per superare queste difficoltà, il modello può essere basato sull’integrazione di numerose osservazioni, perché, nonostante ciascuna di esse possa essere ambigua e rumorosa, tramite ripetizioni, la rappresentazione corretta emergerà. L’integrazione è l’elemento critico del processo di apprendimento ed è realizzato sommando lentamente dei piccoli incrementi nei pesi, che alla fine riprodurranno le statistiche aggregate di un gran numero di campioni distinti di esperienza. La rete, così, finisce col rappresentare i patterns stabili che derivano da un’ampia interazione col mondo. Da sola, quest’operazione di integrazione su molteplici casi di esperienza non è in grado di sviluppare un soddisfacente modello interno, ma si ha bisogno di un’aspettazione a priori sia del tipo di informazione che i patterns portano in sé che di come organizzarli e strutturarli in modo da ricostruire un senso compiuto, una volta data una descrizione generale della costituzione dell’ambiente esterno. Se l’aspettazione

fornisce un rappresentazione ragionevole delle proprietà del mondo attuale, allora il modello diventa più semplice e attendibile di singoli casi.

Per giungere alla formula finale che utilizziamo nel nostro modello, seguiamo, in qualche modo, gli sviluppi storici della teoria dell’apprendimento, partendo proprio dalla forma più semplice di Hebb, fino ad includere, con varie correzioni, problemi che permetteranno ad una rete self-organizing di rappresentare le strutture statisticamente rilevanti dell’ambiente in cui si trova a lavorare. Focalizziamo la nostra attenzione su un singolo neurone che riceve gli ingessi da un insieme formato da k unità, le quali supponiamo siano state a loro volta attivate da un precedente patterns che ha creato una certa correlazione tra le loro attivazioni. Consideriamo per semplicità che la relazione tra net input e attivazione sia lineare, cioè:

j k kj

k

y =

∑

x w (2.3.18)

in cui è omessa la dipendenza esplicita dall’epoca in considerazione, anche se ad ogni passo viene fornito alla rete un pattern diverso. Secondo la regola empirica di Hebb, all’epoca t, l’aggiornamento dei pesi dipende, in modo associativo, sia dall’unità presinaptica che da quella postsinaptica come segue:

twij εx yi j

∆ = (2.3.19)

dove il lerning rate ε indica quanto velocemente variano i pesi. La precedente equazione può essere inserita direttamente nella (2.2.3) per calcolare w tij

(

+1

)

. Dopo t epoche, un

dato peso, complessivamente, avrà subito una variazione pari alla somma delle variazioni:

ij t ij i j

t t

w w ε x y

Si può immaginare che ε sia pari a 1 N , dove N è il numero totale di patterns d’ingresso presentati a y , in modo che la sommatoria diventi un’operazione di media: _j

ij i j t

w x y

∆ = 〈 〉 (2.3.21)

Sostituendo in questa espressione la (2.3.18), si ottiene:

ij i k kj t i k t kj t ik kj t

k k k

w x x w x x w C w

∆ = 〈

∑

〉 =

∑

〈 〉 〈 〉 =

∑

〈 〉 (2.3.22)

dove C è la correlazione di posto _ik

( )

i k, della matrice di correlazione tra l’ingresso i e quello k ed è definita come:

(

)(

)

2 2 i i k k t ik i k x x C µ µ σ σ 〈 − − 〉 = (2.3.23)

con µ e σ rispettivamente valor medio e varianza della variabile x.

Figura 2.13: rappresentazione schematica di come sono calcolate le correlazioni tramite l’algoritmo di

apprendimento hebbiano nella sua versione più semplice.

Il risultato più importante dell’equazione (2.3.22) è che il cambio di peso relativo all’unità ricevente j e la i è proporzionale alla correlazione tra quest’ultima e tutte le altre unità d’ingresso: più è grande la correlazione tra gli ingressi, più i pesi aumenteranno. La cosa

interessante è che, se facciamo durare la fase di training abbastanza a lungo, i pesi saranno dominati da quei sets di ingressi con correlazione più alta, e la distanza tra il primo incremento più grande e il secondo aumenterà considerevolmente. Con la versione standard di Hebb, è come se la rete concentrasse il suo apprendimento sulla prima componente principale della matrice di correlazione degli ingressi. Ci sono due problemi gravi che sorgono con questa regola: il primo è che i pesi aumentano indefinitamente al passare delle epoche, causando una forte instabilità nella rete, per sopperire a cui si deve effettuare una normalizzazione; il secondo è che possiamo considerare solo un neurone di uscita. Infatti, per come è stato costruito, l’algoritmo di apprendimento non può lavorare con un intero strato d’uscita, perché modificherebbe tutti i pesi nello stesso modo, dipendendo esclusivamente dalla correlazione tra gli ingressi. Fra le tante possibilità sviluppate, noi abbiamo scelto per completare il nostro modello la versione dell’apprendimento hebbiano basato sull’analisi condizionale delle componenti principali (CPCA), in cui le dinamiche di attivazione che si accompagnano all’apprendimento determinano quando i singoli neuroni intervengono in risposta a varie caratteristiche dell’ambiente. La potenzialità del metodo CPCA è di specificare sotto quali condizioni una determinata unità dovrebbe realizzare il calcolo delle PCA tramite una funzione di condizionamento. Facciamo un uso combinato di competizione inibitoria e apprendimento hebbiano per implementare una funzione di condizionamento di tipo self-organizing, grazie a cui sono le unità stesse a elaborare le loro funzioni di condizionamento come risultato emergente dall’interazione complessa tra le esperienze apprese e la competizione con le altre unità dello strato.

Prima di costruire la funzione di condizionamento, dobbiamo sviluppare una regola di apprendimento empirica basata sui principi della CPCA. Iniziamo col supporre che la funzione di condizionamento esista e che tenga presente che le unità sono attive quando l’ingresso contiene elementi che potrebbero essere rappresentati utilmente e invece sono disattivate quando ciò non accade. L’algoritmo basato sulla CPCA per implementare l’apprendimento hebbiano in modo più consono si accompagna all’idea che la struttura rilevante dell’ambiente è presente in modo condizionato solo su alcuni patterns d’ingresso e non incondizionatamente su tutti. Assumiamo di volere che i pesi per un dato neurone d’ingresso rappresentino la probabilità condizionata che l’unità d’ingresso x sia attiva _i

dato che lo è anche quella ricevente y , ossia in formula: j

(

1| 1

) (

|

)

ij i j i j

w =P x = y = =P x y (2.3.24)

In questo modo i pesi riprodurranno quanto un dato neurone d’ingresso è attivo tra i patterns d’ingresso rappresentati dall’unità ricevente: se un pattern d’ingresso è aspetto particolarmente tipico di tali ingressi, allora i pesi di queste connessioni saranno grandi (vicini a 1), mentre se non sono tipici, i corrispondenti pesi saranno piccoli (circa 0). La regola di aggiornamento dei pesi su cui si basa la definizione espressa nell’equazione (2.3.24) è la seguente:

(

)

(

)

ij j i j ij j i ij

w ε y x y w εy x w

∆ = − = − (2.3.25)

I pesi sono modificati in accordo con il valore dell’attivazione dell’unità x , minimizzando i

la differenza tra x e _i w , pesati rispetto all’attivazione di _ij y . La cosa interessante è che _j

partendo dalla (2.3.25) si può riottenere la definizione (2.3.24). Si deve innanzitutto esprimere le variabili in gioco in termini statistici, assumendo che le attivazioni delle unità

pre e postsinaptiche rappresentino la probabilità che le corrispondenti unità siano attive. Con P x t

(

_i|

)

e P y

(

_j|t indichiamo rispettivamente la probabilità che l’unità mittente e

)

quella ricevente siano attive una volta presentato il pattern d’ingresso all’epoca t, con P t

( )

invece la probabilità che si presenti il pattern t. La (2.3.25) diventa:

(

)

(

)

(

)

( )

(

)

(

) ( )

(

)

( )

| | | | | | ij j i j ij t j i j ij t t w P y t P x t P y t w P t P y t P x t P t P y t P t w ε ε ⎡ ⎤ ∆ = _⎣ − _⎦ = ⎡ ⎤ = _⎢ − _⎥ ⎣ ⎦

∑

∑

∑

(2.3.26)

Dopo un certo numero di epoche dall’inizio dell’apprendimento, il peso tende ad un valore di equilibrio asintotico e quindi la variazione ∆ tende a 0, per cui: w_ij

(

|

)

(

|

) ( )

(

|

)

( )

0 ij j i j ij t t w ε⎡ P y t P x t P t P y t P t w ⎤ ∆ = _⎢ − _⎥= ⎣

∑

∑

⎦ da cui si ricava:

(

)

(

) ( )

(

)

( )

| | | j i t ij j t P y t P x t P t w P y t P t =

∑

∑

(2.3.27)

Il numeratore rappresenta la definizione di probabilità congiunta dell’unità mittente e ricevente quando entrambe sono attivate dai patterns, mentre il denominatore è la probabilità che l’unità ricevente sia attiva su tutti i patterns. Quindi possiamo riscrivere la (2.3.27) come:

(

)

( )

i, j

(

|

)

ij i j j P x y w P x y P y = = (2.3.28)

che è proprio la funzione di condizionamento da cui eravamo partiti.

Partendo dall’enunciazione di Hebb, siamo arrivati ad un algoritmo di apprendimento abbastanza simile, ma che non è il semplice prodotto dell’attivazione dei neuroni

persinaptici a postsinaptici. Vediamo come può essere interpretato in termini di meccanismi neurali quali LTP e LTD mediati da NMDA, che sappiamo essere le fondamenta dell’apprendimento. Ricordiamo l’equazione (2.3.25):

(

)

ij j i ij

w εy x w

∆ = −

Quando sia l’unità mittente che quella ricevente sono fortemente attive, con x_i >w_ij, il peso aumenta e siamo in presenza di LTP associativo mediato da NMDA.

Se l’unità ricevente è attiva ma quella mittente non lo è, e cioè x_i <w_ij, allora si ha LTD, fenomeno che si verifica con l’apertura dei canali NMDA, in risposta all’ingresso di Mg+ nella membrana postsinaptica, e con una piccolo aumento dell’attività presinaptica dovuta ad un flusso di Ca2+. L’attività postsinaptica attiva altri canali del calcio sensibili al potenziale che potrebbero fornire una debole concentrazione di Ca2+ necessario ad indurre LTD senza la necessità di ulteriore attività presinaptica.

Quando l’unità ricevente non è attiva, y_j = , la probabilità, o in modulo duale l’ampiezza, 0 del cambio di peso è nulla. Questo può essere spiegato dal bloccaggio dei canali NMDA da parte dell’ Mg+ e dalla mancanza di attivazione dei canali del calcio.

L’effetto dell’apprendimento hebbiano con CPCA può essere cosi riassunto: quando il peso è grande, all’incirca 1, ulteriori incrementi si presenteranno poco frequentemente e comunque tenderanno a 0, mentre diminuzioni si avranno con pattern d’ingresso opposti. Al contrario, se i pesi sono piccoli, gli incrementi saranno notevoli e frequenti, e le diminuzioni sporadiche e piccole. Questo è proprio ciò che è stato notato sperimentalmente accadere negli studi su LTP e LTD, ossia una saturazione vreso l’alto e verso il basso rispettivamente.