5. Modelli matematici per la previsione della transizione

5. Modelli matematici per la previsione della

transizione

In questo capitolo sono stati presi in esame i principali metodi sviluppati fino ad oggi per la valutazione della posizione della transizione dello strato limite.

Con particolare interesse sono stati approfonditi i metodi di amplificazione

( )

en .

Il capitolo si conclude illustrando brevemente i più moderni approcci allo studio della transizione e analizzando le potenzialità di un software esistente.

5.1 Correlazioni

Empiriche

I primi metodi sviluppati per la previsione della transizione dello strato limite sono state delle semplici correlazioni tra le dimensioni caratteristiche dello strato limite nel punto di transizione. Questi metodi si basano essenzialmente sul confronto tra i dati sperimentali ed i calcoli effettuati considerando lo strato limite completamente laminare.

La prima correlazione pubblicata fu quella di Michael (1951) [1].

0.4

, ,

Re_θtr =2.9 Re⋅ _{X tr}

Re_θ è il numero di Reynolds riferito allo spessore della quantità di moto mentre R è il numero di Reynolds riferito all’ascissa curvilinea sulla linea di corrente.

e_X , Re 2 Re 2 e e X tr u u X θ θ ⋅ = ⋅ =

Secondo questo modello la transizione avviene quando la relazione è soddisfatta.

Altre correlazioni sono state proposte si riporta a titolo di esempio quella di Cebeci e Smith (1974) [2].

0.46 , , , 22400 Re 1.174 1 Re Re tr X tr X tr θ ⎛ ⎞ = _⎜⎜ + _⎟⎟⋅ ⎝ ⎠

Le correlazioni empiriche, in quanto tali, hanno però la validità limitata al caso particolare studiato. Le due precedenti ad esempio si basano sul flusso bidimensionale su una lastra piana.

Per il caso particolare in esame quindi queste correlazioni non possono essere utilizzate perché risultato di analisi di laboratorio su casi estremamente diversi da quello che deve essere studiato.

5.2 Linear Stability Theory

Il primo strumento teorico che è venuto effettivamente in aiuto per la previsione della transizione è la teoria della stabilità lineare (LST).

Attraverso la LST si studia la stabilità di flussi paralleli rispetto a piccole perturbazioni.

Lo strato limite può essere localmente approssimato ad un profilo di velocità parallelo, e localmente quindi, può essere sottoposto ad analisi di stabilità attraverso la LST.

Le linear stability equation (LSE) si ottengono delle equazioni del moto di un fluido incomprimibile, ipotizzando il campo come somma di una componente media e di una componente di perturbazione, sottraedo il campo medio, adimensionalizzando, facendo l’ipotesi di flusso parallelo e linearizzando rispetto alle perturbazioni.

Nel caso bidimensionale le equazioni che si ottengono sono le seguenti.

2 2 2 2 2 2 2 2 ' ' 0 ' ' ' 1 ' ' ' ' ' 1 ' ' u v x y u u u p u u u v t x y x R x y v v p v v u t x y R x y ∂ ₊∂ ₌ ∂ ∂ ⎛ ⎞ ∂ ₊ ∂ ₊ ∂ _{= −}∂ ₊ ∂ ₊∂ ⎜ ⎟ ∂ ∂ ∂ ∂ _⎝ ∂ ∂ _⎠ ⎛ ⎞ ∂ ∂ ∂ ∂ ∂ + = − + _⎜ + _⎟ ∂ ∂ ∂ _⎝ ∂ ∂ _⎠ '

Dove R è il numero di Reynolds.

In generale si può dire che se un flusso è stabile rispetto ad una perturbazione, significa che la dinamica della perturbazione tende ad estinguersi all’interno del flusso stesso; al contrario, se il flusso tende ad amplificare la perturbazione questo si dice instabile.

Fissato il flusso medio ed il numero di Reynolds al fine di studiare la dinamica delle perturbazioni, a queste deve essere data una formulazione analitica.

Tollmien e Schlichting hanno dimostrato che la forma più generale che possono avere questi disturbi è quella di un’onda la cui ampiezza varia con y e che si muove rispetto alla parete con un angolo γ rispetto all’asse x.

Nella LST infatti, le perturbazioni vengono modellate con un’onda sinusoidale che si muove nel campo. ( ) ( ) '( , , ) ( ) '( , , , ) ( ) i x t i x z t q x y t q y e q x y z t q y e α ω α β ω − + − = = 2 3 D D

Dove α e β sono i numeri d’onda rispetto alla relativa coordinata adimensionalizzati, e ω è la pulsazione adimensionalizzata. * 0 2 2 x z L L L u π α λ π β λ ω ω = = =

Nel caso 2D l’angolo γ è ovviamente nullo mentre nel caso 3D sussistono le seguenti relazioni.

0 0 cos sin arctg α α γ β α γ α γ β = = ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠

Dove α₀ è il numero d’onda lungo la direzione identificata da γ .

Essendo il campo delle perturbazioni solenoidale, posso definire un potenziale le cui componenti del rotore rappresentano le componenti di velocità del campo di perturbazione (questa operazione è permessa grazie al fatto che la divergenza di un rotore è sempre nulla). In generale il potenziale assume la seguente forma.

( ) ( ) ( , , ) ( ) ( , , , ) ( ) i x t i x z t x y t y e x y z t y e α ω α β ω φ φ − + − Ψ = Ψ = 2 3 D D

Facendo le opportune sostituzioni le LSE possono essere ridotte alle note equazioni di Orr-Sommerfeld.

(

)

4 2 2 2 2 4 2 2 2 d d d d iR u iR dy dy dy dy φ φ φ 2 2 u α αφ α ω ⎛ α φ⎞ α φ − + = − _⎜ − _⎟− ⎝ ⎠ 2D

(

)

(

)

4 2 2 2 2 2 1 2 1 3 4 2 2 2 2 2 1 2 2 2 1 3 0 '' '' d d d dy dy dy iR u w iR u w φ _ε φ _ε φ _{ε φ ε} ε α β ε ε α β ω ε α β ⎛ ⎞ − − _⎜ − _⎟+ ⎝ ⎠ = + = + + − = + = 3D

In entrambi i casi sono ODE del quarto ordine per l’ampiezza del potenziale φ( )y ; per risolverle,quindi sono necessarie quattro condizioni al contorno.

Nel caso dello strato limite è necessario imporre che le perturbazioni si annullino sia sulla superficie (y=0) che all’infinito (y= ∞), questo si traduce nelle seguenti condizioni.

0 0 d dy φ φ = = y=0 1 2 2 1 2 2 0 0 d d dy dy d d dy dy ε ε φ ε ε φ ⎛ ⎞⎛ ⎞ + + = ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ ⎛ ⎞⎛ ⎞ − + ⎜ ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠ = y=δ

Le condizioni per il caso 2D si ottengono come caso particolare (w,β =0) del caso 3D.

La condizione al contorno per y=δ deriva dal fatto che se si va a scrivere l’equazione di Orr-Sommerfeld per y=δ si ottiene la seguente espressione.

4 2 2 2 2 2 1 2 1 4 2 2 0 d d d dy dy dy φ _ε φ _ε ⎛ φ _{ε φ}⎞ − − _⎜ − _⎟ ⎝ ⎠= 2

Questa equazione ammette la seguente soluzione generale.

1 1 2

1 2 3 4

( )y A e ε A eε A e ε A e

φ ₌ − _{+ +} − ₊ ε

Quindi è necessario imporre che le parti reali diε₁ e di ε₂ siano strettamente positive e che le costanti ed siano nulle. Tali condizioni si traducono nelle espressioni analitiche sopra riportate.

2

A A₄

La condizione appena illustrata, fa sì che la soluzione all’equazione di Orr-Sommerfeld con le condizioni al contorno imposte, esista solo per opportune combinazioni del numero di Reynolds e dei parametri dei disturbi.

Questo, è dunque un problema agli autovalori; dove, R,α,β ,ω sono gli autovalori e le corrispondenti φ( )y sono le autofunzioni.

In generale questo significa che affinché esista una soluzione R,α,β e ω devono soddisfare una o più condizioni del tipo seguente.

( , , , ) 0

F R α β ω = 3D

( , , ) 0

F R α ω = 2D

5.2.1 Analisi Spaziale ed analisi temporale

Attraverso l’equazione di Orr-Sommerfeld è possibile studiare la stabilità di un flusso da due punti di vista differenti. Infatti è possibile effettuare o un’analisi spaziale o un’analisi temporale.

Nell’analisi temporale si impone α₀ reale mentre ω complesso. Questo fa sì che l’ampiezza della perturbazione vari nel tempo come _eωi_.

( ) ( ) ( ) '( , , ) ( ) r i ( ) r i r i i x y i t i x y t t i q x y t q y e α β ω ω q y e α β ω eω ω ω ω + − + + − = + = =

Nell’analisi temporale, quindi, affinché la perturbazione associata a

(

α β ω, , _r

)

non sia amplificata ma venga smorzata è necessario che la ω_i, identificata dalla F R( , , , )α β ω =0 sia negativa.

Nell’analisi spaziale, invece, si pone la pulsazione reale ed è possibile studiare la stabilità del profilo per perturbazioni che si muovono lungo una direzione considerando immaginario il numero d’onda relativo a tale direzione.

$d $k

γ

i$ $ cos sin $ d = γ⋅ +i$ γ ⋅k ( 0 0)( ) 0 ( ) 0( 0 0 0

( cos( ) sin( ) ) ( cos( ) sin( ) ) cos( ) sin( )

'( , , ) ( ) r i ( ) r i r i i i x z t i x z t x z i q x y t q y e α α γ γ ω q y e α γ γ ω e α γ γ ) α α α + + − + − − + = + = =

Nell’analisi spaziale, quindi, affinché la perturbazione associata a

(

α β ω non sia amplificata è , ,

)

necessario che la α_0i, identificata dalla ( , , , )F Rα β ω = sia positiva. 0

Per quanto concerne il problema riguardante lo strato limite, l’aspetto che più interessa è quello riguardante l’analisi spaziale che, come si vedrà nei prossimi paragrafi sarà necessaria per studiare l’amplificazione e quindi la crescita delle perturbazioni durante il processo di transizione.

5.3.2 Un esempio di analisi di stabilità 2D

A titolo di esempio si riportano i risultati ottenuti dall’analisi di stabilità spaziale per il flusso di Blasius [3].

I risultati relativi all’analisi di stabilità spaziale 2D vengono presentati sui piani

(

α_r,R

)

e

(

ω, R

)

.

Il numero di Reynolds riportato nei grafici è definito come segue. e X u X R R ν = =

La curva per α_i = è detta di stabilità neutra e separa la zona di smorzamento dalla zona di 0 amplificazione dei disturbi. Ovviamente la curva di instabilità neutra è la stessa sia per l’analisi temporale che per l’analisi spaziale dato che è il luogo dei punti nello spazio delle soluzioni di

( , , ) 0

F R α ω = per cui sia la parte immaginaria di α sia la parte immaginaria di ω sono nulle.

Il punto su questa curva in cui il numero di Reynolds assume valore minimo ha un importanza particolare, infatti al di sotto di questo Re, le piccole perturbazioni di qualsiasi frequenza vengono smorzate, mentre per Re maggiori esistono alcune frequenze che vengono amplificate. Tale numero di Reynolds è detto numero di Reyolds critico (Re_cr).

Il identifica l’inizio della transizione con l’inizio dell’amplificazione delle Tollmien-Schlichting waves.

Recr

5.2.3 Stabilità 3D

Per quanto riguarda profili di velocità tridimensionali, è possibile, attraverso l’equazione di Orr-Sommerfeld, studiare la stabilità rispetto alle T-S waves al variare del numero d’onda e della direzione del disturbo.

0

( , , , ) 0 ( , , , ) 0

F R α β ω = _←⎯⎯⎯_⎯→F R α γ ω =

Il teorema di Squire inoltre ci assicura che il minore è dato da disturbi 2D che si muovono nella stessa direzione che vogliamo analizzare.

Re_cr

5.3 Correlazioni Empiriche che utilizzano la LST

Utilizzando l’analisi della stabilità dei flussi paralleli, sono state proposte nuove correlazioni empiriche che utilizzano la valutazione del Re_cr come parametro per fissare la transizione.

A titolo di esempio riportiamo il metodo proposto da Granville [4].

Questo metodo si basa su una curva che lega il ed il al parametro di Pohlhausen medio _ Reθ cr Reθ_tr θ λ . 2 1 cr X e cr X du dx X X dx θ θ λ ν = −

∫

θ

λ , per la soluzione dello strato limite laminare può essere calcolato utilizzando la seguente relazione.

(

)

(

)

2 2 _ _ 2 2 _ _ / 4 1 45 5 / e e cr cr X e e cr X cr R u u R R u u R θ θ θ λ = − ⎢⎡ − ⎤⎥ − ⎢ ⎥ ⎣ ⎦

Nella quale il pedice –cr sta ad indicare la condizione critica alle T-S waves, calcolabile attraverso la LST.

La curva di Granville è invece la seguente.

6.1 55

_ _

Re _tr Re _cr 375 e λθ

θ − θ = + +

Che è stata successivamente estesa da Arnal [5] per tener conto degli effetti della turbolenza.

(

)

25.7

_ _

Re _tr Re _cr 206e λθ ln 16.8Tu 2.77

θ − θ = − ⎡⎣ − λθ⎤⎦

Granville ha inoltre proposto una relazione per valutare direttamente dall’analisi della soluzione dello strato limite senza effettuare l’analisi di stabilità.

_

(

)

_ ₆ 54.2124 31.6 2.591 2.48 Re 520 2.5 10 1 1 2.591 2.591 cr H H H H H H H H θ ⎧ _{+ >} ⎪ ₋ ⎪ = ⎨ ⋅ ⎛ ⎞ ⎪ _{+ − >} ⎜ ⎟ ⎪ _{⎝ ⎠} ⎩

Il metodo di Granville è valido però solo per flussi bidimensionali o assialsimmetrici.

Tra le correlazioni empiriche di questa seconda famiglia che sono state prese in esame, non ne è stata però trovata una utilizzabile nel problema in esame; tutte hanno al più i limiti di validità del metodo di Granville.

5.4 Metodi

di

amplificazione

I metodi di amplificazione, altrimenti detti metodi , si basano sulla LST e se ne servono per studiare la fase di accrescimento dei disturbi durante il processo di transizione.

n

e

L’idea che ne sta alla base è la segente: superata la curva di instabilitè neutra, un disturbo di pulsazione ω che si muove lungo la direzione γ viene localmente amplificato proporzionalmente

0 i

e−α .

Se si vuole studiare l’amplificazione di un disturbo che si muove su una linea, è necessario integrare

0i

α lungo la linea. Tale integrale è detto fattore di amplificazione e viene generalmente indicato con . n 0 ( ; ) _i( ; ) L nω rs = −

∫

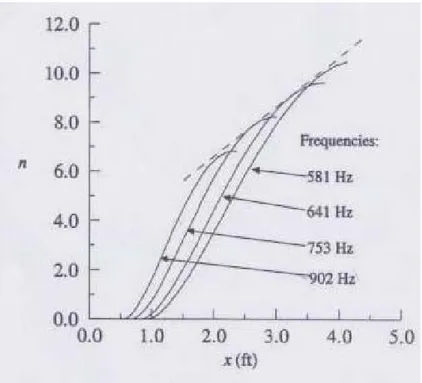
α ω s dr s

A titolo di esempio si riporta l’andamento del fattore di amplificazione ottenuto in [3] per un flusso alla Blasius.

Fig. 5.2 Fattore di amplificazione per il flusso di Blasius

I metodi di amplificazione assumono che la transizione avvenga quando il massimo dei fattori di amplificazione al variare delle pulsazioni raggiunge un valore critico.

max ( ; )n s n_cr

ω ω =

r

Il valore critico è ragionevolmente tra 8 e 9 ma dipende fortemente dalla turbolenza della corrente asintotica.

Per tener conto dell’effetto della turbolenza è stata proposta in [6](Mack 1977) un’espressione generalizzata dell’n_cr per Tu maggiore di 0.1%.

8.43 2.4 ln( )

n= − − Tu

E’ chiaramente visibile come vari fortemente l’ con il livello di turbolenza quindi per flussi dove non è noto a priori il Tu non è possibile conoscere a priori l’ .

cr

n

cr

n

Ulteriori pubblicazioni hanno messo in luce il fatto che l’ può variare fortemente dal problema in esame. In acqua ad esempio può scendere anche sotto 3.

cr

Fig. 5.3 Variazione del n critico con il livello di turbolenza

I metodi sono stati ampliamente utilizzati per studiare la stabilità dello strato limite per casi bidimensionali o assialsimmetrici [3] [7] [8].

n

e

Nel caso di flussi tridimensionali, gli esempi trovati sono molto meno numerosi, probabilmente per la maggiore complessità della procedura e per la non chiara definizione della curva su cui è necessario integrare il rateo di amplificazione.

Sono stati infatti utilizzati in casi in cui il flusso ha una direzione caratteristica come, nello studio della transizione su ali a freccia [9] nel qual caso è possibile effettuare ipotesi semplificative per la procedura e per il calcolo di n.

In casi puramente tridimensionali come un fusiforme ad incidenza, è stata proposta da Cebeci [10] una procedura per il calcolo del fattore di amplificazione che ha dato buoni risultati rispetto ai dati sperimentali.

Cebeci ha proposto di integrare il rateo di amplificazione relativamente ad una frequenza a partire dai punti in cui si verifica l’instabilità neutra, lungo la direzione di massima amplificazione.

In un generico punto in cui si ha instabilità neutra relativamente ad una frequenza lungo una direzione, mentre in tutte le altre direzioni il profilo è stabile (per quella frequenza), parte una curva lungo la quale deve essere integrato il rateo di amplificazione (α_0i).

Tale curva corrisponde ad una frequenza del disturbo e viene definita localmente dalla direzione di massima amplificazione per quella frequenza.

Per chiarire meglio questo concetto facciamo riferimento alla prossima figura.

Fig. 5.4 Procedura utilizzata da Cebeci per l’integrazione del fattore di amplificazione in casi 3D

La curva 1 rappresenta la curva sulla superficie che unisce tutti i punti critici identificati dalla LST. A sinistra di questa linea tutti i disturbi vengono smorzati, a destra invece alcuni, non necessariamente tutti, vengono amplificati.

Il profilo di velocità nel punto A è stabile per disturbi di pulsazione ω in tutte le direzioni eccetto che per la direzione $d rispetto alla quale è in condizioni di instabilità neutra.

Da questo punto quindi parte una linea Γ lungo la quale deve essere integrato il rateo di amplificazione, e tale curva è definita punto per punto dalla direzione di massima amplificazione di un disturbo di pulsazione ω .

La linea di transizione è il luogo dei punti nei quali per prima si raggiunge l’n_cr.

Utilizzano questo metodo, nel caso di un fusiforme ad incidenza Cebeci [10] ha ottenuto risultati ben correlati con le misure sperimentali.

( )

; n sr ω

A

$d

Γ

3) Linea di transizione ( ) 1) Curva di minima instabilità neutra ( Re_cr) cr n=n 2) Curva di instabilità neutra per (ω)

Fig. 5.5 Risultati ottenuti da Cebeci sulla valutazione della transizione nel caso di un fusiforme ad incidenza

I metodi risultano quindi essere un possibile strumento per la valutazione del punto di transizione nel problema in esame.

n

e

L’incertezza dell’ e delle perturbazioni del campo esterno in una condizione operativa richiedono però il supporto di una campagna di prove sperimentali a validazione dei risultati numerici.

cr

n

5.5 PSE e DNS

I più moderni approcci allo studio della trasizione si basano sulla soluzione delle Parabolized Stability Equations (PSE) o delle Direct Navier Stokes Equations (DNS).

Queste equazioni non si limitano all’analisi di flussi paralleli e permettono di tener conto degli effetti non lineari tipici dell’instabilità secondaria.

Questi metodi richiedono elevate potenze di calcolo; i PSE da questo punto di vista sono notevolmente migliori ed è proprio per questo che la maggior parte delle ricerche vanno in questa direzione.

Questi metodi però allo stato dell’arte non sono utilizzabili per casi generali, quale è quello in esame [11] [12] [13].

Intense ricerche sono in corso per rendere facilmente utilizzabili questi metodi che sono stati sviluppati da poco più di un decennio.

Consideriamo quindi, queste tecniche ad oggi non utilizzabili per il problema da affrontare, dati anche i limiti temporali che ci siamo fissati per il termine di questa ricerca.

Lascio quindi ai posteri un’analisi più dettagliata delle capacità future rispetto alle PSE ed alle DNS.

5.6 Un Software, LASTRAC

Langley Stability and Transition Analysis Codes (LASTRAC) è un software sviluppato in linguaggio C++ per l’analisi della transizione del flusso da laminare a turbolento.

Lastrac è un prodotto della NASA Langley research projects finalizzato alla simulazione ed alla modellazione fisica della transizione.

Allo stato attuale Lastrac è capace di effettuare calcoli sulla transizione basandosi sulla LST e sulle PSE sia lineari che non lineari. Può analizzare regimi di flusso completamente diversi, subsonici, supersonici ed ipersionici.

Oggi però si limita allo studio di strati limiti bidimensionali, assialsimmetrici, o di ali a freccia infinite.

Strumenti per calcoli 3D del tutto generali sono però in sviluppo.

Ad oggi quindi ammesso di poter utilizzare questo software, non sarebbe in grado di simulare correttamente il caso in esame.

5.7 Conclusioni

Dopo la ricerca effettuata sullo stato dell’arte dei modelli matematici per la previsione della transizione dello strato limite, concludiamo che l’unica tecnica utilizzabile nel caso in esame risulta essere quella descritta in [10].

Essendo però, i metodi , metodi semiempirici, è necessario affiancare agli esperimenti numerici, un’adeguata campagna di prove sperimentali.

n

Sarebbe inoltre necessario, prima di avviare lo sviluppo di un codice ad hoc per la valutazione della resistenza del bulbo, verificare l’influenza dei moti di beccheggio e di rollio della barca sulla posizione della transizione rispetto al caso stazionario che sarebbe implementato su calcolatore. Qualora infatti una prova full-scale mettesse in luce il fatto che lo strato limite risulta completamente turbolento, non sarebbe necessario lo sviluppo di un software ad hoc, ma risulterebbero utilizzabili i codici rans commerciali.

Nei prossimi capitoli, per questo, ci occuperemo dell’organizzazione della campagna di prove sperimentali da effettuare direttamente sulla barca, i risultati della quale, determineranno gli sviluppi futuri di questa ricerca.

Bibliografia

[1] Michel, R. “Etude de la transition sur les profiles d’aile, etablissement d’un critère de dètermination du point de la transition et calcul de la trainèe de profil incompressible”

[2] Cebeci, T. End Smith, A.M.O., “Analysis of turbulent boundary layer” Academic press, N.Y., 1974 [3] Cebeci, Cousterix “Modeling and Computation of boundary layer flows” ed. Springer 1998

[4] Granville, P.S., “The calcoulation of viscous drag of bodies of revolution” David W. Taylor Model Basin Rept. 849, 1953

[5] Arnal et alt. “Laminar instability theory and transition criteria in two and three dimensional flows” La Rech. Aérosp. N°1984-2, 1984

[6] Mack, L. M., “Transition and laminar instability. Jet propulsion laboratory Pub.” pp. 77-15, Pasadena CA, 1977. [7] S.S. Dodbele “Effects of forebody geometry on subsonic boundary layer stability” NASA contractor report 4314,

1990

[8] Th. Lutz, S. Wagner “Numerical shape optimization of the natural laminar flow bodies” Stutgard, Germany

[9] Cebeci , Chen and Arnal, “A three-dimensional linear stability approach to transition on wings at incidence” AGARD symposium on fluid-dynamics of three dimensional turbulent shear flows and transition, Cesme, Turkey 3-6 October 1988.

[10] Cebeci , Chen and Arnal, “Three-dimensional linear stability approach to transition on wings and body of revolution” AIAA J., vol. 29, No 12, pp 2077-2085, 1991

[11] Herbert, T., “Parabolized stability Equations” Special course on progress in transition modelling, AGARD Report 793, April 1994.

[12] Kleiser, L. Zong, T.A., “Numerical simulation of transition in wall bounded shear flows” Annual review of fluid mechanics, vol. 23, pp 495-538, 1991

[13] Josleen, Street “Spatial direct numerical simulation of boundary layer transition mechanism: validation with PSE theory” NASA Langley research center 1992