Juniode2006 JulioD.PérezTudela Análisisdelainfluenciadelasaberracionesdelsistemadifractorenelreconocimientodeimágenesporcorrelaciónóptica GrupdeRecercaenÒpticaF´ısicaDepartamentdeF´ısicaAplicadaiÒpticaUniversitatdeBarcelona

(1)

Departament de F´ısica Aplicada i `Optica Universitat de Barcelona

An´

alisis de la influencia de las aberraciones del sistema

difractor en el reconocimiento de im´

agenes por

correlaci´

on ´

optica

Julio D. P´erez Tudela

(2)

Parte I

Fundamentaci´

on te´

orica

(3)

(4)

Cap´ıtulo 1

Reconocimiento de formas por

correlaci´

on ´

optica

1.1. Introducci´

on

Dentro de la denominación “reconocimiento de formas” se engloban todos aquellos métodos mediante los cuales es posible detectar la presencia de una determinada ima-gen, denominada imagen de referencia, dentro de otra imagen compleja, que recibe el nombre de escena. En el caso en que dicha imagen de referencia se encuentre presente en la escena, algunos de estos métodos permiten además determinar su posición. Esta disciplina ha ido adquiriendo en los últimos años una relevancia especial dentro del campo del procesado de imágenes debido principalmente a la constante y progresi-va automatización de la mayor´ıa de procesos industriales, as´ı como al desarrollo de nuevas l´ıneas de innovación tecnológica, tales como la inteligencia artificial, la visión por computador o la teledetección.

Existe una gran variedad de técnicas asociadas al reconocimiento de formas y al tratamiento de imágenes, y en función de los elementos que utilizan podemos cla-sificarlas en técnicas ópticas, digitales e h´ıbridas. El primer tipo, como su propio nombre indica, utiliza un conjunto de elementos ópticos para realizar el procesado, lo que garantiza una alta velocidad de procesado, pero plantean problemas debido a su limitada flexibilidad. Por el contrario, las técnicas digitales basan su funcionamiento fundamentalmente en algoritmos ejecutados en un ordenador, aunque el alto coste temporal de algunos de ellos se contrapone a su flexibilidad y potencia. Una buena posibilidad resulta trabajar con técnicas h´ıbridas, las cuales intentan aprovechar las

(5)

ventajas de cada uno de ambos m´etodos y al mismo tiempo minimizar los efectos de sus inconvenientes.

Dentro del conjunto de técnicas ópticas, destacan especialmente aquellas basadas en la comparación entre los elementos de la escena y la imagen que se quiere detec-tar. Esta comparación se realiza fundamentalmente mediante el desplazamiento de la imagen de referencia a lo largo y ancho de la imagen, de manera que se obtiene un conjunto de valores, tanto más elevados cuanto más similares son dicha imagen y la imagen correspondiente presente en la escena compleja. De este modo, la posición del valor máximo obtenido permite determinar la presencia de la imagen a detectar. Este proceso de comparación y asignación posterior de valores recibe el nombre de corre-lación. Presenta una serie de inconvenientes, como por ejemplo que únicamente se puede utilizar para detectar formas del mismo tamaño e idéntica orientación, aunque exiten métodos [HG78, CL78b, HA82a, HA82b] que solventan dichas dificultades.

1.2. Fundamentos de la correlaci´

on ´

optica

La correlaci´on entre dos funciones se puede expresar como: (f ⊗ g)(r) =

Z

Rn

f (r0)g∗(r0− r)dr0 (1.1)

A partir de esta expresión se puede observar cómo la correlación se obtiene al despla-zar la función g∗ _{(conjugada de g), multiplicar su valor en cada punto r}0

por el valor de la función f en dicho punto y realizar la suma para todos los puntos considerados. Los diferentes sumandos serán no nulos sólo si al desplazar la función g∗ _{a un punto}

cualquiera r0 existe una zona com´un entre ambas funciones. Adem´as, cuanto mayor

sea el parecido, mayor ser´a su contribuci´on al total de la suma.

En el caso de que tanto f como g representen imágenes, éstas serán descritas ´ unica-mente mediante funciones bidimensionales, f (x, y) y g(x, y). Puesto que el concepto clásico de imagen va asociado a una distribución bidimensional de valores de trans-misión, estas dos funciones tomarán únicamente valores reales, y serán, por tanto, reales. En este caso, g∗_{(x, y) = g(x, y), y por lo tanto, como se ha comentado}

ante-riormente, tanto mayor será el valor de la correlación cuanto mayor sea la similitud entre las funciones f (x, y) y g(x, y) trasladada. As´ı pues, la correlación resulta a prio-ri un buen mecanismo para reconocer un objeto determinado dentro de una escena formada por varios elementos.

(6)

1.3. Difractómetros 13 Una de las propiedades matemáticas de esta operación es el denominado Teorema de Convolución [Goo68], el cual permite obtener la correlación de dos funciones

f (x, y) y g(x, y) a partir del producto en el espacio complejo de sus transformadas

de Fourier respectivas, F (u, v) y G(u, v).

TF{f (x, y) ⊗ g(x, y)} = F (u, v)G∗(u, v) (1.2) Por lo tanto, es posible realizar este producto en el espacio de Fourier, y posterior-mente, mediante una transformada inversa, obtener el valor de f (x, y) ⊗ g(x, y) sin necesidad de realizar la integral reflejada en la expresi´on 1.1.

La posibilidad de utilizar lentes para realizar las transformadas de Fourier permite diseñar montajes ópticos relativamente simples que posibilitan la obtención práctica-mente en tiempo real de la correlación. Esta propiedad de las lentes podr´ıa generali-zarse del siguiente modo:

al iluminar un objeto f (x, y) situado frente a una lente se obtiene, en el plano focal de la misma, el espectro de frecuencias de dicho objeto, es decir, la amplitud de la transformada de Fourier, multiplicado por una serie de factores de fase que únicamente dependen de las posiciones relativas entre el objeto y la lente. En general se obtendrá una función del tipo:

TF(u, v) ∝ F ( x

λd, y

λd) (1.3)

donde se han omitido términos de proporcionalidad, y el valor de d de-pende de la configuración utilizada (lente anterior o posterior al objeto, iluminación convergente o paralela ...).

1.3. Difract´

ometros

En condiciones de óptica paraxial, se puede considerar el efecto de una lente en un frente de onda incidente como la modificación de dicho frente de onda mediante la inclusión de un término de fase cuadrático de la forma tf(x, y) = e−j

k

2f(x2+y2), donde

f representa la distancia focal de la lente, con signo positivo o negativo seg´un el convenio de signos utilizado. Dicho término de fase se puede considerar como una aproximación cuadrática a una onda esférica. Si la distancia focal f es positiva, la onda esférica es convergente hacia un punto situado en el eje óptico a una distancia

(7)

f posterior a la lente, mientras que si la distancia focal f es negativa, la onda esf´erica

diverge desde un punto situado a una distancia f antes de la lente.

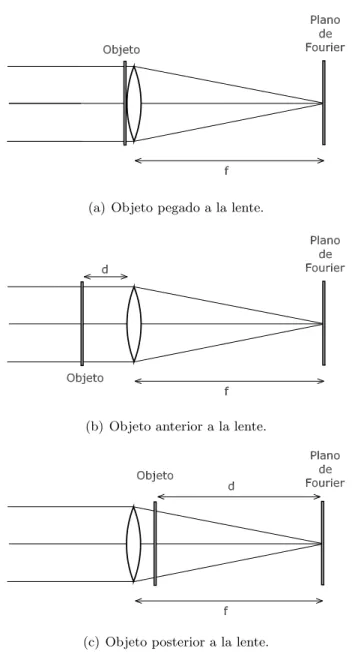
(a) Objeto pegado a la lente.

(b) Objeto anterior a la lente.

(c) Objeto posterior a la lente.

Figura 1.1: Configuraciones b´asicas de difract´ometros.

Como se ha comentado anteriormente, una de las propiedades m´as importantes y ´

utiles de las lentes es la posibilidad que ofrecen para realizar transformadas de Fou-rier bidimensionales de forma extremadamente simple, aprovechando las leyes de la propagaci´on y la difracci´on de la luz. Para ello se utilizan diversas configuraciones, la

(8)

1.3. Difract´ometros 15 geometr´ıa b´asica de tres de las cuales se presenta en la figura 1.1. En los apartados 1.3.1 y 1.3.2 se va a describir el comportamiento de cada una de estas configuraciones, siguiendo el esquema que se puede encontrar en [Goo68].

En los tres casos se utiliza una iluminación monocromática, que se propaga en forma de onda plana colimada, y la función a transformar es introducida en el sistema me-diante la utilización de un dispositivo con una transmisión de amplitud proporcional al valor de dicha función. Estos dispositivos pueden consistir en una simple trans-parencia fotográfica, o bien puede utilizarse SLM. Tanto en un caso como en otro, ´

unicamente se considerar´an como soportes f´ısicos de la funci´on de la cual queremos obtener su transformada.

1.3.1. Objeto anterior a la lente

Se tratará en primer lugar la situación descrita en la figura 1.1(a), donde el objeto se encuentra situado junto a la lente y podemos considerarlo una función t(x, y), que describe la amplitud de transmisión en un punto de coordenadas (x, y), y que se encuentra uniformemente iluminado por una onda plana de amplitud A que incide de forma perpendicular. Por lo tanto, en la lente incide una distribución de luz dada por:

Ul(x, y) = At(x, y) (1.4)

Las dimensiones finitas de la lente pueden ser representadas asociando a la lente una funci´on de pupila P (x, y) del tipo:

P (x, y) =      1 dentro de la lente 0 en otro caso (1.5)

Por lo tanto, podemos escribir la distribuci´on de amplitud detr´as de la lente como:

U_l0(x, y) = Ul(x, y)P (x, y)e[−j k

2f(x2+y2)] (1.6) Para calcular la distribución U_f(u, v) en el plano focal de la lente, aplicamos la ex-presión para la difracción de Fresnel [Mah01]:

Uf(u, v) = e[jkf ]

e[j2fk(u2+v2)]

jλf ×

+∞_{Z Z}

−∞

(9)

Sustituyendo en esta expresi´on la correspondiente a la distribuci´on U0 l(x, y), obtene-mos: U_f(u, v) = e[jkf ]e [jk 2f(u2+v2)] jλf × +∞_{Z Z} −∞

U_l(x, y)P (x, y)e[−jλf2π(xu+yv)]dxdy (1.8)

En el caso en que el objeto sea menor que la apertura de la lente, podemos obviar el t´ermino P (x, y), y por lo tanto:

U_f(u, v) = e[jkf ]e

[j_2fk(u2_+v2_)]

jλf ×

+∞_{Z Z}

−∞

U_l(x, y)e[−j2πλf(xu+yv)]dxdy (1.9)

lo que quiere decir que la distribución de amplitud compleja en el plano focal de la lente equivale a la transformada de Fourier de la distribución de luz transmitida por el objeto, excepto por los términos de fase que preceden a la integral. Estos térmi-nos pueden despreciarse en el caso en que lo que térmi-nos interese sea la distribución de intensidad, y no la amplitud compleja.

En el caso mostrado en la figura 1.1(b) el objeto se encuentra situado tambi´en en una posici´on anterior a la lente, pero a una distancia d de la misma. Si representamos por

Fo(fx, fy) el espectro de Fourier de la luz transmitida a trav´es del objeto (At(x, y)), y

por F_l(fx, fy) el de la luz incidente en la lente (Ul), y asumimos que la aproximaci´on

de Fresnel es v´alida para la propagaci´on del frente de onda a lo largo de la distancia

d, podemos escribir:

F_l(fx, fy) = Fo(fx, fy)e−jπλd(f

2

x+fy2) (1.10)

donde por simplificaci´on se ha omitido un t´ermino de fase.

Si, por el momento, no tenemos en cuenta las dimensiones finitas de la lente (P = 1 para cualquier valor de x e y), resulta:

U_f(u, v) = e [j_2fk(u2_+v2_)] jλf Fl( u λf, v λf) (1.11)

o, sustituyendo la expresi´on para F_l:

Uf(u, v) = e [j_2fk(1−d_f)(u2_+v2_)] jλf Fo( u λf, v λf) (1.12)

(10)

1.3. Difract´ometros 17 Finalmente, esto equivale a escribir:

U_f(u, v) = Ae [j_2fk(1−d_f)(u2_+v2_)] jλf × +∞_{Z Z} −∞ t(ξ, η)e[−j2πλf(ξu+ηv)]dξdη (1.13)

As´ı, la amplitud y la fase de la luz en un punto de coordenadas (u, v) se encuentran relacionadas con la amplitud y la fase del espectro de entrada correspondiente a las frecuencias ( u

λf, v

λf). La integral se encuentra multiplicada por un t´ermino de fase

cuadr´atico que se anula en el caso en que d = f , es decir, cuando el objeto se encuentra situado en el plano focal objeto de la lente. En este caso, el resultado que se obtiene es exactamente la transformada de Fourier del objeto.

1.3.2. Objeto posterior a la lente

Consideremos ahora el caso en el que el objeto se encuentra situado en una posición posterior a la lente, tal y como se muestra en la figura 1.1(c). El objeto, situado a una distancia d del plano focal imagen de la lente, se puede considerar, al igual que en el caso anterior, como una función t(x, y). La lente, a su vez, es iluminada perpen-dicularmente de manera uniforme por una onda plana monocromática de amplitud A. Por lo tanto, la onda incidente en el objeto será una onda esférica convergente con su centro en el punto donde el plano focal imagen de la lente intersecte al eje óptico. Considerando óptica geométrica, la amplitud de la onda esférica que incide en el ob-jeto tiene un valor de Af

d, puesto que las dimensiones geom´etricas del cono de luz se

han reducido en un factor d

f, mientras que su energ´ıa se ha conservado. La regi´on del

objeto que es iluminada viene determinada por la intersecci´on de dicho cono de luz con el plano donde se encuentra situado el objeto. Si la lente es circular y de di´ametro

l, dicha regi´on es circular y con un di´ametro ld f .

Las dimensiones finitas del ´area iluminada pueden ser descritas utilizando una funci´on de pupila del tipo P [ξf

d, η f

d]. Trabajando en la aproximaci´on paraxial, la amplitud

de la onda transmitida por el objeto viene descrita por la expresi´on:

U₀(ξ, η) = ½ Af d P µ ξf d, η f d ¶ e[−j2dk(ξ2+η2)] ¾ t(ξ, η) (1.14)

Si consideramos difracción de Fresnel desde el plano objeto hasta el plano focal ima-gen, el término cuadrático en (ξ, η) presente en la ecuación 1.14 cancela exactamente

(11)

el término cuadrático que aparece en la integral de difracción de Fresnel, y por lo tanto: U_f(u, v) = Ae[j k 2d(u2+v2)] jλd f d× +∞_{Z Z} −∞ t(ξ, η)P µ ξf d, η f d ¶ e[−j2πλd(ξu+ηv)]dξdη (1.15)

Lo cual muestra que, excepto un término de fase cuadrático, la distribución de ampli-tud en el plano focal es la transformada de Fourier de la región del objeto iluminada por el cono de luz que atraviesa la lente.

1.4. Arquitecturas b´

asicas de correlaci´

on

1.4.1. Correlador 4f y correlador convergente

En el apartado 1.3.1 hemos visto c´omo al iluminar con ondas planas un objeto situado en el plano focal objeto de una lente convergente, se obten´ıa en el plano focal imagen la transformada de Fourier exacta de dicho objeto. Una de las propiedades de la transformada de Fourier [Goo68] nos dice que:

TF[TF[f (x, y)]] = f (−x, −y) (1.16) y por lo tanto, acoplando en cascada dos sistemas como el anterior ser´ıa posible re-construir la imagen inicial.

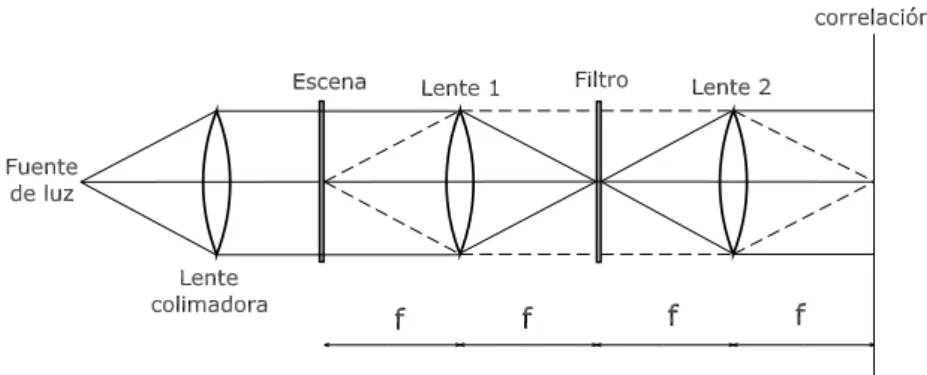
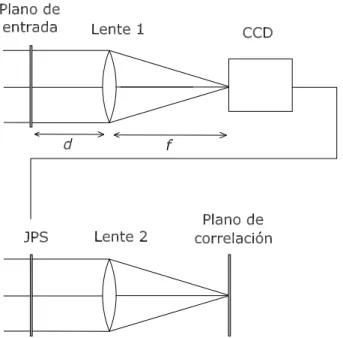
Figura 1.2: Esquema del correlador 4f.

El esquema propuesto es el que se muestra en la figura 1.2, y fue el primer montaje propuesto por VanderLugt en 1964 [Lug64]. Este esquema es el que se utiliza como

(12)

1.4. Arquitecturas básicas de correlación 19 base para desarrollar los dispositivos de filtrado y tratamiento de imágenes mediante métodos ópticos, y debe su nombre (correlador 4f) a la distancia entre el plano de entrada, donde se coloca la escena, y el de salida, o plano de correlación. Esta dis-tancia, en el caso en que trabajemos con dos sistemas ópticos idénticos, equivale a cuatro veces la distancia focal de las lentes.

La escena (función f (x, y)) se sit´ua, como ya hemos dicho, en el plano focal objeto del primer difractómetro, y el filtro codificado (G∗_{(u, v)), que será el encargado de}

modular la información de la transformada de la escena (ver ecuación 1.2), en el plano focal imagen de la primera lente. Como se ha visto anteriormente, con esta configu-ración se obtiene en este plano la transformada de Fourier exacta de la escena, por lo que es aqu´ı donde se realiza el producto F (u, v)G∗_{(u, v). Al realizarse la segunda}

transformaci´on con la segunda lente se obtiene en su plano imagen el producto de correlaci´on f ⊗ g.

A la simplicidad que presenta este dispositivo se ha de contraponer una serie de in-convenientes, la mayor´ıa de los cuales son de tipo práctico, ya que, por ejemplo, la longitud total del montaje es siempre de cuatro veces la focal de las lentes, supo-niéndolas iguales. Además, el acoplamiento de las escalas de la primera transformada y el filtro utilizado para modificar la información resulta un problema nada trivial. Finalmente, y tal vez la dificultad más importante que plantea este montaje, encon-tramos la imposibilidad de modificar la escala de la transformada de Fourier de la escena, puesto que ésta viene determinada por la distancia entre ella y la lente 1, que necesariamente ha de coincidir con la distancia focal del sistema óptico. Puesto que esta escala debe coincidir con la escala del filtro, el no poder modificarla sin reem-plazar el sistema óptico reduce considerablemente la versatilidad del dispositivo. Para solventar este conjunto de dificultades se puede trabajar con un procesador alter-nativo, el denominado correlador convergente. Dicho dispositivo es el que se muestra en la figura 1.3 y se trata también de un sistema óptico con dos lentes convergentes de focales f0

1 y f20, pero que en este caso no se encuentran acopladas por su focal.

El objeto se encuentra situado después de la primera lente, y su transformada de Fourier se forma en el plano imagen de la fuente de luz a través de la primera lente. Es en este mismo plano donde se coloca el filtro. Finalmente, la imagen procesada es obtenida en el plano imagen del objeto a través de la segunda lente.

(13)

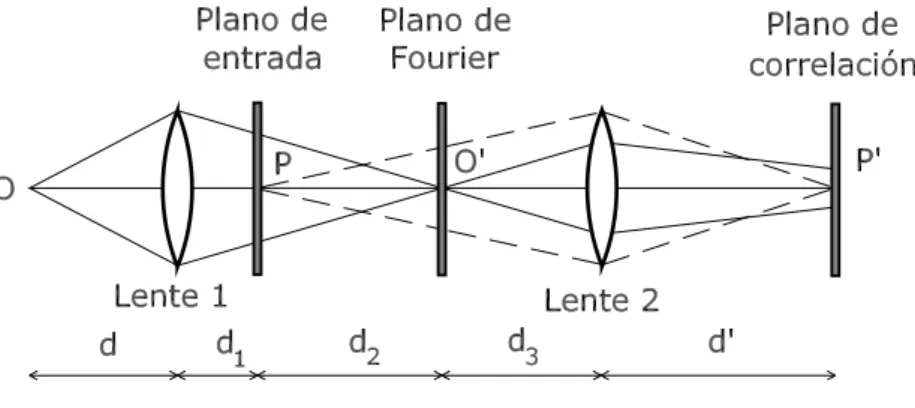
Figura 1.3: Esquema del correlador convergente de Vander Lugt.

Para que el sistema funcione de forma adecuada es necesario, a su vez, que las dis-tancias entre los diferentes planos se encuentren relacionadas seg´un:

           1 d1+ d2 − 1 d = 1 f0 1 − 1 d2+ d3 + 1 d0 = 1 f0 2 (1.17)

El comportamiento de este correlador se puede describir de manera intuitiva del si-guiente modo: el objeto, iluminado por la onda convergente proveniente de la lente 1, forma su imagen a través de la lente 2. En el plano de Fourier obtenemos la figura de difracción del objeto, que incluye su transformada de Fourier, y es donde se coloca la información del filtro. Por lo tanto, en el plano de correlación se formará la imagen del objeto modificada por dicho filtro.

Este procesador presenta una ventaja importante respecto del correlador 4f, y es que la posici´on del plano de entrada puede desplazarse, y puesto que la transformada del objeto tiene un factor de escala λd2, se puede encontrar una distancia d2que se ajuste

a la escala para la cual se ha calculado el filtro. Evidentemente, la modificación de la distancia d2 implica también la variación de la posición del plano de correlación, de

(14)

1.4. Arquitecturas b´asicas de correlaci´on 21

1.4.2. Generaci´on de filtros

Hemos visto anteriormente que para obtener la correlaci´on cruzada entre la imagen

f (x, y) y la referencia a detectar g(x, y) utilizando un correlador 4f se ha de dise˜nar el filtro G∗_{(u, v). As´ı, en el plano de Fourier de la primera lente se obtiene el producto}

F (u, v)G∗_{(u, v) y en el plano imagen de la segunda lente el t´ermino f ⊗ g. Ahora}

bien, en general, la función G∗_{(u, v) es una función compleja, y su codificación}

re-quiere m´etodos especiales, bien de holograf´ıa ´optica o de holograf´ıa digital.

La holograf´ıa óptica fue introducida por Gabor en 1949 [Gab49] como un método pa-ra “registpa-rar y reconstruir frentes de onda”. Dicho método consist´ıa en iluminar un objeto con un haz de luz monocromático y coherente, denominado haz de referencia, y registrar en un soporte adecuado las interferencias entre dicho haz de referencia y el proveniente directamente de la misma fuente de luz.

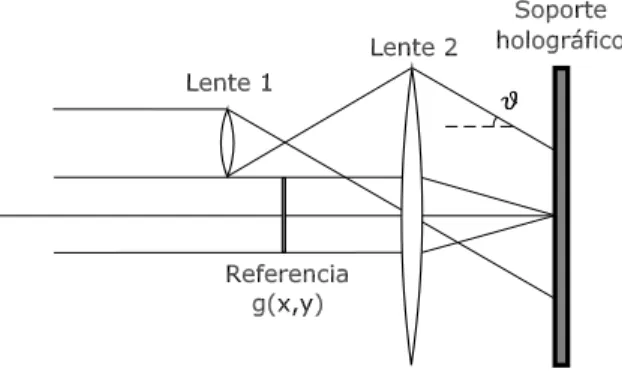
Actualmente las técnicas de holograf´ıa digital generada por ordenador permiten codi-ficar funciones complejas, pero fue VanderLugt [Lug64] en 1964 el primero en describir un experimento de correlación utilizando técnicas ópticas de holograf´ıa para codifi-car el filtro. Para ello, se necesita generar previamente mediante un difractómetro, tal y como se muestra en la figura 1.4, la transformada de Fourier (G(u, v)) de la imagen de referencia (g(x, y)) : en el plano objeto de la lente se coloca dicha imagen de referencia, de modo que en el plano focal imagen se obtiene la transformada de Fourier exacta. En dicho plano se coloca un registro fotográfico que será el encargado de registrar las interferencias entre la función G(u, v) y una onda plana de amplitud

A que incide según una dirección de propagación que forma un ángulo θ con el eje óptico.

(15)

Por lo tanto, el registro de la placa es:

I(u, v) = ¯¯G(u0_{, v}0_{) + Ae}(−j2παv)¯¯2

= |G(u0_{, v}0_)|2_{+ A}2_{+ AG(u}0_{, v}0_)e(j2παv)_{+ AG}∗_(u0_{, v}0_)e(−j2παv) (1.18)

donde se ha definido α = sin θ_λ .

Una vez realizado el proceso de revelado de la placa fotográfica, se sitúa ésta en el plano de Fourier de un procesador 4f en cuyo plano objeto se encuentra la imagen

f (x, y). Para que las escalas de las transformadas de Fourier ´opticas coincidan es

necesario que la focal de la lente con la que se ha generado el filtro y la focal del primer difract´ometro del correlador 4f coincidan.

Finalmente, en el plano focal imagen del segundo difract´ometro se obtiene:

U (u, v) = F (u, v) h |G(u, v)|2+ A2i + Ae(j2παv)_{F (u, v)G(u, v)} + Ae(−j2παv)_{F (u, v)G}∗_{(u, v)} (1.19)

Los tres t´erminos anteriores se pueden interpretar como:

1. El primer término, o término centrado, no aporta información relevante y se difracta en la dirección del eje óptico.

2. El segundo término corresponde al producto de convolución de las funciones f y g, y al encontrarse modulado por una onda plana dirigida seg´un la dirección positiva del eje v, se encontrará situado en uno de los laterales del término central

3. El tercer término incluye la correlación entre la funciones f y g, y se encuentra situado de forma simétrica al término de convolución respecto del eje óptico.

1.4.3. Correlador de transformadas conjuntas

Una arquitectura alternativa al correlador de VanderLugt es el denominado correla-dor de transformadas conjuntas o JTC. La caracter´ıstica principal de este dispositivo la determina el hecho de que no sea necesario diseñar ningún filtro en el espacio de Fourier, tal y como pasaba en el caso anterior, puesto que la introducción de la escena y el objeto a detectar se realiza en el mismo plano de entrada.

(16)

1.4. Arquitecturas básicas de correlación 23 Por otra parte, este correlador no puede trabajar en tiempo real, ya que se hace necesario registrar la intensidad del plano de Fourier en un soporte f´ısico. De todos modos, gracias a la evolución de la tecnolog´ıa de los dispositivos de cristal l´ıquido (ó LCD1_{) y su uso conjunto con cámaras de v´ıdeo (ó CCD}2_{), esta dificultad ya no}

representa un verdadero problema.

Figura 1.5: Esquema del correlador de transformadas conjuntas convencional. Simplificando el proceso, se podr´ıa decir que en un primer paso se registra la dis-tribución de intensidad producida por la transformada de Fourier óptica del plano de entrada o JPS. Esta distribución es nuevamente transformada ópticamente en un segundo paso, y de este modo se obtiene la correlación entre el motivo y la escena. As´ı, el procesador (figura 1.5) consiste en un sistema difractor en el que un haz de ondas planas de longitud de onda λ ilumina conjuntamente la escena f (x, y) y la referencia g(x, y), las cuales se encuentran situadas en el mismo plano, separadas una distancia 2a. Este plano se encuentra situado a una distancia arbitraria d de una lente de focal f , en cuyo plano focal se registra de forma simultánea la información proveniente tanto de la escena como de la referencia.

1_{Liquid Crystal Devices} 2_{Charged-Coupled Device}

(17)

Esta distribuci´on se reintroduce en el plano de entrada, de manera que al iluminar de nuevo el sistema, en el plano focal de la lente se obtiene la siguiente distribuci´on:

U (x, y) = f (−x, −y) ⊗ f (−x, −y) + g(−x, −y) ⊗ g(−x, −y)

+ f (−x, −y) ⊗ g(−x, −y) ∗ δ(x − 2a, y) + g(−x, −y) ⊗ f (−x, −y) ∗ δ(x + 2a, y)

(1.20)

Analizando el resultado, se observa cómo se obtienen los términos de autocorrelación de escena y referencia centrados y, de forma simétrica y centrados en los puntos de coordenadas (±2a, 0), los dos términos de correlación cruzada entre escena y referen-cia.

(18)

Cap´ıtulo 2

Aberraciones geom´

etricas en

sistemas ´

opticos

Conocidas las caracter´ısticas geométricas (radios de curvatura y espesores) y ópticas (´ındice de refracción) de las lentes que forman un sistema óptico es posible deter-minar la posición y tamaño de la imagen de un objeto concreto [Hec00]. Incluso es posible calcular también la distribución de intensidad de la imagen si, además, tanto la posición como el tamaño de las pupilas de salida y de entrada son valores conocidos. En el caso de que los sistemas ópticos utilizados presenten simetr´ıa de revolución y se cumplan las condiciones de óptica paraxial, es posible obtener una representación óptica perfecta entre pares de puntos. Ahora bien, estas condiciones de trabajo son especialmente restrictivas en lo que respecta a los valores de abertura y campo, de modo que resulta complicado ceñirse a ellas. Esto hace que en el caso más general, esta correspondencia exacta entre objeto e imagen se pierda, y las imágenes empie-cen a presentar ”defectos”: as´ı, los planos imagen se curvan, las imágenes se vuelven menos n´ıtidas, la semejanza total entre objeto e imagen desaparece ... Este conjunto de alteraciones que sufre la imagen son debidas principalmente a las caracter´ısticas f´ısicas del sistema óptico y a sus condiciones de trabajo, y reciben el nombre de abe-rraciones geométricas.

Como idea previa, se podr´ıa definir la aberración de un sistema para un determinado objeto puntual como la desviación que experimenta el frente de onda en la pupila de salida respecto del frente de onda ideal. En el caso de aberración nula, este frente de onda ideal es esférico, de modo que todos los rayos provenientes del punto objeto

(19)

convergen en el punto imagen, y el resultado es una imagen puntual. En general, al trabajar con sistemas reales, dicha onda convergente será sólo aproximadamente esférica, y por lo tanto esta correspondencia entre puntos no se conserva. Se puede considerar, por lo tanto, que la calidad de la imagen vendrá determinada por las aberraciones del sistema óptico.

2.1. Aberraciones de rayo y onda

La óptica geométrica basa su estudio de la propagación de la luz en dos concep-tos fundamentales: el de rayo luminoso para caracterizar a la luz, y el de ´ındice de refracción para definir los medios materiales a través de los cuales se realiza dicha propagación. Ambos conceptos se complementan con tres leyes, las cuales rigen la propagación de los rayos en los medios: propagación rectil´ınea, refracción y reflexión. Estas tres leyes no son más que consecuencias del principio de Fermat [Hec00]. Si un rayo de luz recorre un trayecto de longitud s en un medio homogéneo de ´ındice de refracción n, se define el camino óptico < L > de dicho rayo como el producto del ´ındice de refracción del medio y la longitud recorrida:

< L >= n · s (2.1)

Si en su trayectoria atraviesa diferentes medios de ´ındice de refracci´on ni, y recorre

en cada uno de ellos un trayecto de longitud si, el camino ´optico total ser´a:

< L >= n1· s1+ n2· s2+ ... =

X

i

ni· si (2.2)

De todos los rayos trazados desde el punto objeto, se denomina rayo principal a aquel rayo que atraviesa el centro del diafragma de apertura y pasa, real o virtual-mente, por los centros de la pupila de entrada y de la pupila de salida. Si cada uno de los rayos provenientes del objeto es trazado de modo que recorran el mismo camino óptico que el recorrido por el rayo principal, el extremo de cada uno de dichos rayos forma una superficie que recibe el nombre de frente de onda del sistema óptico. Si tras atravesar el sistema óptico dicha superficie es esférica con su centro de curvatu-ra en la posición de la imagen pacurvatu-raxial del punto objeto, la imagen será perfecta. As´ı, los rayos trazados a través del sistema al propagarse desde el punto objeto P hasta el

(20)

2.1. Aberraciones de rayo y onda 27 punto imagen P0 _{recorren el mismo camino ´optico, y todos ellos pasan por P}0_{. Ahora}

bien, si el frente de onda se desv´ıa respecto del frente de ondas esférico, también denominado esfera de referencia, diremos entonces que la imagen está aberrada. En esta situación, los rayos no recorren el mismo camino óptico, y su intersección con el plano imagen paraxial ya no es el punto P0_{, sino puntos más o menos cercanos a}

él. La distancia entre dichos puntos y la posición de la imagen paraxial se denomina aberración del rayo.

Por otro lado, se define [Mah98] la aberración de onda correspondiente a un ra-yo determinado en el punto Q, donde intersecta a la esfera de referencia, como la diferencia de caminos ópticos recorridos por el rayo considerado y el rayo principal al desplazarse ambos desde el punto objeto hasta la intersección con dicha esfera de referencia.

Figura 2.1: Frente de onda aberrado para un objeto puntual situado sobre el eje ´optico.

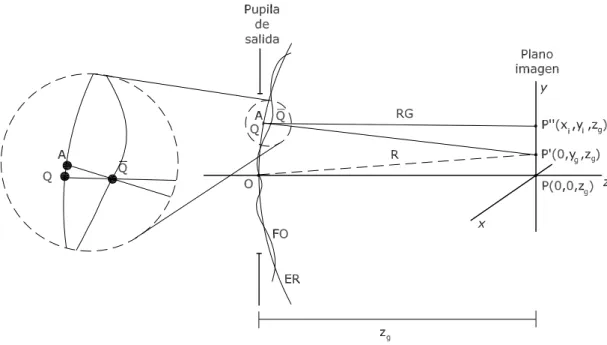
La figura 2.1 muestra el esquema anterior para el caso de un objeto puntual situado sobre el eje ´optico: un rayo arbitrario RG intersecta a la esfera de referencia ER y al frente de onda aberrado F O en los puntos Q y Q, respectivamente, y al plano imagen gaussiano en el punto P00_{. En esta figura se aprecia c´omo la esfera de referencia, de}

(21)

radio de curvatura R, se encuentra centrada en el punto imagen gaussiano, P0_{, y}

c´omo tanto el frente de onda aberrado como la esfera de referencia pasan ambos por el centro O de la pupila de salida.

En base a la definici´on anterior de frente de onda, la longitud del camino ´optico del rayo emergente del punto objeto y con final en Q es la misma que la del rayo principal con final en el punto O (centro de la pupila de salida). De este modo, el producto

nQQ proporciona la aberraci´on de onda del rayo considerado, W .

Ahora bien, existe una definición alternativa [Ray64] para la aberración de onda. En este caso, la aberración de onda se define para un punto Q del frente de onda, en vez de para un punto Q de la esfera de referencia. Seg´un esta definición, la aberración se define como la distancia entre Q y la esfera de referencia medida a lo largo del radio de la esfera que pasa por el punto Q (AQP0). Ésta será la definición que utilizaremos en el siguiente apartado para establecer una relación entre la aberración de rayo y la aberración de onda.

2.1.1. Relación entre aberración de rayo y aberración de onda

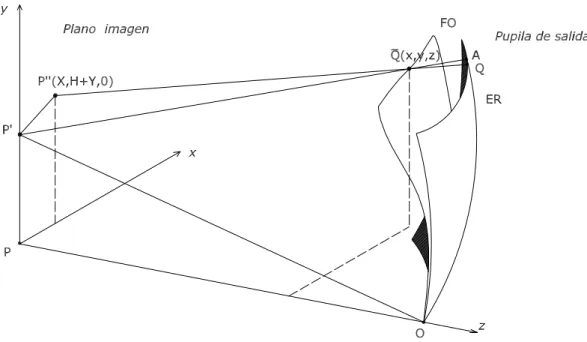
La figura 2.2 muestra de forma más simple el esquema de la figura 2.1. As´ı, F O representa parte de un frente de onda aberrado (propagándose hacia la izquierda) en la pupila de salida del sistema, mientras que ER representa parte de la esfera de referencia. Ambos presentan un punto en común en el centro de la pupila de salida

O. El centro P0 _{de la esfera de referencia coincide con el punto imagen gausiano,}

de modo que el radio de la esfera de referencia es R = OP0 _{= AP}0_{. El sistema de}

coordenadas est´a elegido de tal manera que el eje z coincide con el eje ´optico, el plano

xy es el plano imagen y H = P P0 _{es la altura de la imagen.}

Un rayo cualquiera perpendicular al frente de onda en un punto Q de coordenadas (x, y, z) intersecta al plano imagen en el punto P00_{, de modo que P}0_P00_{es la aberraci´on}

de rayo, y (X, Y ) sus coordenadas ortogonales sobre el plano imagen. La distancia desde el centro de la esfera hasta este punto en el frente de onda es r = P0_{Q, y puesto}

que hemos definido la aberraci´on de onda como la distancia desde ese punto hasta la esfera de referencia, podemos escribir:

W (x, y) = R − r = AP0− P0Q (2.3)

(22)

2.1. Aberraciones de rayo y onda 29

Figura 2.2: Esfera de referencia (ER) y frente de onda (FO).

ecuación del frente de onda en el sistema de coordenadas P xyr, y por lo tanto, obtener la relación entre la aberración de onda y la de rayo se reduce a un problema de derivadas parciales y cambio de variables. Las variables x, y, z, r se encuentran relacionadas según la expresión pitagórica:

x2+ (y − H)2+ z2= r2 (2.4) que tambi´en se puede expresar como:

G(x, y, z, r) = 0 (2.5)

El frente de onda se puede definir a partir de las expresiones:

F (x, y, z) = 0 , z = f (x, y) (2.6)

Si eliminamos la variable z de las ecuaciones 2.4 y 2.6, podemos obtener una nueva expresi´on para el frente de onda:

r = g(x, y) (2.7)

Los diferenciales de las funciones f y g ser´an, por tanto:

dz = ∂z ∂xdx + ∂z ∂ydy dr = ∂r ∂xdx + ∂r ∂ydy            (2.8)

(23)

Y de manera similar, para las funciones F y G: ∂F ∂xdx + ∂F ∂ydy + ∂F ∂zdz = 0 ∂G ∂xdx + ∂G ∂ydy + ∂G ∂zdz + ∂G ∂rdr = 0            (2.9)

Sustituimos en la ecuación anterior las expresiones para dz y dr, y después de agrupar términos: µ ∂F ∂x + ∂F ∂z ∂z ∂x ¶ dx + µ ∂F ∂y + ∂F ∂z ∂z ∂y ¶ dy = 0 µ ∂G ∂x + ∂G ∂z ∂z ∂x+ ∂G ∂r ∂r ∂x ¶ dx + µ ∂G ∂y + ∂G ∂z ∂z ∂y + ∂G ∂r ∂r ∂y ¶ dy = 0 (2.10)

Puesto que dx y dy son infinit´esimos independientes, los coeficientes que les acom-pa˜nan han de ser nulos, y por lo tanto:

∂F ∂x + ∂F ∂z ∂z ∂x = 0 ∂F ∂y + ∂F ∂z ∂z ∂y = 0 ∂G ∂x + ∂G ∂z ∂z ∂x + ∂G ∂r ∂r ∂x = 0 ∂G ∂y + ∂G ∂z ∂z ∂y+ ∂G ∂r ∂r ∂y = 0 (2.11)

La soluci´on del sistema nos lleva a:

∂r ∂x = 1 ∂G ∂r Ã ∂G ∂z ∂F ∂x ∂F ∂z − ∂G ∂x ! ∂r ∂y = 1 ∂G ∂r Ã ∂G ∂z ∂F ∂y ∂F ∂z − ∂G ∂y ! (2.12)

Ahora bien, de la ecuaci´on 2.4 tenemos que:

∂G ∂x = 2x, ∂G ∂y = 2(y − H), ∂G ∂z = 2z, ∂G ∂r = −2r (2.13)

Por otro lado, las derivadas parciales de F y los cosenos directores de la direcci´on perpendicular en Q (es decir, del rayo) se encuentran relacionados seg´un la expresi´on:

∂F ∂x :

∂F ∂y :

∂F

(24)

2.2. Función de aberración de un sistema con simetr´ıa de revolución 31 Y a partir de la geometr´ıa de la figura 2.2:

cos α cos γ = x − X z , cos β cos γ = y − (H + Y ) z (2.15)

Por lo tanto, sustituyendo estos valores en las ecuaciones 2.12, obtenemos:

∂r ∂x = X r , ∂r ∂y = Y r (2.16)

Si recordamos la definición de aberración de onda (ecuación 2.3), r = R − W , y por lo tanto: ∂r ∂x = − ∂W ∂x , ∂r ∂y = − ∂W y (2.17)

Por lo que finalmente llegamos a las relaciones exactas entre la aberraci´on de onda y la aberraci´on de rayo: ∂W ∂x = − X R − W, ∂W ∂y = − Y R − W (2.18)

2.2. Funci´

on de aberraci´

on de un sistema con simetr´ıa

de revoluci´

on

Una vez definidos formalmente los conceptos de aberración de rayo y de onda, as´ı como la relación entre ambos, pasaremos a analizar las aberraciones de un sis-tema óptico con simetr´ıa de revolución. Para ello, el primer paso será determinar la expresión anal´ıtica de la aberración de onda, ya sea como un desarrollo de potencias en función de coordenadas cartesianas, o bien mediante coordenadas polares.

Mediante la introducción de la función caracter´ıstica de Hamilton, se puede demos-trar [BW99] que la aberración de onda depende únicamente de cuatro variables: las coordenadas del rayo en el punto objeto (x0, y0) y sus coordenadas en la intersección

en la pupila de salida (x, y). De este modo, la función de aberración del sistema para el punto objecto considerado, W (~r0), se puede escribir en su forma más general como

una serie de potencias en términos de las coordenadas de los dos puntos anteriores, el punto objeto y el situado en la pupila, según la expresión:

W (x0, y0; x, y) = ∞ X j=0 xj₀ ∞ X k=0 y₀k ∞ X l=0 xl ∞ X m=0 ymajklm (2.19)

donde el t´ermino ajklmrepresenta los coeficientes de la expansi´on, los cuales dependen

(25)

los ´ındices de refracci´on de los medios y el grosor de los mismos, y todas las potencias presentan exponentes enteros no negativos.

Ahora bien, si tenemos en cuenta la simetr´ıa del sistema, esta dependencia se reduce ´

unicamente a tres combinaciones: x2

0+ y02, x2+ y2 y x0x + y0y. Para comprobar

esto resulta m´as adecuado trabajar en coordenadas polares. Sean (r0, θ0) y (r, θ)

las coordenadas polares correspondientes a las coordenadas rectangulares (x0, y0) y

(x, y), respectivamente, del punto objeto y del situado en el plano de la pupila. Las relaciones entre ambos sistemas de coordenadas ser´an:

(

(x0, y0) = r0(cos θ0, sin θ0)

(x, y) = r(cos θ, sin θ) (2.20) De este modo, la aberraci´on depende ahora de r₀, r, θ y θ₀, o lo que es lo mismo,

r0, r, θ0 − θ y θ. Ahora bien, si rotamos ambos sistemas de referencia un mismo

´angulo, las tres primeras variables permanecer´an inalteradas, pero no as´ı el valor de

θ. Esto entrar´ıa en contradicci´on con el hecho de que W sea invariante a rotaciones,

lo que significa que la aberración no puede depender del valor de θ, y por lo tanto, tan sólo es función de r₀, r, θ₀− θ. Esto quiere decir que la función de aberración se

puede expresar en funci´on de los tres productos escalares de los vectores ~r0(x0, y0)

y ~r(x, y), que constituyen los denominados invariantes rotacionales de la función de aberración:      |~r0|2 = r02= p x2 0+ y02 |~r|2 _{= r}2 ₌p_x2_{+ y}2 ~r0· ~r = r0r cos(θ − θ0) = x0x + y0y (2.21) Por lo tanto, si W se expresa mediante un desarrollo en serie de potencias de las cuatro coordenadas, la expansión únicamente contendrá términos de grado par, de manera que será del tipo [BW99]:

W = c(x2₀+ y₀2) + W(4)+ W(6)+ · · · (2.22) donde c es una constante y W(2k) _{representa un polinomio de grado 2k en las}

coorde-nadas, y contiene estas coordenadas ´unicamente en potencias de los tres invariantes. Las aberraciones de orden m´as bajo, representadas por el polinomio W(4)_son

denomi-nadas generalmente aberraciones primarias o aberraciones de Seidel. Este polinomio incluye cinco términos, el coeficiente de cada uno de los cuales corresponde a la dis-torsión, la curvatura de campo, el astigmatismo, el coma y la aberración esférica.

(26)

2.2. Función de aberración de un sistema con simetr´ıa de revolución 33

2.2.1. Polinomios y coeficientes de Zernike

Ya hemos visto en el apartado anterior como para un objeto determinado, la función de aberración W (ρ, θ) de un sistema óptico simétrico respecto de la rotación alrededor del eje óptico puede ser expresada en función de un conjunto completo1 _de

polino-mios. Existen muchos conjuntos de polinomios con estas caracter´ısticas, pero uno de ellos, introducido por primera vez por F. Zernike [Zer34], resulta especialmente útil. Los polinomios de Zernike presentan una serie de caracter´ısticas singulares, puesto que son los ´unicos que, expresados en dos variables, ρ y θ, son ortogonales en el c´ırcu-lo unidad. Esta ortogonalidad provoca que el hecho de añadir o suprimir cualquier término del desarrollo no modifica el ajuste óptimo de la expresión anal´ıtica de la aberración con respecto del polinomio real de aberración. Por otra parte, incluyen un polinomio para cada valor permitido de m y n, los cuales representan la dependencia el grado del polinomio radial y el ´ındice de la dependencia angular, respectivamente. Finalmente, son invariantes respecto a rotaciones de los ejes alrededor del origen. En general, y como ser´ıa de esperar, los polinomios de Zernike circulares son adecuados para representar la función de aberración de sistemas ópticos con simetr´ıa circular. Estos polinomios Rm_n(ρ) cos mθ, expresados en coordenadas polares (ρ, θ), permiten escribir la función de aberración W (ρ, θ) como:

W (ρ, θ) = ∞ X n=0 n X m=0 cnm s 2(n + 1) 1 + δ_m0R m n(ρ) cos mθ (2.23)

donde cnm son los coeficientes de la expansi´on, n y m son enteros positivos (incluido

el cero), de manera que n − m ≥ 0 y par, δij es una delta de Kronecker y

Rm_n(ρ) = n−m 2 X s=0 (−1)s_{(n − s)!} s! µ n + m s − s ¶ ! µ n − m s − s ¶ ! ρn−2s (2.24)

es un polinomio de grado n en ρ con t´erminos en ρn_{, ρ}n−2_{, ... ,ρ}m_{. El hecho de que}

no aparezcan términos dependientes de sin mθ es debido a que todos sus coeficientes son nulos debido a la simetr´ıa de rotación del sistema óptico alrededor del eje.

1_{El t´ermino completo indica que cualquier funci´on continua puede ser expresada como una}

(27)

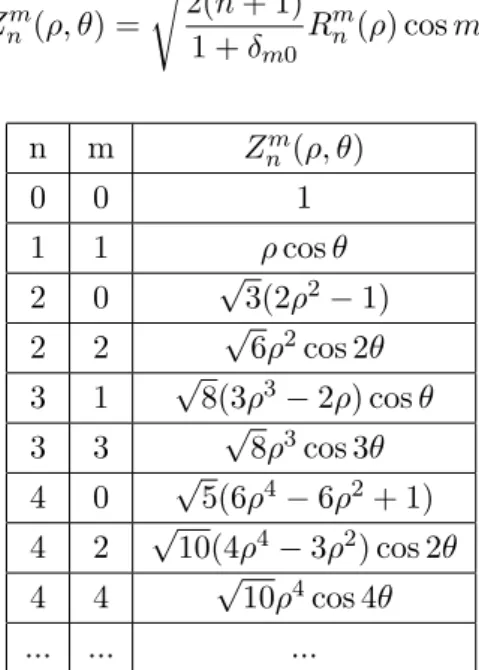
Debido a su ortogonalidad, generalmente los diferentes términos del desarrollo de la aberración en función de los polinomios de Zernike suelen denominarse de forma genérica como aberraciones ortogonales. Algunos de los términos de las aberra-ciones ortonormales de Zernike se muestran en la tabla 2.1. En esta tabla se define Zm n (ρ, θ) como: Z_nm(ρ, θ) = s 2(n + 1) 1 + δm0 Rm_n(ρ) cos mθ (2.25) n m Zm n(ρ, θ) 0 0 1 1 1 ρ cos θ 2 0 √3(2ρ2_{− 1)} 2 2 √6ρ2_{cos 2θ} 3 1 √8(3ρ3_{− 2ρ) cos θ} 3 3 √8ρ3_{cos 3θ} 4 0 √5(6ρ4_{− 6ρ}2_{+ 1)} 4 2 √10(4ρ4_{− 3ρ}2_{) cos 2θ} 4 4 √10ρ4_{cos 4θ} ... ... ...

Tabla 2.1: Aberraciones ortonormales de Zernike (n ≤ 4).

2.3. Propagaci´

on de im´

agenes aberradas

En los apartados anteriores se han analizado tanto la definición como la expresión anal´ıtica de la aberración de onda asociada a un sistema óptico para un punto objeto situado en el eje óptico. Para ello, se ha utilizado la óptica geométrica, a partir del estudio de la marcha de los rayos provenientes del objeto hasta el plano imagen, y relacionando la aberración de rayo en el plano imagen con la aberración de onda en el plano de la pupila de salida. Hasta este momento no se han considerado los efec-tos difractivos asociados a los diferentes elemenefec-tos que conforman el sistema óptico. Será en este apartado donde se tendrán en cuenta estos efectos, agrupándolos de for-ma global en la pupila de salida, y de este modo se calculará la distribución de luz en ella para un sistema aberrado, y posteriormente se realizará su propagación hasta un plano arbitrario.

(28)

2.3. Propagación de imágenes aberradas 35 El primero en asociar estos efectos a la pupila de salida fue Lord Rayleigh en 1896 [Ray96], aunque ya anteriormente Ernst Abbe en 1873 [Abb73] los hab´ıa agrupado en la pupila de entrada. Ambos métodos son equivalentes, puesto que ambas pupilas son imágenes una de la otra, y utilizan la óptica geométrica para describir la propagación de la luz entre la pupila de entrada y la de salida del sistema, mientras que los efectos difractivos únicamente se consideran durante la propagación desde el objeto hasta la pupila de entrada o, de forma alternativa, desde la pupila de salida hasta el plano imagen. El desarrollo que se presenta en este apartado sigue fundamentalmente la notación y el esquema que se puede hallar en [Mah01].

2.3.1. Distribuci´on de luz en la pupila de salida

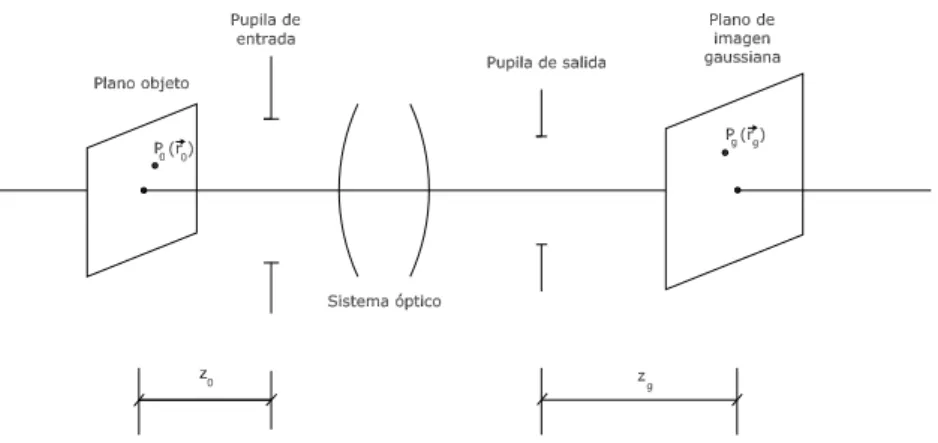
Consideremos un objeto puntual situado en la posición ( ~r₀; z₀), tal y como se mues-tra en la figura 2.3. Una onda esférica divergente, con su centro de curvatura en el objeto, incide en la pupila de entrada. Si el sistema no tiene aberración, una onda esférica de la forma e(−ikrR ), donde R es su radio de curvatura, emerge de la pupila

de salida convergiendo a la imagen gaussiana (o paraxial) del objeto, situada en la posición ( ~r_g; z_g). En el caso real de que el sistema óptico presente aberraciones, este frente de onda emergente ya no será esférico, sino que se distorsionará, tal y como se ha comentado anteriormente.

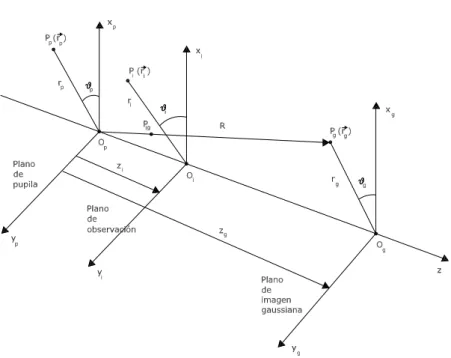
Figura 2.3: Esquema de formación de la imagen gaussiana para un objeto puntual. Fijemos nuestra atención en uno de los múltiples rayos que, provenientes del objeto, atraviesan el sistema óptico, y sea W ( ~r_p; ~r₀) la aberración de onda de un rayo que pasa por el plano de la pupila de salida por un punto Pp cuya posición viene

(29)

Figura 2.4: Sistema de coordenadas en la pupila de salida, en el plano de imagen gaussiana y en un plano imagen cualquiera.

La amplitud compleja en P_p debida a un elemento ∆ ~r₀ centrado en ~r₀ se puede escribir como:

∆Uex( ~rp; ~r0) = P ( ~rp; ~r0)e(−iks) (2.26)

donde s representa la distancia entre el punto considerado y el punto correspondiente en el plano imagen gausiano, Pg, es decir:

s =

q

z2

g+ |~rp− ~rg|2 (2.27)

mientras que P (~r_p; ~r₀), definida como:

P (~r_p; ~r₀) = A(~r_p; ~r₀)e[ikW (~rp;~r0)] _{, en el interior de la pupila de salida}

= 0 , en el exterior de la pupila de salida (2.28) recibe el nombre de funci´on de pupila del sistema. La funci´on de amplitud A(~rp; ~r0),

denominada función de apodización, representa la variación de amplitud de la on-da a lo largo de la pupila de salion-da.

(30)

2.3. Propagaci´on de im´agenes aberradas 37 La intensidad en el punto P_p del plano de la pupila de salida debida al elemento ∆ ~r₀

considerado viene determinada por:

I_p(~r_p; ~r₀) = |∆U_ex(~r_p; ~r₀)|2 = |P (~r_p; ~r₀)|2 = A2(~r_p; ~r₀) (2.29) y la potencia correspondiente en la pupila de salida se obtiene integrando la intensidad para toda la pupila:

Pex(~r0) =

Z

|P (~rp; ~r0)|2d~rp =

Z

A2(~rp; ~r0)d~rp (2.30)

2.3.2. Distribuci´on de luz en un plano arbitrario

Consideremos ahora la propagaci´on de una onda desde el plano de la pupila de salida hasta un plano de observaci´on situado a una distancia arbitraria zi. Para ello

utili-zaremos la f´ormula de Rayleigh - Sommerfeld [BW99] para describir la propagaci´on de una onda desde un plano z = 0 hasta un plano cualquiera situado a distancia z, tal y como se muestra en la figura 2.5.

Figura 2.5: Propagaci´on de una onda. C´alculo de la amplitud compleja en el plano z a partir de la amplitud compleja en el plano z = 0.

Esta relaci´on se puede expresar como:

U (~r; z) = 1 λ Z U (~r0_{; 0)} µ 1 kl − i ¶ z l eikl l d~r0 (2.31)

donde l representa la distancia P0_{P entre el punto origen (~}_r0_{; 0) y el punto de}

obser-vaci´on (~r; z), es decir:

l =

q

(31)

Para valores grandes de z, kl >> 1, y l ≈ z, y por lo tanto, podemos realizar las siguientes aproximaciones:

1. despreciar el valor de _kl1 frente a la unidad, 2. considerar el valor de z

l equivalente a la unidad,

3. sustituir l por z (excepto en el exponente, donde se encuentra multiplicado por

k) para valores de z mucho mayores que el tama˜no de la pupila de salida. Si ahora sustituimos la ecuaci´on 2.26 en la expresi´on 2.31, podemos escribir la am-plitud compleja en el plano zi como:

∆Ui(~ri; ~r0; zi) = −_λz1 i

Z

P (~rp; ~r0)e[ik(l−s)]d~rp (2.33)

donde l corresponde a la distancia desde el punto de observaci´o Pi hasta el punto Pp

situado en la pupila de salida:

l =

q

zi2+ |~rp− ~ri|2 (2.34)

Si ahora desarrollamos el t´ermino l − s obtenemos:

l − s = (zi− zg) +1₂ µ r2 i z_i − r2 g z_g ¶ − 1 z_i~rp· µ ~ri−_zzi g ~rg ¶ +1 2 µ 1 z_i − 1 z_g ¶ r_p2 −1 8 µ r4 i z3 i − r 4 g z3 g ¶ − 1 8 µ 1 z3 i − 1 z3 g ¶ r_p4 +1 2r 3 p µ r_i z3 i cos θpi− r_g z3 g cos θpg ¶ −1 2r 2 p µ r2 i z3 i cos θ2_pi−r 2 g z3 g cos θ_pg2 ¶ −1 4r 2 p µ r2 i z3 i − r 2 g z3 g ¶ + 1 2rp µ r3 i z3 i cos θpi− r3 g z3 g cos θpg ¶ + · · · (2.35)

Cada uno de los términos presentes en el desarrollo depende de las posiciones del plano imagen gaussiano zg y del plano de observación zi, y equivale a un término

de fase al multiplicarse por k, aunque no todos ellos representan aberraciones en el sentido clásico de la acepción. Es interesante destacar el término

Wd(~rp; ~ri; ~rg) = l − s + _z1 i~rp· µ ~ri−_zzi g~rg ¶ (2.36) denominado aberración de la onda difractada [HS78], puesto que esta aberra-ción se encuentra relacionada únicamente con la propagación de la onda, y no con las caracter´ısticas f´ısicas del sistema óptico.

(32)

2.3. Propagación de imágenes aberradas 39 De la expresión 2.35 podemos despreciar todos los términos excepto los cuatro pri-meros en el caso de que se cumpla que:

µ 1 z3 i − 1 z3 g ¶ a4 < λ 8 (2.37)

donde a es el m´aximo valor de rp. Esta condici´on equivale a imponer que la

contri-bución de la aberración esférica sea menor a λ₈. En este caso, la amplitud compleja puede escribirse como:

∆Ui(~ri; ~r0; zi) = −_λzii exp

½ ik · (zi− zg) + 1₂ µ r2 i zi − r2 g zg ¶¸¾ ×R P (~rp; ~r0; zi) exp · −2πi_λzi~rp· µ ~ri−_zgzi~rg ¶¸ d~rp (2.38)

En esta expresi´on, P (~rp; ~r0; zi) corresponde a la denominada funci´on desenfocada

de pupila, e indica que la imagen es observada en un plano diferente del plano ima-gen paraxial. P (~r_p; ~r₀; z_i) = P (~r_p; ~r₀) exp · ik 2 µ 1 zi − 1 zg ¶ r2_p ¸ (2.39) Analizando la expresión 2.39, se puede considerar que se encuentra compuesta de dos términos claramente diferenciados: por un lado, la función pupila del sistema:

P (~rp; ~r0) = A(~rp; ~r0)e[ikW (~rp;~r0)] , en el interior de la pupila de salida

= 0 , en el exterior de la pupila de salida (2.40) donde W (~rp; ~r0) indica la diferencia de caminos ´opticos entre un rayo cualesquiera

y el rayo principal al propagarse hasta la esfera de referencia gaussiana. Por otra parte, en el supuesto de que el plano de observación no coincida con el plano paraxial, aparece el término de desenfoque, el cual representa la longitud del camino óptico añadido que debe recorrer un rayo hasta la nueva esfera de referencia desenfocada, centrada ahora en el nuevo plano de observación:

∆W = 1 2 µ 1 zi − 1 zg ¶ r_p2 (2.41)

As´ı, puesto que el plano de observaci´on no corresponde al paraxial, sino que se en-cuentra desplazado respecto a ´este una distancia ∆z = zi− zg, la esfera de referencia

estará centrada en la posición de dicho plano de observación, con lo que zi = R. Se

debe tener en cuenta, además, que si el objeto es puntual y se encuentra situado sobre el eje óptico, la posición de su imagen gaussiana será ~rg = (0, 0).

(33)

Por lo tanto, considerando todos estos aspectos, la expresión 2.38 se puede reescribir como: ∆U_i= − i λzi exp ½ ik · (z_i− z_g) + r2i 2zi ¸¾ Z P (~r_p; ~r₀; z_i) exp · −2πi λzi ~r_p· ~r_i ¸ d~r_p = − i λzi exp · ik∆z ¸ exp · ikx2i + y2i 2zi ¸ Z P (~rp; ~r0; zi) exp · −2πi µ xpxi+ ypyi λzi ¶¸ d~rp = − i λRexp · 2πi λ ∆z ¸ exp · 2πi λ x2 i + y2i 2R ¸ Z P (~r_p; ~r₀; z_i) exp · −2πi µ x_px_i+ y_py_i λR ¶¸ d~r_p (2.42) Dejando de lado términos constantes irrelevantes, de manera que las expresiones se simplifiquen, y si a partir de ahora denominamos a las coordenadas (x_p, y_p) simple-mente como (x, y) la distribución de luz en el plano imagen se puede escribir como [HY70]: U (xi, yi) = exp · 2πi λ x2 i + y2i 2R ¸ Z Abertura P (x, y) exp · −2πi µ xxi+ yyi λR ¶¸ dxdy (2.43)

donde P(x,y) corresponde a la funci´on generalizada de pupila:

P (x, y) = A(x, y)ei2πλW (x,y) (2.44)

En esta ´ultima expresión, A(x, y) representa la transmitancia de la pupila (que corres-ponderá a la imagen mostrada en el modulador) y W(x,y) la aberración de onda. Por otro lado, el término de fase cuadrática presente en la expresión 2.43 se anula en la segunda etapa de la difracción en un correlador, de manera que de las ecuaciones 2.43 y 2.44 resulta que la calidad de la transformada de Fourier de A(x, y) dependerá ´unica y exclusivamente de la aberración de onda del sistema.