59
4
ANALISI DEL SEGNALE: RICHIAMI
Qualsiasi dato osservato, rappresentante un fenomeno fisico, può essere classificato, in generale, all’interno di due grandi categorie ovvero quella dei dati deterministici e quella dei dati aleatori.
Nella prima categoria rientrano tutti quei dati che possono essere descritti da una relazione matematica esplicita, mentre al contrario nella seconda categoria rientrano quei dati che possono essere descritti soltanto in termini probabilistici e statistici, dati per i quali l’evoluzione futura del fenomeno che li ha generati non può essere predetta utilizzando i dati di un esperimento. Tale classificazione può essere facilmente criticabile in quanto si può pensare che non esistano dati fisici puramente deterministici, poiché vi può essere sempre la possibilità di un evento futuro inaspettato che può mutare le caratteristiche dei dati stessi; è altresì vero che non esistono dati fisici puramente aleatori, in quanto una conoscenza più approfondita del fenomeno potrebbe portare ad una esatta descrizione matematica del medesimo.
L’unico modo per stabilire a quale delle due suddette categorie appartenga un fenomeno fisico, e dunque i dati da esso prodotti, è quello di seguire la via sperimentale; se un esperimento può essere ripetuto molte volte e porta sempre agli stessi risultati (tenendo conto degli errori sperimentali) allora i dati che ne derivarono possono essere generalmente classificati come deterministici, mentre se ciò non si verifica tali dati possono essere considerati aleatori.
60
4.1 Processi aleatori
Un esperimento effettuato su un fenomeno di carattere aleatorio rappresenta soltanto una delle possibili realizzazioni fisiche che il fenomeno poteva avere; pertanto per studiarlo correttamente si dovrebbe considerare l’insieme di tutte le possibili storie che possono essere prodotte.
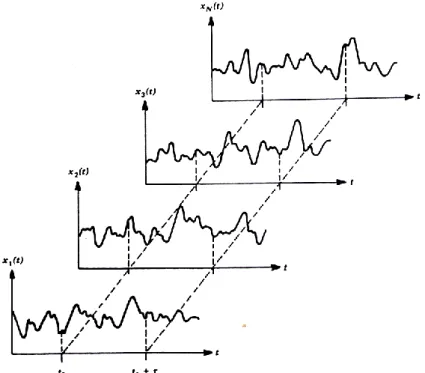
La singola storia temporale è chiamata “funzione campione”, mentre l’insieme di tutte le possibili storie è chiamato “processo aleatorio”.
Figura 4.1: Insieme di storie temporali che definiscono un processo aleatorio (Bendat, 2000).
I processi aleatori possono essere suddivisi in processi non stazionari e processi stazionari; tra quest’ultimi si possono individuare processi non ergodici e processi ergodici. Per poterne definire le peculiarità bisogna prima definire alcune quantità statistiche di interesse.
Siano e una coppia di processi aleatori arbitrari e siano e le funzioni densità di probabilità associate rispettivamente alle variabili aleatorie e
61
Detti e due istanti diversi, si definiscono le funzioni di covarianza:
Nel caso in cui i valori medi e assieme alle funzioni di covarianza , , forniscano lo stesso risultato per qualsiasi valore fissato di t, i due processi si dicono debolmente stazionari. Nel caso in cui tutte le possibili distribuzioni di probabilità coinvolgenti e siano indipendenti dalla traslazione nel tempo, i processi sono detti fortemente stazionari.
I processi stazionari aleatori vengono detti debolmente ergodici se i valori medi e le funzioni di covarianza (o di correlazione), che sono stati in precedenza definiti per mezzo del concetto di media di insieme, possono essere calcolati tramite le corrispondenti medie temporali valutate su una singola ed arbitraria funzione campione. In generale infatti la media temporale, le funzioni di cross-covarianza e di autocovarianza risultano funzione del particolare campione scelto (identificato dall’indice k):
62
dove , , sono le funzioni di autocorrelazione e di cross-correlazione definite, in termini generali, come
Pertanto in termini funzionali i due processi stazionari aleatori in considerazione sono debolmente ergodici se:
Se oltre a quelle suddette anche tutte le altre proprietà statistiche basate sulla media di insieme sono deducibili dalle corrispondenti grandezze basate sulla media temporale, i processi sono detti fortemente ergodici.
Fortunatamente, in pratica, i processi stazionari aleatori rappresentanti fenomeni fisici sono generalmente ergodici.
Le condizioni sufficienti a stabilire l’ergodicità di un processo sono essenzialmente due:
1. condizione sufficiente affinché un processo aleatorio arbitrario sia debolmente ergodico è che esso sia debolmente stazionario e che le medie temporali e le funzioni di autocovarianza siano le stesse per ogni funzione campione k;
2. condizione sufficiente affinché un processo aleatorio Gaussiano sia ergodico è che esso sia debolmente stazionario e la funzione di autocovarianza sia tale che:
Questa ultima condizione viene talvolta indicata come teorema ergodico. Le violazioni all’equazione precedente sono solitamente associate alla presenza di
63
componenti periodiche nei dati. Bisogna però osservare che, essendo questa una condizione sufficiente e non necessaria per l’ergodicità, le medie temporali in luogo delle medie di insieme sono giustificate anche in presenza di violazioni alla precedente equazione e, quindi, anche in presenza di componenti periodiche; in questi casi bisogna verificare che le medie temporali di realizzazioni diverse siano le stesse.
4.2 Correlazione tra due processi aleatori
Siano e due processi aleatori ergodici. Per valori arbitrari di e esiste il seguente legame tra le funzioni di covarianza e di correlazione:
Le funzioni di correlazione pertanto sono uguali a quelle di covarianza solo nel caso in cui i valori medi siano nulli. Due processi stazionari aleatori sono scorrelati se
per ogni τ; ciò avviene nel caso in cui oppure se e . Le funzioni di correlazione nel caso stazionario godono delle seguenti proprietà:
che permettono un indagine completa dal solo studio della τ > 0. Si dimostra valere (Bendat [2]) la disuguaglianza di cross-covarianza
Indicando con la deviazione standard e dunque con la varianza, dal momento che risulta
64 la disuguaglianza di cross-covarianza diventa
In questo modo si giunge alla definizione del coefficiente di correlazione , ovvero la funzione di cross-covarianza normalizzata
Tale coefficiente risulta compreso tra i valori -1 e +1 e rappresenta un indice del grado di dipendenza lineare tra e . Nel caso in cui o siano zero si può scrivere
Si ricorda infine come i concetti di processi scorrelati e di processi indipendenti si basino su due definizioni diverse. Infatti, due variabili aleatorie e si definiscono statisticamente indipendenti se
dove e rappresentano le funzioni densità di probabilità di e mentre rappresenta la funzione densità di probabilità congiunta. Come conseguenza si può scrivere:
Dal momento che la funzione di cross-covarianza può scriversi come
risulta evidente che se due variabili aleatorie sono statisticamente indipendenti esse sono anche scorrelate, essendo nulla la funzione di cross-covarianza. In generale, invece, non è detto che due variabili aleatorie scorrelate siano anche indipendenti (ciò risulta vero nel caso di variabili con distribuzione Gaussiana).
65
4.3 Serie e trasformata di Fourier
Il teorema dello sviluppo in serie di Fourier, che è alla base della moderna teoria dei segnali, afferma che: “Qualunque funzione, purché periodica, può essere scomposta in una somma di termini sinusoidali e cosinusoidali, aventi ampiezze variabili e frequenze tra loro multiple”.
Se , quindi, è una funzione periodica di periodo T definita per , essa può essere rappresentata attraverso la cosiddetta serie di Fourier:
dove
È necessario, inoltre, precisare che la possibilità di calcolare lo sviluppo in serie di Fourier dipende dal verificarsi delle seguenti tre condizioni (dette condizioni di Dirichlet) che si aggiungono a quella della periodicità già indicata:
a) se la funzione ha delle discontinuità, il loro numero deve essere finito in ciascun periodo;
b) la funzione deve contenere, in un periodo, un numero finito di massimi e minimi;
c) la funzione deve essere assolutamente integrabile in un periodo, il che significa che deve valere la seguente condizione:
66
Per facilitare gli sviluppi analitici si preferisce usare una forma alternativa della serie di Fourier. Utilizzando le formule di Eulero e definendo un coefficiente complesso
si può scrivere
Per semplificare la notazione matematica e costruire la serie di Fourier in forma complessa, è utile introdurre, solo matematicamente e senza alcun significato fisico, le frequenze negative; pertanto va considerato compreso tra e . Si può così scrivere la forma complessa della serie di Fourier:
Per rappresentare la sequenza è conveniente tracciare due grafici che prendono il nome di spettro di ampiezza e spettro di fase. Il primo illustra l’andamento dell’ampiezza (modulo) dei coefficienti , il secondo ne illustra l’andamento della fase, entrambi in funzione dell’ordine k del coefficiente o del valore della k-esima frequenza armonica.
Molti segnali che si osservano nei fenomeni naturali non sono però periodici. Sorge allora immediata la questione della possibilità di ottenere una scomposizione simile alla serie di Fourier anche per le forme d’onda non periodiche.
Supponiamo adesso che sia una funzione periodica il cui periodo T diventa sempre più grande; la corrispondente pulsazione, coincidente con la fondamentale dello sviluppo di Fourier, diminuisce e di conseguenza le armoniche successive diverranno sempre più ravvicinate fra di loro. Lo spettro della funzione diventa, quindi, sempre più denso: al limite, per si otterrà una copertura totale dell’asse delle pulsazioni, e la successione delle armoniche tenderà a diventare una funzione continua di .
Da un punto di vista matematico, occorre quindi valutare il limite a cui tende l’espressione dei coefficienti di Fourier.
Per la pulsazione diventa infinitesima ed è valido il seguente insieme di relazioni:
Utilizzando la forma esponenziale dello sviluppo e con queste sostituzioni i coefficienti di Fourier diventano:
67
La sommatoria, originariamente definita per valori finiti di , tende quindi a diventare una somma di infiniti infinitesimi e cioè un integrale. Si può quindi scrivere:
La quantità fra parentesi quadre è una funzione di , che si può chiamare , che sarà definita come:
e che prende il nome di trasformata di Fourier della .
Sostituendo quanto ricavato, nella forma precedente si ha poi:
che prende il nome di antitrasformata di Fourier.
In analogia a quanto visto per i coefficienti di Fourier , si è soliti estrarre dalla funzione complessa le funzioni reali modulo e fase secondo la relazione
La funzione rappresenta lo spettro di ampiezza del segnale, la funzione il suo spettro di fase. Naturalmente, i due spettri forniscono informazioni sull’ampiezza e sulla fase delle componenti frequenziali alla generica pulsazione in cui il segnale viene scomposto dall’operazione di trasformata.
Si può, quindi, indicare la condizione sufficiente per la rappresentazione del segnale attraverso la propria trasformata di Fourier .
Se tale condizione è soddisfatta è possibile affermare che la conoscenza dell’andamento nel tempo del segnale è equivalente alla conoscenza dell’andamento frequenziale della relativa trasformata di Fourier.
68
Riassumendo, se un segnale è di tipo periodico e soddisfa le condizioni dello sviluppo in serie di Fourier, è possibile determinare i coefficienti dello sviluppo delle singole armoniche ed i valori di fase di ciascuno di questi segnali. Viceversa, se il segnale in esame non è periodico (e quindi si può assumere il suo periodo T di valore ) si può ricorrere alla trasformata di Fourier che porta ad una funzione continua nel dominio della frequenza sia per quanto riguarda l’ampiezza sia per quanto riguarda la fase.
Per un processo stazionario , definito teoricamente su un intervallo infinito di tempo, la condizione sufficiente in non è rispettata e quindi la trasformata di Fourier non esiste. Comunque, restringendo il campo di integrazione ad un intervallo di tempo finito, diciamo , allora la può essere stimata calcolando la trasformata finita di Fourier:
Assumendo che venga campionato e rappresentato con valori spaziati di , la lunghezza del campione diviene e la funzione continua viene rimpiazzata dalla sequenza discreta di dati
Per arbitraria, la versione discreta della diviene
Usualmente la scelta delle frequenze discrete per il calcolo di risulta la seguente:
Si hanno così le componenti di Fourier
Alcune conseguenze di questa formula sono riportate di seguito, dove l’asterisco ad apice indica il complesso coniugato:
69
Si noti che i risultati sono unici solo fino in quanto per tale valore si raggiunge la frequenza di Nyquist (definita nel paragrafo 4.5).
4.4 Funzioni di densità spettrale di potenza
La funzione densità spettrale di potenza per un segnale ad energia finita è definita come:
ed ha le seguenti proprietà
1. è una funzione della frequenza reale a valori non negativi: ; 2. se il segnale è reale, la sua densità spettrale di potenza è una funzione
pari: ;
3. la potenza di un segnale si può calcolare integrando la sua densità spettrale di potenza su tutto l’asse delle frequenze: .
Scelto un valore arbitrario di frequenza, la quantità infinitesima
rappresenta il contributo alla potenza totale del segnale fornito dalle componenti frequenziali prossime a .
Per facilitare il calcolo della densità spettrale di potenza si preferisce rifarsi al teorema di Wiener-Khintchine, secondo il quale la densità spettrale è calcolabile come trasformata di Fourier della funzione di correlazione. Quindi dati due segnali e , rappresentanti due fenomeni stazionari ergodici, il cross-spettro è definito da:
70
Dalle proprietà di simmetria delle funzioni di correlazione stazionarie date in segue che (dove l’asterisco ad apice indica il complesso coniugato):
Quindi e sono funzioni non negative a valore reale pari, mentre è una funzione a valori complessi.
Si può dimostrare che
dove e è il quadrato del valor medio dei dati. Quindi, a meno che il valore medio dei dati non sia nullo, lo spettro presenta una funzione nell’origine; per questo motivo ai dati sperimentali conviene sottrarre il valore medio prima di calcolare lo spettro.
Le funzioni di densità spettrale, d’ora in avanti indicate più brevemente come autospettro e cross-spettro, sono definite su tutte le frequenze, sia positive che negative. Per questo motivo la è chiamata spettro a due lati. Si definisce anche la densità spettrale ad un lato tramite:
71
chiamati rispettivamente funzione di densità spettrale coincidente, o cospettro, e funzione di densità spettrale di quadratura. Nella pratica è usuale presentare il cross-spettro in termini di ampiezza e angolo di fase:
dove
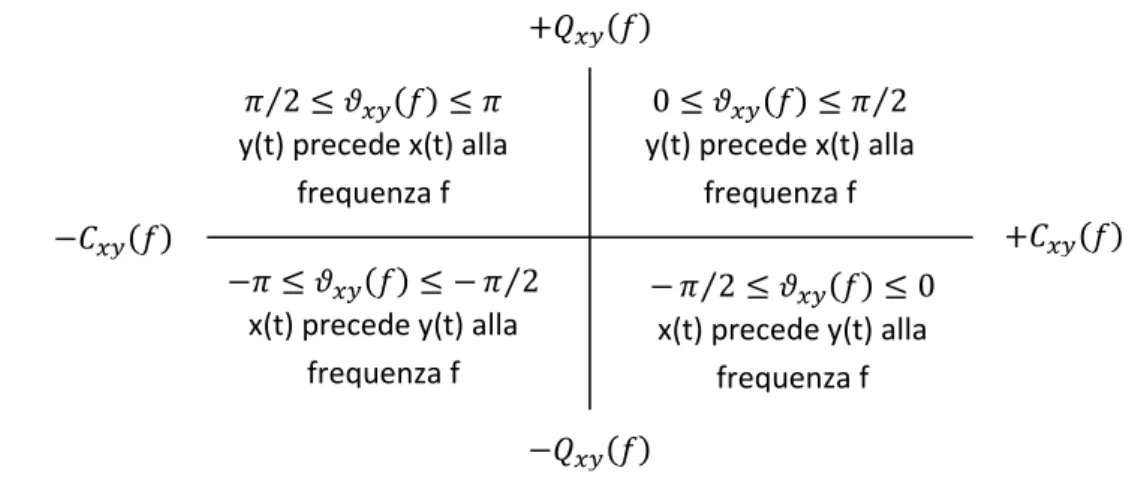
Il segno dei termini e può essere positivo o negativo e determina il quadrante dell’angolo di fase . Il segno determina inoltre, alla generica frequenza f, se x(t) segue y(t) o viceversa (vedi figura sotto).
Figura 4.2: Relazione tra l’angolo di fase e i termini del cross-spettro.
Si fa notare, infine, che nel passato, per il calcolo della densità spettrale, veniva utilizzato il teorema di Wiener-Khintchine portando ad un tempo di calcolo molto lungo. Oggigiorno, invece, il calcolo è basato sull’uso della trasformata rapida di Fourier (FFT) che permette tempi molto più brevi.
Una relazione molto importante che coinvolge l’ampiezza del cross-spettro è la cosiddetta diseguaglianza del cross-spettro:
Questa relazione dà luogo alla definizione di funzione di coerenza, che è una funzione reale tra 0 ed 1 la quale dà una misura della correlazione tra e ad ogni frequenza :
y(t) precede x(t) alla frequenza f
y(t) precede x(t) alla frequenza f
x(t) precede y(t) alla frequenza f
x(t) precede y(t) alla frequenza f
72
Nel caso di sistema lineare la funzione di coerenza tra segnale di ingresso e segnale di uscita avrà valore unitario.
4.5 Teorema del campionamento e sue conseguenze
Si supponga che la trasformata di Fourier di un certo segnale esista solo in un intervallo di frequenze che va da a Hz e sia nulla alle altre frequenze. La reale banda di frequenze realizzabile risulta quella da a Hz. La trasformata inversa di Fourier restituisce x(t)
Si assuma ora che sia continuamente ripetuta in modo da ottenere una funzione periodica in frequenza con periodo di Hz. L’incremento fondamentale di tempo risulta pertanto ed è detto intervallo di Nyquist. Usando l’espansione in serie di Fourier si ha:
dove
Dall’equazione si ha infine:
In questo modo determina e dunque ad ogni ; questa a sua volta determina per ogni . Questo risultato rappresenta il teorema del campionamento nel dominio del tempo. E’ anche possibile sviluppare il teorema del campionamento nel dominio della frequenza (Bendat[2]).
73
Assumendo che il segnale esista solo in un intervallo di tempo da a secondi e supponendo inoltre che la sua trasformata esista soltanto nell’intervallo di frequenze da a Hz (questa doppia assunzione non è teoricamente possibile ma può essere in pratica realizzata adottando intervalli di tempo finiti e filtri passa-banda), occorrono soltanto un numero finito di campionamenti discreti di o di per descrivere completamente il comportamento di per ogni .
Campionando ad intervalli di tempo pari all’intervallo di Nyquist dal tempo fino a , il numero di campionamenti richiesti per descrivere risulta:
Esso rappresenta il numero minimo di valori discreti campionati richiesti per descrivere un segnale di lunghezza ed ampiezza di banda . Il massimo intervallo di campionamento risulta pertanto .
Figura 4.3: Campionamento di un segnale analogico (Bendat, 2000).
Se si adottassero intervalli di campionamento otterremmo valori campionati ridondanti, col rischio di aumentare eccessivamente i tempi di calcolo, mentre se adottassimo ciò porterebbe confusione tra le componenti a bassa ed alta frequenza (aliasing).
74
Il rateo di campionamento risulta sps (punti per secondo) e la più alta frequenza che può essere definita da tale rateo risulta Hz. Frequenze superiori a Hz appariranno così inferiori a Hz e si confonderanno con frequenze più basse. Tale frequenza limite prende il nome di frequenza di Nyquist:
Per ogni frequenza nell’intervallo , le frequenze più alte di , che sono confuse con , sono definite da:
Ad esempio se = 100 Hz allora i dati a 30 Hz saranno confusi e mescolati con i dati a frequenze di 170 Hz, 230 Hz, 370 Hz, 430Hz e così via. Per evitare gli errori dovuti al fenomeno dell’ “aliasing” bisognerebbe rimuovere le informazioni a frequenze maggiori di quella di Nyquist; ciò può essere realizzato ad esempio tramite un filtro passa-basso prima della conversione analogico-digitale, impostando per sicurezza la frequenza di cut-off a circa l’80% di (Bendat[2]).
75
4.6 Bibliografia
[1] M.Antonelli, M.Salsa, “Corso di Telecomunicazioni”,Hoepli, Milano, 2001
[2] J.S.Bendat, A.G.Piersol, “Random Data: Analysis and Measurement Procedures”, Wiley-Interscience, New York, 2000
[3] M.Luise, G.M.Vitetta, “Teoria dei Segnali”, McGraw-Hill, Milano, 1999
[4] D.E.Newland, “An Introduction to Random Vibrations and Spectral Analysis”, Longman, London, 1975