POLITECNICO DI MILANO
Facoltà di Ingegneria Industriale
Corso di Laurea Magistrale in
Ingegneria Spaziale
Caratterizzazione di un polimero ionomerico autoriparante per
applicazioni spaziali
Relatore: Prof. Luca Angelo DI LANDRO Co-relatore: Ing. Antonio Mattia GRANDE
Tesi di Laurea di:
Luca CASTELNOVO Matr. 719498
I
Indice
Indice ... I Indice della tabelle ... V Indice delle figure ... III Sommario ... VI Abstract ... VI
1. Introduzione ... 1
1.1. La gestione del danno ... 1
1.2. Tipologie di materiali autoriparanti ... 1
1.2.1. Microcapsule ... 2
1.2.2. Materiali compositi autoriparanti ... 4
1.2.3. Riparazione mediante riscaldamento ... 7
1.3. Gli ionomeri ... 8
1.3.1. Struttura molecolare ... 8
2. Materiale ... 13
2.1. Surlyn® 8940 ... 13
2.2. Processo di produzione dei campioni ... 13
2.3. Proprietà termiche ... 14
2.4. Proprietà meccaniche ... 16
2.4.1. Prove di torsione in frequenza ... 16
2.4.2. Costruzione della curva maestra ... 17
2.4.3. Prove di trazione veloce ... 21
2.4.4. Prove di trazione in temperatura... 31
3. Modelli analitici ... 33
3.1. Calcolo dello sforzo di snervamento ... 33
3.1.1. Modello di Eyring... 34
3.2. Modello della deformazione plastica ... 38
3.2.1. Modello Johnson-Cook ... 39
3.2.2. Modello Viscoelasto-plastico ... 41
3.2.3. Modello WTS ... 44
3.2.4. Modello a tre reti ... 49
4. Test di qualifica per impiego spaziale ... 57
4.1. L’ambiente spaziale ... 57 4.1.1. Attività solare ... 57 4.1.2. Radiazioni ... 60 4.1.3. Ossigeno atomico ... 62 4.1.4. Pressione ... 62 4.1.5. Impatti... 63
II
4.2. I test di qualifica spaziale ... 65
4.3. Test di outgassing ... 66
4.4. Test di impatto ad ipervelocità ... 69
4.5. Test di tenuta della riparazione ... 71
5. Conclusione ... 75
5.1. Possibilità applicative ... 75
5.1.1. Miscele ... 75
5.1.2. Serbatoi autosigillanti ... 76
5.1.3. Strutture multistrato per applicazioni spaziali ... 77
5.2. Sviluppi futuri ... 79
III
Indice delle figure
Figura 1.1. Processo di autoriparazione con microcapsule[1]. ... 3
Figura 1.2. Processo di autoriparazione con fibre contenenti resina. ... 5
Figura 1.3. Rappresentazione schematica della regione a mobilità ridotta attorno ad un multiplet di polistirene co-metacrilato di sodio[7]. ... 9
Figura 1.4. Rappresentazione schematica della variazione di morfologia interna al variare della concentrazione ionica: (a) bassa, (b) intermedia, (c) elevata. ... 10
Figura 1.5. Rappresentazione schematica del cambiamento della struttura molecolare al variare della temperatura[9]. ... 11
Figura 1.6. Rappresentazione schematica del fenomeno di ion hopping [9]. ... 12
Figura 2.1. Preparazione della fase di stampaggio del materiale. ... 14
Figura 2.2. Risultati della prova al DSC di un campione di Surlyn® 8940. ... 15
Figura 2.3. Risultati sperimentali della prova di trazione in frequenza. ... 17
Figura 2.4. Andamento dello shift factor al variare della temperatura. ... 19
Figura 2.5. Curva maestra 𝐺’ per il Surlyn® 8940 a 23°C. ... 19
Figura 2.6. Curva maestra 𝐺′′ per il Surlyn® 8940 a 23°C. ... 20
Figura 2.7. Andamento del modulo 𝐺′ con la temperatura. ... 20
Figura 2.8. Disegno del campione utilizzato (dimensioni in mm). ... 21
Figura 2.9. Curva sforzo-deformazione ingegneristica a 0.1mm/s. ... 23
Figura 2.10. Curva sforzo-deformazione ingegneristica a 1mm/s. ... 23
Figura 2.11. Curva sforzo-deformazione ingegneristica a 10mm/s. ... 24
Figura 2.12. Curva sforzo-deformazione ingegneristica a 100mm/s. ... 24
Figura 2.13. Curva sforzo-deformazione ingegneristica a 250mm/s. ... 25
Figura 2.14. Curva sforzo-deformazione ingegneristica a 500mm/s. ... 25
Figura 2.15. Curva sforzo-deformazione reale e andamento della temperatura a 0.1mm/s. ... 26
Figura 2.16. Curva sforzo-deformazione reale e andamento della temperatura a 1mm/s. ... 27
Figura 2.17. Curva sforzo-deformazione reale e andamento della temperatura a 10mm/s. ... 27
Figura 2.18. Curva sforzo-deformazione reale a 100mm/s. ... 28
Figura 2.19. Curva sforzo-deformazione reale a 250mm/s. ... 28
Figura 2.20. Curva sforzo-deformazione reale a 500mm/s. ... 29
Figura 2.21. Confronto delle curve sforzo-deformazione reali alle diverse velocità. ... 29
Figura 2.22. Termografia del provino sottoposto a trazione alla velocità di 1mm/s immediatamente prima e dopo la rottura. ... 30
Figura 2.23. Termografia del provino sottoposto a trazione alla velocità di 10mm/s immediatamente prima e dopo la rottura. ... 30
IV
Figura 2.24. Confronto tra le curve sforzo-deformazione ingegneristiche a temperature diverse. ... 31 Figura 2.25. Confronto tra un campione nuovo (a) e i campioni testati alle
temperature di: -40°C (b), -20°C (c), 0°C (d), 23°C (e), 40°C (f) e 60°C (g). ... 32 Figura 3.1. Definizioni dello sforzo di snervamento. ... 34 Figura 3.2. Barriera potenziale nel modello di Eyring. ... 35 Figura 3.3. Andamento dello sforzo di snervamento in funzione della velocità di deformazione a temperature diverse. ... 36 Figura 3.4. Approssimazione dei dati sperimentali con il modello di Eyring. ... 37 Figura 3.5. Confronto tra i dati sperimentali ed il modello di Eyring. ... 38 Figura 3.6. Calcolo delle costanti 𝐴, 𝐵 ed 𝑛. ... 40 Figura 3.7. Confronto tra le curve sforzo-deformazione reali e quelle ottenute
mediante il modello di Johnson-Cook. ... 41 Figura 3.8. Schema del modello viscoelasto-plastico. ... 42 Figura 3.9. Confronto tra i risultati del modello viscoelasto-plastico e le curve
sperimentali. ... 44 Figura 3.10. Confronto tra dati sperimentali e modello WTS per la prova a
0,1mm/s... 47 Figura 3.11. Confronto tra dati sperimentali e modello WTS per la prova a
1mm/s... 48 Figura 3.12. Confronto tra dati sperimentali e modello WTS per la prova a
500mm/s... 48 Figura 3.13. Rappresentazione reologica del modello a tre reti [20]. ... 49 Figura 3.14. Confronto tra il modello a tre reti e i dati sperimentale per la prova
a 0.1mm/s. ... 53 Figura 3.15. Confronto tra il modello a tre reti e i dati sperimentale per la prova
a 1mm/s. ... 53 Figura 3.16. Confronto tra il modello a tre reti e i dati sperimentale per la prova
a 10mm/s. ... 54 Figura 3.17. Confronto tra il modello a tre reti e i dati sperimentale per la prova
a 100mm/s. ... 54 Figura 3.18. Confronto tra il modello a tre reti e i dati sperimentale per la prova
a 250mm/s. ... 55 Figura 3.19. Confronto tra il modello a tre reti e i dati sperimentale per la prova
a 500mm/s. ... 55 Figura 4.1. Rappresentazione dello spettro solare all’esterno dell’atmosfera e al
livello del mare in comparazione con lo spettro di un corpo nero. .. 58 Figura 4.2. Andamento dell’indice F10.7 osservato negli ultimi 60 anni. ... 60 Figura 4.3. Rappresentazione del campo magnetico terrestre. ... 61 Figura 4.4. Flusso complessivo di meteoriti in relazione alla loro massa [15]. . 64 Figura 4.5. Elaborazione grafica degli oggetti monitorati in orbita attorno alla
V
Figura 4.6. Andamento della temperatura durante la prova. ... 67
Figura 4.7. Andamento della pressione in camera durante il test. ... 68
Figura 4.8. Sistema di sparo CISAS... 69
Figura 4.9. Immagine al SEM della zona d’impatto del campione 8813: (a) foro d’ingresso, (b) foro d’uscita. ... 71
Figura 4.10. Immagine al SEM della zona d’impatto del campione 8839: (a) foro d’ingresso, (b) foro d’uscita. ... 71
Figura 4.11. Schema costitutivo del dispositivo di verifica della tenuta della riparazione. ... 72
Figura 4.12. Andamento della pressione durante i test di tenuta dei campioni. . 73
Figura 5.1. Esempio di funzionamento di un serbatoio autosigillante. ... 77
Figura 5.2. Elaborazione grafica di un prototipo di struttura gonfiabile per esplorazione lunare. ... 78
Figura 5.3. Rappresentazione schematica di una struttura multistrato. ... 79
Indice delle tabelle
Tabella 2.1. Campioni utilizzati. ... 22Tabella 3.1. Parametri utilizzati per il modello di Eyring. ... 38
Tabella 3.2. Parametri utilizzati nel modello. ... 52
Tabella 4.1. Risultati del test di outgassing. ... 68
Tabella 4.2. Risultati delle prove d’impatto ad ipervelocità. ... 70
VI
Sommario
In questo lavoro si è studiato il polimero ionomerico EMAA (Polietilene co-metacrilato acido), noto con il nome commerciale di Surlyn® e fornito dalla casa produttrice DuPont™, in relazione alle sue proprietà autoriparanti esibite in caso di impatti balistici. Lo studio si è sviluppato in una prima fase di caratterizzazione meccanica del materiale mediante prove sperimentali di trazione a diverse velocità di deformazione e a diverse temperature. Si è quindi cercato un modello analitico, tra quelli già disponibili in letteratura, che descrivesse al meglio il comportamento esibito dal materiale durante le prove sperimentali, così da poterlo in futuro implementare in un codice ad elementi finiti. Allo stesso tempo si è iniziata una campagna di qualifica del materiale per impiego in applicazioni spaziali attraverso prove di outgassing e di impatto ad ipervelocità, valutando l’efficacia del processo di autoriparazione.
Parole chiave: Polimero autoriparante, Ionomero, Modelli analitici per
materiali, Qualifica spaziale, Outgassing, Impatti ad ipervelocità.
Abstract
In this work Poly(ethylene-co-methacrylic acid) (EMAA) ionomeric polymer, commercially known as Surlyn® provided by DuPont™, was investigated for its self healing behavior exhibited after ballistic impacts. The study consists in a first phase of mechanical characterization of material behavior through experimental tensile tests at different strain rates and temperatures. Next several analytical models, available in literature, were applied to best describe the behavior of the material observed experimentally. The best model could be included in future in a finite element model. Meanwhile a space qualification campaign was started through outgassing and hypervelocity impacts tests, verifying the self healing process effectiveness.
Keywords: Self healing polymer, Ionomer, Analytical material model, Space
1
1. Introduzione
1.1. La gestione del danno
La maggior parte dei progetti strutturali esistenti sono condotti secondo il concetto, ormai assodato in svariati campi dell’ingegneria, di prevenzione del danno (damage prevention), ovvero con l’obiettivo di evitare che le strutture si danneggino sotto l’effetto delle sollecitazioni che si prevede incontreranno durante l’intera vita operativa. In molti casi, però, non è possibile garantire la totale assenza di danni ed è quindi necessario intervenire con opere di manutenzione o riparazione per prolungare la vita operativa delle strutture danneggiate ed evitare conseguenze potenzialmente catastrofiche.
Recentemente tuttavia, il continuo progresso delle tecnologie e dei materiali nonché la continua espansione degli ambiti di utilizzo hanno reso gli interventi di manutenzione sempre più difficili, se non addirittura impossibili. Un chiaro esempio di ciò è costituito dalle strutture operanti nello spazio; quello spaziale, infatti, è un ambiente ostile, non solo per gli esseri viventi, ma anche per i materiali e i dispositivi che compongono un sistema spaziale. In molti casi, dunque, un danno, magari di lieve entità sulla Terra, si può tradurre nel fallimento dell’intera missione e nella perdita dell’intero sistema, con danni elevati. In ambito spaziale, infatti, gli interventi di riparazione sono spesso impossibili o comunque molto complessi e costosi.
Si è dunque affermata una nuova metodologia progettuale basata non più sulla prevenzione ma sulla gestione del danno (damage management); progettando così strutture che possano gestire e porre rimedio all’insorgenza di un danno senza interventi esterni.
In quest’ottica appare evidente come lo studio di materiali in grado di riparare autonomamente (self healing) gli eventuali danni rivesta un ruolo di centrale importanza. La ricerca in questo settore è ancora ad uno stato iniziale e non si possono ancora costruire strutture in grado di autorigenerarsi, ma vi sono tutti i presupposti per importanti sviluppi futuri.
1.2. Tipologie di materiali autoriparanti
La possibilità di conferire capacità autoriparanti ai materiali compositi e polimerici ha favorito, negli ultimi anni, la nascita di un gran numero di nuove ricerche in diverse parti del mondo. Ciò ha portato allo sviluppo di numerose
2
idee e proposte diverse per ottenere materiali autoriparanti che potessero trovare un largo impiego in diversi settori industriali.
In questo paragrafo saranno descritte brevemente alcune soluzioni tra quelle proposte che destano il maggior interesse sia a livello accademico sia in ottica di applicazioni industriali, con particolare riferimento alle problematiche tipiche del settore spaziale.
1.2.1. Microcapsule
La prima idea di molti ricercatori viene direttamente dall’osservazione dei fenomeni di autoriparazione che avvengono spontaneamente in natura e si basa sul concetto di fornire al materiale una riserva di un agente riparante allo stato liquido che, in caso di necessità, potesse raggiungere la zona danneggiata e riparare il danno. La soluzione trovata da White e dai suoi collaboratori nel 2001 consiste nell’inserire all’interno di un materiale polimerico una serie di microcapsule riempite con un monomero liquido che agisca da agente riparante. In caso di danno al materiale, ad esempio una cricca, le capsule si rompono a causa delle concentrazioni di sforzo agenti nella cricca lasciando uscire il liquido all’interno. Il monomero quindi fluisce all’interno della cricca fino ad incontrare un catalizzatore, anch’esso disciolto nella matrice polimerica, che attiva la reazione di polimerizzazione riparando di fatto la cricca e ripristinando le caratteristiche meccaniche del materiale. L’azione autoriparante messa in atto in questo tipo di materiali è ben schematizzata in Figura 1.1.
3
Figura 1.1. Processo di autoriparazione con microcapsule[1].
L’impiego delle microcapsule è di fatto il primo esempio di materiale polimerico autoriparante e costituisce senza dubbio uno dei maggiori progressi compiuti in questo campo. Tuttavia, nonostante molti studi abbiano migliorato significativamente il primo campione, questo tipo di tecnologia conserva ancora alcune criticità specifiche, in particolare:
• Dimensione delle capsule: devono infatti essere sufficientemente grandi per contenere una adeguata quantità di agente riparante ma tali da non influenzare le proprietà meccaniche della matrice
• Spessore delle pareti: devono essere sufficientemente sottili da rompersi in presenza della cricca ma contemporaneamente garantire l’impermeabilità rispetto al liquido contenuto
4
• Catalizzatore: deve poter essere distribuito uniformemente all’interno della matrice polimerica in modo da entrare facilmente in contatto con l’agente riparante
• Reazione di polimerizzazione: deve avvenire spontaneamente al contatto tra monomero liquido e catalizzatore con tempi di reazione molto brevi I migliori risultati in questo campo sono stati ottenuti utilizzando microcapsule realizzate in poli(urea-formaldeide) dell’ordine di 100𝜇𝑚, riempite con
poli(diciclopentadiene) come agente riparante, disperse in una matrice a base
epossidica drogata con un catalizzatore di Grubbs di prima generazione [2]. L’impiego di questo tipo di materiali garantisce una riparazione efficace dei danni di piccole dimensioni ma non consente la riparazione di quelli più grandi, quali ad esempio i fori causati da un impatto balistico. La riparazione mediante microcapsule, inoltre, presenta alcuni svantaggi considerevoli; primo su tutti non garantisce la ripetibilità dell’effetto riparante: una volta rotte le microcapsule, infatti, non è più possibile un’ulteriore riparazione di un altro danno nella stessa porzione di materiale.
Questi materiali sono inoltre stati analizzati in relazione ad un possibile utilizzo in ambito spaziale [3]. Tali studi hanno rilevato alcune problematiche che limitano fortemente le possibilità di utilizzo della tecnologia a microcapsule nell’ambiente spaziale. Il problema principale è dovuto alla coesistenza all’interno del materiale di due fasi distinte, una fase solida costituita dalla matrice e dal catalizzatore e una fase liquida costituita dall’agente riparante. Per garantire tale coesistenza, infatti, è necessario che le temperature operative siano tali da mantenere l’agente riparante in forma liquida; la temperatura inoltre influenza anche l’azione del catalizzatore. Inoltre non è ancora stato stimato con certezza il tempo di vita operativa del materiale; questo dipende soprattutto dalla diffusione del monomero liquido attraverso le pareti delle microcapsule.
In realtà, alcuni di questi problemi potrebbero essere risolti in futuro; attualmente, infatti, esiste una vasta gamma di materiali e processi produttivi per la realizzazione delle microcapsule, la conservazione dell’agente riparante e l’inserimento del catalizzatore che non sono ancora stati analizzati. I materiali autoriparanti con microcapsule, dunque, conservano ancora un notevole potenziale per la ricerca in ambito spaziale.
1.2.2. Materiali compositi autoriparanti
La seconda soluzione proposta si pone l’obiettivo di conferire proprietà autoriparanti ai materiali compositi rinforzati con fibre. Il meccanismo di autoriparazione proposto è molto simile a quello visto per le microcapsule; in questo caso, però, la configurazione del materiale è completamente diversa. L’idea, infatti, è quella di inserire all’interno della matrice di un tradizionale materiale composito rinforzato con fibre un sistema “vascolare” che garantisca
5 l’approvvigionamento dell’agente riparante, in questo caso una resina a bassa viscosità, all’interno del materiale. Anche in questo caso l’ispirazione deriva direttamente dall’osservazione dei fenomeni di autoriparazione naturale tipici degli organismi viventi.
Il vantaggio principale di questa architettura è quello di garantire un afflusso continuo di agente riparante nella zona interessata dal danno consentendo quindi una certa ripetibilità dell’azione riparante, altrimenti impossibile con la tecnologia delle microcapsule. Grazie alla presenza delle tradizionali fibre di rinforzo, poi, questi materiali garantiscono prestazioni meccaniche superiori a qualsiasi altro materiale autoriparante realizzato mediante microcapsule e spesso anche superiori allo stesso materiale composito originale. Le capacità autoriparanti, inoltre, consentono di porre rimedio anche alle delaminazioni interne tipiche dei materiali compositi. La grande versatilità di configurazione dei materiali compositi, poi, consente una progettazione ad hoc del sistema vascolare, ad esempio infittendo il numero dei vasi contenenti la resina nelle zone più esposte a possibili danni o soggette a carichi maggiori.
L’azione autoriparante, come detto, è molto simile a quella delle microcapsule: in caso di rottura l’agente riparante fuoriesce dal sistema vascolare riempiendo la cricca fino ad incontrare il catalizzatore, disciolto nella matrice, che innesca il processo di polimerizzazione (Figura 1.2).
6
L’ampia disponibilità di nuove tecnologie emerse dalla ricerca sui materiali compositi ha reso possibile lo sviluppo di diverse soluzioni per la realizzazione del sistema vascolare [2]. Di seguito saranno brevemente descritte le principali.
Fibre di vetro cave. L’utilizzo delle fibre di vetro cave quali vasi capillari per il
trasporto della resina evidenzia al meglio i vantaggi dei materiali compositi autoriparanti. Infatti, sebbene l’aggiunta di queste fibre comporti una diminuzione della resistenza iniziale del materiale, la maggiore tolleranza ai danni e la conseguente azione riparante compensano ampiamente questo effetto. L’azione riparante, infatti, consente al materiale di recuperare fino al 97% delle sue prestazioni meccaniche originarie.
Nanotubi in carbonio. L’utilizzo dei nanotubi in carbonio a parete singola è
emerso negli ultimi anni e presenta alcuni aspetti molto interessanti. I nanotubi, infatti, conferiscono al materiale resistenza meccanica e conducibilità elettrica e possono essere utilizzati come vasi per l’approvvigionamento dell’agente riparante.
Sistemi microvascolari. Questo tipo di sistemi sono stati studiati per riprodurre
la rete di capillari tipica del derma umano. Questa soluzione molto complessa dal punto di vista realizzativo consente un regolare afflusso di resina in ogni parte del materiale e garantisce un’efficienza di riparazione dell’ 80%.
Per questo tipo di materiali valgono gran parte delle considerazioni già fatte per i materiali con microcapsule; rispetto a questi ultimi, tuttavia, garantiscono prestazioni meccaniche di molto superiori e offrono una certa ripetibilità dell’azione autoriparante, comunque limitata dalla quantità di resina disponibile. I principali svantaggi di questa tecnologia sono dati dalla dimensione dei vasi di contenimento della resina molto superiori rispetto alle normali fibre di rinforzo, dalla necessità di impiego di resine a bassa viscosità e dal processo di riempimento dei vasi. Un ulteriore problema, poi, soprattutto per le applicazioni in ambito spaziale può essere la differenza di coefficiente di dilatazione termica nei materiali “ibridi”, ossia che impiegano materiali diversi per i vasi di contenimento della resina e le fibre di rinforzo.
Molte delle problematiche relative all’utilizzo dei materiali compositi autoriparanti in campo spaziale, infine, sono già state affrontate per materiali compositi tradizionali, già provati ed utilizzati in diverse missioni spaziali. Da questo punto di vista, quindi, i materiali compositi autoriparanti si pongono in una posizione di vantaggio per un possibile impiego operativo in future missioni spaziali [4].
7
1.2.3. Riparazione mediante riscaldamento
I materiali autoriparanti reversibili sono quei materiali che garantiscono una ripetibilità teoricamente infinita dell’azione autoriparante; in questa categoria, dunque, potrebbero rientrare anche gli ionomeri presentati precedentemente. A differenza degli ionomeri, tuttavia, i materiali qui presentati richiedono un intervento esterno per attivare il processo di autoriparazione. Con intervento esterno, in generale, si intende l’apporto di calore o pressione nell’area interessata dal danno. Tale intervento, di fatto, può essere automatizzato implementando un sistema di sensori e attuatori che agiscano autonomamente. Proprio per questo motivo questi materiali rientrano nel novero dei materiali autoriparanti e sono oggetto di numerose ricerche. Tali ricerche hanno portato allo sviluppo di un gran numero di materiali con capacità autoriparanti che richiedono uno stimolo esterno basati su diversi principi di funzionamento. Di seguito saranno descritti brevemente alcuni dei principi che stanno alla base delle proposte più interessanti presentate negli ultimi anni [2].
Reazione di Diels-Alder. La reazione di Diels-Alder, detta più precisamente cicloaddizione, è una reazione termoreversibile tra due reagenti (detti diene e dienofilo) ideale per la sintesi di polimeri riparabili dal momento che non
richiede la presenza di un catalizzatore. Il primo polimero di Diels-Alder con capacità autoriparanti è stato sintetizzato nel 2003 da Wudl; tale materiale, se scaldato ad una temperatura di 120°𝐶, è in grado di riparare le fratture ripristinando l’83% delle proprietà meccaniche iniziali. Da allora sono stati sviluppati numerosi materiali basati sulla reazione di Diels-Alder in grado di recuperare completamente le proprietà iniziali anche dopo un elevato numero di cicli frattura/riparazione.
Legami idrogeno. A differenza dei legami covalenti, i legami idrogeno
presentano un’energia di legame molto più bassa; per questo motivo per rompere e riformare i legami idrogeno è necessaria una quantità di energia molto inferiore di quanto non avvenga per i legami covalenti. Ciò ha consentito lo sviluppo di materiali con capacità autoriparanti che richiedessero uno stimolo esterno di minore entità rispetto ad esempio alla reazioni di Diels-Alder. Tali materiali, infatti, possono essere riparati semplicemente avvicinando i due lembi della frattura per qualche istante. Il processo è riproducibile e consente di ripristinare totalmente le proprietà meccaniche del materiale anche dopo numerose ripetizioni. Tuttavia è necessario che i lembi della frattura siano avvicinati il più rapidamente possibile dopo il danno, in quanto le unità altamente reattive dei legami idrogeno potrebbero reagire con le altre vicine sullo stesso lembo della frattura rendendo impossibile la riparazione. Ciò costituisce un grosso limite alle possibilità di utilizzo di tali materiali che comunque rimangono un settore di ricerca interessante.
8
Questi materiali offrono il grande vantaggio di garantire la ripetibilità dell’azione autoriparante per numero molto elevato di cicli (teoricamente infinito). Per contro, la necessità di disporre di un sistema di controllo automatico che possa fornire lo stimolo richiesto nella zona interessata dal danno costituisce certamente un aggravio importante alla semplicità e soprattutto all’affidabilità del sistema. Per questo motivo, al momento, sembra più difficile un impiego di questi materiali in campo spaziale.
1.3. Gli ionomeri
Gli ionomeri sono una particolare categoria di polimeri che contengono una certa percentuale di ioni (fino al 20%) e costituiscono, finora, il più promettente tra tutti i tipi di materiali autoriparanti. Gli ionomeri sono noti da oltre quarant’anni e sono già utilizzati in numerosi ambiti commerciali: dal confezionamento di alimenti e cosmetici alle attrezzature sportive come scarponi da sci e palline da golf.
Il loro comportamento autoriparante, tuttavia, è stato scoperto di recente e solo da una decina di anni si è approfondito lo studio della struttura degli ionomeri in relazione alle capacità autoriparanti [5] [6]. Il fenomeno di autoriparazione che avviene negli ionomeri, infatti, è di particolare interesse scientifico, in quanto è un fenomeno che si manifesta spontaneamente a seguito di impatti in cui le energie in gioco siano sufficientemente elevate. In particolare, è stato osservato nel caso del passaggio di un proiettile nel materiale, evento molto rapido e che comporta una notevole quantità di energia. Durante l’impatto parte dell’energia cinetica del proiettile è trasferita al materiale sotto forma di energia elastica e calore; sembra essere proprio il giusto bilanciamento tra queste due forme di energia ad attivare il processo di autoriparazione
1.3.1. Struttura molecolare
È ormai assodato che il comportamento autoriparante esibito dagli ionomeri sia dovuto alla loro particolare struttura molecolare, ed in particolare ai gruppi ionici presenti in essa.
Gli ionomeri sono prodotti dalla neutralizzazione dei gruppi ionici di un copolimero contenente ripetizioni di gruppi ionici e non ionici. Tali gruppi ionici, in molti casi, sono inizialmente gruppi acidi attaccati alla catena polimerica che, una volta neutralizzati, danno origine ad una coppia di ioni unita ad un catione metallico. Il processo di neutralizzazione porta quindi alla formazione di un polimero con gruppi ionici all’interno della struttura polimerica, ovvero uno ionomero. Il contenuto ionico di uno ionomero, infine, dipende dal numero di gruppi acidi neutralizzati in fase di produzione.
9 Nel corso degli anni sono stati proposti vari modelli per spiegare la particolare struttura molecolare e le proprietà di questi materiali [7]. Già nel 1970 Eisenberg propose un modello teorico per spiegare la tendenza delle coppie ioniche a raggrupparsi in regioni all’interno del materiale [8]. Questi aggregati, costituiti puramente da materiale ionico, sono chiamati multiplets e sono caratterizzati da una massa piuttosto contenuta e da forti interazioni elettrostatiche. La forma e il numero di coppie ioniche presenti in ciascun multiplet dipende da diversi fattori, tra cui il contenuto ionico, la flessibilità della catena polimerica e la costante dielettrica del materiale. Infatti, una bassa costante dielettrica del polimero e una bassa 𝑇𝑔 favoriscono l’aggregazione delle coppie ioniche, al contrario invece, una costante dielettrica e una 𝑇𝑔 elevate la inibiscono. Anche le forze elettrostatiche rivestono un ruolo di grande importanza nella formazione dei
multiplets; le coppie di ioni piccoli e altamente polari, infatti, interagiscono tra
loro in maniera più forte, portando alla formazione di gruppi ionici più saldi e di dimensioni maggiori.
I multiplets comportano la nascita di una regione a mobilità ridotta all’interno della catena polimerica, come mostrato in Figura 1.3; l’entità di tale riduzione di mobilità è influenzato da diversi fattori come il legame esistente tra catena e
multiplet, la densità e l’estensione della catena polimerica in prossimità del multiplet stesso.
Figura 1.3. Rappresentazione schematica della regione a mobilità ridotta attorno ad un multiplet
10
La dimensione di un singolo multiplet con la relativa regione di mobilità ridotta, riportata in Figura 1.3, non consente di manifestare la propria temperatura di transizione vetrosa. Aumentando il numero di ioni presenti, i multiplets si trovano ad essere molto vicini tra loro e, per effetto delle relazioni elettrostatiche, si genera una regione a mobilità ridotta molto più estesa all’interno della catena polimerica detta cluster.
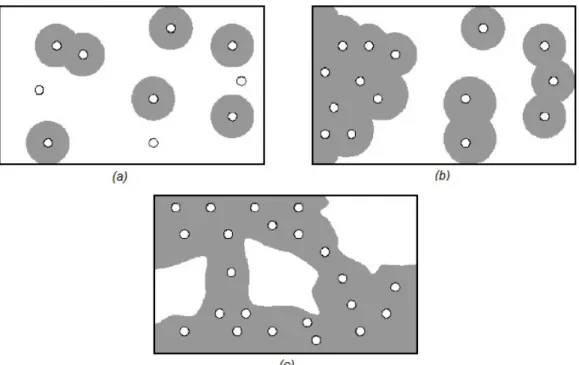
I cluster costituiscono una fase separata all’interno dello ionomero; la loro formazione è dovuta, come detto, alle forze elettrostatiche dei multiplets che prevalgono su quelle elastiche delle catene polimeriche cui i multiplets sono attaccati. Esiste poi una concentrazione critica di ioni al di sopra della quale il processo di formazione dei cluster risulta facilitato. In Figura 1.4 è mostrato come si modifichi la struttura interna del materiale all’aumentare della concentrazione dei gruppi ionici; i cerchi bianchi rappresentano i multiplets, mentre le aree grigie le regioni di mobilità ridotta attorno ad essi. Si può notare come, all’aumentare del numero di multiplets, si creino aggregati sempre più estesi, con relative zone di mobilità ridotta altrettanto estese. Le diverse conformazioni dei multiplets, e quindi degli aggregati ionici che ne derivano, sono responsabili delle proprietà fisiche e meccaniche degli ionomeri.
Figura 1.4. Rappresentazione schematica della variazione di morfologia interna al variare della
concentrazione ionica: (a) bassa, (b) intermedia, (c) elevata.
Un aspetto fondamentale della struttura interna degli ionomeri è dato dal fatto che i legami interni sono termo-reversibili: è questo, infatti, uno dei fattori
11 principali che conferiscono allo ionomero il comportamento autoriparante. Grazie a studi termici e calorimetrici è stato osservato il comportamento della struttura interna del materiale al variare della temperatura.
In condizioni normali, infatti, la struttura molecolare dello ionomero si presenta molto ordinata ed è possibile individuare facilmente al suo interno la struttura cristallina, quella amorfa e i cluster ionici. All’aumentare della temperatura si registra il passaggio da una struttura ordinata dei cluster ad una disordinata; tale passaggio avviene ad una temperatura (per la maggior parte degli ionomeri circa 50°𝐶) detta appunto temperatura di transizione ordine/disordine. Nella struttura disordinata i legami sono allentati e la mobilità molecolare aumenta; i cristalli tuttavia sono ancora visibili all’interno della struttura. Aumentando ulteriormente la temperatura i cristalli spariscono ed il materiale fonde completamente; il valore a cui si osserva questo fenomeno prende quindi il nome di temperatura di fusione (circa 90°𝐶).
In Figura 1.5 è schematizzata la variazione nella struttura interna dello ionomero al variare della temperatura. Si può notare che il fenomeno è reversibile, diminuendo cioè la temperatura si può recuperare la struttura ordinata iniziale. Sebbene la temperatura di ricristallizzazione differisca poco da quella di fusione, la riorganizzazione ordinata dei cluster richiede un tempo molto più lungo rispetto a quello necessario per la transizione ordine/disordine.
Figura 1.5. Rappresentazione schematica del cambiamento della struttura molecolare al variare
della temperatura[9].
Un altro fenomeno importante nella struttura molecolare degli ionomeri è noto con il nome di ion hopping, ovvero la tendenza di uno ione a passare (“saltare”) da un aggregato ionico all’altro (Figura 1.6). In virtù di tale fenomeno, dunque, gli aggregati ionici sono entità dinamiche; esiste quindi un tempo medio 𝜏 che indica il tempo di permanenza di un gruppo ionico in un aggregato prima di passare ad un altro. Questo fenomeno consente il rilassamento del tratto di
12
catena polimerica cui i gruppi ionici sono attaccati; ciò rende possibile la fusione del materiale a prescindere dalla fusione di tutti gli aggregati ionici presenti. La presenza degli aggregati ionici infatti, seppure in configurazione disordinata, è stata osservata anche all’interno dello ionomero fuso fino a temperature piuttosto elevate (circa 300°𝐶, prima del deterioramento del materiale); tale presenza è responsabile della maggiore viscosità degli ionomeri rispetto a polimeri simili non ionici. A livello macroscopico ciò permette al materiale di mantenere un comportamento elastico anche dopo la fusione; tale fattore, come si vedrà in seguito, è estremamente rilevante per il processo di autoriparazione.
13
2. Materiale
2.1. Surlyn
®8940
Gli ionomeri, come detto nel capitolo precedente, sono utilizzati già da parecchi anni in svariati ambiti commerciali; attualmente, dunque, sono disponibili in commercio diverse tipologie di ionomeri sviluppati da molte case produttrici. Per questo lavoro si è utilizzato lo ionomero prodotto dalla compagnia DuPont™ e distribuito con il nome commerciale Surlyn®. Il Surlyn® è una resina ionomerica termoplastica costituita da un copolimero avanzato a base di
etilene e acido metacrilico (EMAA) in cui i gruppi acidi (MAA) sono
parzialmente neutralizzati con ioni metallici. In commercio sono disponibili numerose qualità di Surlyn® che differiscono tra loro per la quantità di gruppi acidi neutralizzati e la tipologia di ioni metallici utilizzati; in questo lavoro si è scelto il Surlyn® 8940 che contiene il 30% di gruppi acidi neutralizzati con cationi di sodio. Questo prodotto, infatti, sembra presentare una migliore capacità di autoriparazione secondo diversi studi condotti negli ultimi dieci anni [6] [5].
Il Surlyn® è un prodotto molto versatile e pertanto trova molte applicazioni nella produzione industriale; presenta, inoltre, una trasparenza cristallina, anche su spessori elevati, che ne favorisce l’impiego come rivestimento su superfici esterne garantendo elevata lucidità, resistenza a impatti, graffi e abrasioni e protezione dagli agenti atmosferici. È particolarmente utilizzato quindi nella produzione di attrezzature sportive quali caschi, sci e palle da golf, come rivestimento in alcune parti di veicoli, oltre che per il confezionamento alimentare e di cosmetici.
2.2. Processo di produzione dei campioni
Il Surlyn® viene fornito in granuli di piccole dimensioni e si presta molto facilmente a diversi processi di lavorazione industriale come stampaggio, laminazione ed estrusione. I campioni per i test effettuati in questo lavoro sono stati prodotti per stampaggio mediante una pressa idraulica con piani riscaldabili elettricamente.
Prima della produzione effettiva il materiale deve essere condizionato per eliminare l’umidità eventualmente assorbita in precedenza. A tale scopo si è scaldato il materiale in forno alla temperatura di 60°𝐶 per circa due ore,
14
estraendo l’aria dall’interno. Una volta condizionato, il materiale è pronto per essere stampato.
Dal momento che la pressa utilizzata non consentiva un controllo sullo spessore dei campioni, tale controllo è stato effettuato pesando la giusta quantità di materiale da inserire nello stampo per ottenere lo spessore desiderato. Lo stampo realizzato in acciaio, è di forma quadrata di 120𝑚𝑚 di lato e può essere riscaldato elettricamente, così come il controstampo.
La procedura di stampaggio utilizzata consiste nell’introdurre il materiale nello stampo preriscaldato alla temperatura di 180°𝐶, quindi abbassare il controstampo, anch’esso alla medesima temperatura, ed esercitare pressione per qualche minuto. Successivamente le piastre della pressa, e quindi il campione, sono raffreddati da un circuito ad acqua che garantisce un rateo di raffreddamento di circa 10°𝐶/𝑚𝑖𝑛. Per evitare l’adesione del materiale alle superfici dello stampo e del controstampo si utilizzano dei fogli di Teflon® che, in questo modo, determinano la finitura superficiale dei campioni.
Il processo di produzione appena descritto è determinato principalmente dalle attrezzature presenti in laboratorio; a livello di produzione industriale, come detto, sono possibili altri tipi di lavorazioni che conferiscono al prodotto finale la forma e la trasparenza volute.
Figura 2.1. Preparazione della fase di stampaggio del materiale.
2.3. Proprietà termiche
La struttura molecolare dei polimeri, come già accennato in precedenza, subisce notevoli modifiche al variare della temperatura a cui si trova il materiale. Tali cambiamenti comportano naturalmente un diverso comportamento del materiale
15 e devono essere studiati attentamente per ciascun materiale, al fine di determinarne con esattezza il relativo campo di impiego. A tale scopo si effettuano delle analisi calorimetriche su un campione di materiale.
In questo caso sono state condotte delle prove al DSC (o Calorimetro
Differenziale a Scansione) per evidenziare le temperature corrispondenti alle
variazioni della struttura interna del materiale [10]. La misura differenziale consiste nel valutare la differenza di flusso termico tra il campione di materiale in analisi ed un campione di riferimento durante un ciclo completo di riscaldamento e raffreddamento del materiale. In Figura 2.2 sono riportati i risultati ottenuti nella prova costituita da due cicli termici completi consecutivi.
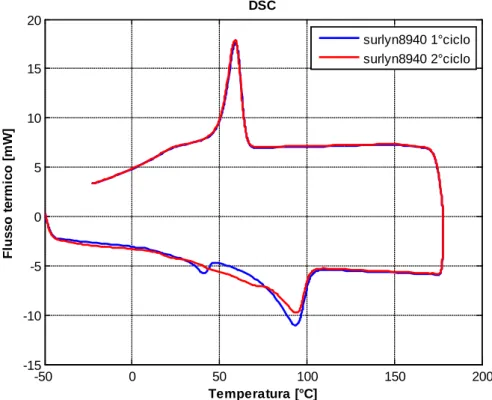
Figura 2.2. Risultati della prova al DSC di un campione di Surlyn® 8940.
Si possono notare tre picchi significativi nell’andamento del flusso termico durante la prova, due nella fase di riscaldamento del materiale (flusso termico negativo) e uno durante la fase di raffreddamento. Tali picchi corrispondono ad altrettanti cambiamenti nelle struttura del materiale.
1. Alla temperatura di circa 42°𝐶 si può notare un primo picco di assorbimento di calore da parte del materiale; ciò corrisponde al passaggio da una configurazione ordinata dei cluster ionici ad una configurazione disordinata. Tale temperatura prende quindi il nome di
temperatura di transizione ordine/disordine.
-50 0 50 100 150 200 -15 -10 -5 0 5 10 15 20 DSC Temperatura [°C] F lu sso t er m ico [ m W ] surlyn8940 1°ciclo surlyn8940 2°ciclo
16
2. Alla temperatura di circa 94°𝐶 si registra un altro picco di assorbimento di calore molto più intenso del precedente. La reazione endotermica che avviene qui è la fusione del materiale e la temperatura corrispondente è dunque la temperatura di fusione.
3. Alla temperatura di circa 60°𝐶 durante il processo di raffreddamento del materiale si registra un picco di cessione di calore da parte del materiale. In questo caso la reazione esotermica corrisponde alla formazione di una struttura cristallina all’interno del materiale; tale temperatura è quindi chiamata temperatura di cristallizzazione.
È interessante notare, infine, che nel secondo ciclo termico (identificato dalla curva rossa nel grafico di Figura 2.2) non compare più il picco corrispondente alla temperatura di transizione ordine/disordine. Questo effetto è dovuto al fatto che, a seguito del primo ciclo termico, non si è ancora recuperata la configurazione ordinata dei cluster ionici iniziale. Ciò conferma quanto anticipato in nel capitolo precedente, ovvero che il passaggio dallo stato disordinato allo stato ordinato richiede un tempo maggiore rispetto al passaggio inverso. Questa considerazione, infine, suggerisce anche di prevedere un periodo di invecchiamento del materiale, successivamente alla fase di produzione, affinché possa recuperare una struttura completamente ordinata dei
cluster. Il tempo necessario per questo processo è stato valutato in circa 38
giorni [11].
2.4. Proprietà meccaniche
2.4.1. Prove di torsione in frequenza
Per determinare il modulo di elasticità tangenziale del materiale non è possibile eseguire una semplice prova a sforzo di taglio, in quanto la forza necessaria per indurre una deformazione significativa nel materiale sarebbe troppo elevata. Per questo motivo il modulo 𝐺 è solitamente determinato attraverso prove di torsione. Lo stato di sforzo di puro taglio generato in queste prove è confermato dal fatto che durante le prove stesse non si osservino significative variazioni del volume del provino oggetto della prova.
Si sono dunque condotte prove di torsione su un provino di Surlyn® 8940 di forma rettangolare mediante l’uso di un reometro. Questo strumento, infatti, consente di imporre al provino, a diverse temperature, una deformazione torsionale con andamento sinusoidale del tipo:
17 Tale deformazione comporta la nascita di uno sforzo di puro taglio, anch’esso armonico di frequenza pari a quella della deformazione:
𝜏 = (𝐺𝑠(𝜔) + 𝑖𝐺𝑙(𝜔))𝛾0𝑒𝑥𝑝 (𝑖𝜔𝑡) (2.2)
In cui 𝐺𝑠 e 𝐺𝑙 sono rispettivamente la componente conservativa e dissipativa del modulo di elasticità tangenziale:
𝐺∗(𝜔) = 𝐺
𝑠(𝜔) + 𝑖𝐺𝑙(𝜔) (2.3)
Il modulo di elasticità tangenziale, tuttavia, non dipende solamente dalla frequenza (e quindi dal tempo) ma anche dalla temperatura. Per questo motivo sono state condotte prove a diverse temperature nell’intervallo compreso tra −150°𝐶 e 80°𝐶, considerando per ciascuna di esse un intervallo di frequenze tra 0.5𝐻𝑧 e 50𝐻𝑧. I risultati della prova in termini di 𝐺′ sono riportati in Figura 2.3.
Figura 2.3. Risultati sperimentali della prova di trazione in frequenza.
2.4.2. Costruzione della curva maestra
Per la costruzione della curva maestra del materiale in esame si è sfruttato il postulato di equivalenza tempo-temperatura tipico dei materiali polimerici. Esso pone in relazione l’influenza che la temperatura ed il tempo (o in questo caso la frequenza) hanno sulla risposta del materiale. Si nota, infatti, che il tempo e la
10-2 10-1 100 101 102 103 0 500 1000 1500 2000 2500 3000 Frequenza [Hz] G '[ M P a]
Prova di torsione in frequenza
-153°C 23°C 78°C
18
temperatura hanno lo stesso effetto sui materiali polimerici mentre la frequenza (che dimensionalmente è l’inverso di un tempo) ha l’effetto opposto. In particolare, quindi, l’effetto delle temperature basse è lo stesso dei tempi brevi (e quindi delle frequenze alte) e comporta una risposta più fragile del materiale; l’effetto delle alte temperature, invece, è lo stesso dei tempi lunghi (e quindi delle frequenze basse) e presuppone un comportamento più elastico. La spiegazione di questa correlazione va cercata a livello della struttura molecolare dei polimeri: la temperatura infatti influenza la mobilità molecolare del materiale che a sua volta comporta una variazione della cinetica (dipendenza dal tempo) con cui il materiale risponde ad una sollecitazione meccanica.
Il postulato di equivalenza tempo-temperatura è estremamente importante nella sperimentazione sui materiali polimerici in quanto consente di prevederne il comportamento. Infatti, se l’effetto della temperatura è solo quello di variare la velocità dei fenomeni viscoelastici interni al materiale, si può prevedere la risposta a tempi non accessibili sperimentalmente effettuando esperimenti a temperature diverse: più alte per ottenere la risposta a tempi lunghi, più basse per i tempi brevi.
I dati ottenuti sperimentalmente a temperature diverse (mostrati in Figura 2.3), dunque, possono essere considerati come tratti della medesima curva alla temperatura di riferimento (in questo caso 23°C) traslati per effetto della temperatura lungo l’asse logaritmico delle frequenze. Sulla base di queste considerazioni si può quindi ricostruire la curva completa della risposta del materiale alla temperatura di riferimento, nota come curva maestra (master
curve). Per poter effettuare la traslazione è necessario definire uno shift factor,
ovvero un fattore di spostamento definito come il rapporto tra le due frequenze a cui il modulo 𝐺′ assume, a temperature differenti, lo stesso valore. Mediante lo
shift factor, quindi si possono traslare le porzioni di curva a temperature diverse
lungo l’asse delle frequenze così che i valori coincidenti di 𝐺’ vadano a sovrapporsi. Costruendo la curva maestra si verifica sperimentalmente il postulato di equivalenza tempo-temperatura.
In Figura 2.4 è riportato l’andamento dello shift factor in funzione della temperatura; in Figura 2.5 e Figura 2.6 sono riportate le curve maestre rispettivamente delle componenti conservativa e dissipativa del modulo di elasticità tangenziale. In Figura 2.7, infine, è riportato ancora l’andamento del modulo 𝐺′ in funzione della temperatura: si può notare l’effetto inverso rispetto all’andamento in frequenza (Figura 2.5) a ulteriore conferma della validità del principio di equivalenza tempo-temperatura.
19
Figura 2.4. Andamento dello shift factor al variare della temperatura.
Figura 2.5. Curva maestra 𝑮’ per il Surlyn® 8940 a 23°C.
-200 -150 -100 -50 0 50 100 10-10 10-5 100 105 1010 1015 1020 1025 1030 Shift Factor T [°C] [-] 10-10 100 1010 1020 1030 100 101 102 103 104 Master curve G' Frequenza [Hz] G '[ M P a]
20
Figura 2.6. Curva maestra 𝑮′′ per il Surlyn® 8940 a 23°C.
Figura 2.7. Andamento del modulo 𝑮′ con la temperatura.
10-20 10-10 100 1010 1020 1030 1040 10-2 10-1 100 101 102 103 Master curve G" Frequenza [Hz] G "[M P a ] -200 -150 -100 -50 0 50 100 100 101 102 103 104 Master curve G' T [°C] G '[ M P a]
21
2.4.3. Prove di trazione veloce
Nei polimeri le prestazioni meccaniche, quali ad esempio il modulo elastico e lo sforzo di snervamento, non sono costanti ma dipendono contemporaneamente da diversi parametri tra cui la velocità di deformazione del materiale e la temperatura. Nel caso degli ionomeri, poi, esiste anche una correlazione diretta tra velocità di deformazione e temperatura. Si è osservato, infatti, che durante il processo di deformazione il materiale si scalda progressivamente e il fenomeno diventa sempre più evidente all’aumentare della velocità di deformazione. Tale riscaldamento è probabilmente dovuto allo svolgimento delle catene polimeriche che allineandosi rilasciano energia e quindi calore.
Per analizzare meglio questi fenomeni si sono condotte delle prove di trazione a diverse velocità di deformazione; tali prove sono anche state registrate con l’ausilio di una termo camera ad infrarossi per evidenziare i cambiamenti di temperatura. Le velocità utilizzate nelle diverse prove sono riportate in Tabella 2.1; per ciascuna velocità si sono testati tre campioni.
I campioni impiegati nelle prove sono stati ricavati da lastre di Surlyn® 8940, prodotte come descritto nel paragrafo 2.2, dello spessore di circa 2mm e presentano la forma riportata in Figura 2.8, in accordo con la normativa ASTM D1708.
22
Tabella 2.1. Campioni utilizzati.
Campione Velocità di allungamento [mm/s] Velocità di deformazione [s-1] Spessore [mm] 1 A 0.1 0.0045 2.08 2 B 0.1 0.0045 1.87 3 C 0.1 0.0045 2.13 4 A 1 0.0455 2.00 5 B 1 0.0455 1.97 6 C 1 0.0455 1.95 7 A 10 0.4545 1.90 8 B 10 0.4545 2.04 9 C 10 0.4545 1.80 10 A 100 4.5455 1.86 11 B 100 4.5455 2.10 12 C 100 4.5455 2.09 13 A 250 11.3636 2.04 14 B 250 11.3636 2.00 15 C 250 11.3636 1.87 16 A 500 22.7273 1.82 17 B 500 22.7273 2.02 18 C 500 22.7273 1.85
Le prove sono state effettuate utilizzando uno strumento MTS modello 858; le immagini termiche, invece, sono state ottenute mediante una termo camera Nikon Laird S270.
Nelle figure da 2.9 a 2.14 sono riportate le curve sforzo-deformazione relative alle prove effettuate calcolate con il metodo ingegneristico, secondo le relazioni:
𝜎𝑒=𝐴𝐹
0 (2.4)
𝜀𝑒 =𝐿∆𝑙
0 (2.5)
In cui 𝐴0 è l’area iniziale della sezione del provino e 𝐿0 è la lunghezza iniziale del tratto utile del provino.
23
Figura 2.9. Curva sforzo-deformazione ingegneristica a 0.1mm/s.
Figura 2.10. Curva sforzo-deformazione ingegneristica a 1mm/s.
0 0.5 1 1.5 2 2.5 3 3.5 4 0 5 10 15 20 25 30 0.1 mm/s εe [-] σe [ M P a] A B C 0 0.5 1 1.5 2 2.5 3 3.5 4 0 5 10 15 20 25 30 1 mm/s εe [-] σe [ M P a] A B C
24
Figura 2.11. Curva sforzo-deformazione ingegneristica a 10mm/s.
Figura 2.12. Curva sforzo-deformazione ingegneristica a 100mm/s.
0 0.5 1 1.5 2 2.5 3 3.5 4 0 5 10 15 20 25 30 10 mm/s εe [-] σe [ M P a] A B C 0 0.5 1 1.5 2 2.5 3 3.5 4 0 5 10 15 20 25 30 100 mm/s εe [-] σe [ M P a] A B C
25
Figura 2.13. Curva sforzo-deformazione ingegneristica a 250mm/s.
Figura 2.14. Curva sforzo-deformazione ingegneristica a 500mm/s.
0 0.5 1 1.5 2 2.5 3 3.5 4 0 5 10 15 20 25 30 250 mm/s εe [-] σe [ M P a] A B C 0 0.5 1 1.5 2 2.5 3 3.5 4 0 5 10 15 20 25 30 500 mm/s εe [-] σe [ M P a] A B C
26
L’approccio ingegneristico, però, non consente di identificare correttamente gli sforzi reali all’interno del materiale; durante la prova, infatti, il tratto utile del provino, sottoposto a trazione, subisce una strizione che ne fa variare l’area della sezione. Per tener conto di questa variazione è necessario calcolare gli sforzi e le deformazioni effettive all’interno del campione attraverso le relazioni [12]:
𝜀𝑡 = ln(1 + 𝜀𝑒) (2.6)
𝜎𝑡 = 𝜎𝑒exp (𝜀𝑒) (2.7)
Nelle figure da 2.15 a 2.20 sono riportate le curve sforzo-deformazione reali per le prove effettuate; per le velocità più basse, finché è stato possibile acquisire i dati con la termo camera, è riportato anche l’incremento di temperatura registrato in funzione della deformazione. In Figura 2.21, poi, è riportato un confronto tra le curve sforzo-deformazione reali ottenute a diverse velocità di deformazione.
Figura 2.15. Curva sforzo-deformazione reale e andamento della temperatura a 0.1mm/s.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 0 50 100 150 0.1 mm/s ε t [-] σt [ M P a] 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 ∆ T [ °C] 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 A B C
27
Figura 2.16. Curva sforzo-deformazione reale e andamento della temperatura a 1mm/s.
Figura 2.17. Curva sforzo-deformazione reale e andamento della temperatura a 10mm/s.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 0 50 100 150 1 mm/s εt [-] σt [ M P a] 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 ∆ T [ °C] 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 A B C 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 0 50 100 150 10 mm/s εt [-] σt [ M P a] 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 ∆ T [ °C] 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.60 20 40 60 A B C
28
Figura 2.18. Curva sforzo-deformazione reale a 100mm/s.
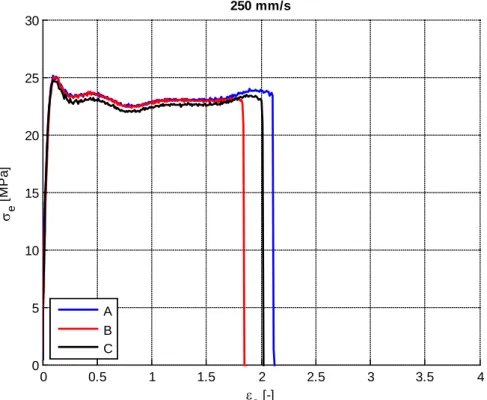
Figura 2.19. Curva sforzo-deformazione reale a 250mm/s.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 0 50 100 150 100 mm/s εt [-] σt [ M P a] A B C 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 0 50 100 150 250 mm/s εt [-] σt [ M P a] A B C
29
Figura 2.20. Curva sforzo-deformazione reale a 500mm/s.
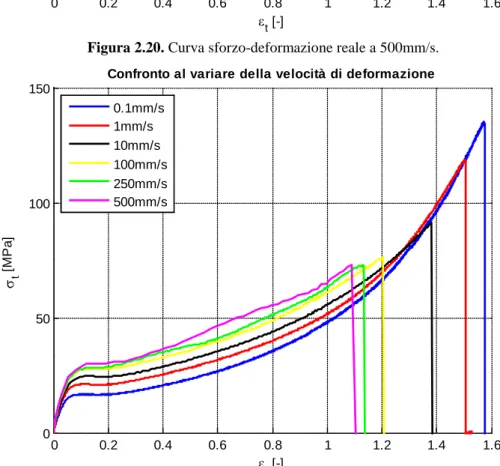
Figura 2.21. Confronto delle curve sforzo-deformazione reali alle diverse velocità.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 0 50 100 150 500 mm/s εt [-] σt [ M P a] A B C 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 0 50 100 150 εt [-] σt [ M P a]
Confronto al variare della velocità di deformazione 0.1mm/s 1mm/s 10mm/s 100mm/s 250mm/s 500mm/s
30
Di seguito, infine, sono riportate alcune immagini più significative registrate dalla termo camera. Il fenomeno risulta particolarmente evidente all’aumentare della velocità di deformazione; a basse velocità, infatti, il riscaldamento interno del materiale è più lento dei fenomeni convettivi esterni che riportano immediatamente il materiale all’equilibrio termico con l’ambiente circostante. Per le velocità molto alte, invece, la dinamica della prova è risultata troppo veloce per il sistema di acquisizione della termo camera e quindi non è stato possibile registrare interamente il fenomeno; le immagini acquisite immediatamente prima ed immediatamente dopo la rottura comunque confermano un forte aumento di temperatura.
Figura 2.22. Termografia del provino sottoposto a trazione alla velocità di 1mm/s
immediatamente prima e dopo la rottura.
Figura 2.23. Termografia del provino sottoposto a trazione alla velocità di 10mm/s
31
2.4.4. Prove di trazione in temperatura
Per approfondire meglio la dipendenza della risposta meccanica del Surlyn 8940 dalla temperatura, si sono effettuate delle altre prove di trazione a diverse velocità, costanti durante la prova, e a diverse temperature. Per queste prove si è utilizzato un dispositivo Instron modello 4302 che dispone di una camera climatica di cui si può controllare la temperatura (modello 3119.006). Tale dispositivo consente velocità di trazione più basse rispetto ai test descritti precedentemente; potendo però effettuare prove a diversa temperatura, grazie al postulato di equivalenza tempo-temperatura descritto precedentemente, si può ricostruire il comportamento del materiale in un campo di velocità molto più vasto. Questo procedimento sarà descritto in dettaglio successivamente, nel paragrafo 3.1.1.
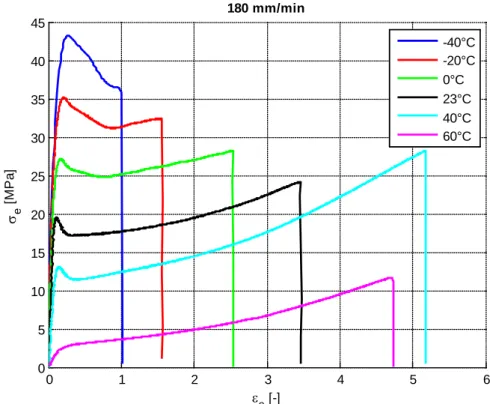
Le velocità utilizzate, scelte in modo tale da garantire una spaziatura uniforme lungo l’asse logaritmico delle velocità di deformazione, sono 500𝑚𝑚/𝑚𝑖𝑛, 180𝑚𝑚/𝑚𝑖𝑛, 65 𝑚𝑚/𝑚𝑖𝑛, 25𝑚𝑚/𝑚𝑖𝑛 e 10𝑚𝑚/𝑚𝑖𝑛. Per ciascuna velocità sono state effettuate prove alle temperature di −40°𝐶, −20°𝐶, 0°𝐶, 23°𝐶, 40°𝐶 e 60°𝐶. Per garantire una certa validità statistica, infine, sono stati testati tre campioni per ciascuna combinazione di temperatura e velocità per un totale di 90 campioni. Per brevità non si riportano le curve sforzo-deformazione di tutte le prove effettuate ma solamente un confronto tra le prove alla velocità di 180mm/min alle diverse temperature.
Figura 2.24. Confronto tra le curve sforzo-deformazione ingegneristiche a temperature diverse.
0 1 2 3 4 5 6 0 5 10 15 20 25 30 35 40 45 180 mm/min ε e [-] σe [ M P a] -40°C -20°C 0°C 23°C 40°C 60°C
32
In Figura 2.25, infine, sono confrontati visivamente i campioni impiegati nelle prove alle diverse temperature e alla stessa velocità di deformazione (500𝑚𝑚/ 𝑚𝑖𝑛, in questo caso). Osservando attentamente la zona di rottura si intuisce un comportamento differente del materiale al variare della temperatura. In particolare, si osserva la presenza di una strizione notevole alle temperature più basse che diventa via via meno evidente all’aumentare della temperatura. Alle temperature più alte, invece, si può osservare uno scorrimento maggiore delle catene polimeriche, evidenziato da un allungamento maggiore, fino alla cristallizzazione alle temperature più elevate, evidenziato dal colore bianco assunto dal materiale (g). A titolo di esempio, per valutare l’allungamento, si è inserito anche un provino non testato (a).
Figura 2.25. Confronto tra un campione nuovo (a) e i campioni testati alle temperature di: -40°C
33
3. Modelli analitici
In questo capitolo saranno presentate le analisi effettuate per arrivare a definire un modello analitico che possa descrivere, nel miglior modo possibile, il comportamento meccanico del Surlyn® 8940. La definizione di un modello, infatti, è un passo fondamentale nella caratterizzazione di un materiale in quanto consente di prevederne il comportamento anche in condizioni non provate sperimentalmente.
3.1. Calcolo dello sforzo di snervamento
Lo sforzo di snervamento è uno dei parametri fondamentali per definire le proprietà meccaniche di un materiale. Può essere tradizionalmente definito come il minimo valore di sforzo per cui si produce una deformazione permanente nel materiale, una volta rimosso il carico. Questa definizione è valida per i metalli, in cui esiste una distinzione netta tra il comportamento puramente elastico e la deformazione plastica permanente; per i polimeri, tuttavia, questa distinzione non è così netta e la definizione di sforzo di snervamento deve quindi essere rivista.
Nei polimeri il concetto di snervamento è fortemente legato a quello di instabilità. La comparsa di una strizione nella sezione del provino durante i test di trazione è un chiaro esempio di instabilità causata dalle fondamentali proprietà di snervamento del materiale. Lo snervamento, infatti, può portare ad un massimo nello sforzo applicato che consente alla deformazione nel provino di aumentare senza incremento di forza (condizione instabile). Snervamento ed instabilità, tuttavia, sono fenomeni qualitativamente differenti: lo snervamento è una caratteristica intrinseca del materiale, mentre l’instabilità dipende dalla geometria e dalle condizioni di carico specifiche del campione [13]. Una definizione più corretta dello sforzo di snervamento può quindi essere quella di sforzo corrispondente al punto di massimo (relativo) nella curva di carico (Figura 3.1 A). Riferendosi, più adeguatamente, alla definizione di sforzo ingegneristico lo sforzo di snervamento può essere definito come:
𝜎𝑦=𝑃𝑀𝐴𝑋𝐴
0 (3.1)
In alcuni casi, tuttavia, non si osservano massimi nella curva sforzo-deformazione, è quindi necessaria un’altra definizione dello sforzo di snervamento. Un possibile approccio è quello di individuare lo sforzo di
34
snervamento dall’intersezione delle tangenti ai due tratti di curva precedente e successivo (Figura 3.1 B). Un’altra possibilità è quella di definire la pendenza iniziale della curva sforzo-deformazione e tracciarne una parallela ad un determinato valore di deformazione (es. 2%); l’intersezione di questa retta con la curva identifica lo sforzo di snervamento (Figura 3.1 C).
Figura 3.1. Definizioni dello sforzo di snervamento.
In questo lavoro si è scelto di definire lo sforzo di snervamento mediante la prima definizione (A), ovvero come il punto di massimo relativo nella curva sforzo-deformazione calcolata con approccio ingegneristico.
3.1.1. Modello di Eyring
Il modello di Eyring assume che la deformazione di un polimero sia un processo attivato termicamente che riguarda il moto di un segmento di una catena molecolare al di sopra di una barriera a potenziale. Il modello può quindi essere rappresentato con una molla e uno smorzatore non lineare governato dal processo di attivazione e descrive un comportamento viscoelastico.
Il modello di Eyring può essere utilizzato per descrivere il comportamento meccanico di un polimero. Si assume che le deformazioni macroscopiche del materiale siano il risultato di processi sia intermolecolari (ad esempio lo scorrimento delle catene) sia intramolecolari (ad esempio un cambiamento nella conformazione delle catene) la cui frequenza 𝜈 dipende dalla facilità con cui un segmento di catena può oltrepassare una barriera energetica di altezza ∆𝐻. In assenza di sforzo esiste un equilibrio dinamico tale per cui un egual numero si segmenti si muove in ogni direzione sulla barriera ad una frequenza data da:
𝜈 = 𝜈0exp �−Δ𝐻𝑅𝑇� (3.2)
Applicando uno sforzo 𝜎 si produce uno spostamento lineare 𝛽𝜎 della barriera in modo simmetrico, come mostrato in Figura 3.2, dove 𝛽 ha le dimensioni di un volume.
35
Figura 3.2. Barriera potenziale nel modello di Eyring.
Il flusso nella direzione dello sforzo applicato è quindi dato da:
𝜈1 = 𝜈0𝑒𝑥𝑝 �−(∆𝐻 − 𝛽𝜎)𝑅𝑇 � (3.3)
Mentre il flusso in direzione contraria è dato da:
𝜈2 = 𝜈0𝑒𝑥𝑝 �−(∆𝐻 + 𝛽𝜎)𝑅𝑇 � (3.4)
Il flusso netto quindi sarà dato da: 𝜈′= 𝜈
1 − 𝜈2 = 𝜈0𝑒𝑥𝑝 �−𝛥𝐻𝑅𝑇� �𝑒𝑥𝑝 �𝛽𝜎𝑅𝑇� − 𝑒𝑥𝑝 �−𝛽𝜎𝑅𝑇�� (3.5)
Assumendo che il flusso netto nella direzione dello sforzo applicato è direttamente legato alla velocità di deformazione, si ottiene:
𝜀̇ = 𝜀̇0𝑒𝑥𝑝 �−∆𝐻𝑅𝑇� 𝑠𝑖𝑛ℎ �𝛽𝜎𝑅𝑇� (3.6)
In cui 𝜀̇0 è una costante moltiplicativa; il parametro 𝛽 è definito volume di
attivazione per l’evento molecolare.
Rielaborando l’equazione (3.6) e applicandola allo snervamento, si ottiene l’equazione di Eyring per lo sforzo di snervamento:
𝜎𝑦 𝑇 = 𝑅 𝛽 𝑠𝑖𝑛ℎ−1� 𝜀̇ 𝜀̇0𝑒𝑥𝑝 � ∆𝐻 𝑅𝑇�� (3.7)
36
𝜀̇ ≅ 𝜀̇0𝑒𝑥𝑝 �−∆𝐻𝑅𝑇�12 𝑒𝑥𝑝 �𝛽𝜎𝑅𝑇� (3.8)
Da cui si può ricavare una nuova equazione di Eyring per lo sforzo di snervamento: 𝜎𝑦 𝑇 = 𝑅 𝛽 𝑙𝑛 � 2𝜀̇ 𝜀̇0𝑒𝑥𝑝 � ∆𝐻 𝑅𝑇�� (3.9)
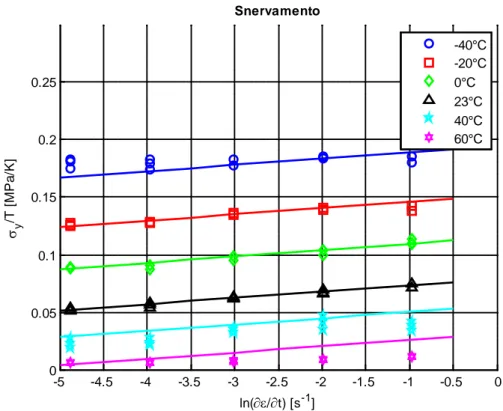
L’equazione di Eyring mette in relazione lo sforzo di snervamento con la temperatura e la velocità di deformazione; il modello può quindi essere verificato sperimentalmente utilizzando i risultati delle prove di trazione effettuate a diverse temperature e presentate nel paragrafo 2.4.4. In Figura 3.3 sono riportati i valori dello sforzo di snervamento ottenuti per ciascuna prova nelle diverse condizioni di temperatura e velocità di deformazione.
Figura 3.3. Andamento dello sforzo di snervamento in funzione della velocità di deformazione a
temperature diverse.
Osservando il grafico si nota immediatamente un andamento lineare dello sforzo di snervamento con il logaritmo della velocità di deformazione per ciascuna temperatura, e un andamento decrescente al crescere della temperatura. Si nota inoltre che gli andamenti a diverse temperature sono tra loro paralleli, e approssimabili con il modello di Eyring, come evidenziato in Figura 3.4.
-5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0 0.05 0.1 0.15 0.2 0.25 Snervamento ln(∂ε/∂t) [s-1] σy /T [M P a /K ] -40°C -20°C 0°C 23°C 40°C 60°C
37
Figura 3.4. Approssimazione dei dati sperimentali con il modello di Eyring.
Si può quindi pensare di utilizzare il postulato di equivalenza tempo-temperatura, già citato in precedenza, per traslare i dati relativi alle diverse temperature lungo l’asse delle ascisse così da ricostruire una sorta di curva maestra dello sforzo di snervamento ad una temperatura di riferimento (23°C in questo caso) in un range di velocità molto più ampio, analogamente a quanto fatto nel paragrafo 2.4.2. Per far ciò è necessario calcolare uno shift factor, ovvero un fattore di spostamento che definisca la traslazione dei segmenti di curva; questo fattore può essere calcolato mediante l’espressione di Arrhenius [14]:
𝑠𝑥 = −∆𝐻𝑅 �𝑇1 𝑟𝑒𝑓−
1
𝑇� (3.10)
In Figura 3.5 è riportato un confronto tra i dati sperimentali, traslati come descritto pocanzi, e il modello di Eyring.
-5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0 0.05 0.1 0.15 0.2 0.25 Snervamento ln(∂ε/∂t) [s-1] σy /T [M P a /K ] -40°C -20°C 0°C 23°C 40°C 60°C
38
Figura 3.5. Confronto tra i dati sperimentali ed il modello di Eyring.
I parametri utilizzati nel modello di Eyring, infine, sono riportati in Tabella 3.1.
Tabella 3.1. Parametri utilizzati per il modello di Eyring.
Parametro Valore Unità di misura
𝛽 5.0038 [𝑛𝑚3]
∆𝐻 190.16 [𝑘𝐽/𝑚𝑜𝑙]
𝜀̇0 2.28 ∙ 1027 [𝑠−1]
3.2. Modello della deformazione plastica
Il problema principale nella modellazione analitica del Surlyn® 8940 è costituito dal comportamento del materiale nel campo di deformazione plastica. Durante questo processo, infatti, la risposta del materiale dipende da numerosi fattori che la influenzano in diversi modi; gli effetti principali sono dovuti alla velocità di deformazione e alla temperatura. Proprio la temperatura rappresenta probabilmente il fattore più critico in quanto subisce notevoli variazioni durante la deformazione plastica, come evidenziato nel capitolo 2. Di seguito saranno presentati i modelli analitici, reperiti in letteratura, che hanno mostrato i risultati
-20 -15 -10 -5 0 5 10 15 20 25 0 0.05 0.1 0.15 0.2 0.25 Modello di Eyring ln(∂ε/∂t) [s-1] σy /T [M P a /K ] -40°C -20°C 0°C 23°C 40°C 60°C Modello di Eyring
39 migliori in relazione alle prove sperimentali condotte e descritte nel capitolo precedente.
3.2.1. Modello Johnson-Cook
Il modello di Johnson-Cook fu proposto negli anni ’80 come modello costitutivo per materiali soggetti a grandi deformazioni, alte velocità di deformazione e temperature elevate, con il preciso intento di fornire un modello, sufficientemente accurato, che potesse essere facilmente implementato negli emergenti codici di calcolo automatizzato.
Sebbene fosse pensato per i materiali metallici, il modello di Johnson-Cook può essere utilizzato, con buoni risultati, anche per descrivere il comportamento di alcuni materiali polimerici. Costituisce quindi un’ottima base di partenza nella ricerca di un modello analitico che descriva le caratteristiche del Surlyn® 8940. Il modello fornisce una legge che descrive la risposta del materiale in campo plastico al variare della velocità di deformazione e della temperatura, espressa dalla relazione [15]:
𝜎 = [𝐴 + 𝐵 ∙ 𝜀𝑛][1 + 𝐶 ∙ 𝑙𝑛(𝜀̇∗)][1 − 𝑇∗𝑚] (3.11)
Dove 𝜀 è la deformazione plastica, ε̇∗ è il rapporto adimensionale tra la velocità di deformazione 𝜀̇ e una velocità di deformazione di riferimento 𝜀̇0, e 𝑇∗ è la temperatura omologa definita come:
𝑇∗ = 𝑇 − 𝑇𝑎𝑚𝑏
𝑇𝑓𝑢𝑠− 𝑇𝑎𝑚𝑏 (3.12)
In cui 𝑇𝑎𝑚𝑏 è la temperatura ambiente e 𝑇𝑓𝑢𝑠 è la temperatura di fusione del materiale. Le cinque costanti 𝐴, 𝐵, 𝑛, 𝐶 e 𝑚 dipendono dal materiale considerato e devono quindi essere determinate.
Osservando la legge espressa nell’equazione (3.11) si nota che l’espressione all’interno della prima parentesi descrive la risposta del materiale alla velocità di deformazione di riferimento (ε̇∗ = 1) e a temperatura ambiente (𝑇∗ = 0). Le altre due espressioni tra parentesi rappresentano rispettivamente l’effetto della velocità di deformazione e della temperatura su tale risposta.
Per poter definire completamente il modello per il materiale considerato, quindi, è necessario definire le cinque costanti del materiale sulla base dei dati sperimentali. In questo caso si sono utilizzati i dati delle prove di trazione veloce descritte nel paragrafo 2.4.3; tali prove sono state condotte alla medesima temperatura, pertanto non saranno utilizzate per il calcolo del parametro 𝑚. Il primo passo di questo processo è la scelta di una velocità di riferimento e la determinazione delle costanti 𝐴, 𝐵 ed 𝑛.
Si è scelta come riferimento la velocità di deformazione di 0.0045𝑠−1, corrispondente al test di trazione a 0.1𝑚𝑚/𝑠. Le prime tre costanti, quindi, sono
![Figura 1.3. Rappresentazione schematica della regione a mobilità ridotta attorno ad un multiplet di polistirene co-metacrilato di sodio[7]](https://thumb-eu.123doks.com/thumbv2/123dokorg/7520122.105977/17.892.307.623.609.1033/figura-rappresentazione-schematica-regione-mobilità-multiplet-polistirene-metacrilato.webp)
![Figura 1.5. Rappresentazione schematica del cambiamento della struttura molecolare al variare della temperatura[9]](https://thumb-eu.123doks.com/thumbv2/123dokorg/7520122.105977/19.892.178.751.621.875/figura-rappresentazione-schematica-cambiamento-struttura-molecolare-variare-temperatura.webp)