Appendice A
Termopile
Il principio di funzionamento delle termopile integrate `e basato sullo stesso princi-pio di trasduzione delle termocoppie: l’effetto Seebeck. La struttura tipica consiste in strisce di silicio drogato p in una well di silicio drogato n, interconnesse da alluminio (Fig. A.1). Connettendo pi`u strisce si ottiene una sensitivit`a n volte pi`u grande, con n numero di termocoppie. L’effetto Seebeck non necessita di alimenta-zione esterna, ma la potenza necessaria per fornire il segnale d’uscita viene fornita dal principio di trasduzione. Le termopile offrono un segnale di uscita virtualmente senza offset n´e drift poich´e non vi pu`o essere un segnale senza alcun ingresso. Non soffrono di interazioni con altri effetti fisici o chimici, n´e con le alimentazioni, eccetto l’interazione con la luce del silicio. Inoltre la sensibilit`a delle termopile `
e difficilmente influenzata da variazioni nei parametri elettrici sulla superficie del
wafer o dalla temperatura, rispetto all’uso di transistori o di resistori integrati.
In-fine `e importante sottolineare che la fabbricazione delle termopile `e completamente compatibile con i processi standard bipolari e CMOS. Gli svantaggi legati all’uso
Figura A.1: Termopila integrata p-Si/Al 146
147
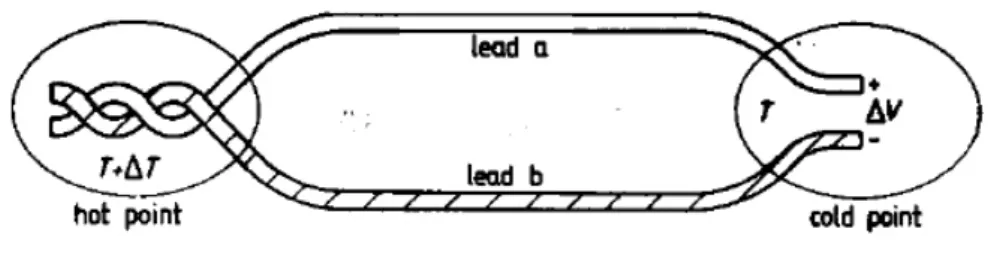
Figura A.2: L’effetto Seebeck: una tensione ∆V si instaura a causa di un differenza di temperatura ∆T
delle termopile, rispetto ai resistori integrati o ai transistori, sono da imputare alla resistenza termica del sensore. Infatti, per come `e fatta la termopila, `e necessario un collegamento fra il contatto caldo e quello a temperatura di riferimento. Inoltre la resistenza elettrica della termopila pu`o essere piuttosto elevata se sono state utilizzate molte termocoppie per aumentare la sensibilit`a.
Nel caso in cui due semiconduttori a e b sono uniti insieme ad una estremit`a (hot point) e una differenza di temperatura ∆T `e mantenuta fra questa estremit`a e l’altra (cold point), come in figura A.2, si ha una tensione a circuito aperto ∆V fra i due semiconduttori all’estremit`a aperta. Questo effetto, chiamato effetto Seebeck, pu`o essere espresso come:
∆V = αS∆T (A.1)
dove αS `e il coefficiente di Seebeck espresso in V /K o pi`u comunemente in µV /K .
L’effetto Seebeck `e una propriet`a del bulk e pu`o essere espressa come:
∇EF
q = αS∇T (A.2)
con EF livello di Fermi. Per silicio non degenere il coefficiente di Seebeck pu`o
essere approssimato usando la statistica di Maxwell-Boltzmann; tre effetti sono presenti:
• con l’aumento della temperatura il silicio diviene pi`u intrinseco;
• l’aumento della temperatura comporta l’aumento della velocit`a media dei por-tatori di carica, che porta all’accumularsi di carica sulla giunzione fredda. In realt`a essendo lo scattering dei portatori di carica dipendente dall’ener-gia, e quindi dalla temperatura, l’instaurarsi di un accumulo di carica sulla
148 giunzione calda o fredda dipende se i portatori caldi possono muoversi pi`u liberamente di quelli freddi, o sono intrappolati dall’aumento di scattering;
• la differenza di temperatura nel silicio provoca inoltre un flusso di fononi dalla
giunzione calda a quella fredda. Per certe temperature (10-500 K) e per silicio non degenere, un trasferimento di quantit`a di moto fra i fononi e i portatori di carica pu`o avvenire. Questo pu`o far s`ı che dei portatori siano trascinati verso la giunzione fredda.
Sommando questi effetti il coefficiente di Seebeck pu`o essere espresso secondo la seguente relazione [9]:
αS = −k
q{ln(Nc/n) + 2.5 + sn+ φn} (A.3)
con q la carica elementare, k la costante di Boltzmann, Nc la densit`a degli stati
nella banda di conduzione e n la densit`a degli elettroni (fissata dalla concentra-zione). Il fattore sn `e l’esponente nella relazione esponenziale fra il mean-free-time
fra due collisioni e l’energia, e varia da −1 a 2. L’effetto di trascinamento dei fononi `
e rappresentato da φn e va da 0, per drogaggi elevati, a 5 per bassi drogaggi e
temperatura ambiente. Per il silicio drogato p l’espressione `e la stessa, cambia solo il segno del coefficiente.
Per applicazioni pratiche `e possibile usare una relazione semi-empirica che lega il coefficiente di Seebeck alla resistivit`a elettrica [9]:
αS = mk
q ln(ρ/ρ0) (A.4)
con ρ0' 5 × 10−6Ωm e m ' 2.6.
Per quanto riguarda il polisilicio, anch’esso pu`o essere usato insieme all’alluminio per la costruzione di termopile. Il vantaggio di usare termopile di solo polisilicio, o di polisilicio e alluminio, `e la possibilit`a di realizzarle su strati di ossido o nitruro con bassa conducibilit`a termica, e di rimuovere il silicio sottostante. Un’espressione per il coefficiente di Seebeck del polisilicio drogato `e presente in letteratura [10]:
αi = ±k
q · [5/2 + s − ζi] ζe = − ln(Nc/ne) ζh= − ln(Nv/nh) (A.5)
con i che rappresenta sia gli elettroni, e, che le lacune, h; il segno meno `e per gli elettroni e il pi`u per le lacune come per il silicio. Per scattering dovuto solo a
149 fononi, vero per concentrazioni al di sotto 1018cm−3, s = −1/2; per concentrazioni pi`u elevate prevale lo scattering con le impurit`a e s = 3/2.
In tabella A.1 possiamo leggere dei valori di coefficienti di Seebeck, per un processo CMOS standard (ALP2LV) [10], per differenti coppie di materiali.
Tabella A.1: Coefficienti di Seebeck per differenti coppie di materiali.
Termocoppie αab[µV /K ] n- Poly/n+ Poly 413 n- Poly/Metal 1 519 n- Poly/Metal 2 519 n- Poly/p+ Poly 856 n+ Poly/Metal 1 106 n+ Poly/Metal 2 106 n+ Poly/p+ Poly 443 p+ Poly/Metal 1 337 p+ Poly/Metal 2 337 Metal 1/Metal 2 0